Числа фибоначчи золотое сечение: Ошибка 404. Запрашиваемая страница не найдена

Золотое сечение и числа Фибоначчи

Законы природы и законы Жизни до сих пор не разгаданы. И каждый новый взгляд на обычные вещи отображается новым открытием или новыми изобретениями. Жизнь интересная штука! И каждый раз узнаешь о чем-то новом.

Для меня было большим открытием узнать о золотом сечение и числах Фибоначчи. Я до сих пор под впечатлением. И спешу рассказать Вам об этом обычном (для мира) и уникальном (для человечества) явлении.

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.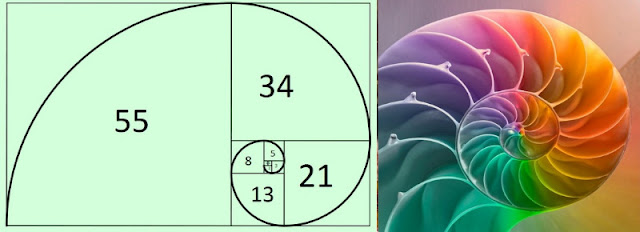

И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами.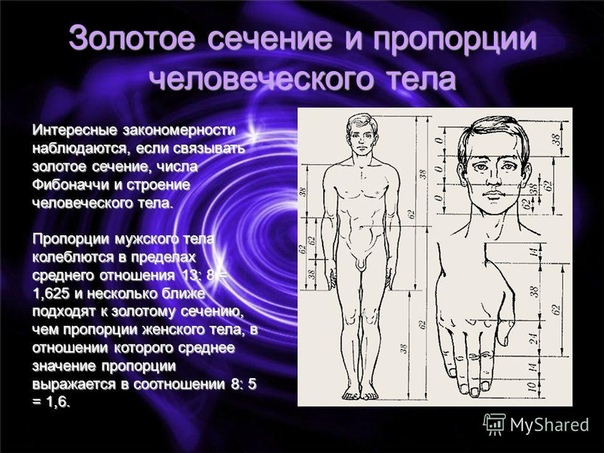

В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 … и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 … и т.д.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … и т.д.

Набор этих чисел известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом

Ф.

Последовательность Фибоначчи —  это числовой ряд, в котором каждый последующий член представляет собой сумму двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.

• каждое последующее число в числовом ряду приблизительно в 1.618 раз больше предыдущего, а каждое предыдущее составляет приблизительно 0.618 от следующего.
• Отношение через одно число составляет 0.382, а обратное ему число = 2.618. За исключением нескольких первых чисел последовательности.

Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.

Еще Гете подчеркивал тенденцию природы к спиральности.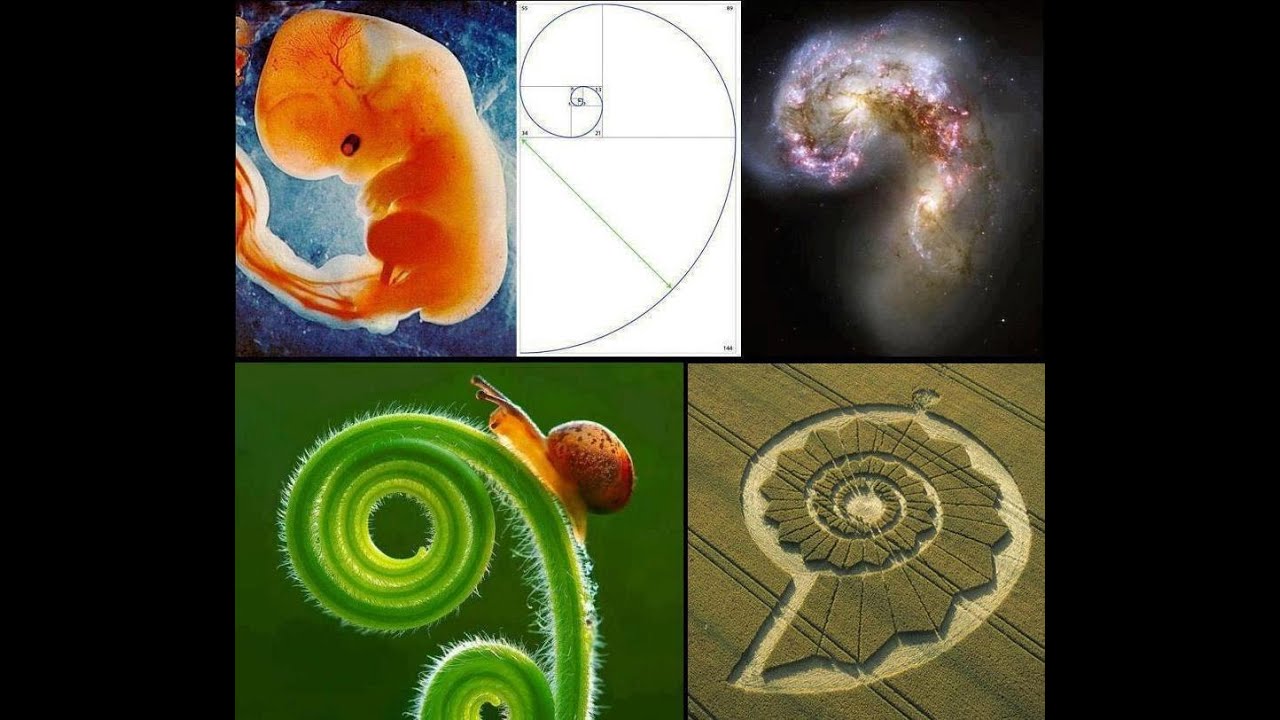 Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы.

Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.

Понравилась статья? Расскажи о ней своим друзьям в социальных сетях, жми соответствующую кнопку ниже!

Tags: Законы Успеха, Золотое сечение, Колесо Жизненного Баланса, Правила Жизни, ряд Фибоначчи

Что такое числа Фибоначчи, золотое сечение? ⋆ FutureNow

Последовательность Фибоначчи – одна из самых известных формул математики. Так, что такое числа Фибоначчи, золотое сечение и какая их интересная стория?

Что такое числа Фибоначчи?

Каждое число в последовательности Фибоначчи – это сумма двух чисел, предшествующих ему.

 

Итак, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Математическое уравнение, описывающее число Фибоначчи: Xn + 2 = Xn + 1 + Xn    

Фибоначчи числа иногда называют “секретным кодом природы” и “общем правилом природы”. Говорят, что данная последовательность руководит размерами всего сущего, в том числе обьясняет Великую пирамиду в Гизе, так и многие вещи, с которыми мы сталкиваемся каждый день.   

Числа Фибоначчи: богатая история

Поэтому какова реальная история стоит за этой знаменитой последовательностью?

Многие источники утверждают, что ее впервые обнаружил или “изобрел” Леонардо Фибоначчи. 

Итальянский математик, родился около 1170 года нашей эры и первоначально был известен как Леонардо из Пизы. Лишь в 19 веке историки придумали прозвище Фибоначчи, чтобы отличить математика от другого известного Пизарського Леонардо.  

Но Леонардо из Пизы на самом деле не изобрел последовательность.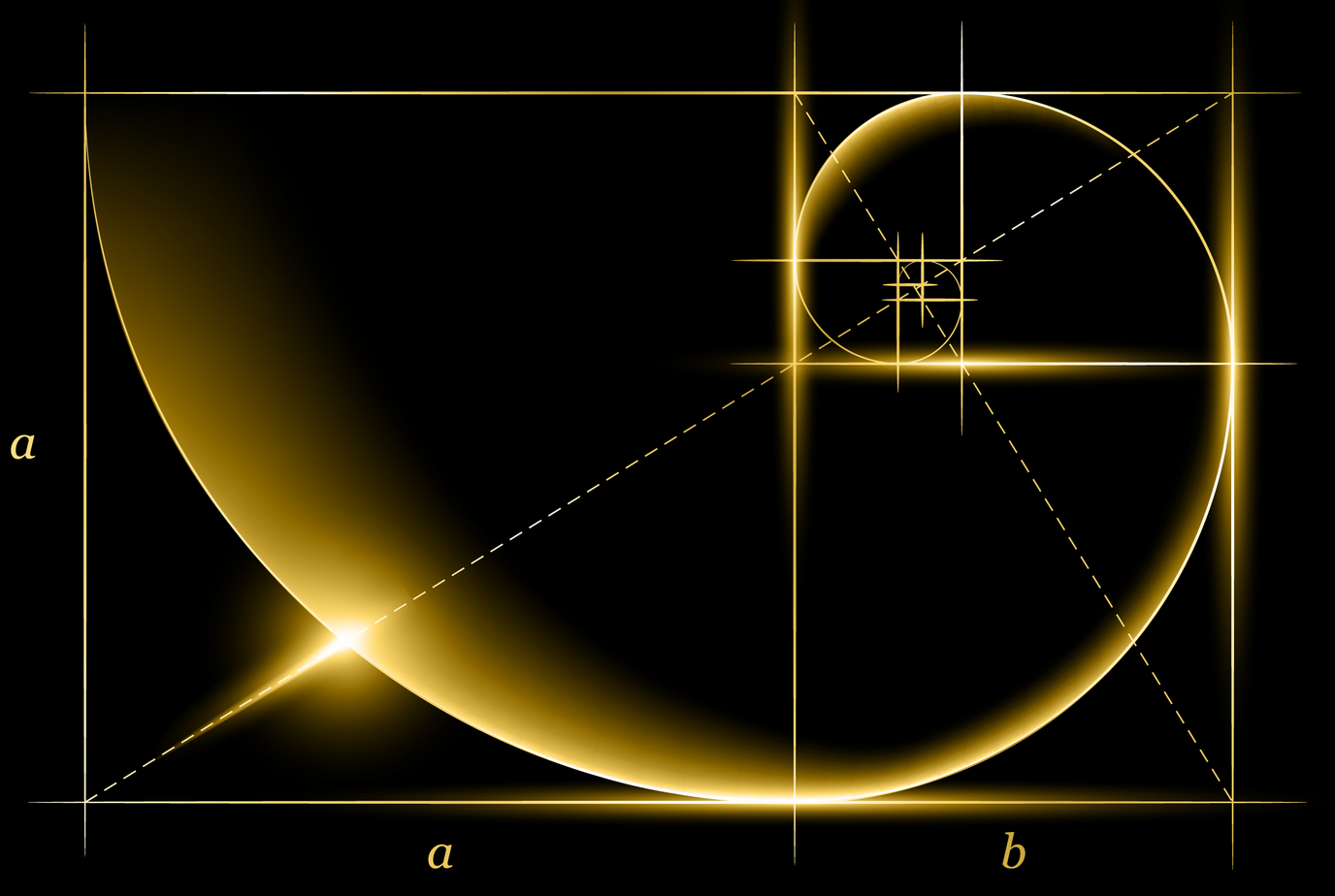

 Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.     

Однако в 1202 Леонардо из Пизы опубликовал большой том “Liber Abaci,” книгу по математике “о том, как производить вычисления”. “Liber Abaci”, написанная для торговцев, где изложена индуистско-арабский арифметика, которая является полезной для отслеживания прибыли, убытков, остатков по кредитам и тому подобное.  

ЧТО ТАКОЕ ШАРОВАЯ МОЛНИЯ: СУЩЕСТВУЕТ ЛИ ОНА?

В книге Леонардо из Пизы вводит последовательность с задачей о кроликах. Проблема заключается в следующем: начнем с самца и самки кролика. Через месяц они созревают и дают помет в результате которого мы имеем еще самца и самку кролика. Через месяц эти кролики размножаются и получается – вы догадались – еще один самец и самка, которые также могут спариваться через месяц. Через год сколько бы у вас было кроликов? Ответ, 144, спрятан в формуле, которая сейчас известна как последовательность Фибоначчи.

     

“Liber Abaci” впервые представила эту последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы больше никогда не вспоминал ее. 

На самом деле эти числа Фибоначчи были забыты до 19 века, когда математики подробнее изучили математические свойства последовательности. В 1877 году французский математик Эдуард Лукас официально назвал задачу о кроликах “последовательностью Фибоначчи”.   

Числа Фибоначчи и золотое сечение

Мы узнали что такое числа Фибоначчи, но какое же значение имеет последовательность Фибоначчи? 

Кроме как учебный инструмент, она проявляется во многих случаях в природе. Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.  

Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как “золотое сечение”. Проще говоря, отношение чисел в последовательности, поскольку последовательность идет к бесконечности, приближается к золотому сечению, который составляет +1,6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмической спирали, коэффициент роста которой равен золотому сечению.

    

Золотое сечение объясняет рост некоторых растений. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Но есть также растения, которые не соблюдают этого правила.  

Мистификации и выдумки

Когда люди начинают связывать человеческое тело, искусство и архитектуру, много вымышленных теорий и мистификаций ссылаются на последовательность Фибоначчи.

“Понадобится большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, многие из которой – это просто повторение одних и тех же фантазий разных авторов”, – написал Джордж Марковский, математик из университета Мэн в 1992 году. 

Значительная часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Зейзинга. Он утверждал, что пропорции человеческого тела основана на золотом сечении. 

Золотое соотношение проросло в “золотые прямоугольники”, “золотые треугольники” и всевозможные теории об этих знаковых размерах.  

С тех пор люди говорят, что золотое соотношение или золотое сечение можно найти в размерах Пирамиды в Гизе, Парфеноне, “Витрувийським человеке” Леонардо да Винчи и ренессансных сооружениях. 

Под сомнение можно поставить и беспрекословное утверждение о том, что золотое сечение является “однозначно приятным” для человеческого глаза – на чем часто настаивают фотографы.          

Часто все эти утверждения, когда их проверяют, являются ошибочными. Люди часто выдают желаемое за действительное.

Источник: www.livescience.com/ 

Разметчик Фибоначчи

Разметчик Фибоначчи — это устройство, позволяющее вам всегда иметь под рукой соотношениие размеров для ваших изделий, удовлетворяющее принципам Золотого Соотношения. Если вы хотите, чтоб мебель, которую вы делаете, была не только функциональна, но и по-настоящему красива, то начинать нужно с пропорций предмета в целом и его частей. Если эти пропорции правильны, ваше произведение будет радовать глаз, иначе — может быть ужасным. Разметчик Фибоначчи — отличное подручное средство для проектирования красивых изделий.

Разметчик Фибоначчи, специальный инструмент, назван по имени итальянского математика Фибоначчи, жившего в  XIII веке.  «Фибоначчи» у этого учёного — это псевдоним, происхождение которого не известно он же — Fibonacci, он же — Леона́рдо Пиза́нский, он же — Leonardo Pisano. В честь учёного назван и числовой ряд, в котором каждое последующее число равно сумме двух предыдущих. Эта числовая последовательность носит название чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, …  Хотя этот ряд и был известен ещё в Древней Индии, т.е. задолго до рождения умного Фибоначчи, но, тем не менее, своё нынешнее название числа Фибоначчи получили благодаря исследованию свойств этих чисел, проведённому именно этим учёным в его труде «Книга абака» (Издательство РИМГНИЗ «Римское Государственное Народное Издательство», 1202 г. ).  Ряды Фибоначчи, спирали Фибоначчи, уровни Фибоначчи — об этом много можно прочитать.

К чёму всё это? Одна закономерность упомянута, но можно заметить и другую — деление числа в ряду Фибоначчи на предыдущее даёт практически постоянный результат — 1,618 — проверьте, если не лень. С этими последовательностями много чего связано — от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции. Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.

Даже если вы одарены превосходным видением, не так-то просто спроектировать предмет мебели без использования основополагающих принципов для определения размеров этого предмета мебели и, главное, пропорций между его элементами. Будет ли это подход к проектированию, который передаётся от мастера к ученику или ваше врожденное чувство равновесия и гармонии, которым обладают лишь некоторые одарённые люди, в любом случае без такой совокупности знаний и опыта вы не сможете создать совершенное изделие, которое будет радовать ваш глаз и вызывать восхизение окружающих и ваших друзей.  Можно создать изделие, которое будет прочно и функционально адекватно, но не будет радовать и вызывать приятные чувства. Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.

Главным среди множества совокупностей фундаментальных установок, сложившихся за сотни лет представлений и понятий, которые разработчики предметов мебели использовали и продолжают использовать  для обеспечения баланса и хороших пропорций в дизайне мебели является золотая пропорция или соотношение (также называемое золотой серединой или золотым сечением). Обозначается эта пропорция греческой буквой ∳ (фи). Золотое соотношение может быть выражено уравнением ∳ (фи)= [1 + √ 5] / 2. Для простоты практического применения, мы можем взять лишь результирующее значение ∳ (фи), равное 1,618. Т.е. одно значение к другому должно относится как 1 к 1,618. Одна длина, к другой, например.

Один из многих замечательных принципов золотой пропорции является то, что коротий отрезок прямой линии по отношению к длинному отрезку этой же линии относится так же, как длинный отрезок линии относится к общей длине линии, и это соотношение равно ∳ (фи) = 1,618:

Именно это соотношение заложено в самой конструкции замечательного разметочного инструмента — Разметчика Фибоначчи:

Исходя из описанного принципа, Золотым (или гармоничным) Прямоугольником является такой, стороны в котором соотносятся как 1 : 1,618, т. е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:

Узнаёте? Это же столешница гармоничного стола! Или фасад тумбы и много чего ещё.

Аналогично, Золотым (или гармоничным) Параллелепипедом является тот, стороны в котором тоже соотносятся как 1 : 1,618, т.е. длина большей стороны параллелепипеда равна высоте параллелепипеда, умноженной на ∳ (фи)=1,618, а ширина параллелепипеда равна высоте параллелепипеда, поделённой на ∳ (фи)=1,618:

Узнаёте? Это же мебельная тумба, пристенный стол (консоль) и т.д.

Золотая Пропорция лежит в основе многих (если не всех) естественных соотношений и даже построения нашей Вселенной. Примеры есть в изобилии на каждом уровне, от размножения кроликов, расположения семян в подсолнухе и орешков в шишке, до астрофизики и квантовой механики. Планетарные орбиты и даже структура человеческой фигуры являются ещё одним подвержедния соблюдения этой замечательной пропорции.

Соотношение между соседними фалангами пальцев — это ∳ (фи) = 1,618, Соотношение между локтем и кистью — это ∳ (фи) = 1,618, соотношение расстояния от макушки до глаз и растояния от глаз до подбородка — это ∳ (фи) = 1,618, соотношение расстояния от макушки до пупка и растояния от пупка до пяток — это опять-таки ∳ (фи) = 1,618:

 

Дистанции между солнцем и первыми пяти планетами в солнечной системе так же соотносятся (примерно) как ∳ (фи) = 1,618, поэтому, как безусловно известно, астронометрия использует золотое соотношение при определении планет на их орбитах:

Будучи столь фундаментальным и столь широко распространённым в природе, это отношение просто призывает нас на подсознательном уровне как абсолютно правильное, которому надо следовать. Как таковое, это соотношение было использовано на протяжении веков дизайнерами и архитекторами, от пирамид до мебельных шедевров.

Большая пирамида в Гиза, как теперь понятно, тоже построена в соответствии с Золотым Сечением: высота стороны пирамиды равна длине основания стороны пирамиды, умноженной на всё ту же величину ∳ (фи) = 1,618:

 

При строительстве Парфенона (древнегреческий храм, расположенный на афинском Акрополе, главный храм в древних Афинах) использовалось соотношение ∳ (фи) = 1,618 при определении внешних размеров и соотношения его частей:

Достоверно не известно, применялись ли при построении Парфенона калькуляторы или Разметчики Фибоначчи, но соотношение точно применялось. Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:

В вышеприведённом ролике, наконец-то, дело дошло и до предмета мебели, пусть и простого. Главное — соотношение всё то же — ∳ (фи) = 1,618.

В одном из видов комода с множеством ящиков называемом в разных изданиях как Highboy или Popadour («Высокий парень» или «Помпадур»), сделанном в Филадельфии в промежутке между 1762 и 1790 годами, используется Золотая Пропорция в соотношении размеров многих из его элементов. Каркас — это Золотой прямоугольник, положение сужения («талии» шкафа) определяется делением общей высоты шкафа на ∳ (фи) = 1,618. Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:

 

Золотое Сечение применяется при изготовлении мебели чаще всего в качестве некоего прямоугольника, который строится с помощью ∳ (фи) = 1,618 для двух его измерений, т.е. уже упоминаемого Золотого прямоугольника, где длина в 1,618 раз больше ширины (или наоборот). Эти пропорции могут быть использованы для определения габаритных размеров мебели, а также деталей интерьера, таких как двери и ящики. Можно применять рассчёты, деля и умножая на такое «круглое» и удобное число, как 1,618, но можно просто использовать Разметчик Фибоначчи, просто снимая размеры бОльшего предмета и откладывая после этого размер меньшего предмета. Или наоборот. Быстро, просто и удобно.

Предметы мебели являются трехмерными и Золотое Соотношение может быть применено ко всем трем измерениям, т.е. предмет мебели становится Золотым Параллелепипедом, если сделать его по правилам Золотого Соотношения. К примеру, в простом случае, глядя на предмет мебели сбоку, его высота может быть наибольшим измерением в Золотом  Прямоугольнике.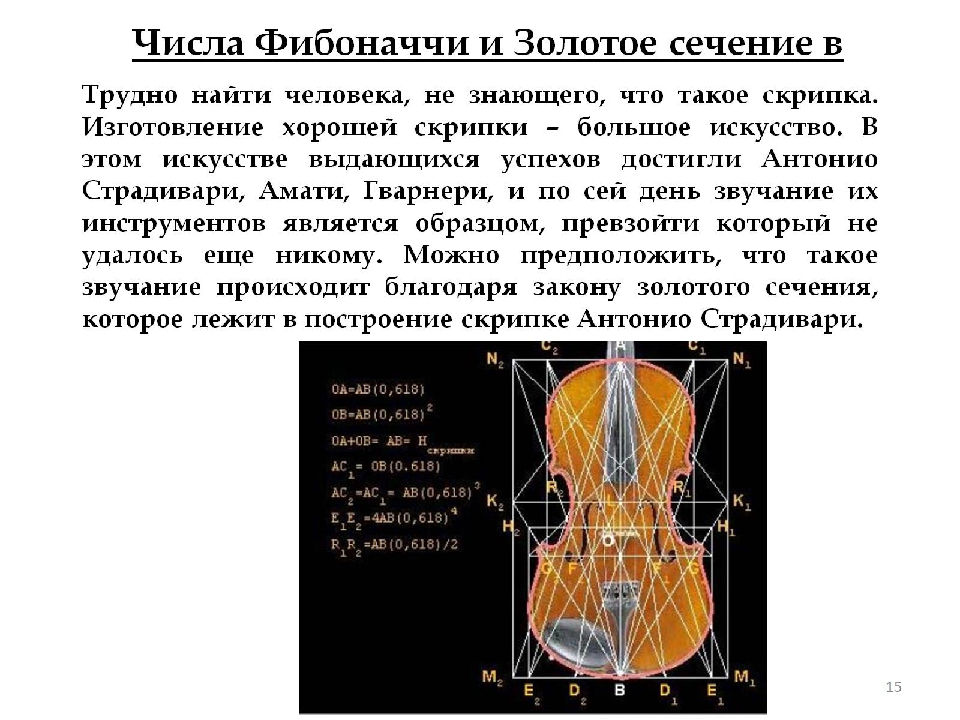 Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.

Необходимо отметить, однако, что форма предмета должна следовать за его функцией. Даже превосходные пропорции мебели могут оказаться быть бессмысленными, если этот предмет не может быть использован, например потому, что он слишком маленький или слишком большой или по другим причинам не может быть использован с комфортом. Следовательно, практические соображения должны быть на первом месте. В самом деле, большинство проектов мебели требуют, чтоб вы начали проектирование с некоторых заданных размеров: стол должен быть определенной высоты, шкаф возможно, придется приноравливать к конкретному пространству, а в книжном шкафу может потребоваться определенное количество полок. Но почти наверняка вы вынуждены будете определять множество других размеров, в отношении которых можно применить правильные пропорции. Но результат будет стоит затраченных усилий, чтоб в результате увидеть, как Золотое Соотношение может работать для всех этих элементов. Принятие решения о размерах «на глаз» или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.

Итак, размеры отдельных частей мебели должны быть пропорциональны в соответствии с Золотым Соотношением. Такие элементы, как ножки стола, относительные размеры элементов каркаса, такие как вертикальные и горизонтальные части фасадов, проноги, царги и т.д., могут быть рассчитаны с применением Золотой Пропорции. Золотое сечение также предлагает один из способов решение проблемы проектирования ящиков в комоде с ступенчатым увеличением высоты ящиков. С помощью Разметчика Фибоначчи легко осуществить такую разметку — надо просто взять размер бОльшего ящика и по разметчику отложить размеры двух соседних ящиков и т.д. После этого, взяв размер ящика, по разметчику отложить расстояние от верха ящика до места расположения его ручки.

Такой метод использования Разметчика Фибоначчи, как инструмента для практического применения Золотого Соотношения будут эффективен для определения и других размеров, таких, как положение полок в шкафу, разделителей между ящиками и т. д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части — дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.

Спроектировать что-то с абсолютно совершенными пропорциями редко удается в реальности. Почти каждый предмет мебели или дерева придётся соотносить с ограничениями, накладываемыми функциональностью, возможностями столярных соединений или  экономией средств. Но даже попытка приблизиться к совершенству, которое может быть определено как размеры, в точности соответствующие Золотому Соотношению гарантирет вам получение лучшего результата по сравнению с разработкой без внимания к этим основополагающим принципам. Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.

Наконец, мы часто корректируем вещи на глаз, чтобы сделать предмет легче и лучше сбалансированным, и делаем мы это с помощью методов, которые являются повседневными в деревообработке. Эти методы включают в себя учёт изменения размеров заготовки, исходя из направления волокон древесины, учёт рисунка древесины, с помощью которого можно предмет мебели сделать более привлекательным, отделку краёв и углов, которая создаст впечатление большей или меньшей толщины элемента изделия, использование молдингов для более точного соответствия изделия Золотому Прямоугольнику или Параллелепипеду, использование сужающихся ножек, чтобы сделать ощущение большего приближения предмета мебели к идеальной пропорции, и, в конце концов, смешивание всех этих методов для достижения идеального дизайна. Использование Золотого Сечения и инструмента для его применения — Разметчика Фибоначчи — начало этого стремления к совершенству.

В статье использованы материалы главы «A Guide to Good Design» из книги «Practical Furniture Design», написанной Graham Blackburn — признанным мебельным мастером, популяризатором деревообработки и издателем.

Евгений Фукс

технический консультант
LeighJigs.ru
[email protected]

Золотое сечение. Числа Фибоначчи в техническом анализе Текст научной статьи по специальности «Математика»

УДК 81:72.013 К.Ю. Баклина

Омский государственный технический университет, г. Омск

ЗОЛОТОЕ СЕЧЕНИЕ.

ЧИСЛА ФИБОНАЧЧИ В ТЕХНИЧЕСКОМ АНАЛИЗЕ

Предмет общей теории терминологии составляет изучение формирования и употребления специальных слов, с помощью которых передаются накопленные человечеством знания, а так же отражаются взаимоотношения человека и общества. Термины отрасли, будь то наука или производство, формируют свои системы, которые определяются понятийными связями профессионального знания при стремлении выразить эти связи языковыми средствами. Тем самым, язык оказывается структурным элементом научного знания. Чем наука «научнее», тем больше вес языка в ее структуре. Язык входит в науку прежде всего терминами. Обратимся к терминам «Золотое сечение» и «Числа Фибоначчи».

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление), термин относящийся к древней проблеме, решенной пифагорейцами, о делении отрезка на части в таком соотношении, при котором большая часть относится к меньшей, как сумма к большей. Принцип золотого сечения — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Золотым сечением интересовались по разным причинам. Исходя из золотого сечения, Платон пришел к представлению об основах знания; Аристотель извлек из золотого сечения этические аналогии, а некоторые средневековые мыслители называли его божественной пропорцией. Ныне золотое сечение привлекает внимание главным образом в связи с определением гармонических пропорций в архитектуре и других видах искусств.

Термин «золотое сечение» был введен Леонардо да Винчи, который использовал золотое сечение как пропорции «идеального человеческого тела». Американский математик Марк Барр, предложил называть отношение двух отрезков, образующих золотое сечение,

числом . Буква (фи) — первая буква в имени великого Фидия, который, по преданию, часто использовал золотое сечение в своих скульптурах.

Чему же равно ? PHI — число, по всеобщему мнению, признано самым красивым во вселенной. Пирамида Хеопса, самая известная из египетских пирамид, знаменитый греческий храм Парфенон, большинство греческих скульптурных памятников, «Джоконда» Леонардо да Винчи, картины Рафаэля, Шишкина, этюды Шопена, музыка Бетховена, Чайковского, стихи Пушкина и Шота Руставели — вот далеко не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией, основанной на Золотом Сечении. Число PHI, равное 1.618, получено из последовательности Фибоначчи. Сам ряд последовательности выглядит как вид: 1-1-2-3-5-8-13-21-34-55-89-144-…. Здесь каждый следующий элемент является сложенной суммой двух предыдущих чисел. Отношение любого числа из последовательности к предыдущему, стремится всегда к значению 1.618. Существует еще одна закономерность — любое число ряда соотносится к следующему примерно как 0.618. Это и есть всем известное «золотое сечение» или «божественная пропорция».

Многие математики, жившие в средние века и в эпоху Возрождения, были настолько

увлечены исследованием необычайных свойств числа , что это походило на легкое помешательство.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. Адольф Цейзинг доказывает, что из всех пропорций именно золотое сечение дает наибольший художественный эф-

фект и доставляет наибольшее удовольствие при восприятии.

Так же пример использования золотого сечения для получения гармоничного фотоснимка. Он основан на подмеченном психологами и искусствоведами правиле — расположении основных компонентов кадра в особых точках — зрительных центрах. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.

7

8

Человек всегда акцентирует свое внимание на этих точках, независимо от формата кадра или картины.

В настоящее время числа Фибоначчи усиленно изучаются бизнесменами и экономистами. Разбираясь с числами Фибоначчи и волнами Эллиота, вы можете разбогатеть, играя на бирже ценных бумаг.

Ральф Нельсон Эллиотт (американский финансист) еще в 30-е годы высказал свою мысль использования последовательности Фибоначчи при прогнозировании цены, то есть техническом анализе. С тех пор конкретная польза применения этой идеи практически во всех методах технического анализа не вызывает сомнения.

Этот шанс предсказать движения цен побуждает аналитиков трудиться денно и ношно. Эллиоттписал: «любой человеческой деятельности присущи три отличительных особенности: форма, время и отношение, — и все они подчиняются суммационной последовательности Фибоначчи».

Один из простейших способов применения чисел Фибоначчи на практике — определение отрезков времени, через которое произойдет то или иное событие, например, изменение тренда. Аналитик отсчитывает определенное количество фибоначчиевских дней или недель (13, 21, 34, 55 и т.д.) от предыдущего сходного события.

Числа Фибоначчи имеют широкое применение при определении длительности периода в Теории Циклов. За основу каждого доминантного цикла берется определенное количество дней, недель, месяцев, связанное с числами Фибоначчи.

К сожалению, волны Эллиота очень хорошо просматриваются на «старом» рынке и туманно видны для будущего. В связи с этим практическое использование волновой теории Эллиота зачастую проблематично и требует специальных знаний. Если вы не обладаете последними, то можете воспользоваться прогнозами аналитических фирм, которые опираются исключительно на теории Эллиота.

Необходимо отметить также тот факт, что свою теорию Эллиот вывел на основе анализа фондового рынка. Для валютного рынка волны Эллиота могут, очевидно, иметь как прямое их сопоставление, так и обратное. Это будет выражаться в том, что 8 волн (5 бычьих и 3 медвежьих), характерных для анализа фондового рынка, на валютном рынке могут иметь свою противоположность — 5 медвежьих и 3 бычьих волны. Связано это с тем, что любая из котировок валют имеет как прямое свое обозначение, так и обратное.

Библиографический список

1. Дональд Кнут, Рональд Грэхем, ОренПаташник- Конкретнаяматематика. Основание-информатики = Concrete Mathematics. A Foundationfor Computer Science. — М.:Мир; Бином. Лабораториязнаний, 2006.- 303с.

2. Knuth, D. E., Fibonacci multiplication, Appl. Math. Lett.1, Zeckendorf, E., 1988.- 57-60с.

3. Рудаков, А. Н. Числа Фибоначчи и простота числа 2127/ А. Н. Рудаков // Математическое просвещение, третья серия. — 2000. — Т. 4.

4 Фишер, Р.Новые методы торговли по Фибоначчи / Р. Фишер.- М.:»ИК «Аналитика», 2002.- 384 с.

Числа Фибоначчи и золотое сечение окружают нас повсюду. Вот примеры | Хакнем Школа

Дэн Браун «Код да Винчи»

#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳

Недавно, читая роман Дэна Брауна «Код да Винчи», я по-новому посмотрела на известные со школы: последовательность чисел Фибоначчи, «золотое сечение» и число Фи. Герой романа использует в качестве кода несколько чисел этого ряда.

Своими новыми для себя открытиями я решила поделиться с нашими читателями.

Удивительную последовательность чисел открыл итальянский математик Леонардо Пизанский, более известный под именем Фибоначчи (родился около 1170 — умер после 1228).

Числа, образующие последовательность:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … называются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи. Что же в них такого удивительного?

Числовая последовательность Фибоначчи в задачке с размножением кроликов

1) В этой последовательности первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число получается из суммы двух предыдущих чисел: 1 = 0 +1, 2 = 1 + 1, 3 = 1 +2, 5 = 2 + 3, 8 = 3 +5, и т. д.

2) Ещё одна особенность в том, что при делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то — превосходящая, то — не достигающая его. После 13-ого числа этот результат деления становится постоянным до бесконечности ряда.

Именно это постоянное число деления в средние века было названо Божественной пропорцией, а в наши дни именуется, как золотое сечение. В алгебре это число обозначается греческой буквой фи (φ).

Итак, Золотая пропорция = 1 : 1,618

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618 и т.д., можете проверить сами…

Но самое интересное, что меня поразило, это то, что золотая пропорция есть как в нашем теле, так и в природе.

Тело человека и золотое сечение«Витрувиа́нский человек» — изображение, созданное Леонардо да Винчи

Оказывается, художники, учёные, модельеры и дизайнеры делают свои расчёты, чертежи или наброски, исходя из соотношения золотого сечения, так как пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению.

Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенным.

Несколько основных золотых пропорций нашего тела:

· расстояние от кончиков пальцев до запястья равно 1:1,618;

· расстояние от уровня плеча до макушки головы и размера головы равно 1:1,618;

· расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1,618;

· расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1,618 и др.

Формулу золотого сечения можно найти в других частях тела человека: и в руках человека, и ушах, и в строении лёгких и даже в строении молекулы ДНК (если интересно, можно найти информацию самостоятельно).

Золотой прямоугольникЗолотой прямоугольник

В геометрии есть такой прямоугольник, который называют золотым прямоугольником, его длинные стороны соотносятся с короткими сторонами в соотношении 1,168:1.

Он обладает удивительными свойствами — отрезав от золотого прямоугольника квадрат, строна которого равна меньшей стороны прямоугольника, мы снова получим золотой прямоугольник, но меньшего размера. Продолжая отрезать квадраты, мы будем получать всё меньшие и меньшие золотые прямоугольники.

Причём, располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).

ПРИРОДАИдеальную пропорцию создала сама природа

В природе, лежащее в основе строения спирали, правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях:

• числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи;
• расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи;
• семена в центре подсолнуха организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки;
• у большинства улиток, которые обладают раковинами, раковина растёт в форме логарифмической спирали.

Наутилус раковина

Оказывается, числа Фибоначчи повсюду вокруг нас!

#хакнем_математика 👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳

Автор: #ирина_чудневцева 41 год, город Ярославль, мама 16-летнего подростка.

Золотое сечение в природе, науке, искусстве

В природе Просто удивительно, сколько постоянных можно вычислить пpи помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Источник:http://forexaw.com/TERMs/People/Scientists_and_economists_theorists/l725_%D0%A4%D0%B8%D0%B1%D0%BE%D0%BD%D0%B0%D1%87%D1%87%D0%B8_Fibonacci_%D1%8D%D1%82%D0%BE В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы. Pаковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см.Cпирали очень распространены в природе. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали.Cпираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике. Спираль Архимеда Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать 55 и 89. Источник:http://forexaw.com/TERMs/People/Scientists_and_economists_theorists/l725_%D0%A4%D0%B8%D0%B1%D0%BE%D0%BD%D0%B0%D1%87%D1%87%D0%B8_Fibonacci_%D1%8D%D1%82%D0%BE

В искусстве  В архитектуре: Гармония в архитектурном произведении зависит не столько от размеров самого сооружения, сколько от соотношений между размерами составляющих его частей. Для того чтобы выполнялся основной принцип гармонии «все во всем» , взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение. В живописи: Искусствоведы дружно утверждают, что на живописном полотне существуют четыре точки повышенного внимания. Располагаются они по углам четырехугольника, и зависят от пропорций подрамника. Считается, что какими бы ни были масштабы и размеры холста, все четыре точки обусловлены золотым сечением. Все четыре точки (их называют зрительными центрами) расположены на расстоянии 3/8 и 5/8 от краев (на рисунках в этой книжке золотые точки выделены оранжевым цветом). Полагают, что это матрица композиции любого произведения изобразительного искусства. В скульптуре: Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. В музыке: Трудно найти человека, не знающего, что такое скрипка. Изготовление хорошей скрипки – большое искусство. В этом искусстве выдающихся успехов достигли Антонио Страдивари, Амати, Гварнери, и по сей день звучание их инструментов является образцом, превзойти который не удалось еще никому. Можно предположить, что такое звучание происходит благодаря закону золотого сечения, которое лежит в построение скрипке Антонио Страдивари.

В науке  Математические свойства Отношение большей части к меньшей в золотом сечении выражается квадратичной иррациональностью и, наоборот, отношение меньшей части к большей

Фибоначчи повсюду!. Числа Фибоначчи названы в честь… | by Сергей Базанов | Paradox Review

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.

Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

7.2: Золотое сечение и последовательность Фибоначчи

В этом разделе мы обсудим очень особое число, называемое золотым сечением. Это иррациональное число, немного больше 1,6, и оно (что несколько удивительно) имело огромное значение в мире науки, искусства и музыки. Также было обнаружено, что это число имеет удивительную связь с так называемой последовательностью Фибоначчи, первоначально изученной в контексте биологии много веков назад. Эта неожиданная связь между алгеброй, биологией и искусством предполагает математическое единство мира и иногда также обсуждается в философии.

Золотое сечение

Для одного числа \ (a \) и другого меньшего числа \ (b \) соотношение этих двух чисел находится путем их деления. Их соотношение равно \ (a / b \). Другое соотношение получается сложением двух чисел \ (a + b \) и делением на большее число \ (a \). Новое соотношение — \ ((a + b) / a \). Если эти два соотношения равны одному и тому же числу, то это число называется золотым соотношением. Греческая буква \ (\ varphi \) (фи) обычно используется для обозначения золотого сечения.

Например, если \ (b = 1 \) и \ (a / b = \ varphi \), то \ (a = \ varphi \).Второе соотношение \ ((a + b) / a \) тогда будет \ ((\ varphi + 1) / \ varphi \). Поскольку эти два соотношения равны, это правда:

\ [\ varphi = \ dfrac {\ varphi + 1} {\ varphi} \ nonumber \]

(У этого уравнения есть два решения, но только положительное решение называется золотым сечением \ (\ varphi \)).

Один из способов написать это число —

\ [\ varphi = \ dfrac {1+ \ sqrt {5}} {2} \ nonumber \]

\ (\ sqrt {5} \) — положительное число, которое при умножении на само себя дает \ (5: \ sqrt {5} \ times \ sqrt {5} = 5 \).

Золотое сечение — иррациональное число. Если человек попытается записать его десятичное представление, оно никогда не остановится и никогда не создаст шаблон, но начнется так: 1.6180339887 … Интересная особенность этого числа заключается в том, что вы можете вычесть из него 1 или разделить 1 по нему, и результат будет таким же.

\ [\ varphi-1 = 1,6180339887 \ ldots-1 = 0,6180339887 \ nonumber \]

\ [1 / \ varphi = \ frac {1} {1.6180339887} = 0,6180339887 \ nonumber \]

Золотой прямоугольник

Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник называется «золотым прямоугольником».«Если квадрат отрезать от одного конца золотого прямоугольника, то другой конец станет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) — это золотой прямоугольник, потому что \ (a / b = \ varphi \). Синяя часть (B) — квадрат. Сама по себе розовая часть (A) — это еще один золотой прямоугольник, потому что \ (b / (a ​​- b) = \ varphi \). {2} — \ varphi-1 = 0 \).{2} \). Тогда мы получим \ (\ dfrac {a} {b} = \ dfrac {b} {a-b} \). Обе стороны: \ (\ varphi \) .

Последовательность Фибоначчи

Последовательность Фибоначчи — это список чисел. Начните с 1, 1, а затем вы сможете найти следующее число в списке, сложив два последних числа вместе. Результирующая (бесконечная) последовательность называется последовательностью Фибоначчи. Поскольку мы начинаем с 1, 1, следующее число будет 1 + 1 = 2. Теперь у нас есть 1, 1, 2. Следующее число 1 + 2 = 3. Теперь у нас есть 1, 1, 2, 3. Следующее число 2 + 3 = 5.Следующее — 3 + 5 = 8 и так далее. Каждое из этих чисел называется числом Фибоначчи. Первоначально Фибоначчи (Леонардо Пизанский, живший около 800 лет назад) придумал эту последовательность для изучения популяций кроликов! Он, вероятно, понятия не имел, что произойдет, если вы разделите каждое число Фибоначчи на предыдущее, как показано ниже.

Таблица \ (\ PageIndex {1} \):

Число Фибоначчи	делится на число до	соотношение
1
1	1/1	= 1.0000
2	1/2	= 2,0000
3	3/2	= 1,5000
5	5/3	= 1.6667
8	8/5	= 1,6000
13	13/8	= 1,6250
21	21/13	= 1.6154 …
34	34/21	= 1,6190 …
55	55/34	= 1,6177 …
89	89/55	= 1.6182 …
…	…	…
		= 1,6180 …

Вот очень удивительный факт:

Примечание

Отношение двух последовательных чисел Фибоначчи приближается к золотому сечению.

Оказывается, числа Фибоначчи довольно часто встречаются в природе. Некоторые примеры — узор листьев на стебле, части ананаса, цветение артишока, распускание папоротника и расположение сосновой шишки. Числа Фибоначчи также встречаются в генеалогическом древе пчел.

Между тем, многие художники и исследователи музыки изучали художественные произведения, в которых золотое сечение играет важную роль. К ним относятся работы Микеланджело, Да Винчи и Моцарта.Заинтересованные читатели могут найти в Интернете множество ресурсов и видео. Возможно, неудивительно, что числа вроде 3, 5, 8 и 13 очень важны в теории музыки; просто взгляните на клавиши пианино!

Номер ссылки

1. Список литературы (17)

Авторы и ссылки

10.4: Числа Фибоначчи и золотое сечение

Известной и важной последовательностью является последовательность Фибоначчи, названная в честь итальянского математика Леонардо Пизано по прозвищу Фибоначчи, жившего с 1170 по 1230 год.Эта последовательность:

\ [\ {1,1,2,3,5,8,13,21,34,55, \ ldots \ ldots \ ldots \} \]

Эта последовательность определяется рекурсивно. Это означает, что каждый термин определяется предыдущими терминами.

и так далее.

Последовательность Фибоначчи определяется, для всех, когда и.

Другими словами, чтобы получить следующий член в последовательности, сложите два предыдущих члена.

\ [\ {1,1,2,3,5,8,13,21,34,55,55 + 34 = 89,89 + 55 = 144, \ cdots \} \]

Обозначения, которые мы будем использовать для представления последовательности Фибоначчи, следующие:

\ [f_ {1} = 1, f_ {2} = 1, f_ {3} = 2, f_ {4} = 3, f_ {5} = 5, f_ {6} = 8, f_ {7} = 13, f_ {8} = 21, f_ {9} = 34, f_ {10} = 55, f_ {11} = 89, f_ {12} = 144, \ ldots \]

Пример \ (\ PageIndex {1} \): Рекурсивный поиск чисел Фибоначчи

Найдите 13, 14 и 15 числа Фибоначчи, используя приведенное выше рекурсивное определение последовательности Фибоначчи.

Во-первых, обратите внимание, что уже есть 12 чисел Фибоначчи, перечисленных выше, поэтому, чтобы найти следующие три числа Фибоначчи, мы просто складываем два предыдущих члена, чтобы получить следующий член, как указано в определении. {n} \ right]} {\ sqrt {5}} \]

Формула Бине является примером последовательности , явно определенной .Это означает, что условия последовательности не зависят от предыдущих условий.

Иногда вместо приведенной выше формулы иногда используется несколько более удобная и упрощенная версия формулы Бине.

Упрощенная формула Бине : n-е число Фибоначчи определяется по следующей формуле: Примечание. Символ означает «округление до ближайшего целого числа.”

Пример \ (\ PageIndex {2} \): поиск явно

Найдите ценность использования упрощенной формулы Бине.

Рисунок \ (\ PageIndex {1} \): Работа калькулятора для

Пример \ (\ PageIndex {3} \): Поиск Явно

Найдите значение , используя упрощенную формулу Бине.

Рисунок \ (\ PageIndex {2} \): Работа калькулятора для

Пример \ (\ PageIndex {4} \): Поиск Явно

Найдите значение , используя упрощенную формулу Бине.

Рисунок \ (\ PageIndex {3} \): Работа калькулятора для

Мы можем найти числа Фибоначчи в природе повсюду вокруг нас. Количество ветвей на некоторых деревьях или количество лепестков некоторых ромашек часто являются числами Фибоначчи

.

Рисунок \ (\ PageIndex {4} \): числа Фибоначчи и ромашки

а. Ромашка с 13 лепестками б. Ромашка с 21 лепестком

а. б.

(Ромашки, н.о.)

Числа Фибоначчи также появляются в схемах спирального роста, таких как число спиралей на кактусе или на грядках с семенами подсолнечника.

Рисунок \ (\ PageIndex {5} \): числа Фибоначчи и спиральный рост

а. Кактус с 13 спиралями по часовой стрелке b. Подсолнечник с 34 спиралями по часовой стрелке и 55 спиралями против часовой стрелки

а. б.

(Кактус, н.о.) (Подсолнечник, н.о.)

Другой интересный факт возникает при рассмотрении соотношений последовательных чисел Фибоначчи.

Похоже, что эти коэффициенты приближаются к цифре. Число, к которому приближаются эти отношения, — это особое число, называемое золотым сечением, которое обозначается (греческой буквой фи).Вы видели это число в формуле Бине.

Золотое сечение: \ [\ phi = \ frac {1+ \ sqrt {5}} {2} \] Золотое сечение имеет десятичное приближение \ (\ phi = 1,6180339887 \).

Золотое сечение является особым числом по разным причинам. Его также называют божественной пропорцией, и он проявляется в искусстве и архитектуре.Некоторые утверждают, что это самое приятное для глаз соотношение. Чтобы найти это соотношение, греки разрезали отрезок на две части и позволили меньшему отрезку равняться одной единице. Самый приятный крой — это когда отношение полной длины к длинной части такое же, как отношение длинной части к короткой 1.

1

перемножим, чтобы получить

переставить, чтобы получить

решите это квадратное уравнение, используя формулу корней квадратного уравнения.

Золотое сечение — это решение квадратного уравнения, означающее, что оно обладает свойством. Это означает, что если вы хотите возвести золотое сечение в квадрат, просто добавьте к нему единицу. Чтобы проверить это, просто подключите.

Сработало!

Еще одна интересная связь между золотым сечением и последовательностью Фибоначчи возникает при использовании степеней.

И так далее.

Обратите внимание, что коэффициенты и числа, добавленные к члену, являются числами Фибоначчи.{n} = f_ {n} \ phi + f_ {n-1} \)

, где \ (f_ {n} \) — это n-е число Фибоначчи, а \ (\ phi \) — это золотое сечение .

Пример \ (\ PageIndex {5} \): Степени золотого сечения

Найдите следующее, используя правило золотой силы: a. и б.

Понимание последовательности Фибоначчи и золотого сечения

Последовательность Фибоначчи

Последовательность Фибоначчи, возможно, является самым простым рекуррентным соотношением, встречающимся в природе.Это 0,1,1,2,3,5,8,13,21,34,55,89, 144… каждое число равно сумме двух чисел перед ним и разности двух следующих за ним чисел. Это бесконечная последовательность, которая продолжается вечно по мере своего развития.

Золотое сечение / Божественное сечение или Золотое сечение

Частное любого числа Фибоначчи и его предшественника приближается к Фи, представленному как ϕ (1,618), золотое сечение. Золотое сечение геометрически лучше всего можно понять по золотому прямоугольнику.

Прямоугольник, неравномерно разделенный на один квадрат и один прямоугольник, стороны квадрата будут иметь соотношение 1: 1, а новый прямоугольник будет точно пропорционален исходному прямоугольнику — 1: 1.618.

Эта итерация может продолжаться в обоих направлениях бесконечно. Если вы построите четверть круга внутри каждого квадрата, когда они повторяются, образуется золотая спираль. Золотая спираль, возможно, является самым простым математическим узором, который встречается в природе, как раковины улиток, морские раковины, рога, цветы, растения. Числа — это только то, что мы используем для организации количественной информации.

Золотое сечение можно увидеть от наутилуса с камерой к спиральной галактике

Золотое сечение можно применять к любому количеству геометрических форм, включая круги, треугольники, пирамиды, призмы и многоугольники.

Золотое сечение образовано третями внутри третей, шестыми, связью между двумя и тремя, включая каждое четное и нечетное число. Само соотношение представляет собой превосходство чисел, понимание нашего мира — это не числа, а то, что они представляют.

Через спираль соотношение показывает, насколько числа, все количества, являются качеством. В конце концов, все качество можно представить через количество. Качественные и количественные свойства — всего лишь информационные ярлыки, собранный нами неоспоримый факт.

Подсолнухи имеют расположение семян золотой спирали. Это обеспечивает биологическое преимущество, так как максимально увеличивает количество семян, которые можно упаковать в семенную головку.

Если вы изобразите любую систему счисления, в конечном итоге появятся шаблоны. В математике числа и их модели не только бесконечно линейны, но и распространяются во всех направлениях. Например, учитывая бесконечное десятичное разложение, даже самые короткие отрезки имеют бесконечное количество точек.

Наша Вселенная и числа не только бесконечно линейны, но даже в ее коротких отрезках есть бесконечные точки.

(Красивый короткометражный фильм о последовательности Фибоначчи в природе — «Природа по числам»)

Золотое сечение — не единственная математическая модель, которая достигает бесконечности, существует множество других моделей, которые достигают бесконечности. Зная это, спросите себя, как бесконечность может возникнуть дважды? Если что-то должно происходить бесконечно, как это могло случиться дважды?

Ответ прост: бесконечность представляет то, что вечно, то, что действительно цельно. Например, если бы бесконечность использовалась как переменная в математике, как и все другие числа, она была бы обозначена как 1∞, 2∞, 3∞, 4∞ и т. Д.

Единство всего фактического — это то, что вы знаете, что вы воспринимаете, что вы осознаёте, — это вся вселенная, смотрящая на себя. Это вселенная, даже вы — вселенная, мы и все, что мы знаем, — это одно и то же.

Поскольку числа везде, все является частью узора. Отражения отражений, колеса в колесах. Сама жизнь — фрактал.

Источник изображения

Золотое сечение Фи

Последовательность Фибоначчи влияет на фондовый рынок | Наука

В пятницу, 20 марта, как сообщает U.Южный фондовый рынок завершил свою худшую неделю с 2008 года на фоне беспорядков, связанных с коронавирусом (до некоторого восстановления в начале следующей недели), перед инвесторами остался вопиющий вопрос: все ли идет под откос? В условиях такой экономической нестабильности некоторые исследователи рынка обращаются к знакомому мощному набору чисел для предсказания будущего.

«Коррекция Фибоначчи» — это инструмент, который технические аналитики используют для определения своих взглядов на поведение покупателей и продавцов на рынках.Этот метод назван в честь известной последовательности Фибоначчи, набора чисел, свойства которой связаны со многими природными явлениями. Хотя использование этих чисел для прогнозирования рыночных движений гораздо менее надежно, чем их использование для расчета структуры семян подсолнечника, появление последовательности в области финансов является еще одним свидетельством ее способности захватывать человеческое воображение.

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — это известная группа чисел, начинающаяся с 0 и 1, в которой каждое число является суммой двух перед ним.Он начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21 и продолжается бесконечно. Шаблон скрывает мощный секрет: если вы разделите каждое число в последовательности на его предшественник (кроме 1, деленного на 0), то по мере продвижения к более высоким числам результат сходится к константе phi или приблизительно 1,61803, в противном случае известное как золотое сечение.

Последовательность имеет долгую историю. В Европе это было решение проблемы кролиководства, описанной в книге Liber Abaci итальянского математика Леонардо Пизанского в 1202 году A.Д. Но этот узор был известен в Индии гораздо раньше, возможно, даже в седьмом веке. Название последовательности происходит от прозвища Фибоначчи, что означает «сын Боначчи», данного Леонардо в 19 веке, согласно книге Кейта Девлина В поисках Фибоначчи: В поисках нового забытого математического гения, изменившего мир . Затем математик Эдуоард Лукас в 1870-х годах дал название «последовательность Фибоначчи» последовательности, полученной из сценария с кроликом.(Это также проявилось при подсчете количества пчел в последовательных поколениях).

Между тем, золотое сечение может быть записано как половина суммы 1 плюс квадратный корень из 5. И хотя фи не дает такого праздника с начинкой из теста, как пи, константа появляется в природных явлениях. Число спиралей в шишках — это числа Фибоначчи, как и количество лепестков в каждом слое определенных цветов. У спиралевидных растений каждый лист растет под углом по сравнению с его предшественником, равным 360 / phi ² , и семена подсолнечника упакованы в спиралевидное образование в центре их цветка, геометрия которого также регулируется золотым сечением.

«Привлекательность золотого сечения проистекает в первую очередь из того факта, что оно имеет почти сверхъестественный способ появиться там, где его меньше всего ждут», — пишет Марио Ливио в книге «» Золотое сечение: история самого удивительного числа в мире Фи. .

Но почему эта последовательность так повсеместна? «Многие вещи в математике и, вероятно, в реальном мире регулируются простыми рекурсивными правилами, где каждое вхождение регулируется простой формулой с точки зрения предыдущего вхождения», — сказал Кен Рибет, профессор математики Калифорнийского университета. Беркли.«И у числа Фибоначчи есть простейшая из возможных формул, просто сумма двух предыдущих».

Фибоначчи выходит на рынок

Люди запрограммированы на идентификацию закономерностей, и когда дело доходит до чисел Фибоначчи, мы не ограничиваемся поиском и восприятием последовательности в природе. Фибоначчи и фи можно найти в некоторых произведениях искусства, архитектуры и музыки (хотя это миф, что пирамиды Египта имеют к этому какое-то отношение).И хотя поведение покупателей и продавцов в значительной степени непредсказуемо, некоторые финансовые аналитики клянутся, что они тоже могут увидеть эти цифры в игре, в том числе в нынешнем экономическом кризисе.

Крупный план подсолнечника (Wiki Commons / Alex M3rcer)

Инвестиционные исследователи, которых называют «техническими аналитиками», смотрят на исторические формы графиков, чтобы определить, будет ли текущая тенденция покупки или продажи продолжаться или измениться.Некоторые делают свои прогнозы, используя «уровни восстановления Фибоначчи», полученные из известной последовательности.

Технические аналитики могут смотреть на целый набор чисел, соответствующих соотношениям чисел в последовательности Фибоначчи, но есть пара важных — 61,8% и 38,2%. Любое данное число Фибоначчи, деленное на его преемник, составляет приблизительно 1 / фи, или 0,618. Число Фибоначчи, деленное на число на два разряда выше в последовательности, приблизительно равно 0.382.

Например, рассмотрим S&P 500. В разгар рецессии 2008 года индекс достиг своей самой низкой точки в 2009 году — 666 пунктов. С тех пор он, как правило, находится на длительном подъеме, достигнув пика в 3393 человека до резкого падения, вызванного коронавирусом в последние недели.

Чтобы понять тенденции нынешнего спада, Кэти Стоктон, основатель и управляющий партнер фирмы технического анализа Fairlead Strategies, LLC в Стэмфорде, штат Коннектикут, изучает, пробиваются ли ключевые индексы и акции через различные уровни.Если вы возьмете минимум 2009 года в 666 за нижнюю (0 процентов) и максимум 2020 года в 3393 как за верхнюю (100 процентов), Стоктон будет следить за тем, закрывается ли S&P 500 две пятницы подряд ниже того, что она определяет как « уровень поддержки »38,2 процента. Этот уровень соответствует максимуму 3393 минус 1042 (38,2 процента разницы между максимумом и минимумом), что составляет 2351.

Пока что во время кризиса цены не падали так низко две пятницы подряд, хотя 20 марта индекс закрылся на мрачном уровне 2304.92. Если 27 марта он закроется ниже этого уровня Фибоначчи 2351, это будет второй страйк подряд. Для таких аналитиков, как Стоктон, это будет указывать на то, что S&P рискует упасть ниже уровня 61,8 процента, или около 1708 года, что, согласно этой точке зрения, делает сейчас менее оптимальным временем для покупок.

Самореализующееся пророчество?

Рибет, математик, отвергает идею поиска паттернов, связанных с последовательностью Фибоначчи, для прогнозирования рынков.Но даже если это неправда, что числа Фибоначчи связаны с фундаментальными рыночными силами, рынки по своему замыслу реагируют на убеждения своих игроков. Поэтому, если инвесторы массово покупают из-за анализа Фибоначчи, они в любом случае создают восходящий тренд; аналогично для продажи.

Стоктон признает, что это, по крайней мере, частично объясняет движение золота в прошлом году, когда инвесторы внимательно отслеживали, поднимется ли цена унции выше определенного уровня Фибоначчи. Цена на золото значительно упала с 2012 по 2015 год, а затем колебалась в пределах от 1200 до 1400 долларов за унцию в течение четырех лет до июня 2019 года, когда, похоже, она снова начала расти.

«Это был большой прорыв Фибоначчи, за которым наблюдали многие люди, даже до такой степени, что он стал настолько широко отслеживаемым уровнем, что, я думаю, он становится неким самореализующимся свойством», — сказал Стоктон.

Идея о том, что числа Фибоначчи управляют торговлей акциями людей, может быть волшебным мышлением, но достаточное количество людей с таким же магическим мышлением может двигать рынки. Готовясь к еще большему хаосу, мы, по крайней мере, можем успокоиться, зная, что сами числа Фибоначчи вечны.

Что такое последовательность Фибоначчи и почему она является секретом музыкального величия?

22 ноября 2018, 16:21 | Обновлено: 28 января 2019, 09:23

Последовательность Фибоначчи часто встречается в музыке и искусстве. Картина: Getty Images / Классический FM

Гении от Моцарта до Леонардо да Винчи использовали последовательность Фибоначчи. Но что это такое и почему из него получается отличная музыка?

Последовательность Фибоначчи получила прозвище «код природы», «божественная пропорция», «золотое сечение», «спираль Фибоначчи» и другие.

Что такое последовательность Фибоначчи?

Проще говоря, это ряд чисел:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…

Следующее число в последовательности можно найти по после сложения двух чисел перед . Соотношение для этой последовательности составляет 1,618 . Это то, что некоторые называют «божественной пропорцией» или «золотым сечением».

Когда вы строите квадраты из этих значений, получается красивая спираль:

Спираль Фибоначчи.Картина: Классический FM

Знакомо? Вы, наверное, видели это раньше …

Басовый ключ и спираль Фибоначчи. Картина: Классический фм

Эта последовательность, узор и спираль возникают во многих вещах, которые вы, возможно, никогда не замечали. Используется в искусстве и музыке; просто посмотрите, как Леонардо да Винчи использовал его в одной из своих самых известных картин, «Мона Лиза»:

Использование Леонардо да Винчи последовательности Фибоначчи в «Джоконде» (Мона Лиза). Картина: Getty Images / Классический FM

Последовательность Фибоначчи в музыке

Последовательность Фибоначчи играет большую роль в западной гармонии и музыкальных гаммах.Вот факты:

— октава на фортепиано состоит из 13 нот. Восемь — белые клавиши, а пять — черные.
— Шкала состоит из восьми нот, из которых третья и пятая ноты составляют основу основного аккорда
— В гамме доминирующей является пятая нота, которая также является восьмой из всех 13 нот, составляющих вверх на октаву.
— Восемь, разделенная на 13, равняется 0,61538 … приблизительное золотое сечение )

Начинаете видеть закономерность? Это все числа в последовательности Фибоначчи: 3, 5, 8, 13.

Последовательность Фибоначчи можно увидеть на клавиатуре фортепиано. Картина: Классический FM

Кто использовал последовательность Фибоначчи?

Композиторы и производители инструментов использовали последовательность Фибоначчи и золотое сечение на протяжении сотен лет для сочинения и создания музыки.

Моцарт, например, основал многие свои произведения на золотом сечении, особенно его сонаты для фортепиано.

Традиционная соната состоит из двух частей:
1. Экспозиция — где представлена ​​музыкальная тема
2. Развитие и перепросмотр — где тема развивается и повторяется

А вот интересный момент …

Моцарт расположил свои фортепианные сонаты таким образом, чтобы количество тактов в развитии и перепросмотре делилось на количество тактов в экспозиции будет равно примерно 1,618 , золотому сечению.

В качестве примера возьмем первую часть сонаты для фортепиано № 1 до мажор Моцарта.

Золотое сечение в сонате Моцарта No.1. Картина: Классический FM

На приведенной выше диаграмме C — это первая часть сонаты в целом, B — это развитие и повторение , и A — это экспозиция .

Экспозиция состоит из 38 тактов, а development and recapitulation состоит из 62. Первый механизм в целом состоит из 100 тактов.

62 делить на 38 равно 1,63 (приблизительно золотое сечение )

Эксперты утверждают, что Бетховен, Барток, Дебюсси, Шуберт, Бах и Сати (и это лишь некоторые из них) также использовали эту технику для написания своих сонат, но никто точно знает, почему это так хорошо работает.

Stradivari

Прославленный как мастер изготовления скрипок, Антонио Страдивари создал одни из самых красивых и звучных скрипок на свете.

Чтобы сохранить звук Страдивари, весь этот итальянский город молчит.

Есть причина, по которой покупка скрипки Страдивари будет стоить вам несколько миллионов фунтов — и ее ценность частично зависит от последовательности Фибоначчи и ее золотого Соотношение.

Страдивари использовал последовательность Фибоначчи и золотое сечение для создания своих скрипок.Картина: Getty Images / Классический FM

Золотое сечение можно найти во всей скрипке, разделив длины отдельных частей скрипки. Некоторые думают, что это одна из причин, по которой это звучит так хорошо.

Золотое сечение, которое исходит из последовательности Фибоначчи, используется не только для изготовления скрипок, но и для мундштуков саксофона, проводов динамиков и даже в акустическом оформлении некоторых соборов.

Даже Леди Гага использовала его в своей музыке — узнайте, как это сделать здесь>

Золотое сечение / последовательность Фибоначчи: что это значит для фотографов | Стив и Марни Харкеры (SweetHark Crafts) | PHLEARN Magazine

Как начинающие, так и опытные фотографы всегда открывают для себя новые способы экспериментировать с фотографической композицией.Мы ищем правила композиции во время съемки и монтажа, изучаем соответствующие концепции и изучаем работы известных фотографов, иллюстраторов и художников, чтобы определить, как они использовали эти идеи в своих интересах.

Золотое сечение, также известное как последовательность Фибоначчи, является одним из наименее понятных правил композиции. Что это? Что оно делает? Как мы можем это использовать? Здесь мы ответим на эти и другие вопросы.

Фото Кристиана Ламберта на Unsplash

Вы можете вздрогнуть при мысли о том, чтобы заниматься математикой, когда все, что вам нужно, — это делать потрясающие снимки, но золотое сечение и последовательность Фибоначчи связаны друг с другом визуально и могут быть определены математически. как та же идея.Композиционная двойка!

Прежде всего, давайте разберемся с сырой математикой. Золотое сечение описывается делением линии на две части, так что длинная часть, разделенная на короткую, также равна всей длине, разделенной на длинную часть. Фактическое число, используемое для описания символа, — это иррациональное число, которое бесконечно повторяется, 1.6180339887498… и так далее.

Взаимосвязь между математикой и формой видна здесь:

Изображение Рафаэля Хавьера с сайта Pixabay

Делает меня иррациональным, позвольте мне вам сказать! Но композиционно он производит очень приятное впечатление.Это соотношение прослеживается как в классической, так и в современной архитектуре, а также в природных сооружениях.

Эта концепция также известна как спираль Фибоначчи, которую чрезвычайно просто описать как математически, так и визуально. Это последовательность чисел, в которой следующее число находится путем сложения двух чисел перед ним. Итак, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Намного проще, чем в предыдущем уравнении.

Почему золотое сечение и последовательность Фибоначчи так важны в фотографии? На самом деле все сводится к балансу и закономерностям против хаоса.От скоплений галактик до субатомных частиц — почти все, что нас окружает, вписывается в определенный узор. Так что искать и создавать закономерности в окружающем мире — это вполне нормальная реакция.

Эту последовательность можно встретить повсюду в природе. Лепестки растущего цветка, сосновая шишка, раковина морской улитки, паутина и листья куста или дерева — все следуют этой последовательности. Если вы находитесь рядом с подсолнухом, присмотритесь к одному из них. Я считаю, что изображение подсолнечника иллюстрирует концепцию золотого сечения и последовательности Фибоначчи.

Фотография Марджори Бертран на Unsplash

Если вы поищете, вы можете найти вхождения золотого сечения вокруг себя. Но как заставить его работать в ваших собственных композициях? Частично ответ на этот вопрос состоит в том, чтобы иметь хорошее представление о том, что такое золотое сечение в первую очередь. Вы можете сделать это, сделав себе визуальное упражнение.

Совершите путешествие без камеры, чтобы увидеть, сколько раз вы можете заметить пропорции и спираль в природе и в архитектуре. Возьмите с собой блокнот, чтобы делать наброски.Что вы будете вознаграждены, так это оценка этого фантастического композиционного инструмента и способность видеть его, когда он появляется перед вашим объективом.

Изображение Dimitris Vetsikas с сайта Pixabay

Затем дайте себе задание фотографировать. Найдите все естественные и искусственные золотые сечения, скажем, в пяти милях от вашего дома или студии. Сфотографируйте их и распечатайте. Их не нужно печатать на фотобумаге; для этого упражнения будет достаточно обычной копировальной бумаги.

А теперь самое сложное.Нарисуйте или распечатайте спираль Фибоначчи или версию с линиями и блоками. Вы можете распечатать эти изображения:

Изображение Nicolás Damián Visceglio с сайта Pixabay Изображение Peter Kertesz с сайта Pixabay

Сделайте отпечатки своих изображений и наложите график на отпечаток. Вы также можете нарисовать спираль прямо на отпечатке, соединив кривые от мала до велика.

Это упражнение прочно закрепит в вашем воображении, что такое золотое сечение и как оно работает. Когда у вас есть эта концепция, вы можете начать целенаправленно применять ее.

Эту композиционную технику можно использовать и в портретах. Групповые портреты поддаются ему почти естественно. Если вы просто не выстраиваете людей в ряд или группируете их по росту, скорее всего, вы уже используете золотое сечение в своих групповых снимках. Как это так?

Когда группам комфортно друг с другом и комфортно с фотографом, они, как правило, естественным образом тяготеют к этому золотому сечению, когда собираются для портрета. Просто небольшое указание от вас, как от фотографа, — это все, что нужно для точной настройки для приятной аранжировки.

Когда вы смотрите в видоискатель, обратите внимание на то, как все естественным образом распределяются по меньшим группам внутри большей группы. Вы можете взять эту естественную тенденцию и настроить ее, чтобы усилить спираль, отрегулировав положение их головы и плеч в кадре.

Последовательность Фибоначчи | Винодельня Мира

Последовательность Фибоначчи лежит в основе архитектуры, искусства и природы. Он также лежит в основе Mira с момента нашего первого знакомства, дизайна нашего поместья и того, как мы определяем цены на наши вина.

Последовательность Фибоначчи в финансах

Mira Winery использует последовательность Фибоначчи для определения цены на наши вина.

«Коррекция Фибоначчи» — это инструмент, который технические аналитики используют для определения своих взглядов на поведение покупателей и продавцов на рынках. Этот метод назван в честь известной последовательности Фибоначчи, набора чисел, свойства которой связаны со многими природными явлениями. Хотя использование этих чисел для прогнозирования рыночных движений гораздо менее надежно, чем их использование для расчета структуры семян подсолнечника, появление последовательности в области финансов является еще одним свидетельством ее способности захватывать человеческое воображение.

Последовательность Фибоначчи в архитектуре

Поместье Мира было спроектировано в соответствии с золотым сечением и его можно увидеть во время посещения.

Золотое сечение основано на последовательности Фибоначчи и используется в архитектуре и искусстве, поскольку считается, что оно создает эстетически приятные деления и пропорции. … Во многих случаях золотое сечение применялось позже при анализе произведения искусства / здания, и глаз видит то, что он хочет видеть.

Последовательность Фибоначчи в природе

Многие примеры чисел Фибоначчи можно найти в фенотипических структурах растений и животных.Действительно, числа Фибоначчи часто появляются в количестве лепестков цветов, спиралей на раковине подсолнечника или наутилуса, морских звезд и фракциях, которые появляются при филлотаксисе [4, 18, 10].

Другой простой пример, в котором можно найти последовательность Фибоначчи в природе, — это количество лепестков цветов. У большинства их три (например, лилии и ирисы), пять (парнасия, плоды шиповника) или восемь (космея), 13 (некоторые маргаритки), 21 (цикорий), 34, 55 или 89 (сложноцветные).

Последовательность Фибоначчи в искусстве

Одна очень известная фигура, известная как Мона Лиза, написанная Леонардо да Винчи, нарисована в соответствии с золотым сечением.