Число фи равно: Число ФИ: значение золотого сечения

Число ФИ: значение

Число ФИ или латинскими буквами PHI – это число, которое обозначает все красивое во Вселенной. Что же это за необычное число, и какие другие названия у него существуют?

Число Фи обозначает все красивое во Вселенной

Почему это число называют золотым сечением?

Это число получил исследователь Фибоначчи

В древней Греции был один скульптор Фидий, который обладал удивительным талантом. Все восхищались его скульптурами и пытались разгадать, как этому творцу удается каждый раз делать настоящее произведение искусства. Позже стало известно, что в каждой своей скульптуре Фидий придерживается определенного числа в пропорциях.

Затем оказалось, что не только этот творец использовал в своем искусстве это необыкновенное число. Оно было обнаружено в произведениях искусства художника Рафаэля, русского художника Шишкина, число гнездилось в музыкальных произведениях Бетховена, Шопена и Чайковского. Знаменитая «Джаконда» Леонардо Да Винчи тоже содержит в себе это число. Его еще называют золотым сечением.

ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ [Число ФИ и Золотое сечение]

Тайна числа 1.618034 — самое ВАЖНОЕ число в мире

ЗОЛОТОЕ СЕЧЕНИЕ

По математическим меркам число ФИ равно 1.618, его получил исследователь Фибоначчи. Этот ученый в результате своих исследований пришел к тому, что все числа имеют четкую последовательность. Каждый следующий член, начиная с третьего числа, несет в себе сумму двух прошлых членов. А частное двух соседних чисел представляет собой максимально приближено к числу 1.618, то есть к тому самому числу ФИ.

Золотое сечение и пропорции человеческого тела

Человеческое тело сотворено по принципу золотого сечения

Наверное, все видели знаменитую картину Леонардо Да Винчи, где расчерчено человеческое тело. Именно при помощи этой знаменитой схеме Леонардо доказал, что человеческое тело сотворено по принципу золотого сечения. Пропорции тела человека всегда дают то самое число красоты ФИ.

При желании такую теорию можно легко проверить на практике. Нужно измерить при помощи сантиметра длину от плеча до кончика самого длинного пальца, а потом поделить его на длину от локтя до кончика того же самого пальчика. Удивительно, но в результате вы получите как раз 1.618! То самое число красоты. Это не единственный пример. Измерьте расстояние от верхней части бедра, поделите его на длину от колена до пола, вы получите такое же значение. Таким образом, легко доказать, человек полностью состоит из божественной пропорции.

Кроме того на теле человека легко можно обнаружить признак того самого золотого сечения. Это наш пупок. Интересно отметить, что замеры тела мужчин чуть больше приближены к заветному числу. Это примерно 1.625. Женские же пропорции больше подходят под значение 1.6.

Секреты пирамид

На принципе числа Фи построены пирамиды в Гизе

На протяжении многих лет люди пытались открыть загадку Пирамиды в Гизе. Но на этот раз пирамида интересовала человечество не в качестве склепа, а как уникальная комбинация числовых значений. Эту пирамиду возвел мастер, который обладает удивительной изобретательностью, он не пожалел труда и времени для этого произведения. На ее сотворение были пущены лучшие архитекторы, которых удалось найти. Долго современные ученые недоумевали как древним египтянам, у которых не было письменности, удалось придумать такой сложный геометро-математический ключ. После длительных просчетов оказалось, что и в этом случае не обошлось без золотого сечения и числа ФИ. Как раз на этом принципе и основана эта пирамида. Некоторые современные ученые считают, что посредством этого произведения древние египтяне пытались передать своим современникам секрет природной красоты и гармонии.

Не исключительно в Гизе существуют пирамиды, которые выстроены, пирамиды, которые расположены в Мексике, тоже выстроены таким образом. Именно поэтому современные исследователи приходят к выводу, что пирамиды на этих территориях были построены народом, который имеет общие корни.

Число ФИ в космосе

В астрономии тоже присутствует число Фи

Астроном из Германии Тициус в XVIII столетии заметил, что ряд числовых значений Фибоначчи присутствует и в расстоянии между планетами всей солнечной системы. В этом не было бы ничего удивительного, если бы такая закономерность не шла в противостоянии с одним законом. Дело в том, что между Марсом и Юпитером планеты нет, так раньше думали астрономы. Однако после выведения этой закономерности, они тщательно исследовали эту область галактики и обнаружили там ряд астероидов. К сожалению, такое важное открытие произошло, когда тот самый Тициус уже ушел из жизни.

Теперь в астрономии при помощи числовых соотношений Фибоначчи представляют строение Галактик. Такой факт свидетельствует о независимости данных числовых соотношений от условий проявления, тем самым доказывается их универсальность.

Примеры числа ФИ из природы

Существуют интересные примеры числа ФИ из самой природы

Вот интересные примеры числа ФИ из самой природы:

• Если взять пчелиный улий, пересчитать в нем количество пчел-мальчиков и пчел-девочек, потом мальчиков поделить на девочек, то каждый раз вы получить 1,618.
• Семечки в подсолнухе расположены по принципу спирали, против направления часовой стрелки. Диаметр каждой спирали в подсолнухе равен следующей спирали тоже 1.618.
• Тот же принцип со спиралями действует на панцире улитки.
• Если провести анализ, как вытягивается к небу каждое растение, то можно заметить, что маленький росточек делает большой рывок вверх, затем следует остановка и выпускание одного листочка, который будет несколько короче первого росточка. Потом снова следует бросок вверх, но уже с меньшей силой. Если все это перевести в математическое значение, то первый бросок будет равен 100, второй 62, третий 38 единицам, четвертый 24 и так дальше. Это значит, что рывки в росте уменьшаются по тому же принципу золотого сечения.
• Живородящая ящерица. В таком удивительном существе, как ящерица можно даже невооруженным взглядом заметить божественные пропорции. Соотношение длины хвоста этого животного равно длине всего остального тела этого существа, как 62 относится к 38.

Исходя из всех этих примеров, их на самом деле гораздо больше ученые делают вывод, что в мире растений и мире животных присутствует симметрия в отношении роста и движения. Золотое сечение проявлено здесь перпендикулярно к направлению роста.

Золотое сечение и теория Хаоса

В каждом природном явлении присутствует свое золотое соотношение чисел

Одни ученые заметили, что все в мире происходит хаотично. А другие подвели итог, что даже в хаосе, которому подвержен весь мир, можно найти свои конкретные закономерности. Эти самые закономерности тоже выражены в числовых значениях Фибоначчи. В каждом природном явлении присутствует свое золотое соотношение чисел. В этом смысле природа не может соревноваться с сухой и скучной геометрией.

Геометрия при всей своей точности и конструктивности не способна описать форму облака, дерева или горы. Облако не может быть представлено сферой, гора конусом, берег моря не может найти свое выражение в геометрической окружности. Кора дерева не может быть выражена этой наукой, потому что она не гладкая, а молния никогда не будет двигаться по прямой. Природные явления представляют собой не только более высокую степень, а совершенно новый уровень сложности. В природе представлены наборы масштабов, разные длины объектов, поэтому они способны закрывать неисчислимое количество потребностей. Такой набор масштабов и измерений несет название фрактал. Именно при помощи фракталов ученые не оставляют попытки сделать описание объектов, которые не доступны линейной геометрии. Это фрактальная геометрия. Каждый человек тоже представляет собой фрактал.

А еще интересно то, что число ФИ имеет бесконечную природу, это означает, что мы бесконечно можем делать новые открытия во Вселенной и в себе самом.

Загадка числа Фи — Bad Android

Число Фи есть самым точным, загадочным и интригующим значением в природе. Оно играет уникальную роль — основы в построении всего живого.

Число Фи (Φ), или как его еще называют «число Бога», получено из последовательности Фибоначчи, математической прогрессии, известной не только тем, что сумма двух соседних чисел в ней равна последующему числу, но и потому, что частное двух соседствующих чисел обладает уникальным свойством — приближенностью к числу 1,618, то есть к числу Фи!

Эта вездесущность Фи в природе указывает на связь всех живых существ.

Вездесущее число Фи

Немного истории

Это число имеет множество названий и знакомо человечеству более 2500 лет.

Впервые упоминание об этом числе встречается в труде древнегреческого математика Евклида «Начала» (примерно 300 лет до н. э.). Там это число используется для построения правильного пятиугольника, положенного в основу идеального «Платонового тела» — додекаэдра, символа совершенной Вселенной.

Леонардо Пизанский, более известный как Фибоначчи, назвал это число «божественной пропорцией». Позже на значении константы «фи» было основано «золотое сечение».

Термин «золотого сечения» был введен в 1835 году Мартином Омом.

Постоянную константу «фи» использовали в построении пирамиды Хеопса, а также для создания барельефов, предметов быта и украшений из гробницы Тутанхамона. Пропорция «золотого сечения» используется в произведениях художников, скульпторов, архитекторов и даже хореографов и музыкантов.

Золотое сечение Леонардо да Винчи

Математические расчеты

Фибоначчи в результате своих исследований пришел к тому, что все числа имеют четкую последовательность.

Каждое следующее число, начиная с третьего, несет в себе сумму двух предыдущих. А частное двух соседних чисел представляет собой максимально приближенное к числу 1.618, то есть к тому самому числу ФИ.

Вселенная влияет на каждое живое существо на планете. Закономерности и пропорции, которые прослеживаются в природе, часто остаются незамеченными.

Ученые заметили, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках расположены по двойным спиралям, завивающимся навстречу друг другу. При этом числа «правых» и «левых» спиралей всегда относятся друг к другу, как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34).

Многочисленные примеры двойных спиралей, встречающихся повсюду в природе, всегда соответствуют этому правилу.

Золотое сечение

Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».

Пьер Kюри в начале ХХ века сформулировал ряд глубоких идей симметрии. Согласно его утверждению нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

ЗНАЧЕНИЕ ЧИСЛА ФИ И «РУССКАЯ МАТРИЦА» А. Ф. ЧЕРНЯЕВА

                                                                                                              Вымысел — не есть обман.
                                                                                                              Замысел — еще не точка.
                                                                                                              Дайте дописать роман
                                                                                                              до последнего листочка.
                                                                                                                                                Б. Окуджава
  
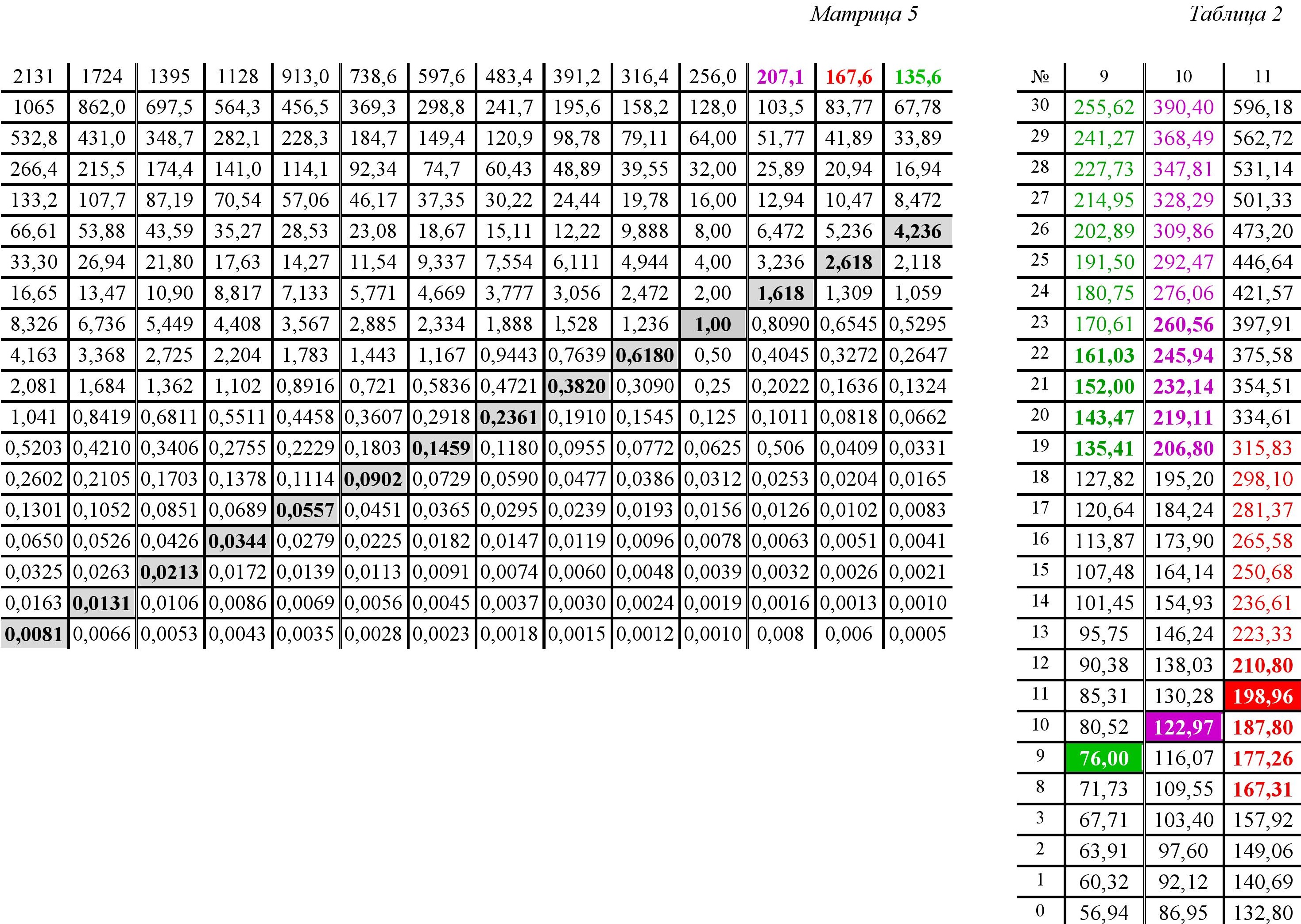
              Через несколько дней после окончания предыдущей статьи я заметила то, что могла бы увидеть ранее: значения чисел в таблице 2 отличаются от значений, стоящих в матрице 5. Например, в левом верхнем углу матрицы 5 стоят числа 207,1; 167,6; 135,6. В таблице 2 соответственно имеем 206,80; 167,31; 135,41, то есть имеется устойчивое расхождение значений в пределах 0,14-0,17%. Но так как матрица 5 есть «свертка» матрицы 6, а таблица 2 – это фрагмент матрицы 6, то соответствующие значения в матрице 5 и таблице 2 должны совпадать.

   
              Причина возникшего несоответствия в неточно определенном значении числа Фи.
              Дабы не повторяться, приведу цитату из главы Живого журнала «Золотой вурф. Живые и мертвые тела и объемы»:
              «Проясним теперь вопрос с истинным значением числа Фи. Дело в том, что истинное значение числа Фи невозможно определить просто математическим методом, без проникновения в его суть. Так значение Фи не определяется ни из ряда Фибоначчи, ни из решения квадратного уравнения. Оно может быть определено через коэффициент перехода от саженей одной группы к саженям другой группы как степень энергетического соответствия разных групп саженей:
1.     А_2i / А_3i = Фи / 2, или А_1i / А_2i = Фи / 2;
2.     А_3i+1 / А_1i = Фи, или А_1i+12 / А_2i = Фи, или А_2i+12 / А_3i = Фи.
              Все они дают значение Фи, ОТЛИЧНОЕ от так называемого общепринятого, а между собой отличаются только в силу точности определения размера саженей.
              Если размер саженей определен в сантиметрах с точностью до второго знака после запятой, то значение Фи может быть определено с точностью до четырех знаков после запятой и оно будет соответствовать величине 1,6182…
              Общепринятое значение Фи принимается за 1,6180…
              Казалось бы, незначительное отличие. Но это РАЗНЫЕ величины!
              Определить значение Фи с любой мыслимой точностью можно, используя коэффициент перехода от данной сажени к правой рядом стоящей, который равен малой секунде равномерно темперированного строя:
              k_Г. = ¹²√2 = Фи³/4.
              Отсюда получим значение Фи, например, с точностью до 16 знака после запятой: 1,6182611502319232…»
              Все расчеты в предыдущей статье, также как и расчеты в книге «Золото Древней Руси» были сделаны со значением числа Фи, округленным с точностью до трех знаков после запятой 1,618… Такая точность является недостаточной, поэтому в матрицах 5, 6 и 7 и таблице 2 возникли отклонения в значениях величин. Данная неточность вычислений, связанная с округлением значения числа Фи до трех знаков после запятой, была принята А. Ф. Черняевым за процесс появления новых величин. Необходимо заметить, что данные отклонения сильнее проявляются в матрицах 6 и 7 и таблице 2 как части матрицы 6, чем в матрице 5, так как в них чрезвычайно быстро возрастает степень числа Фи – каждый переход со строки на строку – это ¹²√2 = Фи³/4.
              Ниже приведены матрица 5 и таблица 2, пересчитанные со значением Фи, принятом за 1,61826…. При этом границы матрицы 5 были еще значительно расширены вправо.

         При сопоставлении полученных результатов видно, что соответствующие значения в матрице 5 и таблице 2 совпадают с точностью до двух знаков после запятой. Например, вышеприведенные три значения теперь выглядят следующим образом: 207,14; 167,60; 135,61.
              Далее при сопоставлении расширенного варианта матрицы 5 и таблицы 2 можно заметить, что в каждом столбце матрицы 5 проявляется одно из значимых, несущих информационную новизну, значений таблицы 2 – эти цифры выделены жирным шрифтом в матрице 5 и таблице 2. При этом четко прослеживается разбивка матрицы 5 на тройки столбцов, что выделено соответствующими цветами цифр и в таблице 2, и в матрице 5.
              Легко предположить, что через 36 столбцов или 12 троек столбцов закончатся значения, имеющие информационную новизну, и, как следствие, закончится данный цикл и начнется его повторение. Действительно, столбцы 37, 38 и 39 есть отражение столбцов 1, 2 и 3 со сдвигом вверх на 11 строк.
              Итак, «Русская матрица» и в виде «матрицы 5» матрицей не является, так как на самом деле представляет собой повторяющееся бесчисленное множество столбцов из 36 бесконечных последовательностей чисел, сдвинутых друг относительно друга на 11 строк.
              Таким образом, мысли А. Ф. Черняева по поводу «Русской матрицы» и выводы, сделанные на их основании, нуждаются в корректировке и пересмотре.
              Сделаем некоторые уточненные выводы, основываясь на материале двух последних глав.
              Применение в расчетах так называемого «общепринятого значения» числа Фи с точностью до трех знаков после запятой в виде 1,618… приводит к значительным отклонениям в результатах вычислений и, как следствие, программирует неправильные выводы.
              В книге «Золото Древней Руси» имеем как раз такой случай, когда циклические вычисления со значением Фи, определенным как 1,618…, продолжались до тех пор, пока на каком-то витке вычислений достаточно случайным образом не был получен результат, подтверждающий вывод, который автор желал получить, в котором он даже не сомневался, а именно, что Русские сажени есть часть «Русской матрицы».
              Взгляд человека на проистекающую вокруг него действительность не свободен, а жестко спрограммирован его желаниями, то есть человек видит не то, что есть на самом деле, а то, что он хочет видеть.
              «Русская матрица» есть яркий пример такого запрограммированного желанием взгляда, хотя для объективизации восприятия надо было всего лишь раздвинуть рамки «матриц» 5 и 6…

.

Самая красивая теорема математики: тождество Эйлера / Хабр

Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.

Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».

Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.

Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».

Рисунок 2.0: обложка журнала The Mathematical Intelligencer
Рисунок 3.0: опрос Дэвида Уэллса из журнала

Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой».

Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».

Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.
Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.

Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«.

Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.
Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.

Почему уравнение Эйлера так важно?

Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.

• Константа e связана со степенными функциями.
• Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
• Знаменитая константа π (пи) связана с окружностями.

Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.

e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ

Рисунок 8.0: экспоненциальная функция y=e^x.
Рисунок 8.1: график тождества Эйлера.
Рисунок 8.2: частоты, испускаемые LC-цепью.

Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.

1: число для счёта

Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.

Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.

323 = (3*100) + (2*10) + (3*1)

Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:

1001 = (2³) + (0²) + (0¹) + (2⁰) = [9 в системе с основанием 10]

Кто создал системы исчисления? Как первые люди считали предметы или животных?

Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.

Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).
Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.

В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.

Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).

Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.

Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления
Рисунок 15: таблица преобразования из арабских в римские числа

Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.

Рисунок 15: таблица букв древних греков.

В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.

Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.

Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.

Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами
Рисунок 18: ещё один способ записи чисел майя.

0: число для обозначения ничего

Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.
Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.
Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.

Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.

Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.

Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.
Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.

Пи (π): самое известное иррациональное число

Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.

π = окружность / диаметр ИЛИ π = площадь круга / радиус²

Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.

Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).

Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.
Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.

На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.

Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.

Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.
Рисунок 25: Numberwarrior

Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:

Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:

Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).

Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.

Рисунок 26: математический папирус Ахмеса.

Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.

Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2⁶²-сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.

В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно
Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.
Рисунок 29: Формула Мэчина для пи

Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!

Рисунок 30: Juliabloggers

В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.

Рисунок 31: комната пи

С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.

Рисунок 32.0: Science Friday

А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.

Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи

e: история экспоненциального роста

e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.

Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.

Рисунок 33: источник

Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2⁰ зерна на первую клетку шахматной доски, 2¹ зерна на вторую клетку доски, 2² зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2⁶³ зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!

Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.

Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.

Рисунок 34: источник: Wikipedia

Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.

Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.

В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.

Рисунок 35: закон Ньютона-Рихмана
Рисунок 36: мальтузианская катастрофа

Мнимость числа: i, квадратный корень -1

Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.

Лейбниц дал такой комментарий о мнимом числе √-1:

Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.

Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i² будет равно -1.

После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).

Рисунки 37 и 38: комплексные числа

В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.

Самое красивое уравнение: тождество Эйлера

Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений

Рисунок 39: открытие тождества Эйлера

Рисунок 40: тождество Эйлера

Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.

Что считается PHI согласно HIPAA?

Опубликовано HIPAA Journal 28 декабря, 2017

Поделиться этой статьей на:

В сфере здравоохранения вы, вероятно, услышите медицинскую информацию, называемую защищенной медицинской информацией или PHI, но что считается PHI в соответствии с HIPAA?

Что считается PHI согласно правилам HIPAA?

Согласно HIPAA PHI считается любой идентифицируемой медицинской информацией, которая используется, обслуживается, хранится или передается организацией, покрытой HIPAA — поставщиком медицинских услуг, планом медицинского страхования или страховщиком здоровья, или информационным центром здравоохранения — или деловым партнером Лицо, имеющее покрытие HIPAA, в отношении предоставления медицинских услуг или оплаты медицинских услуг.

В соответствии с правилами HIPAA PHI считается не только прошлая и текущая медицинская информация, но и будущая информация о медицинских состояниях или физическом и психическом здоровье, связанная с предоставлением ухода или его оплатой. PHI — это медицинская информация в любой форме, включая физические записи, электронные записи или устную информацию.

Таким образом, PHI включает медицинские записи, истории болезни, результаты лабораторных анализов и медицинские счета. По сути, вся медицинская информация считается PHI, если она включает индивидуальные идентификаторы.Демографическая информация также считается PHI согласно правилам HIPAA, как и многие распространенные идентификаторы, такие как имена пациентов, номера социального страхования, номера водительских прав, сведения о страховке и даты рождения, если они связаны с медицинской информацией.

18 идентификаторов, из которых состоит PHI, содержащая медицинскую информацию:

• Имена
• Даты, кроме
года
• Номера телефонов
• Географические данные
• Номера факсов
• Номера социального страхования
• Адреса электронной почты
• Номера медицинских карт
• Номера счетов
• Номера получателей плана медицинского страхования
• Номера сертификатов / лицензий
• Идентификаторы и серийные номера автомобилей, включая номерные знаки
• Интернет-адреса
• Идентификаторы и серийные номера устройств
• Адреса интернет-протокола
• Фотографии анфас и сопоставимые изображения
• Биометрические идентификаторы (т.е. сканирование сетчатки, отпечатки пальцев)
• Любой уникальный идентификационный номер или код

Один или несколько из этих идентификаторов превращают медицинскую информацию в PHI, и PHI вступают в силу ограничения Правил конфиденциальности HIPAA, которые ограничивают использование и раскрытие информации. Организации, на которые распространяется действие HIPAA, и их деловые партнеры также должны будут обеспечить выполнение соответствующих технических, физических и административных мер безопасности для обеспечения конфиденциальности, целостности и доступности PHI, как это предусмотрено в Правиле безопасности HIPAA.

Когда PHI не является PHI?

Существует распространенное заблуждение, что вся медицинская информация считается PHI согласно HIPAA, но есть некоторые исключения.

Во-первых, это зависит от того, кто записывает информацию. Хорошим примером могут служить трекеры здоровья — физические устройства, которые можно носить на теле, или приложения на мобильных телефонах. Эти устройства могут записывать медицинскую информацию, такую ​​как частота сердечных сокращений или артериальное давление, которая будет считаться PHI в соответствии с правилами HIPAA, если информация была записана поставщиком медицинских услуг или использовалась планом медицинского страхования.

Однако HIPAA применяется только к организациям, покрытым HIPAA, и их деловым партнерам, поэтому, если производитель устройства или разработчик приложения не заключил договор с организациями, покрытыми HIPAA, и является деловым партнером, записанная информация не будет считаться PHI в соответствии с HIPAA. .

То же самое относится к записям об образовании или занятости. Больница может хранить данные о своих сотрудниках, которые могут включать некоторую медицинскую информацию — например, аллергии или группу крови, — но HIPAA не распространяется на записи о занятости и об образовании.

Согласно HIPAA PHI перестает быть PHI, если она лишена всех идентификаторов, которые могут связать информацию с человеком. Если вышеупомянутые идентификаторы удалены, медицинская информация называется обезличенной PHI. Для обезличенных PHI правила HIPAA больше не применяются.

.

Произношение Фи — Золотое сечение: Фи, 1,618

Фи, Фи, Фо, Фум ™… или как сказать Φ?

Общепринятое произношение слова «фи» — фи, как и «летать».

Большинство людей знают фи как «фи», рифмуясь со словом «муха», как это произносится в «Фи-бета-каппа». Однако в бестселлере Дэна Брауна «Код да Винчи» фи произносится как фи, как гонорар.

В ответ на вопросы, полученные о правильном произношении фи, предлагается следующее:

Dictionairies либо перечисляют fi как единственное произношение для phi, либо, если указаны оба слова fi и fe, как основное произношение.См. Списки на Merriam-Webster и Dictionary.com.

Ведущие авторы по теме phi предложили следующие комментарии:

• Двое в США и Великобритании подтвердили, что предпочтительным произношением является fi.
• Один заметил, что в Великобритании «фи» всегда произносилось как рифма к «пирогу», но что некоторые американцы на конференциях произносили это «гонорар».
• Другой заметил, что на греческом языке буква PHI действительно произносится как PHEE. Однако в греческом языке буква, которую мы называем PI, также произносится как PEE.Следовательно, в зависимости от того, хотите ли вы использовать греческое или американское произношение, вы можете произносить его как PHEE или PHI. В математических кругах буква, используемая для золотого сечения, обычно TAU.

Чтобы усложнить ситуацию, когда он используется в связи с братствами и женскими обществами, его использование также варьируется, и оно произносится как PHEE, когда оно идет после гласной, как в Alpha Phi.

Мой греческий друг Тассос Спилиотопулос предлагает следующее: Буквы греческого алфавита записываются как слова, а не как отдельные буквы, например, первая буква A пишется AΛΦA и звучит как Альфа.Когда дело доходит до таких букв, как, Χ, Φ (пишущихся соответственно I, ΧI и ΦI), недоразумение возникает из-за произношения буквы «I», которая в английском языке рифмуется со словом fly, а в греческом — EE. Буква Φ всегда произносится на греческом языке как PHEE, и она не отличается, если за ней следует гласная или согласная.

Итак, вот оно. Хотя пурист-лингвист может выбрать гонорар на греческом языке, большинство математиков знают фи как фи. Любой из этих вариантов верен, но если мы хотим быть совместимыми с общепринятым использованием выражения «пи» как «пирог», мы должны произносить фи как фи.

Или, как говорится в тексте песни: «PotAto, potAHto, tomAto, tomAHto, давай прекратим все».

---

Большое спасибо доктору Марио Ливио (автору «Золотого сечения»), доктору Рону Нотту (автору «Чисел Фибоначчи и золотого сечения»), Стиву Макинтошу (автору «Золотого сечения» и президенту Now & Zen) и доктору Эдди. Левину (изобретателю шкалы золотого сечения) за их вклад и Джени Флауэрс за то, что вдохновили меня получить ответ.

.

Что такое защищенная медицинская информация (PHI)?

Аббревиатура : PHI означает P rotected H ealth I информация — не личная медицинская информация (хотя, по сути, это то, что она подразумевает), не личная информация о здоровье (я видел, что она использовалась, хотя технически это будет PIHI), и я уверен, что есть варианты этого, которые вы тоже слышали.

Определение : Вот определение из Википедии.Защищенная медицинская информация (PHI) — это любая информация о состоянии здоровья, предоставлении медицинских услуг или оплате медицинских услуг, которая может быть связана с конкретным человеком. HHS предоставляет еще более простую PHI — индивидуально идентифицируемую медицинскую информацию, передаваемую или сохраняемую в любой форме или на любом носителе Защищенной организацией или ее Деловым партнером; определение «делового партнера» было расширено правилом HIPAA Omnibus, которое вступило в силу в 2013 году. Этот термин «информация» интерпретируется довольно широко и включает любую часть медицинской карты пациента или истории платежей.Ключевым моментом здесь является фраза «что может быть связано с конкретным человеком». Здесь становится актуальным другой акроним, PII (личная информация) — вот ссылка на статью в Википедии по этому поводу. Основное различие между PHI и PII заключается в том, что PII — это юридическое определение, то есть PII — это все, что может использоваться для однозначной идентификации человека. PHI является подмножеством PII в том смысле, что медицинская карта может использоваться для идентификации человека, особенно если заболевание или состояние встречается достаточно редко.

Защита

Ядром правил HIPAA является обеспечение того, чтобы право собственности на любые и все медицинские данные принадлежало исключительно физическому лицу. Затем человек может решить предоставить доступ другим — поставщикам услуг, членам семьи, работодателям, если это необходимо или необходимо, или просто по желанию владельца записи. Только физическое лицо имеет право предоставить доступ к своим медицинским данным. В основном это было сделано по следующим причинам:

1. Конфиденциальность : Очевидно, мы предпочли бы, чтобы наш сосед (или, в некоторых случаях, члены семьи) не знали о том, от какого состояния мы можем страдать, или о принимаемых нами лекарствах.

2. Предубеждение и дискриминация : СПИД, психическое здоровье и другие состояния имеют некоторую (хотя и снижающуюся) социальную стигму, связанную с этим. Положения HIPAA PHI гарантируют, что работодатели и другие лица не имеют доступа к чьей-либо медицинской карте и используют информацию, содержащуюся в ней, для дискриминации человека на основе его медицинской информации.

Уникальность

Очевидно, что защита и конфиденциальность вступают в игру после того, как индивидуум может быть однозначно идентифицирован.В конце концов, 25,8 миллиона американцев страдают диабетом. Это приводит к вопросу о том, какие данные можно использовать для однозначной идентификации человека. Общепринятый набор индивидуально уникальных элементов данных включает следующее:

#	Идентификатор	Описание
1	Имя	Ну, конечно, то есть имя, фамилия, девичья фамилия комбинации. Можно возразить, что любой или из вышеперечисленных не могут однозначно идентифицировать человека, в конце концов, «Джеймс» — довольно распространенное имя.Но можно было бы идентифицировать человека, используя комбинацию данных, например имя, почтовый индекс, почтовый адрес и т. Д.
2	Географические указатели	Все (почтовый адрес, город, район, почтовый индекс, широта) -длинные координаты и т. д.) считается PII. Первые три цифры почтового индекса обычно считаются приемлемыми для использования, за исключением определенных почтовых индексов, предназначенных для небольшой группы населения (менее 20 000 человек). В настоящее время этому профилю подходят 17 почтовых индексов — 036, 692, 878, 059, 790, 879, 063, 821, 884, 102, 823, 890, 203, 830, 893, 556, 831.Таким образом, можно использовать трехзначные почтовые индексы, за исключением перечисленных выше.
3	Даты	Относящиеся к значительным событиям в жизни человека — рождению, смерти, браку, поступлению, выписке и т. Д. Только год обычно считается годным для использования, за исключением очень пожилых людей (> 89 лет, в этом случае они будут представлены совокупной категорией, например <90)
4	Номера телефонов	Ну, конечно.
5	Номера факсов	Это, ИМХО, пережиток старых времен. Вы знаете много людей, у которых есть личный номер факса? Но в этом есть смысл.
6	Адреса электронной почты (email)	Чек
7	Номера социального страхования	Чек
8	Номера медицинских карт	Это обычно «случайное» число и можно было бы использовать, если бы также было известно учреждение, которое его назначило.
9	Номера получателей плана медицинского обслуживания	Это ваша страховая карта / идентификатор участника.
10	Номера счетов	Номера банков и т. Д.
11	Номера свидетельств / лицензий	Водительские права, номер свидетельства о рождении и т. Д.
12	Идентификаторы и серийные номера транспортных средств, включая номерные знаки	Если это достаточно для полиции, чтобы выследить кого-то…
13	Идентификаторы и серийные номера устройств	Медицинские устройства имеют уникальные серийные номера. Идентификатор MAC вашего компьютера также уникален.
14	Универсальные веб-указатели ресурсов (URL-адреса)	Это немного неясно, но здесь описаны все возможности. http://www.facebook.com не очень уникален. Но если войти в конкретное приложение, он действительно может быть уникальным для человека.
15	Номера адресов Интернет-протокола (IP)	Ваш IP-адрес может использоваться для простой идентификации вашего адреса.Есть несколько бесплатных сервисов, которые предлагают это (выполните быстрый поиск в Google адреса с IP и попробуйте это в качестве примера
16	Биометрические идентификаторы, включая отпечатки пальцев и голоса	Не забудьте изображения сетчатки глаза.
17	Фотографические изображения лица и любые сопоставимые изображения	Проверка
18	Любой другой уникальный идентификационный номер, характеристика или код	Перекодировать — обратите внимание, что это не означает уникальный код, присвоенный системой для закодируйте данные.

Эти 18 элементов представляют собой основной набор элементов данных, которые по отдельности или в комбинации могут использоваться для уникальной идентификации человека. И, учитывая тот факт, что в приведенном выше списке идентификаторов есть номеров факсов , а не имена @usernames Twitter, идентификаторы Facebook или множество других современных, более распространенных идентификаторов, ясно, что список PII не самый современный и нужно еще подумать о распознавании и защите идентифицируемой информации.Однако, поскольку данные о пациентах важны для клинических испытаний, медицинских исследований и т. Д., Приведенный выше список используется в качестве руководства для обеспечения конфиденциальности. Это приводит к …

Анонимизация и деидентификация

Анонимизация — это процесс, с помощью которого элементы PHI удаляются или изменяются с целью минимизации / исключения возможности возврата к исходному набору данных. Это включает удаление всех идентифицирующих данных для создания несвязанных данных.

Деидентификация по HIPAA происходит, когда данные были удалены от общих идентификаторов двумя способами:

1. Удалите 18 элементов, перечисленных выше;

2. Если используется другой подход, обеспечьте статистически небольшой / незначительный риск повторной идентификации, который подтвержден экспертом по статистике (вам должна понравиться интерпретируемость этого правила).

Разработка решений, совместимых с HIPAA

Учитывая указанные выше ограничения, важно, чтобы любое разрабатываемое вами приложение учитывало эти требования к анонимности и / или деидентификации, прежде чем какие-либо данные будут переданы какому-либо внешнему объекту. Данные PHI могут быть «переданы» внешнему лицу при условии, что у вас есть BAA (соглашение о деловом сотрудничестве) и данное лицо подписало соответствующие документы о согласии. Как управлять PHI в соответствии с HIPAA — это отдельная тема.Найдите в нашем блоге сообщение, в котором вкратце описывается, как мы обеспечиваем соблюдение требований HIPAA и упрощаем соблюдение буквы и духа закона в Datica.

.

Символ Фи — Золотое сечение: Фи, 1,618

В текстах Древней Греции буква фи выглядела так:

Φ

Когда вы видите греческую букву фи на братстве или женском обществе, это обычно выглядит так:

Φ

Когда вы видите Фи на веб-сайте, он часто выглядит так:

Ø

Какой уклон на этот счет?

Фи больше не тот честный персонаж, каким был раньше? Неужели Фи превратилась в пустую оболочку самого себя? (Маленький юмор для вас, математиков.) Склоняется ли Фи вправо в своей политической ориентации? Чтобы уберечь Фи от кризиса «идентичности» (немного больше математического юмора), вот объяснение того, что происходит и что вы можете сделать, чтобы быть уверенным, что Фи останется в хорошей репутации.

Как и гольф, все в ходу

Простая правда заключается в том, что базовый западный набор символов на компьютерах не включает символ греческой буквы фи. Единственный базовый символ ASCII, который по внешнему виду приближается к Phi Φ, — это буква O с зачеркнутой чертой или Ø.В результате Ø маскировался под Φ с первых дней использования компьютеров.

Наберите на клавиатуре настоящую Φ с помощью Alt-1000

Теперь, когда расширенные наборы символов доступны на большинстве ПК и в большинстве браузеров, можно снова позволить Phi быть Phi. Все, что вам нужно сделать, это удерживать клавишу Alt и затем ввести 1000 на цифровой клавиатуре.

Если на вашем ПК не установлены необходимые для этого наборы символов, вы можете использовать программу Windows Character Map. Чтобы открыть «Карту символов», нажмите «Пуск», выберите «Все программы», «Стандартные», «Системные инструменты» и затем нажмите «Карта символов».Прокрутите вниз, чтобы найти символ phi, нажмите «Выбрать», затем скопируйте и вставьте его в свое приложение.

Обозначение Φgønes равным Φgønes

И хотя изменение всегда неизбежно вызывает споры, в конце концов, лучше позволить Φgønes быть Φgønes.

Символьный шрифт и Phi: Alt-618 дает… j, то есть phi, 0,618!

На ПК с использованием шрифта Symbol вы можете создать символ phi следующими способами:

Соответственно, фи в нижнем регистре, или 0,618, и величина, обратная Фи, 1.618, можно создать с помощью Alt-618: j

Другие символы фи могут быть созданы с помощью:

Альт-70: F

Alt-102: f

Alt-106 или Alt-618: j

Alt-232: Φ

Альт-237: φ

Примечание. Alt-618 означает, что удерживая клавишу Alt, введите 618 на цифровой клавиатуре и затем отпустите. Это понимание было внесено В. Натаном Сондерсом.

Запуск проверки символов на Phi

Письмо	Греческая буква фи		Латинская буква O со штрихом
Корпус	Верхний корпус	Нижний регистр	Верхний корпус	Нижний регистр
Карта символов Windows	Alt-03A6 (0934 десятичное в HTML)	Alt-03C6 (0966 десятичное в HTML)	Alt-0216	Alt-0248
Введите с клавиатуры с помощью	Альт-1000	Alt-1005	Alt-0216	Alt-0248
Verdana шрифт	Φ	φ	Ø	ø
Шрифт Arial	Φ	φ	Ø	ø
Times New Roman	Φ	φ	Ø	ø

На клавиатуре Windows вы можете

Эта страница посвящена Кэти (а.k.a. Принцесса Кейт), старшеклассница, которая написала, ставя под сомнение использование Ø, и вдохновила меня глубже вникнуть в причины того, что символ Φ мало использовался на веб-сайтах … до сих пор. (15.03.2003, Мартовские «Фиды», дата, составленная из чисел серии Фибоначчи 0, 1, 2, 3 и 5)

.