Что такое Числа Фибоначчи — Узнай Что Такое
Числа Фибоначчи — это последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … Следующее число можно посчитать, сложив два числа перед ним.
Т. е. 0 + 1 = 1; 1 + 1 = 2, 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; …
Более формальное определение ряда Фибоначчи можно показать следующим равенством:
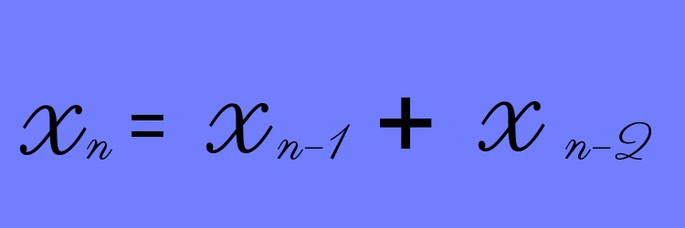
Более длинный список последовательности чисел Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811,…
Запомнить его довольно просто: нужно только помнить, что первые два числа — это 0 и 1, и начать складывать. И за этим занятием можно просидеть сутками.
«Золотое число» или «Золотое сечение»
Если разделить два последовательных числа друг на друга (например 55 разделить на 34), всегда получится приблизительно
1,618 называется «Золотое число» или «Золотое сечение«.
55 / 34 = 1,6176
89 / 55 = 1,61818
377 / 233 = 1,618
Использование золотого сечения для вычисления чисел Фибоначчи
Можно вычислить любое число Фибоначчи, используя золотое сечение следующими способами
Формулой
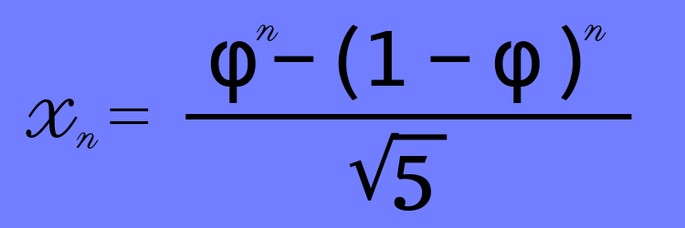
Например, можно попробовать посчитать для n = 10 (внимание, это будет одиннадцатое число в ряду!)
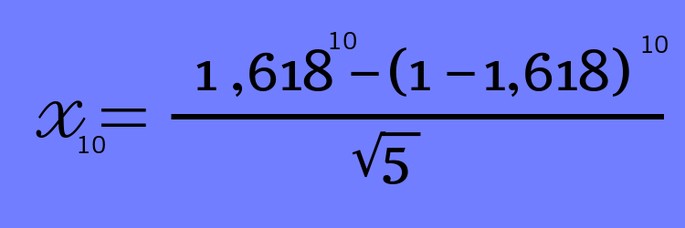
Получился такой ответ:

Умножением предыдущего числа на золотое сечение
Этот способ работает для чисел выше 1. Можно рассчитать число Фибоначчи, умножив предыдущее число на золотое сечение (1,618), а затем округлив полученный результат.
Например:
13 x 1,618 = 21,034 ≈ 21
55 x 1,618 = 88,99 ≈ 89
377 x 1,618 = 609,986 ≈ 610
Золотая спираль Фибоначчи
Это спираль, которая выглядит следующим образом:
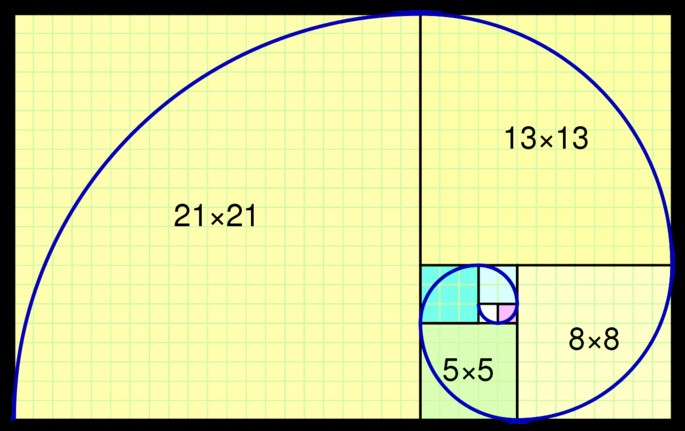 Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …Как можно видеть на изображении, тут представлен числовой ряд Фибоначчи как спираль. Она начинается в центре с двух квадратов 1×1, за ними следуют квадраты 2×2, 3×3, 5×5 и так далее.
Числа Фибоначчи в природе
 Фотография «Алоэ многолистное» (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе.
Фотография «Алоэ многолистное» (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе. 
В этом видео «ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ» ещё больше примеров чисел Фибоначчи в природе и в мире вокруг нас.
Числа Фибоначчи в архитектуре
В строениях древней архитектуры мы зачастую можем ощущать некую гармонию пропорций. И это неслучайно, ведь на протяжении многих веков архитекторы пользуются этим магическим числом золотого сечения. Число 1,618 можно заметить и в творчестве средневековья, и в современных произведениях архитектурного искусства.
 Здание SOMISA в Буэнос-Айресе, Аргентина; архитектор Марио Роберто Альварес, окончание строительства 1977 г.
Здание SOMISA в Буэнос-Айресе, Аргентина; архитектор Марио Роберто Альварес, окончание строительства 1977 г.Пример использования золотого числа в древней архитектуре:
 Пантеон в Париже
Пантеон в ПарижеЛюбопытные факты
Давайте ещё раз посмотрим на последовательность чисел Фибоначчи:
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
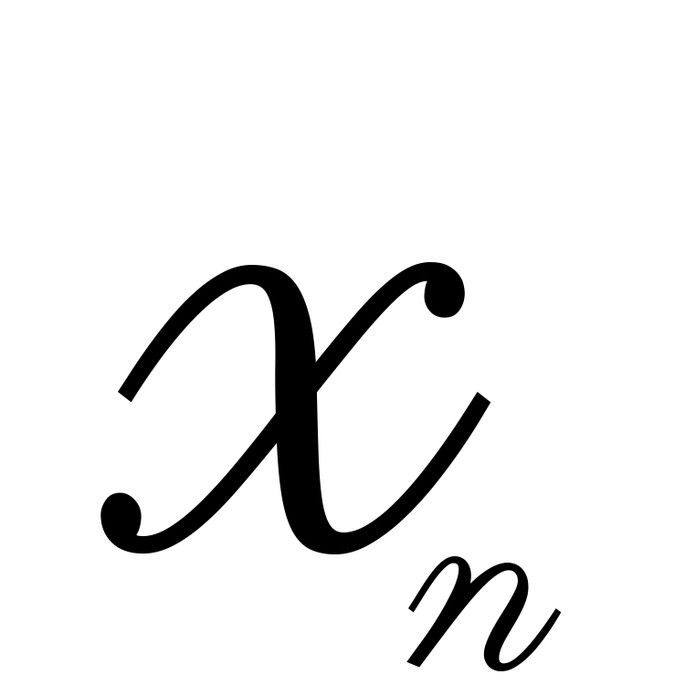 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 |
Каждое n-е число кратно 
Если внимательно посмотреть на цифры, можно рассмотреть удивительную закономерность:
- посмотрите на
 , а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!
, а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2! - посмотрите на
 , а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!
, а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3! - посмотрите на
 , а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
, а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
Первые 6 цифр Фибоначчи — 1/89
Если посчитать на калькуляторе 1 : 89 будет ответ 0,011235955… Заметили, что первые 6 цифр после запятой — ряд Фибоначчи?
День Фибоначчи 23/11
День Фибоначчи — 23 ноября (11/23; в американском формате дат месяц идёт первым, а день вторым), так как в нём присутствуют цифры «1, 1, 2, 3», которые являются частью последовательности. 23 ноября можно всех поздравлять с Днём Фибоначчи!
Смотрите также значения Числа Пи и Экспоненты.
Цифровой ряд чисел Фибоначчи. Правда и вымысел
Из статьи ты узнаешь :
Добрый день сегодня блог веб-мастера Максима расскажет о понятии ряд Фибоначчи и как оно связанно с теорией волн, а также приведет опровержение применимости ряда к природным процессам.
Волновая теория Элиота, которую мастер разработал в 30-х годах прошлого века – это один из самых захватывающих разделов технического анализа. Сама по себе она была выделена в новую главу науки, которая изучает графики. В её основе лежат разработки других специалистов в области теории (советую прочитать – книгу под авторством Денис Стукалов теория волн Эллиотта).
Так, например, великого итальянского математика Леонардо Фибоначчи причисляют к ученым (о котором я уже говорил в статьях – Фибоначчи на форекс, Индикатор уровней Фибоначчи, Веер Фибоначчи ), создавшим основу для теории Элиота.
 Цифровой ряд чисел Фибоначчи – золотое сечение и коэффициенты или уровни коррекции + видео. Числа Фибоначчи в природе.
Цифровой ряд чисел Фибоначчи – золотое сечение и коэффициенты или уровни коррекции + видео. Числа Фибоначчи в природе.Специалист жил ещё в XIII веке. Ученый опубликовал труд, который называется «Книга вычислений». Эта книга представила Европе важное для тех времен и не только открытие – десятичную систему счисления. Эта система ввела привычные для нас числа от нуля до девяти в обращение.
Появление этой системы было первым важным достижений Европы со времён падения Рима. Фибоначчи сохранил числовую науку для средневековья. А также заложил глубокие основы для развития других наук, таких как высшая математика, физика, астрономия, машиностроение.
 ряд чисел Фибоначчи
ряд чисел ФибоначчиСмотреть видео
А вот эти книги я рекомендую вам прочитать:
Как появились числа и их производные
Решая прикладную задачу, Леонардо наткнулся на любопытный ряд чисел Фибоначчи, вначале которого находятся две единицы.
Каждый последующий член – это сумма двух предыдущих. Самое любопытное, что числовой ряд Фибоначчи – примечательная последовательность тем, что если любой член поделить на предыдущий, то получится число, которое близко к 0,618. Этому числу дали имя «Золотое сечение».
Оказалось, что это число было известно человечеству очень давно. Например, в древнем Египте строили пирамиды с его использованием, а древние греки возводили по нему свои храмы. Леонардо да Винчи показал, как строение тела человека подчиняется этом числу.
Природа применяет числа из ряда Фибоначчи в своих наиболее сокровенных и продвинутых областях. От атомных структур и других мелких форм, как молекулы ДНК и микрокапилляры мозга до огромных, как планетарные орбиты и структуры галактик. Ряд примеров настолько велик, что следует утверждать, что в природе действительно присутствует некий основной закон пропорций.
Поэтому не удивительно, что ряд Фибоначчи и золотое сечение пробралось и на биржевые графики. И не одно число 0,618, но и его производные.
Если число золотого сечения возвести в первую, вторую, третью и четвертую степень и вычесть результат из единицы, то получиться новый ряд, который носит название «коэффициенты коррекции Фибоначчи». Осталось только добавить отметку пять десятых – это пятидесятипроцентная коррекция Чарльза Доу.
Однако, это не все, что можно сделать с золотым сечением. Если единицу разделить на 0,618 то получается 1,618, если возведем в квадрат, то у нас получится 2,618, если возведем в куб, то получим число 4,236. Это коэффициенты расширения Фибоначчи. Тут не хватает только числа 3,236, которое было предложено Джоном Мёрфи.


Что думают о последовательности специалисты
Кто-то скажет, что эти числа уже знакомы, потому что они используются в программах технического анализа, для определения величины коррекции и расширения. Кроме того эти же ряды играют важную роль в волновой теории Элиота. Они являются его числовой основой.
Наш эксперт Николай Проверенный портфельный менеджер инвестиционной компании Восток.
- – Николай, как вы думаете, случайно ли появление чисел Фибоначчи и его производных на графиках различных инструментов? И можно ли сказать: «Ряд Фибоначчи практическое применение» имеет место?
- – К мистике отношусь плохо. А на графиках биржи тем более. У всего есть свои причины. Джо Ди Наполи в книге «Уровни Фибоначчи» красиво рассказывал, где появляется золотое сечение, что не стал удивляться тому, что оно появилось на графиках котировок биржи. А зря! Во многих примерах, которые он привел, часто появляется число Пи. Но его почему-то нет в ценовых соотношениях.
- – То есть вы не верите в действенность волнового принципа Элиота?
- – Да нет же, не в этом дело. Волновой принцип – это одно. Численное соотношение – это другое. А причины их появления на ценовых графиках – третье
- – Каковы на ваш взгляд причины появления золотого сечения на биржевых графиках?
- – Правильный ответ на этот вопрос может быть в силах заслужить Нобелевскую премию по экономике. Пока мы можем догадываться об истинных причинах. Они явно не в гармонии природы. Моделей биржевого ценообразования много. Они не объясняют обозначенный феномен. Но не понимание природы явления не должно отрицать явление как таковое.
- – А если когда – либо этот закон будет открыт, то сможет ли это разрушить биржевой процесс?
- – Как показывает та же теория волн закон изменения биржевых цен – это чистая психология. Мне кажется, знание данного закона ничего не изменит и не сможет разрушить биржу.
Материал предоставлен блогом веб-мастера Максима.


Совпадения основ принципов математики в самых разных теориях кажется невероятным. Может быть это фантастика или подгонка под конечный результат. Поживем – увидим. Многое из того, что раньше считалось необычным или было не возможно: освоение космоса, например, стало привычным и никого не удивляет. Также и волновая теория, может быть непонятная, со временем станет доступней и понятней. То, что раньше было не нужным, в руках аналитика с опытом станет мощным инструментом прогнозирования дальнейшего поведения рынка форекс.
Числа Фибоначчи в природе.
Смотреть
А теперь, давайте поговорим о том, как можно опровергнуть то, что цифровой ряд Фибоначчи причастен к каким-либо закономерностям в природе.
Возьмем любые другие два числа и выстроим последовательность с той же логикой, что и числа Фибоначчи. То есть, следующий член последовательности равен сумме двух предыдущих. Для примера возьмем два числа: 6 и 51. Теперь выстроим последовательность, которую завершим двумя числами 1860 и 3009. Заметим, что при делении этих чисел, мы получаем число близкое золотому сечению.
При этом числа, которые получались при делении других пар уменьшались от первых к последним, что позволяет утверждать, что если этот ряд продолжать бесконечно, то мы получим число равное золотому сечению.
Таким образом, числа Фибоначчи ни чем сами по себе не выделяются. Существует другие последовательности чисел, которых бесконечное множество, что дают в результате тех же операций золотое число фи.


Фибоначчи не был эзотериком. Он не хотел вложить никой мистики в числа, он просто решал обыкновенную задачу о кроликах. И написал последовательность чисел, которые вытекали из его задачи, в первый, второй и другие месяца, сколько будет кроликов после размножения. В течение года он получил ту самую последовательность. И не делал отношений. Никакой золотой пропорции, Божественном отношении речи не шло. Все это было придумано после него в эпоху Возрождения.
Перед математикой достоинства Фибоначчи огромны. Он от арабов перенял систему чисел и доказал её справедливость. Была тяжелая и долгая борьба. От римской системы счисления: тяжелой и неудобной для счета. Она исчезла после французской революции. Никакого отношения именно к золотому сечению Фибоначчи не имеет.
И несколько слов о золотой спирали Фибоначчи (перейдите по ссылке, там более подробно). Она не является полноценным математическим объектом.
Спиралей бесконечно много, наиболее популярны: спираль натурального логарифма, спираль Архимеда, гиперболическая спираль.
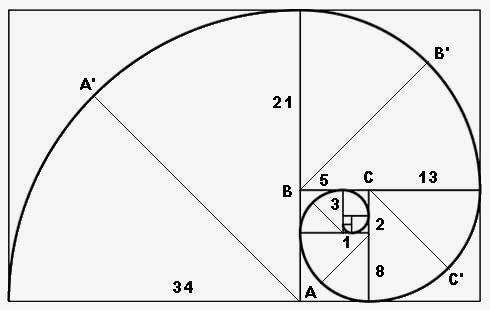

А теперь давайте взглянем на спираль Фибоначчи. Данный кусочно-составной агрегат складывается из нескольких четвертей окружностей. И не является спиралью, как таковой.
Вывод
Как бы долго мы не искали подтверждение или опровержение применимости ряда Фибоначчи на бирже, такая практика существует.
Огромные массы людей действуют согласно линейке Фибоначчи, которая находится во многих пользовательских терминалах. Поэтому хотим мы или нет: числа Фибоначчи оказывают влияние на движение цены, а мы можем воспользоваться этим влиянием.
В обязательном порядке читаем статью – линии фибоначчи как строить.
ПредыдущаяФорекс для начинающихЧто такое просадка на Форекс — друг или враг?
СледующаяФорекс для начинающихАдаптивная система принятия решений на рынке Форекс
Похожие статьи Епсель-моксель! Рекомендую
Фибоначчи — Финансовый словарь смарт-лаб.
Николас Фибоначчи — родился в Италии в 1175 году.В 1202 году он издал книгу Liber Abaci (Книга о счётах). Книга была посвещена истории появления арабских цифр в Европе. В ней Фибоначчи описал ряд своих открытий мистических числовых моделей, имеющих выражение в природе, сооружениях, Вселенной.
Числа Фибоначчи
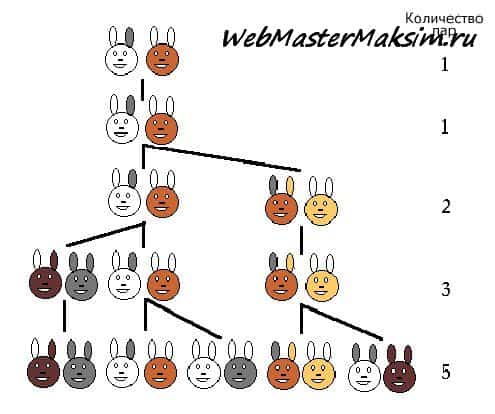
Ф. обнаружил интересный ценовой ряд, пытаясь решить задачу размножения кроликов. Задача была такой:
Есть пара кроликов. Сколько пар кроликов родится в течение года, если ежемесячно каждая пара кроликов производит другую пару кроликов.
Ответ: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
Числа Фибоначчи обладают рядом интересных характеристик:
- сумма двух последовательных чисел представляет собой следующее число в последовательности, то есть: M(N)+M(N-1)=M(N+1)
- после первых 4 чисел, отношение каждого числа последовательности к предыдущему равно 1,618, ко второму слева = 2,618, то есть: M(N)/M(N-1)=1,618; M(N)/M(N-2)=2,618
- Отношение каждого числа к последующему примерно равно 0,618, чем дальше пара чисел стоит в ряду, тем ближе соотношение к 0,618.
- Каждое число делится на второе число слева с остатком, в точности совпадающим с числом, стоящим на позиции перед числом-делителем.
- разница между квадратом числа последовательности и квадратом числа, которое стоит на 2 позиции дальше, всегда является числом Фибоначчи.
- сумма квадратов любых стоящих рядом чисел (после 1) будет равняться числу. стоящему через две позиции после большего из этой пары.
число 0,618 из п.3 — волшебное. Его называют золотым сечением.
Отношение 0,618 к 1 представляет собой решение математического уравнения, которое описывает совершенство.
Где встречается золотое сечение?
- заложено в расчет формы здания Парфенона
- определяет расположение семечек в подсолнухе
- определяет соотношение толщины витков спирали на панцире улитки
- определеяет соотношение больших спиралей космических галактик
- лежит в основе форм, которые наиболее приятно воспринимаются человеческим глазом.
- великая пирамида в Гизе спроектирована с учетом соотношения: Отношение высоты к основанию равно 0,618. высота пирамиды равна корню из увеличенной в 161,8 раза половины ее основания. Высота пирамиды = 5813 дюймов. (5,8,13-числа Фибоначчи).
- Леонрадо Да Винчи использовал золотой прямоугольник 1,618 к 1 для многих своих картин (описано в бестселлере «Код Да Винчи»)
Золотое сечение и числа последовательности Фибоначчи.
Некоторое время назад я обещала прокомментировать утверждение Толкачева о том, что Питер построен по принципу Золотого Сечения, а Москва – по принципу симметрии, и что именно поэтому столь ощутимы различия в восприятии этих двух городов, и именно поэтому петербуржец, приезжая в Москву «заболевает головой», а москвич «заболевает головой», приезжая в Питер. Требуется некоторое время для сонастройки с городом (как при перелете в штаты – требуется сонастройка со временем).Дело в том, что наш глаз смотрит — ощупывая пространство с помощью определенных движений глаз – саккад (в переводе – хлопок паруса). Глаз совершает «хлопок» и посылает сигнал в мозг «сцепление с поверхностью произошло. Все в порядке. Информация такая-то». И в течение жизни глаз привыкает к определенной ритмике этих саккад. И когда эта ритмика кардинально меняется (с городского пейзажа на лес, с Золотого Сечения на симметрию) – тут то и требуется некоторая работа мозга по перенастройке.
Теперь подробности:
Определение ЗС — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
То есть, если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382. Таким образом, если взять строение, например, храм, построенный по принципу ЗС, то при его высоте скажем 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6, 18 см. (понятно, что цифры я взяла ровными для наглядности)
Далее можно рассчитать высоту двери, окон, креста. И везде будет просматриваться принцип ЗС.
А какова связь между ЗС и числами Фибоначчи?
Числа последовательности Фибоначчи это:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Закономерность чисел в том, что каждое последующее число равно сумме двух предыдущих чисел.
0 + 1 = 1;
1 + 1 = 2;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21 и т.д.,
а отношение смежных чисел приближается к отношению ЗС.
Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.
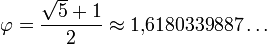
То есть в основе ЗС лежат числа последовательности Фибоначчи.
Вот этот ролик ещё раз наглядно демонстрирует эту связь ЗС и чисел Фибоначчи
Где ещё встречаются принцип ЗС и числа последовательности Фибоначчи?
• Листья у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.
• Яйцо птицы
• Длины фаланг пальцев человека относятся примерно как числа Фибоначчи. Золотое сечение просматривается в пропорциях лица.
• Эмиль Розенов исследовал ЗС в музыке эпохи Барокко и классицизма на примере произведений Баха, Моцарта, Бетховена.
• Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам ЗС. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.
• Многие элементы декора, а так же шрифты, созданы с использованием ЗС. Например шрифт А.Дюрера (в рисунке буква «А»)
• Считается, что термин «Золотое сечение» ввел Леонардо Да Винчи, который говорил, «пусть никто, не будучи математиком, не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Знаменитый портрет Моны Лизы или Джоконды (1503) создан по принципу золотых треугольников.
Собственно говоря сама звезда или пентакль представляет собой построение ЗС.
Ряд чисел Фибоначчи наглядно моделируется (материализуется) в форме спирали
А в природе спираль ЗС выглядит вот так:
При этом, спираль наблюдается повсеместно (в природе и не только):
— Семена в большинстве растений расположены по спирали
— Паук плетет паутину по спирали
— Спиралью закручивается ураган
— Испуганное стадо северных оленей разбегается по спирали.
— Молекула ДНK закручена двойной спиралью. Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.
— Эмбрион развивается в форме спирали
— Спираль «улитки во внутреннем ухе»
— Вода уходит в слив по спирали
— Спиральная динамика показывает развитие личности человека и его ценностей по спирали.
— Ну и конечно, сама Галактика имеет форму спирали
Таким образом можно утверждать, что сама природа построена по принципу Золотого Сечения, оттого эта пропорция гармоничнее воспринимается человеческим глазом. Она не требует «исправления» или дополнения получаемой картинки мира.
Теперь о Золотом сечении в архитектуре
• Пирамида Хеопса представляет собой пропорции ЗС. (Фотография нравится – с заваленным песком Сфинксом).
• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции.
Собор «Нотредам де Пари» в Париже, Франция.
Одно из выдающихся строений, выполненных по принципу ЗС – Смольный Собор в Питере. К собору ведут по краям две дорожки и если приближаться по ним к собору, то тот будто приподнимается в воздухе.
В Москве также есть строения выполненные с использованием ЗС. Например, Храм Василия Блаженного
Однако застройка, использующая принципы симметрии преобладает.
Например, Кремль и Спасская башня.
Высота стен Кремля также нигде не отражает принципа ЗС относительно высоты башен, например. Или взять гостиницу Россия, или гостиницу Космос.
При этом здания, построенные по принципу ЗС представляют больший процент в Питере, при этом это здания уличной застройки. Литейный проспект.
Таким образом, Золотое Сечение использует коэффицент 1,68, а симметрия 50/50.
То есть симметричные здания построены по принципу равенства сторон.
Ещё одной важной характеристикой ЗС является её динамичность и стремление к разворачиванию, за счет последовательности чисел Фибоначчи. Тогда как симметрия – наоборот представляет собой стабильность, устойчивость и неподвижность.
Кроме этого, дополнительное ЗС вносит в план Питера обилие водных пространств, расплескавшихся по городу и диктующих подчиненность города их изгибам. Да и сама схема Питера напоминает спираль или зародыш одновременно.
***
Папа, правда, высказал другую версию, отчего у москвичей и питерцев «голова болит» при посещении столиц. Папа относит это к энергиям городов:
Санкт-Петербург – имеет мужской род и соответственно мужские энергии,
Ну а Москва – соответственно – женского рода и обладает женскими энергиями.
Так жителям столиц, настроившимся на свой определенный баланс женского и мужского в своих организмах – сложно перестраиваться при посещении города-соседа, а у кого-то может и сложности какие-то имеются с восприятием одной или другой энергий и оттого город сосед могут и вовсе не любить!
В подтверждение этой версии говорит и то, что все российские императрицы правили именно в Питере, тогда как Москва видела лишь царей мужского пола!
Использованные ресурсы:
Последовательность Фибоначчи, проиллюстрированная природой.
Золотое сечение в живописи и архитектуре.
Золотое сечение и симметрия
Геометрия в архитектуре древнерусского творчества
Число Фибоначчи: Золотое сечение бога | Математика
Философы Древней Греции часто спорили: что занимает главенствующую позицию в мире — истина или красота. Возможно, истина заключает в себе красоту, а возможно, красота — истину. Масла в огонь подлил Пифагор Самосский, категорически заявивший, что миром правят числа. Правят в том смысле, что заключают в себе и красоту, то есть гармонию, и истину.
Деревце на террасе
У Пифагора, жившего в VI веке до н.э., было множество последователей. Его считают родоначальником всей западной нумерологии. Нумерология же, как известно, описывает влияние на жизнь человека, его прошлое и будущее тех чисел, под которыми он родился.
Но этим роль чисел в мире далеко не исчерпывается. Истина или красота, красота или истина — все в какой-то степени подчиняется числам… или по крайней мере может быть описано ими.
Такой вывод сделал другой великий математик прошлого, Леонард Пизанский. Леонард Пизанский, живший в XIII веке н.э. (то есть на 18 столетий позднее Пифагора), больше известен нам по своему прозвищу — Фибоначчи. Ну и, разумеется, как первооткрыватель знаменитой «последовательности Фибоначчи», которая, как мы увидим, действительно находит своё отражение во всех уровнях живой и неживой природы — от структуры ДНК до формы спиральных галактик.
Однако же обо всём по порядку.
По легенде, Фибоначчи открыл свою последовательность, наблюдая за ростом деревца в горшке у себя на террасе. На дереве сначала не было листьев; затем появился один листок, затем ещё один, затем два, потом их стало три, пять, восемь… Если записать количество листьев, появившихся со временем на дереве, то получится следующая последовательность: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… и так далее.
Количество листьев на молодом деревце ограничено; а вот последовательность Фибоначчи — нет. Как легко заметить, каждое последующее число в ней равно сумме двух предыдущих: 2+3 = 5, 3+5 = 8, 5+8 = 13…
Фибоначчи и «золотое сечение»
Но Фибоначчи не был бы великим математиком, если бы ограничился просто вычислением все новых чисел своей последовательности. Он заметил, что с возрастанием чисел отношение последующего к предыдущему все более и более приближается к значению 1,618.
В самом деле, округляя до тысячных значений после запятой, получаем:
34:21 = 1,619, 55:34 = 1,618, 89:34 = 1,618, 144 89 = 1,618…
Что же это за число такое — 1,618? Имеет ли оно какое-то особое значение, встречается ли где-нибудь ещё, кроме последовательности Фибоначчи?
Как выяснилось, имеет, и весьма важное. Настолько важное, что даже получило собственное название — число Фи, или число Фибоначчи.
Справедливости ради надо сказать, что само число Фи (то есть его значение) было известно задолго до Фибоначчи и даже задолго до Пифагора. Его использовали архитекторы древних усыпальниц, храмов и дворцов. Намётанный глаз архитектора оценивал постройку в первую очередь по гармонии всех её составляющих. А гармония заключалась в том, чтобы пространства, площади и отрезки разбивать не точно посредине, а по следующему правилу: отношение большей части отрезка к меньшей должно быть равно отношению целого к большей части. И это отношение составляло именно число Фи, которое со временем получило ещё несколько названий — «золотое сечение», «точка мирового равновесия» и даже «божественная пропорция».
От египетских пирамид до Джоконды
Один из самых древних известных нам египетских памятников, гробница Хесира в Саккаре (XXVIII век до н.э.), по сей день считается «академией архитектурного канона». Все внешние и внутренние размеры гробницы выполнены с практически идеальным соответствием «золотому сечению».
«Учебником» древних архитекторов могли служить и знаменитые пирамиды Гизы (XXVI-XXIII вв, до н.э.), и более поздние египетские постройки, такие как храм фараона Сети I в Абидосе (XIII век до н.э.). В храме Сети I канону «золотого сечения» были подчинены как само здание, так и обширная прихрамовая территория со всеми пилонами, статуями и пальмовыми аллеями (не сохранившимися, к сожалению, до наших дней).
Главный строитель афинского Парфенона Фидий (500-430 гг. до н.э.) использовал «золотое сечение» не только в зданиях, но и в своих скульптурах. Он открыл для потомков совершенную красоту гармонично развитого человеческого тела, пропорции которого соответствовали как числу Фи, так и общей последовательности Фибоначчи. Две с половиной тысячи лет спустя в Германии был проведён грандиозный опыт, доказавший, что телу человека с нормальным развитием действительно свойственны пропорции Фибоначчи, — но об этом несколько ниже.
Истинным фанатиком, если можно так выразиться, «золотого сечения» и геометрических фигур на его основе был величайший гений всех времён и народов — Леонардо да Винчи. В его живописи гармония Фибоначчи присутствует повсюду, в самих фигурах, их расположении на полотне, соотношениях фигур и фоИа.
Исследователи самого известного портрета кисти Леонардо да Винчи — Моны Лизы (Джоконды) не устают восторгаться композицией картины, основанной на «золотых треугольниках», которые в свою очередь являются частями правильного звездчатого пятиугольника. Лицо и фигура Моны Лизы также идеальным образом вписываются в «золотые прямоугольники».
Число Фи в природе…
Чтобы увидеть число Фибоначчи в живой и неживой природе, нужно обратить внимание на такую популярную структуру, как спираль. Спиралью закручиваются витки раковины, ростки папоротника, атмосферные циклоны и даже галактики. Семечки подсолнуха в его головке выложены по спирали, спиралью закручены листья початка кукурузы; и если вы понаблюдаете за тем, как вода из ванны уходит в сливное отверстие, вы также увидите спираль.
Эти примеры природных спиралей объединяет одно — число Фи. Если измерить витки раковин, то мы увидим, что отношение диаметра каждого последующего витка к диаметру предыдущего будет равно (или очень близко) 1, 618.
Самое интересное заключается в том, что «божественной пропорции» подчиняется и первооснова жизни — ДНК. Молекула ДНК состоит из двух вертикально переплетённых между собой спиралей. Длина каждой из этих спиралей в развёрнутом виде составляет 34 ангстрема (1 ангстрем равен одной десятимиллиардной доле метра), а ширина — 21 ангстрем.
Вам эти числа — 21 и 34 — ничего не напоминают? Правильно, это соседние члены последовательности Фибоначчи. И если вы разделите длину на ширину, то получите… 1,619. Практически число Фи.
…и в теле человека
А ещё можно внимательно посмотреть на себя в зеркало. Пропорции вашего лица и фигуры, если вы взрослый человек нормального телосложения, ещё раз продемонстрируют вам «вездесущность» чисел Фибоначчи.
В 1855 году немецкий исследователь Адольф Цейзинг измерил пропорции более 2000 человеческих тел, а также множества античных статуй. Он сделал однозначный вывод: «золотое сечение» проявляет себя как единая формообразующая закономерность. В пропорционально развитом теле человека ему подчинены практически все части, но главный «золотой» показатель — это деление тела по высоте в точке пупка. Если у мраморных и бронзовых богов это отношение в точности равно 1,618, то у обычных людей, измеренных Цейзингом, оно составило в среднем 1,625 — результат, по мнению учёных, достаточно близкий.
Последние исследования ритмов головного мозга человека показывают, что и здесь, возможно, присутствует число Фи. Частота электрических колебаний, оказывается, зависит от того, чем занят в данный момент человек — спит, бодрствует, развлекается, предаётся пассивному созерцанию или решает сложные задачи. Измерение частоты колебаний для каждого состояния показывает, что границы диапазонов альфа-, бета-, гамма- и других ритмов, возможно, соотносятся как число Фи.
Число Фибоначчи проявляется и как следующий скрытый психологический механизм. Прогуливаясь по парку и видя пустую скамью, мы чаще всего садимся не ровно посередине, а несколько вправо или влево. То же самое происходит в пустом кинотеатре или на выставке — мы подсознательно выбираем для себя не центральную, а «сдвинутую» позицию. Угадайте: каково при этом отношение большей части нашего пространственного расположения к меньшей?…
Ограниченный объём журнальной статьи позволяет привести лишь несколько из необозримого моря доказательств «всеобщности и универсальности» числа Фибоначчи. Неудивительно, что находятся люди, считающие это число одним из доказательств бытия Божия и прямо так его и называющие — «число Бога». Или просто — «Само совершенство».
Журнал: Тайны 20-го века №31, июль 2020 года
Рубрика: Нумерология
Автор: Ольга Строгова
Метки: Древний Египет, число, Тайны 20 века, Древняя Греция, живопись, природа, математика, архитектура, музыка, ДНК, Пифагор, Саккара, последовательность, Фибоначчи, пропорция, золотое сечение, сечение
Золотое сечение и числа Фибоначчи
Золотое сечение и числа Фибоначчи

Золотое сечение
 ) — это иррациональное число с несколькими любопытными свойствами. Его можно определить как число, равное его собственному обратному значению плюс один:
) — это иррациональное число с несколькими любопытными свойствами. Его можно определить как число, равное его собственному обратному значению плюс один:  = 1/
= 1/ + 1 . Умножая обе части этого же уравнения на золотое сечение, мы получаем интересное свойство, что квадрат золотого сечения равен самому простому числу плюс один:
+ 1 . Умножая обе части этого же уравнения на золотое сечение, мы получаем интересное свойство, что квадрат золотого сечения равен самому простому числу плюс один:  2 =
2 =  + 1 .Поскольку это уравнение может быть записано как
+ 1 .Поскольку это уравнение может быть записано как  2 —
2 —  — 1 = 0 , мы можем вывести значение золотого сечения из квадратного уравнения
— 1 = 0 , мы можем вывести значение золотого сечения из квадратного уравнения  , где a = 1 , b = -1 , и c = -1 :
, где a = 1 , b = -1 , и c = -1 :  . Золотое сечение — это иррациональное число, но не трансцендентное (например,
. Золотое сечение — это иррациональное число, но не трансцендентное (например,  ), поскольку оно является решением полиномиального уравнения.
), поскольку оно является решением полиномиального уравнения. Это дает нам либо 1,618 033 989 , либо -0,618 033 989 .Первое число обычно рассматривается как само золотое сечение, второе — как отрицательное значение его обратной величины — или мы можем использовать второе само по себе, как число « », которое будет использоваться ниже. Золотое сечение также может быть получено из тригонометических функций:
», которое будет использоваться ниже. Золотое сечение также может быть получено из тригонометических функций:  = 2 sin 3
= 2 sin 3  /10 = 2 cos
/10 = 2 cos 
 = 2 sin
= 2 sin  /10 = 2 cos 2
/10 = 2 cos 2  /5 . Углы в тригонометрических уравнениях в градусах, а не в радианах, равны 54 o , 36 o , 18 o и 72 o соответственно.
/5 . Углы в тригонометрических уравнениях в градусах, а не в радианах, равны 54 o , 36 o , 18 o и 72 o соответственно.Золотое сечение, кажется, получило свое название от Golden Rectangle , прямоугольника, стороны которого пропорциональны золотому сечению. Теория Золотого Прямоугольника — эстетическая, что соотношение является эстетически приятным и поэтому может быть обнаружено спонтанно или намеренно в большом количестве произведений искусства. Так, например, фасад Парфенона удобно оформить золотым прямоугольником.
Насколько приятен золотой прямоугольник, как часто он действительно появляется в искусстве и действительно ли он обрамляет фасад Парфенона, может быть во многом вопросом интерпретации и предпочтений.Однако построение золотого прямоугольника — интересное упражнение в геометрии золотого сечения,  , как показано справа. Начиная с единичного квадрата, сначала квадрат делится пополам, затем в полуквадрате проводится диагональ. Длину диагонали можно рассчитать с помощью теоремы Пифагора, основанной на треугольнике, который составляет ,5 с одной стороны и 1 с другой. Таким образом, диагональ равна
, как показано справа. Начиная с единичного квадрата, сначала квадрат делится пополам, затем в полуквадрате проводится диагональ. Длину диагонали можно рассчитать с помощью теоремы Пифагора, основанной на треугольнике, который составляет ,5 с одной стороны и 1 с другой. Таким образом, диагональ равна  (1 + 0,5 2 ) =
(1 + 0,5 2 ) =  (1,25) = 1,118033989 .Если мы просто прибавим ,5 , то получим золотое сечение 1,6l8033989 . Таким образом, если мы продолжим сторону единичного квадрата и нарисуем круг с радиусом диагонали и его центром в средней точке на единичной стороне, круг будет пересекать сторону в точке, которая будет на 1,6 л8033989 единиц от угла. площади. По сути, это дает нам уравнение для золотого сечения:
(1,25) = 1,118033989 .Если мы просто прибавим ,5 , то получим золотое сечение 1,6l8033989 . Таким образом, если мы продолжим сторону единичного квадрата и нарисуем круг с радиусом диагонали и его центром в средней точке на единичной стороне, круг будет пересекать сторону в точке, которая будет на 1,6 л8033989 единиц от угла. площади. По сути, это дает нам уравнение для золотого сечения:  = 0,5 +
= 0,5 +  1,25 . Однако мы можем легко превратить это в предыдущее уравнение, просто умножив числа, чтобы получить целые числа:
1,25 . Однако мы можем легко превратить это в предыдущее уравнение, просто умножив числа, чтобы получить целые числа:  = 1/2 + 2
= 1/2 + 2  1.25/2 = (1 + 2
1.25/2 = (1 + 2  1,25) / 2 = (1 +
1,25) / 2 = (1 +  (4 * 1,25)) / 2 = (1 +
(4 * 1,25)) / 2 = (1 +  5) / 2 .
5) / 2 .
Независимо от того, имеют ли золотое сечение или золотой прямоугольник эстетическое значение, соотношение действительно имеет важное значение в задачах естественной симметрии.  Например, поверхность может быть полностью и симметрично облицована треугольниками, квадратами и шестиугольниками, но не пятиугольниками. Периодическая пятикратная симметрия в природе не встречается. Однако в начале 70-х годов Роджер Пенроуз обнаружил, что поверхность может быть полностью облицована асимметричным и непериодическим способом всего двумя формами, называемыми «воздушными змеями» и «дротиками» — «плиткой Пенроуза» — как показано на право.Однако внутри этой мозаики могут быть небольшие области пятикратной симметрии. Может возникнуть несколько декагонов, некоторые из которых на расстоянии могут выглядеть как пятиугольники.
Например, поверхность может быть полностью и симметрично облицована треугольниками, квадратами и шестиугольниками, но не пятиугольниками. Периодическая пятикратная симметрия в природе не встречается. Однако в начале 70-х годов Роджер Пенроуз обнаружил, что поверхность может быть полностью облицована асимметричным и непериодическим способом всего двумя формами, называемыми «воздушными змеями» и «дротиками» — «плиткой Пенроуза» — как показано на право.Однако внутри этой мозаики могут быть небольшие области пятикратной симметрии. Может возникнуть несколько декагонов, некоторые из которых на расстоянии могут выглядеть как пятиугольники.
Так уж вышло, что, учитывая достаточно большую площадь, соотношение воздушных змеев и дротиков составляет всего , золотое сечение . Почему это могло произойти? Итак, полный круговой угол (360 o ), разделенный на пять, равен 72 o , что произошло выше как один из углов, тригонометрическая функция которого — золотое сечение.Что еще более очевидно, сама иррациональность золотого сечения является результатом квадратного корня из пяти:  . Если золотое сечение встречается в примерах пятикратной симметрии, это вполне может быть связано с тем, что само число фундаментально связано с числом пять.
. Если золотое сечение встречается в примерах пятикратной симметрии, это вполне может быть связано с тем, что само число фундаментально связано с числом пять.
Теперь числа Фибоначчи встречаются в природе.Спирали, видимые в головке ромашки, состоят из отдельных «цветочков», которые считаются числами Фибоначчи. Это важно, потому что соотношение между любыми двумя последовательными числами Фибоначчи приближается к пределу по мере увеличения числа, и этот предел составляет золотого сечения . Таким образом, 6765/4181 (20-й и 19-й уровни Фибоначчи) равно 1,618033963, что отличается от золотого сечения только на 0,000000025 .
Таблица справа иллюстрирует интересный способ естественного возникновения чисел Фибоначчи по отношению к золотому сечению.Это основано на уже отмеченном выше свойстве золотого сечения:  2 =
2 =  + 1 . Точно так же любую степень золотого сечения можно разбить на сумму меньших степеней, например
+ 1 . Точно так же любую степень золотого сечения можно разбить на сумму меньших степеней, например  5 =
5 =  4 +
4 +  3 . Из-за этого любая степень золотого сечения может быть в конечном итоге уменьшена до суммы , целого числа и целочисленного числа , кратного золотого сечения.Пример прохождения всего этого процесса для большой державы приведен в сноске. Любопытно, что все эти числа оказываются числами Фибоначчи . Таким образом,
3 . Из-за этого любая степень золотого сечения может быть в конечном итоге уменьшена до суммы , целого числа и целочисленного числа , кратного золотого сечения.Пример прохождения всего этого процесса для большой державы приведен в сноске. Любопытно, что все эти числа оказываются числами Фибоначчи . Таким образом,  7 равно 13
7 равно 13  + 8 . Это можно обобщить так, чтобы для каждой степени
+ 8 . Это можно обобщить так, чтобы для каждой степени  :
:
 n = f n
n = f n  + f n-1 .
+ f n-1 .
Поскольку, как мы видели выше, есть два решения квадратного уравнения для  , также верно, что
, также верно, что  n = f n
n = f n  + f n-1 .Если вычесть одно уравнение из другого, мы получим интересный результат:
+ f n-1 .Если вычесть одно уравнение из другого, мы получим интересный результат:
 n = f n
n = f n  + f n-1
+ f n-1
— ( n = f n
n = f n  + f n-1 )
+ f n-1 )
_______________
 n —
n —  n = f n (
n = f n ( —
—  ) ,
) ,
или f n = ( n —
n —  n ) / (
n ) / ( —
—  ) .Если вернуться к квадратному уравнению,
) .Если вернуться к квадратному уравнению,
 —
—  = (1 +
= (1 +  5) / 2 — (1 —
5) / 2 — (1 —  5) / 2 =
5) / 2 =  5 . Таким образом, мы получаем общее уравнение для чисел Фибоначчи: f n = (
5 . Таким образом, мы получаем общее уравнение для чисел Фибоначчи: f n = ( n —
n —  n ) /
n ) /  5 . При использовании этого уравнения необходимо учитывать, что
5 . При использовании этого уравнения необходимо учитывать, что  на самом деле является отрицательным числом и поэтому становится отрицательным или положительным в зависимости от степени, в которую оно возведено. Это формула « Бине », названная в честь математика Жака Бине.
на самом деле является отрицательным числом и поэтому становится отрицательным или положительным в зависимости от степени, в которую оно возведено. Это формула « Бине », названная в честь математика Жака Бине.
Хотя мы видим, что ряд Фибоначчи естественно возникает при оценке степеней золотого сечения, это не обязательно проясняет, почему отношение членов ряда Фибоначчи должно приближаться к золотому сечению как пределу. Как это случается, связь может быть проиллюстрирована с помощью техники непрерывных дробей , которая представляет собой устройство для сокращения неповторяющихся десятичных дробей до дробей, то есть до отношений целых чисел. Техника сокращения повторяющихся десятичных знаков до дробей обсуждалась в другом месте.При неповторяющихся десятичных дробях целая часть числа последовательно удаляется, а из оставшейся десятичной дроби берется обратная величина , образуя новое целое число, которое затем удаляется, и процесс повторяется. Это может продолжаться до тех пор, пока не будет достигнута желаемая точность или мощность калькулятора не будет превышена — поскольку я предполагаю, что большинство людей сегодня будет использовать калькулятор для получения обратных величин (в противном случае это не очень удобная процедура). Как только получено достаточное количество целых чисел, соответствующая дробь со всеми вложенными дробями может быть решена для простой целочисленной дроби.
 Например, справа представлена непрерывная дробь для отношения между продолжительностью лунного (синодического) месяца (29,530588 дней) и продолжительностью солнечного (тропического) года (365,24219878 дней). Это говорит нам о количестве лунных месяцев в солнечном году; а в целочисленной форме дробная часть сообщила бы нам, сколько дополнительных лунных месяцев (более 12 в год) нужно добавить в определенный период солнечных лет, чтобы приблизиться к истинному соотношению. Истинное соотношение — 12.368267058. Удаление 12, а затем последовательное взятие обратного и удаление целой части снова дает нам целые числа после 12, 2, 1, 2, 1, 1 и 17 (как минимум). Последовательные приближения могут быть сделаны, останавливаясь на каждом новом целом числе. Таким образом, имея только 2 , мы будем иметь приближение 12 + 1/2 . Остановившись со следующим 1 , 1 добавляется к 2 , и следующее приближение составляет 12 + 1/3 . Добавление следующего числа, 2 , дает долю 3/8 , что исторически очень важно, потому что популярное древнее устройство для приближения лунного календаря к солнечному году должно было добавлять 3 дополнительных месяца каждые 8 лет. .Однако более важным было дробление на два шага дальше. Добавление 7 лунных месяцев каждые 19 лет было приемом, принятым в Вавилонском календаре. Это правило было унаследовано и используется даже сегодня по еврейскому календарю и христианскому исчислению Пасхи. Следующая дробь в серии, 123/334 , слишком велика, чтобы ее можно было использовать в календарных целях. (Непрерывная дробь для
Например, справа представлена непрерывная дробь для отношения между продолжительностью лунного (синодического) месяца (29,530588 дней) и продолжительностью солнечного (тропического) года (365,24219878 дней). Это говорит нам о количестве лунных месяцев в солнечном году; а в целочисленной форме дробная часть сообщила бы нам, сколько дополнительных лунных месяцев (более 12 в год) нужно добавить в определенный период солнечных лет, чтобы приблизиться к истинному соотношению. Истинное соотношение — 12.368267058. Удаление 12, а затем последовательное взятие обратного и удаление целой части снова дает нам целые числа после 12, 2, 1, 2, 1, 1 и 17 (как минимум). Последовательные приближения могут быть сделаны, останавливаясь на каждом новом целом числе. Таким образом, имея только 2 , мы будем иметь приближение 12 + 1/2 . Остановившись со следующим 1 , 1 добавляется к 2 , и следующее приближение составляет 12 + 1/3 . Добавление следующего числа, 2 , дает долю 3/8 , что исторически очень важно, потому что популярное древнее устройство для приближения лунного календаря к солнечному году должно было добавлять 3 дополнительных месяца каждые 8 лет. .Однако более важным было дробление на два шага дальше. Добавление 7 лунных месяцев каждые 19 лет было приемом, принятым в Вавилонском календаре. Это правило было унаследовано и используется даже сегодня по еврейскому календарю и христианскому исчислению Пасхи. Следующая дробь в серии, 123/334 , слишком велика, чтобы ее можно было использовать в календарных целях. (Непрерывная дробь для  приведена в сноске.)
приведена в сноске.)
 Золотое сечение обладает уникальным свойством: его обратная величина всегда дает то же десятичное число , а обратная десятичная дробь всегда дает целое число 1 .Это означает, что непрерывную дробь можно построить, не беспокоясь о калькуляторе! Непрерывная дробь однозначно содержит только 1 . Это также означает, что последовательные дроби могут быть получены без обращения к диаграмме. Для каждой дроби мы добавляем 1 , а затем переворачиваем ее (делаем обратное) для каждой новой дроби. Таким образом, первое число 1 , что дает дробь 1/1 . Это само по себе обратное. К этому добавляется 1 ( 1/1 ), в результате получается дробь 2/1 .Обратная величина — 1/2 , наша вторая дробь. К этому добавляется снова 1 (теперь 2/2 ), в результате получается дробь 3/2 . Обратной величиной будет 2/3 , наша третья дробь. К этому снова добавляется 1 (теперь 3/3 ), в результате получается дробь 5/3 . Обратная величина — 3/5 , наша четвертая дробь. По мере того как это продолжается, мы можем заметить, что процедура генерирует дроби, состоящие из последовательных чисел Фибоначчи ! Вот почему отношения чисел Фибоначчи приближаются к золотому сечению, все они представляют собой решений уникальной непрерывной дроби для золотого сечения!
Золотое сечение обладает уникальным свойством: его обратная величина всегда дает то же десятичное число , а обратная десятичная дробь всегда дает целое число 1 .Это означает, что непрерывную дробь можно построить, не беспокоясь о калькуляторе! Непрерывная дробь однозначно содержит только 1 . Это также означает, что последовательные дроби могут быть получены без обращения к диаграмме. Для каждой дроби мы добавляем 1 , а затем переворачиваем ее (делаем обратное) для каждой новой дроби. Таким образом, первое число 1 , что дает дробь 1/1 . Это само по себе обратное. К этому добавляется 1 ( 1/1 ), в результате получается дробь 2/1 .Обратная величина — 1/2 , наша вторая дробь. К этому добавляется снова 1 (теперь 2/2 ), в результате получается дробь 3/2 . Обратной величиной будет 2/3 , наша третья дробь. К этому снова добавляется 1 (теперь 3/3 ), в результате получается дробь 5/3 . Обратная величина — 3/5 , наша четвертая дробь. По мере того как это продолжается, мы можем заметить, что процедура генерирует дроби, состоящие из последовательных чисел Фибоначчи ! Вот почему отношения чисел Фибоначчи приближаются к золотому сечению, все они представляют собой решений уникальной непрерывной дроби для золотого сечения!
 Теперь я получил от Девина Чалмерса из Джуно, Аляска, вывод
Теперь я получил от Девина Чалмерса из Джуно, Аляска, вывод  непосредственно из определения ряда Фибоначчи (уравнение 1 ).Уравнение 2 перемещает определение по одному в ряду; затем мы делим обе части на a (n) в уравнении 3 , которое мы обрабатываем с помощью алгебры. Предел обоих соотношений в уравнении 4 должен быть одним и тем же числом, поэтому мы заменяем их переменной
непосредственно из определения ряда Фибоначчи (уравнение 1 ).Уравнение 2 перемещает определение по одному в ряду; затем мы делим обе части на a (n) в уравнении 3 , которое мы обрабатываем с помощью алгебры. Предел обоих соотношений в уравнении 4 должен быть одним и тем же числом, поэтому мы заменяем их переменной  в уравнении 5 . Это эквивалентно уравнению 6 , которое, как мы видели выше, можно подставить в квадратное уравнение, чтобы получить уравнение 7 .
в уравнении 5 . Это эквивалентно уравнению 6 , которое, как мы видели выше, можно подставить в квадратное уравнение, чтобы получить уравнение 7 .
Таким образом, хотя золотое сечение может быть не так важно, как другие математические константы, оно претендует на известность и имеет свои уникальные свойства.И, если подумать еще раз, мы действительно можем превратить это в очень серьезную компанию. Таким образом, если мы определим золотое сечение как число, которое при вычитании на равно его собственному обратному (  — 1 = 1/
— 1 = 1/ ), мы можем спросить, в свою очередь, какое число, если умножить на . на минус один, равно собственной обратной величине ( x * -1 = 1 / x ). Оказывается, это мнимое число , i =
), мы можем спросить, в свою очередь, какое число, если умножить на . на минус один, равно собственной обратной величине ( x * -1 = 1 / x ). Оказывается, это мнимое число , i =  -1: — i = l / i .Это гораздо более значимое и загадочное число, чем золотое сечение — неплохое в качестве своего рода родственника.
-1: — i = l / i .Это гораздо более значимое и загадочное число, чем золотое сечение — неплохое в качестве своего рода родственника.
Философия науки, математика
Философия науки
Домашняя страница
Copyright (c) 1999, 2003, 2008, 2011, 2012, 2019 Келли Л. Росс, доктор философии Все права защищены

Золотое сечение и числа Фибоначчи, Примечание 1

Вернуться к тексту

Золотое сечение и числа Фибоначчи, Примечание 2;
Непрерывная дробь для числа Пи

 Непрерывная дробь для
Непрерывная дробь для  представляет некоторый интерес, потому что греческие попытки получить значение для
представляет некоторый интерес, потому что греческие попытки получить значение для  всегда давали его в форме дроби — у древних не было десятичной записи.Лучшее, что они могли сделать, согласно Айзеку Азимову («Часть Пи», 1964), было 22/7 , что является лишь самой маленькой дробью в ряду (конечно, после 3/1 ). Архимед обнаружил, что
всегда давали его в форме дроби — у древних не было десятичной записи.Лучшее, что они могли сделать, согласно Айзеку Азимову («Часть Пи», 1964), было 22/7 , что является лишь самой маленькой дробью в ряду (конечно, после 3/1 ). Архимед обнаружил, что  было меньше, чем 22/7 , и больше, чем 223/71 , но этого все еще было недостаточно, чтобы найти следующую дробь в ряду. Только в 16 веке было обнаружено значение 355/113 . Как видите, на самом деле это лучшее, что можно сделать с относительно простой дробью, и современные математики в любом случае имеют новые обозначения и методы для решения проблемы
было меньше, чем 22/7 , и больше, чем 223/71 , но этого все еще было недостаточно, чтобы найти следующую дробь в ряду. Только в 16 веке было обнаружено значение 355/113 . Как видите, на самом деле это лучшее, что можно сделать с относительно простой дробью, и современные математики в любом случае имеют новые обозначения и методы для решения проблемы  , не продолжая вообще определять ее как дробь.Однако следующая пара дробей в серии дает чрезвычайно точные значения. 104,348 / 33,215 отличается от
, не продолжая вообще определять ее как дробь.Однако следующая пара дробей в серии дает чрезвычайно точные значения. 104,348 / 33,215 отличается от  всего на 1 / 3,030,303,030 ; и 103,993 / 33,102 отличается всего на 1 / 1,724,137,931 . Для сравнения: 355/113 отличается от
всего на 1 / 3,030,303,030 ; и 103,993 / 33,102 отличается всего на 1 / 1,724,137,931 . Для сравнения: 355/113 отличается от  на 1 / 3,748,688 ; 333/106 по 1/12 016 ; и 22/7 по 1/791 . Таким образом, легко удовлетворяется любое желание использовать целочисленные значения
на 1 / 3,748,688 ; 333/106 по 1/12 016 ; и 22/7 по 1/791 . Таким образом, легко удовлетворяется любое желание использовать целочисленные значения  в широком диапазоне точности.
в широком диапазоне точности.
Вернуться к тексту золотого сечения
Текст непрерывной дроби для синодического месяца
Философия науки
Домашняя страница
Copyright (c) 1999 Келли Л. Росс, доктор философии. Все права защищены
.89, 109 и последовательность Фибоначчи
Число, обратное 89, число Фибоначчи, основано на рядах Фибоначчи.
Это небольшое любопытство, связанное с числом 89, одним из чисел ряда Фибоначчи.
1/89 — повторяющаяся десятичная дробь из 44 символов:
.01123595505617977528089887640449438202247191
Вы можете увидеть начало последовательности Фибоначчи в первых 6 цифрах десятичного эквивалента 1/89. (т.е. 0,1,1,2,3,5 отображается как 0.8) +
. . .
0,011235955… =
0,0 +
0,01 +
0,001 +
0,0002 +
0,00003 +
0,000005 +
0,0000008 +
0,00000013 +
. . .
Джон Халберт, который опубликовал подобные последовательности в Бюллетене Института математики и его приложений, отмечает, что эта взаимосвязь была представлена в книге У. «Заклинание математики».J.Reichmann, издано издательством Pelican books в 1972 г.
Обратная величина 109 также основана на рядах Фибоначчи, вперед и назад
Вот еще одна любопытная вещь, связанная с числом 109, обнаруженным и внесенным (20.10.2003) Риком Тэйвсом.
1/109 — повторяющаяся десятичная дробь из 108 символов:
.009174311926605504587155963302752293577981651376146788
990825688073394495412844036697247706422018348623853211
Вы можете увидеть начало последовательности Фибоначчи в ПОСЛЕДНИХ 6 цифрах десятичного эквивалента 1/109, которые появляются в ОБРАТНОМ порядке, начиная с КОНЕЦ десятичной дроби.(т.е. 0,1,1,2,3,5, 8 отображается как… 853211)
Если вы возьмете каждое число Фибоначчи, разделите его на 10 в степени 109 МИНУС его позиции в последовательности Фибоначчи (начиная с 0) и сложите их все вместе, вы получите величину, обратную 109.
Обратите внимание на серию Фибоначчи Обратите внимание на последовательность | … 18348623853211 = … 000000000000000 + .. . |
И, наконец, еще одно любопытство, связанное с числом 109.
Если вы возьмете каждое число Фибоначчи, разделите его на 10 в степени его позиции в последовательности Фибоначчи и сложите и вычтите каждый альтернативный член вместе, вы получите 0,00917431… опять же, обратная величина 109.
Обратите внимание на ряд Фибоначчи зеленым цветом Обратите внимание на порядковый номер ряда Фибоначчи в Red . | 1/109 = 0 / (10 ^ 1) + .. . | 0,00917431… = 0,0 + . . . |

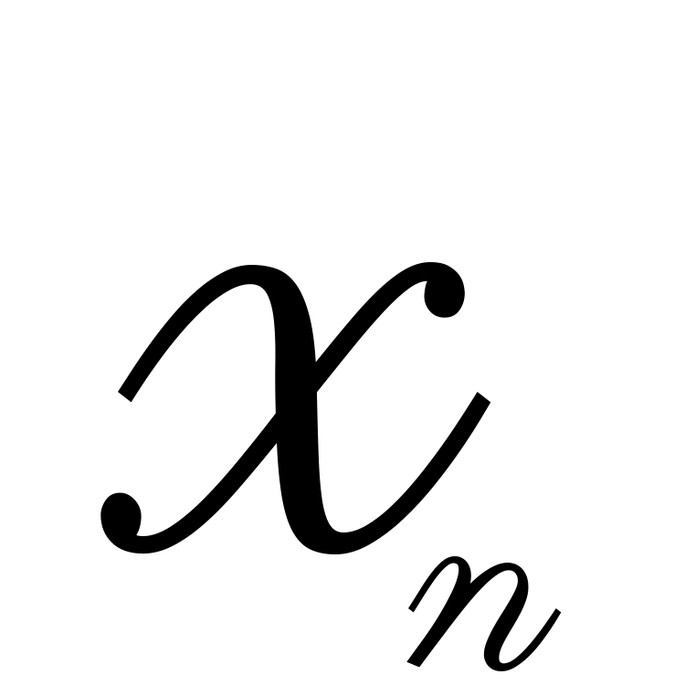
 , а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!
, а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!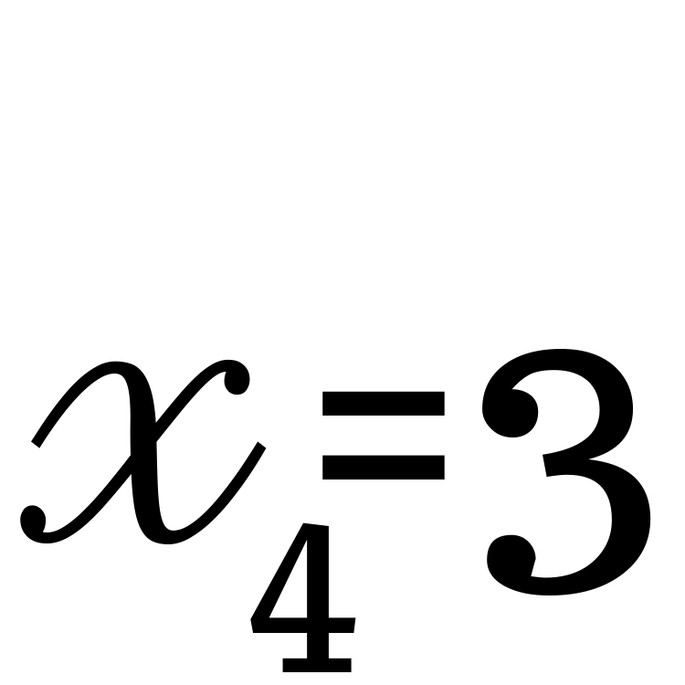 , а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!
, а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!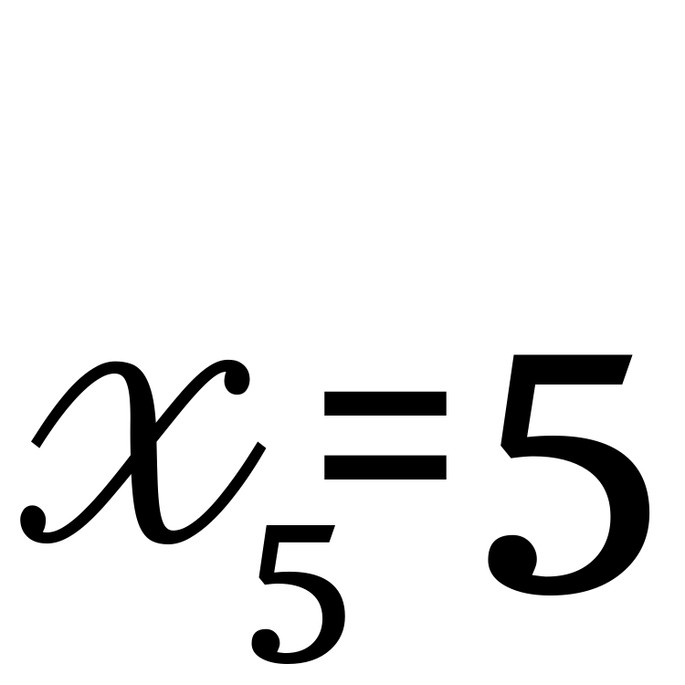 , а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
, а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!