Информация о золотом сечении: Золотое сечение и симметрия — Мастерок.жж.рф — LiveJournal

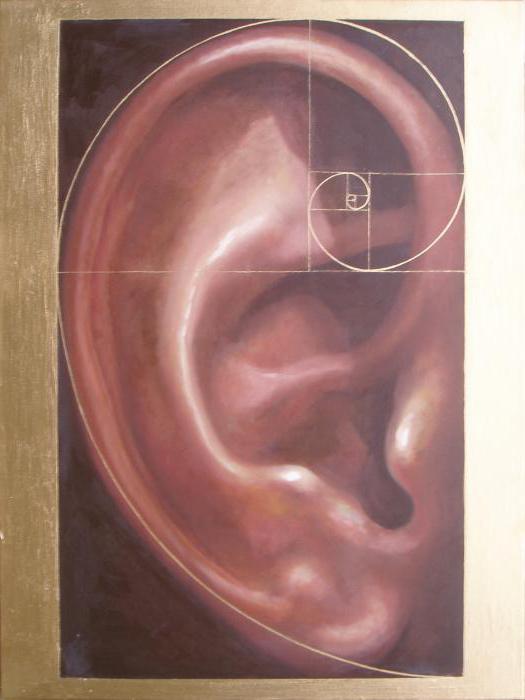
Золотая пропорция

Золотое сечение – это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всём, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Наиболее ёмкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

История

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция», иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д.

На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до безконечности». Сейчас ряд Фибоначчи – это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Самым удивительным в золотом сечении является то, что оно может рассматриваться как естественное явление в природе. Золотое сечение выражается в расположении ветвей вдоль стволов деревьев, прожилок в листьях. Его можно увидеть в строении скелетов животных и людей, в разветвлении их вен и нервов.

Оно даже может быть замечено в пропорции химических соединений и геометрии кристаллов.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять своё место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Ещё Архимед, уделяя внимание спирали, вывел на основе её формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни».

Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.

Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента

Формы временного искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера.

Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

В фотографии и видеопроизводстве методика золотого сечения также используется повсеместно.

По сути, Золотая пропорция вокруг и внутри нас, и по этой причине немецкий психолог Адольф Цейзинг (1810 – 1876 гг.) назвал его «универсальным законом, в котором содержится основной принцип формирования всего, стремление к красоте и полноте в природе и искусстве, который пронизывает, как первостепенный духовный идеал, все структуры, формы и пропорции, будь то космические или индивидуальные, органические или неорганические, акустические или оптические; который полностью реализован в теле человека».

Благодаря уникальным свойствам золотого сечения многие считают его священным или божественным, позволяющим обрести более глубокое понимание красоты и духовности в жизни, увидеть скрытую гармонию и связность во всём, что нас окружает.

Источник: http://econet.ru/articles/149170-zolotoe-sechenie-kak-eto-rabotaet

ЧТО ТАКОЕ ЗОЛОТОЕ СЕЧЕНИЕ

ЧТО ТАКОЕ ЗОЛОТОЕ СЕЧЕНИЕ

Что такое Золотое Сечение? Что такое Золотая Пропорция? Это одно и то же, просто кто и как больше любит называть.

Попробую в публицистической манере, просто, по-житейски ответить на вопросы, которые часто задают люди, в частности слушатели моих курсов.

Для начала просто полезно знать, что в интернете, объективно, запросов на Золотое Сечение в десять раз больше чем на Золотую Пропорцию, но при этом есть специалисты, которые считают определение — Золотое Сечение — вообще ошибочным, искажающим суть данной пропорции и не имеющее права на жизнь.

Что такое Золотое Сечение или Золотая Пропорция простыми словами? В примитиве, это отношение одной части, чего либо, к другой с коэффициентом 1,618 (это 61,8%), или 62% на 38%, грубо принято округлять 60% на 40%.

Важно понимать, что в Золотой Пропорции «части» всегда три, третье – это целое (100%).

Классическое определение Золой Пропорции: меньшее относится к большему так, как большее относится к целому, с коэффициентом 1,618.

Что такое число ФИ? Это и есть этот самый коэффициент 1,618 между двумя частями. Он показывает, на сколько одна часть отличается от другой. Золотое Число — так часто называют этот коэффициент.

Золотое Сечение – Пропорция Гармонии Природы. Золотое Сечение в Природе проявится во всём, если поискать. Даже можно сказать, если есть Золотая Пропорция с рядом проявлений своих свойств, то есть «жизнь», и есть Природная красота.

Формула Золотого Сечения, Золотое Сечение в математике – это раскрытие в цифрах закономерностей проявлений отношения частей в Природе. Основные формулы проявлений Золотого Сечения есть даже в детских учебниках.

Гуманитарных объяснений смысла Золотого Сечения, в глубоком смысле, значительно меньше и они часто овеяны вековыми тайнами, но это время осталось в прошлой эпохе, теперь выявлена простота на уровне букваря.

Золотое Сечение Фибоначчи, Золотая пропорция Фибоначчи, или Ряд Фибоначчи. Это проявление шагов Золотой пропорции в целых числах, которая становится точной 62% на 38%, или 1,618 — только к десятому шагу. По шагу Фибоначчи изменяется вся Природа, растут веточки, листики, плодятся кролики, насекомые и т.д.                      

Опять уточню, что детские учебники красочно показывают это.

Главное надо знать, что начиная с 0 и 1, все дальнейшие цифры – это сумма двух последних… 0,1,1,2,3,5,8,13,21,34,55…

Поскольку в Природе всё начинается с двух единиц, то соответственно к любому числу из ряда надо прибавлять – 1, например, 21 – это не 21, а 21 +1 (коварное очко и не только очко, но и любое число из ряда). То есть, если нам надо 21 яблоко, то с точки зрения Природы, по ряду Фибоначчи, их надо взять 22 = 21 + 1. Всегда на одну единицу больше.

Эта, на первый взгляд, странная тонкость, имеет принципиальное значение для поиска «постоянных» и «переменных» состояний. Например, какая зарплата нас удовлетворит, или сколько яблок надо купить, чтобы быть довольным. Купив «постоянное» количество (из ряда Фибоначчи) – будешь удовлетворён, даже если купил меньше планируемого.

Золотое Сечение Леонардо да Винчи. Так часто люди отождествляют гения и пропорцию. Да, это справедливо, хотя, намного раньше, по ходу истории, разные цивилизации использовали Пропорцию Бога, это и шумеры, и египтяне…

Мы привыкли, что Золотое Сечение в архитектуре, это удел специалистов, и то редких, или сумасшедших гениев. Это ошибка. Любому человеку, даже детям, надо знать элементарные проявления закона Золотого Сечения – базовые приёмы Природоподобных Технологий, как таблицу умножения.

Это позволит в психологии понимать причино-следственность поступка в программном смысле, а также это позволит легко ориентироваться в городе на предмет зданий, несущих положительные состояния или за городом, на дачном участке на предмет получения удовлетворения от пребывания на природе и от ведения хозяйства. Золотое Сечение в Природе и Золотое Сечение в доме, станут одинаково положительно влиять на ощущения.

Теперь пару слов о Золотом Сечении в искусстве. Хорошо когда произведение искусства завораживает. Завораживать может только «жизнь», проявленная в произведении, которая включается исключительно проявлениями Золотого Сечения, то есть Природоподобия.

Есть интересный пример проявления Золотого Сечения в фотографии. Стоит взять по Природоподобию «правильные» размеры рамки, самой фотографии и изображения, то одна и та же фотография, которая только что была скучной, вдруг заживёт притягательной магией.

В итоге, еще раз повторю, Золотая Пропорция – это выключатель или включатель всей полноты Природоподобия, Гармонии, Красоты, Жизни — с больших букв: равновесия, сил, здоровья, удовлетворения, доходности, счастья и любви. Собственно, это и есть маркер Любви. Причина этого в том, что правило Золотой Пропорции отражает мирозданческий принцип Триединства, но об этом я расскажу в другой статье.

Полезные статьи:

— Человек в золотом сечении;

— Метод Аркадия Осипова;

— Заказать индивидуальный проект;

— Что такое Закон Триединства;

— Улей для пчел по Золотому Сечению;

— Отзывы;

— Семинары;

— На главную

Золотое сечение – это… Золотое сечение пирамиды. Формула золотого сечения

Геометрия – точная и достаточно сложная наука, которая при всем этом является своеобразным искусством. Линии, плоскости, пропорции – все это помогает создавать много действительно прекрасных вещей. И как ни странно, в основе этого лежит именно геометрия в самых разных ее формах. В этой статье мы рассмотрим одну очень необычную вещь, которая непосредственно связанна с этим. Золотое сечение – это именно тот геометрических подход, о котором пойдет речь.

Форма предмета и ее восприятие

Люди чаще всего ориентируются на форму предмета для того, чтобы распознавать его среди миллионов других. Именно по форме мы определяем, что за вещь лежит перед нами или стоит вдали. Мы в первую очередь узнаем людей по форме тела и лица. Поэтому с уверенностью можем утверждать, что сама форма, ее размеры и вид – одна из самых важных вещей в восприятии человека.

Для людей форма чего бы то ни было представляет интерес по двум главным причинам: либо это диктуется жизненной необходимостью, либо же вызывается эстетическим наслаждением от красоты. Самое лучшее зрительное восприятие и ощущение гармонии и красоты чаще всего приходит, когда человек наблюдает форму, в построении которой использовались симметрия и особое соотношение, которое и называется золотым сечением.

Понятие золотого сечения

Итак, золотое сечение – это золотая пропорция, которая также является гармоническим делением. Для того чтобы объяснить это более понятно, рассмотрим некоторые особенности формы. А именно: форма является чем-то целым, ну а целое, в свою очередь, всегда состоит из некоторых частей. Эти части, вероятнее всего, обладают разными характеристиками, по крайней мере разными размерами. Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.

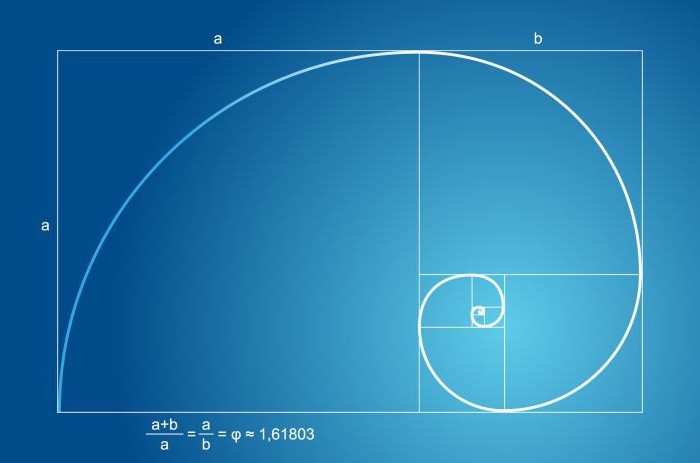
Значит, другими словами, мы можем утверждать, что золотое сечение – это соотношение двух величин, которое имеет свою формулу. Использование такого соотношения при создании формы помогает сделать ее максимально красивой и гармоничной для человеческого глаза.

Из древней истории золотого сечения

Соотношение золотого сечения часто используют в самых разных сферах жизни прямо сегодня. Но история этого понятия уходит еще в древние времена, когда только зарождались такие науки, как математика и философия. Как научное понятие золотое сечение вошло в обиход во времена Пифагора, а именно в VI веке до нашей эры. Но еще до того знания о подобном соотношении на практике использовали в Древнем Египте и Вавилоне. Ярким свидетельством этого являются пирамиды, для построения которых использовали именно такую золотую пропорцию.

Новый период

Эпоха Возрождения стала новым дыханием для гармонического деления, особенно благодаря Леонардо да Винчи. Это соотношение все больше начали использовать как в точных науках, таких как геометрия, так и в искусстве. Ученные и художники стали более глубоко изучать золотое сечение и создавать книги, рассматривающие этот вопрос.

Одна из самых важных исторических работ, связанных с золотой пропорцией, – это книга Луки Панчоли под названием «Божественная пропорция». Историки подозревают, что иллюстрации этой книги были выполнены самим Леонардо до Винчи.

Математика дает очень четкое определение пропорции, которое говорит о том, что она является равенством двух соотношений. Математически это можно выразить таким равенством: а:b=с:d, где а, b, с, d – это некоторые определенные значения.

Если рассматривать пропорцию отрезка, разделенного на две части, то можем встретить всего несколько ситуаций:

• Отрезок разделен на две абсолютно ровные части, а значит, АВ:АС= АВ:ВС, если АВ – это точна начала и конца отрезка, а С – точка, которая и разделяет отрезок на две равные части.
• Отрезок разделен на две неравные части, которые могут находиться в самом разном соотношении между собой, а значит, здесь они абсолютно непропорциональны.
• Отрезок разделен так, что АВ:АС= АС:ВС.

Что же касается золотого сечения, то это такое пропорциональное деление отрезка на неравные между собой части, когда весь отрезок относится к большей части, как и сама большая часть относится к меньшей. Существует и другая формулировка: меньший отрезок так относится к большему, как и больший ко всему отрезку. В математическом соотношении это выглядит следующим образом: а:b = b:с или с:b = b:а. Именно такой вид имеет формула золотого сечения.

Золотая пропорция в природе

Золотое сечение, примеры которого мы сейчас рассмотрим, относится к невероятным явлениям в природе. Это очень красивые примеры того, что математика – это не просто цифры и формулы, а наука, которая имеет более чем реальное отражение в природе и нашей жизни вообще.

Для живых организмов одна из главных жизненных задач – это рост. Такое стремление занять свое место в пространстве, по сути, осуществляется в нескольких формах – рост вверх, практически горизонтальное расстилание по земле или закручивание по спирали на некой опоре. И как бы ни было это невероятно, много растений растут в соответствии с золотой пропорцией.

Еще один почти невероятный факт – это соотношения в теле ящериц. Их тело выглядит достаточно приятно для человеческого глаза, и это возможно благодаря тому же золотому соотношению. Если быть точнее, то длина их хвоста относится к длине всего тела как 62 : 38.

Интересные факты о правилах золотого сечения

Золотое сечение – это поистине невероятное понятие, а значит, на протяжении всей истории мы можем встретить много действительно интересных фактов о такой пропорции. Представляем вам некоторые из них:

• Правило золотого сечения активно применялось в построении пирамид. Например, всемирно известные гробницы Тутанхамона и Хеопса возводили с использованием такого соотношения. И золотое сечение пирамиды до сих пор остается загадкой, ведь по сей день не известно, случайно или же специально выбирались такие размеры для их оснований и высот.
• Правило золотого сечения четко видно в фасаде Парфенона – одного из самых красивых сооружений в архитектуре Древней Греции.
• То же касается здания собора Парижской Богоматери (Нотр-Дам де Пари), то здесь не только фасады, но и другие части конструкции возводили, опираясь на эту невероятную пропорцию.
• В русской архитектуре можно встретить невероятно много примеров зданий, полностью соответствующих золотому сечению.
• Гармоничное деление присуще также и человеческому телу, а значит, и скульптуре, в частности, статуям людей. Например Аполлон Бельведерский – статуя, где у человека рост делится пупочной линией в золотом сечении.
• Живопись – отдельная история, особенно если учесть роль Леонарда да Винчи в истории золотого соотношения. Его известная Джоконда, конечно же, подлежит этому закону.

Золотое сечение в человеческом теле

В этом разделе нужно упомянуть очень значимую персону, а именно – С. Цейзинга. Это немецкий исследователь, который провел огромнейшую работу в сфере изучения золотой пропорции. Он опубликовал труд под названием «Эстетические исследования». В своей работе он представил золотое сечение как абсолютное понятие, которое является универсальным для всех явлений как в природе, так и в искусстве. Здесь можно вспомнить золотое сечение пирамиды наряду с гармоничной пропорцией человеческого тела и так далее.

Именно Цейзинг смог доказать, что золотое сечение, по сути, есть средним статистическим законом для человеческого тела. Это было показано на практике, ведь во время своей работы ему пришлось измерять очень много человеческих тел. Историки считают, что в этом опыте принимали участие более двух тысяч людей. По исследования Цейзинга, главный показатель золотого соотношения – это деление тела точкой пупка. Так, мужское тело со средним соотношением 13:8 немного ближе к золотому сечению, чем женское, где число золотого сечения составляет 8:5. Также золотую пропорцию можно наблюдать в других частях тела, таких как, например, рука.

О построении золотого сечения

На самом деле, построение золотого сечения – дело нехитрое. Как мы видим, еще древние люди справлялись с этим довольно легко. Что уже говорить о современных знаниях и технологиях человечества. В этой статье мы не будем показывать, как подобное можно сделать просто на листке бумаги и с карандашом в руках, но с уверенностью заявим, что это, на самом деле, возможно. Более того, сделать это можно далеко не одним способом.

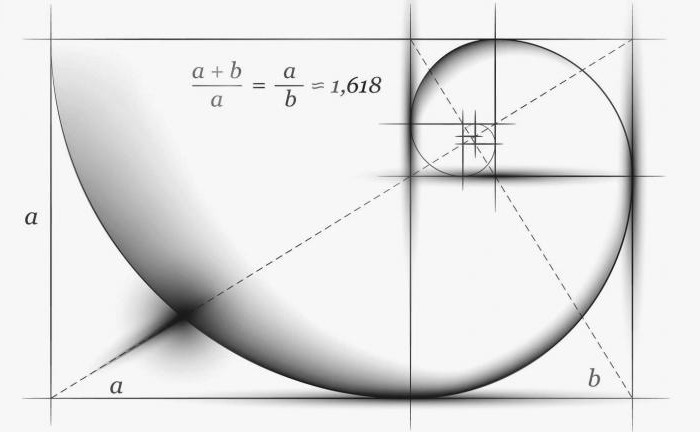
Так как это достаточно несложная геометрия, золотое сечение является довольно простым для построения даже в школе. Поэтому информацию об этом можно легко найти в специализированных книгах. Изучая золотое сечение 6 класс полностью способен понять принципы его построения, а значит, даже дети достаточно умны для того, чтобы осилить подобную задачу.

Золотая пропорция в математике

Первое знакомство с золотым сечением на практике начинается с простого деления отрезка прямой все в тех же пропорциях. Чаще всего это реализуется с помощью линейки, циркуля и, конечно же, карандаша.

Отрезки золотой пропорции выражают как бесконечную иррациональную дробь AE = 0,618…, если АВ принимается за единицу, ВЕ = 0,382… Для того чтобы сделать эти вычисления более практическими, очень часто используют не точные, а приближенные значения, а именно – 0,62 и 0,38. Если же отрезок АВ принимать за 100 частей, то большая его часть будет равна 62, ну а меньшая – 38 частям соответственно.

Главное свойство золотого соотношения можно выразить уравнением: х²-х-1=0. При решении мы получаем следующие корни: х_1,2=. Хотя математика и есть точной и строгой наукой, как и ее раздел – геометрия, но именно такие свойства, как закономерности золотого сечения, наводят таинственность на эту тему.

Гармония в искусстве через золотое сечение

Для того чтобы подвести итоги, рассмотрим коротко то, о чем уже говорили.

В основном под правило золотого соотношения подпадает много образцов искусства, где соблюдается соотношение близкое к 3/8 и 5/8. Это и есть грубая формула золотого сечения. В статье уже очень много упоминалось о примерах использования сечения, но мы еще раз посмотрим на него через призму древнего и современного искусства. Итак, самые яркие примеры из древних времен:

• Золотое сечение пирамиды Хеопса и Тутанхамона выражается буквально во всем: храмы, барельефы, предметы быта и, конечно же, украшения самых гробниц.
• Храм фараона Сети І в Абидосе славится рельефами с разными изображениями, и все это соответствует все тому же закону.

Что касается уже наверняка сознательного использования пропорции, то, начиная с времен Леонардо да Винчи, она вошла в использование практически во всех отраслях жизни – от науки и до искусства. Даже биология и медицина доказали, что золотое соотношение работает даже в живых системах и организмах.

К понятию о Золотом сечении



«Геометрия владеет двумя сокровищами:

одно из них — теорема Пифагора,

другое — деление отрезка в среднем и крайнем отношении»

Иоганн Кеплер

Золотое сечение – это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Авторы статьи исследуют литературу, находят связи между науками, касающиеся Золотого сечения, выявляют практический смысл золотых пропорций.

Ключевые слова: золотое сечение, золотые пропорции, научный феномен.

Целью нашей работы является исследование источников информации, касающихся «Золотого сечения» в различных областях знаний, выявление закономерностей и нахождение связей между науками, выявление практического смысла Золотого сечения.

Актуальность данного исследования определяется многовековой историей использования золотого сечения в математике и искусстве. То, над чем ломали голову древние, остается актуальным и вызывающим интерес современников.

Во все времена люди пытались находить закономерности в окружающем их мире. Окружали себя предметами «правильной» с их точки зрения формы. Лишь с развитием математики людям удалось измерить «золотое соотношение», которое впоследствии получило название «Золотое сечение».

Золотое сечение— гармоническая пропорция

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или, другими словами, меньший отрезок так относится к большему, как больший ко всему (Рис.1).

a:b = b:c

Рис. 1. Деление отрезка по золотым пропорциям

Напомним Вам, что же такое золотое сечение. Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62 % на 38 %. Это соотношение действует в формах пространства и времени [1].

Золотой треугольник ипрямоугольник

Кроме деления отрезка на неравные части (золотое сечение) рассматривают золотой треугольник и золотой прямоугольник [3].

Золотой прямоугольник — это прямоугольник, длины сторон которого находятся в золотой пропорции (Рис.2).

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения (Рис.3).

Рис.2. Золотой прямоугольник

Рис.3 Золотой треугольник

Пентакль

В правильной пятиконечной звезде, каждый сегмент делится пересекающим его сегментом в золотом сечении, т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618 (Рис.4).

Рис.4. Пентаграмма-гигиея

Пифагор утверждал, что пентаграмма, или, как он ее называл, гигиея представляет собой математическое совершенство, так как скрывает в себе золотое сечение. Отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому и есть золотая пропорция.

Ряд Фибоначчи

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления.

Так, 21: 34 = 0,617

34: 55 = 0,618.

История золотого сечения

Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Золотые пропорции вчастях тела человека

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».

Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон (Рис.5).

Рис.5 Золотые пропорции в частях тела человека

Золотое сечение вживой природе

Удивительно, как всего одно математическое понятие встречается во многих разделах человеческого знания. Оно как бы пронизывает все в мире, соединяя между собой гармонию и хаос, математику и искусство [2].

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38 (Рис.6).

Рис.6 Золотые пропорции в частях тела ящерицы

Золотое сечение вархитектуре

В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (Рис.7). Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.

Другим примером из архитектуры древности является пирамида Хеопса (Рис.8).

Пропорции Великой Пирамиды выдержаны в » Золотом соотношении»

Древние строители ухитрились возвести этот величественный монумент практически с идеальной инженерной точностью и симметричностью.

Рис.7. Парфенон

Рис.8. Пирамида Хеопса

Золотое сечение вскульптуре

Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям (Рис.9).

Рис.9 Статуя Аполлона Бельведерского

Золотое сечение вживописи

Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину «Джоконда». Композиция портрета построена на золотых треугольниках (Рис.10).

Рис.10 Леонардо да Винчи «Джоконда»

Еще один пример золотого сечения в живописи – это полотно Рафаэля «Избиение младенцев» (Рис.11). На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается…золотая спираль!

Рис.11. Рафаэль «Избиение младенцев»

Золотое сечение влитературных произведениях

Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так, в повести «Пиковая дама» 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения.

Золотое сечение вкинокартинах

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей.

Заключение

О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом ученые — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения. Бесконечный ряд после запятой — 1,6180339887… Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»? Что это за идеальное, божественное сочетание? Может быть, это закон красоты? Или все-таки он — мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно… И в этом его подлинная загадка, его великая тайна.

Литература:

1. Виленкин Н. Я., Жохов В. И. и др. Математика — 6. — М.: Мнемозина, 2015
2. Корбалан Ф. Золотое сечение. Математический язык красоты. (Мир математики Т.1). — М.: ДеАгостини, 2014
3. Тимердинг Г. Е. Золотое сечение. — М.: Либроком, 2009

Основные термины (генерируются автоматически): золотое сечение, золотое деление, Золотой треугольник, золотая пропорция, золотой прямоугольник, деление отрезка, пропорция, научный феномен, синий отрезок, золотой.

Золотое сечение

Золотое сечение

Бабенко П.Д. 1

---

1КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ И.Т. ТРУБИЛИНА

Мамась Н.Н. 1

---

1КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ И.Т. ТРУБИЛИНА

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение: «Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением…»

«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».

Иоганн Кеплер

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Цели:

1. Измерить гармонию алгеброй.

2. Изучить разнообразие применения золотого сечения и связанные с ним соотношения в реальной жизни;

2. Разобраться в пропорциях человека как гармонии и красоты.

Задачи:

1. Познакомиться с понятием золотого сечения и с историей его развития;

2. Получить представление о практическом применении золотого сечения в реальной жизни;

3. Выяснить, почему с этим понятием связана гармония и красота.

Предметом исследования является золотое сечение, объектом – гармоническая пропорция.

Актуальность работы – гармония и красота в жизни всегда актуальны

Гипотеза: в окружающем мире “золотое сечение” является основополагающим принципом красоты, прочности, надежности и позволяет осознать связь мира искусства и мира чисел. 

1. Понятие «золотое сечение».

«Золотым сечением» и даже «божественной пропорцией» называли математики древности и средневековья такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

а :b = b : c или с : b = b : а

Итак, золотая пропорция = 1 :1,618. Это отношение приближенно равно 0,618 ≈ 5/8.В алгебре это число обозначается греческой буквой фи (φ). Полученное значение есть знаменитое число «фи», названное так американским математиком Марком Баром по первой букве имени великого скульптора Фидия, который, по преданию, использовал «золотое сечение» в своих работах.

Замечательный пример «золотого сечения» представляет собой правильный пятиугольник — выпуклый и звездчатый.

Из подобия треугольников АСD и ABE можем вывести уже известную пропорцию:

AB/AC=AC/BC

Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.

Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

1.1. Задачи на построение.

В геометрии есть понятия: «деление отрезка в золотом отношении», «золотой треугольник», «золотой прямоугольник», «золотая логарифмическая спираль». Мне Dзахотелось научиться строить эти фигуры. Я разобрала три задачи.

Задача №1. «Деление отрезка в золотом отношении»

Дано : Отрезок АВ. E

A CB Построить: золотое сечение отрезка АВ, то есть точку С так, чтобы Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.

Задача №2. Построение «золотого треугольника».

Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d₁ соединяем прямыми с точкой А. Отрезок dd₁откладываем на линию Ad₁, получая точку С. Она разделила линию Ad₁ в пропорции «золотого сечения». Линиями Ad₁ и dd₁ пользуются для построения «золотого» прямоугольника

2. История развития «золотого сечения».

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети 1 в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответсвуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Также о золотом делении знал Платон. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во второй книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипеикл (2 в. до н.э.), Папп (3 в. н.э.) и др.

В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж.Кампано из Наварры (3 в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре. В 1509 г. В Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства Бог сын, Бог отец и Бог дух святой (подразумевалась, что малый отрезок есть олицетворение Бога сына, большой отрезок – Бога отца, а весь отрезок – Бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название Золотое Сечение. Так оно и держится до сих пор как самое популярное.

В 1855 г. Немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.

В конце 19 – начале 20 вв. появилось немало чисто формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры.

3. «Золотое сечение» в разных сферах

3.1.«Золотое сечение» в скульптуре.

Скульптурное сооружение, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Ещё в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Они утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения».

Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самая знаменитая статуя Зевса Олимпийского и Афины Парфенос (которые считались одним из чудес света). Было проведено большое число измерений на помещённых в журналах крупных портретах мужчин и женщин, на многих их низ указанные отношения представляют «золотое сечение».

3.2.«Золотое сечение» в архитектуре.

Парфенон.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (5 в. До н. э.).

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон(синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.

Дом Пашкова.

Одним из шедевров архитектуры в Москве – дом Пашкова- является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.

Баженов говорил: «Архитектура – главнейшее имеет три предмета; красоту, спокойность и прочность здания… К достижению сего служит руководством здание пропорций, перспектива, механика или вообще физика, а всем им общим является рассудок».

3.3. «Золотое сечение» в живописи.

«Золотое сечение» в живописи, проглядывалось в работах и творчесте великого Леонардо да Винчи. Он говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».

Одним из таких портретов является Монны Лизы (Джоконды), долгие годы привлекают внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует много версий об истории этого портрета. Одна из них:

Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекало простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.

3.4. «Золотое сечение» в природе.

«Золотое сечение» — один из основополагающих принципов природы. Красота природных форм во взаимодействии двух физических сил – тяготения и инерции. Золотое сечение – символ этого взаимодействия, поскольку диктуемое ею отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный рост побега до зрелости и замедленный рост до момента цветения, когда достигшее полной силы растение готовится дать жизнь новому побегу.

Одним из первых проявления золотого сечения в природе подметил немецкий математик и астроном Иоганн Кеплер (1570-1630 гг.). С ХVII в. наблюдение математических закономерностей в ботанике и зоологии стали быстро накапливаться.

В 1850 г. немецкий ученый А. Цейзинг открыл так называемый закон углов, согласно которому средняя величина углового отклонения ветки растения равно примерно 138 градусов.

Допустим, что две соседние ветки растения исходят из одной точки (на самом деле это не так: в реальности ветви располагаются выше или ниже друг друга). Обозначим одну из них через ОА, другую через ОВ. Угол между лучами – ветками обозначим через а, а угол, дополняющий его до 360 , — через Р.

Составим золотую пропорцию деления полного угла, считая, что угол К – большая часть этой величины.

360/Р=Р/360-Р.

Получаем квадратное уравнение: Р² + 360 – Р360² =0. Положительный корень Р= -180+√180²+360²= 180·±√5= 180·1,236= 222,48.

а=360°-222,48°=137,52°≈138°.

Таким образом, величина среднего углового отклонения ветки соответствует меньшей из двух частей, на которые делится полный угол при золотом сечении.

5. Экспериментальная часть

Изучив теорию вопроса, я решила провести исследование и найти пропорции золотого сечения в живой природе (на примере комнатных растений).

Эксперимент №1

Цель: проверить есть ли «золотое сечение» в растительном мире, у комнатных растений.

В первую очередь я заинтересовалась, как проявляется принцип формообразования в живой природе. Выяснилось, что комнатные растения растут и занимают место в пространстве в основном в двух вариантах — рост вверх или расстилание по поверхности, либо закручивание по спирали (вьющиеся растения). Меня заинтересовал первый вариант. Для этого было изучено 6 комнатных растений (среди них бегония клубневая, диффенбахия, традесканция, глоксиния белоцветковая, каланхое, роициссус).

Приглядимся внимательно к схематично изображённому фрагменту комнатного растения. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.

Если измерить расстояние АС и расстояние ВС, и найти отношение

ВС.: АС, то оно приближённо равно 0,618, т.е. подчиняется золотой пропорции.

Вывод: результаты измерений показывают, что в росте, завоевании пространства, растение сохраняет определенные пропорции. Импульсы его роста постепенно уменьшаются в пропорции «золотого сечения».

Заключение.

В своей работе я хотел продемонстрировать красоту и широту «Золотого сечения» в реальной жизни. Проведенные исследования доказали, что многое в окружающем мире подчиняется правилу золотого сечения.

Физика исследует реальный мир. Биология – живой мир органической природы. Предмет исследования математики нематериальны, в природе нет логарифмов, синус не рассмотришь под микроскопом и при этом математика – самое могущественное орудие познания, созданное человеком, и любая наука достигает совершенства, когда начинает говорить на языке математики.

Значение золотого сечения в современной науке очень велико. Эта пропорция используется практически во всех областях знаний.

Я говорила только об его эстетическом значении, но существуют примеры его чисто практического применения. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью и т.д.

Список литературы:

Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014.

Пидоу Д. Геометрия и искусство. – М.: Мир, 1989.

Виленкин Н. и др. «Математика», 5, «Мнемозина», 2001

«Энциклопедический словарь юного математика», Москва, «Педагогика», 1985

Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988.

Интернет сайты:

http://www.abc-people.com/idea/zolotsech/

 http://n-t.ru/tp/iz/zs.htm

http://tmn.fio.ru/works/04x/304/p3_4.htm

Просмотров работы: 541

Золотое сечение: Самый раздутый миф в дизайне

Золотое сечение – это полный нонсенс в дизайне. И вот почему.

В мире искусства, архитектуры и дизайна золотое сечение завоевало потрясающую репутацию. Великие гении, включая Корбюзье и Сальвадора Дали, использовали эту пропорцию в своих работах. Парфенон, Пирамиды в Гизе, полотна Микелянджело, Мона Лиза и даже логотип Apple якобы построены на его основе.

Это бред. Эстетика золотого сечения – это просто современная байка, миф. Многие дизайнеры им пренебрегают, а если и используют, то не стесняются преуменьшать его значение. Кроме того, у этой пропорции нет никакой научной подоплеки. Те, кто верят, что за красотой золотого сечения кроется математика, попались на крючок 150-летней давности.

Пользователь FlickrSébastien Bertrand

Что такое золотое сечение?

Изначально описанный в Элементах Эвклида 2300 лет назад, этот термин гласит: два объекта находятся в золотой пропорции, если соотношение между ними идентично отношению их суммы к большему из двух элементов. Обычно эта пропорция составляет 1.6180. Самое известное применение золотого сечения – так называемый золотой прямоугольник, который может быть разделен на идеальный квадрат и меньший прямоугольник тех же пропорций, что и “родительский” прямоугольник. Вы можете применить эту теорию к большему разнообразию объектов, также разделяя их на компоненты.

Золотое сечение всегда немного неточное.

Простым языком: если у вас есть два объекта (или один объект, который можно разделить на два, по аналогии с золотым прямоугольником), и если после вышеописанной математики, вы получите число 1.6180, обычно считается, что два объекта демонстрируют золотое сечение. Но есть одна проблема. Когда вы все-таки посчитаете, то сама пропорция не равна 1.6180. Она равна 1.6180339887… И десятичная часть уходит в бесконечность.

“Собственно говоря, невозможно подобрать примеры золотого сечения в реальном мире, потому что это иррациональное число”, – заявляет Кит Девлин, профессор математики Стэнфордского университета. Вы можете только приблизиться к более стандартным пропорциям. Стороны экрана iPad соотносятся как 3:2, пропорция HDTV составляет 16:9, и все это “вокруг да около”, по словам Девлина. Но само золотое сечение – это как число “пи”. Как нельзя найти идеальный круг в реальном мире, так и нельзя применить точное золотое сечение к любому объекту в реальном мире. Оно всегда будет немного смещаться.

Золотое сечение – это как эффект Моцарта

Конечно, это педантизм. Неужели 1.6180 – недостаточно точно? Возможно, и достаточно, если бы было какое-то научное обоснование того, что именно золотое сечение позволяет нам считать объекты вроде Парфенона или Моны Лизы эстетически приятными.

Но это не так. Девлин считает, что сама идея, будто золотое сечение имеет какое-то отношение к эстетике, исходит от двух людей, один из которых был неправильно истолкован, а второй это толкование и обнародовал.

Первый человек – Лука Пачоли, францисканский монах, который написал книгу под названием De Divina Proportione в далком 1509 году, и она была названа в честь золотого сечения. Примечательно то, что в своей книге Пачоли не отстаивал теорию эстетики этого сечения в отношении к искусству, архитектуре и дизайну: вместо этого он поддерживал Витрувианскую систему рациональных пропорций, основанную римским архитектором первого века, Витрувием. Золотое сечение ошибочно было приписано Пачоли в 1799 году, согласно Марио Ливио, который буквально написал книгу по золотому сечению. Но Пачоли был близким другом Леонардо да Винчи, чьи работы получили огромное признание и популярность в 19 веке. Так как Да Винчи проиллюстрировал De Divina Proportione, вскоре начали говорить, что и сам Да Винчи применил золотое сечение как секретную математику в своих восхитительно красивых творениях.

Адольф Цейзинг был тем, кто в это поверил. “Это человек, который хотел сжечь себя на костре во имя репутации золотого сечения” – шутит Девлин. Цейзинг был немецким психологом, который отстаивал идею, что золотое сечение является универсальным законом, описывающим “красоту и завершенность в природе и в искусстве… оно проходит красной нитью как первостепенный духовный идеал во всех структурах, формах и пропорциях, космических и индивидуальных, органических и неорганических, акустических или оптических”.

Он был очень многословным. Единственной проблемой Цейзинга было то, что он видел закономерности там, где их не было. Например, Цейзинг доказывал, что золотое сечение можно применить к человеческому телу, взяв рост человека от пупка до пальцев ног, поделив его на полный рост. По словам Девлина, это всего лишь произвольные части тела, слепленные в формулу. Он говорит: “При замерах чего-то столь сложного, как человеческое тело, очень легко найти примеры разных пропорций, близких к 1.6”.

В моей собственной работе я даже не найду примера использования золотого сечения.

Но это не имеет никакого значения. Теории Цейзинга стали невероятно популярны, и Девлин называет их “эквивалентом эффекта Моцарта 19-го века”. Эффект Моцарта гласит, что прослушивание классической музыки повышает интеллект. В 20 веке известный швейцарско-французский архитектор Ле Корбузье положил золотое сечение в основу своей системы антропометрических пропорций “Модулора”. Дали нарисовал свой шедевр “Тайная вечеря” на холсте в форме золотого прямоугольника. Тем временем историки искусства начали просматривать и другие шедевры, пытаясь отыскать золотое сечение в Стоунхендже, полотнах Рембранта, Шартрском соборе и работах Сёра. Связь между золотым сечением и красотой превратилась в самую раздутую утку в мире искусства, архитектуры и дизайна.

Ian Yen на Yanko Design

На самом деле, вы не очень-то и предпочитаете золотое сечение

В реальном мире людям не особо необходимо золотое сечение.

Девлин совместно с кафедрой психологии Стенфордского университета в течение многих лет опрашивал сотни студентов, какой прямоугольник их любимый. Он показывал разные прямоугольники студентам, а затем просил их выбрать наиболее понравившийся. Если бы оды золотому сечению были оправданы, студенты бы выбирали прямоугольники, близкие к золотому. Но это было не так. Они выбирают их произвольно. И если вы попросите их повторить свой выбор, они выберут другие прямоугольники. “Это очень полезный пример для демонстрации сложности человеческого восприятия”. Кроме того, это отличная демонстрация того, что золотое сечение не является более приятным для людей с эстетической точки зрения.

Эксперименты Девлина не единственные в исследовании золотого сечение. Исследование, проведенное специалистами Школы бизнеса имени Уолтера Хааса в Беркли, показало, что в среднем потребители предпочитают прямоугольники, пропорция которых между 1.414 и 1.732. Золотое сечение входит в этот диапазон, но не является явным “любимчиком” публики.

Многие современные дизайнеры не считают его полезным

Дизайнеры, с которыми мы обсуждали золотое сечение, не видят в нем особой пользы.

Ричард Мейер, легендарный архитектор, автор Центра Гетти и Музея современного искусства в Барселоне, отмечает, что в начале своей карьеры у него был архитекторский треугольник, который соответствовал золотому сечению, но он никогда не создавал свои здания по золотому сечению. “В мире такое множество других чисел и формул, которые важнее при проектировании зданий”, – говорит Мейер, ссылаясь на формулы по расчету максимальных допустимых размеров пространств зданий, или на формулы расчета структурной нагрузки.

Алиса Андрасек, дизайнер из Biothing, онлайн-репозитория машинного проектирования, соглашается с этим: “В своей работе я даже не найду примера использования золотого сечения. Я могу представить, что эту пропорцию можно встроить в разные системы в качестве ‘изюминки’, но мне сложно вообразить, чтобы весь дизайн был построен именно на золотом сечении, как это случалось в истории… это слишком уж упрощенно”.

Джорджия Лупи из Accurat, итальянской дизайн-фирмы, говорит, что в лучшем случае золотое сечение так же важно для дизайнеров, как и любое другое композиционное правило, например, правило третей: отличное распространенное правило, которое хорошие дизайнеры могут с таким же успехом проигнорировать. “Я не знаю, сколько дизайнеров на практике специально внедряют золотое сечение в свои работы. Лично я никогда не работала с этой пропорцией в своих проектах”.

Из всех опрошенных дизайнеров, индустриальный дизайнер Ив Бехар из Fuseproject теплее всех относится к золотому сечению: “Иногда я действительно вижу золотое сечение в пропорциях продуктов и графики, которую мы создаем, но это скорее просто случайность, чем догма. Это важный инструмент, но не правило”.

Даже дизайнеры, которые по совместительству являются математиками, скептически относятся к использованию золотой пропорции в дизайне. Эдмуд Харрис – клинический доцент кафедры математики в Университете Арканзаса, который использует множество формул для создания новых произведений искусства. Но и Харрис говорит, что золотое сечение, в лучшем случае, всего лишь один из множества инструментов в руках дизайнеров, склонных к математике: “Во многих смыслах это просто число, и оно, как и другие числа, часто встречается в разных местах… [Но] это точно не универсальная формула эстетической красоты”.

Тайная вечеря, 1955, Сальвадор Дали

Почему этот миф так популярен?

Если ценность золотого сечения так незначительна, почему же этот миф процветает?

Девлин поясняет это просто: “Мы создания, генетически запрограммированные видеть паттерны и искать смысл. В нашей ДНК не зашифрована способность мириться с условными вещами вроде эстетики, поэтому мы пытаемся доказать их с помощью нашего часто ограниченного математического видения. Большая часть людей не понимает математику, и даже не может понять, как формула вроде золотого сечения применяется к сложной системе, так что и проверить себя они не могут. Люди думают, что повсюду видят золотое сечение, в природе и в любимых объектах, но они не могут это обосновать. Они – жертвы своего природного желания найти смысл в разных объектах вселенной, но из-за недостаточной математической грамотности они не могут понять, что обнаруживаемые закономерности иллюзорны”.

Золотое сечение — подробное объяснение

Золотое сечение, также известное как золотая пропорция, золотая середина, золотое сечение, золотое число и божественная пропорция, представляет собой деление данной единицы длины на две части таким образом, чтобы отношение более короткой к более длинному равняется отношению более длинной части к целому или, когда линия разделена таким образом, что отношение более длинной части линии ко всему целому точно такое же, как отношение более короткой части линии к более длинной часть.

Это число, которое часто встречается при измерении отношений расстояний в простых геометрических фигурах, таких как пятиугольник, пентаграмма, десятиугольник и додекаэдр.Это соотношение или пропорция, определяемая числом Phi = 1,618033988749895 … Это иррациональное число, то есть это число, которое нельзя записать как простую дробь — десятичная дробь продолжается бесконечно, не повторяя. Фи, как и Пи, представляет собой отношение, определяемое геометрической конструкцией.

Точно так же, как Pi — это отношение длины окружности к ее диаметру, Phi — это просто отношение отрезков линии, которые возникают при разделении линии одним очень особым и уникальным способом.

Фигура золотого сечения иллюстрирует геометрическую связь, определяющую эту константу.Выражается алгебраически:

Уникальным положительным решением этого уравнения является алгебраическое иррациональное число

Формы, пропорциональные золотому сечению, долгое время считались эстетически приятными во многих культурах и до сих пор часто используются в искусстве и дизайне, что предполагает естественный баланс между симметрией и асимметрией.

Древние пифагорейцы, которые определяли числа как выражения соотношений (а не как единицы, как это принято сегодня), считали, что реальность является числовой и что золотое сечение выражает основную истину о существовании.

Золотое сечение, кажется, получило свое название от золотого прямоугольника, прямоугольника, стороны которого пропорциональны золотому сечению.

Теория Золотого Прямоугольника — эстетическая, что соотношение является эстетически приятным и поэтому может быть обнаружено спонтанно или намеренно в большом количестве произведений искусства. Фасад Парфенона удобно оформить золотым прямоугольником. Дополнительные классические части прямоугольника идеально сочетаются с основными архитектурными особенностями строения.

Золотой прямоугольник можно использовать для создания спирали, Золотой спирали. Начиная с одного золотого прямоугольника, второй золотой прямоугольник может быть прикреплен к первому, используя самую длинную сторону прямоугольника, сторону A как самую короткую сторону B следующего прямоугольника. Для этого второй прямоугольник строят под углом 90 градусов перпендикулярно первому. Если продолжить этот процесс, называемый спиралью Золотого прямоугольника, через углы прямоугольников можно провести изогнутую линию, создав спираль Золотого Сечения.Спираль золотой середины продолжается бесконечно во внутреннем и внешнем направлениях, она становится все меньше и меньше по спирали внутрь и все больше и больше по спирали наружу.

Другая связь золотого сечения с частичными симметриями в природе — это числа Фибоначчи. Это числовой ряд, в котором каждый член представляет собой просто сумму двух предыдущих чисел. Спирали Фибоначчи и отношения золотого сечения появляются повсюду во Вселенной. Спираль — это естественная форма потока воды, когда она стекает в канализацию.Это также естественная форма потока воздуха во время торнадо и ураганов. Вот еще один прекрасный пример спирали Фибоначчи в природе, это оболочка Наутилуса, и каждая книга о сакральной геометрии содержит ее:

Размеры Великой пирамиды Гизы также основаны на золотом сечении. Если мы возьмем поперечное сечение Великой пирамиды, мы получим прямоугольный треугольник, так называемый Египетский треугольник. Отношение наклонной мета-высоты пирамиды (гипотенузы треугольника) к расстоянию от центра земли (половина размера основания) равно 1.61804 … который отличается от фи только на одну единицу пятого знака после запятой. Если мы допустим базовое измерение равным 2 единицам, тогда стороны прямоугольного треугольника будут иметь пропорцию 1: sqrt (phi): phi, а мета-высота пирамиды будет равна sqrt (phi).

Леонардо да Винчи демонстрировал золотое сечение во многих своих картинах и иллюстрациях, назвав его De Divina Proportione или «божественная пропорция». Он провел полное исследование человеческого тела и соотношения длин различных частей тела.

© Token Rock, Inc. Все права защищены.

.

Золотое сечение

Подкаст Skeptoid # 325
28 августа 2012 г.
Расшифровка подкаста | Подписывайся
Также доступно на русском языке | Арабский

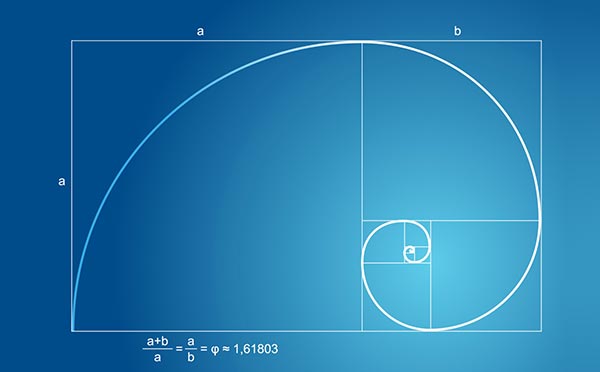
Спирали Фибоначчи в семенах подсолнечника Фото: Викимедиа

Вы, наверное, слышали, что в течение тысяч лет человечество очаровывалось золотым сечением, которое значение от 1 до φ (фи, произносится как «гонорар» в США и их родном греческом языке, и «фи» во многих других странах).φ составляет около 1,618. Это иррациональное число, которое продолжается вечно и определяется как

.

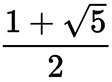
Золотой прямоугольник, стороны которого пропорциональны золотому сечению, чуть более приземистый, чем экран вашего телевизора высокой четкости. Этот прямоугольник считается наиболее эстетичным и, более того, встречается в природе, определяя пропорции всех видов живых существ, включая идеальное человеческое лицо. Говорят, что великие композиторы, художники и архитекторы основывали свои работы на этом соотношении.Игроки финансовых рынков создают формулы, которые полагаются на это. Повсюду в вашем доме вы найдете множество предметов, соблазнительно напоминающих золотой прямоугольник: книги, приборы, крышки электрических розеток, игральные карты, картины, окна. Люди нашли его в структуре ДНК и расположении молекул в кристаллах. Самый известный из них — греческий Парфенон, выдающийся образ архитектуры, который, как говорят некоторые, почти полностью основан на золотом сечении. Многие считают, что это соотношение настолько распространено как в природе, так и в дизайне, что его также называют божественной пропорцией.

φ и золотое сечение известны своими уникальными математическими и геометрическими свойствами. Если вы возьмете прямоугольник, стороны которого пропорциональны золотому сечению, вы можете отрезать квадрат с одного его конца, и полученный маленький прямоугольник, который останется, будет иметь те же пропорции, что и оригинал. Вы можете вырезать из него квадрат, и вы получите прямоугольник золотого сечения еще меньшего размера, и вы можете сделать это до бесконечности. Это его основное геометрическое свойство.

Важнейшим математическим свойством φ является то, что это отношение последовательных чисел в ряду Фибоначчи.Ряд Фибоначчи состоит из значений, равных сумме двух предыдущих значений: 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. 5 + 8 = 13, 8 + 13 = 21, 13 + 21 = 34 и так далее. Поскольку этот ряд продолжается бесконечно, отношение каждого числа к предыдущему становится все ближе и ближе к φ; но, поскольку серия бесконечна, она никогда не достигает цели. Итак, φ — это предел отношения этой последовательности. По 40-му значению в ряду Фибоначчи, которое составляет 102 334 155, φ имеет точность до 15 знаков после запятой.

Вот, пожалуй, самое интересное проявление фи в природе.Это связано с эффективной упаковкой. Когда вы смотрите прямо на дерево сверху, дерево будет наиболее эффективным, если видно как можно больше листьев и не затенено другими листьями. По мере роста стебля необходимо знать, как часто следует производить лист и под каким углом от предыдущего листа, согласно генетической формуле. Если бы он производил каждый лист с интервалом, например, 1/4 оборота, каждый лист заканчивался бы затенением четвертого листа над ним. Фактически, какую бы целую долю полного оборота мы ни использовали, мы в конечном итоге повторяем узор и закрашиваем листья.Таким образом, эволюция в конечном итоге привела к более эффективной генетической инструкции: φ. Производите φ листьев за оборот — чуть более 137,5 ° между последовательными листьями — и никакие два листа никогда не затенят друг друга. Этот угол называется золотым углом.

Мы видим очень конкретный и очевидный пример этого рисунка в семенах в центре подсолнечника. Соцветия, которые созревают в семена, вырастают из центра подсолнечника, и каждый новый из них выталкивает существующие семена наружу. В результате каждого нового семени, растущего под золотым углом от своего предшественника, получается подсолнечник, семена которого максимально эффективно упакованы в круглую головку цветка, независимо от того, насколько большим становится цветок.Этот тип насадки создает видимые перекрещивающиеся спиральные узоры в обоих направлениях вокруг головы. Не случайно, что для цветка любого размера количество спиральных рукавов по часовой стрелке и спиральных рукавов против часовой стрелки всегда является двумя последовательными числами Фибоначчи. Семена в сосновой шишке и другие подобные структуры из растительного мира следуют той же схеме.

Эта тенденция для соотношений, основанных на φ, для устранения повторения имеет инженерное применение. Один из наиболее известных — это дизайн звуковых комнат для прослушивания музыки или просмотра фильмов, комнат, в которых мы хотим подавить стоячие звуковые волны и резонансы.Аудиоинженеры ссылаются на золотое соотношение комнаты, которое устанавливает базовые идеальные размеры звуковой комнаты 10 × 16 × 26. Высота комнаты 10 × φ ≈ 16, что дает длину комнаты, и 16 × φ ≈ 26, что дает ширину комнаты. Любой диагональный прямой путь, пройденный внутри золотого прямоугольника, будет отражаться бесконечно, никогда не повторяя свой курс, поэтому звуковые волны внутри комнаты таких размеров всегда рассеиваются с максимальной эффективностью.

Несмотря на то, что многие книги и статьи утверждают иное, точная история понимания человеком золотого сечения неизвестна.Около 500 г. до н. Э. Греческий математик Пифагор основал пифагорейскую школу мысли, символом которой была пентаграмма. Когда вы вписываете звезду в пятиугольник, соотношение всех отрезков прямой является золотым сечением; поэтому, хотя кажется, что он должен был знать об этом соотношении, сам Пифагор не оставил никаких работ, которые бы рассказывали нам наверняка. Более конкретное раннее определение исходит от Евклида, который установил золотое сечение в своей книге Elements около 300 г. до н.э., назвав его крайним и средним соотношением.Кажется почти наверняка, что они должны были знать о рядах Фибоначчи; однако только примерно в 1200 году Леонардо Фибоначчи описал знаменитую последовательность, которая теперь носит его имя, но ни одно из работ Фибоначчи не показывает, что он когда-либо устанавливал ее связь с φ или золотым сечением. Сегодня концепции и отношения хорошо изучены, и теперь они представляют собой обычные математические приемы.

Появление золотого сечения в мире природы почти неизбежно привело к его принятию и кооптированию многими альтернативными исследователями практически во всех дисциплинах.Возможно, самым известным псевдонаучным утверждением о золотом сечении является то, что греческий Парфенон, знаменитый храм с колоннами на вершине Акрополя в Афинах, спроектирован вокруг этого соотношения. Многие любители накладывают золотые прямоугольники на все изображения Парфенона, утверждая, что нашли совпадение. Но если вы когда-либо изучали такие изображения, вы видели, что они никогда не подходят полностью, по крайней мере, не лучше, чем любой другой прямоугольник, который вы можете попробовать. Это потому, что нет достоверных исторических или документальных свидетельств того, что дизайнеры Парфенона, которые работали более века до рождения Евклида, когда-либо использовали золотое сечение каким-либо образом или даже знали о его существовании.

Еще одно псевдонаучное утверждение состоит в том, что золотое сечение присутствует во всем человеческом теле. Написаны целые тома чепухи, утверждающей, что всевозможные произвольные измерения тела выдают золотое сечение. Ширина плеч по сравнению с высотой головы; высота пупка относительно высоты всего тела; длина предплечья по сравнению с расстоянием от головы до кончиков пальцев; и так далее, и так далее, и так далее. Очевидно, что эти измерения у всех разные; вероятно, нет ни одного живого человека, для которого эти многочисленные утверждения верны.Более того, это совершенно произвольно. Дайте мне любое число, любое соотношение или любую форму, и я с таким же легкостью смогу составить такой же длинный список черт тела, который одинаково точен.

Еще один хороший пример — книга. Высота и ширина обычной книги определяется удобством; мы хотим, чтобы он имел удобные пропорции в закрытом (не слишком высоком) и открытом (не слишком широком) положении. Некоторые называют 1: φ идеальной формой книги, но это неверно. Размер книги такой, чтобы ее пропорции были одинаковыми независимо от того, открыта она или закрыта — 1: √2, а не 1: φ.φ значительно больше √2. В бумажной промышленности соотношение 1: √2 называется отношением Лихтенберга.

Простой факт заключается в том, что прямоугольники, которые не являются ни слишком квадратными, ни слишком узкими, являются наиболее привлекательными и часто наиболее удобными в дизайне. Золотое сечение попадает в диапазон обычно приятных прямоугольников, но также и √2, √3 и многие другие числа. Нет необходимости утверждать, что существует единственное идеальное соотношение, которое лучше всего подходит для всех приложений.

Хороший способ отличить реальные проявления золотого сечения от выдуманных или предполагаемых — служит ли оно цели, которой не может служить подобное число.Подсолнухи используют золотой угол для очень конкретной цели, и для этого абсолютно необходимо число φ. Примером ошибочного проявления является утверждение, что каждый сустав вашего пальца длиннее другого по золотому сечению. Это не только измеримо неверно, но и не принесет особой пользы в этом случае, и, следовательно, ничего подобного не произошло. Преимущество повышенной точности при все более малых масштабах манипуляции означает, что полезно иметь постепенно уменьшающиеся сегменты пальцев, так что это то, что у нас есть.Но нет необходимости в том, чтобы это было золотое сечение или даже все в точности одинаковыми, так что это не так.

Еще один псевдонаучный пример из природы — это спиралевидная морская ракушка. Золотая спираль — это спираль, которая становится в φ раз шире с каждой четвертью оборота, и часто говорят, что раковина наутилуса следует за ней. Не правда. Золотая спираль — это только одна из бесконечного числа возможных логарифмических спиралей. Для наутилуса полезно иметь возможность сохранять ту же форму во время роста, и этой цели служит любая приблизительно логарифмическая спираль.Основание фактора роста спирали на φ не принесет дополнительных преимуществ.

φ, золотое сечение и ряд Фибоначчи математически интересны и имеют естественные проявления. Это не значит, что все или даже что-либо еще основано на них. Популярность и «громкое имя» «божественной пропорции» были реальной движущей силой ее псевдонаучного назначения практически всему и чему угодно. Те, у кого программное обеспечение сопоставления с образцом в мозгу перегружено, вероятно, слышали о золотом сечении, и поэтому они думают о нем всякий раз, когда видят прямоугольник или великое произведение искусства (например, Мона Лизу, которая не основана на золотое сечение), или модели на фондовом рынке (которые вообще не существуют, не говоря уже о золотом сечении), или в нумерологии Библии (если любое другое число не может считаться столь же значимым).Не все утверждения о золотом сечении являются результатом гиперактивного сопоставления с образцом, но большинство из них. Как минимум, такое заявление — всегда хороший сигнал, к которому вы должны относиться скептически.

.

Руководство по золотому сечению (также известное как Золотое сечение или Золотое сечение) для художников

Дайанн Мизе в Уроки рисования> Уроки рисования

Существует математическое соотношение, обычно встречающееся в природе — отношение 1 к 1,618, — которое имеет много названий. Чаще всего мы называем его золотым сечением , золотым сечением или золотым сечением, , но иногда его также называют золотым числом, божественной пропорцией, золотой пропорцией, числом Фибоначчи и фи.

Обычно золотое сечение изображается как один большой прямоугольник, образованный квадратом и другим прямоугольником. Уникальность этого заключается в том, что вы можете повторять последовательность бесконечно и идеально в каждом разделе.

Быстрое объявление — EmptyEasel создала более быстрый и простой способ для художников иметь собственный сайт об искусстве. Щелкните здесь, чтобы узнать больше и получить собственный простой художественный сайт!

Если убрать большой квадрат слева, останется еще один золотой прямоугольник., , и так далее.

Золотое сечение в искусстве и архитектуре

Появление этого соотношения в музыке, в моделях человеческого поведения, даже в пропорциях человеческого тела, — все указывает на его универсальность как принцип хорошей структуры и дизайна.

Золотое сечение, используемое в искусстве, является наиболее загадочной из всех композиционных стратегий. Мы знаем, что создавая изображения на основе этого прямоугольника, наше искусство будет более привлекательным для человеческого глаза, но мы не знаем почему.

Некоторые ученые утверждают, что египтяне применяли золотое сечение при строительстве великих пирамид еще в 3000 году до нашей эры.

В 300 г. до н. Э. Евклид описал золотое сечение в своих стихах Евклида, а до этого, около 500 г. до н.э., Пифагор утверждал, что золотое сечение является основой пропорций человеческой фигуры.

Древние греки также использовали золотое сечение при строительстве Парфенона.

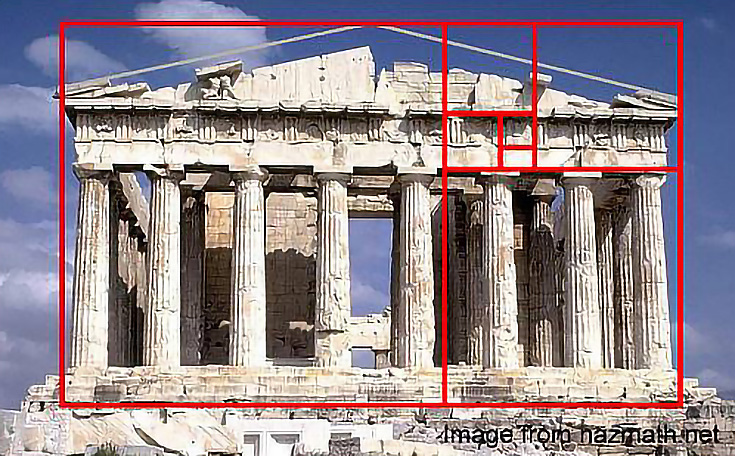
Художники на протяжении всей истории, такие как Боттичелли и Леонардо да Винчи, использовали золотой прямоугольник или его вариации в качестве основы для своих композиций.

Вот картина да Винчи, Тайная вечеря , с выделенными золотыми сечениями.

Золотые прямоугольники по-прежнему остаются самыми красивыми из известных прямоугольников, и, хотя они основаны на математическом соотношении, вам не понадобится ни йоты математики, чтобы создать его.

Как сделать прямоугольник по золотому сечению

Если вы хотите использовать золотой прямоугольник в своих композициях, вот как это сделать без каких-либо специальных инструментов или математических формул.

1. Начните с квадрата, который будет длиной короткой стороны прямоугольника.

2. Затем нарисуйте линию, разделяющую ее пополам (образуя два прямоугольника).

3. Проведите линию от угла к противоположному углу одной из этих половинок.

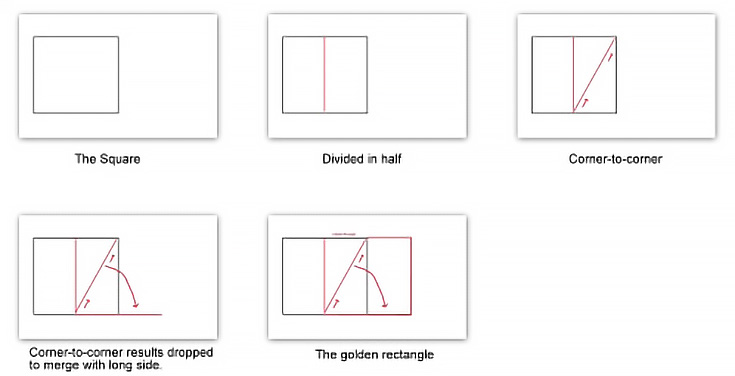
4. Поверните верхнюю точку диагональной линии вниз, пока она не расширит ваш квадрат.

5. Закончите прямоугольник, используя длину диагонали в качестве ориентира для длинной стороны вашего золотого прямоугольника.Это так просто.

Визуальные объекты внутри золотого прямоугольника

Любой квадрат или прямоугольник (но особенно те, которые основаны на золотом сечении) содержат области внутри, которые также привлекают нас визуально. Вот как вы их найдете:

1. Проведите по прямой от каждого нижнего угла к противоположному верхнему углу с каждой стороны. Они пересекутся точно в центре формата.

2. Найдите середину каждого противоположного угла от центра к каждому углу.

Эти точки, представленные зелеными точками на диаграмме выше, называются «глазами прямоугольника».

Как использовать «глаза» золотого прямоугольника

Одна из стратегий, часто используемых художниками, заключается в размещении фокусных точек или областей акцента вокруг и внутри этих глаз, создавая сильный визуальный путь в своих композициях.

Композиция Эдварда Хоппера, приведенная ниже, устанавливает парусную лодку прямо над правым нижним глазом (кончики парусов доходят почти до правого верхнего глаза).

На этой картине Кэролайн Андерсон тоже кладет руки своего объекта на это место.

J.M.W. Тернер использует угол своих волн, чтобы создать дугу, проходящую через нижний правый и нижний левый глаза.

Обратите внимание, что фокус сцены также фиксируется всеми четырьмя глазами.

Использование золотого сечения или этих «глаз» для направления визуального пути зрителя ограничено только вашим воображением.Попробуйте использовать глаза прямоугольника на следующем рисунке и посмотрите, как это может повлиять на силу вашей композиции.

ПОЛУЧИТЬ ЛИСТНИК В СВОЕМ ЯЩИКЕ

Мы будем отправлять вам статьи и руководства сразу после их публикации, чтобы вы не пропустили ни одной публикации! Отпишитесь здесь в любое время.

ПРИМЕЧАНИЕ. Вас также может заинтересовать пошаговое руководство по рисованию от EE для художников. Нажмите ниже, чтобы узнать больше!

Этот пост может содержать партнерские ссылки.

.