Определение расстояния до недоступной точки: Презентация к уроку (геометрия, 8 класс) на тему: Определение расстояния до недоступной точки.

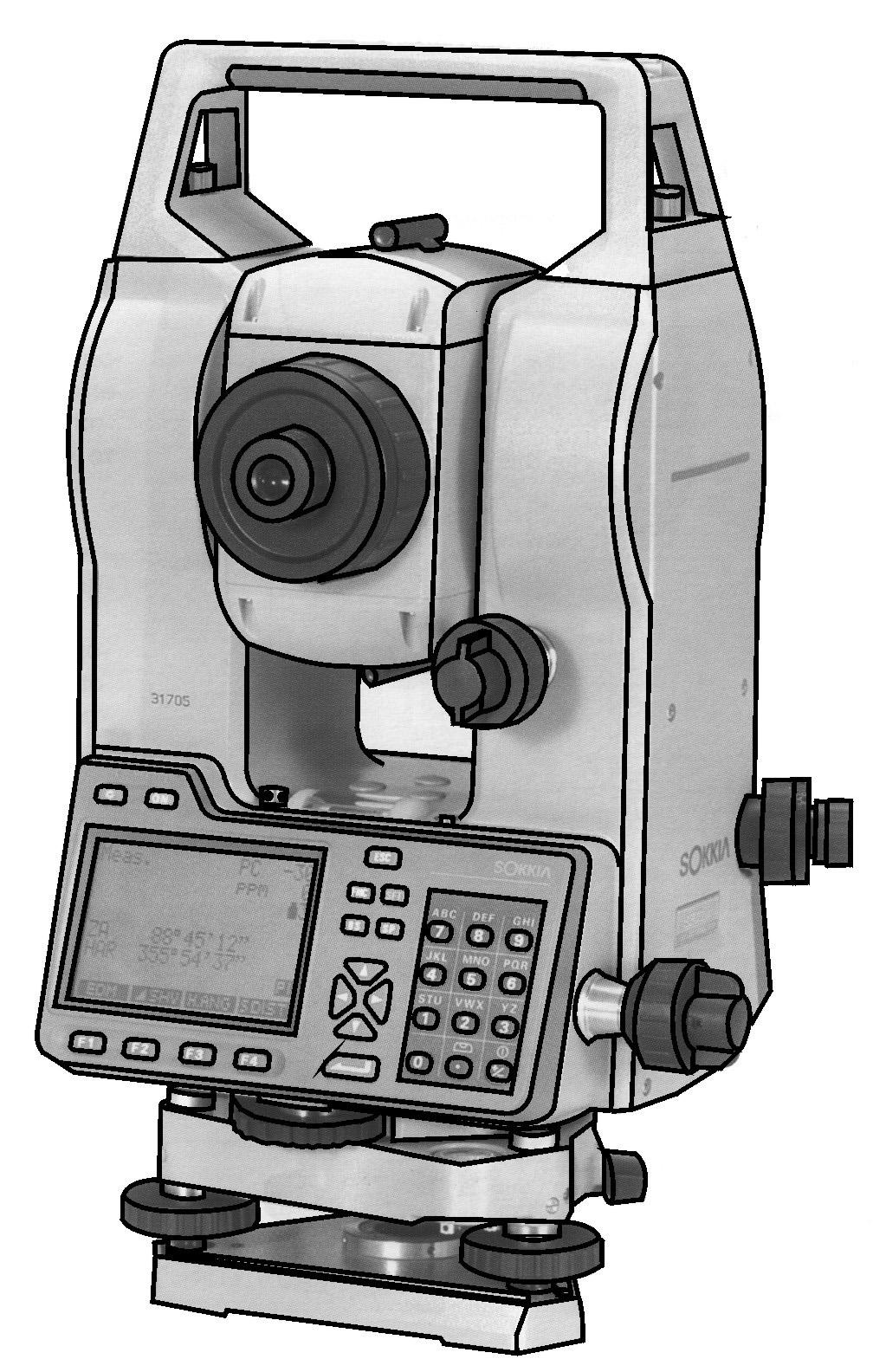
Презентация к уроку (геометрия, 8 класс) на тему: Определение расстояния до недоступной точки.

Слайд 1

И змерение расстояния до недоступной точки

Слайд 2

Определение расстояния до недоступной точки. Геометрическое объяснение «способа козырька». Этот способ часто применяется военными и туристами, для определения расстояния до недоступной точки. Задача №1

Слайд 3

Луч зрения, касающийся обреза козырька (ладони, записной книжки), первоначально направлен на линию противоположного берега. Когда человек поворачивается, то луч зрения, подобно ножке циркуля, как бы описывает окружность, и тогда расстояние до предмета на том берегу равно расстоянию до предмета на этом берегу.

Слайд 4

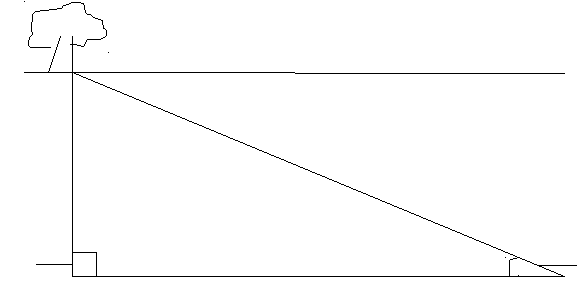
Определение высоты предмета. Задача №2 Своеобразный способ определения высоты дерева — при помощи зеркала . На некотором расстоянии от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку Д, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ЕД), во сколько раз расстояние ВС от зеркала до дерева больше расстояния СД от зеркала до наблюдателя. Почему?

Слайд 5

Способ основан на законе отражения света. Вершина А отражается в точке А’ так, что АВ=А’В. Из подобия же треугольников ВСА’ и СЕД следует, что АВ’:ЕД=ВС:СД. В этой пропорции остается лишь заменить А’В равным ему АВ, чтобы обосновать указанное в задаче соотношение . Этот удобный и нехлопотливый способ можно применять во всякую погоду, но не в густом насаждении, а к одиноко стоящему дереву.

Слайд 6

Задача №3 Определение высоты предмета по способу Жюля Верна Следующий – тоже весьма несложный – способ измерения предметов картинно описан у Жюля Верна в известном романе «Таинственный остров». «- Сегодня нам надо измерить высоту площадки Далекого Вида, — сказал инженер. — Вам понадобится для этого инструмент? — спросил Герберт. — Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. — Тебе знакомы зачатки геометрии? — спросил он Герберта, поднимаясь с земли. — Да. — Помнишь свойства подобных треугольников? — Их сходственные стороны пропорциональны. — Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч. У другого основания треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мой луч зрения, совпадающий с направлением гипотенузы первого треугольника.

Слайд 7

-Понял! — воскликнул юноша — Расстояние от колышка до шеста так относится к расстоя­нию от колышка до основания стены, как высота шеста к высоте стены. — Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты». Оба горизонтальных расстояния были измерены: меньшее — 15 футов, большее — 500 футов. По окончании измерений инженер составил следующую запись: 15:500=10:х, 500∙10=5000, 5000:15=333,3 Значит, высота гранитной стены равнялась 333 футам.

Определение недоступных расстояний. | Инженерная геодезия. Часть 1.

Если препятствие (река, обрыв, здание) делает расстояние недоступным для измерения лентой, то его измеряют косвенным методом.

Так, для определения недоступного расстояния d измеряют лентой длину базиса b (рис. 8.3, а, б) и углы a и b . Из DABC находят

d = b sin a / sin (a + b),

где учтено, что sin g = sin (180°-a-b) = sin (a + b).

 

Рис. 8.3. Определение недоступного расстояния

 

Для контроля расстояние d определяют ещё раз из треугольника ABC₁ и при отсутствии недопустимых расхождений вычисляют среднее.

8.3. Нитяный дальномер

Теория нитяного дальномера. Зрительные трубы многих геодезических приборов снабжены нитяным дальномером. Сетка нитей зрительной трубы, кроме основных штрихов (вертикальных и горизонтальных), имеет дальномерные штрихи

a и b (рис. 8.4, а). Расстояние D от оси вращения прибора MM (рис. 8.4, б) до рейки AB равно

D = L + f + d ,

где L — расстояние от фокуса объектива до рейки; f — фокусное расстояние; d — расстояние между объективом и осью вращения прибора.

Лучи, идущие через дальномерные штрихи сетки a и b параллельно оптической оси, преломляются объективом, проходят через его фокус F и проецируют изображения дальномерных штрихов на точки A и B, так что дальномерный отсчёт по рейке равен n. Обозначив расстояние между дальномерными штрихами p, из подобных треугольников ABF и a¢b¢F находим L = n f / p. Обозначив f / p = K и f +

d = c , получаем

D = K n + c ,

где K — коэффициент дальномера и c — постоянная дальномера.

 

Рис. 8.4. Нитяный дальномер: а) – сетка нитей; б) – схема определения расстояния

При изготовлении прибора f и p подбирают такими, чтобы K=100, а постоянная c была близкой к нулю. Тогда D = 100 n.

Точность измерения расстояний нитяным дальномером » 1/300.

Определение горизонтального проложения линии, измеренной нитяным дальномером. При измерении наклонной линии отсчёт по рейке это отрезок n = AB (рис. 8.5). Если бы рейку наклонить на угол n, то отсчёт был бы равен n₀ = A₀B₀ = n cosn и наклонное расстояние

D=Kn₀+c = Kn×cosn+c.

Рис. 8.5. Измерение нитяным дальномером наклонного расстояния

Умножив наклонное расстояние D на cosn, получим горизонтальное расстояние d = K n cos² n + c cos n.

Прибавив и отняв с× cos²n, после преобразований получим

d = (Kn + с) cos²n + 2c cosn sin²(n¤2).

Вторым слагаемым по его малости пренебрежем. Получим

d = (Kn + с) cos²n .

Вычисления упрощаются, если воспользоваться составленными с использованием этой формулы «Тахеометрическими таблицами».

НАХОЖДЕНИЕ РАССТОЯНИЯ ДО НЕДОСТУПНОЙ ТОЧКИ. ИЗМЕРЕНИЕ ШИРИНЫ РЕКИ ИВИНКА

НАХОЖДЕНИЕ РАССТОЯНИЯ ДО НЕДОСТУПНОЙ ТОЧКИ. ИЗМЕРЕНИЕ ШИРИНЫ РЕКИ ИВИНКА

Корженевский Д.А. 1

---

1

Каменская З.А. 1

---

1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Цель проекта:  

• Научиться измерять ширину реки Ивинка разными способами без специальных приборов;

• Применять математические знания для решения задач реальной жизни.

Задачи проекта:

• познакомиться с историческим и теоретическим материалом по вопросу измерения ширины реки;

• применить математические знания в решении практических задач;

• измерить ширину реки Ивинка разными способами, найти наиболее простой способ измерения и сопоставить точность разных методов;

• научиться проводить измерительные работы на местности.

Основополагающий вопрос:

Как можно измерить ширину реки, находясь на одной стороне реки?

Гипотеза:

Применяя признаки равенства треугольников и подобие треугольников, мы сможем найти ширину реки!

Объектом исследования нашей работы является река Ивинка.

Предметом исследования – нахождение ширины реки Ивинка.

Методы исследования:

• обобщение научной литературы по данной теме;

• практическая работа на местности;

• решение задачи, сравнение, анализ;

• использование технических средств видео и фотосъемки.

Актуальность исследования:

• Данная тема является дополнением и углублением изученных в курсе геометрии методов измерения расстояния до недоступной точки;

• Полученный опыт позволит находить без каких-либо сложных технических устройств расстояние до недоступной точки;

• Изучение данной темы поможет более глубоко подготовиться к выпускным экзаменам в 9 и 11 классах.

Введение:

Часто в походе возникает ситуация, когда необходимо определить расстояние до недоступной точки, но нет возможности применить технические средства. Например: требуется определить ширину реки. Это можно сделать с помощью подручных средств или на глаз.

Способы определения расстояния до недоступной точки:

• Измерение ширины реки при помощи травинки;

• При помощи двух равных прямоугольных треугольников;

• В зимнее время можно измерить ширину реки с помощью рулетки, проходя с одного берега реки до другого по льду.

1. Измерение ширины реки при помощи травинки.

Выбираем на противоположном берегу, в непосредственной близости от него, два заметных предмета и, стоя по другую сторону реки с вытянутыми руками, в которых зажата травинка, закрываем промежуток между выбранными предметами. Один глаз должен быть закрыт.

После этого сложив травинку пополам, отходим от берега реки до тех пор, пока расстояние между выбранными предметами не закроется сложенной травинкой. Затем измеряем промежуток между двумя точками своего стояния. Расстояние между ними будет равно ширине реки.

Нами снят учебный фильм « Измерение ширины реки Ивинка при помощи травинки» (смотри Приложение 1).

1. Способ измерения ширины реки, основанный на построении равнобедренных треугольников.

Попробуем измерить ширину реки в походных условиях. Ширину реки можно определить геометрическим глазомерным способом, путём построения вдоль её берега двух равных прямоугольных треугольников.

Нами снят учебныйфильм: «Измерение ширины реки Ивинка при помощи двух равных прямоугольных треугольников»

(смотри Приложение 2).

1. Способ измерения ширины реки с помощью рулетки.

Результат: 42 метра.

Анализ результатов измерения ширины реки Ивинка:

Способы измерения	Ширина реки
Измерение ширины реки при помощи травинки	47 м
При помощи двух равных прямоугольных треугольников.	37 м
С помощью рулетки по льду.	42 м

Заключение.

Мы рассмотрели разные способы измерения ширины реки, описанные в научной литературе.

Реализовали на практике 3 способа. Как показал результат, точность измерения 1 и 2 способом недостаточна. Мы видим, что наиболее точный способ измерения ширины реки — с помощью рулетки, но этот способ возможен только зимой, значит, в реальных условиях можно найти ширину реки, находясь на одном берегу, используя знание геометрии, при помощи двух равных прямоугольных треугольников.

Для нас наиболее простым и приемлемым оказался способ измерения ширины реки, основанный на построении двух равных прямоугольных треугольников.

Таким простым способом можно измерить примерную ширину реки в походных условиях.

Мы выдвинули гипотезу:

Применяя признаки равенства треугольников и подобие треугольников, мы сможем найти ширину реки!

Наша гипотеза подтвердилась!

Ипользуемые ресурсы:

1. Учебник Геометрия 7-9, автор: Атанасян Л.С.

2. http://ru.wikipedia.org

3. Презентация Проекта, для создания которой использована программа PowerPoint из пакета программ Microsoft Office.

Приложение:

1. Фильм « Измерение ширины реки при помощи травинки»;

2. Фильм «Измерение ширины реки при помощи прямоугольных треугольников».

Просмотров работы: 3034

Определение недоступных расстояний — Студопедия.Нет

Если препятствие (река, обрыв, здание) делает расстояние недоступным для измерения лентой, то его измеряют косвенным методом.

Так, для определения недоступного расстояния d измеряют лентой длину базиса b (рис. 8.3, а, б) и углы a и b . Из DABC находят

d = b sin a / sin (a + b),

где учтено, что sin g = sin (180°-a-b) = sin (a + b).

 

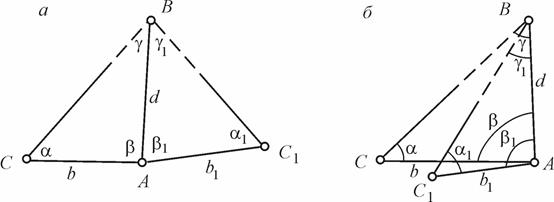
Рис. 8.3. Определение недоступного расстояния

 

Для контроля расстояние d определяют ещё раз из треугольника ABC1 ипри отсутствии недопустимых расхождений вычисляют среднее.

Нитяный дальномер

Теория нитяного дальномера. Зрительные трубы многих геодезических приборов снабжены нитяным дальномером. Сетка нитей зрительной трубы, кроме основных штрихов (вертикальных и горизонтальных), имеет дальномерные штрихи a и b (рис. 8.4, а). Расстояние D от оси вращения прибора MM (рис. 8.4, б) до рейки AB равно

D = L + f + d ,

где L — расстояние от фокуса объектива до рейки; f — фокусное расстояние; d — расстояние между объективом и осью вращения прибора.

Лучи, идущие через дальномерные штрихи сетки a и b параллельно оптической оси, преломляются объективом, проходят через его фокус F и проецируют изображения дальномерных штрихов на точки A и B, так что дальномерный отсчёт по рейке равен n. Обозначив расстояние между дальномерными штрихами p, из подобных треугольников ABF и a¢b¢F находим L = n f / p. Обозначив f / p = K и f + d = c , получаем

D = K n + c ,

где K — коэффициент дальномера и  c — постоянная дальномера.

 

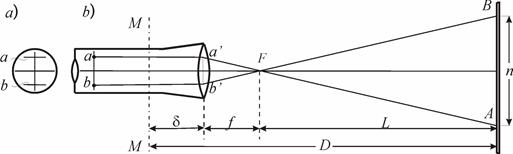
Рис. 8.4. Нитяный дальномер: а) – сетка нитей; б) – схема определения расстояния

При изготовлении прибора f и p подбирают такими, чтобы K=100, а постоянная c была близкой к нулю. Тогда D = 100 n.

Точность измерения расстояний нитяным дальномером » 1/300.

Определение горизонтального проложения линии, измеренной нитяным дальномером. При измерении наклонной линии отсчёт по рейке это отрезок n = AB (рис. 8.5). Если бы рейку наклонить на угол n, то отсчёт был бы равен n₀ = A₀B₀ = n cosn и наклонное расстояние D = Kn₀+ c = Kn ×cosn+c.

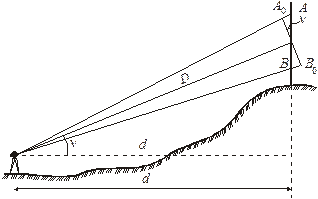
Рис. 8.5. Измерение нитяным дальномером наклонного расстояния

Умножив наклонное расстояние D на cosn, получим горизонтальное расстояние d = K n cos2 n + c cos n.

Прибавив и отняв с × cos2n, после преобразований получим

d = (Kn + с) cos²n + 2c cosn sin²(n¤2).

Вторым слагаемым по его малости пренебрежем. Получим

d = (Kn + с) cos²n .

Вычисления упрощаются, если воспользоваться составленными с использованием этой формулы «Тахеометрическими таблицами».

Светодальномеры, электронные тахеометры                   

Светодальномер – прибор, измеряющий расстояние по времени прохождения его световым сигналом.

В комплект светодальномера входят приёмопередатчик и отражатель. Приемопередатчик 1 (рис. 8.6) устанавливают на штативе на одном конце измеряемой линии, а отражатель 2 на специальной вешке или тоже на штативе – на другом.

Рис. 8.6. Измерение расстояния светодальномером

Приёмопередатчик излучает световой сигнал, принимает его после возвращения от отражателя, измеряет время t, прошедшее от излучения до приёма, и вычисляет расстояние

D = vt/2.

Здесь v – скорость света (при средних условиях v » 299710 км/с).

Время t необходимо измерять с высокой точностью. Так, для точности в расстоянии 1 см время надо знать с ошибкой не более 10-10 с. Измерение времени выполняется фазовым или импульсным методом.

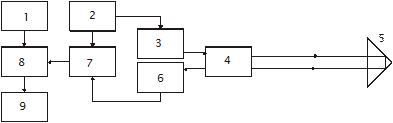
Рис. 8.7. Схема импульсного светодальномера

В импульсном светодальномере (рис. 8.7) лазерный источник излучения 3 под воздействием генератора импульсов 2 периодически посылает через объектив 4 световой импульс. Одновременно переключатель 7 запускает счётчик 8 временны¢х импульсов, поступающих от высокочастотного генератора 1. Световой импульс, отразившись от отражателя 5, поступает на преобразователь 6, который через переключатель 7 останавливает счётчик 8. Число импульсов, сосчитанное счётчиком 8, пропорционально прошедшему времени и, следовательно, измеряемому расстоянию. Для повышения точности измерения выполняются многократно и результаты осредняются процессором 9. Измеренное расстояние высвечивается на табло.

Измеренное расстояние исправляют поправками за атмосферное давление, температуру и влажность воздуха, влияющие на скорость света. Для получения горизонтального проложения вводят поправку за наклон.

Конструктивно приемопередатчик представляет собой отдельный прибор, насадку на теодолит или блок, входящий в состав электронного тахеометра.

По их назначению принято различать светодальномеры для построения государственных геодезических сетей, светодальномеры для прикладной геодезии и маркшейдерии и светодальномеры для топографических съёмок.

Точность топографических светодальномеров 2 – 3 см, а применяемых в прикладной геодезии 2 – 3 мм.

Отражатели бывают призменные и плёночные. Основным элементом призменного отражателя (рис. 8.8 б) является стеклянная трипельпризма отражающая световые лучи в тех направлениях, откуда они пришли. Для увеличения дальности измерений изготавливают многопризменные отражатели.

Плёночный отражатель представляет собой отражающую свет пластиковую плёнку размером 1´1 см и больше, на которую нанесены штрихи (например, вертикальный и горизонтальный). Дальность измерений с пленочными отражателями меньше, чем с призменным. Но зато пленочный отражатель можно закрепить там, где установить призменный отражатель невозможно, например – приклеить в нужном месте на сооружение. Кроме того, пленочные отражатели гораздо дешевле призменных. При выполнении угловых измерений центр штрихов на отражателе служит визирной целью.

Существуют светодальномеры, использующие диффузное отражение сигнала от предметов и не требующие отражателя. Таким дальномером является «лазерная рулетка» Disto фирмы Leica (Швейцария). Прибор используют без штатива, с руки. Световой луч наводят на нужные объекты и на шкале читают расстояния до 200 м с точностью 1,5 мм.

Электронные тахеометры. Электронным тахеометром (рис. 8.8) называется прибор, объединяющий в себе светодальномер, электронный теодолит и микро-ЭВМ. Светодальномер прибора измеряет расстояние до отражателя. Датчики горизонтального и вертикального кругов электронного теодолита выдают отсчеты по кругам. Отсчеты расстояния и углов передаются на индикацию и регистрацию. Микро-ЭВМ обеспечивает возможность решения целого ряда стандартных геодезических задач, для чего прибор снабжен набором необходимых прикладных программ. Полученная в результате измерений и вычислений информация высвечивается на цифровом табло, а также регистрируется во внутренней памяти прибора и на флэш-картах для последующего ввода в компьютер для дальнейшей обработки.

Электронный тахеометр имеет, как правило, две панели управления, расположенные с обеих сторон прибора. На панели управления расположены дисплей и клавиатура для управления процессом измерений и ввода информации вручную. Ввод информации и управление возможны и с дистанционного пульта управления (контроллера). Тахеометр может иметь световой указатель створа, облегчающий установку вехи с отражателем на линию, по которой направлена труба прибора.

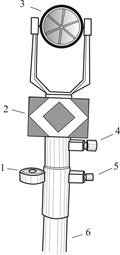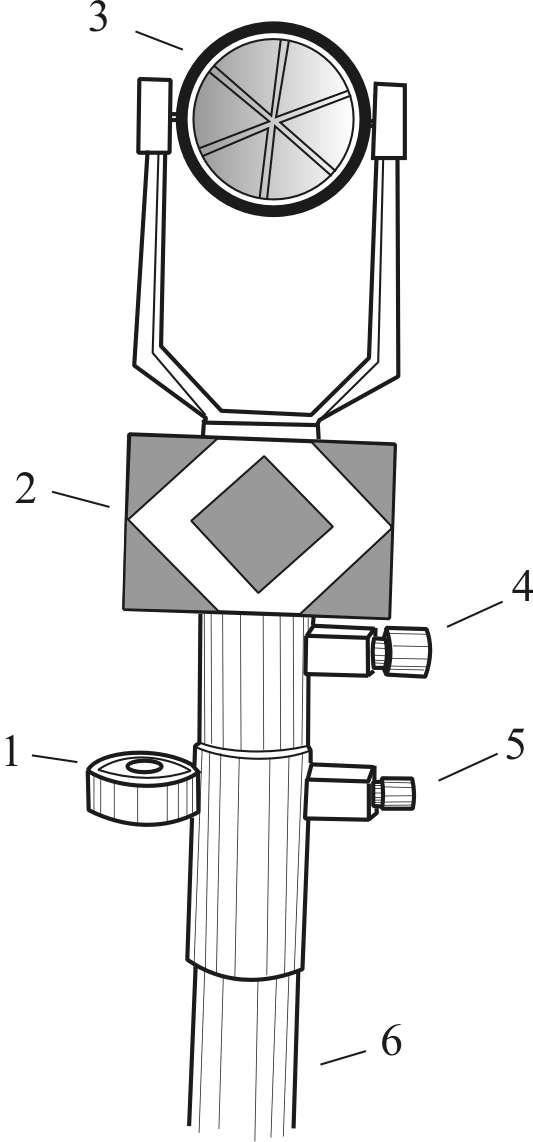
Рис. 8.8. Электронный тахеометр: а) – основной прибор; б) — однопризменный отражатель: 1 – уровень; 2 – визирная марка; 3 – призма; 4, 5 – закрепительные винты; 6 — штанга.

Программное обеспечение электронных тахеометров поддерживает решение достаточно широкого круга задач. Обычно бывает предусмотрен ввод и сохранение данных о станции: ее координат, номера точки, высоты прибора, имени оператора, даты, времени, сведений о погоде (ветре, температуре, давлении). По результатам измерений выполняется вычисление горизонтальных и вертикальных углов, дирекционных углов линий, горизонтальных проложений, превышений, высот точек, где установлен отражатель, приращений координат, плоских и пространственных координат наблюдаемых точек. Предусмотрена возможность вычисления координат по результатам засечек, вычисления расстояния до недоступной для установки отражателя точки и координат недоступной точки, определения высоты недоступного объекта. Для обеспечения разбивочных работ служат программы вычисления угла и расстояния для выноса точки с заданными координатами. При решении задач учитывается рефракция световых лучей в атмосфере.

В настоящее время на рынке имеется широкий выбор электронных тахеометров, выпускаемых разными фирмами, в числе которых Уральский оптико-механический завод (Россия), Sokkia (Япония), Trimble (США), Leica (Швейцария) и др. Характеристики приборов разных марок различаются. Средние квадратические погрешности измерения углов тахеометров лежат в пределах от 1² до 6². Максимальные дальности измерения расстояний на однопризменный отражатель различаются от 1600 до 5000 м. При этом, точность измерений в среднем характеризуется ошибкой 2 мм + 2´10^-6D, где D – расстояние. Многие из электронных тахеометров позволяют измерять расстояния без отражателя. Дальность таких измерений меняется в разных приборах в пределах 70 – 350 м.

Использование электронных тахеометров значительно повышает производительность труда, упрощает и сокращает время на обработку результатов измерений, исключает такие ошибки исполнителя, которые имеют место при визуальном взятии отсчетов, при записи результатов измерений в журналы, в вычислениях. При работе с электронным тахеометром отпадает необходимость иметь калькулятор для выполнения полевых вычислений.

 

9. НИВЕЛИРОВАНИЕ

Методы нивелирования

Нивелированием называется измерение превышений с целью определения высот точек. Путем нивелирования значения высот передают от исходных точек с известными высотами на точки, высоты которых надо определить.

В зависимости от применяемых приборов и методов различают следующие виды нивелирования.

Геометрическое нивелирование — метод определения превышений путем взятия отсчетов по вертикальным рейкам при горизонтальном луче визирования. Это — основной метод нивелирования. Методом геометрического нивелирования создана государственная нивелирная сеть, создаются инженерно-геодезические высотные сети различного назначения.

 Тригонометрическое нивелирование — метод определения превышения путем измерения вертикального угла и расстояния. Метод используют при создании высотного обоснования топографических съемок, а также при определении превышений и передаче высот на строительных площадках.

Барометрическое нивелирование основано на зависимости между высотой и атмосферным давлением. Для определения превышений измеряют атмосферное давление и температуру в точке с известной высотой и в точках, высоты которых определяют. По разностям давлений вычисляют превышения. Метод применяют при работах в труднодоступной местности, им пользуются геологи, геофизики. Точность измерений этим методом невысокая: на равнинной местности — 0.5 м, в горной — 1.5 м.

Гидростатическое нивелирование основано на свойстве жидкости в сообщающихся сосудах устанавливаться на одном уровне. Простейший  гидростатический нивелир представляет собой два сосуда с делениями, соединенные шлангом. Систему заполняют дистиллированной водой. Точность метода очень высокая (0,1 мм), поэтому он применяется при монтаже и выверке конструкций по высоте, особенно при работе в стесненных условиях, при передаче отметок через водные преграды, для наблюдений за деформациями сооружений (плотин, мостов, ускорителей частиц и пр.).

Определение превышений и высот точек с помощью спутниковых измерений. Автономное определение высот точек аппаратурой ГЛОНАСС и GPS выполняется с точностью нескольких метров, а определение превышений между точками — с точностью 10 — 15 мм.

Геометрическое нивелирование

Геометрическое нивелирование выполняют, используя нивелир и нивелирные рейки. Нивелир – прибор, в котором визирный луч приводится в горизонтальное положение. Отсчеты берут по шкалам устанавливаемых вертикально нивелирных реек. Оцифровка шкал на рейках возрастает от пятки рейки вверх. Если на пятке рейки расположен ноль шкалы, то отсчет по рейке равен расстоянию от пятки до луча визирования.

Геометрическое нивелирование выполняют двумя способами — “из середины” и “вперед”.

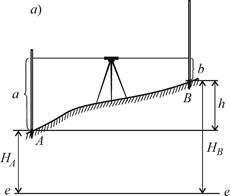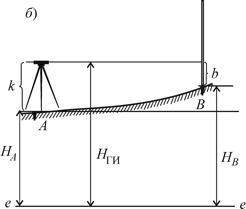Рис. 9.1. Нивелирование: а — из середины; б — вперед; ee – исходная уровенная поверхность

Нивелирование из середины – основной способ. Для измерения превышения точки B над точкой A (рис. 9.1 а) нивелир устанавливают в середине между точками (как правило, на равных расстояниях) и приводят его визирную ось в горизонтальное положение. На точках А и В устанавливают нивелирные рейки. Берут отсчет a по задней рейке и отсчет b по передней рейке. Превышение вычисляют по формуле

h = a — b

Обычно для контроля превышение измеряют дважды – по черным и красным сторонам реек. За окончательный результат принимают среднее.

    Если известна высота H_A точки А, то высоту H _В точки В вычисляют по формуле

H_B = H_A + h_AB .                                  (9.1)

     При нивелировании вперед (рис. 9.1 б) нивелир устанавливают над точкой A и измеряют (обычно с помощью рейки) высоту прибора k. В точке B, высоту которой требуется определить, устанавливают рейку. Приведя визирную ось нивелира в горизонтальное положение, берут отсчет b по черной стороне рейки. Вычислив превышение

h = k – b,

по формуле (9.1) находят высоту точки В.

На строительной площадке, где на земляных работах, укладке бетона или асфальта и пр. требуется с одной стоянки нивелира определить высоты многих точек, сначала вычисляют общую для всех точек высоту H_ГИ горизонта инструмента, то есть высоту визирной оси нивелира

H_ГИ = H_A + k,

а затем – высоты определяемых точек

H₁ = H_ГИ — b₁, H₂ = H_ГИ — b₂, …,

где 1, 2, … — номера определяемых точек.

Если точки А и В, расположены так, что измерить между ними превышение с одной установки нивелира невозможно, превышение измеряют по частям, то есть прокладывают нивелирный ход (рис. 9.2).

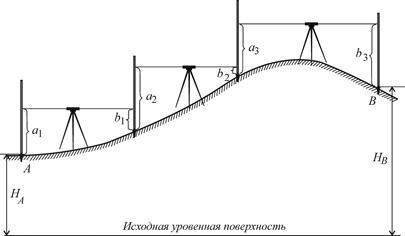
Рис. 9.2. Нивелирный ход

    Превышения вычисляют по формулам (см. рис. 9.2):

h₁ = a₁ — b₁;

h₂ = a₂ — b₂;

h₃ = a₃ — b₃;

Превышение между конечными точками хода А и В равно сумме вычисленных превышений

h_AB = h₁ + h₂ + h₃,

а высота точки В определится по формуле (9.1).

Нивелиры

Исследовательская работа «измерительные работы на местности»

Муниципальное образовательное учреждение

«Великодворская основная общеобразовательная школа»

Измерительные работы на местности

Работу выполнил:

Анфалов Сергей Васильевич, 8

класс

Великодворская ООШ Бабушкинского

района

Дата рождения: 16.06.1995

Домашний адрес: 161344, Вологодская

область, Бабушкинский р-н, д. Великий

Двор, д.76.

Руководитель:

Беляева Елена Васильевна,

учитель физики и математики

МОУ «Великодворская основная

общеобразовательная школа»

Адрес школы: 161344, Вологодская

область Бабушкинский р-н, д. Великий

Двор, д.72

д. Великий Двор

2009

ВВЕДЕНИЕ.

В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. Практические работы на местности являются одной из наиболее активных форм связи обучения с жизнью, теории с практикой. Мы учимся пользоваться справочниками, применять необходимые формулы, овладевать практическими приёмами геометрических измерений и построений. Практические работы с использованием измерительных инструментов повышают интерес к математике, а решение задач на измерение ширины реки, высоты предмета и определение расстояния до недоступной точки позволяют применить их в практической деятельности, увидеть масштаб применения математике в жизни человека. По мере изучения материала способы решения этих задач изменяются, одну и ту же задачу можно решить многими способами. При этом используются следующие вопросы геометрии: равенство и подобие треугольников, соотношения в прямоугольном треугольнике, теорема синусов и теорема косинусов(9 кл.), теорема Пифагора, свойства прямоугольных треугольников и т. д. В школе мы довольно подробно геометрические построения с помощью циркуля и линейки и решаем много задач. А как решить такие же задачи на местности? Ведь возможно вообразить себе такой огромный циркуль, который мог бы очертить окружность школьного стадиона или линейку для разметки дорожек парка. На практике картографам для составления карт, геодезистам для того, чтобы размечать участки на местности, например, для закладки фундамента дома, приходится использовать специальные методы.

Тема нашего реферата: Измерительные работы на местности.
Цель: изучение некоторых методов решения геометрических задач на местности.

Для реализации поставленной цели мы определили следующие задачи:

● Изучить теоретическую и методическую литературу по данному вопросу.

● Показать взаимосвязь математики и основ безопасности жизнедеятельности.

● Применить на практике теоретические знания.

Объектом моих наблюдений стали:

● Определение высоты предмета.

● Расстояние до недоступной точки.

ОСНОВНАЯ ЧАСТЬ.

Одной из наиболее активных форм связи обучения с жизнью, теории с практикой является выполнение на уроках геометрии практических работ, связанных с измерением, построением, изображением. Эти же вопросы рассматриваются и в курсе основ безопасности жизнедеятельности, но все измерения проходят без специальных приборов. Работа проводится как на местности, так и решение задач в классе различными способами на нахождение высоты предмета и определение расстояния до недоступной точки. По программе в курсе геометрии рассматриваются следующие вопросы:
7 класс
● «Провешивание прямой на местности» (п.2).
● «Измерительные инструменты» (п.8).
● «Измерение углов на местности» (п.10).
● «Построение прямых углов на местности» (п.13) ● « Задачи на построение. Окружность» (п.21).
● « Практические способы построения параллельных прямых» (п.26).
● «Уголовный отражатель» (п.36).
● «Расстояние между параллельными прямыми» (п.37 – рейсмус).
● «Построение треугольника по трём элементам» (п.38).
8 класс
● «Практические приложения подобия треугольников» (п.64 – измерение высоты предмета, определение расстояния до недоступной точки).
9 класс
● «Измерительные работы» (п.100 — измерение высоты предмета, определение расстояния до недоступной точки).

Измерительные инструменты, используемые при измерении на местности:

● РУЛЕТКА – лента, с нанесёнными на ней делениями, предназначена для построения прямых углов на местности.
● ЭКЕР – прибор для измерения прямых углов на местности.
● АСТРОЛЯБИЯ – прибор измерения углов на местности.
● ВЕХИ (ВЕШКИ) – колья, которые вбивают в землю.
● ЗЕМЛЯНОЙ ЦИРКУЛЬ (ПОЛЕВОЙ ЦИРКУЛЬ – САЖЕНЬ) – инструмент в виде буквы А высотой 1,37 м. и шириной 2 м. для измерения на местности.

ЭКЕР.

Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них взаимно перпендикулярны.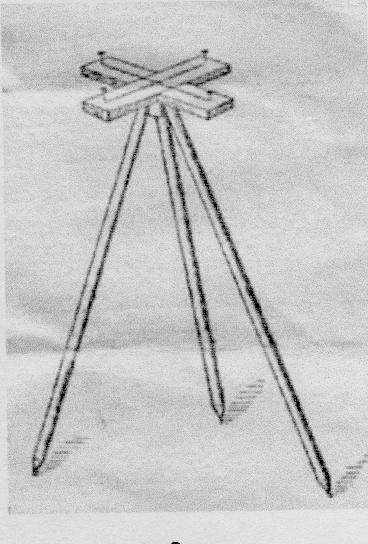


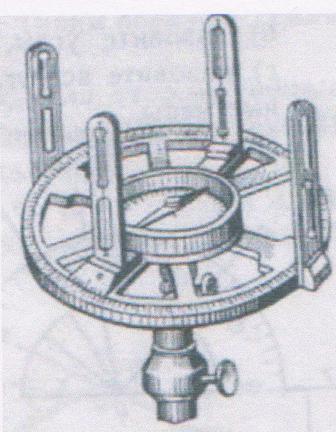
АСТРОЛЯБИЯ.

Устройство астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.

ПОСТРОЕНИЕ ОКРУЖНОСТИ НА
МЕСТНОСТИ.

На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки, двигаясь вокруг колышка, можно описать окружность.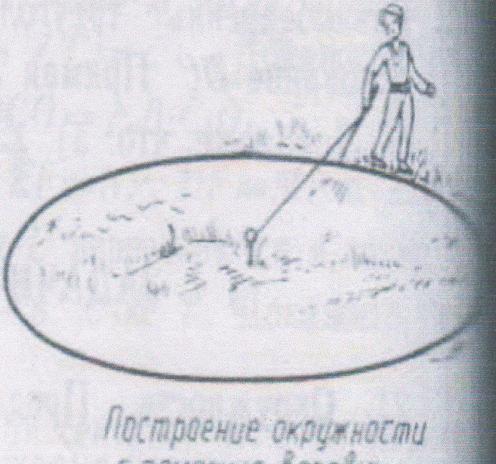



ПРАКТИЧЕСКАЯ РАБОТА.

І. Измерение высоты объекта.

Способы:

1 Измерение высоты столба при помощи плоского зеркала.

Согласно законам отражения (оптика, физика), угол падения солнечного луча равен углу отражения этого луча от зеркала.

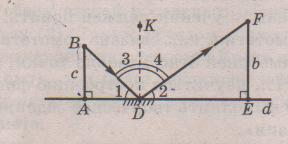
∟3 = ∟4, где DK ┴ d, d – горизонтальная плоскость.

С – человек; b – предмет; а – зеркало.

∟ADB=∟FDF, так как углы падения и отражения солнечного луча равны, а ∟1 = ∟2 = 90º-∟3, ∟A = ∟E = 90º, значит, треугольники ABD и EFD подобны по двум углам.

Из подобия треугольников следует AB:AD = FE:DE EF = (AB·DE):AD, где AB – «рост» человека – расстояние от земли до глаз, EF – измеряемая высота, AD и DE – соответственно расстояния от человека, отражённого в зеркале до измеряемого предмета.

2. Измерение высоты предмета при помощи тени.

С

N

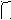
В М А

СВ – высота телеграфного столба.

МN – рост человека (1,6м.).

АМ – тень человека (3,35м.).

АВ – тень столба (15,3м.).

Человек встаёт в область тени столба так, что тень его макушки головы совпадала с концом тени от столба.

Рассмотрим треугольники АВС и АМN.

∟АВС =∟АМN = 90º. По двум равным

∟ВАС – общий. углам.

Треугольники АВС и АМN подобны.

Можно записать соотношение сторон AB:AM = CB:MN

CB = (AB·MN):AM

СВ = (15,3 · 1,6) : 3,35

СВ = 7,3м.

3. Измерение высоты предмета при помощи вехи.

Используем способ, основанный на измерении тени, отбрасываемой объектом.

● Измерить расстояние от дерева до точки, где заканчивается его тень.

● Взять веху и, наблюдая за её тенью, двигаться обратно к дереву до точки полного перекрытия их теней.

● Установить в этом месте веху, измерить расстояние до неё.

●Из подобия треугольников следует, что длина вехи относится к длине своей тени также как и высота дерева к своей.

● Определяем высоту дерева по формуле:

СЕ:BC = AD:AB, отсюда AD = (CE·AB):BC.

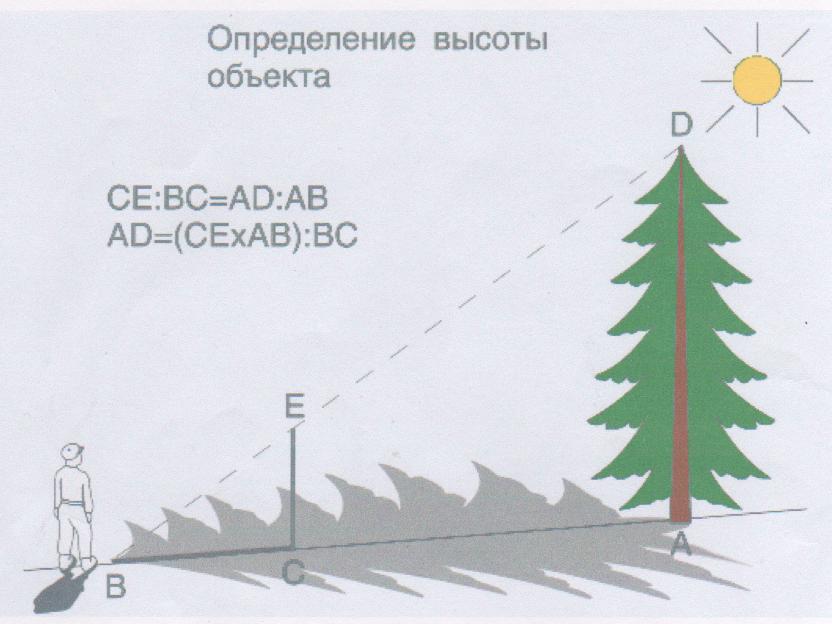
4. Измерение высоты предмета при помощи отсутствии тени.

При отсутствии тени высота вертикальных предметов определяется следующим образом.

Рядом с измеряемым предметом установить вертикально палку известной длины и отойти на 25 – 30 шагов. В вытянутой руке держать перед глазами вертикально карандаш или ровную палочку. Отметить на карандаше высоту вертикальной палки и измерить это расстояние. Мысленно умножить это расстояние на измеренный предмет. Умножив полученное количество раз на длину палки, можно получить искомую величину. На этом опыте мы определили, что высота столба равна 6,89 м.

II. Измерение расстояния до недоступной точки.

Способы:

1. Измерение расстояния до недоступной точки при помощи глазомера.

Отчётливо видны:

● на расстоянии 2 – 3 км – очертания больших деревьев;

● на расстоянии 1 км – стволы деревьев;

● на расстоянии 0,5 км – большие сучья;

● на расстоянии 300 м – можно различить листья на деревьях.

2. Измерение расстояния до недоступной точки с помощью подобия треугольников.

А) Для измерения ширины реки на берегу измеряем расстояние АС, с помощью астролябии устанавливаем угол А = 90˚ (направив на объект В на противоположном берегу), измеряем угол С. На листке бумаги строим подобный треугольник в масштабе 1:1000 и вычисляем АВ (ширину реки).

В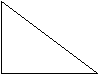1

А1 С1

Запишем отношение сторон АВ: А1В1 = АС: А1С1

АВ = (АС·АВ1) : А1С1

Б) Ширину реки можно определить и так: рассматривая два подобных треугольника АВС и АВ1С1. Точка А выбрана на берегу реки, В1 и С у кромки поверхности воды, ВВ1 – ширина реки.

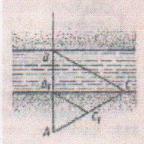
3. Измерение расстояния до недоступной точки способом «кепки».

Для определения ширины реки (оврага) необходимо встать на берег и надвинуть кепку на лоб так, чтобы из-под козырька был виден только обрез воды на противоположном берегу. Далее не меняя наклона головы и положения кепки, следует повернуть голову вправо (влево), заметить предмет, который находится на том же берегу, что и наблюдатель, и виден из-под края козырька. Расстояние до этого предмета равно ширине реки. На опыте мы определили, что ширина реки равна 6 м.

5. Измерение расстояния до недоступной точки с помощью равенства треугольников.

Один из способов определения расстояния до недоступной точки связан с законами геометрии и основан на равенстве треугольников.

● Встать напротив предмета на противоположном берегу реки.

● Повернувшись на 90˚, пройти вдоль берега 20 метров и поставить веху О.

● В том же направлении пройти ещё столько же.

● Повернувшись на 90˚, идти пока веха О и предмет на противоположном берегу не будут на одной линии.

● Расстояние СЕ равно ширине реки ВD.

ВD равно 5,78 м.

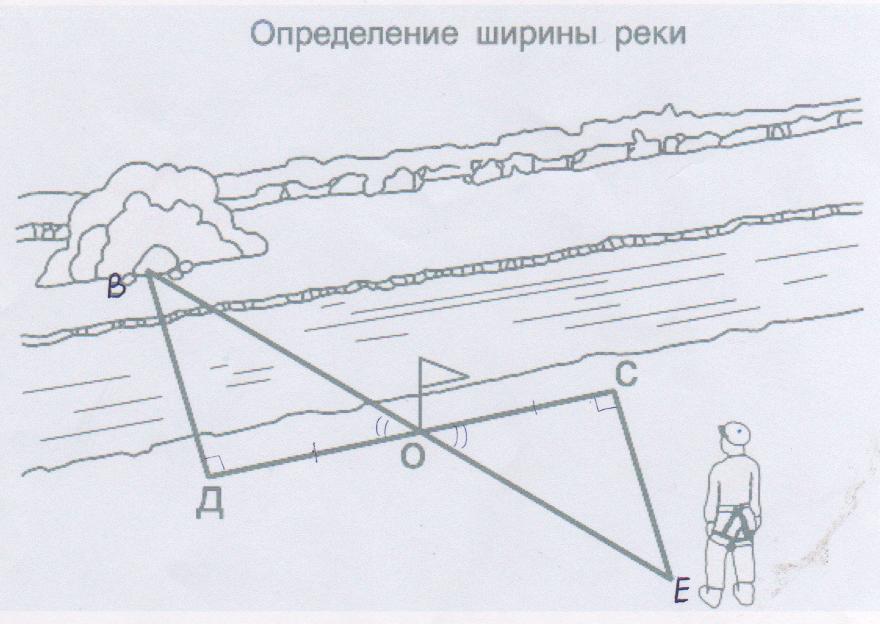
6. Измерение расстояния до недоступной точки способом «травинки».

Наблюдатель стоит в точке А и выбирает на противоположном берегу около воды два неподвижных предмета (ориентира), затем, держа в руке травинку (проволоку), которая закрывает промежуток между ориентирами, складывают её пополам и отходят от реки до тех пор, пока расстояние между ориентирами не уложится в сложенную пополам травинку В. Расстояние от А до В равно ширине реки. АВ равно 5,96 м.

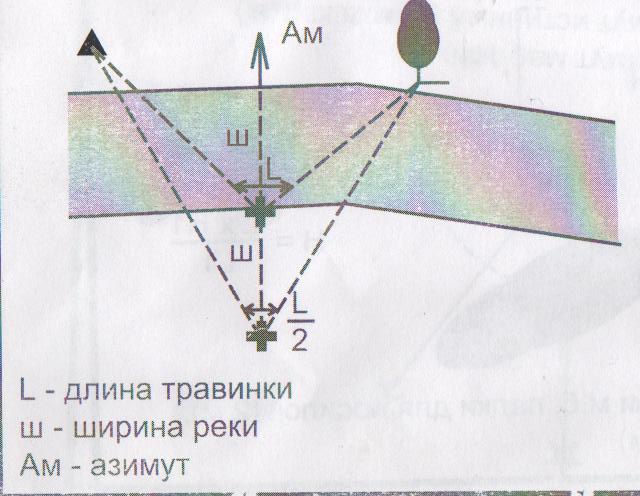
ЗАКЛЮЧЕНИЕ.

В этом реферате рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – измерением высоты предмета, определения расстояния до недоступной точки. Приведённые задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.

Литература

Атанасян Л. С. Геометрия 7-9. – М.: Просвещение, 2003.

Юрченко О. Методы мотивации и стимулирования деятельности учащихся. // Математика в школе, №1, 2005

СD-диск «Школа безопасности».

8.2. Определение недоступных расстояний

Если препятствие (река, обрыв, здание) делает расстояние недоступным для измерения лентой, то его измеряют косвенным методом.

Так, для определения недоступного расстояния dизмеряют лентой длину базисаb(рис. 8.3, а, б) и углыи. ИзABCнаходят

d = b sin  / sin ( + ),

где учтено, что sin  = sin (180) = sin ( + ).

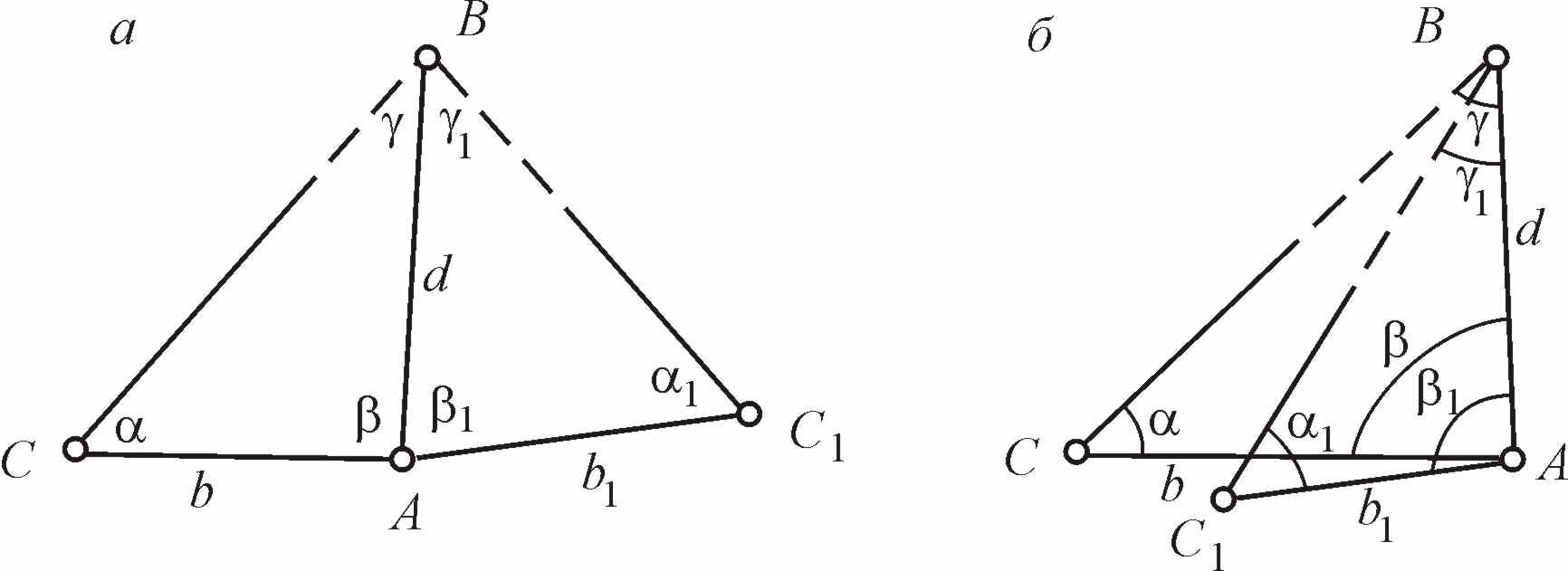
Рис. 8.3. Определение недоступного расстояния

Для контроля расстояние d определяют ещё раз из треугольника ABC₁ и при отсутствии недопустимых расхождений вычисляют среднее.

8.3. Нитяный дальномер

Теория нитяного дальномера. Зрительные трубы многих геодезических приборов снабжены нитяным дальномером. Сетка нитей зрительной трубы, кроме основных штрихов (вертикальных и горизонтальных), имеет дальномерные штрихи a и b (рис. 8.4, а). Расстояние D от оси вращения прибора MM (рис. 8.4, б) до рейки AB равно

D = L + f +  ,

где L  расстояние от фокуса объектива до рейки; f  фокусное расстояние;   расстояние между объективом и осью вращения прибора.

Лучи, идущие через дальномерные штрихи сетки a и b параллельно оптической оси, преломляются объективом, проходят через его фокус F и проецируют изображения дальномерных штрихов на точки A и B, так что дальномерный отсчёт по рейке равен n. Обозначив расстояние между дальномерными штрихами p, из подобных треугольников ABF и abF находим L = n f / p. Обозначив f / p = K и f +  = c , получаем

D = K n + c ,

где K  коэффициент дальномера и c  постоянная дальномера.

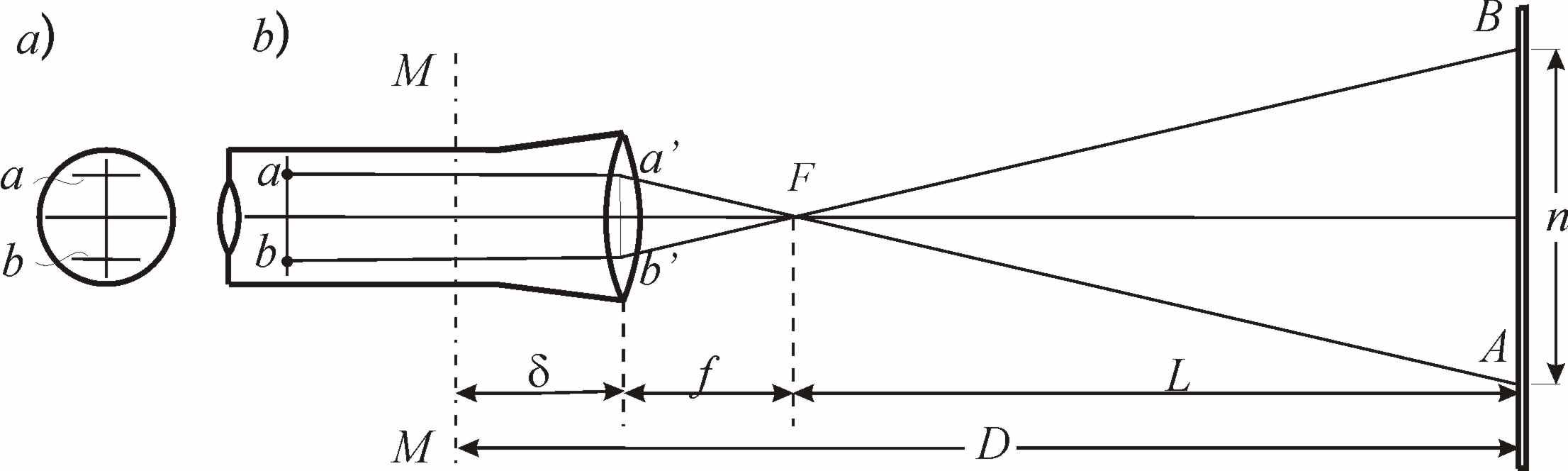
Рис. 8.4. Нитяный дальномер: а) – сетка нитей;б) – схема определения расстояния

При изготовлении прибора f и p подбирают такими, чтобы K=100, а постоянная c была близкой к нулю. Тогда D = 100 n.

Точность измерения расстояний нитяным дальномером  1/300.

Определение горизонтального проложения линии, измеренной нитяным дальномером. При измерении наклонной линии отсчёт по рейке это отрезок n = AB (рис. 8.5). Если бы рейку наклонить на угол , то отсчёт был бы равен n₀ = A₀B₀ = n cos и наклонное расстояние D=Kn₀+c = Kncos+c.

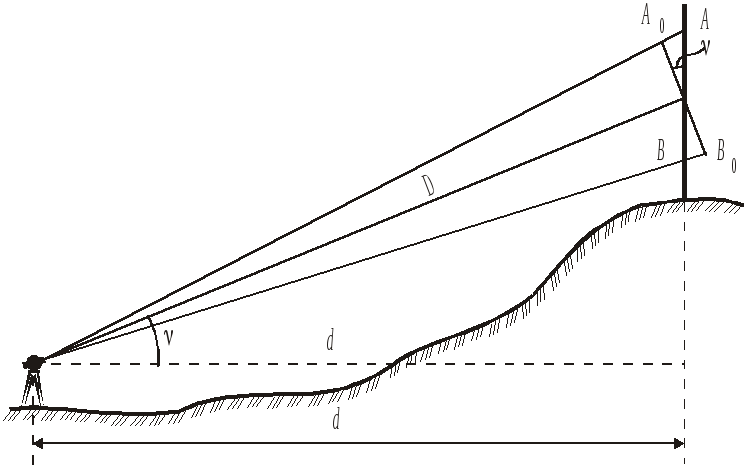
Рис. 8.5. Измерение нитяным дальномером наклонного расстояния

Умножив наклонное расстояние D на cos, получим горизонтальное расстояние d = K n cos²  + c cos .

Прибавив и отняв с cos², после преобразований получим

d = (Kn + с) cos² + 2c cos sin²(2).

Вторым слагаемым по его малости пренебрежем. Получим

d = (Kn + с) cos² .

Вычисления упрощаются, если воспользоваться составленными с использованием этой формулы «Тахеометрическими таблицами».

8.4. Светодальномеры, электронные тахеометры

Светодальномер – прибор, измеряющий расстояние по времени прохождения его световым сигналом.

В комплект светодальномера входят приёмопередатчик и отражатель. Приемопередатчик 1 (рис. 8.6) устанавливают на штативе на одном конце измеряемой линии, а отражатель 2 на специальной вешке или тоже на штативе – на другом.

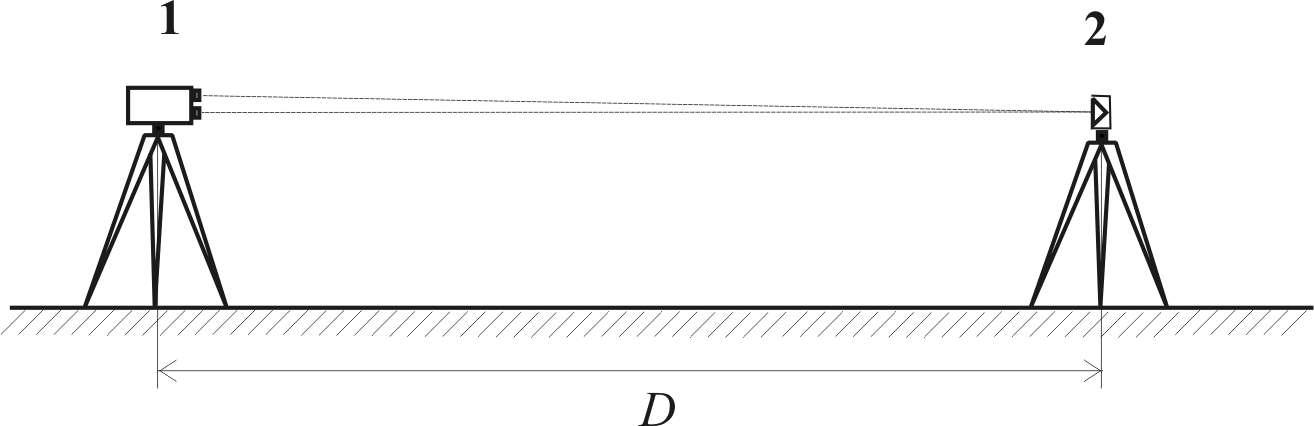
Рис. 8.6. Измерение расстояния светодальномером

Приёмопередатчик излучает световой сигнал, принимает его после возвращения от отражателя, измеряет время t, прошедшее от излучения до приёма, и вычисляет расстояние

D = vt/2.

Здесь v – скорость света (при средних условиях v  299710 км/с).

Время t необходимо измерять с высокой точностью. Так, для точности в расстоянии 1 см время надо знать с ошибкой не более 10^-10 с. Измерение времени выполняется фазовым или импульсным методом.

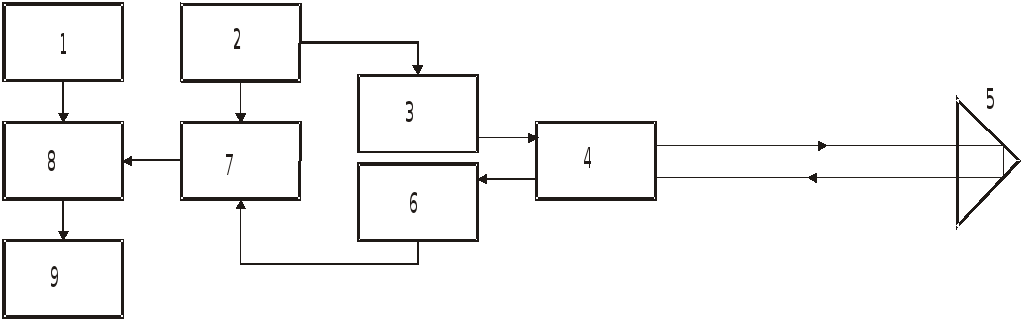
Рис. 8.7. Схема импульсного светодальномера

В импульсном светодальномере (рис. 8.7) лазерный источник излучения 3 под воздействием генератора импульсов 2 периодически посылает через объектив 4 световой импульс. Одновременно переключатель 7 запускает счётчик 8 временных импульсов, поступающих от высокочастотного генератора 1. Световой импульс, отразившись от отражателя 5, поступает на преобразователь 6, который через переключатель 7 останавливает счётчик 8. Число импульсов, сосчитанное счётчиком 8, пропорционально прошедшему времени и, следовательно, измеряемому расстоянию. Для повышения точности измерения выполняются многократно и результаты осредняются процессором 9. Измеренное расстояние высвечивается на табло.

Измеренное расстояние исправляют поправками за атмосферное давление, температуру и влажность воздуха, влияющие на скорость света. Для получения горизонтального проложения вводят поправку за наклон.

Конструктивно приемопередатчик представляет собой отдельный прибор, насадку на теодолит или блок, входящий в состав электронного тахеометра.

По их назначению принято различать светодальномеры для построения государственных геодезических сетей, светодальномеры для прикладной геодезии и маркшейдерии и светодальномеры для топографических съёмок.

Точность топографических светодальномеров 2 – 3 см, а применяемых в прикладной геодезии 2 – 3 мм.

Отражатели бывают призменные и плёночные. Основным элементом призменного отражателя (рис. 8.8 б) является стеклянная трипельпризма отражающая световые лучи в тех направлениях, откуда они пришли. Для увеличения дальности измерений изготавливают многопризменные отражатели.

Плёночный отражатель представляет собой отражающую свет пластиковую плёнку размером 11 см и больше, на которую нанесены штрихи (например, вертикальный и горизонтальный). Дальность измерений с пленочными отражателями меньше, чем с призменным. Но зато пленочный отражатель можно закрепить там, где установить призменный отражатель невозможно, например – приклеить в нужном месте на сооружение. Кроме того, пленочные отражатели гораздо дешевле призменных. При выполнении угловых измерений центр штрихов на отражателе служит визирной целью.

Существуют светодальномеры, использующие диффузное отражение сигнала от предметов и не требующие отражателя. Таким дальномером является «лазерная рулетка» Disto фирмы Leica (Швейцария). Прибор используют без штатива, с руки. Световой луч наводят на нужные объекты и на шкале читают расстояния до 200 м с точностью 1,5 мм.

Электронные тахеометры. Электронным тахеометром (рис. 8.8) называется прибор, объединяющий в себе светодальномер, электронный теодолит и микро-ЭВМ. Светодальномер прибора измеряет расстояние до отражателя. Датчики горизонтального и вертикального кругов электронного теодолита выдают отсчеты по кругам. Отсчеты расстояния и углов передаются на индикацию и регистрацию. Микро-ЭВМ обеспечивает возможность решения целого ряда стандартных геодезических задач, для чего прибор снабжен набором необходимых прикладных программ. Полученная в результате измерений и вычислений информация высвечивается на цифровом табло, а также регистрируется во внутренней памяти прибора и на флэш-картах для последующего ввода в компьютер для дальнейшей обработки.

Электронный тахеометр имеет, как правило, две панели управления, расположенные с обеих сторон прибора. На панели управления расположены дисплей и клавиатура для управления процессом измерений и ввода информации вручную. Ввод информации и управление возможны и с дистанционного пульта управления (контроллера). Тахеометр может иметь световой указатель створа, облегчающий установку вехи с отражателем на линию, по которой направлена труба прибора.

Рис. 8.8. Электронный тахеометр: а) – основной прибор;б)однопризменный отражатель: 1 – уровень; 2 – визирная марка; 3 – призма; 4, 5 – закрепительные винты; 6 — штанга.

Программное обеспечение электронных тахеометров поддерживает решение достаточно широкого круга задач. Обычно бывает предусмотрен ввод и сохранение данных о станции: ее координат, номера точки, высоты прибора, имени оператора, даты, времени, сведений о погоде (ветре, температуре, давлении). По результатам измерений выполняется вычисление горизонтальных и вертикальных углов, дирекционных углов линий, горизонтальных проложений, превышений, высот точек, где установлен отражатель, приращений координат, плоских и пространственных координат наблюдаемых точек. Предусмотрена возможность вычисления координат по результатам засечек, вычисления расстояния до недоступной для установки отражателя точки и координат недоступной точки, определения высоты недоступного объекта. Для обеспечения разбивочных работ служат программы вычисления угла и расстояния для выноса точки с заданными координатами. При решении задач учитывается рефракция световых лучей в атмосфере.

В настоящее время на рынке имеется широкий выбор электронных тахеометров, выпускаемых разными фирмами, в числе которых Уральский оптико-механический завод (Россия), Sokkia (Япония), Trimble (США), Leica (Швейцария) и др. Характеристики приборов разных марок различаются. Средние квадратические погрешности измерения углов тахеометров лежат в пределах от 1 до 6. Максимальные дальности измерения расстояний на однопризменный отражатель различаются от 1600 до 5000 м. При этом, точность измерений в среднем характеризуется ошибкой 2 мм + 210^-6D, где D – расстояние. Многие из электронных тахеометров позволяют измерять расстояния без отражателя. Дальность таких измерений меняется в разных приборах в пределах 70 – 350 м.

Использование электронных тахеометров значительно повышает производительность труда, упрощает и сокращает время на обработку результатов измерений, исключает такие ошибки исполнителя, которые имеют место при визуальном взятии отсчетов, при записи результатов измерений в журналы, в вычислениях. При работе с электронным тахеометром отпадает необходимость иметь калькулятор для выполнения полевых вычислений.

math — Грубое вычисление расстояния между 2 точками

Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Общественные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним возможности технической карьеры
5. Талант Нанять технических талантов
6. реклама Обратитесь к разработчикам по всему миру

Загрузка…

.

Расстояние между 2 точками

Краткое объяснение

Когда мы знаем расстояния по горизонтали и по вертикали между двумя точками, мы можем вычислить расстояние по прямой следующим образом:

расстояние = √ a ² + b ²

Представьте, что вы знаете расположение двух точек (A и B), как здесь.

Какое расстояние между ними?

Мы можем провести линии вниз от A и вдоль от B, чтобы получился прямоугольный треугольник.

И с небольшой помощью Пифагора мы знаем, что:

a ² + b ² = c ²

Теперь отметьте координаты точек A и B.

x _A означает координату x точки A
y _A означает координату y точки A

Горизонтальное расстояние a равно (x _A — x _B )

Расстояние по вертикали b равно (y _A — y _B )

Теперь мы можем найти c (расстояние между точками):

Начнем с: c ² = a ² + b ²

Поместите в вычисления для a и b: c ² = (x _A — x _B ) ² + (y _A — y _B ) ²

Квадратный корень из обеих сторон: Готово!

Примеры

Пример 1

Введите значения:

Пример 2

Неважно, в каком порядке расположены точки, потому что возведение в квадрат удаляет любые негативы:

Введите значения:

Пример 3

А вот еще пример с некоторыми отрицательными координатами… все еще работает:

Введите значения:

(Примечание √136 может быть дополнительно упрощено до 2√34, если хотите)

Попробуйте сами

Перетащите точки:

Три или более измерения

Отлично работает в 3 (и более!) Измерениях.

Возвести в квадрат разность для каждой оси, затем просуммировать их и извлечь квадратный корень:

Расстояние = √ [(x _A — x _B ) ² + (y _A — y _B ) ² + (z _A — z _B ) ² ]

Пример: расстояние между двумя точками (8,2,6) и (3,5,7) составляет:

= √ [(8−3) 2 + (2−5) 2 + (6−7) 2 ]

= √ [5 2 + (−3) 2 + (−1) 2 ]

= √ (25 + 9 + 1)

= √35

Что примерно равно 5.9

,