Что такое золотое сечение: определение и история
С проявлениями принципа «Золотого сечения» человек ежедневно сталкивается в своем окружении. Увидев яркие краски крыльев бабочки или распускающийся бутон цветка, мы произносим: «Как красиво!». Что же мы называем «красивым», а от чего брезгливо отворачиваемся? Ответ на подобные вопросы был найден в законах, как его еще называют, Божественного сечения.
Определение
Ощущение совершенства и гармонии вызывают у нас предметы, отдельные части которых объединены друг с другом и с целым строгими соотношениями.
Язык беспристрастных математических формул иллюстрирует это правило вот этим рисунком.
Большая часть отрезка относится к меньшей в пропорции 1,6180339887. Это же правило справедливо для общей длины и большей части. В процентном варианте пропорция выглядит как 62% к 38%.
Философский взгляд и широкое понимание правил Золотого сечения можно сформулировать так – большее так относится к меньшей части, как целое к большему.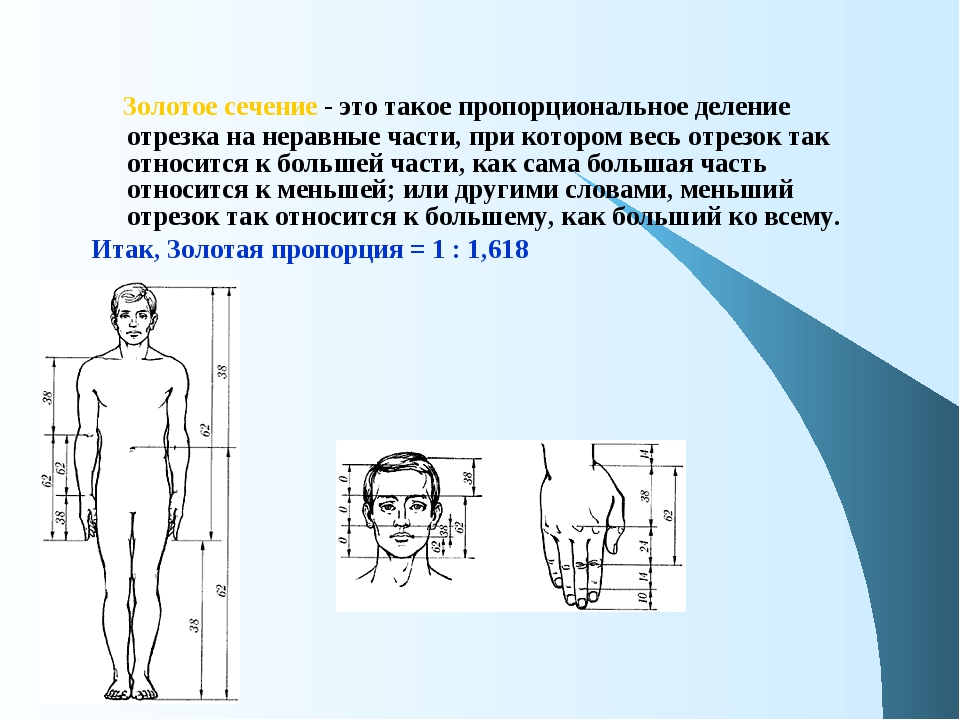
По большому счету – это универсальное определение, справедливое для всего мироустройства. Такую гармонию можно встретить везде – от законов астрономической механики до узоров паутины.
История
О том, что наши предки были знакомы с гармоничным соотношением большего и меньшего говорят многие мировые шедевры архитектуры и искусства. Пропорции золотого сечения можно найти в древнеегипетских храмах и фресках, предметах быта и украшениях.
Фасад сохранившегося до наших дней храма Парфенона подтверждает, что древние греки пользовались законами геометрических пропорций при его строительстве. Лишним свидетельством тому являются циркули, найденные при раскопках.
Определение гармоничных пропорций дал великий итальянский математик эпохи Возрождения – монах Лука Пачолли. В своей книге «Божественная пропорция» он описывает золотое сечение как «божественную суть» всех законов природы.
Свое восхищение золотыми пропорциями Леонардо да Винчи выразил в своем рисунке «Витрувианский человек», который стал гимном гармонии и совершенству человеческого тела.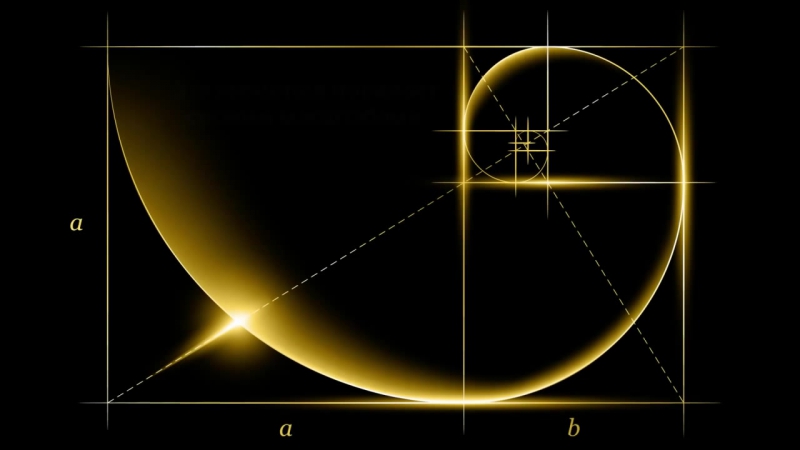
Природа и человек
Не прибегая к математическим выкладкам, проявления золотого сечения можно найти в явлениях природы, растительном и животном мире.
Построению спирали уделял внимание еще Архимед. На основе ее формы он вывел уравнение, которое используется в техническом моделировании до настоящего времени.
Современные исследования подтверждают, что законы золотой спирали справедливы для семян подсолнечника и лепестков розы, строения сосновой шишки и человеческого уха.
Гармонии человеческого тела посвятили свои работы многие великие художники и архитекторы. Наиболее лаконично она отражена в знаменитом «Модулоре» французского архитектора Ле Корбюзье. Детально познакомиться с красотой природных пропорций человека можно в этом видеоматериале.
youtube.com/embed/h9GwRwJ8Q_c?rel=0″/>Понять значение слова «красота» — это лишь первый шаг. Пропорции золотого сечения совершенны, и с этим трудно спорить. Принять его, осмыслить и созидать – не это ли может быть целью человечества?
Прежде всего, что такое Золотое сечение?
По материалам Википедии:
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление, число Фидия, ?) — деление отрезка на части в таком соотношении, при котором большая часть относится к меньшей, как сумма к большей. Например, деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ (т. е. |АВ| / |ВС| = |АС| / |АВ|).
Эту пропорцию принято обозначать греческой буквой ? (встречается также обозначение ?) и она равна 1.618…
В дошедшей до нас античной литературе золотое сечение впервые встречается в «Началах» Евклида (3 в. до н.э.). Термин «золотое сечение» был введён гораздо позднее Леонардо да Винчи, который использовал золотое сечение как пропорции «идеального человеческого тела».
Например, пропорции мужского тела колеблются в пределах отношения 13 : 8 = 1,625 и немного ближе подходят к золотому сечению, чем пропорции женского тела, выражающиеся в соотношении 8 : 5 = 1,6.
Золотое сечение можно найти практически везде в живой природе.
Можно увидеть его и в самых удачных творениях человеческих рук — принципы золотого сечения легли в основу композиционного построения многих произведений архитектуры, живописи, даже в поэзии.
Давайте проведем эксперимент: какой прямоугольник из ниже расположенных, с вашей точки зрения, имеет идеальные пропорции?
По результатам опросов, большинство людей признает самым гармоничным прямоугольник под номером 2. Именно он построен в соответствии с правилом «золотого сечения».
Вы можете спросить, зачем дизайнеру эта математика, и какой в ней практический смысл? А смысл есть. Например, отношение сторон у iPod Shuffle 1.59, iPod Classic 1.67, а у iPhone4 1.7 — объем продаж за первые 4 дня торговли превысил 1 миллион 700 тысяч штук. Даже логотип Apple построен по принципам золотого сечения.
Даже логотип Apple построен по принципам золотого сечения.
Одной из главных задач эффективного дизайна в Web — это ясность и интуитивность. А также концентрация внимания пользователя на нужных местах страницы. Как этого добиваются?
Существует множество путей, например, использовать сетки, можно предпочесть самые элементарные решения или сосредоточится на простоте и удобстве.
Но в любом случае, Вы должны быть уверены, что у пользователей присутствует ощущение баланса, порядка, гармонии и комфорта. Как раз в этом случае применение золотого сечения становится важным этапом при разработке дизайна web-страницы. Итак, принцип золотого сечения на практике в Web поможет нам определить, какого размера должны быть элементы на странице, в каком месте и на каком расстоянии они должны располагаться друг от друга, чтобы не нарушать баланс, чтобы наш сайт выглядел гармоничным.
Воспользуемся правилом третей, основанном на применении золотого сечения. Это правило позволит нам вычислить центры внимания на странице. Для этого поделим страницу на три части по горизонтали и вертикали.
Для этого поделим страницу на три части по горизонтали и вертикали.
На пересечении линий находятся 4 важные точки, которые можно использовать для выделения основных деталей макета сайта.
Как правило, не стоит использовать сразу все четыре точки, но одну или две — обязательно.
Какую то важную деталь лучше поместить в левый верхний угол, т. к. пользователи начинают просматривать сайт именно оттуда — логотип, если у нас имиджевый сайт или контактную информацию, если сайт продающий.
Навигационное меню можем расположить на первой горизонтальной линии. Еще один-два важных элемента располагаем на точках пересечения горизонтальных и вертикальных линий.
Что нам дало такое расположение блоков?
Мы поместили наиболее важные вещи в местах наибольшего внимания пользователя. При таком расположение элементов, наш сайт становится более удобным и более структурированным для просмотра.
Что это дает нам, как владельцам сайта?
Например, дополнительный доход, если мы разместим рекламные блоки в тех местах, где их с большей вероятностью увидят посетители сайта.
2/3 страницы займет центральная колонка и 1/3 отведем под сайдбар.
Еще один пример: создадим трехколоночный шаблон.
Разделим по предыдущему принципу страницу на две колонки.
А дальше центральную колонку опять поделим вертикальными линиями на три равные части, первая из которых будет сайдбаром, а две остальные — центральной частью.
В первом сайдбаре можно расположить основное меню сайта, содержащее самые важные ссылки. Их посетитель сайта увидит в первую очередь, (поскольку он привык читать текст слева направо), а всякую дополнительную информацию поместить во второй сайдбар.
В некоторых случаях применение Золотого сечения и Правила третей может значительно улучшить взаимосвязь вашего проекта с посетителями.
При пропорции 1:1.62, ваш сайт становится более удобным и более структурированным для просмотра. И это работает не только в Web-дизайне.
Автор: Максим, Менеджер интернет-проектов
Золотое сечение
Золотое сечение
Р. Мурадова,
Мурадова,
г. Ногинск
План урока
1. Вступительное слово учителя.
2. «Золотое сечение» в математике – постановка задачи, аналитическое и геометрическое решение пропорции
3. «Золотое сечение» в скульптуре.
4. «Золотое сечение» в архитектуре.
5. «Золотое сечение» в живописи.
Ход урока
1. Вступительное слово учителя
Вопрос о математических предпосылках прекрасного, о роли математики в искусстве волновал еще древних греков, причем свой интерес они унаследовали от предшествующих цивилизаций. В наше время геометрия – необходимый элемент общего образования и культуры, представляет большой исторический интерес, имеет серьезное практическое применение и обладает внутренней красотой.
Начиная с шестого класса, мы в
общих чертах говорили о золотом сечении, решали
задачу о делении отрезка в среднем и крайнем
отношении.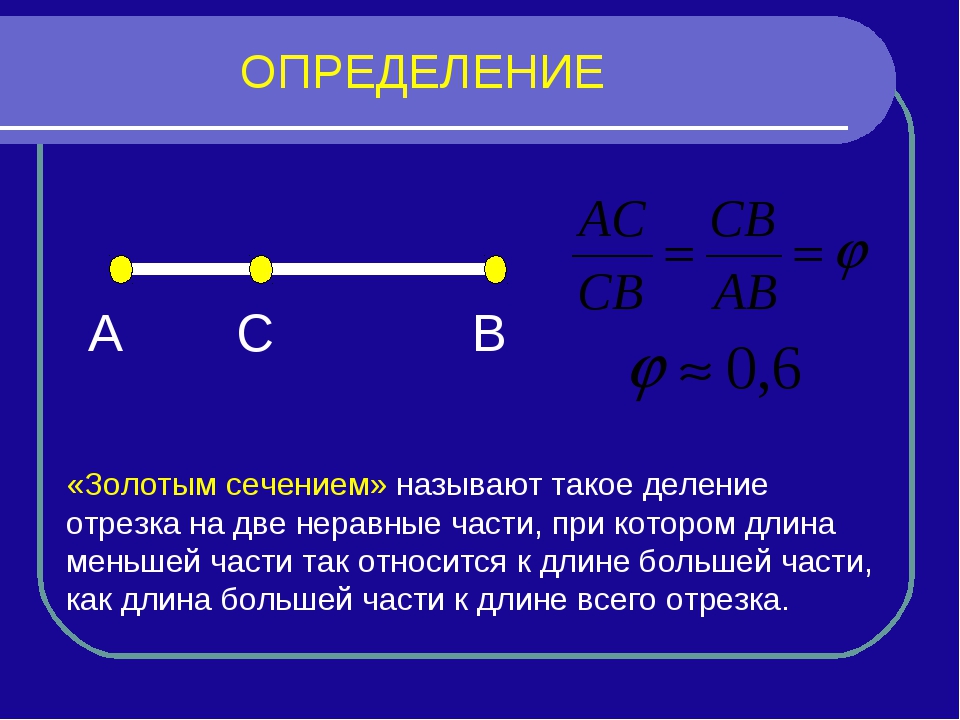 Сегодня мы обобщим пройденный
материал, привлекая дополнительные сведения из
различных источников [1–4] . Приведем примеры
золотого сечения в скульптуре, архитектуре и
живописи.
Сегодня мы обобщим пройденный
материал, привлекая дополнительные сведения из
различных источников [1–4] . Приведем примеры
золотого сечения в скульптуре, архитектуре и
живописи.
2. «Золотое сечение» в математике
1-й ведущий:
– Иоган Кеплер говорил, что геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем.
Теорему Пифагора знает каждый, а вот что такое «золотое сечение» – далеко не все. Расскажем вам об этом «драгоценном камне».
2-й ведущий (объявляет математическую часть урока):
– Что такое «золотое сечение»? Говорят, что точка C производит «золотое сечение» отрезка AB, если
AC : AB = CB : AC. (1)
Учитель:
– Итак, «золотое сечение» – это такое деление целого на две неравные части, при котором большая часть так относится к целому, как меньшая к большей.
В геометрии «золотым
сечением» называется также деление отрезка в
среднем и крайнем отношениях (рис. 1).
1).
Если длину отрезка AB
обозначить через a, а длину отрезка AC – через x, то
a – x – длина отрезка CB,
и пропорция (1) принимает вид
(2)
Из этой пропорции следует, что при золотом сечении длина большего отрезка есть среднее геометрическое, или, как часто говорят, среднее пропорциональное длин всего отрезка и его меньшей части:
Геометрически «золотое сечение» отрезка AB можно построить следующим образом: восстановить в точке B перпендикуляр к AB (рис. 2) и на нем отложить далее, соединив точки A и D, отложить DE = BD, и, наконец, AC = AE. Точка C является искомой, она производит «золотое сечение» отрезка AB.
В самом деле, заметим, что по теореме Пифагора
(AE + ED)2 = AB2 + BD2,
а по построению AE = AC, Из этих равенств следует, что
AC2 + AC•AB = AB2,
а отсюда легко получить
равенство (1).
Решив уравнение (2) относительно x, находим
значит, a – x»0,38a.
Таким образом, части «золотого сечения» составляют приблизительно 62% и 38% всего отрезка.
Рассмотренная задача очень древняя, она присутствует в «Началах» Евклида, который решил ее геометрически (рис. 3).
На отрезке AB построен квадрат ABDC. Требуется найти точку Y, делящую AB в среднем отношении. Соединим точку E – середину AC – с точкой B. На продолжении стороны CA квадрата отложим отрезок EJ = BE. На отрезке AJ построим квадрат AJHY. Продолжение стороны HY до пересечения с CD в точке K делит квадрат ABCD на два прямоугольника AYKC и YBDK. Существует чисто геометрическое доказательство, что прямоугольник YBDK равновелик квадрату AJHY.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 4).
Из подобия треугольников ACD и ABE можем вывести уже известную пропорцию:
Таким образом, звездчатый
пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно
продолжить строить пятиугольники, и это
отношение будет сохраняться.
Интересно, что внутри пятиугольника можно
продолжить строить пятиугольники, и это
отношение будет сохраняться.
Ученик А:
– Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
Бытует легенда о том, что один из пифагорейцев больным попал в дом к незнакомым людям. Они старались его выходить, но болезнь не отступала. Не имея средств заплатить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле, через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина дома о том, каким образом она появились у входа. После рассказа хозяина гость щедро вознаградил его.
Пентаграмма была хорошо
известна и в Древнем Египте. Но непосредственно
как эмблема здоровья она была принята лишь в
Древней Греции.
В настоящее время существует гипотеза, что пентаграмма – первичное понятие, а «золотое сечение» вторично. Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая» пропорция.
3. «Золотое сечение» в скульптуре
2-й ведущий:
– Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения.
Ученик Б:
– Пропорции «золотого
сечения» создают впечатление гармонии красоты,
поэтому скульпторы использовали их в своих
произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения». Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям (объяснение проводится с использованием рис. 1).
Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос (объяснение проводится с использованием рис. 2).
Измерения нескольких тысяч человеческих тел позволили обнаружить, что для взрослых мужчин это отношение равно = 1,625, а для взрослых женщин оно составляет = 1,6. Так что пропорции мужчин ближе к «золотому сечению», чем пропорции женщин. Было проведено большое число измерений на помещенных в журналах крупных портретах мужчин и женщин, на многих из них указанные отношения представляют «золотое сечение».
4. «Золотое сечение» в архитектуре
1-й ведущий:
– В книгах о «золотом
сечении» можно найти замечание о том, что в
архитектуре, как и в живописи, все зависит от
положения наблюдателя, и что, если некоторые
пропорции в здании с одной стороны кажутся
образующими «золотое сечение», то с других точек
зрения они будут выглядеть иначе. «Золотое
сечение» дает наиболее спокойное соотношение
размеров тех или иных длин.
«Золотое
сечение» дает наиболее спокойное соотношение
размеров тех или иных длин.
Ученик В:
– Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада.
Другим примером из архитектуры древности является Пантеон.
Ученик Г:
– Известный русский
архитектор М. Казаков в своем творчестве широко
использовал «золотое сечение». Его талант был
многогранным, но в большей степени он раскрылся в
многочисленных осуществленных проектах жилых
домов и усадеб. Например, «золотое сечение» можно
обнаружить в архитектуре здания сената в Кремле.
По проекту М. Казакова в Москве была построена
Голицынская больница, которая в настоящее время
называется Первой клиничес-
Например, «золотое сечение» можно
обнаружить в архитектуре здания сената в Кремле.
По проекту М. Казакова в Москве была построена
Голицынская больница, которая в настоящее время
называется Первой клиничес-
кой больницей имени
Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.
Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г. При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.
Многие высказывания зодчего
заслуживают внимание и в наши дни. О своем
любимом искусстве В. Баженов говорил:
«Архитектура – главнейшие имеет три предмета:
красоту, спокойность и прочность здания. .. К
достижению сего служит руководством знание
пропорции, перспектива, механика или вообще
физика, а всем им общим вождем является
рассудок».
.. К
достижению сего служит руководством знание
пропорции, перспектива, механика или вообще
физика, а всем им общим вождем является
рассудок».
5. «Золотое сечение» в живописи
1-й ведущий:
– Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в. Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете».
Он писал справа налево
неразборчивым почерком и левой рукой.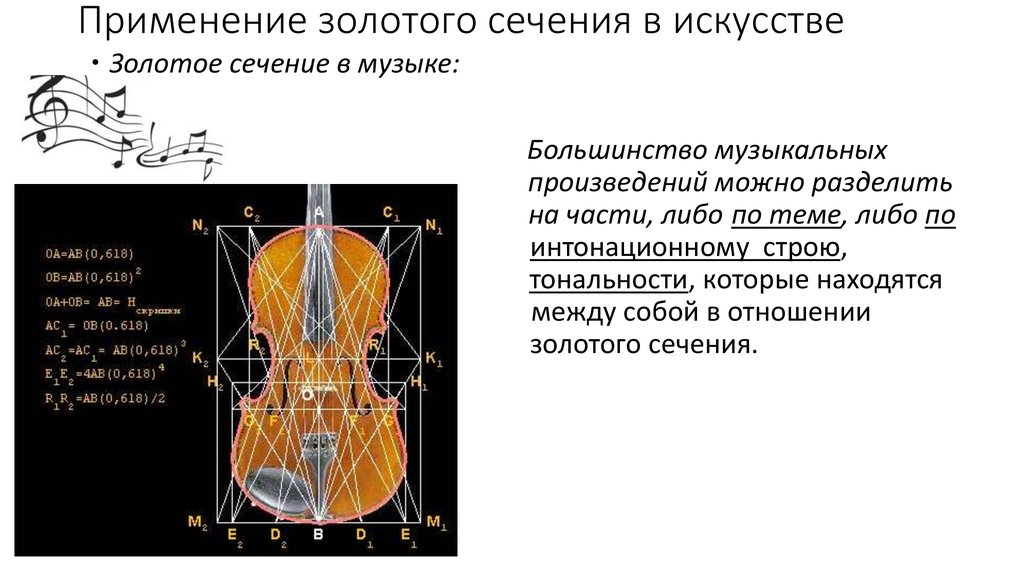 Это самый
известный из существующих образец зеркального
письма.
Это самый
известный из существующих образец зеркального
письма.
Ученик В:
– Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них.
Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.
Сказка
Жил-был один бедный человек,
было у него четыре сына: три умных, а один из них и
так, и сяк. И вот пришла за отцом смерть. Перед тем,
как расстаться с жизнью, он позвал к себе детей и
сказал: «Сыны мои, скоро я умру. Как только вы
схороните меня, заприте хижину и идите на край
света добывать себе счастья. Пусть каждый из вас
чему-нибудь научится, чтобы мог кормить сам
себя». Отец умер, а сыновья разошлись по свету,
договорившись спустя три года вернуться на
поляну родной рощи.
Как только вы
схороните меня, заприте хижину и идите на край
света добывать себе счастья. Пусть каждый из вас
чему-нибудь научится, чтобы мог кормить сам
себя». Отец умер, а сыновья разошлись по свету,
договорившись спустя три года вернуться на
поляну родной рощи.
Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула.
Братья бросились к ней и
каждый кричал одно и то же: «Ты должна быть моей
женой».
Но женщина ответила: «Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями. А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь».
Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество.
Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель…
Трудно отметить, что замечали
в этом шедевре искусства, но все говорили о том
глубоком знании Леонардо строения человеческого
тела, благодаря которому ему удалось уловить эту,
как бы загадочную, улыбку. Говорили о
выразительности отдельных частей картины и о
пейзаже, небывалом спутнике портрета. Толковали
о естественности выражения, о простоте позы, о
красоте рук. Художник сделал еще небывалое: на
картине изображен воздух, он окутывает фигуру
прозрачной дымкой.
Говорили о
выразительности отдельных частей картины и о
пейзаже, небывалом спутнике портрета. Толковали
о естественности выражения, о простоте позы, о
красоте рук. Художник сделал еще небывалое: на
картине изображен воздух, он окутывает фигуру
прозрачной дымкой.
Несмотря на успех, Леонардо был мрачен, положение во Флоренции показалось художнику тягостным, он собрался в дорогу. Не помогли ему напоминания о нахлынувших заказах.
Учитель подводит итог урока и благодарит ведущих и активных участников в подборе материала и проведении урока.
Литература
1. Из опыта проведения внеклассной работы по математике в средней школе. Сб. статей под ред. П. Стратилатова. – М. : Учпедгиз, 1955.
2. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1989.
3. Журнал «Квант», 1973, № 8.
4. Журнал «Математика в школе», 1994, № 2; № 3.
Золотое сечение | Belcanto.ru
Категории словаря
Золотое сечение в музыке — обнаруживающаяся во мн.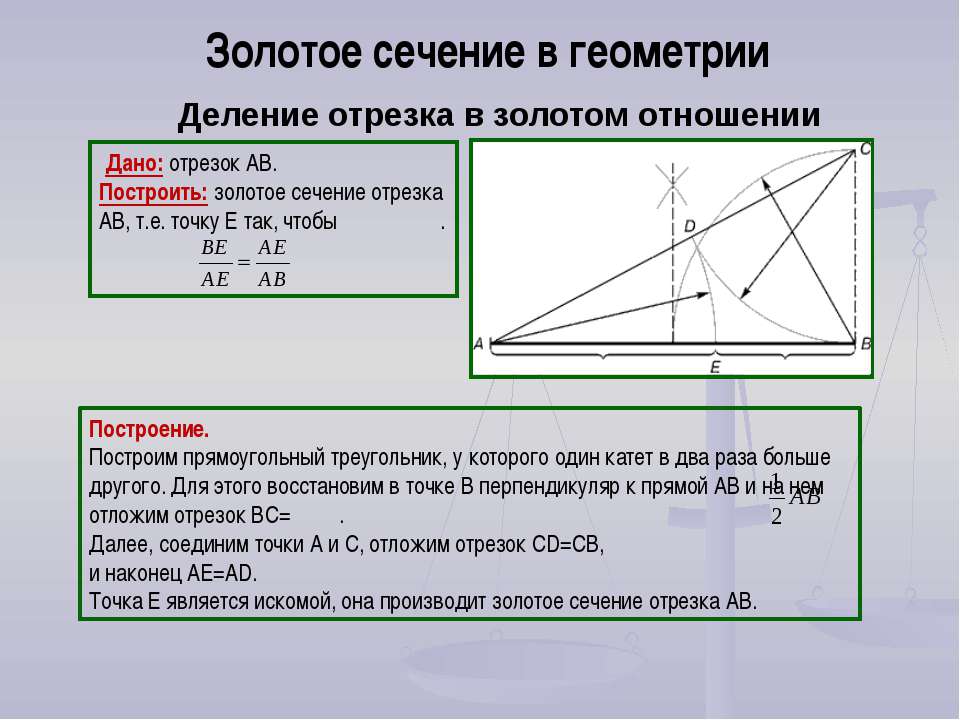 муз. произв.
связь важных особенностей построения целого или его частей с т.н.
золотым сечением. Понятие З. с. относится к области геометрии; З.
с. называют деление отрезка на две части, при к-ром целое так
относится к большей части, как бульшая часть к меньшей (гармонич.
деление, деление в крайнем и среднем отношении). Если целое
обозначить буквой а, бульшую часть буквой b и меньшую — буквой c,
соотношение это выражается пропорцией а:b=b:с. В числовом выражении
отношение b:a составляет непрерывную дробь, приближённо равную
0,618034…
муз. произв.
связь важных особенностей построения целого или его частей с т.н.
золотым сечением. Понятие З. с. относится к области геометрии; З.
с. называют деление отрезка на две части, при к-ром целое так
относится к большей части, как бульшая часть к меньшей (гармонич.
деление, деление в крайнем и среднем отношении). Если целое
обозначить буквой а, бульшую часть буквой b и меньшую — буквой c,
соотношение это выражается пропорцией а:b=b:с. В числовом выражении
отношение b:a составляет непрерывную дробь, приближённо равную
0,618034…
В эпоху Возрождения было установлено, что З. с. находит применение в изобразит. иск-вах, в особенности в архитектуре. Было признано, что подобное соотношение частей производит впечатление гармонии, соразмерности, изящества. Композиторы нидерландской школы (Я. Обрехт) сознательно применяли З. с. в своих произв.
Первую попытку обнаружить проявление З. с. в музыке сделал в сер.
19 в. нем. учёный А. Цейзинг, к-рый неоправданно объявил З. с.
всеобщей, универсальной пропорцией, проявляющейся как в иск-ве, так
и в мире природы. Цейзинг нашёл, что близкое к З. с. соотношение
обнаруживает мажорное трезвучие (интервал квинты как целое, большая
терция как большая часть, малая терция — как меньшая часть).
Цейзинг нашёл, что близкое к З. с. соотношение
обнаруживает мажорное трезвучие (интервал квинты как целое, большая
терция как большая часть, малая терция — как меньшая часть).
Более определённое проявление соотношений З. с. в музыке было открыто в нач. 20 в. рус. исследователем Э. К. Розеновым в области муз. формы. По Розенову, оно сказывается уже в рамках периода, где мелодич. кульминация обычно располагается в точке, близкой к точке З. с. Нередко вблизи точки З. с. обнаруживаются переломные моменты и в более крупных разделах муз. формы (З. с. проявляется во временном соотношении частей, к-рое в случае изменения темпа не совпадает с соотношением числа тактов) и даже в целых одночастных произв. Хотя анализы Розенова порой чрезмерно детализированы и не лишены натяжек, в целом его наблюдения о проявлениях З. с. в музыке были плодотворными и обогатили представление о временных муз. закономерностях.
Позднее З. с. в музыке изучали В. Э. Ферман, Л. А. Мазель и др.
Развивая и уточняя высказанные Розеновым положения, Мазель
установил, что деление в отношении З. с. является признаком
устойчивости, внутр. завершённости мелодии. Он показал, что в точке
З. с. муз. периода может находиться мелодич. вершина не только
всего периода, но и 2-го предложения, что точка эта может являться
моментом, с к-рого 2-е предложение развивается иначе сравнительно с
1-м (эти проявления З. с. могут совмещаться). В масштабах сонатного
allegro и в трёхчастной форме, по Мазелю, точка З. с. в классич.
музыке обычно приходится на начало репризы (конец разработки), в
музыке композиторов-романтиков — располагается в репризе, ближе к
коде. Мазель ввёл понятие З. с. в курс анализа муз. произведений;
постепенно оно прочно вошло в обиход сов. музыкознания.
с. является признаком
устойчивости, внутр. завершённости мелодии. Он показал, что в точке
З. с. муз. периода может находиться мелодич. вершина не только
всего периода, но и 2-го предложения, что точка эта может являться
моментом, с к-рого 2-е предложение развивается иначе сравнительно с
1-м (эти проявления З. с. могут совмещаться). В масштабах сонатного
allegro и в трёхчастной форме, по Мазелю, точка З. с. в классич.
музыке обычно приходится на начало репризы (конец разработки), в
музыке композиторов-романтиков — располагается в репризе, ближе к
коде. Мазель ввёл понятие З. с. в курс анализа муз. произведений;
постепенно оно прочно вошло в обиход сов. музыкознания.
Литература: Розенов Э. К., О применении закона «золотого деления» к
музыке, «Известия СПб. Общества музыкальных собраний», 1904, вып.
июнь — июль — август, с. 1-19; Tимердинг Г. Е., Золотое сечение,
пер. с нем., П., 1924; Мазель Л., Опыт исследования золотого
сечения в музыкальных построениях в свете общего анализа форм,
«Музыкальное образование», 1930, No 2.
Я рекомендую
Это интересно
Твитнуть
реклама
вам может быть интересно
Золотое сечение в процентах
Число Бога, числа Фибоначчи, Золотое Сечение
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.
Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.
Числа Фибоначчи
Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Также ученый привел ряд закономерностей:
Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.
Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.
Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.
Для практических целей ограничиваются приблизительным значением Φ = 1,618 или Φ = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Число Φ называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства.
Теперь подробности:
Определение ЗС — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
То есть, если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382. Таким образом, если взять строение, например, храм, построенный по принципу ЗС, то при его высоте скажем 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6, 18 см. (понятно, что цифры взяты ровными для наглядности)
Далее можно рассчитать высоту двери, окон, креста. И везде будет просматриваться принцип ЗС.
А какова связь между ЗС и числами Фибоначчи?
Числа последовательности Фибоначчи это:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Закономерность чисел в том, что каждое последующее число равно сумме двух предыдущих чисел.0 + 1 = 1;1 + 1 = 2;2 + 3 = 5;3 + 5 = 8;5 + 8 = 13;
8 + 13 = 21 и т.д.,
а отношение смежных чисел приближается к отношению ЗС.Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.
То есть в основе ЗС лежат числа последовательности Фибоначчи.
Считается, что термин «Золотое сечение» ввел Леонардо Да Винчи, который говорил, «пусть никто, не будучи математиком, не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Ряд чисел Фибоначчи наглядно моделируется (материализуется) в форме спирали.
А в природе спираль ЗС выглядит вот так:
При этом, спираль наблюдается повсеместно (в природе и не только):
— Семена в большинстве растений расположены по спирали- Паук плетет паутину по спирали- Спиралью закручивается ураган- Испуганное стадо северных оленей разбегается по спирали.- Молекула ДНK закручена двойной спиралью. Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.- Эмбрион развивается в форме спирали- Спираль «улитки во внутреннем ухе»- Вода уходит в слив по спирали- Спиральная динамика показывает развитие личности человека и его ценностей по спирали.
— Ну и конечно, сама Галактика имеет форму спирали
Таким образом можно утверждать, что сама природа построена по принципу Золотого Сечения, оттого эта пропорция гармоничнее воспринимается человеческим глазом. Она не требует «исправления» или дополнения получаемой картинки мира.
Фильм. Число Бога. Неопровержимое доказательство Бога; The number of God. The incontrovertible proof of God.
Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).
21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618
Золотое сечение в строении микромиров
Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.
В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.
Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.
Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:
«Доктор Каспар и я показали, что для сферической оболочки вируса самой оптимальной формой является симметрия типа формы икосаэдра. Такой порядок сводит к минимуму число связующих элементов… Большая часть геодезических полусферических кубов Букминстера Фуллера построены по аналогичному геометрическому принципу. 14 Монтаж таких кубов требует чрезвычайно точной и подробной схемы-разъяснения. Тогда как бессознательные вирусы сами сооружают себе столь сложную оболочку из эластичных, гибких белковых клеточных единиц.»
Комментарий Клюга еще раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который ученые классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует четкий замысел и осуществлен разумный проект 16. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру проектами, созданными гениальным архитектором Букминстером Фуллером.
Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.
Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.
В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.
Золотое сечение в физике
Последовательность чисел Фибоначчи и формула золотого сечения непосредственным образом затрагивает и сферу физики и физических законов:
«Представим две соприкоснувшиеся между собой стеклянные пластины. Теперь направим на них луч света. Часть луча пройдет сквозь стекло, другая часть поглотиться, оставшаяся же часть отразится от стекла. Произойдет явление «множественного отражения». Количество путей, которые проходит луч внутри стекла, прежде чем пройти и выйди сквозь стекло, зависит от количества лучей, который не прошли сквозь стекло, а подверглись отражению. Если подсчитать количество лучей, отразившихся от стекла и прошедших сквозь него, то опять же мы получим последовательность чисел Фибоначчи в соотношении 1:1.618.»
Строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле. Это является самым ярким доказательством их осознанной сотворенности согласно некоему проекту, замыслу. Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.
Любая помощь проекту — это добрый шаг с Вашей стороны, Вы становитесь хотя бы немного, но соавтором проекта и непосредственным образом влияете на его дальнейшее развитие. Если Вы готовы оказать поддержку нашему проекту, мы с благодарностью примем любую посильную помощь! Заранее сердечно благодарим Вас за участие!
Как использовать Золотое Сечение в Дизайне
Золотое сечение – это то, о чем должен знать каждый дизайнер. Мы объясним, что это такое, и как вы можете его использовать.
Существует общее математическое соотношение, найденное в природе, которое может быть использовано в дизайне для создания приятных, натурально-выглядящих композиций. Его называют Золотым Сечением или греческой буквой “фи”. Если вы иллюстратор, арт директор или графический дизайнер, вам определенно стоит использовать Золотое Сечение в каждом проекте.
В этой статье мы объясним, как его использовать, а также поделимся несколькими отличными инструментами для дальнейшего вдохновения и изучения.
Тесно связанная с Последовательностью Фибоначи (Fibonacci Sequence), которую вы, возможно, помните из уроков математики или романа Дэна Брауна “Код Да Винчи”, Золотое Сечение описывает идеально симметричное взаимоотношение между двумя пропорциями.
Приблизительно равное соотношению 1 : 1.61, Золотое Сечение может быть иллюститровано как Золотой Прямоугольник: большой прямоугольник, включающий квадрат (в котором стороны равны длине самой короткой стороны прямоугольника) и прямоугольник поменьше.
Если убрать квадрат из прямоугольника, останется другой, маленький Золотой Прямоугольник. Этот процесс может продолжаться до бесконечности, как и цифры Фибоначи, которые работают в обратном порядке. (Добавление квадрата со сторонами, равными длине самой длинной стороны прямоугольника, приближает вас к Золотому Прямоугольнику и Золотому Сечению.)
Золотое Сечение в действии
Считается, что Золотое Сечение используется уже около 4000 лет в искусстве и дизайне. Однако, многие люди соглашаются, что при строительстве Египетских Пирамид также использовался этот принцип.
В более современные времена это правило может быть замечено в музыке, искусстве и дизайне вокруг нас. Применяя аналогичную рабочую методологию, вы можете привнести в свою работу те же особенности дизайна. Давайте взглянем на несколько вдохновляющих примеров.
Греческая архитектура
В древнегреческой архитектуре Золотое Сечение использовалось для определения приятных пространственных отношений между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих структуру.
В результате получается идеально пропорциональное строение. Движение неоклассической архитектуры также использовало эти принципы.
Тайная вечеря
Леонардо Да Винчи, как и многие другие художники прошлых лет, часто использовал Золотое Сечение для создания приятных композиций.
В Тайной вечере фигуры расположены в нижних двух третях (самая большая из двух частей Золотого Сечения), а Иисус идеально зарисован между золотых прямоугольников.
Золотое сечение в природе
Существует множество примеров Золотого Сечения в природе – их вы можете обнаружить вокруг себя. Цветы, морские раковины, ананасы и даже пчелиные соты демонстрируют одинаковое соотношение.
Как рассчитать Золотое Сечение
Рассчет Золотого Сечения достаточно прост, и начинается с простого квадрата:
01. Нарисуйте квадрат
Он образует длину короткой стороны прямоугольника.
02. Разделите квадрат
Разделите квадрат пополам с помощью вертикальной линии, образуя два прямоугольника.
03. Проведите диагональ
В одном из прямоугольников проведиде линию из одного угла в противоположный.
04. Поверните
Поверните эту линию так, чтобы она легла горизонтально по отношению к первому прямоугольнику.
05. Создайте новый прямоугольник
Создайте прямоугольник, используя новую горизонтальную линию и первый прямоугольник.
Как использовать Золотое Сечение
Использовать этот принцип проще, чем вы думаете. Существует пара быстрых трюков, которые вы можете использовать в своих макетах, или потратить немного больше времени и полностью раскрыть концепт.
Быстрый способ
Если вы когда-нибудь сталкивались с “Правилом третей”, то вам будет знакома идея разделения пространства на равные трети по вертикали и горизонтали, при этом места пересечения линий создают естественные точки для объектов.
Фотограф размещает ключевой объект на одной из этих пересекающихся линий, чтобы создать приятную композицию. Этот прицип может также использоваться в вашей разметке страниц и дизайне постеров.
Правило третей можно применять к любой форме, но если вы примените его к прямоугольнику с пропорциями примерно 1 : 1.6, вы окажетесь очень близко к золотому прямоугольнику, что сделает композицию более приятной для глаз.
Полная реализация
Если вы хотите реализовать Золотое Сечение в вашем дизайне в полной мере, то просто расположите основной контент и сайдбар (в веб дизайне) в соотношении равном 1 : 1.61.
Можно округлить значения в меньшую или большую стороны: если контент-зона равна 640px, а сайдбар 400px, то эта разметка вполне подойдет под Золотое Сечение.
Разумеется, вы также можете разделить области контента и боковой панели на одно и то же отношение, а связь между заголовком веб-страницы, областью содержимого, футером и навигацией также может быть спроектирована с использованием того же приципа.
Полезные инструменты
Вот несколько инструментов, которые помогут вам в использовании Золотого Сечения в дизайне и создании пропорциональных проектов.
01. goldenRATIO
GoldenRATIO – это приложение для создания дизайна веб сайтов, интерфейсов и шаблонов, подходящих под Золотое Сечение. Доступно в Mac App Store за 2,99$. Включает визуальный калькулятор Золотого Сечения.
Так же в приложении есть функция “Избранное”, которое сохраняет настройки для повторяющихся задач и “Click-thru” мод, позволяющий сворачивать приложение в Photoshop.
02. Golden Ratio Typography Calculator
Этот калькулятор Золотого Сечения от Pearsonified помогает в создании идеальной типографики для вашего сайта. Введите размер шрифта, ширину контейнера в поле, и нажмите кнопку Set my type! Если вам нужно оптимизировать количество букв в строчке, вы можете дополнительно ввести значение CPL.
03. Phicalculator
Это простое, полезное и бесплатное приложение доступно для Mac и PC. Введите любое число, и приложение вычислит вторую цифру в соответствии с приципом Золотого Сечения.
04. Atrise Golden Section
Это приложение позволяет проектировать с золотыми пропорциями, экономя кучу времени на вычислениях.
Вы можете менять формы и размеры, фокусируясь на работе над своим проектом. Постоянная лицензия стоит 49$, но вы можете скачать бесплатную версию на месяц.
Обучение Золтому Сечению
Вот несколько полезных туториалов по Золотому Сечению (английский язык):
01. Graphic design, illustration and art
В этом туториале для Digital Arts Роберто Маррас (Roberto Marras) показывает, как использовать Золотое Сечение в художественной работе.
02. Web design
Туториал от Tuts+, рассказывающий, как использовать золотые принципы в веб дизайн проектах.
03. More web design
Туториал от Smashing Magazine, рассказывающий о пропорциях и правиле третей.
Перевод статьи The designer’s guide to the Golden Ratio
Автор оригинального текста Creative Bloq Staff
Божественная гармония
Эта гармония поражает своими масштабами…
Здравствуйте, друзья!
Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.
Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)
Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».
До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.
Золотое сечение в математике
Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.
В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.
Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:
Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.
Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ — Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».
Сама последовательность выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… и дальше до бесконечности.
Если словами, то последовательность Фибоначчи — это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.Причем здесь золотое сечение? Сейчас увидите.
Спираль Фибоначчи
Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.
Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.
Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».
Золотая спираль — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение.В общем и целом, с точки зрения математики, золотое сечение — идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.
Золотое сечение в природе, человеке, искусстве
Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.
И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.
Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.
Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.
Пропорции золотого сечения в человеке
Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.
Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:
от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618
Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».
Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.
Золотое сечение в природе и ее явлениях
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:
в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.
Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.
Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:
Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.
Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.
Золотое сечение в искусстве
Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.
Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.
Золотые котики Фибоначчи
Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)
А все дело в том, что кошки — идеальны! Не верите? Сейчас докажу вам это математически!
Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)
* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.
На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!
P. S. Изображения взяты с сайта medium.com.
Золотое сечение
Калькулятор ниже находит параметры, соответствующие золотому сечению. Про само золотое сечение рассказано под калькулятором
ТипДлинный отрезок Короткий отрезок Суммарный отрезок Точность вычисленияЗнаков после запятой: 8
Золотое сечение — термин, обозначающий деление отрезка на два в соотношении, при котором большая часть относится к меньшей также как весь отрезок относится к большей. Также употребляют термин деление в крайнем и среднем отношении.
Отношение это фиксированное, его можно найти. Представим, что b у нас единица. Тогда значение a должно равняться искомому отношению, и его надо найти — переименуем его в более привычное x и проведем ряд преобразований:Последнее есть квадратное уравнение. Его положительный корень: и есть отношение золотого сечения. Число это иррациональное:
Для практических целей иногда используют приближение — большая часть равна 0,62 всей величины, меньшая — 0,38 (это видно, если ввести длину 1, и выбрать тип «суммарный отрезок» в калькуляторе сверху).
Золотое сечение известно еще со времен Евклида (ок. 300 лет до н. э.), и у него много забавных свойств, про которые можно почитать в: Википедии, например, к нему стремится отношение последовательных чисел Фибоначчи.
Для полноты ликбеза скажем, что почему-то считается, что объекты, содержащие золотое сечение, воспринимаются людьми как наиболее гармоничные. Ну а вот целая занятная статья, где золотое сечение находят буквально во всем.
ЗОЛОТОЕ СЕЧЕНИЕ ИЛИ НОВЫЙ МЕТОД РАСЧЕТА БОЖЕСТВЕННОЙ ПРОПОРЦИИ
ЗОЛОТОЕ СЕЧЕНИЕ ИЛИ НОВЫЙ МЕТОД РАСЧЕТА БОЖЕСТВЕННОЙ ПРОПОРЦИИ
Васильев К.С. 11Муниципальное общеобразовательное бюджетное учреждение «Средняя общеобразовательная школа №1» пгт. Пойковский, 11класс
Яблокова Е.Л. 11Муниципальное общеобразовательное бюджетное учреждение «Средняя общеобразовательная школа №1» пгт.Пойковский
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Исследовательская работа посвящена божественной пропорции и использованию ее при анализе живописного произведения искусства.
В ходе работы решаются актуальные вопросы в области искусства, связанные с анализом картин, нахождением нового способа вычисления золотого сечения. Прослеживается интерес к культуре, искусству и к точным наукам. В ходе исследования нашла подтверждение идея о том, что используя новый способ определения золотого сечения, человек, не знакомый со сложными расчетами божественной пропорции, способен выполнить композиционный анализ полотна.
Работа может быть интересна специалистам широкого круга: научным деятелям, искусствоведам, учителям, учащимся, т.к. она затрагивает многие области наук.
Золотое сечение и новый метод расчета божественной пропорции
Васильев Кирилл Станиславович
Россия, Ханты-Мансийский автономный округ-Югра, поселок городского типа Пойковский, Муниципальное общеобразовательное бюджетное учреждение «Средняя общеобразовательная школа №1», 11 класс
Оглавление
Введение………………………………………………………………………………………… 1
Глава 1. Суть понятия «божественная пропорция»…………………………………………….. 3
Глава 2. Применение божественной пропорции в жизни человека………………………… 4
Глава 3. Новый способ определения золотого сечения……………………………………….5
Заключение………………………………………………………………………………………10
Список используемой литературы………………………………………………………… 12
Приложение……………………………………………………………………………………..13
1
Золотое сечение и новый метод расчета божественной пропорции
Васильев Кирилл Станиславович
Россия, Ханты-Мансийский автономный округ-Югра, поселок городского типа Пойковский, Муниципальное общеобразовательное бюджетное учреждение «Средняя общеобразовательная школа №1», 11 класс
Научная статьяВведение
Актуальность работы. Испокон веков золотое сечение проявляется во всем сущем: начиная от строения одноклеточных организмов, заканчивая человеком. Несмотря на то что в некоторых ситуациях божественная пропорция невидима для невооруженного глаза, известно, что она существует в других биосистемах, например, на молекулярном уровне. Большую популярность вопрос о золотом сечении получил в XIX веке. Известный немецкий профессор Адольф Цейзинг обнаружил некоторые особенности, касающиеся золотой пропорции в далеком 1855 году. Он утверждал универсальность и практичность сечения в природе и искусстве, измерив около двух тысяч людских тел. Наука в XIX веке начинает искать ответы на «вечные» вопросы, установленные еще древними греками. Конечно, не все ответы найдены на сегодняшний день, но утверждение, что в мире главенствует закон ритма и числа, обуславливающий структурное и функциональное совершенство, безусловно, существует. Проблема золотого сечения актуальна в наше время, поэтому я решил выяснить, на какой стадии разрешения она находится.
В ходе проведенных исследований было выявлено, что из 50-ти учащихся большинство незнакомо с понятием «золотого сечения», но подсознательное чутье к божественной пропорции у десятиклассников присутствует. Знания о золотом сечении являются не только интересными и познавательными, по мнению учащихся, но и нужными. Треть респондентов хорошо знакома с произведениями искусства, но выполнение анализа картин у большинства вызывает затруднение. (Приложение №1, график 1-5).
Гипотеза: мы предполагаем, что возможно вывести новый способ определения золотого сечения, который окажется прост в использовании и послужит основой для построения других сечений. Любой человек способен произвести формальный анализ
2
живописного полотна посредством золотого сечения, пользуясь выведенным способом.Основные тенденции:
— Использование золотого сечения в фотографии и типографии через «правило третей» — Применение божественной пропорции в разработке дизайна сайтов и логотипов, в проектировании архитектурных сооружений, создании музыкальных произведений и в промышленности.
Цель исследования: популяризировать тему божественной пропорции для людей, не имеющих глубоких знаний в области искусства и математики, посредством вычисления золотого сечения новым и обычным методами, определив связь этого соотношения с картинами Югорских художников.
Объект исследования: картинаА.А. Иванова «Явление Христа народу» и работы Югорских художников Митрофана Тебетева, Владимира Видинеева, Виктора Банникова.
Предмет исследования: способы расчетов божественной пропорции.К достижению цели ведет решение следующих задач:
-
рассмотреть понятие «золотое сечение»;
-
выявить геометрические разновидности построения пропорции и способы его применения;
-
проанализировать примеры анализов картин на основе божественной пропорции;
-
вывести новый метод определения божественной пропорции;
-
определить точки последующих сечений, используя новый способ;
-
создать алгоритм построения сечений для искусствоведческого анализа живописного полотна.
Теоретическая значимость работы: исследование золотого сечения вносит определенный вклад в развитие искусства, т.к. любая теория развивается на основе фактов, предоставляемых частными исследованиями. Результаты, полученные в работе, могут быть использованы также при решении теоретической проблемы в построении божественной пропорции и последующих сечений.Практическая значимость работы: возможность использования результатов и положений исследования на уроках МХК, математики, изобразительного искусства,
3
семинарах, мастер-классах и в деятельности, связанной с дизайном.
Методы исследования: анкетирование, опрос, эксперимент, анализ, синтез, прием статистического подсчета, искусствоведческий анализ.
Глава 1. Суть понятия «божественная пропорция»
Наше видение уникально. Оно позволяет нам получать информацию о форме предмета, соразмерности каких-либо отдельных частей. Человеческий глаз устроен таким образом, что он лучше всего воспринимает гармоничную и эстетически совершенную форму. Она представляет собой высшую гармонию целого и его частей, встречающуюся во всех сферах человеческой деятельности: в науке, искусстве и др. Это соотношение целого и частей именуется золотым сечением. Золотая пропорция, гармоническое деление или божественная пропорция в математике и искусстве является соотношением числовых величин. Например, деление отрезка на две неравные части в отношении 62:38. (Приложение №2, рис.1) Божественная пропорция обозначается буквой φ (фи), названной в честь архитектора Фидия, и имеет собственную константу — 1,618. Такое деление отрезка впервые встречается в «Началах»1 древнегреческого математика Евклида, где пропорция применяется в построении пятиугольника. (Приложение №2, рис.2) Интерес к пропорции возрастает в далеком 1202 году, когда известный математик Леонардо Пизанский (известный как Фибоначчи) издает главный труд всей своей жизни «Книга Абака»2, в которой он исследует особый ряд чисел, именуемый как последовательность Фибоначчи.
Последовательность имеет такой вид: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377…
Ряд содержит две важнейшие особенности:1) каждое последующее число равно сумме двух предыдущих чисел;2) если взять две последовательные пары из ряда и разделить большее число на меньшее, результат будет постепенно приближаться к числу золотого сечения. В эпоху Возрождения на свет выходит трактат величайшего математика современности Луки Пачоли под названием «О божественной пропорции» с изумительными
4
иллюстрациями, автором которых является сам Леонардо да Винчи. (Приложение №2, рис.3) Принято считать, что именно Леонардо ввел термин «золотое сечение» в научный обиход благодаря своему рисунку витрувианского человека. (Приложение №2, рис.4) Исследуя объемные тела посредством сечения, он получал фигуры со строго выверенными отношениями сторон.
Глава 2. Применение божественной пропорции в жизни человека
Не секрет, что божественная пропорция создает впечатление гармонии форм и единства, непревзойденного баланса и красоты, поэтому многие известные деятели искусства применяли ее в своих произведениях. Мастера, прежде всего, опирались на теорию пропорций и вдохновлялись совершенством человека и природы. Основываясь на результатах эксперимента Адольфа Цейзинга, можно утверждать, что отношение частей человеческого тела было непосредственно связано с формулой золотого сечения. (Приложение №2, рис.5) Следовательно, формула находила свое активное применение как в скульптуре, так и в архитектуре. Ярким примером применения математической пропорции может послужить статуя Аполлона Бельведерского, где рост от макушки до земли делится ровно по линии пупка. (Приложение №2, рис.6) Сергей Эйзенштейн, как известный советский режиссер театра и кино, снял фильм «Броненосец Потёмкин» по канонам золотой пропорции. Лента фильма включает в себя пять частей, на трех из них сюжет развивается на корабле. Это свидетельствует о том, что режиссер прибегал к последовательности Фибоначчи. Можно заметить применение божественной пропорции в кинематографе и музыке в местах перелома сюжета либо развития темы или настроения.
Доклад Эмилия Розенова о наличии божественной пропорции в музыке стал весьма популярным в 1903 году. Он, как ярый исследователь загадочной пропорции, на примере произведений «венской классической школы» делится результатами, которые впоследствии будут описаны в статье «Закон золотого сечения в поэзии и музыке»3.
Геометрические разновидности построения золотого сечения.
На сегодняшний день существует большое количество способов построения божественной пропорции. Все они имеют, как правило, треугольную, прямоугольную, или квадратную основы построения. Первый способ осуществляет деление отрезка прямой по
5
золотому сечению с помощью циркуля и линейки. (Приложение №2, рис.7) Второй способ вытекает из основного сечения и дает отношение отрезка, равное 44:56. Его название — «второе золотое сечение». Этот способ был описан в статье журнала «Отечество» болгарским иллюстратором Цветаном Цековым-Карандашом в 1983 году. Такая пропорция чаще всего используется при построении композиций изображений удлинённого формата. (Приложение №2, рис.8).
Также геометрическим способом нахождения отрезков божественной пропорции считается построение пентаграммы. Этот способ построения разработал знаменитый немецкий живописец Альбрехт Дюрер. (Приложение №2, рис.9) Каждый конец пентаграммы, как известно, представляет собой золотой треугольник. Его основание, отложенное на боковую сторону, делит её в пропорции гармонического деления. (Приложение №2, рис.10).
Казимир Малевич считал, что именно квадрат является основой всех форм, поэтому, проанализировав все общедоступные способы построения, я предположил, что точкой опоры для нового способа определения божественной пропорции послужит квадрат.
Глава 3. Новый способ определения золотого сечения
В ходе работы было рассмотрено около 30 полотен с готовым искусствоведческим анализом, где применялись способы определения золотого сечения. Путем экспериментального подбора геометрических фигур к точкам золотого деления, математических расчетов было выявлено, что полуокружность является необходимым элементом при построении точки божественной пропорции, т.к. окружность – это замкнутая кривая, константой которой является иррациональное число «пи».Синтез рациональности и иррациональности дает возможность создания точки золотого деления. Таким образом был выведен новый способ определения точек божественной пропорции и создан алгоритм построения золотого и последующих сечений. (Приложение №2, рис.11)
-
Полотно делится вертикально на 3 равные части;
-
Отмечаем точки пересечения вертикальных линий с основанием. Боковые стороны полотна тоже считать за вертикальные линии;
-
Образуются 4 точки, лежащие на основании полотна;
-
Обозначаем их буквами произвольно: A1, A2, A3, A4;
6
-
Откладываем высоту, равную расстоянию между точками A1 и A2;
-
Верхнюю точку высоты обозначаем буквой B1;
-
Из точки B1 проводим горизонтальную линию, параллельную основанию.
-
Точку пересечения обозначим B2;
-
Образуется прямоугольник B1B2A4A1, состоящий из трех равных квадратов;
-
Строим полуокружность, радиусом A1B1 и центром в точке A2;
-
Отрезок A1B1 делим пополам точкой С;
-
Из точки C проводим горизонтальную линию, параллельную основанию
-
Точку пересечения обозначим С2;
-
Находим точку пересечения полуокружности с линией CC2, расположенную в среднем квадрате;
-
Обозначаем точку пересечения буквой С1;
-
Из точки C1 строим перпендикуляр к основанию A1A4;
-
Точку, лежащую на основании A1A4 обозначим буквой Z;
-
Точка Z является точкой золотого деления.
Анализ композиционно-ритмического строя картины А. А. Иванова «Явление Христа народу» по Ф.В. Ковалеву
История: Знаменитый художник Александр Андреевич Иванов создавал свой венец творения «Явление Христа народу» порядка 20 лет. Это редчайший случай, когда мастер настолько глубоко проникся темой полотна. Прежде чем оживлять картину красками, художник создал около 260 эскизов. Проживая в Италии, Александр Иванов познакомился с Николаем Васильевичем Гоголем. Впоследствии писатель согласился помочь ему в написании картины. Он позировал для создания образа на полотне. Человек, похожий на Гоголя, стоит ближе всех к Иисусу Христу. Особенность полотна заключается в том, что на нем изображены исключительно мужские лица, но прообразом для художника являлись лица представительниц прекрасного пола. По мнению творца, лица девушек итальянского происхождения имеют больше евангельских черт, нежели лица мужчин.
Анализ полотна: фигура Иоанна Крестителя – главный композиционный центр на полотне. Наиболее важные события происходят в правой части картины. От Иоанна Крестителя мы плавно переносим взгляд к фигуре Иисуса Христа. (Приложение №2, рис.12) Эффект весов на полотне создается путем правильного композиционного решения.
7
Наиболее ярко это проявляется между выходящим из воды юношей со стариком слева и двух обнаженных фигур справа. Весы, как правило, имеют центр. Центром здесь является фигура Иоанна Крестителя, указывающая на Христа. Если внимательно рассмотреть расположение людей на полотне, то можно выделить несколько весов:1. Иоанн Креститель и Христос. Фигура Христа значительно меньше Иоанна.
2. Христос и юноша в синем плаще.
3. Гоголь и Христос. Очень маленькое расстояние между ними.
4. Всадник и Христос. Относительно одинаковые по размеру объекты, находящиеся на одном расстоянии от переднего плана.
Если зритель рассматривает картину с 10 метров, то, согласно формуле глубины картинного пространства получается, что расстояние от Иоанна до Христа – около 24 метров; от юноши в плаще — 10 метров; от Гоголя — 2 метра; от всадника — 0 метров. Итак, на картине Александра Иванова «Явление Христа народу» линии золотого сечения пересекаются на фигуре Христа вдали. Фигуры переднего плана значительно больше по размерам и выписаны, но взгляд притягивает именно фигура Иисуса, т.к. она находится в зрительном центре.
Анализ композиционно-ритмического строя картины А. А. Иванова «Явление
Христа народу» по новому способу определения божественной пропорцииПостроим точки золотого сечения по новому способу. Определим композиционные центры полотна благодаря образовавшимся квадратам, оценим композиционное решение и расположение объектов на полотне. (Приложение №2, рис.13) Анализ полотна: на переднем плане изображен иудейский народ и фигура Иоанна Крестителя, которая, как было сказано выше, является главным композиционным центром полотна. Рассмотрим точки золотого деления. Левая точка расположена там, где находится Иоанн Креститель. Правая точка приходится на сидящего человека в синем одеянии. Сравнивая эти две фигуры, несложно догадаться, что автор использовал прием контраста, выделяя их цветом. Затем обращаем внимание на вертикальные линии квадратов. Линия квадрата в левой части картины приходится на человека, отвернувшего голову и находящегося в движении. Далее смотрим на линию квадрата в правой части картины. Она приходится ровно на Иисуса Христа. В данном случае мастер использует зеркальный эффект. Человек в золотистом одеянии смотрит в сторону, откуда виднеется силуэт Спасителя. В левой руке Иисуса находится крест, олицетворяющий символ нового
8
вероучения. Вероучения, открытого для всех. Поэтому человек является прообразом верующего народа, идущего за Христом. Таким образом, точки божественной пропорции, вычисленные Ф.В. Ковалевым путем наложения сетки золотого сечения и «правила весов» совпадают с точками золотого деления, определенными новым способом.
Определение других сечений посредством нового метода
Знаменитый британский художник Уильям Хогарт считал, что прямые, параллельные либо пересекающиеся под прямым углом линии, создают подсознательное впечатление застоя, искусственности и торможения. В то время, как волнообразная линия была для него воплощением единства и разнообразия, элементом всех живых и изменяющихся природных объектов. Мнение Хогарта подтолкнуло к новому подходу построения последовательных сечений.
На сегодняшний день в мире насчитывают десять видов сечений. Наряду с божественной пропорцией существует последовательность родственных сечений, таких как серебряное, бронзовое, медное, никелевое и так далее. Каждое сечение, исходя из ряда, имеет свои особенности и характерные черты. Как известно, сечение имеет собственное иррациональное число – константу. Наличие иррациональности говорит о постоянном движении без пауз и остановок, а также о траектории движения числа. Точка золотого сечения образуется путем слияния статичных и динамичных элементов. В роли статичных элементов построения играют квадраты, параллельные линии и перпендикуляр. Роль динамичного элемента отведена полуокружности. Отсюда следует вывод, что точка божественной пропорции самопроизвольно возникла из неживого. Последующие сечения строятся, опираясь на уже возникшее золотое сечение. От статичных элементов они образовываться не могут. Золотое сечение положило начало возникновению новой жизни.
Пошаговое построение последовательных сечений на основе нового метода определения золотой пропорции
-
Отправной точкой для построения последовательных сечений будет являться построенное золотое сечение;
-
В прямоугольнике B1B2A4A1 необходимо разделить отрезок B1C точкой S на две равные части;
9
-
Из точки S проводим горизонтальную линию, параллельную основанию;
-
Точку пересечения обозначим S1;
-
Из точки A3 провести диагональ к точке B2;
-
Образуется пересечение линии CC1 с диагональю A3B2 и линии SS1 с диагональю A3B2;
-
Точки пересечения зафиксированы. Обозначим их как: M и N;
-
Из обеих точек пересечения опускается перпендикуляр к основанию A1A4;
-
Точки, лежащие на основании, обозначим, как: R и T;
-
Точка R (левее, чем T) является точкой серебряного сечения, а точка T (правее, чем R) является точкой бронзового сечения.
-
Точки построены. (Приложение №2, рис.14)Применим новый метод для анализа смысловых центров в композиции произведений Югорских художников. (Выбор произведений искусства произвольный)
Митрофан Тебетев «На пристани» (Приложение №3)Год создания: 1969 г.Материал, техника: холст, маслоРазмеры: 33х80 см
На этом полотне можно увидеть последовательное расположение точек сечения по обеим сторонам. Вероятнее всего, автор применил зеркальный эффект изображения. На переднем плане расположены люди. Точки золотого сечения попадают на двух детей и на мужчину с велосипедом. Автор полотна связывает такие понятия, как «детство» и «воспоминания». Велосипед здесь является символом беззаботного детства. На точки серебряного сечения приходятся две подруги, изображенные на заднем плане полотка и две женщины в правой части. Художник призывает к общению. В одной ситуации две идущие подруги разговаривают, делятся впечатлениями, в другой ситуации женщина стоит, будто отгорожена от общества. На точки бронзового сечения приходятся мальчик с собакой и одинокий мужчина. Собака как символ верности и дружбы противопоставляется одиночеству. (Приложение №2, рис.15)Владимир Видинеев «Церковь сорока мучеников»
Год создания: 2008 г.
Материал, техника: холст, масло
10
Размеры: 80×90 см
Золотое сечение: линия горизонта, средняя линия церкви, окно, вогнутая арка. Продуманное композиционное решение полотна. Однородность предметов.Серебряное сечение: основание церкви, синонимичные четверики, комбинация цветов.Бронзовое сечение: стихия воды, стихия воздуха, символизм, небо и земля. (Приложение №2, рис.16)
Виктор Банников «Ярославль. Ночь»
Год создания: 2004 г.
Материал, техника: медь/полудрагоценные эмали высокого обжига
Размеры: 42×32см
Золотое сечение: два барабана, два креста.Серебряное сечение: боковые барабаны. На каждом барабане по 3 креста.Бронзовое сечение: точка с левой стороны служит границей храма. По правой точке располагается крыша деревенского дома. Связь мира духовного и мира земного. (Приложение №2, рис.17)
Результаты эксперимента по определению композиционных центров картин посредством применения нового способа вычисления точек золотого и последующих сечений.
50 респондентам, ранее участвовавшим в опросе и эксперименте после обучения новому способу вычисления точек золотого и последующих сечений, было предложено определить и проанализировать композиционные центры трех репродукций: картина Репина И.Е «Пушкин на лицейском экзамене в Царском селе» (Приложение №3.1, рис.1), картина Сурикова В.И «Боярыня Морозова» (Приложение №3.1, рис.2) и произведение прикладного декоративного искусства (батик) Банникова В.Н. «Энергия сотворения» (Приложение №3.1, рис.3). В ходе эксперимента выяснилось, что 100% участников смогли, используя алгоритм, определить точки сечений, но только 34 ученика (68%) выполнили формальный анализ композиционно-ритмического строя произведений. (Приложение №1, график 6)
Заключение. Тема золотого сечения раскрыта еще с глубокой древности, но люди, живущие в 21 веке воспринимают это математическое и эстетическое сокровище как тайну. Божественная пропорция иррациональна. Она в движении всегда. То, что мы создаем сегодня, вписывается ли в рамки золотой пропорции? Быть может это предметы
11
«мертвые», в которых нет живости и той самой частицы Бога? Следовательно, говоря об искусстве, хочется заметить, что оно не утратило эту способность к созданию великолепных произведений, созданных по пропорциям. Но тот вклад, который был вложен художниками, воспринимается людьми как обычное деяние. Возможно, с психологической точки зрения, картины с золотым сечением запоминаются подсознательно у людей, но мы внутри чувствуем, «а знать не знаем». Вывод.1. Экспериментальным путем доказана возможность выведения нового способа определения золотого и последующих сечений.2. Способ прост в использовании и не требует математических расчетов.3. Создан алгоритм построения точек золотого и последующих сечений для композиционного анализа полотна.
4. Данный способ позволяет определить главное в целом и показывает, вокруг чего объединены части целого.
5. Анализ картины посредством нового способа обращает внимание на законы композиции, которые организуют изображение в соответствии со смыслом и законами зрительного восприятия.
12
Список используемой литературы и источников
-
Андрей Чернов. Заметки о вечном. «Серебряное сечение (введение в проблему)»URL: http://chernov-trezin.narod.ru/ZS_1_4.htm
-
Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с.
-
Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973URL: http://kvant.mccme.ru/1973/08/zolotoe_sechenie.htm
-
В. Лаврус, Золотое сечениеURL: http://n-t.ru/tp/iz/zs.htm
-
Ковалев Ф.В. К56 Золотое сечение в живописи: Учеб. пособие.- К.: Вы-ща шк. Головное изд-во, 1989. – 143 с, 90 ил., табл. – Библиогр.: 77 назв.ISBN-11-001336-5.
-
Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с
URL: https://books.google.ru/books?id=t9lICAAAQBAJ&redir_esc=y
-
Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.URL: http://kvant.mccme.ru/pdf/1997/06/kv0697kaleid.pdf
-
Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
URL: http://314159.ru/tsvetkov/tsvetkov2.htm
-
J. J. O’Connor, E. F. Robertson. Golden ratio. MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland.URL: http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Golden_ratio.html
-
https://ru.wikipedia.org/wiki/Золотое_сечение
-
Roger Herz-Fischler. A Mathematical History of the Golden Number. — Courier Corporation, 2013. — 228 с.
URL: https://books.google.ru/books?id=aYjXZJwLARQC&redir_esc=y
13
Приложение №1
График 1
График 2
14
График 3
График 4
15
График 5
График 6 16
Приложение №2
(рис.1)
(рис.2) 17
(рис.3)
(рис.4) 18
(рис.5)
19
(рис.6)
(рис.7)
(рис.8)
20
(рис.9)
(рис.10)
(рис.11) 21
(рис.12)
22
(рис.13)
(рис.14)
23
(рис.15)
(рис.16)
(рис.17) 24
Приложение №3
Тебетев Митрофан Алексеевич — член Союза художников России с 1993 г. Участник региональных, окружных и городских выставок.
Владимир Видинеев – член Союза Художников России, член Международной ассоциации изобразительный искусств – АИАП ЮНЕСКО, Заведующий кафедрой изобразительного искусства, доцент Нижневартовского Государственного гуманитарного университета.
Банников Виктор Николаевич — кандидат педагогических наук, доцент (2000), член «Союза художников России» (2002), дипломант «Союза художников России» (2003, 2005), дипломант Российской Академии художеств (2005). В 2007 году награжден Почетной грамотой Министерства культуры и массовых коммуникаций Российской Федерации. Академик Европейской академии естественных наук (секция культурологии). В настоящее время работает заведующим кафедрой художественного образования и эстетического воспитания ГОУДПО Институт повышения квалификации и развития регионального образования.
Приложение №3.1 25
(рис.1)
(рис.2)
(рис.3) 27
1 «Начала» (лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. о построении геометрии. Является эталоном античной математики в целом и основой для последующих исследований.
2 «Книга абака» (лат. Liber abaci) — главный труд Фибоначчи, посвященный десятичной арифметике и знаменитой последовательности Фибоначчи.
3 «Закон золотого сечения в музыке и поэзии» — доклад музыковеда Розенова Э.К, который положил начало исследованиям математических закономерностей, связанных с золотой пропорцией в музыке.
Просмотров работы: 1134
Золотое сечение в теле человека
В процессе работы над индивидуальным исследовательским проектом по математике на тему «Золотое сечение в теле человека» автором была поставлена цель, выяснить, действительно ли золотое сечение делает человеческое тело более гармоничными, разобраться в истории золотого сечения и его роли в окружающем мире.
Подробнее о работе:
В ученическом проекте по математике «Золотое сечение в теле человека» автором была изучена история золотого сечения, дано определение того, что принято считать золотым сечением, рассматривается принцип золотого сечения в теле человека на примере определения симметрии на лице и руках человека.
Учебная исследовательская работа по математике на тему «Золотое сечение в теле человека» будет интересна учащимся 8, 9 и 10 класса, рассматривает симметрию как основу красоты и совершенства человеческого тела.
В работе автор приводит информацию, найденную в различных исторических, научных, энциклопедических источниках и примеры использования золотой пропорции в человеческом теле, проводит исследование применения принципа золотого сечения в теле человека.
Оглавление
Введение
1. Золотое сечение.
1.1 История золотого сечения.
1.2 Что такое золотое сечение?
1.3 Золотое сечение в теле человека.
2. Результаты исследования.
2.1 Практические знания о золотом сечении в нашем теле.
2.2 Определение золотого сечения в теле человека.
Заключение
Используемая литература
Введение
Как вы думаете, что общего между древнеегипетскими пирамидами, полотном Леонардо да Винчи «Святой Иерахим», подсолнухом, улиткой, сосновой шишкой и пальцами человека?
Ответ на этот вопрос можно найти в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, известным под именем Фибоначчи. После его открытия числа эти так и стали называться именем известного математика. Удивительная суть последовательности чисел состоит в том, что каждое число в этой последовательности равно сумме двух предыдущих. В числах Фибоначчи
при делении любого числа на предыдущую величину всегда получается 1, 618..
Эту пропорцию можно увидеть и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»?..
Гипотеза исследования: подчиняется ли красота и гармоничность человеческого тела математическим законам?
Объект исследования: человеческое тело.
Предмет исследования: использование золотого сечения в теле человека.
Цели: установить, действительно ли золотое сечение делает человеческое тело наиболее гармоничными; формирование навыков самостоятельной исследовательской деятельности; обучение работе с информацией и медиасредствами для расширения кругозора и развития творческих способностей.
Задачи работы:
- Найти в различных исторических, научных, энциклопедических источниках примеры использования золотой пропорции в человеческом теле.
- Провести исследование применение принципа золотого сечения в теле человека.
Материал для исследования:
- Автор работы, ученик 7 Б класса, соседи и родственники старшего возраста.
Методы исследования:
Эмпирические:
- изучение научной, художественной, познавательной литературы;
- наблюдение.
История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его
имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Что такое золотое сечение?
Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Что такое золотое сечение?
Золотое сечение, или божественная пропорция — это идеальное соотношение величин, наилучшая и единственная пропорция, уравнивающая отношения частей какой-либо формы между собой и каждой части с целым, — основа гармонии.
Золотое сечение — это такое пропорциональное деление отрезка на неравные части. При этом весь отрезок так относится к большей части, как большая часть относится к меньшей, или наоборот, меньший отрезок так относится к большему, как больший ко всему. Её примерное числовое значение колеблется около 1.61… если отношение большей части к меньшей, а если наоборот меньшая часть к большей, то 0.61…
Золотое сечение в теле человека
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.
Рассмотрим тело человека. Верхушка головы до пупа относится к уровню пупа и до подошвы ног, как 38:62, то есть 0.63157894…Золотое сечение.
От верхушки головы и до кончиков пальцев к кончикам пальцев и до ступни, относится, как 62:38, то есть 1.6315… Золотое сечение.
От плеча до локтя к локтю и до кончиков пальцев относится, как 38:62, то есть 0.6315… Золотое сечение.
От локтя до кисти руки к кисти руки и до кончиков пальцев относится, как 62:38, то есть 1.631… Золотое сечение.
Возьмём лицо человека.
От верхушки головы и до бровей к бровям и до подбородка относится, как 38:62, то есть 0.631… Золотое сечение.
От кончика носа до губ к губам и до подбородка относится, как 38:62, то есть 0.631… Золотое сечение.
Посмотрим на наши кисти рук. От начала кисти руки до середины пальцев к началу кисти руки до костяшек относится, как 62:38, то есть 1.631… Золотое сечение.
От начала кисти руки и до первых костяшек к костяшкам и до середины пальцев относится, как 38:24, то есть 1.583… Золотое сечение.
Расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618, то есть 0.618… Золотое сечение.
Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).
Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.
Пропорции мужского тела колеблются в пределах среднего отношения 13:8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5 = 1,6. У новорожденного пропорции тела составляют отношение 1:1, к 13 годам они равны 1,6, а к 21 году равны мужской.
Практические знания о золотом сечении в нашем теле
Давайте проведём исследование, чтобы доказать выдвинутую гипотезу.
Для этого измерим пропорции моего тела.
Измерим тело:
1) Рост – 168см 2) от пупа и до ступни – 102 см
1:2=167:102=1.63… – золотое сечение.
2) От макушки головы до пупа – 63 см
2:3=102:63=1.62… — золотое сечение.
3) от макушки головы и до кончиков рук – 104 см
4) от кончиков пальцев и до стопы – 63 см
3:4=104:63=1.65 => на моём теле этот закон не соблюдается.
5) От плеча до локтя – 36 см
6) От локтя до кончиков пальцев – 44 см
6:5=44:36=1.22… — здесь закон не соблюдается.
7) От локтя до начала кисти руки – 27 см
6:7=44:27=1.63… — золотое сечение
8) От начала кисти руки и до кончиков пальцев – 17 см
7:8=27:17=1.58… — близко к золотому сечению.
9) вся голова – 22 см
10) от бровей и до подбородка – 14 см
11) от макушки головы и до бровей – 8.5 см
9:10=22:14=1.57… — близко к золотому сечению
10:11=14:8.5=1.64… — золотое сечение
12) от кончика носа и до подбородка – 52 мм
13) от губ до подбородка – 32 мм
14) от кончика носа и до губ – 20 мм
12:13=52:32=1.625 – золотое сечение
13:14=32:20=1.6 – золотое сечение
15) от начала кисти руки и до конца первого фаланга пальцев – 13 см
16) от начала кисти руки и до костяшек – 8 см
17) от костяшек до конца первого фаланга – 5 см
15:16=13:8=1.625 – золотое сечение
16:17=8:5=1.6 – золотое сечение
Вывод: выполнив измерения, можно убедиться, что не все части человеческого тела имеют пропорции золотого сечения.
Определение золотого сечения в теле человека
Проведем измерения у взрослых старше 19 лет.
| № ученика | Рост (см) | Расстояние от пупа до стопы (см) | Золотое сечение (есть или нет) |
|---|---|---|---|
| 1 | 165 | 101 | есть |
| 2 | 180 | 111 | есть |
| 3 | 156 | 95 | есть |
| 4 | 177 | 108 | есть |
| 5 | 160 | 98 | есть |
| 6 | 157 | 82 | нет |
| 7 | 165 | 103 | есть |
| 8 | 187 | 116 | есть |
Используя данные, построим диаграмму 1. Примерный возраст 19лет и старше.
Диаграмма 1
Мы можем сделать вывод о том, что количество людей, имеющих золотое сечение – большинство.
Получив данные двух исследований, можем сделать вывод об изменении тела человека. С возрастом золотое сечение более ярко выражено.
Заключение
Золотое сечение божественное творение мира красоты. Строение всех живых
организмов и неживых объектов не имеющих никакой связи и подобия между собой спланировано по определенной математической формуле. По этому закону созданы галактики, сотворены растения, микроорганизмы, тело человека, живые существа. Люди изучают этот закон и стараются подражать ему и воплощать этот закон в жизнь.
По результатам исследования я сделал следующий вывод: красота и гармоничность человеческого тела подчиняется математическим законам. С возрастом пропорции золотого сечения в теле человека носят более выраженный характер.
В следующем году я хотел бы обратиться к архитектуре, вершине прикладного искусства. Если золотое сечение и вправду создаёт некую гармонию во всех её проявлениях, то, возможно, я увижу это в геометрических формах самых известных в мире зданий.
Литература
- Кеплер И. О шестиугольных снежинках. – М., 1982.
- Фернандо Корбалан. Золотое сечение. Математический язык красоты./Пер.с англ. – М.: Де Агостини, 2014 .-160 с..
- Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
- Стахов А. Коды золотой пропорции.
- Интернет
Если страница Вам понравилась, поделитесь в социальных сетях:
Реальный номер | математика | Britannica
Действительное число , в математике величина, которая может быть выражена как бесконечное десятичное разложение. Действительные числа используются в измерениях непрерывно меняющихся величин, таких как размер и время, в отличие от натуральных чисел 1, 2, 3,…, возникающих в результате подсчета. Слово , вещественное число отличает их от комплексных чисел, содержащих символ i , или квадратный корень из √ −1, используемых для упрощения математической интерпретации эффектов, например, возникающих в электрических явлениях.Действительные числа включают положительные и отрицательные целые числа и дроби (или рациональные числа), а также иррациональные числа. У иррациональных чисел есть десятичные разложения, которые не повторяются, в отличие от рациональных чисел, разложения которых всегда содержат повторяющуюся цифру или группу цифр, например, 1/6 = 0,16666… или 2/7 = 0,285714285714…. Десятичная дробь, образованная как 0,42442444244442… не имеет регулярно повторяющейся группы и поэтому является иррациональной.
Наиболее известные иррациональные числа — это алгебраические числа, которые являются корнями алгебраических уравнений с целыми коэффициентами.Например, решение уравнения x 2 — 2 = 0 является алгебраическим иррациональным числом, обозначенным квадратным корнем из √2. Некоторые числа, такие как π и e , не являются решениями любого такого алгебраического уравнения и поэтому называются трансцендентными иррациональными числами. Эти числа часто можно представить в виде бесконечной суммы дробей, определенных определенным образом, и десятичное разложение — одна из таких сумм.
Действительные числа можно охарактеризовать важным математическим свойством полноты, означающим, что каждое непустое множество, имеющее верхнюю границу, имеет наименьшую такую границу, свойство, которым не обладают рациональные числа.Например, набор всех рациональных чисел, квадраты которых меньше 2, не имеет наименьшей верхней границы, потому что квадратный корень из √2 не является рациональным числом. Иррациональные и рациональные числа бесконечно многочисленны, но бесконечность иррациональных чисел «больше», чем бесконечность рациональных чисел, в том смысле, что рациональные числа могут быть спарены с подмножеством иррациональных чисел, в то время как обратное спаривание невозможно.
Золотое сечение: как и зачем его использовать в дизайне | Мэтт Рэй | Мыслительный дизайн
Теория золотого сечения исторически восходит к временам Пи.Это соотношение на протяжении всей истории использовалось философами, архитекторами и дизайнерами для создания привлекательных, приятных дизайнов и структур. Некоторыми историческими примерами являются Парфенон в Греции и пирамиды в Египте, где архитекторы использовали это соотношение для создания баланса между структурными элементами. Причина популярности золотого сечения заключается в убеждении, что оно естественно и создает эстетически приятный баланс для зрителя.
Как и в архитектуре, мы можем использовать золотое сечение в цифровом дизайне, независимо от того, работаем ли мы над макетами, разработкой бренда или созданием готовых готовых дизайнов.Вот как.
Само соотношение определено как 1: 1,618033987 и представлено греческим символом Phi . Это означает, что если длина A составляет 100 пикселей, то длина B будет 161,80 пикселей. Это может применяться к фигурам или объектам, расположенным рядом друг с другом (сравнивая их ширину или длину), или для формирования единой формы, такой как прямоугольник (т.е.длина = 1,618x ширины).
Формула для расчета отношения: A / B = (A + B) / A = 1,6180033987, хотя в практических приложениях это число часто округляется, чтобы с ним было легче работать.В этих случаях можно использовать 1: 1.618 или 1: 1.62.
Формула золотого сечения показывает, что длина A в 1,618 раза больше длины B. Вы можете проверить, соответствуют ли две длины соотношению, разделив их длины.Еще один термин, связанный с вычислением золотого сечения, — это последовательность Фибоначчи, определенная математиком Фибоначчи. В этой последовательности указано, что каждое число в последовательности представляет собой сумму двух предшествующих значений. Например, 1 + 1 = 2, поэтому первые три числа в последовательности — 1, 1, 2, а следующее будет 3 (1 + 2 = 3).Это продолжается, создавая первые 10 цифр 1,1,2,3,5,8,13,21,34,55.
Последовательность Фибоначчи — это то, что создает золотую спираль, которая является логарифмической спиралью, которая увеличивается в разы золотого сечения. В большинстве изображений золотого сечения показана золотая спираль, как показано ниже. Это создает еще одно руководство при создании макетов или ресурсов логотипа и помогает определить баланс.
. Аппроксимация золотой спирали, созданной путем рисования дуг окружности, соединяющих противоположные углы квадратов в мозаике Фибоначчи.Хотя вы можете подумать, что это просто причудливая формула, разработанная математиками, она обычно встречается в природе, в первую очередь спираль. Его можно увидеть на растениях, в панцире «Наутилуса» и даже в облачных образованиях во время ураганов. Если вникнуть в это, то золотое сечение окружает нас повсюду, как искусственное, так и естественное. Взгляните на логотип National Geographic — это пропорциональный прямоугольник, соответствующий золотому сечению.
Использовать золотое сечение в вашей дизайнерской работе проще, чем может показаться.Поскольку все дело в соотношении, вы можете использовать формулу для создания столбцов и пропорциональных макетов. Например, если вы хотите создать макет с боковой панелью и областью основного содержимого шириной 960 пикселей, вы должны рассчитать ширину основного столбца как 960 пикселей / 1,618. Это создаст ширину 593 пикселей. Вы должны сделать то же самое с шириной основного столбца, чтобы получить ширину боковой панели (593 пикселей / 1,618), чтобы получить 367 пикселей. Конечно, при этом не учитываются поля или отступы, и вы можете округлить эти измерения, чтобы они были четными числами, или учесть кратное в зависимости от вашей системы.Однако это дает представление о наиболее приятном балансе между этими столбцами.
Еще несколько примеров использования золотого сечения в дизайне веб-сайтов. Хижина дизайна кредита изображения.В этом сценарии вы, вероятно, захотите, чтобы эти столбцы прокручивались, а не фиксировались на определенной высоте. Если у вас есть блоки содержимого или виджеты боковой панели, вы можете использовать формулу для определения наилучшей высоты для этих блоков на основе их ширины (умножьте или разделите на значение 1,618, чтобы получить расположение, подходящее для вашего приложения).
Хотя использование этого соотношения в вашем дизайне — это здорово, применение его ко всей странице или макету может быть затруднено, поскольку многие дизайны являются динамическими и реагируют на изменение размеров области просмотра или макета. Если вы сосредоточите свое соотношение сторон на компонентах в дизайне и воспользуетесь сеткой, основанной на соотношении, чтобы выровнять эти компоненты, вы сможете извлечь выгоду с меньшим напряжением.
Отличный и простой способ начать работу — использовать шаблоны и примеры каркасов, в которых используется соотношение для создания макетов и размещения элементов.Это отличная отправная точка для начала работы над дизайном, так как вы можете увидеть, как это работает на практике.
Есть также много калькуляторов для вставки измерений и расчета соответствующих размеров на основе соотношения. Если вы используете для проектирования такие приложения, как Adobe XD, вы можете загрузить такие шаблоны, как эта Golden Grid, от Джона Варгаса. Что бы вы ни создавали, мы надеемся, что благодаря этому вы сможете создавать потрясающие сбалансированные макеты.
Что такое золотое сечение ?. Вы знаете, что по-настоящему нервничаете, когда… | Бретт Берри | Math Hacks
Золотое сечение веками считалось самым красивым соотношением в искусстве и архитектуре.От Парфенона до произведения Сальвадора Дали Таинство Тайной вечери золотое сечение было обнаружено в некоторых из самых знаменитых творений мира.
Теперь, верите ли вы, что эта божественная пропорция действительно является признаком красоты или просто предвзятостью выбора, зависит от вас, но, без сомнения, это одно из самых интригующих чисел из существующих.
Обозначается греческой буквой фи (φ), золотое сечение является иррациональным значением:
Золотое сечениеВ книге 6 из «Элементы » Евклид дает нам определение золотого сечения.
Он инструктирует нас взять линейный сегмент и разделить его на два меньших сегмента таким образом, чтобы отношение целого линейного сегмента ( a + b) к сегменту a было таким же, как отношение сегмента a к сегменту b , например:
Или, что эквивалентно как пропорция:
Также известна как Золотая Пропорция или Золотое Сечение(Вы, любители геометрии, вероятно, знаете, что a — это среднее геометрическое a + b и b 🙌🏼 )
Золотое сечение чаще всего представлено как золотой прямоугольник , прямоугольник с соотношением сторон 1.618: 1.
Золотые прямоугольники также обладают тем свойством, что если вы отрежете квадрат, у вас останется еще один золотой прямоугольник.
Золотые прямоугольникиЧтобы найти значение 1.618034…, мы должны вычислить пропорцию. Для простоты предположим, что b = 1 и a = x , чтобы вы могли решить для x .
a = x и b = 1Шаг 1
Возьмите перекрестные произведения.
Шаг 2
Вычтите x + 1, чтобы приравнять уравнение к нулю.
Теперь у нас есть стандартный квадратичный с a = 1, b = -1 и c = -1 .
Шаг 3
Подставьте эти значения в формулу корней квадратного уравнения и решите.
Поскольку мы работаем с длинами, нам нужно только положительное решение.
И вот оно! Золотое сечение, как и было обещано!
Для правильного измерения вставьте a = 1,618 и b = 1 , чтобы убедиться, что пропорция сохраняется.
Обратите внимание на что-нибудь интересное в (1.618 + 1) /1.618 = 1.618?Мы можем записать золотое сечение в терминах самих себя! Что совершенно потрясающе.
Переписано с φ вместо 1.618.Или, что то же самое,
А теперь давайте сойдем с ума. Подставляем φ = 1 + 1 / φ вместо φ в знаменатель.
Здорово! Давай сделаем это снова!
Мы можем продолжать заниматься этим вечно. Что довольно впечатляюще. Оказывается, золотое сечение можно записать в виде бесконечной непрерывной дроби .
Мы можем использовать непрерывную дробь для аппроксимации золотого сечения и раскрыть интересную связь с последовательностью Фибоначчи.
Step 1
Для начала мы немного изменим нашу непрерывную дробь.
Вместо того, чтобы писать формулу, вложенную в себя, мы добавим индексы, чтобы указать, что следующее значение (φ_n + 1) может быть сгенерировано из предыдущего значения (φ_n).
Поскольку это бесконечная непрерывная дробь, по мере увеличения n приближение приближается к истинному значению φ.
Шаг 2
Определите φ_0 = 1 . Чтобы найти φ_1 , вставьте n = 0.
Шаг 3
Повторите процесс, чтобы найти φ_2 с n = 1, поскольку φ_2 = φ_1 + 1. Используйте результат шага 2 для φ_1.
Шаг 4
Продолжайте повторять этот процесс.
Step 5
Проверьте это. Вот последовательность Фибоначчи ! Каждое приближение — это отношение двух соседних чисел Фибоначчи. Нам больше не нужно беспокоиться о включении значений в непрерывную дробь, мы можем просто разделить последовательные члены последовательности Фибоначчи.
Золотое сечение в фотографии
Некоторые утверждают, что правило третей является чрезмерным упрощением более сложного математического уравнения, известного как золотое сечение (также известное как золотая середина). Золотое сечение — это соотношение, которое веками удивляло художников, ученых, музыкантов и математиков. Причина в том, что золотое сечение, кажется, появляется повсюду. Мало того, что золотое сечение появляется повсюду, также кажется, что человеческий глаз очень привлекает результаты этого соотношения.
Например, на лицах моделей есть размеры, которые удивительно близки к золотому сечению. В природе мы видим золотое сечение в растениях и ветвлениях деревьев, спирали раковин, кривые волн, в нашей ДНК и в Солнечной системе. Он также использовался в архитектуре, искусстве и музыке. Золотое сечение, кажется, есть повсюду.
Он использовался в архитектурных шедеврах, таких как греческий Парфенон, пирамиды, а позже в таких великих произведениях искусства, как Нотр-Дам.Есть также основания полагать, что его использовали великие художники Микеланджело и Леонардо де Винчи.
Спорный вопрос о том, была ли Мона Лиза намеренно создана с использованием пропорций золотого сечения. См. Ниже
Золотой прямоугольник — это прямоугольник, длина сторон которого находится в золотом сечении.
Проще говоря, золотое сечение — это отношение примерно 1,618 к 1. Эта пропорция создает ощущение гармонии и баланса.
Хотя это соотношение было вновь в течение времени, один бесспорный вехой в его истории была серия чисел Фибоначчи.В XII веке Фибоначчи произвел ряд чисел, сложив пары чисел.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
(0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8)
Соотношение между каждой последовательной парой становится все ближе и ближе к Фи по мере прохождения серии.
Как только вы начнете разбивать золотой прямоугольник по соотношению, вы можете продолжать делить его на части бесконечно. Спираль, которую это производит, точно соответствует росту раковины наутилуса в природе.Да, сейчас все становится немного странно.
Скажем так, это математическое уравнение эстетически приятной композиции.
Ниже показано, как Картье-Брессон использовал пропорции золотого прямоугольника для создания своей композиции.
Примечательно, что этот образец также встречается в природе:
Вот видео по теме золотого сечения:
Как получить золотое сечение в Adobe Lightroom:
Знаете ли вы, что при кадрировании можно даже включить наложение золотого сечения в Adobe Lightroom?
Это выглядит так:
Просто нажмите клавишу O при кадрировании изображения.Нажимайте клавишу O, пока не увидите свое золотое сечение. О как буква, а не цифра. Насколько это удобно ?!
Также продолжайте нажимать кнопку O, и он будет циклически перемещаться по различным направляющим кадрирования. Еще один совет — нажмите Shift-O, и ваше руководство по обрезке золотого сечения изменит местоположение. Просто продолжайте нажимать Shift-O, и Adobe Lightroom перебирает все ваши варианты.
Наконец, мне пришлось поместить это сюда, потому что я думаю, что это весело:
Другие интересные страницы фотографий:
Правило третей
Фотография в высоком и низком ключе
Как использовать негативное пространство в фотографии
Ритм и узор в фотографии
Школа фотографии Icon
Школа фотографии Icon — это онлайн-школа фотографии.Вы можете правильно изучить фотографию в Интернете. Начни изучать фотографию уже сегодня!
Золотое сечение — Go Рисунок
→ Версия для печати
Золотое сечение — очень красивая математическая тема во многих отношениях. Во-первых, его давно используют для анализа нашего чувства прекрасного. Во-вторых, с математической точки зрения это очень красивая тема.
Золотое сечение часто определяется как отношение a / b, где отношение a к b такое же, как отношение всего сегмента к a.Зеленый — к красному, красный — к синему.
Мы можем использовать это определение, чтобы получить значение золотого сечения — все, что нужно, — это немного алгебры. Я не буду здесь описывать все шаги, но достаточно сказать, что вы можете использовать это определение, чтобы установить пропорцию и решить, чтобы найти, что золотое сечение равно
.Ну, это не так уж и хорошо. Но мы сможем лучше понять это, если перенесем это определение из одного измерения в два. Существует прямоугольная версия золотого сечения, называемая (соответственно) золотым прямоугольником.
Вот как это работает: средняя линия разделяет большой прямоугольник пополам, поэтому левая часть представляет собой квадрат, а правая — меньший прямоугольник. Золотой прямоугольник получается, когда пропорции маленького прямоугольника совпадают с пропорциями большого прямоугольника.
Почему это то же самое соотношение, которое мы определили ранее? Что ж, если мы назовем длину стороны квадрата «a» и ширину маленького прямоугольника «b», тогда длина большого прямоугольника будет a + b.Тогда пропорции большого прямоугольника равны от a + b до a, а пропорции маленького прямоугольника — от a до b. Зеленый — к красному, красный — к синему.
Это определение означает, что маленький прямоугольник имеет те же пропорции, что и большой прямоугольник — другими словами, это еще один золотой прямоугольник. Это означает, что мы также можем разделить его на квадрат и золотой прямоугольник меньшего размера.
А так как новый маленький прямоугольник также является Золотым прямоугольником, мы можем его тоже разделить.
И мы можем продолжать так долго, как захотим.
Более того, мы можем нарисовать четверть круга во всех квадратах:
И получаем спираль.
Ну что ж. Те из вас, кто читал страницу о моделях чисел Фибоначчи, могут заметить, что это очень похоже на спираль Фибоначчи. На самом деле, обе спирали очень-очень-очень хорошие приближения к логарифмической спирали. Логарифмическая спираль пройдет через все те же углы, что и наши четверть круга, но она плавно изменит свою кривизну, вместо того, чтобы прыгать от размера четверти круга к размеру четверти круга.
Раковина наутилуса (похожая на ту, что изображена выше) растет по логарифмической спирали, всегда увеличиваясь в размерах, но сохраняя те же пропорции, как растет эта золотая спираль. В природе можно найти множество других примеров логарифмических спиралей. И это не единственный способ проявления золотого сечения в природе — обратите внимание на его близкого родственника — золотой угол.
Вы также можете найти интригующие параллели с золотым сечением во многих произведениях искусства, часто с использованием золотого прямоугольника. Некоторые люди утверждают, что золотое сечение заложено в нашем эстетическом восприятии как самой красивой пропорции и поэтому проявляется в таких местах, как Мона Лиза и Парфенон.
Это правда или это просто шумиха? Честно говоря, никто не знает наверняка. До сих пор остается загадкой, насколько золотое сечение действительно связано с нашим чувством красоты. По крайней мере, его художественные параллели очаровывали и вдохновляли людей на протяжении веков. Но одно можно сказать наверняка: с математической точки зрения он заслуживает своего названия.
Например, возьмите пентаграмму, пятиконечную звезду, состоящую из пяти прямых линий.
Эта фигура — , пронизанная с золотым сечением.Например: AD для AC, как AC для CD, как CD для BC. Чем больше вы это ищете, тем больше находите!
Но это еще не все! Если присмотреться, то можно найти еще одно удивительное место…
Золотое сечение — принципы формы и расположения
Теперь мы рассмотрим предмет, который исходит непосредственно из математики и который мы также можем найти повсюду, — золотое сечение . Не волнуйтесь; мы не вернемся в класс надолго.Мы рассмотрим, что это за концепция и насколько она является фундаментальной частью создания дизайна, приятного для глаз пользователя.
История золотого сечения стала легендой. Имея историю, восходящую почти ко времени Pi (еще одна великая математическая формула, которая необходима для понимания свойств кругов), ученые, в том числе Пифагор и Евклид, назвали ее многими именами, включая золотую середину , и божественный раздел .
В чем привлекательность этого соотношения? На протяжении веков считалось, что искусство, архитектура и природа более привлекательны для глаз, когда пропорции конструкций и сооружений основаны на золотом сечении. Вы можете найти примеры золотого сечения в человеческих усилиях еще в Древней Греции. Статуи Парфенона, кажется, демонстрируют золотое сечение в своей форме, и некоторые из пяти тел Платона (включая куб и додекаэдр) тоже связаны с ним. Золотое сечение было популяризировано в эпоху Возрождения, и художники того периода стремились использовать его для создания эстетически привлекательных работ.Сегодня мы можем использовать золотое сечение в дизайне наших веб-сайтов и приложений для улучшения макета и привлекательности для глаз, полностью доверяя этому проверенному временем факту.
Что такое золотое сечение?
Золотое сечение использовалось на протяжении всей истории для создания визуально привлекательных дизайнов. В эпоху Возрождения это стало формализованной частью теории дизайна. Его частое появление в геометрии (в форме пятиугольника и пентаграммы) привлекло внимание древнегреческих математиков, которые начали изучать его по крайней мере 2400 лет назад.Отношение основано на соотношении между последовательными числами в последовательности Фибоначчи. Фибоначчи был средневековым итальянским математиком; однако, вам не нужно быть математиком, чтобы понять эту последовательность, поскольку она очень проста.
Каждое число в последовательности Фибоначчи — это просто сумма двух чисел перед ним. Он начинается с 1, 1 (т. Е. 1 + невидимый 0 = 1), а первые 10 членов последовательности — это 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Он продолжается бесконечно. .Мы можем рассчитать это соотношение, используя формулу выше (мы используем греческую букву Phi для представления выходных данных). Отношение составляет примерно 1,618, хотя, как и Pi , оно имеет длинную строку чисел после десятичной точки. Однако для наших целей нам не нужно беспокоиться о выходе за пределы 1.618.
Как соотношение используется в дизайне? Представьте себе прямоугольник с короткой стороной длиной 1. Чтобы вычислить наиболее эстетичный прямоугольник, вы просто умножаете длину короткой стороны на приближение золотого сечения, равное 1.618. Таким образом, в данном случае длинная сторона будет иметь длину 1,618.
Если у вас под рукой есть карандаш, бумага и линейка, попробуйте нарисовать прямоугольник такого масштаба. Или, если вы можете перейти на другой экран, создайте его в приложении для рисования. То, что вы увидите перед собой, — это не просто прямоугольник, а идеальный прямоугольник !
Золотое сечение можно найти во всем мире дизайна. Архитекторы того времени использовали его для основания и высоты Акрополя в Греции.Он используется для определения формата подавляющего большинства книг на вашем физическом книжном шкафу. Это буквально везде, куда ни глянь. Возможно, потому, что мы окружены фигурами и формами, полученными из золотого сечения, мы особенно привыкли к нему. Как дизайнеры, мы должны помнить об этой концепции комфорта и удобства для наших пользователей. Глаза мира благосклонно относятся к этому соотношению. Фактически, буквально: в журнале National Geographic используется желтый прямоугольник, пропорциональный золотому сечению.
Однако золотое сечение не помогает нам просто создавать красивые прямоугольники. Вы также можете сформировать спираль, используя длины сторон, основанные на порядке убывания последовательности Фибоначчи. Итак, если мы возьмем длину 55 в качестве отправной точки, мы можем сделать нашу спираль, потянув ее внутрь, так что, когда она пройдет эту начальную точку, новая длина будет 34. Мы продолжаем работать внутрь с длинами 21, 13, 8, 5 и т. Д., Пока не дойдем до середины (длина = 1). Эта спираль также основана на золотом сечении и может быть более интересной для человеческого глаза, чем столь же сбалансированная спираль.Он присутствует в природе, от растений до моллюсков и моллюсков. Часто говорят, что даже определенные пропорции многих более крупных животных (включая людей!) Пропорциональны золотому сечению. В этом смысле можно сказать, что это часть нас. Итак, вы, как дизайнер, можете использовать эту спираль, чтобы привлечь внимание пользователей из любой точки мира и сосредоточить их на определенной точке вашего дизайна. Исследования показали, что человеческий глаз распознает (а мозг интерпретирует и обрабатывает) изображения, основанные на золотом сечении, быстрее, чем изображения, которые не включают это соотношение.
Мы также можем использовать золотое сечение, чтобы сбалансировать элементы в других элементах. Логотипы Toyota и Pepsi используют этот факт. Toyota использует соотношение, чтобы сбалансировать овалы в своем логотипе, а Pepsi использует его, чтобы сбалансировать круги в своем логотипе. Можете ли вы назвать другие бренды, которые используют это «волшебное» соотношение? Возможно, это то, что может сделать логотипы по-настоящему знаковыми!
Расчет золотого сечения
Давайте теперь вкратце перейдем к математике. Как и в случае с изображением, показанным в верхней части этого урока, уравнение для расчета коэффициента простое.Это отношения между двумя сторонами дизайна (обычно горизонтальной и вертикальной). Неважно, какую сторону мы выберем как самую длинную (A), а какую — как самую короткую (B). (Хотя, если вы пытаетесь увидеть, использовалось ли золотое сечение в другом произведении, вам нужно будет проследить, какая сторона самая длинная или самая короткая.)
Формула для этого:
A / B = (A + B) / A = 1,618033987 = Φ
Φ — это греческая буква Phi — , как мы представляем золотое сечение. Почему делает A / B = (A + B) / A? Это происходит потому, что мы следуем последовательности Фибоначчи, а A и B (если они выражены целыми числами) — это просто два последовательных числа в этой последовательности. К счастью, мы можем приблизить это к 1,6, 1,61 или 1,618 в дизайне, не отказываясь от эстетической привлекательности золотого сечения. Наши глаза не беспокоят такие незначительные отклонения.
Как использовать золотое сечение в ваших проектах
Вы можете легко использовать золотое сечение в своих проектах.Используя такие приложения, как Adobe Photoshop и Adobe Illustrator, вы можете создавать направляющие или слои, которые помогут вам создавать дизайн с использованием золотого сечения.
Если ваше программное обеспечение не вычисляет золотое сечение автоматически, вы всегда можете использовать онлайн-инструмент, который поможет указать соотношение длин сторон. Вот три таких инструмента:
GoldenRATIO
Phicalculator
Atrise Золотое сечение
The Take Away
Золотое сечение, которое философы, математики, архитекторы, художники и дизайнеры использовали уже более двух тысяч лет, является фундаментальным как для дизайнеров, так и для пользователей.Нас окружают такие узоры, как логотип Pepsi, и даже естественные образования, несущие пропорции золотого правила, такие как раковина наутилуса.
Поскольку эти формы настолько распространены, наши глаза быстро распознают их, и мы склонны воспринимать их как знакомые и приятные. Хотя золотое сечение было предметом изучения на протяжении веков и было известно древним грекам, средневековый итальянский математик Фибоначчи определил свою знаменитую последовательность. Использование этого (где ряд чисел, начинающийся с 1,1, таков, что мы добавляем предыдущее число к следующему) является ключом к пониманию золотого сечения (которое мы представляем греческой буквой Phi ).
Мы широко используем золотое сечение в веб-дизайне и дизайне приложений. В частности, его очень легко использовать при создании каркасов. Вы можете убедиться, что нужный вам контент правильно расставлен по приоритетам и что эстетические требования макета будут удовлетворены, не выполняя поначалу слишком много дизайнерской работы. Только когда вы, например, решите, где вы будете размещать элементы и функции над этой структурой, работа станет более сложной.
На верхнем изображении в приведенном выше примере соотношение между областью содержимого и боковой панелью равно Phi (1.618). Вы можете проверить это с помощью измерений ниже:
- Общая ширина фиксированного макета составляет 960 пикселей. Вы разделяете это на область содержимого и боковую панель. Область содержимого является более длинной из двух областей.
- Если вы разделите общую ширину 960 пикселей на 1,618, вы получите 593 пикселей. Затем вы назначаете эту длину области содержимого.
- Вы назначаете оставшиеся 367 пикселей боковой панели.
Поскольку это соотношение, оно гибкое. Это означает, что вы можете легко применить его для создания множества макетов дизайна, поскольку нет необходимости использовать фиксированные числа.Все, что вам нужно сделать, это указать, что более длинная область в 1,618 раза длиннее, чем более короткая.
Золотое сечение можно применить к любой части макета страницы. Например, вы можете использовать золотое сечение в заголовке, чтобы привлечь внимание пользователя, а затем повторить его и в теле.
На нижнем рисунке (вверху) мы также видим спиральную форму, в которой используется золотое сечение. Используя последовательность Фибоначчи в порядке убывания применительно к длинам стороны спирали, мы можем легко создавать спиральные конструкции на основе золотого сечения.
Как дизайнеры, мы находим множество доступного программного обеспечения, которое помогает нам раскрыть потенциал золотого сечения в наших творениях и оптимизировать взаимодействие с пользователем. Adobe с Photoshop и Illustrator — такая компания, предлагающая такую большую помощь.
Ссылки и где узнать больше
- Изображение героя: Автор / Правообладатель: Мэтью Олифант. Условия авторских прав и лицензия: CC BY-ND 2.0
- Фридман В. (2008) Применение божественной пропорции к вашим веб-дизайнам. Smashing Magazine. Получено с: http://www.smashingmagazine.com/2008/05/29/applying-divine-proportion-to-web-design/. [1 августа 2014]
Золотое сечение — священное число, связывающее прошлое с настоящим
Древних греков, художников эпохи Возрождения, астрономов 17 века и архитекторов 21 века объединяло одно — все они использовали золотое сечение, также известное как золотое сечение, божественная пропорция или золотое сечение.
Точнее, это число 1.61803399, представленное греческой буквой Фи и считающееся поистине уникальным по своим математическим свойствам, распространенности в природе и способности создавать идеальную эстетическую композицию.
По словам астрофизика Марио Ливио в его книге «Золотое сечение: история PHI, самого удивительного числа в мире» :
Некоторые из величайших математических умов всех времен, от Пифагора и Евклида в Древней Греции, до средневекового итальянского математика Леонардо Пизанского и астронома эпохи Возрождения Иоганна Кеплера, до современных ученых, таких как оксфордский физик Роджер Пенроуз, потратили бесконечные часы над этим простым соотношением и его свойствами.Но увлечение золотым сечением не ограничивается только математиками. Биологи, художники, музыканты, историки, архитекторы, психологи и даже мистики размышляли и обсуждали причины его повсеместности и привлекательности. Фактически, будет справедливо сказать, что золотое сечение вдохновляло мыслителей всех дисциплин, как никакое другое число в истории математики.
Что такое золотое сечение?
В математике и искусстве две величины находятся в золотом сечении, если их соотношение совпадает с отношением их суммы к большему из двух величин.Когда Золотая Середина концептуализируется в двух измерениях, она обычно представляется как правильная спираль, определяемая серией квадратов и дуг, каждая из которых образует «Золотые прямоугольники».
Этот символический потенциал возникает из-за того, что спиралевидная форма среднего напоминает закономерности роста, наблюдаемые в природе, а его пропорции напоминают пропорции человеческих тел. Таким образом, эти простые спирали и прямоугольники, которые служили признаком наличия универсального порядка, лежащего в основе мира, были названы «золотыми» или «божественными».
Форма спирали Золотого сечения напоминает закономерности роста, наблюдаемые в природе. (Дин Марстон / Adobe Stock)
Золотое сечение в истории
Золотое сечение очаровывало западных интеллектуалов с самыми разными интересами как минимум 2400 лет. Самыми ранними известными памятниками, которые, как считается, были построены в соответствии с этим заманчивым числом, являются статуи Парфенона в Греции, датируемые периодом между 490 и 430 годами до нашей эры. Тем не менее, многие утверждают, что оно восходит к гораздо более древним временам, чем это, и что египтяне хорошо разбирались в свойствах этого уникального числа.
Согласно некоторым историкам, египтяне считали золотое сечение священным. Поэтому это было очень важно в их религии. Они использовали золотое сечение при строительстве храмов и мест для усопших.
Считается, что древние египтяне использовали золотое сечение в своих зданиях. (Джон Смит / Adobe Stock)
Кроме того, египтяне нашли золотое сечение приятным для глаз. Они использовали его в своей системе письма и в устройстве своих храмов.Египтяне знали, что использовали золотое сечение, но они называли его «священным сечением».
Первое записанное определение золотого сечения относится к тому периоду, когда греческий математик Евклид (ок. 325 – ок. 265 г. до н.э.) описал то, что он назвал «крайним и средним отношением». Тем не менее, уникальные свойства пропорции стали популяризованы в 15 веке, когда эстетика была жизненно важным компонентом искусства эпохи Возрождения, а геометрия служила как практическим, так и символическим целям. Как писал известный математик, астроном и астролог Иоганн Кеплер (1571 — 1630):
У геометрии есть два великих сокровища: одно — это теорема Пифагора, а другое — деление прямой на крайнее и среднее отношение; первое мы можем сравнить с мерой золота, второе — с драгоценным камнем.
Золотое сечение в архитектуре
Многие художники и архитекторы составили пропорции своих работ, приближенные к золотому сечению, с верой в то, что результат будет более эстетичным. Используя любое из этих соотношений, архитектор может спроектировать дверную ручку, которая имеет дополнительные отношения к своей двери, которая, в свою очередь, имеет аналогичное отношение к ее ограждающей стене и т. Д.
Более того, золотое сечение использовалось для фасадов великих зданий — от Парфенона до Великой мечети Кайруана и вплоть до современных достопримечательностей, таких как Сиднейский оперный театр и Национальная галерея в Лондоне.
Золотое сечение присутствует в Сиднейском оперном театре. (Марко Бривио / Adobe Stock)
Золотое сечение в природе
Возможно, самое удивительное в золотом сечении — это то, что его можно рассматривать как естественное явление в природе. Золотое сечение выражается в расположении ветвей вдоль стеблей растений и прожилках на листьях.
Его также можно увидеть на скелетах животных и людей, а также на разветвлениях их вен и нервов.Это видно даже по пропорциям химических соединений и геометрии кристаллов.
По сути, золотое сечение повсюду вокруг нас и внутри нас, и по этой причине немецкий психолог Адольф Цейзинг (1810–1876) назвал его «универсальным законом»:
, в котором содержится основной принцип всех формирующих стремлений к красоте и полноте в сферах как природы, так и искусства, и который пронизывает, как высший духовный идеал, все структуры, формы и пропорции, космические или индивидуальные, органические. или неорганические, акустические или оптические; которое, однако, находит свое наиболее полное воплощение в человеческой форме.
В результате уникальных свойств этой золотой пропорции многие считают золотое сечение священным или божественным, а некоторые даже считают, что это дверь к более глубокому пониманию красоты и духовности в жизни, раскрывающей скрытую гармонию или взаимосвязь во многих отношениях.
