Расстояние до луны от марса: «Сколько километров от Луны до Марса?» – Яндекс.Кью

Сколько километров до Луны от Марса

Луна с незапамятных времен была постоянным спутником нашей планеты и самым близким к ней небесным телом. Естественно, человеку всегда хотелось там побывать. Но далеко ли туда лететь и какое до нее расстояние?

Блок: 1/9 | Кол-во символов: 208
Источник: https://SpaceGid.com/rasstoyanie-ot-zemli-do-lunyi.html

Марс и Луна в сравнении

Для грамотного планирования межпланетного перемещения, специалистам необходимо представление о размерах небесных тел, знать, что расположено дальше от Земли, и четко понимать, что все-таки больше Луна или Марс.
Ошибочно может сложиться мнение о том, что Луна является большим светилом в сравнении с другими планетами. Подобные мысли обусловлены ее расположением на максимально близком расстоянии к Земле, 384 407 километров. На самом деле, по своим астрономическим размерам Луна не превышает 27% общих параметров нашей планеты.
Лунная площадь составляет примерно 38 миллионов км2.

Данный показатель сам по себе меньше размеров любого континента на Земле.
Марс находится на четвертом месте по удаленности от Солнца и на лидирующих позициях по своей величине. Показатель его площади составляет почти 145 миллионов километров, что чуть больше половины размера нашей планеты.
Исходя из представленной выше информации, можно сделать вывод, что Марс существенно больше Луны по своим размерам, однако находится на гораздо более дальнем расстоянии от нашей планеты именно по этому мы видим его таким маленьким. Хотите знать больше о других характеристиках Марса!?

Блок: 2/4 | Кол-во символов: 1188
Источник: https://MarsPlaneta.ru/perelet-ot-luny-do-marsa

Кто впервые измерил расстояние до Марса

Протяженность пути от Земли до Марса, впервые было измерено Джованни Кассини. Он вел вычисления при помощи методики параллакса. Астроном, договорился со своим другом Жаном Рише о том, что они будут наблюдать из двух разных точек. Джованни поехал в Париж, а друга отправил во французскую Гвиану.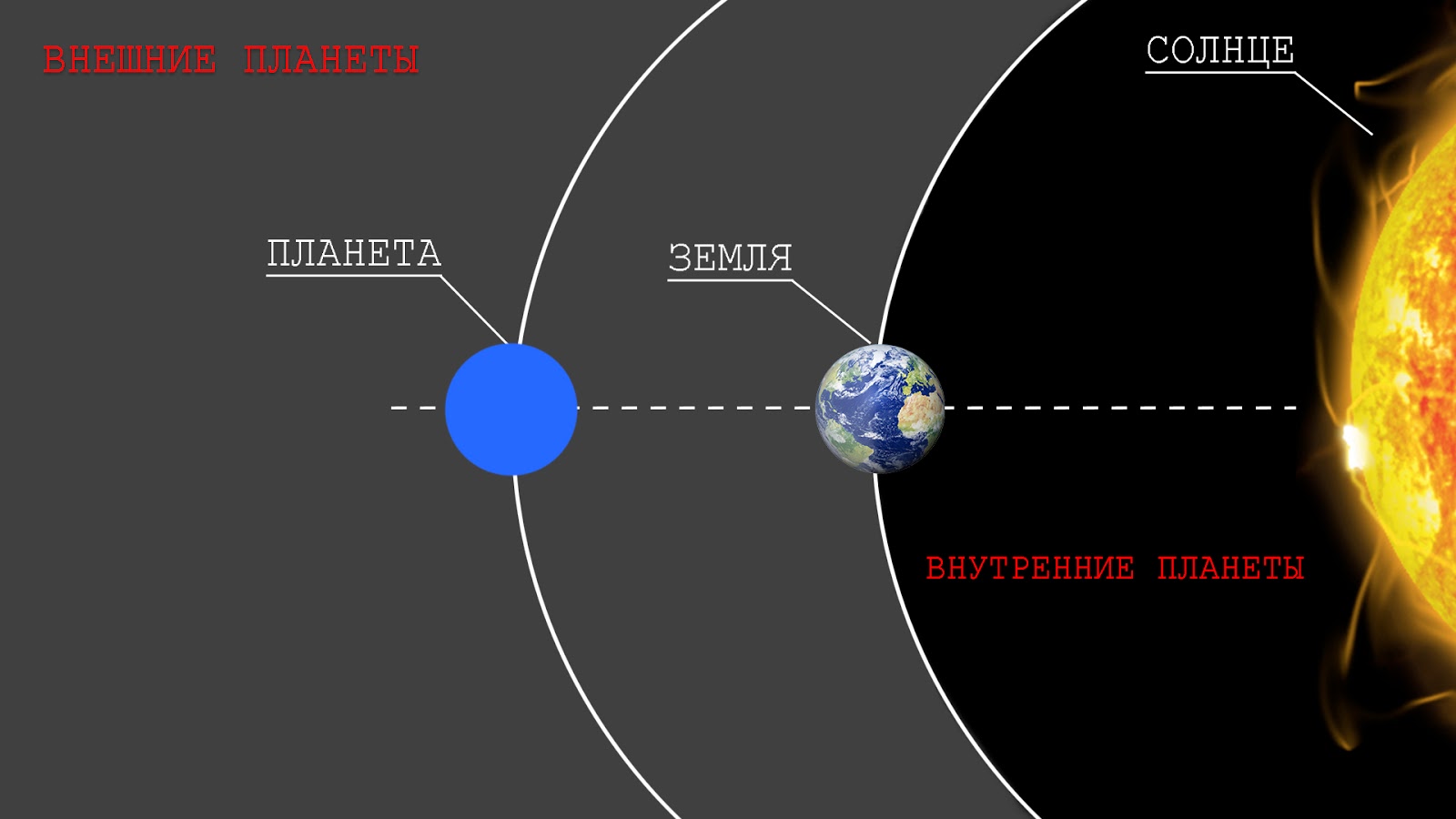

Расчеты оказались впечатляющими для XVII века – Кассини удалось вычислить путь от марса до земли с погрешностью 7%.

Блок: 2/8 | Кол-во символов: 451
Источник: https://oplanetah.ru/mars/rasstoyanie-do-marsa

Необходимое время

Скорость света достигает практически 300 тысяч километров в секунду. Поэтому свет от Земли до Марса доберется за:

• в случае минимальной дистанции – 3,03 минуты;
• в случае средней дистанции – 12,52 минут;
• в случае максимальной дистанции – 22,37 минуты.

Наиболее мощным космическим аппаратом на данный момент считается «New Horizons», принадлежащий НАСА. Он способен развивать скорость до 58 000 км/час, что более чем в 18 тысяч раз уступает скорости света.

Учитывая реальную мощность «New Horizons», можно высчитать количество времени, которое потребуется ему для того, чтобы с Земли добраться до четвертой от Солнца планеты:

• в случае минимальной дистанции – чуть больше 39 дней;
• в случае средней дистанции – 162 дня;
• в случае максимальной дистанции – немного больше 289 суток.

Важно знать: стоит учитывать тот факт, что расчеты произведены из условия движения по прямой линии от одной планеты к другой. Поэтому данные по времени могут несколько отличаться при планировании реального полета.

За последние несколько десятков лет космическая отрасль притормозила в своем развитии.

Ведь после высадки на луну года больше не происходило столь резонансных событий, связанных с космосом.

В 21 веке больший скачок произошел в других сферах, например, в развитии пользовательской электроники и коммуникационных сетей.

Такой ход истории не устраивает НАСА и SpaceX, которые стараются наверстать упущенное и активно развивать космическую промышленность. Некоторые даже планируют превращение Марса в колонию, однако произойти это может не ранее как через 100 лет.

Блок: 3/3 | Кол-во символов: 1560
Источник: https://samsebevoin. ru/interesnoe/skolko-letet-do-marsa.html

Сколько по времени лететь на Марс

Сколько времени понадобится, чтобы преодолеть расстояние между Землей и Марсом? Для начала представим, что корабль, везущий космических путешественников, развивает такую же скорость, как самый скоростной космический зонд «Новые горизонты». Его максимальная скорость равнялась 58*103км/ч.

Следовательно, при минимальном удалении двух планет друг от друга при полете по прямой полет на Марс для человека займет 941 час или почти 40 суток. При максимальной удаленности долететь на Красную планету можно будет за 6920 часов или 288 суток.

Блок: 3/7 | Кол-во символов: 589
Источник: https://spaceworlds.ru/solnechnaya-sistema/planeta-mars/skolko-letet-do-marsa.html

Сложности вычислений расстояния от Земли

Ответить на вопрос, сколько составляет расстояние между Землей и Марсом, можно в том случае, если примерно знать, где они должны находиться. Было бы гораздо проще ответить, где планета находится сейчас, если бы на конфигурацию ее орбиты не влияло Солнце. Но даже звезда, расположенная в своей системе, не вращается по кругу, а совершает движение по эллипсу. У красной планеты средний эксцентриситет.

И если смотреть на цифры, полученные в вычислениях, то выходит, что данный счет идет на миллионы условных человеческих единиц (в космических масштабах он маленький). Орбиты смещены и в сторону Солнца, а если учесть, что скорость Земли выше, ее величина больше, а орбита расположена ближе к светилу и короче, то становится понятным, почему у Марса год длиннее (686,98 суток), а максимально возможное сближение происходит крайне редко.

Дистанция между планетами

Удаленность в 55.75 млн км, именуемая еще противостоянием, наступает намного чаще, но измеряется другими цифрами. Это случается в определенный период нахождения обеих планет на одной линии с Солнцем, когда Земля находится в перигелии, а Марс – в афелии.

Если это происходит наоборот и Солнце располагается между ними, то самый короткий путь, который придется преодолеть, составит 102,1 млн км.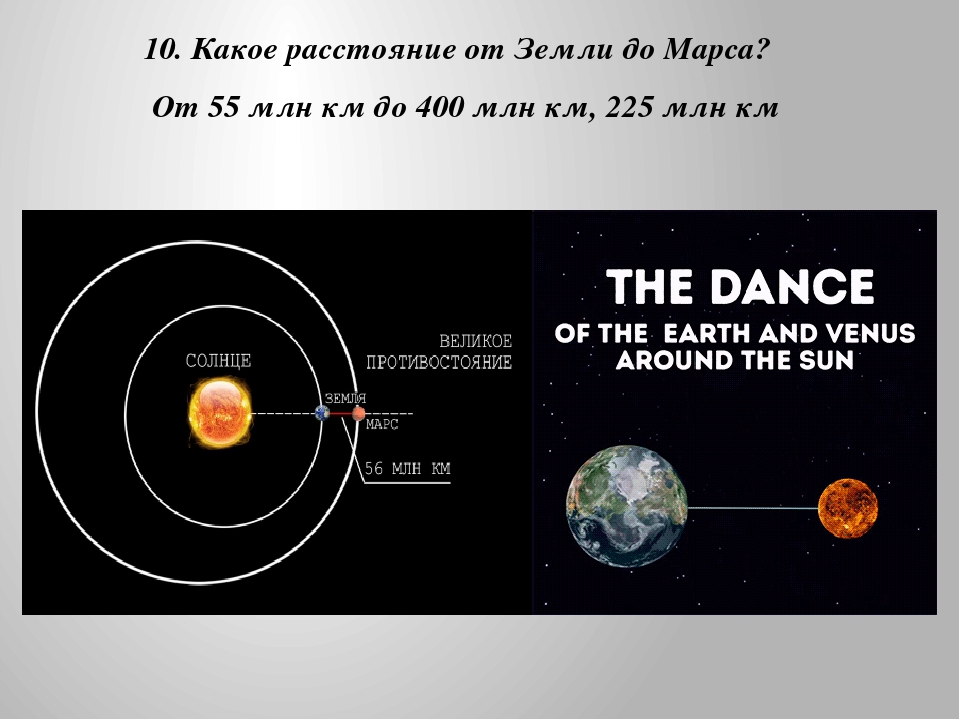 При этом космическому аппарату все равно нужно будет пролетать в течение значительного периода времени. Когда обе планеты будут в афелии по разные стороны от своего светила, расстояние, по астрономическим наблюдениям и подсчетам, будет в 401,3 млн км.

Световой год равен 9 460 730 472 580 800 км.

Радиосигнал до Марса и обратно поступает за 11 минут, а свет долетает за 3 минуты. Современный космический корабль летит в зависимости от скорости и массы разное время. Самым быстрым полетом, когда вес космического аппарата составил 412 кг, был полет Маринера-6 еще в прошлом веке – 131 сутки.

В космосе

Смотрите видео на эту тему.

Блок: 4/5 | Кол-во символов: 1925
Источник: https://ProNormy.ru/nauka/kosmos/rasstoyanie-ot-zemli-do-marsa

Чему равно

Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд

Космическим кораблям придется потратить на полет к земному спутнику немало времени.   До Луны нельзя лететь по прямой – планета будет уходить по орбите в сторону от точки назначения, и путь придется корректировать. При второй космической скорости в 11 км/с (40 000 км/ч) полет теоретически займет около 10 часов, но на деле это будет происходить дольше. Все потому, что корабль на старте постепенно наращивает скорость в атмосфере, доводя ее до значения в 11 км/с, чтобы вырваться из поля тяготения Земли. Затем  кораблю придется тормозить при подлете к Луне. Кстати, эта скорость- максимум, чего удалось добиться современным космическим кораблям.

Пресловутый полет американцев на Луну в 1969 году, согласно официальным данным, занял 76 часов. Быстрее всех до Луны удалось долететь аппарату НАСА «Новые горизонты» — за минут. Правда, он не приземлился на планетоид, а пролетел мимо – у него была другая миссия.

Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд. Но полеты на световых скоростях – пока что из области фантастики.

Можно попытаться представить путь до Луны в привычных величинах. Пешком при скорости 5 км/ч дорога до Луны займет порядка девяти лет. Если поехать на машине на скорость в 100 км/ч, то добираться до земного спутника придется 160 дней. Если бы на Луну летали самолеты, то рейс до нее продлился бы где-то 20 дней.

Блок: 4/9 | Кол-во символов: 1442
Источник: https://SpaceGid.com/rasstoyanie-ot-zemli-do-lunyi.html

Как в древней Греции астрономы рассчитывали расстояние до Луны

Расстояние от Земли до Луны

Луна стала первым небесным телом, до которого удалось рассчитать расстояние от Земли. Считается, что первыми это сделали астрономы в Древней Греции.

Измерить расстояние до Луны пытались с незапамятных времен – первым это попытался сделать Аристарх Самосский. Он оценил угол между Луной и Солнцем в 87 градусов, поэтому вышло, что Луна ближе Солнца в 20 раз (косинус угла равного 87 градуса равен 1/20). Ошибка измерений угла привела к 20-кратной ошибке, сегодня известно, что это отношение на самом деле равно 1 к 400 (угол равен примерно 89. 8 градусов). Большая ошибка была вызвана трудностью оценок точного углового расстояния между Солнцем и Луной с помощью примитивных астрономических инструментов Древнего мира. Регулярные солнечные затмения к этому времени уже позволили древнегреческим астрономам сделать вывод о том, что угловые диаметры Луны и Солнца примерно одинаковы. В связи с этим Аристарх сделал вывод, что Луна меньше Солнца в 20 раз (на самом деле примерно в 400 раз).

Для вычисления размеров Солнца и Луны относительно Земли Аристарх использовал другой метод. Речь идет о наблюдениях лунных затмений. К этому времени древние астрономы уже догадались о причинах этих явлений: Луна затмевается тенью Земли.

На схеме выше хорошо видно, что разность расстояний с Земли до Солнца и до Луны пропорциональна разнице между радиусами Земли и Солнца и радиусами Земли и её тени на расстояние Луны. Во времена Аристарха уже удалось оценить, что радиус Луны равен примерно 15 угловым минутам, а радиус земной тени составляет 40 угловых минут. То есть размер Луны получался примерно в 3 раза меньше размера Земли. Отсюда зная угловой радиус Луны можно было легко оценить, что Луна находится от Земли примерно в 40 диаметрах Земли. Древние греки могли лишь приблизительно оценить размеры Земли. Так Эратосфен Киренский (276 – 195 годы до нашей эры) на основе различий в максимальной высоте Солнца над горизонтом в Асуане и Александрии во время летнего солнцестояния определил, что радиус Земли близок к 6287 км (современное значение 6371 км). Если подставить это значение в оценку Аристарха насчет расстояния до Луны, то оно будет соответствовать примерно 502 тысяч км (современное значение среднего расстояния от Земли до Луны составляет 384 тысяч км).

Чуть позже математик и астроном II века до н. э. Гиппарх Никейский подсчитал, что расстояние до земного спутника в 60 раз больше, чем радиус нашей планеты. Его расчеты основывались на наблюдениях за движением Луны и его периодических затмениях.

Блок: 5/9 | Кол-во символов: 2589
Источник: https://SpaceGid.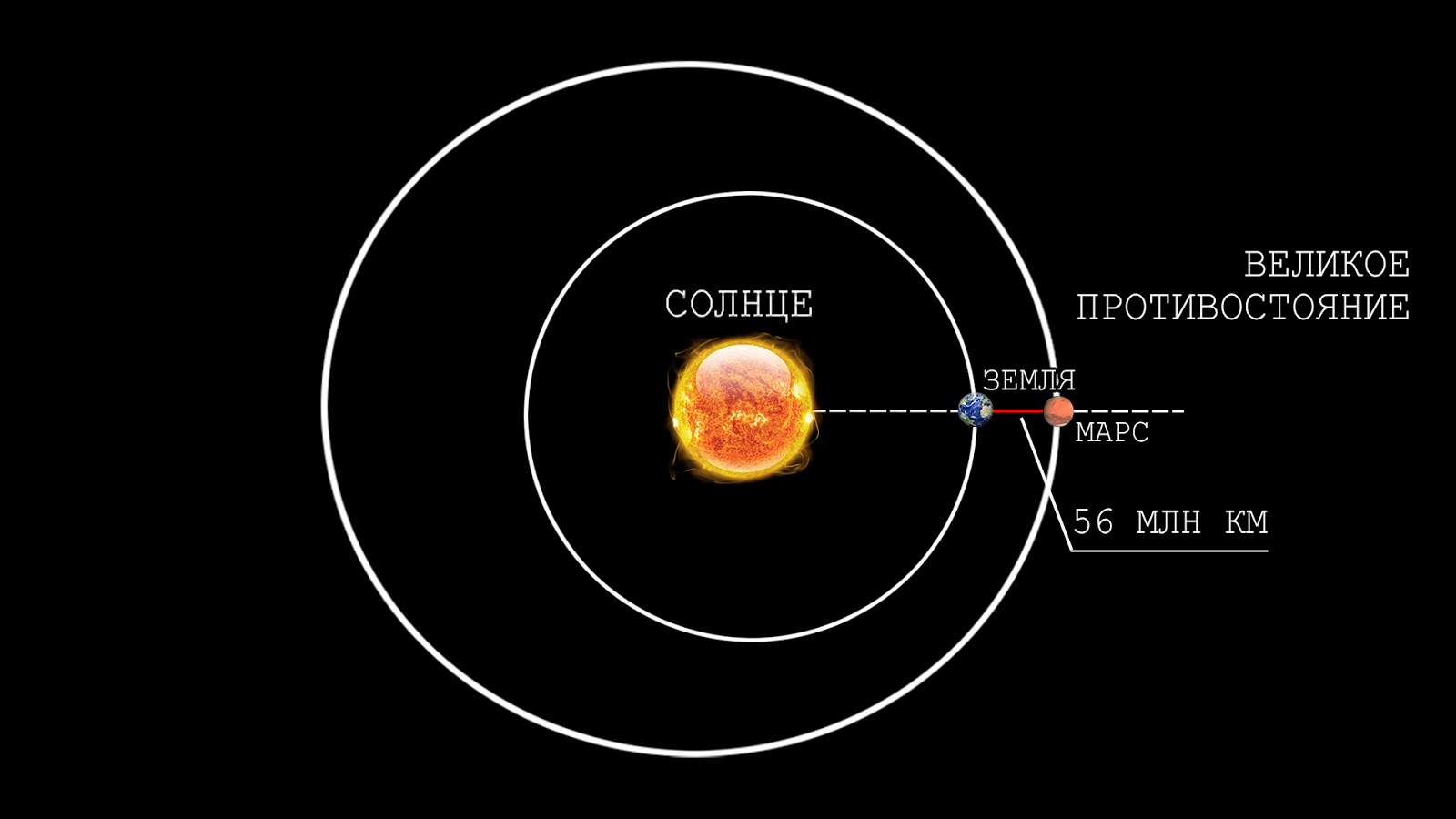 com/rasstoyanie-ot-zemli-do-lunyi.html

Зачем лететь на Марс

Мы уже разобрались, сколько километров лететь до Марса и как долго продлится такое путешествие. Но стоит ли оно всех затрат? Ведь для создания корабля с мощными ионными двигателями, подготовки экипажа и всех запасов топлива и продовольствия, нужно потратить просто астрономические суммы. Так зачем лететь на Марс?

Первая цель – исследования. По мнению многих исследователей, планета некогда имела атмосферу и развитую гидросферу. Также экспериментально было доказано, что в марсианском грунте способны прижиться и вырасти некоторые виды земных растений. Путешествие могло бы пролить свет на прошлое этого небесного тела. Кроме того, ученые могли бы продолжить эксперименты по заносу живых организмов на марсианскую поверхность.

Вторая цель – колонизация. Человечество уже давно ищет место для переселения, куда можно будет экстренно эвакуироваться в случае глобальной катастрофы на Земле. Условия на четвертой планете Солнечной системы, конечно, далеки от идеала. Но уже есть несколько теорий о том, как можно создать на нем искусственную атмосферу и создать человеческое поселение.

Третья цель – туризм. Пока туристические круизы к марсианским кратерам кажутся вымыслом писателей-фантастов. Но туристы уже не раз посещали международную космическую станцию. Полеты к нашему красному соседу – следующий этап этого прибыльного и перспективного направления.

Блок: 5/7 | Кол-во символов: 1401
Источник: https://spaceworlds.ru/solnechnaya-sistema/planeta-mars/skolko-letet-do-marsa.html

Материалы по теме

Так как в момент затмения Солнце и Луна будут иметь одинаковые угловые размеры, то по правилам подобия треугольников можно найти отношение расстояний до Солнца и до Луны. Эта разница составляет 400 раз. Применяя еще раз эти правила, только уже по отношению к диаметрам Луны и Земли, Гиппарх вычислил, что диаметр Земли больше диаметра Луны в 2,5 раза. Т.е Rл = Rз/2,5.

Под углом в 1′ можно наблюдать предмет, размеры которого в 3 483 раза меньше, чем расстояние до него – эта информация во времена Гиппарха была всем известна.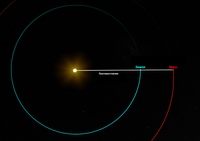 То есть, при наблюдаемом радиусе Луны в 15′ она будет ближе к наблюдателю в 15 раз. Т.е. отношение расстояния до Луны к ее радиусу будет равно 3483/15= 232 или Sл= 232Rл.

Соответственно, дистанция до Луны – это 232* Rз /2,5= 60 радиусов Земли. Это получается 6 371*60=382 260 км. Самое интересное, что измерения, выполненные при помощи современных инструментов, подтвердили правоту античного ученого.

Сейчас измерение дистанции до Луны проводится при помощи лазерных приборов, позволяющих измерить его с точностью до нескольких сантиметров. При этом измерения происходят за очень короткое время – не более 2 секунд, за которое Луна удаляется по орбите примерно на 50 метров от точки отправки лазерного импульса.

Блок: 6/9 | Кол-во символов: 1252
Источник: https://SpaceGid.com/rasstoyanie-ot-zemli-do-lunyi.html

Опасность марсианского путешествия

Как мы уже выяснили, полет до Марса займет не менее 80 суток. И такое долгое космическое путешествие не может не иметь последствий для экипажа корабля. Кроме того, сам полет может пойти совсем не по плану, ведь все опасности и трудности просто невозможно спрогнозировать. Чем может быть опасен полет к Марсу?

Влияние на психическое и физическое здоровье

Космическая радиация пагубно влияет на живые организмы. Астронавты будут в некоторой степени защищены от нее, находясь в переделах космического корабля.  Но исследователи подчитали, что за время полета до марсианской орбиты они получат дозу облучения, равную 1 Зв. Для сравнения, годовая доза облучения на Земле составляет 2,5 мЗв. Такое облучение может оказать крайне негативное влияние на нервную, сосудистую и пищеварительную систему путешественников. Кроме того, риск развития у них злокачественных опухолей возрастет в десятки раз. Если же корабль попадет под поток  высокоэнергетического солнечного ветра, никакая защита не защитит экипаж от смерти в результате острой лучевой болезни.

Кроме радиации, опасность для здоровья астронавтов несет длительное состояние невесомости. В отсутствие силы притяжения, опорно-двигательный аппарат и кровеносная система быстро теряют свой тонус. Реабилитация после полета займет не менее 2 лет, а последствия для здоровья могут преследовать путешественников всю оставшуюся жизнь.

Изолированное пространство, однообразное питание, переутомление и другие издержки длительного космического полета негативно скажутся на психике первых марсианских путешественников. Это может привести к конфликтам в команде и даже к реальным психическим расстройствам.

Технические трудности

Невозможно предугадать точный сценарий полета. В любой момент может наступить поломка двигателя или столкновения корабля с мелким космическим телом. Кроме того он может попасть под поток солнечного ветра или в эпицентр марсианской песчаной бури.

Чтобы отправить людей на красную планету, ученые должны оснастить корабль резервными двигателями. Кроме того защитить его жилые помещения от излучения и пыли. Это сложный и затратный процесс и здесь нет права на ошибку. Поэтому полет состоится только тогда, когда все технические системы будут доведены практически до совершенства. И даже в этом случае, риск гибели экипажа очень высок.

Блок: 6/7 | Кол-во символов: 2378
Источник: https://spaceworlds.ru/solnechnaya-sistema/planeta-mars/skolko-letet-do-marsa.html

Интересные факты

Между Землей и Луной можно поместить все остальные планеты Солнечной системы

Каждый год расстояние до земного спутника возрастает в среднем на 4 см. Причины – движение планетоида по спиральной орбите и постепенно падающая мощность гравитационного взаимодействия Земли и Луны.

Между Землей  и Луной теоретически можно разместить все планеты Солнечной системы. Если сложить диаметры всех планет, включая  Плутон, то получится величина в 382 100 км.

comments powered by HyperComments

Блок: 9/9 | Кол-во символов: 498
Источник: https://SpaceGid. com/rasstoyanie-ot-zemli-do-lunyi.html

Почему расстояние между Солнцем и Марсом не постоянно

Марс, как и любые другие планеты, входящие в Солнечную систему, имеет орбиту эллипсовидной формы. Такая особенность в астрономии называется – эксцентриситет. Существует много факторов, которые способствуют такому перемещению. К примеру, на Землю влияет Луна, взаимодействуя с ней, на нашей планете случаются приливы и отливы. Примерно такое же влияние другие планеты оказывают на Марс. За весь период существования, орбита красной звезды несколько раз подвергалась сжатию и растягиванию. Различные формы оказывают на скорость перемещения и на температурные показатели. К примеру, сближаясь с центром Солнечной системы — скорость передвижения наращивается, и понижается, если планета отдаляется. Также эти факторы воздействуют на смену сезонов.

Блок: 7/8 | Кол-во символов: 798
Источник: https://oplanetah.ru/mars/rasstoyanie-do-marsa

Эволюция системы Луна и Земля

Главной целью всё более точных измерений расстояния до Луны являются попытки более глубокого понимания эволюции орбиты Луны в далеком прошлом и в отдаленном будущем. К настоящему времени астрономы пришли к выводу, что в прошлом Луна находилась в несколько раз ближе к Земле, а так же обладала значительно более коротким периодом вращения (то есть не была приливно захваченной).  Этот факт подтверждает импактную версию образования Луны из выброшенного вещества Земли, которая преобладает в наше время. Кроме того, приливное воздействие Луны приводит к тому, что скорость вращения Земли вокруг своей оси постепенно замедляется. Скорость этого процесса составляет увеличение земных суток каждый год на 23 микросекунды. За один год Луна отдаляется от Земли в среднем на 38 миллиметров. Оценивается, что в случае если система Земля-Луна переживет превращение Солнца в красный гигант, то через 50 миллиардов лет земные сутки сравняются с лунным месяцем. В результате Луна и Земля будут всегда повернуты к друг другу только одной стороной, как сейчас наблюдается в системе Плутон-Харон. К этому времени Луна отдалится до, примерно, 600 тысяч километров, а лунный месяц увеличится до 47 суток. Кроме того, предполагается, что испарение земных океанов через 2.3 миллиардов лет приведет к ускорению процесса удаления Луны (земные приливы значительно тормозят процесс).

Кроме того, расчеты показывают, что в дальнейшем Луна снова начнет сближаться с Землей по причине приливного взаимодействия с друг другом. При приближении к Земле на 12 тысяч км Луна будет разорвана приливными силами, обломки Луны образуют кольцо наподобие известных колец вокруг планет-гигантов Солнечной Системы. Другие известные спутники Солнечной Системы повторят эту судьбу гораздо раньше. Так Фобосу отводят 20-40 миллионов лет, а Тритону около 2 миллиардов лет.

Блок: 8/9 | Кол-во символов: 1856
Источник: https://SpaceGid.com/rasstoyanie-ot-zemli-do-lunyi.html

Расстояние от Луны до Марса

Учитывая, что орбита космических тел имеет эллипсовидную форму, то расстояние между планетами варьируется. Так при максимальном сближении, протяженность пути будет равна 55.7 млн. км, тогда как на максимальном удалении Марса от Луны — 400 млн. км.

Блок: 8/8 | Кол-во символов: 283
Источник: https://oplanetah.ru/mars/rasstoyanie-do-marsa

Кол-во блоков: 27 | Общее кол-во символов: 35375
Количество использованных доноров: 6
Информация по каждому донору:

1. https://MarsPlaneta.ru/perelet-ot-luny-do-marsa: использовано 1 блоков из 4, кол-во символов 1188 (3%)
2. https://spaceworlds.ru/solnechnaya-sistema/planeta-mars/skolko-letet-do-marsa.html: использовано 4 блоков из 7, кол-во символов 5589 (16%)
3. https://samsebevoin.ru/interesnoe/skolko-letet-do-marsa.html: использовано 1 блоков из 3, кол-во символов 1560 (4%)
4. https://ProNormy.ru/nauka/kosmos/rasstoyanie-ot-zemli-do-marsa: использовано 3 блоков из 5, кол-во символов 7312 (21%)
5. https://SpaceGid.com/rasstoyanie-ot-zemli-do-lunyi.html: использовано 9 блоков из 9, кол-во символов 13894 (39%)
6. https://oplanetah.ru/mars/rasstoyanie-do-marsa: использовано 6 блоков из 8, кол-во символов 5832 (16%)

Расстояние от Земли до Луны

Луна с незапамятных времен была постоянным спутником нашей планеты и самым близким к ней небесным телом. Естественно, человеку всегда хотелось там побывать. Но далеко ли туда лететь и какое до нее расстояние?

Что такое

Расстояние от Земли до Луны теоретически измеряется от центра Луны до центра Земли. Измерить это расстояние обычными методами, используемыми в обычной жизни, невозможно. Поэтому дистанция до земного спутника вычислялась по тригонометрическим формулам.

Перигей и апогей Луны

Аналогично Солнцу, Луна испытывает постоянное движение на земном небе вблизи эклиптики. Тем не менее, это движение значительно отличается от движения Солнца. Так плоскости орбит Солнца и Луны различаются на 5 градусов. Казалось бы, вследствие этого траектория Луны на земном небе должна быть похожа в общих чертах на эклиптику, отличаясь от нее только сдвигом на 5 градусов:

В этом движение Луна напоминает движение Солнца – с запада на восток, в противоположном направлении суточному вращению Земли. Но кроме того Луна движется по земному небу гораздо быстрее Солнца. Это связано с тем, что Земля совершает оборот вокруг Солнца примерно за 365 суток (земной год), а Луна вокруг Земли всего за 29 суток (лунный месяц). Это различие и стало стимулом к разбивке эклиптики на 12 зодиакальных созвездий (за один месяц Солнце смещается по эклиптике на 30 градусов). За время лунного месяца происходит полная смена фаз Луны:

Лунные фазы

В дополнение к траектории движения Луны добавляется ещё и фактор сильной вытянутости орбиты. Эксцентриситет орбиты Луны составляет 0.05 (для сравнения у Земли этот параметр равен 0.017). Отличие от круговой орбиты Луны приводит к тому, что видимый диаметр Луны постоянно меняется от 29 до 32 угловых минут.

В конечном итоге траектория положения Луны на земном небе постоянно мигрирует относительно фоновых звезд и эклиптики

За сутки Луна смещается относительно звезд на 13 градусов, за час примерно на 0.5 градусов. Современные астрономы часто используют покрытия Луны для оценок угловых диаметров звезд вблизи эклиптики.

От чего зависит движение Луны

Важным моментом теории движения Луны является факт того, что орбита Луны в космическом пространстве не является неизменной и стабильной. По причине сравнительно небольшой массы Луны, она подвержена постоянным возмущениям от более массивных объектов Солнечной Системы (прежде всего Солнца и Луны). Кроме того, на орбиту Луны оказывают влияние сплюснутость Солнца и гравитационные поля других планет Солнечной Системы. В результате этого величина эксцентриситета орбиты Луны испытывает колебания между 0.04 и 0.07 с периодом в 9 лет. Следствием этих изменений стало такое явление, как суперлуние. Суперлунием называется астрономическое явление, в ходе которого полная луна в несколько раз больше по угловым размерам, чем обычно. Так во время полнолуния 14 ноября 2016 года Луна находилась на рекордно близком расстоянии с 1948 года. В 1948 году Луна была на 50 км ближе, чем в 2016 году.

Сравнение видимого диаметра Луны на земном небе в перицентре и апоцентре лунной орбиты

Кроме того наблюдаются и колебания наклонения лунной орбиты к эклиптике: примерно на 18 угловых минут каждые 19 лет.

График изменения расстояния между Землей и Луной за 2 года

Чему равно

Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд

Космическим кораблям придется потратить на полет к земному спутнику немало времени.   До Луны нельзя лететь по прямой – планета будет уходить по орбите в сторону от точки назначения, и путь придется корректировать. При второй космической скорости в 11 км/с (40 000 км/ч) полет теоретически займет около 10 часов, но на деле это будет происходить дольше. Все потому, что корабль на старте постепенно наращивает скорость в атмосфере, доводя ее до значения в 11 км/с, чтобы вырваться из поля тяготения Земли. Затем  кораблю придется тормозить при подлете к Луне. Кстати, эта скорость- максимум, чего удалось добиться современным космическим кораблям.

Пресловутый полет американцев на Луну в 1969 году, согласно официальным данным, занял 76 часов. Быстрее всех до Луны удалось долететь аппарату НАСА «Новые горизонты» — за 8 часов 35 минут. Правда, он не приземлился на планетоид, а пролетел мимо – у него была другая миссия.

Свет от Земли до нашего спутника доберется очень быстро – за 1,255 секунд. Но полеты на световых скоростях – пока что из области фантастики.

Можно попытаться представить путь до Луны в привычных величинах. Пешком при скорости 5 км/ч дорога до Луны займет порядка девяти лет. Если поехать на машине на скорость в 100 км/ч, то добираться до земного спутника придется 160 дней. Если бы на Луну летали самолеты, то рейс до нее продлился бы где-то 20 дней.

Как в древней Греции астрономы рассчитывали расстояние до Луны

Расстояние от Земли до Луны

Луна стала первым небесным телом, до которого удалось рассчитать расстояние от Земли. Считается, что первыми это сделали астрономы в Древней Греции.

Измерить расстояние до Луны пытались с незапамятных времен – первым это попытался сделать Аристарх Самосский. Он оценил угол между Луной и Солнцем в 87 градусов, поэтому вышло, что Луна ближе Солнца в 20 раз (косинус угла равного 87 градуса равен 1/20). Ошибка измерений угла привела к 20-кратной ошибке, сегодня известно, что это отношение на самом деле равно 1 к 400 (угол равен примерно 89.8 градусов). Большая ошибка была вызвана трудностью оценок точного углового расстояния между Солнцем и Луной с помощью примитивных астрономических инструментов Древнего мира.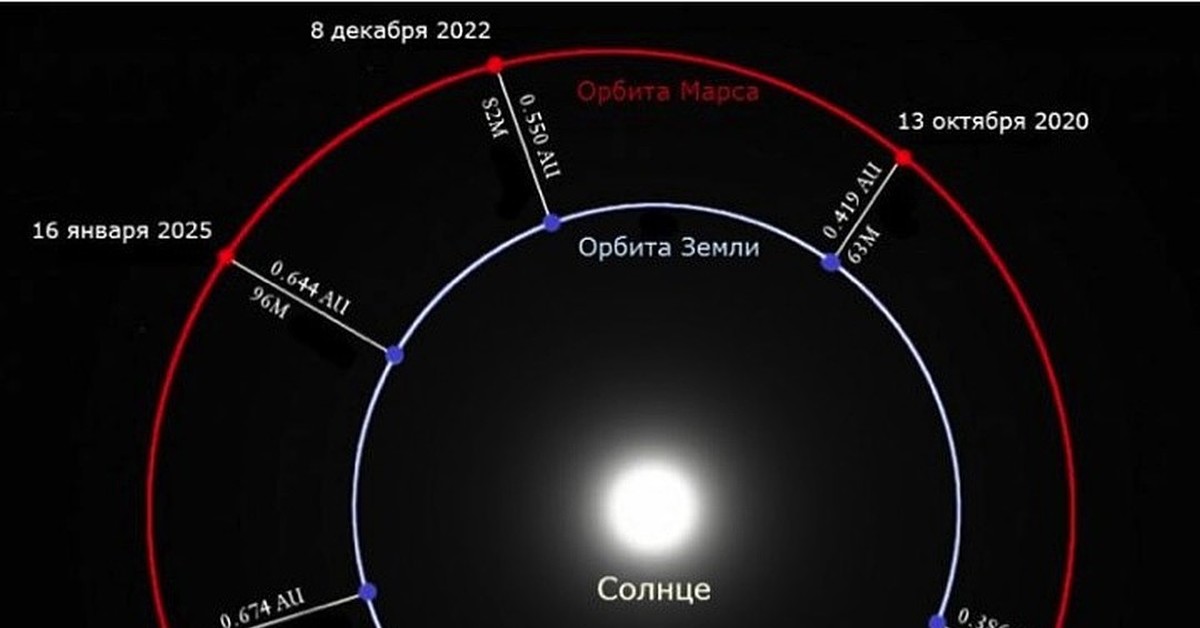 Регулярные солнечные затмения к этому времени уже позволили древнегреческим астрономам сделать вывод о том, что угловые диаметры Луны и Солнца примерно одинаковы. В связи с этим Аристарх сделал вывод, что Луна меньше Солнца в 20 раз (на самом деле примерно в 400 раз).

Для вычисления размеров Солнца и Луны относительно Земли Аристарх использовал другой метод. Речь идет о наблюдениях лунных затмений. К этому времени древние астрономы уже догадались о причинах этих явлений: Луна затмевается тенью Земли.

На схеме выше хорошо видно, что разность расстояний с Земли до Солнца и до Луны пропорциональна разнице между радиусами Земли и Солнца и радиусами Земли и её тени на расстояние Луны. Во времена Аристарха уже удалось оценить, что радиус Луны равен примерно 15 угловым минутам, а радиус земной тени составляет 40 угловых минут. То есть размер Луны получался примерно в 3 раза меньше размера Земли. Отсюда зная угловой радиус Луны можно было легко оценить, что Луна находится от Земли примерно в 40 диаметрах Земли. Древние греки могли лишь приблизительно оценить размеры Земли. Так Эратосфен Киренский (276 – 195 годы до нашей эры) на основе различий в максимальной высоте Солнца над горизонтом в Асуане и Александрии во время летнего солнцестояния определил, что радиус Земли близок к 6287 км (современное значение 6371 км). Если подставить это значение в оценку Аристарха насчет расстояния до Луны, то оно будет соответствовать примерно 502 тысяч км (современное значение среднего расстояния от Земли до Луны составляет 384 тысяч км).

Чуть позже математик и астроном II века до н. э. Гиппарх Никейский подсчитал, что расстояние до земного спутника в 60 раз больше, чем радиус нашей планеты. Его расчеты основывались на наблюдениях за движением Луны и его периодических затмениях.

Материалы по теме

Так как в момент затмения Солнце и Луна будут иметь одинаковые угловые размеры, то по правилам подобия треугольников можно найти отношение расстояний до Солнца и до Луны. Эта разница составляет 400 раз. Применяя еще раз эти правила, только уже по отношению к диаметрам Луны и Земли, Гиппарх вычислил, что диаметр Земли больше диаметра Луны в 2,5 раза. Т.е R_л = R_з/2,5.

Под углом в 1′ можно наблюдать предмет, размеры которого в 3 483 раза меньше, чем расстояние до него – эта информация во времена Гиппарха была всем известна. То есть, при наблюдаемом радиусе Луны в 15′ она будет ближе к наблюдателю в 15 раз. Т.е. отношение расстояния до Луны к ее радиусу будет равно 3483/15= 232 или S_л= 232R_л.

Соответственно, дистанция до Луны – это 232* R_з /2,5= 60 радиусов Земли. Это получается 6 371*60=382 260 км. Самое интересное, что измерения, выполненные при помощи современных инструментов, подтвердили правоту античного ученого.

Сейчас измерение дистанции до Луны проводится при помощи лазерных приборов, позволяющих измерить его с точностью до нескольких сантиметров. При этом измерения происходят за очень короткое время – не более 2 секунд, за которое Луна удаляется по орбите примерно на 50 метров от точки отправки лазерного импульса.

Эволюция методик измерения расстояния до Луны

Только с изобретением телескопа астрономы смогли получить более-менее точные значения параметров орбиты Луны и соответствия её размеров с размером Земли.

Пример эволюции астрономической единицы со временем

Более точный метод измерения расстояния до Луны появился в связи с развитием радиолокации. Первая радиолокация Луны была проведены в 1946 году в США и Великобритании. Радиолокация позволяла измерить расстояние до Луны с точностью в несколько километров.

Ещё более точным методом измерения расстояния до Луны стала лазерная локация. Для его реализации в 1960х годах на Луне было установлено несколько уголковых отражателей. Интересно отметить, что первые эксперименты по лазерной локации были проведены ещё до установки уголковых отражателей на поверхности Луны. В 1962-1963 годах в Крымской обсерватории СССР были проведены несколько экспериментов по лазерной локации отдельных лунных кратеров с использованием телескопов диаметром от 0. 3 до 2.6 метров. Эти эксперименты смогли определять расстояние до поверхности Луны с точностью в несколько сотен метров. В 1969-1972 годы астронавты программы “Аполлон” доставили на поверхность нашего спутника три уголковых отражателя. Среди них наиболее совершенным был отражатель миссии “Апполон-15”, так как он состоял 300 призм, тогда как два других (миссии “Апполон-11” и “Апполон-14”) только из ста призм каждый.

Карта положения уголковых отражателей

Кроме того в 1970 и 1973 годах СССР доставил на поверхность Луны ещё два французских уголковых отражателя на борту самоходных аппаратов “Луноход-1” и “Луноход-2”, каждый из которых состоял из 14 призм. Использование первого из этих отражателей обладает незаурядной историей. За первые 6 месяцев работы лунохода с отражателем удалось провести около 20 сеансов лазерной локации. Однако затем из-за неудачного положения лунохода вплоть до 2010 года не удавалось использовать отражатель. Лишь снимки нового аппарата LRO помогли уточнить положение лунохода с отражателем, и тем самым возобновить сеансы работы с ним.

В СССР наибольшее количество сеансов лазерной локации было проведено на 2.6-метровом телескопе Крымской обсерватории. Между 1976 и 1983 годами на этом телескопе было проведено 1400 измерений с погрешностью в 25 сантиметров, затем наблюдения были прекращены в связи со свертыванием советской лунной программы.

Всего же с 1970 по 2010 годы в мире было проведено примерно 17 тысяч высокоточных сеансов лазерной локации. Большинство из них было связано с уголковым отражателем “Аполонна-15” (как говорилось выше, он является наиболее совершенным – с рекордным количеством призм):

Из 40 обсерваторий, способных выполнять лазерную локацию Луны лишь несколько могут выполнять высокоточные измерения:

Большинство сверхточных измерений выполнено на 2-метровом телескопе в техасской обсерватории имени Мак Дональда:

В то же время наиболее точные измерения выполняет инструмент APOLLO, который был установлен на 3.5-метровом телескопе обсерватории Апач Пойнт в 2006 году. Точность его измерений достигает одного миллиметра:

Эволюция системы Луна и Земля

Главной целью всё более точных измерений расстояния до Луны являются попытки более глубокого понимания эволюции орбиты Луны в далеком прошлом и в отдаленном будущем. К настоящему времени астрономы пришли к выводу, что в прошлом Луна находилась в несколько раз ближе к Земле, а так же обладала значительно более коротким периодом вращения (то есть не была приливно захваченной).  Этот факт подтверждает импактную версию образования Луны из выброшенного вещества Земли, которая преобладает в наше время. Кроме того, приливное воздействие Луны приводит к тому, что скорость вращения Земли вокруг своей оси постепенно замедляется. Скорость этого процесса составляет увеличение земных суток каждый год на 23 микросекунды. За один год Луна отдаляется от Земли в среднем на 38 миллиметров. Оценивается, что в случае если система Земля-Луна переживет превращение Солнца в красный гигант, то через 50 миллиардов лет земные сутки сравняются с лунным месяцем. В результате Луна и Земля будут всегда повернуты к друг другу только одной стороной, как сейчас наблюдается в системе Плутон-Харон. К этому времени Луна отдалится до, примерно, 600 тысяч километров, а лунный месяц увеличится до 47 суток. Кроме того, предполагается, что испарение земных океанов через 2.3 миллиардов лет приведет к ускорению процесса удаления Луны (земные приливы значительно тормозят процесс).

Кроме того, расчеты показывают, что в дальнейшем Луна снова начнет сближаться с Землей по причине приливного взаимодействия с друг другом. При приближении к Земле на 12 тысяч км Луна будет разорвана приливными силами, обломки Луны образуют кольцо наподобие известных колец вокруг планет-гигантов Солнечной Системы. Другие известные спутники Солнечной Системы повторят эту судьбу гораздо раньше. Так Фобосу отводят 20-40 миллионов лет, а Тритону около 2 миллиардов лет.

Интересные факты

Между Землей и Луной можно поместить все остальные планеты Солнечной системы

Каждый год расстояние до земного спутника возрастает в среднем на 4 см. Причины – движение планетоида по спиральной орбите и постепенно падающая мощность гравитационного взаимодействия Земли и Луны.

Между Землей  и Луной теоретически можно разместить все планеты Солнечной системы. Если сложить диаметры всех планет, включая  Плутон, то получится величина в 382 100 км.

Понравилась запись? Расскажи о ней друзьям!

Просмотров записи: 72760

Запись опубликована: 05.04.2018
Автор: Максим Заболоцкий

Измерение расстояний в мировом пространстве

У каждого, кто начинает знакомиться с астрономией и узнает, что до Луны 380 тыс., а до Солнца 150 млн. км, что звездные расстояния измеряются вместо километров сотнями, тысячами и миллионами «световых лет» и «парсеков», возникает вполне естественное и законное сомнение: «А как же измерили эти расстояния, эти миллионы и миллиарды километров? Ведь до Луны, а тем более до Солнца и звезд добраться нельзя, следовательно, нельзя применить и обычные способы измерения расстояний».

Наука и жизнь // Иллюстрации

Рис. 1. Измерение расстояния до недоступного предмета.

Рис. 2. Измерение расстояния до Луны (относительное расстояние Луны и звезды Е сильно искажено).

Наука и жизнь // Иллюстрации

Рис. 3. Прохождение Венеры по диску Солнца (относительные размеры Солнца, Земли и Венеры не в масштабе).

Рис. 4. Противостояние Марса.

Рис. 5. Расположение орбит Марса, Эроса и Земли.

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

‹

›

Цель этой статьи — изложить вкратце способы, которыми астрономы измеряют расстояния до тел солнечной системы — Луны и Солнца. Определению расстояний более отдаленных объектов — звезд и туманностей — мы посвятим другую статью в с дном из ближайших номеров нашего журнала.

Измерение расстояния до Луны

Способы, применяемые астрономами для определения расстояния до близких к нам небесных тел, в принципе те же самые, которые применяют геодезисты при съемочных работах, землемеры, саперы, артиллеристы и т. д.

Как измерить расстояние до предмета, подойти к которому нельзя, например, до дерева на противоположной стороне реки (рис. 1)?

Топограф или землемер поступит просто. Он отложит на «своем» берегу линию АВ и измерит ее длину. Затем, став на один конец линии в точку А, измерит угол CAB — между направлением своей линии и направлением на предмет С. Перейдя в точку В он измерит угол СВА. А дальше можно поступить двумя способами: можно отложить на бумаге линию АВ в масштабе и построить на ее концах углы CAB и СВА, пересечение сторон которых и дает на плане точку С. Расстояние ее от точек А и В (да и от любой другой точки, отмеченной на плане) представит соответствующее действительное расстояние в том же самом масштабе, в котором изображена линия АВ. Или же можно по формулам тригонометрии, зная одну сторону треугольника и два его угла, вычислить все другие его линии, в том числе и высоту СН — расстояние точки С — далекого дерева до проведенной землемером линии АВ.

Точно так же поступили и астрономы, определяя расстояние до Луны. Если в один и тот же момент два наблюдателя сфотографируют небо с Луной из двух далеких друг от друга мест А и В (рис. 2) и затем сравнят свои снимки, они увидят, что положение Луны относительно звезд несколько различно. Например, звезда Е на снимке наблюдателя А будет видна к северу от Луны, а у наблюдателя В — к югу.

Измеряя снимки или, что проще, определяя положение Луны на небе в двух местах с помощью специальных телескопов, снабженных угломерными приспособлениями, можно по видимому смещению Луны найти и ее расстояние до Земли. Вспомним одну простую теорему из геометрии — сумма углов в четырехугольнике равна 360° — и применим ее к Земле и Луне.

Измерения дадут величину углов z₁ и z₂ — углов между вертикальным направлением в обоих местах и направлением на Луну. Предположим, для простоты, что места А и В лежат на одном меридиане, т. е. на круге, проходящем через оба полюса Земли. ЕЕ — земной экватор и утлы φ ₁ и φ₂ —географические широты обоих мест.

Применяя теорему к четырехугольнику OALB, где О — центр Земли, найдем, что

[(180° — z₁)+φ ₁ + φ ₁₂+ (180°—z₂)[+] p]= 360°

или

р = (z₁+ z₂) — (φ₁+ φ₂)

По известным углам найдем угол р, под которым из центра Луны видна линия АВ. Длина линии АВ известна, так как известен радиус Земли и положение мест наблюдения А и В. По длине этой линии и углу р, так же как и в случае недоступного предмета, можно вычислить расстояние до Луны.

Угол, под которым из центра Луны или другого небесного тела видна линия, длиной равная радиусу Земли, называется параллаксом этого небесного светила. Измерив угол р для любой линии АВ, можно вычислить и параллакс Луны.

Такие измерения были сделаны еще древними греками. Современные точные намерения дают для параллакса Луны на ее среднем расстоянии от Земли величину немного меньше градуса — 57′ 2″,7, т. е. Земля видна с Луны как диск диаметром почти в 2° (в 4 раза больше диаметра видимого нами диска Луны).

Отсюда следует между прочим тесьма интересный вывод: жители Луны (если бы они были там) с большим правом смогли бы сказать, что Земля служит для освещения Луны, чем мы говорим обратное. В самом деле: диск Земли, видимый с Луны, по площади в 14 раз больше видимого нами диска Луны; а так как каждый участок поверхности диска Земли отражает в 6 раз больше света (из-за наличия атмосферы), чем такой же участок диска Луны, то Земля посылает на Луну в 80 раз больше света, чем Луна на Землю (при одинаковых фазах).

По параллаксу Луны сейчас же находим, что расстояние до нее в 60,267 раз больше радиуса Земли или равно 384 400 км.

Однако — это среднее расстояние: путь Луны не точный круг, и Луна, обращаясь вокруг Земли, то подходит к ней на 363000 км, то удаляется на 405 000 км.

Так решается первая, самая простая задача — измерение расстояния до самого близкого к нам небесного тела.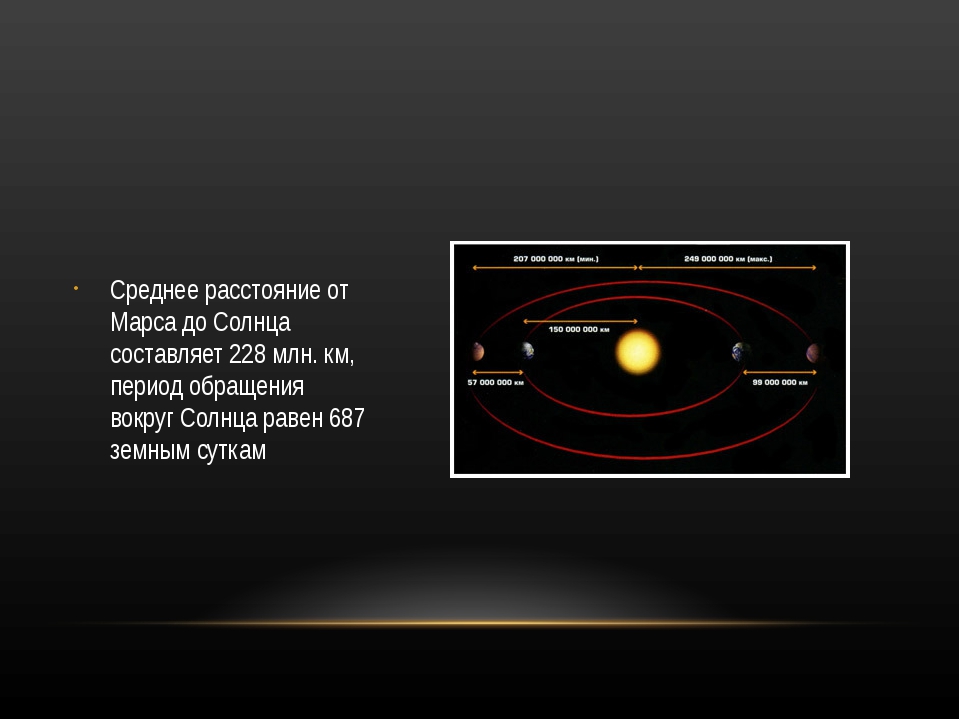 Это сравнительно не трудно, потому что видимое смещение Луны велико, и его можно было измерить с помощью даже тех примитивных приборов, которыми пользовались древние астрономы.

Чему равно расстояние до Солнца

Казалось бы, можно применить тот же самый способ и для измерения расстояния: до Солнца — произвести одновременные наблюдения в двух местах, вычислить углы четырехугольников и треугольников, и задача решена. На деле, однако, обнаружилось весьма много трудностей.

Уже древние греки установили, что Солнце во много раз дальше Луны, но во сколько именно — установить не смогли.

Древнегреческий астроном Аристарх нашел, что Солнце в 20 раз дальше Луны; это измерение было неверно. В 1650—1675 гг. голландские и французские астрономы показали, что Солнце дальше Луны примерно в 400 раз. Стало понятным, почему не удавались попытки обнаружить видимое смещение Солнца, как это удалось сделать для Луны. Ведь параллакс Солнца в 400 раз меньше параллакса Луны, всего около 1/400 градуса, или 9 сек. дуги. А это значит, что даже при наблюдении с двух мест Земли, лежащих на противоположных концах диаметра Земли, например с северного и южного полюсов, видимое смещение Солнца было бы равно видимой толщине проволоки в 0,1 мм (человеческий волос) при рассматривании ее с расстояния в 1,5 м. Величина ничтожная, и заметить ее трудно, хотя и возможно с помощью точного угломерного прибора.

Но возникают большие добавочные трудности. Луну наблюдают ночью и ее положение сравнивают с положениями соседних звезд. Днем звезд не видно, и сравнивать положение Солнца не с чем, приходится целиком полагаться на разделенные круги самого прибора. Прибор нагревается лучами Солнца, различные части его деформируются, вызывая появление новых ошибок. Да и сам воздух, нагретый лучами Солнца, неспокоен, край Солнца кажется волнующимся, дрожащим, по небу как бы бегут волны. Погрешности наблюдений будут больше той величины, которую необходимо измерить. От самого простого метода пришлось отказаться и пойти обходными путями.

Наблюдения видимых движений планет производились еще в глубокой древности. Из сравнения этих наблюдений с современными удалось с очень большой точностью определить время обращения планет вокруг Солнца. Так например, мы знаем что Марс совершает свой оборот в 1,8808 земных года. Но третий закон Кеплера говорит: «Квадраты времен обращения планет относятся, как кубы их средних расстояний от Солнца». Отсюда, принимая за единицу среднее расстояние Земли от Солнца, можно вычислить, что среднее расстояние Марса равно 1,5237. Таким путем можно построить точный «план» солнечной системы, нанести орбиты планет, Земли, комет, но у плана будет не хватать «мелочи» — масштаба. Мы сможем уверенно сказать, что Венера в 1,38 раза ближе к Солнцу, чем Земля, а Марс в 1,52 раз дальше, но ничего не будем знать о том, сколько же километров от Венеры или Земли до Солнца. Достаточно, однако, найти хотя бы одно из расстояний в километрах: мы получим в свои руки масштаб и, пользуясь им, сможем измерить любое расстояние на плане.

Именно этот способ был применен для измерения расстояния от Солнца до Земли. Меркурий и Венера находятся ближе к Солнцу, чем Земля. Может оказаться, что когда Земля и Венера будут находиться по одну сторону от Солнца, — центры Солнца и обеих планет окажутся на одной «прямой линии (рис. 3). Венера будет видна с Земли на диске Солнца. Расстояние от Земли до Венеры будет почти в 4 раза меньше расстояния до Солнца, а параллакс ее почти в 4 раза больше параллакса Солнца. Кроме того, нужно будет определить положение Венеры относительно центра Солнца, что можно сделать гораздо точнее, чем определение видимого положения Солнца (ошибки, присущие инструменту, влияют значительно меньше при определении относительного положения двух небесных тел).

Если бы движение Земли и Венеры происходило в одной и той же плоскости, то «прохождения Венеры по диску Солнца» наблюдались бы каждый раз, когда Венера, движущаяся быстрее Земли, обгоняет ее, т. е. примерно раз в 1 год и 7 мес. Но плоскости путей Земли и Венеры наклонены друг к другу. Обгоняя Землю, Венера проходит выше или ниже Солнца и не может быть наблюдаема, так как она повернута к Земле темной, не освещенной Солнцем стороной. Мы увидим ее на диске Солнца лишь в том случае, если и «обгон» будет происходить вблизи линии пересечения плоскостей орбит обеих планет.

Такое «счастливое совпадение» случается не часто. После одного прохождения второе следует через 8 лет, но зато следующее — лишь через 105—120 лет. Впервые явление наблюдали в 1639 г. Следующие прохождения — 1761, 1769, 1874 и 1882 гг. наблюдались уже весьма тщательно для определения точного расстояния до Солнца. Для наблюдения последних двух прохождений было снаряжено большое число специальных экспедиций. Наблюдатели в далеко расположенных пунктах с наибольшей доступной точностью наблюдали моменты начала и конца явления, а также положение Венеры на диске Солнца. При наблюдениях последних прохождений применялось уже фотографирование Солнца. Видимый путь Венеры по диску Солнца будет несколько смещен у обоих наблюдателей (рис. 3). Из величины смещения можно вычислить расстояние от Земли до Венеры, т. е. найти тот ключ, масштаб, которого недоставало в построенном плане солнечной системы. Наблюдений прохождений Венеры дали для параллакса Солнца величину 8″,86 и для расстояния Солнца — 148 000 000 км.

Два ближайших прохождения Венеры по диску Солнца будут наблюдаться 8 июня 2004 г. и 6 июня 2012 г.

Могут наблюдаться и прохождения по диску Солнца ближайшей к Солнцу планеты — Меркурия. Они бывают значительно чаще, чем прохождения Венеры, но представляют несравненно меньше интереса для определения расстояния до Солнца: в момент прохождения расстояние от Земли до Меркурия составляет около 90 млн. км, и параллакс его лишь в 1,5 раза больше параллакса Солнца.

Другое удобное расположение планет бывает тогда, когда Земля, двигаясь быстрее Марса, перегоняет его (рис. 4). В это время Марс виден на ночном небе в противоположном от Солнца направлении, почему такие положения его и называются противостояниями.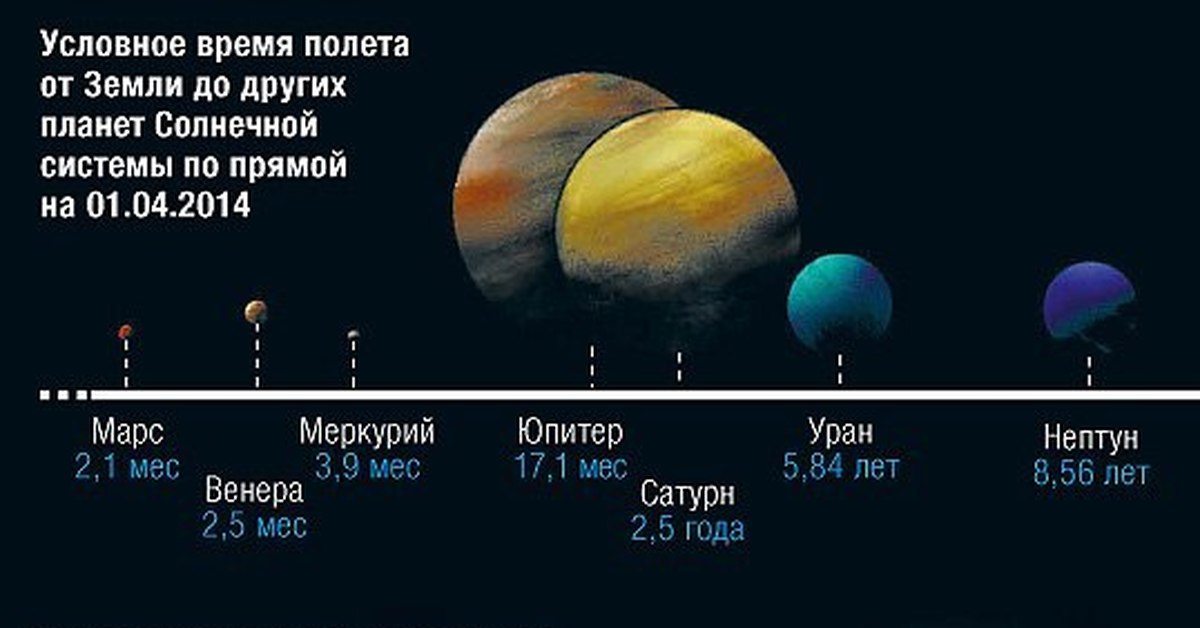 Расстояние между Землей и Марсом уменьшается в среднем до 78 млн. км. Однако орбита Марса сильно отлична от круга, и если сближение Марса и Земли происходит в августе — сентябре, расстояние до Марса может быть всего 56 млн. км. Марс виден всю ночь, и его положение можно очень точно определить, пользуясь как опорными точками близкими звездами.

Наблюдения из двух пунктов дадут параллакс Марса, а отсюда можно вычислить его расстояние и по нему — масштаб к плану солнечной системы. Приближения Марса и Земли — противостояния Марса — повторяются приблизительно через 2 года и 2 мес., а так называемые «великие противостояния», когда Марс ближе всего к Земле, — раз в 15 —17 лет. Последнее «великое противостояние» было 24 августа 1924 г., а следующее будет 23 июля 1939 г. Каждое противостояние используется не только для определения расстояния, но и для физических наблюдений самого Марса.

Еще ближе к Земле может подойти Эрос, одна из семейства малых планет, орбиты большинства которых лежат между орбитам Марса и Юпитера. Орбита Эроса очень сильно отлична от круга, и значительная часть ее лежит даже внутри орбиты Марса (рис. 5). В некоторых случаях расстояние между Землей и Эросом может уменьшаться до 22 млн. км, т. е. до 1/7 расстояния Солнца, довольно близко Эрос подходил к Земле в 1900—1901 гг. (на 48 млн. км) и в 1930— 1931 гг. (на 26 млн. км). Эрос наблюдался в это время, как звездочка, положение которой среди других звезд может быть определено весьма точно.

Нужно заметить, что для определения параллакса по наблюдениям Эроса не нужно обязательно производить наблюдения из двух далеких пунктов. Вращение Земли вокруг оси уносит с собой наблюдателя и, если он находится на экваторе, за 12 час. вращение Земли перенесет его на расстояние, равное диаметру Земли, или 12,7 тыс. км. Наблюдатель, расположенный к северу или к югу от экватора, переместится меньше. И если снимки Эроса произведены в начале и в конце ночи, — они равносильны снимкам, сделанным на большом расстоянии друг от друга. Нужно, конечно, принять во внимание движение Земли и Эроса по орбитам за время между снимками.

Существуют ещё другие способы измерения расстояния до Солнца, но они не являются основными, и рассматривать их мы не имеем возможности. Между прочим такой же метод использовался древними и для определения параллакса Луны.

Сопоставление всех наиболее точных определений дает для параллакса Солнца величину 8″,803 с возможной ошибкой в 0″,001, а отсюда — среднее расстояние Земли равно 149 450 000 км с возможной ошибкой в 17 000 км.

Среднее расстояние Солнца—Земля является основным для выражения других расстояний в солнечной системе и названо «астрономической единицей». Но действительное расстояние до Солнца может отличаться от среднего, так как путь Земли около Солнца — не круг, а эллипс. В июле расстояние до Солнца на 2,5 млн. км больше среднего, а в январе на столько же меньше.

Астрономическая единица есть та мера, которой мы измеряем «не только все расстояния до тел солнечной системы, но и расстояния самых далеких звезд, туманностей и звездных скоплений. Словом, это та мера, при помощи которой мы определяем масштаб строения вселенной. Поэтому на определения ее потрачено много усилий, и известна она современной науке с большой точностью.

Может показаться, что указанная выше ошибка в 17 000 км велика; но не надо забывать, что эта ошибка составляет лишь немногим больше 0,0001 всей астрономической единицы. Представим себе, что мы измерили длину комнаты в 9 м и при этом измерении ошиблись всего лишь на 1 мм. По сравнению с длиной комнаты эта ошибка соответствует точности, с которой известно среднее расстояние Земли от Солнца. Но если попробовать на самом деле измерить длину в 9 м с ошибкой в 1 мм, — это окажется совсем не так просто: потребуется большое внимание и хорошие измерительные инструменты, чтобы обеспечить такую точность при обыкновенном измерении по гладкому полу, во всех точках доступному измерителю. Тем более нужно отдать должное точности, с которой произведено измерение через межпланетное пространство расстояния до Солнца, к которому ни один человек ее приближался ближе чем на 147 млн. км, — расстояние, которое пушечное ядро сможет пролететь, двигаясь со скоростью 1000 м/сек, только в 4,5 года.

Геометрия звездного неба

Владимир Юрьевич Протасов
«Квант» №2, 2010

Небо над головой — самый древний учебник геометрии. Первые понятия, такие как точка и круг, — оттуда. Скорее даже не учебник, а задачник. В котором отсутствует страничка с ответами. Два круга одинакового размера — Солнце и Луна — движутся по небу, каждый со своей скоростью. Остальные объекты — светящиеся точки — движутся все вместе, словно они прикреплены к сфере, вращающейся со скоростью 1 оборот в 24 часа. Правда, среди них есть исключения — 5 точек движутся как им вздумается. Для них подобрали особое слово — «планета», по-гречески — «бродяга». Сколько человечество существует, оно пытается разгадать законы этого вечного движения. Первый прорыв произошел в III веке до н.э., когда греческие ученые, взяв на вооружение молодую науку — геометрию, смогли получить первые результаты об устройстве Вселенной. Об этом и пойдет речь.

Чтобы иметь некоторое представление о сложности задачи, рассмотрим такой пример. Представим себе светящийся шар диаметром 10 см, неподвижно висящий в пространстве. Назовем его S. Вокруг него на расстоянии чуть больше 10 метров обращается маленький шарик Z диаметром 1 миллиметр, а вокруг Z на расстоянии 6 см обращается совсем крохотный шарик L, его диаметр — четверть миллиметра. На поверхности среднего шарика Z живут микроскопические существа. Они обладают неким разумом, но покидать пределы своего шарика не могут. Всё, что они могут, — смотреть на два других шара — S и L. Спрашивается, могут ли они узнать диаметры этих шаров и измерить расстояния до них? Сколько ни думай, дело, казалось бы, безнадежное. Мы нарисовали сильно уменьшенную модель Солнечной системы (S — Солнце, Z — Земля, L — Луна).

Вот такая задача стояла перед древними астрономами. И они ее решили! Более 22 веков назад, не пользуясь ничем, кроме самой элементарной геометрии — на уровне 8 класса (свойства прямой и окружности, подобные треугольники и теорема Пифагора). И, конечно, наблюдая за Луной и за Солнцем.

Над решением трудились несколько ученых. Мы выделим двух. Это математик Эратосфен, измеривший радиус земного шара, и астроном Аристарх, вычисливший размеры Луны, Солнца и расстояния до них. Как они это сделали?

Как измерили земной шар

То, что Земля не плоская, люди знали давно. Древние мореплаватели наблюдали, как постепенно меняется картина звездного неба: становятся видны новые созвездия, а другие, напротив, заходят за горизонт. Уплывающие вдаль корабли «уходят под воду», последними скрываются из вида верхушки их мачт. Кто первый высказал идею о шарообразности Земли, неизвестно. Скорее всего — пифагорейцы, считавшие шар совершеннейшей из фигур. Полтора века спустя Аристотель приводит несколько доказательств того, что Земля — шар. Главное из них: во время лунного затмения на поверхности Луны отчетливо видна тень от Земли, и эта тень круглая! С тех пор постоянно предпринимались попытки измерить радиус земного шара. Два простых способа изложены в упражнениях 1 и 2. Измерения, правда, получались неточными. Аристотель, например, ошибся более чем в полтора раза. Считается, что первым, кому удалось сделать это с высокой точностью, был греческий математик Эратосфен Киренский (276–194 до н. э.). Его имя теперь всем известно благодаря решету Эратосфена — способу находить простые числа (рис. 1).

Если вычеркнуть из натурального ряда единицу, затем вычеркивать все четные числа, кроме первого (самого числа 2), затем все числа, кратные трем, кроме первого из них (числа 3), и т. д., то в результате останутся одни простые числа. Среди современников Эратосфен был знаменит как крупнейший ученый-энциклопедист, занимавшийся не только математикой, но и географией, картографией и астрономией. Он долгое время возглавлял Александрийскую библиотеку — центр мировой науки того времени. Работая над составлением первого атласа Земли (речь, конечно, шла об известной к тому времени ее части), он задумал провести точное измерение земного шара. Идея была такова. В Александрии все знали, что на юге, в городе Сиена (современный Асуан), один день в году, в полдень, Солнце достигает зенита. Исчезает тень от вертикального шеста, на несколько минут освещается дно колодца. Происходит это в день летнего солнцестояния, 22 июня — день наивысшего положения Солнца на небе. Эратосфен направляет своих помощников¹ в Сиену, и те устанавливают, что ровно в полдень (по солнечным часам) Солнце находится точно в зените. Одновременно (как написано в первоисточнике: «в тот же час»), т. е. в полдень по солнечным часам, Эратосфен измеряет длину тени от вертикального шеста в Александрии. Получился треугольник ABC (АС — шест, АВ — тень, рис. 2).

Итак, солнечный луч в Сиене (N) перпендикулярен поверхности Земли, а значит, проходит через ее центр — точку Z. Параллельный ему луч в Александрии (А) составляет угол γ = ACB с вертикалью. Пользуясь равенством накрест лежащих углов при параллельных, заключаем, что AZN = γ. Если обозначить через l длину окружности, а через х длину ее дуги AN, то получаем пропорцию . Угол γ в треугольнике АВС Эратосфен измерил, получилось 7,2°. Величина х — не что иное, как длина пути от Александрии до Сиены, примерно 800 км. Ее Эратосфен аккуратно вычисляет, исходя из среднего времени движения верблюжьих караванов, регулярно ходивших между двумя городами, а также используя данные бематистов — людей специальной профессии, измерявших расстояния шагами. Теперь осталось решить пропорцию , получив длину окружности (т. е. длину земного меридиана) l = 40000 км. Тогда радиус Земли R равен l/(2π), это примерно 6400 км. То, что длина земного меридиана выражается столь круглым числом в 40000 км, не удивительно, если вспомнить, что единица длины в 1 метр и была введена (во Франции в конце XVIII века) как одна сорокамиллионная часть окружности Земли (по определению!). Эратосфен, конечно, использовал другую единицу измерения — стадий (около 200 м). Стадиев было несколько: египетский, греческий, вавилонский, и каким из них пользовался Эратосфен — неизвестно. Поэтому трудно судить наверняка о точности его измерения. Кроме того, неизбежная ошибка возникала в силу географического положения двух городов. Эратосфен рассуждал так: если города находятся на одном меридиане (т. е. Александрия расположена в точности к северу от Сиены), то полдень в них наступает одновременно. Поэтому, сделав измерения во время наивысшего положения Солнца в каждом городе, мы должны получить правильный результат. Но на самом деле Александрия и Сиена — далеко не на одном меридиане. Сейчас в этом легко убедиться, взглянув на карту, но у Эратосфена такой возможности не было, он как раз и работал над составлением первых карт. Поэтому его метод (абсолютно верный!) привел к ошибке в определении радиуса Земли. Тем не менее, многие исследователи уверены, что точность измерения Эратосфена была высока и что он ошибся менее чем на 2%. Улучшить этот результат человечество смогло только через 2 тысячи лет, в середине XIX века. Над этим трудилась группа ученых во Франции и экспедиция В. Я. Струве в России. Даже в эпоху великих географических открытий, в XVI веке, люди не смогли достичь результата Эратосфена и пользовались неверным значением длины земной окружности в 37000 км. Ни Колумб, ни Магеллан не знали, каковы истинные размеры Земли и какие расстояния им придется преодолевать. Они-то считали, что длина экватора на 3 тысячи км меньше, чем на самом деле. Знали бы — может, и не поплыли бы.

В чем причина столь высокой точности метода Эратосфена (конечно, если он пользовался нужным стадием)? До него измерения были локальными, на расстояниях, обозримых человеческим глазом, т. е. не более 100 км. Таковы, например, способы в упражнениях 1 и 2. При этом неизбежны ошибки из-за рельефа местности, атмосферных явлений и т. д. Чтобы добиться большей точности, нужно проводить измерения глобально, на расстояниях, сравнимых с радиусом Земли. Расстояние в 800 км между Александрией и Сиеной оказалось вполне достаточным.

Упражнения
1. Как вычислить радиус Земли по следующим данным: с горы высотой 500 м просматриваются окрестности на расстоянии 80 км?
2. Как вычислить радиус Земли по следующим данным: корабль высотой 20 м, отплыв от берега на 16 км, полностью исчезает из вида?
3. Два друга — один в Москве, другой — в Туле, берут по метровому шесту и ставят их вертикально. В момент, в течение дня, когда тень от шеста достигает наименьшей длины, каждый из них измеряет длину тени. В Москве получилось а см, а в Туле — b см. Выразите радиус Земли через а и b. Города расположены на одном меридиане на расстоянии 185 км.

Как видно из упражнения 3, опыт Эратосфена можно проделать и в наших широтах, где Солнце никогда не бывает в зените. Правда, для этого нужны две точки обязательно на одном меридиане. Если же повторить опыт Эратосфена для Александрии и Сиены, и при этом сделать измерения в этих городах одновременно (сейчас для этого есть технические возможности), то мы получим верный ответ, при этом будет не важно, на каком меридиане находится Сиена (почему?).

Как измерили Луну и Солнце. Три шага Аристарха

Греческий остров Самос в Эгейском море — теперь глухая провинция. Сорок километров в длину, восемь — в ширину. На этом крохотном острове в разное время родились три величайших гения — математик Пифагор, философ Эпикур и астроном Аристарх. Про жизнь Аристарха Самосского известно мало. Даты жизни приблизительны: родился около 310 до н.э., умер около 230 до н.э. Как он выглядел, мы не знаем, ни одного изображения не сохранилось (современный памятник Аристарху в греческом городе Салоники — лишь фантазия скульптора) . Много лет провел в Александрии, где работал в библиотеке и в обсерватории. Главное его достижение — книга «О величинах и расстояниях Солнца и Луны», — по единодушному мнению историков, является настоящим научным подвигом. В ней он вычисляет радиус Солнца, радиус Луны и расстояния от Земли до Луны и до Солнца. Сделал он это в одиночку, пользуясь очень простой геометрией и всем известными результатами наблюдений за Солнцем и Луной. На этом Аристарх не останавливается, он делает несколько важнейших выводов о строении Вселенной, которые намного опередили свое время. Не случайно его назвали впоследствии «Коперником античности».

Вычисление Аристарха можно условно разбить на три шага. Каждый шаг сводится к простой геометрической задаче. Первые два шага совсем элементарны, третий — чуть посложнее. В геометрических построениях мы будем обозначать через Z, S и L центры Земли, Солнца и Луны соответственно, а через R, R_s и R_l — их радиусы. Все небесные тела будем считать шарами, а их орбиты — окружностями, как и считал сам Аристарх (хотя, как мы теперь знаем, это не совсем так). Мы начинаем с первого шага, и для этого немного понаблюдаем за Луной.

Шаг 1. Во сколько раз Солнце дальше, чем Луна?

Как известно, Луна светит отраженным солнечным светом. Если взять шар и посветить на него со стороны большим прожектором, то в любом положении освещенной окажется ровно половина поверхности шара. Граница освещенной полусферы — окружность, лежащая в плоскости, перпендикулярной лучам света. Таким образом, Солнце всегда освещает ровно половину поверхности Луны. Видимая нам форма Луны зависит от того, как расположена эта освещенная половина. При новолунии, когда Луна вовсе не видна на небе, Солнце освещает ее обратную сторону. Затем освещенная полусфера постепенно поворачивается в сторону Земли. Мы начинаем видеть тонкий серп, затем — месяц («растущая Луна»), далее — полукруг (эта фаза Луны называется «квадратурой»). Затем день ото дня (вернее, ночь от ночи) полукруг дорастает до полной Луны. Потом начинается обратный процесс: освещенная полусфера от нас отворачивается. Луна «стареет», постепенно превращаясь в месяц, повернутый к нам левой стороной, подобно букве «С», и, наконец, в ночь новолуния исчезает. Период от одного новолуния до другого длится примерно четыре недели. За это время Луна совершает полный оборот вокруг Земли. От новолуния до половины Луны проходит четверть периода, отсюда и название «квадратура».

Замечательная догадка Аристарха состояла в том, что при квадратуре солнечные лучи, освещающие половину Луны, перпендикулярны прямой, соединяющей Луну с Землей. Таким образом, в треугольнике ZLS угол при вершине L — прямой (рис. 3). Если теперь измерить угол LZS, обозначим его через α, то получим, что  = cos α. Для простоты мы считаем, что наблюдатель находится в центре Земли. Это несильно повлияет на результат, поскольку расстояния от Земли до Луны и до Солнца значительно превосходят радиус Земли. Итак, измерив угол α между лучами ZL и ZS во время квадратуры, Аристарх вычисляет отношение расстояний до Луны и до Солнца. Как одновременно застать Солнце и Луну на небосводе? Это можно сделать ранним утром. Сложность возникает по другому, неожиданному, поводу. Во времена Аристарха не было косинусов. Первые понятия тригонометрии появятся позже, в работах Аполлония и Архимеда. Но Аристарх знал, что такое подобные треугольники, и этого было достаточно. Начертив маленький прямоугольный треугольник Z’L’S’ с тем же острым углом α = L’Z’S’ и измерив его стороны, находим, что , и это отношение примерно равно 1/400.

Получается, что Солнце в 400 раз дальше от Земли, чем Луна. Эту константу — отношение расстояний от Земли до Солнца и от Земли до Луны — мы будем обозначать буквой κ. Итак, мы нашли, что κ = 400.

Шаг 2. Во сколько раз Солнце больше Луны?

Для того чтобы найти отношение радиусов Солнца и Луны, Аристарх привлекает солнечные затмения (рис. 4). Они происходят, когда Луна загораживает Солнце. При частичном, или, как говорят астрономы, частном, затмении Луна лишь проходит по диску Солнца, не закрывая его полностью. Порой такое затмение даже нельзя разглядеть невооруженным глазом, Солнце светит как в обычный день. Лишь сквозь сильное затемнение, например, закопченное стекло, видно, как часть солнечного диска закрыта черным кругом. Гораздо реже происходит полное затмение, когда Луна на несколько минут полностью закрывает солнечный диск.

В это время становится темно, на небе появляются звезды. Затмения наводили ужас на древних людей, считались предвестниками трагедий. Солнечное затмение наблюдается по-разному в разных частях Земли. Во время полного затмения на поверхности Земли возникает тень от Луны — круг, диаметр которого не превосходит 270 км. Лишь в тех районах земного шара, по которым проходит эта тень, можно наблюдать полное затмение. Поэтому в одном и том же месте полное затмение происходит крайне редко — в среднем раз в 200–300 лет. Аристарху повезло — он смог наблюдать полное солнечное затмение собственными глазами. На безоблачном небе Солнце постепенно начало тускнеть и уменьшаться в размерах, установились сумерки. На несколько мгновений Солнце исчезло. Потом проглянул первый луч света, солнечный диск стал расти, и вскоре Солнце засветило в полную силу. Почему затмение длится столь короткое время? Аристарх отвечает: причина в том, что Луна имеет те же видимые размеры на небе, что и Солнце. Что это значит? Проведем плоскость через центры Земли, Солнца и Луны. Получившееся сечение изображено на рисунке 5a. Угол между касательными, проведенными из точки Z к окружности Луны, называется угловым размером Луны, или ее угловым диаметром. Так же определяется угловой размер Солнца. Если угловые диаметры Солнца и Луны совпадают, то они имеют одинаковые видимые размеры на небе, а при затмении Луна действительно полностью загораживает Солнце (рис. 5б), но лишь на мгновение, когда совпадут лучи ZL и ZS. На фотографии полного солнечного затмения (см. рис. 4) ясно видно равенство размеров.

Вывод Аристарха оказался поразительно точен! В реальности средние угловые диаметры Солнца и Луны отличаются всего на 1,5%. Мы вынуждены говорить о средних диаметрах, поскольку они меняются в течение года, так как планеты движутся не по окружностям, а по эллипсам.

Соединив центр Земли Z с центрами Солнца S и Луны L, а также с точками касания Р и Q, получим два прямоугольных треугольника ZSP и ZLQ (см. рис. 5a). Они подобны, поскольку у них есть пара равных острых углов β/2. Следовательно, . Таким образом, отношение радиусов Солнца и Луны равно отношению расстояний от их центров до центра Земли. Итак, R_s/R_l = κ = 400. Несмотря на то, что их видимые размеры равны, Солнце оказалось больше Луны в 400 раз!

Равенство угловых размеров Луны и Солнца — счастливое совпадение. Оно не вытекает из законов механики. У многих планет Солнечной системы есть спутники: у Марса их два, у Юпитера — четыре (и еще несколько десятков мелких), и все они имеют разные угловые размеры, не совпадающие с солнечным.

Теперь мы приступаем к решающему и самому сложному шагу.

Шаг 3. Вычисление размеров Солнца и Луны и расстояний до них

Итак, нам известно отношение размеров Солнца и Луны и отношение их расстояний до Земли. Эта информация относительна: она восстанавливает картину окружающего мира лишь с точностью до подобия.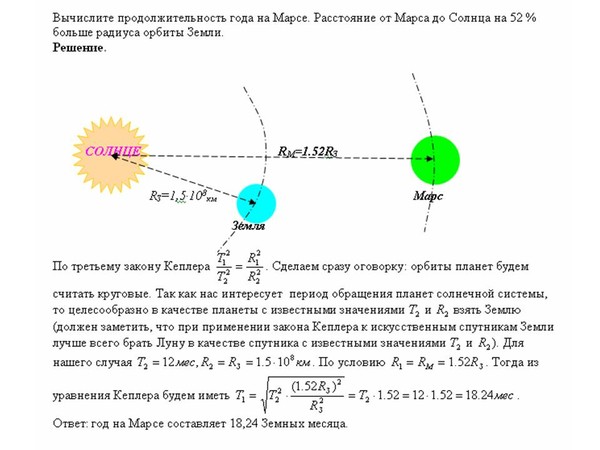 Можно удалить Луну и Солнце от Земли в 10 раз, увеличив во столько же раз их размеры, и видимая с Земли картина останется такой же. Чтобы найти реальные размеры небесных тел, надо соотнести их с каким-то известным размером. Но из всех астрономических величин Аристарху пока известен только радиус² земного шара R = 6400 км. Поможет ли это? Хоть в каком-то из видимых явлений, происходящих на небе, появляется радиус Земли? Не случайно говорят «небо и земля», имея в виду две несовместные вещи. И всё же такое явление есть. Это — лунное затмение. С его помощью, применив довольно хитроумное геометрическое построение, Аристарх вычисляет отношение радиуса Солнца к радиусу Земли, и цепь замыкается: теперь мы одновременно находим радиус Луны, радиус Солнца, а заодно и расстояния от Луны и от Солнца до Земли.

При лунном затмении Луна уходит в тень Земли. Спрятавшись за Землю, Луна лишается солнечного света, и, таким образом, перестает светить. Она не исчезает из вида полностью, поскольку небольшая часть солнечного света рассеивается земной атмосферой и доходит до Луны в обход Земли. Луна темнеет, приобретая красноватый оттенок (через атмосферу лучше всего проходят красные и оранжевые лучи). На лунном диске при этом отчетливо видна тень от Земли (рис. 6). Круглая форма тени еще раз подтверждает шарообразность Земли. Аристарха же интересовал размер этой тени. Для того, чтобы определить радиус круга земной тени (мы сделаем это по фотографии на рисунке 6), достаточно решить простое упражнение.

Упражнение 4. На плоскости дана дуга окружности. С помощью циркуля и линейки постройте отрезок, равный ее радиусу.

Выполнив построение, находим, что радиус земной тени примерно в раза больше радиуса Луны. Обратимся теперь к рисунку 7. Серым цветом закрашена область земной тени, в которую попадает Луна при затмении. Предположим, что центры окружностей S, Z и L лежат на одной прямой. Проведем диаметр Луны M₁M₂, перпендикулярный прямой LS. Продолжение этого диаметра пересекает общие касательные окружностей Солнца и Земли в точках D₁ и D₂. Тогда отрезок D₁D₂ приближенно равен диаметру тени Земли. Мы пришли к следующей задаче.

Задача 1. Даны три окружности с центрами S, Z и L, лежащими на одной прямой. Отрезок D₁D₂, проходящий через L, перпендикулярен прямой SL, а его концы лежат на общих внешних касательных к первой и второй окружностям. Известно, что отношение отрезка D₁D₂ к диаметру третьей окружности равно t, а отношение диаметров первой и третьей окружности равно ZS/ZL = κ. Найдите отношение диаметров первой и второй окружностей.

Если решить эту задачу, то будет найдено отношение радиусов Солнца и Земли. Значит, будет найден радиус Солнца, а с ним и Луны. Но решить ее не удастся. Можете попробовать — в задаче не достает одного данного. Например, угла между общими внешними касательными к первым двум окружностям. Но даже если этот угол был бы известен, решение будет использовать тригонометрию, которую Аристарх не знал (мы формулируем соответствующую задачу в упражнении 6). Он находит более простой выход. Проведем диаметр A₁A₂ первой окружности и диаметр B₁B₂ второй, оба — параллельные отрезку D₁D₂. Пусть C₁ и С₂ — точки пересечения отрезка D₁D₂ с прямыми A₁B₁ и А₂В₂ соответственно (рис. 8). Тогда в качестве диаметра земной тени возьмем отрезок C₁C₂ вместо отрезка D₁D₂. Стоп, стоп! Что значит, «возьмем один отрезок вместо другого»? Они же не равны! Отрезок C₁C₂ лежит внутри отрезка D₁D₂, значит C₁C₂ < D₁D_2. Да, отрезки разные, но они почти равны. Дело в том, что расстояние от Земли до Солнца во много раз больше диаметра Солнца (примерно в 215 раз). Поэтому расстояние ZS между центрами первой и второй окружности значительно превосходит их диаметры. Значит, угол между общими внешними касательными к этим окружностям близок к нулю (в реальности он примерно 0,5°), т. е. касательные «почти параллельны». Если бы они были в точности параллельны, то точки A₁ и B₁ совпадали бы с точками касания, следовательно, точка C₁ совпала бы с D₁, а C₂ с D₂, и значит, C₁C₂ = D₁D₂. Таким образом, отрезки C₁C₂ и D₁D₂ почти равны. Интуиция и здесь не подвела Аристарха: на самом деле отличие между длинами отрезков составляет менее сотой доли процента! Это — ничто по сравнению с возможными погрешностями измерений. Убрав теперь лишние линии, включая окружности и их общие касательные, приходим к такой задаче.

Задача 1′. На боковых сторонах трапеции А₁А₂С₂С₁ взяты точки B₁ и В₂ так, что отрезок В₁В₂ параллелен основаниям. Пусть S, Z u L — середины отрезков А₁А₂, B₁B₂ и C₁C₂ соответственно. На основании C₁C₂ лежит отрезок М₁М₂ с серединой L. Известно, что и . Найдите А₁А₂/B₁B₂.

Решение. Так как , то , а значит, треугольники A₂SZ и M₁LZ подобны с коэффициентом SZ/LZ = κ. Следовательно, A₂SZ = M₁LZ, и поэтому точка Z лежит на отрезке M₁A₂. Аналогично, Z лежит на отрезке М₂А₁ (рис. 9). Так как C₁C₂ = t·М₁М₂ и , то .

Далее, треугольники A₂C₂M₁ и A₂B₂Z подобны. Их коэффициент подобия равен

Следовательно,

С другой стороны,

Значит, . Из этого равенства сразу получаем, что .

Итак, отношение диаметров Солнца и Земли равно , а Луны и Земли равно .

Подставляя известные нам величины κ = 400 и t = 8/3, получаем, что Луна примерно в 3,66 раза меньше Земли, а Солнце в 109 раз больше Земли. Так как радиус Земли R нам известен, находим радиус Луны R_l = R/3,66 и радиус Солнца R_s = 109R.

Теперь расстояния от Земли до Луны и до Солнца вычисляются в один шаг, это может быть сделано с помощью углового диаметра. Угловой диаметр β Солнца и Луны составляет примерно полградуса (если быть совсем точным, 0,53°). Как древние астрономы его измеряли, об этом речь впереди. Опустив касательную ZQ на окружность Луны, получаем прямоугольный треугольник ZLQ с острым углом β/2 (рис. 10).

Из него находим , что примерно равно 215R_l, или 62R. Аналогично, расстояние до Солнца равно 215R_s  = 23 455R.

Всё. Размеры Солнца и Луны и расстояния до них найдены.

Упражнения
5. Докажите, что прямые A₁B₁, A₂B₂ и две общие внешние касательные к первой и второй окружностям (см. рис. 8) пересекаются в одной точке.
6. Решите задачу 1, если дополнительно известен угол между касательными между первой и второй окружностью.
7. Солнечное затмение может наблюдаться в одних частях земного шара и не наблюдаться других. А лунное затмение?
8. Докажите, что солнечное затмение может наблюдаться только во время новолуния, а лунное затмение — только во время полнолуния.
9. Что происходит на Луне, когда на Земле происходит лунное затмение?

О пользе ошибок

На самом деле всё было несколько сложнее. Геометрия только формировалась, и многие привычные для нас еще с восьмого класса школы вещи были в то время совсем не очевидны. Аристарху потребовалось написать целую книгу, чтобы изложить то, что мы изложили на трех страницах. И с экспериментальными измерениями тоже всё было непросто. Во-первых, Аристарх ошибся с измерением диаметра земной тени во время лунного затмения, получив отношение t = 2 вместо . Кроме того, он, вроде бы, исходил из неверного значения угла β — углового диаметра Солнца, считая его равным 2°. Но эта версия спорная: Архимед в своем трактате «Псаммит» пишет, что, напротив, Аристарх пользовался почти правильным значением в 0,5°. Однако самая ужасная ошибка произошла на первом шаге, при вычислении параметра κ — отношения расстояний от Земли до Солнца и до Луны. Вместо κ = 400 у Аристарха получилось κ = 19. Как можно было ошибиться более чем в 20 раз? Обратимся еще раз к шагу 1, рисунок 3. Для того чтобы найти отношение κ = ZS/ZL, Аристарх измерил угол α = SZL, и тогда κ = 1/cos α. Например, если угол α был бы равен 60°, то мы получили бы κ = 2, и Солнце было бы вдвое дальше от Земли, чем Луна. Но результат измерения оказался неожиданным: угол α получался почти прямым. Это означало, что катет ZS во много раз превосходит ZL. У Аристарха получилось α = 87°, и тогда cos α =1/19  (напомним, что все вычисления у нас — приближенные). Истинное значение угла , и cos α =1/400. Так погрешность измерения менее чем в 3° привела к ошибке в 20 раз! Завершив вычисления, Аристарх приходит к выводу, что радиус Солнца равен 6,5 радиусов Земли (вместо 109).

Ошибки были неизбежны, учитывая несовершенные измерительные приборы того времени. Важнее то, что метод оказался правильным. Вскоре (по историческим меркам, т. е. примерно через 100 лет) выдающийся астроном античности Гиппарх (190 – ок. 120 до н.э.) устранит все неточности и, следуя методу Аристарха, вычислит правильные размеры Солнца и Луны. Возможно, ошибка Аристарха оказалась в конце концов даже полезной. До него господствовало мнение, что Солнце и Луна либо вовсе имеют одинаковые размеры (как и кажется земному наблюдателю), либо отличаются несильно. Даже отличие в 19 раз удивило современников. Поэтому не исключено, что, найди Аристарх правильное отношение κ = 400, в это никто бы не поверил, а может быть, и сам ученый отказался бы от своего метода, сочтя результат несуразным. Известный принцип гласит, что геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах. Перефразируя, можно сказать, что наука в целом — это искусство делать верные выводы из неточных, или даже ошибочных, наблюдений. И Аристарх такой вывод сделал. За 17 веков до Коперника он понял, что в центре мира находится не Земля, а Солнце.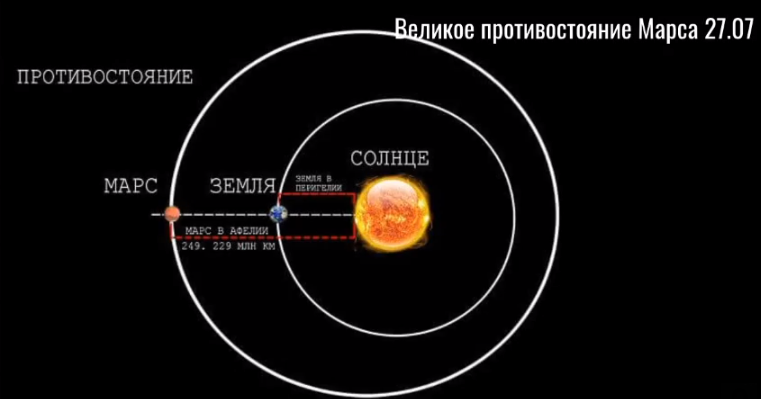 Так впервые появилась гелиоцентрическая модель и понятие Солнечной системы.

Что в центре?

Господствовавшее в Древнем Мире представление об устройстве Вселенной, знакомое нам по урокам истории, заключалось в том, что в центре мира — неподвижная Земля, вокруг нее по круговым орбитам вращаются 7 планет, включая Луну и Солнце (которое тоже считалось планетой). Завершается всё небесной сферой с прикрепленными к ней звездами. Сфера вращается вокруг Земли, делая полный оборот за 24 часа. Со временем в эту модель многократно вносились исправления. Так, стали считать, что небесная сфера неподвижна, а Земля вращается вокруг своей оси. Затем стали исправлять траектории движения планет: круги заменили циклоидами, т. е. линиями, которые описывают точки окружности при ее движении по другой окружности (об этих замечательных линиях можно прочитать в книгах Г. Н. Бермана «Циклоида», А. И. Маркушевича «Замечательные кривые», а также в «Кванте»: статья С. Верова «Тайны циклоиды» №8, 1975, и статья С.  Г. Гиндикина «Звездный век циклоиды», №6, 1985). Циклоиды лучше согласовывались с результатами наблюдений, в частности, объясняли «попятные» движения планет. Это — геоцентрическая система мира, в центре которой — Земля («гея»). Во II веке она приняла окончательный вид в книге «Альмагест» Клавдия Птолемея (87–165), выдающегося греческого астронома, однофамильца египетских царей. Со временем некоторые циклоиды усложнялись, добавлялись всё новые промежуточные окружности. Но в целом система Птолемея господствовала около полутора тысячелетий, до XVI века, до открытий Коперника и Кеплера. Поначалу геоцентрической модели придерживался и Аристарх. Однако, вычислив, что радиус Солнца в 6,5 раз больше радиуса Земли, он задал простой вопрос: почему такое большое Солнце должно вращаться вокруг такой маленькой Земли? Ведь если радиус Солнца больше в 6,5 раз, то его объем больше почти в 275 раз! Значит, в центре мира должно находиться Солнце. Вокруг него вращаются 6 планет, включая Землю.³ А седьмая планета, Луна, вращается вокруг Земли. Так появилась гелиоцентрическая система мира («гелиос» — Солнце). Уже сам Аристарх отмечал, что такая модель лучше объясняет видимое движение планет по круговым орбитам, лучше согласуется с результатами наблюдений. Но ее не приняли ни ученые, ни официальные власти. Аристарх был обвинен в безбожии и подвергся преследованиям. Из всех астрономов античности только Селевк стал сторонником новой модели. Больше ее не принял никто, по крайней мере, у историков нет твердых сведений на этот счет. Даже Архимед и Гиппарх, почитавшие Аристарха и развившие многие его идеи, не решились поставить Солнце в центр мира. Почему?

Почему мир не принял гелиоцентрической системы?

Как же получилось, что в течение 17 веков ученые не принимали простой и логичной системы мира, предложенной Аристархом? И это несмотря на то, что официально признанная геоцентрическая система Птолемея часто давала сбои, не согласуясь с результатами наблюдений за планетами и за звездами. Приходилось добавлять всё новые окружности (так называемые вложенные циклы) для «правильного» описания движения планет. Самого Птолемея трудности не пугали, он писал: «К чему удивляться сложному движению небесных тел, если их сущность нам неизвестна?» Однако уже к XIII веку этих окружностей накопилось 75! Модель стала столь громоздкой, что начали раздаваться осторожные возражения: неужели мир в самом деле устроен так сложно? Широко известен случай с Альфонсом X (1226–1284), королем Кастилии и Леона, государства, занимавшего часть современной Испании. Он, покровитель наук и искусств, собравший при своем дворе пятьдесят лучших астрономов мира, на одной из научных бесед обмолвился, что «если бы при сотворении мира Господь оказал мне честь и спросил моего совета, многое было бы устроено проще». Подобная дерзость не прощалась даже королям: Альфонс был низложен и отправлен в монастырь.⁴ Но сомнения остались. Часть из них можно было бы разрешить, поставив Солнце в центр Вселенной и приняв систему Аристарха. Его труды были хорошо известны. Однако еще много веков никто из ученых не решался на такой шаг. Причины были не только в страхе перед властями и официальной церковью, которая считала теорию Птолемея единственно верной. И не только в инертности человеческого мышления: не так-то просто признать, что наша Земля — не центр мира, а лишь рядовая планета. Все-таки для настоящего ученого ни страх, ни стереотипы — не препятствия на пути к истине. Гелиоцентрическая система отвергалась по вполне научным, можно даже сказать, геометрическим причинам. Если допустить, что Земля вращается вокруг Солнца, то ее траектория — окружность с радиусом, равным расстоянию от Земли до Солнца. Как мы знаем, это расстояние равно 23 455 радиусов Земли, т. е. более 150 миллионов километров. Значит, Земля в течение полугода перемещается на 300 миллионов километров. Гигантская величина! Но картина звездного неба для земного наблюдателя при этом остается такой же. Земля то приближается, то удаляется от звезд на 300 миллионов километров, но ни видимые расстояния между звездами (например, форма созвездий), ни их яркость не меняются.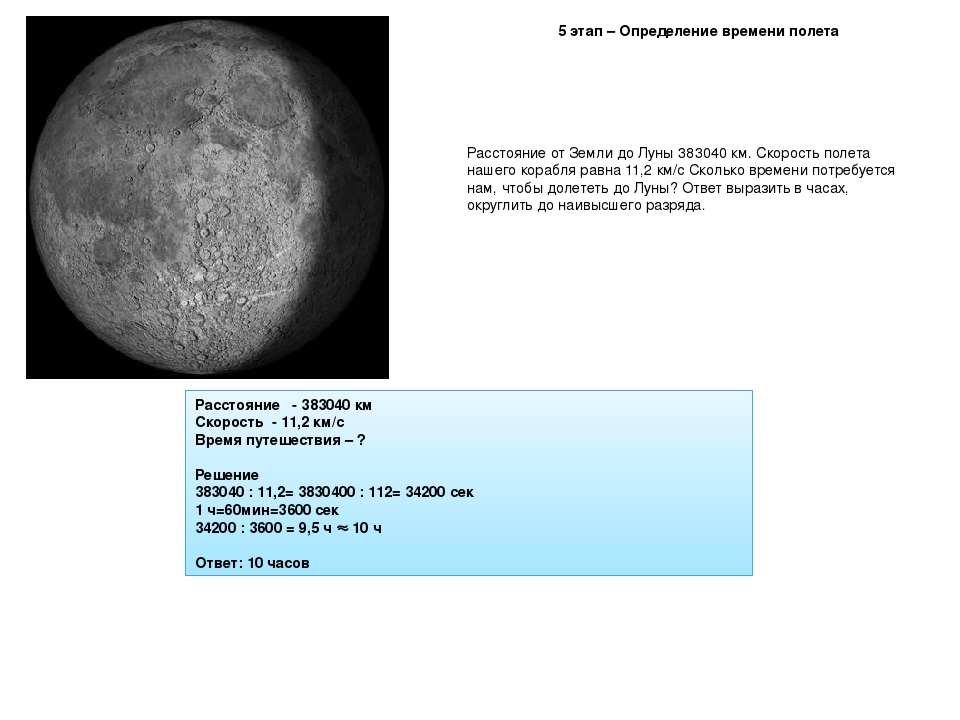 Это означает, что расстояния до звезд должны быть еще в несколько тысяч раз больше, т. е. небесная сфера должна иметь совершенно невообразимые размеры! Это, между прочим, осознавал и сам Аристарх, который писал в своей книге: «Объем сферы неподвижных звезд во столько раз больше объема сферы с радиусом Земля-Солнце, во сколько раз объем последней больше объема земного шара», т. е. по Аристарху выходило, что расстояние до звезд равно (23 455)²R, это более 3,5 триллионов километров. В реальности расстояние от Солнца до ближайшей звезды еще примерно в 11 раз больше. (В модели, которую мы представили в самом начале, когда расстояние от Земли до Солнца равно 10 м, расстояние до ближайшей звезды равно … 2700 километров!) Вместо компактного и уютного мира, в центре которого находится Земля и который помещается внутри относительно небольшой небесной сферы, Аристарх нарисовал бездну. И эта бездна испугала всех.

Венера, Меркурий и невозможность геоцентрической системы

Между тем невозможность геоцентрической системы мира, с круговыми движениями всех планет вокруг Земли, может быть установлена с помощью простой геометрической задачи.

Задача 2. На плоскости даны две окружности с общим центром О, по ним равномерно движутся две точки: точка М по одной окружности и точка V по другой. Докажите, что либо они двигаются в одном направлении с одинаковой угловой скоростью, либо в некоторый момент времени угол MOV тупой.

Решение. Если точки движутся в одном направлении с разными скоростями, то через некоторое время лучи ОМ и OV окажутся сонаправленными. Далее угол MOV начинает монотонно возрастать до следующего совпадения, т. е. до 360°. Следовательно, в некоторый момент он равен 180°. Случай, когда точки движутся в разных направлениях, рассматривается так же.

Теорема. Ситуация, при которой все планеты Солнечной системы равномерно вращаются вокруг Земли по круговым орбитам, невозможна.

Доказательство. Пусть О — центр Земли, М — центр Меркурия, а V — центр Венеры. Согласно многолетним наблюдениям, у Меркурия и Венеры разные периоды обращения, а угол MOV никогда не превосходит 76°. В силу результата задачи 2 теорема доказана.

Конечно, древние греки неоднократно встречались с подобными парадоксами. Именно поэтому, чтобы спасти геоцентрическую модель мира, они заставили планеты двигаться не по окружностям, а по циклоидам.

Доказательство теоремы не совсем честно, поскольку Меркурий и Венера вращаются не в одной плоскости, как в задаче 2, а в разных. Хотя плоскости их орбит почти совпадают: угол между ними — всего несколько градусов. В упражнении 10 мы предлагаем вам устранить этот недостаток и решить аналог задачи 2 для точек, вращающихся в разных плоскостях. Другое возражение: может быть, угол MOV бывает тупым, но мы этого не видим, поскольку на Земле в это время день? Принимаем и это. В упражнении 11 нужно доказать, что для трех вращающихся радиусов всегда настанет момент времени, когда они будут образовывать друг с другом тупые углы. Если на концах радиусов — Меркурий, Венера и Солнце, то в этот момент времени Меркурий и Венера будут видны на небе, а Солнце — нет, т. е. на земле будет ночь. Но должны предупредить: упражнения 10 и 11 значительно сложнее задачи 2. Наконец, в упражнении 12 мы предлагаем вам, ни много ни мало, вычислить расстояние от Венеры до Солнца и от Меркурия до Солнца (они, конечно, вращаются вокруг Солнца, а не вокруг Земли). Убедитесь сами, насколько это просто, после того, как мы узнали метод Аристарха.

Упражнения
10. В пространстве даны две окружности с общим центром О, по ним равномерно с разными угловыми скоростями движутся две точки: точка М по одной окружности и точка V по другой. Докажите, что в некоторый момент угол MOV тупой.
11. На плоскости даны три окружности с общим центром О, по ним равномерно с разными угловыми скоростями движутся три точки. Докажите, что в некоторый момент все три угла между лучами с вершиной О, направленными в данные точки, тупые.
12. Известно, что максимальное угловое расстояние между Венерой и Солнцем, т. е. максимальный угол между лучами, направленными с Земли к центрам Венеры и Солнца, равно 48°. Найдите радиус орбиты Венеры. То же — для Меркурия, если известно, что максимальное угловое расстояние между Меркурием и Солнцем равно 28°.

Последний штрих: измерение угловых размеров Солнца и Луны

Следуя шаг за шагом рассуждениям Аристарха, мы упустили лишь один аспект: как измерялся угловой диаметр Солнца? Сам Аристарх этого не делал, пользуясь измерениями других астрономов (по-видимому, не совсем верными). Напомним, что радиусы Солнца и Луны он смог вычислить, не привлекая их угловые диаметры. Посмотрите еще раз на шаги 1, 2 и 3: нигде значение углового диаметра не используется! Он нужен только для вычисления расстояний до Солнца и до Луны. Попытка определить угловой размер «на глазок» успеха не приносит. Если попросить несколько человек оценить угловой диаметр Луны, большинство назовут угол от 3 до 5 градусов, что в разы больше истинного значения. Сказывается обман зрения: ярко-белая Луна на фоне темного неба кажется массивной. Первым, кто провел математически строгое измерение углового диаметра Солнца и Луны, был Архимед (287— 212до н.э.) Он изложил свой метод в книге «Псаммит» («Исчисление песчинок»). Сложность задачи он осознавал: «Получить точное значение этого угла — дело нелегкое, потому что ни глаз, ни руки, ни приборы, при помощи которых производится отсчет, не обеспечивают достаточной точности». Поэтому Архимед не берется вычислить точное значение углового диаметра Солнца, он лишь оценивает его сверху и снизу. Он помещает круглый цилиндр на конце длинной линейки, напротив глаза наблюдателя. Линейка направляется на Солнце, и цилиндр придвигается к глазу до тех пор, пока он не заслонит собой Солнце полностью. Затем наблюдатель уходит, а на конце линейки отмечается отрезок MN, равный размеру человеческого зрачка (рис. 11).

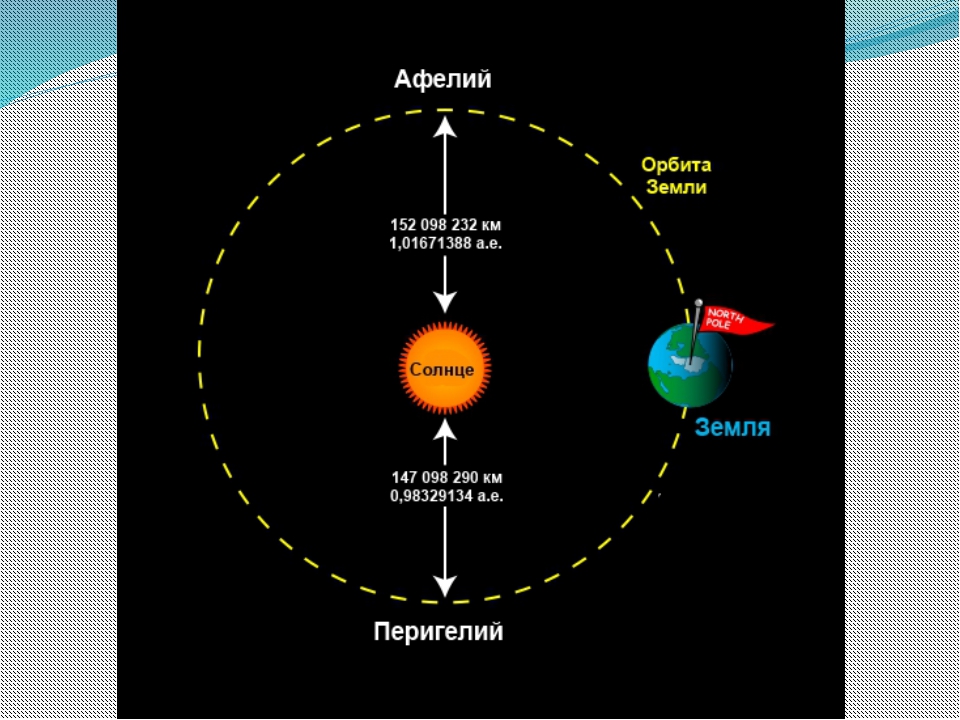Тогда угол α₁ между прямыми МР и NQ меньше углового диаметра Солнца, а угол α₂ = POQ — больше. Мы обозначили через PQ диаметр основания цилиндра, а через О — середину отрезка MN. Итак, α_1 2 (докажите это в упражнении 13). Так Архимед находит, что угловой диаметр Солнца заключен в пределах от 0,45° до 0,55°.

Неясным остается, почему Архимед измеряет Солнце, а не Луну. Он был хорошо знаком с книгой Аристарха и знал, что угловые диаметры Солнца и Луны одинаковы. Луну же измерять гораздо удобнее: она не слепит глаза и границы ее видны отчетливее.

Некоторые древние астрономы измеряли угловой диаметр Солнца, исходя из продолжительности солнечного или лунного затмения. (Попробуйте восстановить этот способ в упражнении 14.) А можно сделать то же, не дожидаясь затмений, а просто наблюдая закат Солнца. Выберем для этого день весеннего равноденствия 22 марта, когда Солнце восходит точно на востоке, а заходит точно на западе. Это означает, что точки восхода Е и заката W диаметрально противоположны. Для земного наблюдателя Солнце движется по окружности с диаметром EW. Плоскость этой окружности составляет с плоскостью горизонта угол 90° – γ, где γ — географическая широта точки М, в которой находится наблюдатель (например, для Москвы γ = 55,5°, для Александрии γ = 31°). Доказательство приведено на рисунке 12. Прямая ZP — ось вращения Земли, перпендикулярная плоскости экватора. Широта точки М — угол между отрезком ZP и плоскостью экватора. Проведем через центр Солнца S плоскость α, перпендикулярную оси ZP.

Плоскость горизонта касается земного шара в точке М. Для наблюдателя, находящегося в точке М, Солнце в течение дня движется по окружности в плоскости α с центром Р и радиусом PS. Угол между плоскостью α и плоскостью горизонта равен углу MZP, который равен 90° – γ, поскольку плоскость α перпендикулярна ZP, а плоскость горизонта перпендикулярна ZM. Итак, в день равноденствия Солнце заходит за горизонт под углом 90° – γ. Следовательно, во время заката оно проходит дугу окружности, равную β/cos γ, где β — угловой диаметр Солнца (рис. 13). С другой стороны, за 24 часа оно проходит по этой окружности полный оборот, т. е. 360°.

Получаем пропорцию где Т — продолжительность заката (единица измерения — час). Зная γ и измерив время Т, находим β = 0,53°.

Упражнения
13. Докажите, что угол α₁ между прямыми МР и NQ (см. рис. 11) меньше углового диаметра Солнца, а угол α₂ = POQ — больше.
14. Предложите способ измерения угловых размеров Луны во время лунного затмения.

С автором статьи можно связаться по адресу: [email protected].

---

¹ В некоторых источниках сообщается легенда о том, что одним из них был друг Эратосфена — великий Архимед.
² Неизвестно, знал ли Аристарх об измерении Эратосфена или пользовался другим значением радиуса Земли. Это не так важно, поскольку он брал радиус Земли в качестве единицы длины.
³ Именно шесть, а не девять, поскольку Уран, Нептун и Плутон были открыты гораздо позже. Совсем недавно, 13 сентября 2006 года, по решению Международного астрономического союза (IAU) Плутон лишился статуса планеты. Так что планет в Солнечной системе теперь восемь.
⁴ Истинной причиной опалы короля Альфонса была, видимо, обычная борьба за власть, но его ироничное замечание об устройстве мира послужило веским поводом для его недругов.

Как измерили расстояние до Солнца / Хабр

Сегодня, когда астрономию вернули в школьную программу, любой старшеклассник (ну, в теории, любой) должен знать: расстояние от нашей планеты до Солнца составляет примерно 149,5 млн километров. Это расстояние еще принято называть астрономической единицей.
Но, понятно, что этот ответ как-то надо было получить и астрономам потребовалось на это несколько шагов, растянувшихся не одно тысячелетие.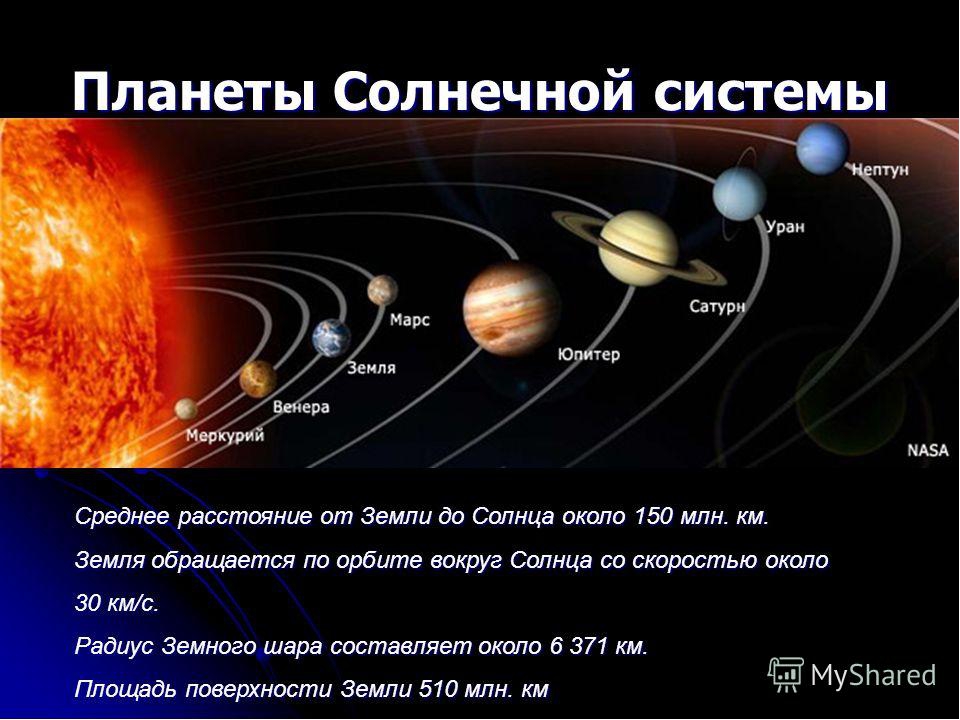 Ниже — о каждом шаге подробнее.

Шаг первый – безбожник Аристарх и Луна

Аристарх Самосский жил в III веке до нашей эры и был по-настоящему выдающимся астрономом. Задолго до Коперника он построил гелиоцентрическую модель устройства мира. Довольно точно определил продолжительность года в 365 + (1/4) + (1/1623) дней. Усовершенствовал солнечные часы. А еще он предпринял попытку измерить расстояние от Земли до Солнца и Луны. Этому Аристарх посвятил целый трактат (кстати, единственная письменная работа этого автора, дошедшая до нас).

С Луной у него получилось довольно близко к правильному ответу: 486400 км (по расчетам Аристарха), 380000 км (среднее расстояние по современным данным). Спустя сто лет другой античный астроном Гиппарх, кстати, уточнил эти цифры. А вот с Солнцем у Аристарха получилась нехилая промашка.

Но сначала о том, как вообще древнегреческий астроном измерял это расстояние. Известно, что иногда Солнце и Луну можно наблюдать одновременно. Причем, бывают моменты, когда Солнце освещает ровно половину Луны. Тогда угол «Земля-Луна-Солнце» — прямой, и измеряя угол «Луна-Земля-Солнце» можно с помощью тригонометрических соотношений, зная расстояние Земля-Луна, найти расстояние Земля-Солнце.

Но «гладко было на бумаге». Во-первых, Аристарху надо было поймать момент, когда освещена ровно половина Луны, а сделать это без телескопа было практически невозможно. А во-вторых, опять же без серьезной измерительной аппаратуры, точно измерить все параметры. Не удивительно, что грек ошибся, причем, очень сильно: угол α у него получился целых три градуса (в реальности он равен 10 минутам), а расстояние до Солнца всего 7,5 млн километров. Опираясь на это расстояние, Аристарх пришел к выводу, что Солнце намного больше Земли. Это и стало главным аргументом его гелиоцентризма (в центре мироздания должен быть самый большой объект).

Впрочем, ошибка в определении расстояния большой роли в науке не сыграла, вычисления Аристарха вообще не получили широкой известности (даже среди образованной части населения античных городов). Причина была скорее политической, все дело в его гелиоцентрической модели мироздания. Она противоречила геоцентрической модели, которой придерживался тогдашний научный консенсус. И есть упоминания, что его даже пытались привлечь к суду как безбожника. Спустя некоторое время сначала Гиппарх подверг критике его взгляды, а позже Птолемей (чья геоцентрическая модель успешно дожила до Коперника) и вовсе проигнорировал результаты Аристарха, способствуя их забвению на долгое время.

Шаг второй — смотрим на Венеру (Кеплер и Хоррокс)

Человечеству потребовалось почти две тысячи лет, чтобы сделать этот следующий шаг к ответу, но будем справедливы, это было нелегкое время и хватало других проблем.

И для начала, надо было выбрать другой объект, на который опираться в своих вычислениях. В 1626 году известный немецкий астроном и математик Иоганн Кеплер предложил в качестве кандидата Венеру. К тому времени астрономы уже знали про одно довольно редкое астрономическое явление – прохождение Венеры по диску Солнца, причем, оно случается дважды с разницей в несколько лет, а потом следует значительный перерыв. Предложенный Кеплером метод заключался в следующем: надо измерить время прохождения Венеры по диску Солнца из разных точек Земли. И сравнивая эти времена можно найти расстояние от Земли до Венеры и до Солнца.

Впрочем, это только звучит просто. Как минимум, надо было дождаться этого явления. Это удалось британскому астроному Джереми Хороксу, который переписывался с Кеплером и знал про его метод. Сначала британец уточнил частоту этого явления: «дубль» случается с разницей в восемь лет каждые полтора столетия. И ближайшее должно было состояться в 1639 году. Хоррокс подготовился к этому событию, он наблюдал за небом из своего дома в Мач Хул, близ Престона, а его друг делал то же самое из Солфорда, близ Манчестера. Сначала, казалось, что удача от них отвернулась, поскольку в этот день была сильная облачность, но за полчаса до захода Солнца облака разошлись и пара астрономов сумела-таки осуществить свой план. На основании наблюдений, Хоррокс рассчитал, что нашу планету от Солнца отделяет 95,6 млн км. Это было уже гораздо ближе к истине, но все равно неверно.

Шаг третий – смотрим на Марс (Кассини)

До следующего венерианского «дубля» надо было ждать полтора века и пока шло время астрономы тратили его на поиск других способов вычислить искомое расстояние. И это удалось французскому астроному итальянского происхождения Джованни Доменико Кассини. Он вообще отметился в астрономии как талантливый наблюдатель (например, это он первым увидел Большое Красное пятно на Юпитере). К тому времени астрономы уже оценили возможности, которые дает одновременное наблюдение за одним и тем же объектом из отдаленных друг от друга мест. В 1672 году Кассини на пару с другим французским астрономом Жаном Рише осуществили такой проект: первый остался в Париже, а второй отправился в Южную Африку, где у Франции были свои колонии. Они одновременно наблюдали Марс и, вычислив параллакс, определили его расстояние от Земли. Параллакс, если кто не знает, это смещение или разница в видимом положении объекта, рассматриваемого на двух разных линиях зрения. Ну а вычислять расстояние до объекта по параллаксу умели уже давно.

И поскольку относительные отношения различных расстояний между Солнцем и планетами уже были известны из геометрии, рассчитав по параллаксу расстояние до Марса, Кассини смог сделать то же самое и для Солнца. Его результат — 146 млн км – был уже очень близок к современным оценкам. Что интересно, в то время, когда Кассини проводил эти расчеты, он был приверженцем геоцентрической системы, то есть, расстояния он получал близкие к верным, но карту Солнечной системы строил по старинке, с Землей в центре. Позже он признал правоту Коперника, но в ограниченной степени.

Шаг четвертый – снова Венера и астрономы всего мира

Тем временем близился очередной венерианский «дубль» (в 1761 и 1769 годах) и астрономы были намерены выжать из этого события максимум. Чтобы не зависеть от погодных условий и собрать данные с разных точек на Земле, был организован большой международный проект (его считают чуть ли не первым в истории) под эгидой Французской академии наук. Заблаговременно были подготовлены и отправлены научные экспедиции к местам наблюдений. Не все закончилось гладко – экспедиция, отправленная в Новую Гвинею, без вести пропала в джунглях.

Но в целом проект удался.

Кстати, активно в нем участвовала и Россия. В нашей стране им руководил человек необычайных талантов и энергии – Михайло Ломоносов (это он, кстати, обнаружил атмосферу на Венере).

Ломоносову удалось получить аудиенцию у императрицы Екатерины II и убедить ее в важности этой работы как для науки, так и для государственного престижа. Получив поддержку казны, Ломоносов смог развернуть на территории Российской империи 40 наблюдательных пунктов. На один из них, вблизи Петербурга, приезжала сама Екатерина и с интересом смотрела в телескоп.
Вот в итоге этой большой работы астрономов по всему миру и было получено то число, которое сегодня включено в учебники. Но нет предела совершенству, и еще через сто пятьдесят лет, 8 декабря 1874 года и 6 декабря 1882 года, очередные прохождения Венеры по диску Солнца вновь наблюдали научные экспедиции по всему миру, уточняя полученные данные. А потом еще раз в 2004 и 2012 году. Впрочем, в ходе этих наблюдений получали и другие полезные данные, но это уже другая тема.

Марса размером с Луну не будет — Российская газета

Ночью 27 августа 2014 года в небе можно будет наблюдать появление сразу двух лун — нашего естественного спутника и Марса, сообщили некоторые СМИ. Причем Красная планета, приблизившись к Земле, будет выглядеть якобы такой же большой, как Луна. Для подогрева интереса в Интернете даже появились фотографии с двумя лунами.

Однако новость о Марсе размером с Луну на самом деле не соответствуют действительности, указывают профессиональные астрономы. Так, директор астрономической обсерватории ИГУ Сергей Язев на своей странице в Facebook заявил: «Дикое сообщение о том, что Марс будет на небе, как Луна — это невежественный фейк, как сейчас принято говорить о фальсификациях в интернете».

По его словам, сейчас планеты расходятся, и 27 августа расстояние между Землей и Марсом составит более 200 млн километров. В этот момент Земля подойдет ближе всего к перигелию орбиты Марса, однако Марса в этой точке не окажется. «Для того чтобы планеты оказались близко друг к другу, надо же, чтобы и Марс находился в точке перигелия своей орбиты в тот же самый момент! А это бывает нечасто», — указывает ученый.

Максимальное сближение Марса и Земли называют противостоянием. Оно происходит примерно раз в два года. Великие противостояния, когда дистанция между планетами уменьшается примерно до 55 — 56 млн километров, случаются раз в 15- 17 лет. Причем и в эти моменты Марс виден всего лишь как яркая оранжевая звезда. Последнее противостояние произошло в апреле этого года — тогда Марс был удален от нас более чем на 90 млн километров.

В августе 2003 года произошло одно из великих противостояний планет — в тот момент расстояние между ними уменьшилось до 55 млн километров.

«Кто-то из популяризаторов писал, что в это время Марс в телескоп с 75-кратным увеличением был виден на небе как Луна  невооруженным глазом. Повторяю: Марс как Луна, но только Луна без телескопа, а Марс в телескоп, да еще и с сильным увеличением. Тот, кто запустил фейк, видимо, решил, что ситуация всегда повторяется 27 августа. При этом почему-то забыл упомянуть про телескоп», — пишет Язев.

Очередное великое противостояние ожидается в июле 2018 года. «Тогда расстояние будет 57 с половиной млн километров, а не 200 млн, как сейчас. Вот тогда и посмотрим в телескоп», — заметил астроном.

Модель Солнечной системы — Oficiální stránky obce Hýsly

Модель Солнечной системы

Солнечной системой называется система планет вращающихся вокруг звезды Солнца. Среди этих планет — и наша Земля. Солнечная Система состоит из солнца и небесных тел удерживаемых солнечным притяжением. Масса солнца примерно в 330 000 раз превышает земную массу и составляет 99.8% массы всей солнечной системы. Диаметр солнца — порядка 1 400 000 км, т. е. примерно 109 диаметров Земли. В солнечную систему кроме солнца также входят восемь планет, более 150 лун и множество малых тел — таких как астероиды, кометы и метеоры.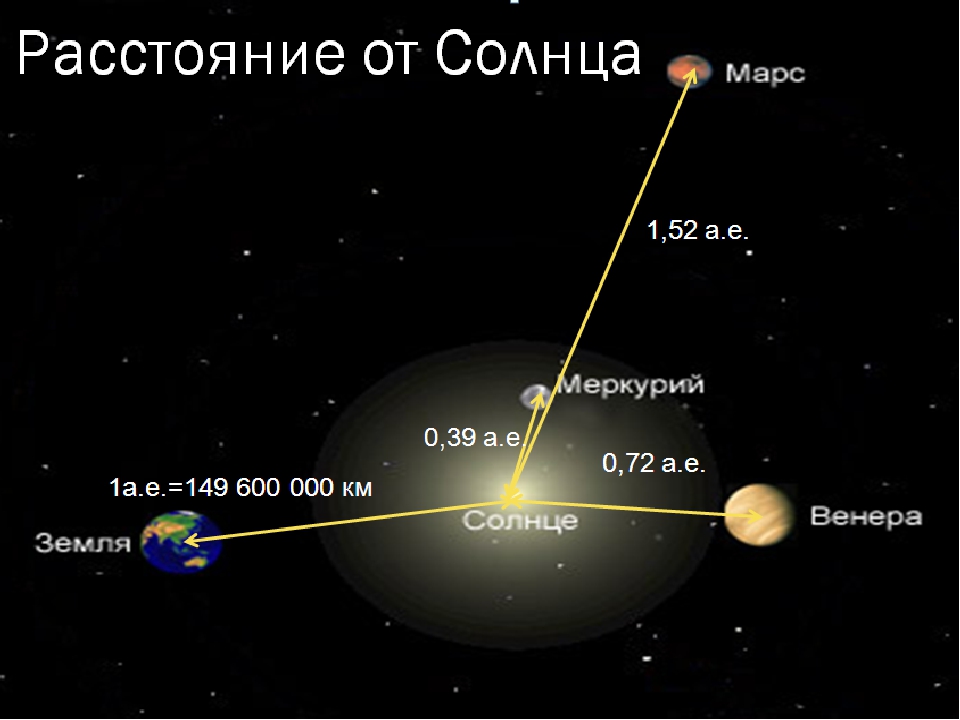

По порядку близости к Солнцу, восемь планет солнечной системы это Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран и Нептун.

Для измерения расстояний в солнечной системе используется «астрономическая единица» (АЕ). Одна АЕ соответствует расстоянию от Земли до Солнца. Таким образом, расстояние в одну АЕ — это почти 150 миллионов километров. Например, Юпитер вращается на орбите 5.2 АЕ — то есть на расстоянии от Солнца в 5.2 раза большем чем Земля.

Планеты в солнечной системе иногда делят на две группы. В первую включают четыре планеты земного типа (внутренние планеты), а во вторую — четыре газовых гиганта (внешние планеты). Четыре внутренние планеты состоят из плотных, каменистых материалов. Газовые гиганты в основном состоят из водорода, гелия, воды, аммиака и метана и не имеют твердой поверхности.

Планеты земного типа

Меркурий — наименьшая по размеру из восьми планет, и также ближайшая к солнцу. Поверхность Меркурия в целом напоминает поверхность нашей Луны. Меркурий усеян кратерами и не имеет ни естественных спутников ни существенной атмосферы. Температура на его поверхности весьма различна в дневное и в ночное время. Орбита Меркурия составляет 0.387 АЕ, его диаметр — примерно треть от Земного (точнее, 0.38 земного), орбитальный период — 0.24 земного года.

Венера близка по размеру, силе притяжения и минералогическому составу к Земле. Однако условия на венерианской поверхности радикально отличаются от земных. Это самая горячая планета. Температура ее поверхности достигает 400 градусов по Цельсию, видимо из-за насыщенности углекислым газом. Венера вращается вокруг Солнца на среднем расстоянии около 0.72 АЕ; ее диаметр — 0.95 от земного. Венерианский год составляет 0.615 от земного года.

Земля — самая большая и плотная из четыре внутренних планет. Земля вращается вокруг Солнца на расстоянии 1АЕ = 150 млн. км. Диаметр Земли — около 12700км, а орбитальный период равен, естественно, одному земному году. У земли есть один естественный спутник — Луна, единственный большой спутник у планет земного типа в с. системе. Среднее расстояние от центра Земли к центру Луны равно 380 000км = 0.0026АЕ, то Луна примерно в 400 раз ближе к Земле чем Солнце. Это самый крупный спутник во всей с. системе относительно к размеру планеты вокруг которой он вращается. Диаметр Луны — 3476км, т.е. чуть больше четверти земного (0.273). Луна совершает полный круг вокруг Земли за 29.5 дней (примерно за месяц).

Марс — после Меркурия самая малая планета солнечной системы. У Марса есть две луны, Фобос (диаметр 22км) и Деймос (диаметр 12.6км) — маленькие и неправильной формы. Атмосфера Марса состоит в основном из углекислого газа со следами водяных паров. Среди всех планет, климатические сезоны на Марсе более всего напоминают земные. Большее удаление Марса от Солнца объясняет пониженные температуры на его поверхности. В среднем они колеблются около -30C, но днем могут подниматься до 15C. На Марсе, как и на Земле, есть полярные ледники, но там они состоят частично из воды, а частично из углекислого газа. Эти ледники можно наблюдать в телескоп, где они видны как белые пятна.

Газовые гиганты.

Юпитер это самая большая планета солнечной системы. Он состоит в основном из водорода и гелия. Юпитер состоит в основном из водорода с малой примесью гелия. Возможно, у него есть также каменистое ядро из более тяжелых элементов под большим давлением. Юпитер окружен неплотной системой планетарных колец. У Юпитера более 60 спутников, включая четыре большие Галлилеевы луны, открытые Галлилео Галлилеем в 1610 году. Ио обрашается на расстоянии 3643 км от Юпитера, Европа — 3122 км, Ганимед 5262 км и Каллисто — 4821 км. Среднее расстояние между Юпитером и Солнцем в 5.2 раза больше земного (5.2АЕ)и его орбитальный период составляет 11.86 земного года. Диаметр Юпитера в 11.2 раза больше земного.

Сатурн — вторая по величине планета солнечной системы. Сатурн известен своей системой колец, которые превратили его в наиболее визуально примечательный объект солнечной системы. Кольца состоят в основном из частиц льда, а также осколков минералов и пыли. Диаметр кольца более 420000 км, но толщина его всего несколько сотен метров. У Сатурна множество спутников. Известно 60, но число это растет по мере совершенствования телескопов. Титан — наибольшая луна Сатурна, его диаметре 5150 км. Другие крупные луны — Мимас, Енцеладус, Тетис, Диона, Реа, Иапетус. Среднее расстояние между Сатурном и Солнцем — 9.53 АЕ; диаметр его в 9,45 раз больше земного и сатурнианский год в 29.65 раза больше земного.

Уран — третья по величине планета солнечной системы. Атмосфера Урана содержит в основном, подобно Юпитеру и Сатурну, водород (83%) и гелий (15%), но также и воду, аммиак и метан. Уран также имеет неплотную систему планетарных колец, состоящих из частиц и осколков размером до 10 метров. У Урана открыто 27 спутников. Пять основных это Миранда, Ариель, Умбриель, Оберон и Титаниа. Среднее расстояние от Урана до Солнца около 19,2 АЕ. Его диаметр в 4 раза больше земного, а период обращения вокруг Солнца равен 84. 1 земному году.

Нептун — восьмая и наиболее удаленная от Солнца планета солнечной системы. Диаметр и химический состав Нептун весьма напоминают Уран. В отличие от Урана, атмосфера Нептуна характеризуется частыми мощными штормами. У Нептуна также есть неплотная и фрагментированная системе колец, что было подтверждено при пролете аппарата Вояджер 2. У Нептуна известно 13 спутников. Самый крупный из них, Тритон, является также самым холодным телом известным сегодня в солнечной системе. Температура его поверхности равна -228 C. Среднее расстояние от Нептуна до солнца — 30.0 АЕ, его диаметр в 4 раза больше земного и период обращения вокруг Солнца составляет 164.9 земных лет.

Марс такой же БОЛЬШОЙ, как Лунная мистификация

Эта тема вызывает сожаление у астрономов с 2003 года, когда она впервые появилась в электронных письмах и в социальных сетях. С тех пор мы видели множество любительских и профессиональных астрономических веб-сайтов, пытающихся бороться с этим продолжающимся бедствием городских легенд. А поскольку мы являемся астрономами-любителями, то каждый год в августе мы неизменно получаем уведомления и электронные письма с вопросами об этом «единственном в жизни событии»? Это наша попытка сообщить людям факты.

---

Электронная почта (или сообщение):

Правда:

1. Марс не такой большой, как Луна на небе.


2. Марс никогда не может быть таким большим, как Луна в небе.


3. Вам понадобится приличный телескоп, чтобы даже увидеть Марс в виде диска, а не маленького оранжевого светового шара.


4. Если Марс выглядел таким большим, как Луна, нас ждал целый ряд неприятностей.


5. Марс сейчас даже не приближается к Земле по своей орбите.Мы приближались к нему, как машина на внутренней трассе на гоночной трассе, но это будет январь 2010 года, пока мы не приблизимся. Даже тогда это будет за десятки миллионов миль.

Проблема:
Упоминаемая дата «27 августа» на самом деле 27 августа 2003 .

Еще в 2003 году Марс в ту ночь исторически «близко» прошел мимо Земли (35 миллионов миль или 56 миллионов км). Это был исторически близкий перевал и самый близкий за последние 50 000 лет! Но даже тогда невооруженным глазом Марс казался не более чем чрезвычайно яркой желтовато-оранжевой звездой, совсем не похожей на «Полнолуние», как утверждается.

С точки зрения реальных размеров Марс (примерно 4213 миль или 6780 км в диаметре) всего примерно в два раза больше нашей Луны (примерно 2160 миль или 3475 км). Но из-за большого расстояния между Марсом и Землей, с нашей точки зрения, визуальная перспектива никогда не позволила бы Марсу казаться хоть сколько-нибудь крупным, как Луна на нашем небе.

Фактическое расстояние от Земли до Луны — в масштабе

Среднее расстояние от Луны до Земли составляет 238 000 миль (382 900 км).А Марс примерно в два раза больше Луны. Таким образом, чтобы Марс выглядел таким же большим, как Луна от Земли, он должен быть примерно вдвое больше Луны, или примерно 476 000 миль (766 000 км).

Этого никогда не будет! (прокрутите вправо)

Кроме того, если бы Марс находился на расстоянии всего в два раза дальше от Земли, чем Луна, гравитационное влияние Марса создало бы ужасающие приливные катастрофы и погоду. Подобно тому, как Луна создает приливы, которые влияют на нашу погоду, приливы из-за столь близкой гравитации Марса могут создать хаос и глобальный погодный хаос.

Фактическое расстояние Марса от Земли в среднем составляет примерно 140 миллионов миль (225 миллионов км). Это МИЛЛИОНЫ миль (километров)! Или примерно в 102 раза дальше, чем Луна!

Эксперимент:
Возьмите полдоллара США (Марс) и поместите его на расстоянии около 20 футов (попросите друга подержать его или установить на что-нибудь, чтобы вы могли его видеть). Затем возьмите 10 центов США (Луна) и держите на расстоянии вытянутой руки. Когда полдоллара находится всего в 20 футах, а десять центов — на расстоянии вытянутой руки, закройте один глаз и посмотрите вниз по руке туда, где вы можете увидеть обе монеты в одном поле зрения. Вы увидите, что полдоллара, который примерно в два раза больше десятицентовика, теперь на самом деле выглядит меньше, чем десять центов.

Теперь, если бы мы ДЕЙСТВИТЕЛЬНО собирались быть точными в этой шкале (десять центов и полдоллара), вам нужно было бы разместить десятицентовую монету в 9 футах от вас (расстояние Земля-Луна), а полдоллара на расстоянии 1877 футов (примерно 1/3 мили). ) вдали, чтобы представить приблизительные расстояния между Землей, Луной и Марсом. Дайм все еще виден с девяти футов, но полдоллара будет трудно увидеть невооруженным глазом.Вот почему электронная почта Mars фактически неточна. Точно так же, как все большие объекты кажутся меньше, чем дальше они находятся; объекты меньшего размера также выглядят больше, чем ближе они к зрителю. Это называется перспектива.

Заявление в письме было вырвано из контекста его фактического происхождения. То, что опущено во фразе, будет выглядеть таким же большим, как полная луна, если вы смотрите в телескоп с увеличением как минимум 75X.

И даже при этом следует отметить, что при просмотре в телескоп с увеличением как минимум 75х он будет размером с полную луну невооруженным глазом.

ФАКТИЧЕСКОЕ ИЗОБРАЖЕНИЕ ТЕЛЕСКОПА: Марс и Луна вместе
(Обратите внимание на разницу в размерах между ними. Луна кажется намного больше, потому что она намного ближе к нам, чем Марс). МАРС С ОБНАРУЖЕННЫМ ГЛАЗОМ

ЛОЖЬ	ИСТИНА (в лучшем случае)

Этот обман / дезинформация неоднократно подтверждалась ошибкой на различных астрономических веб-сайтах и ​​может быть найдена со ссылками в таких местах, как:

• SNOPES.com (http://www.snopes.com/science/astronomy/brightmars.asp)
• Википедия (http://en.wikipedia.org/wiki/Mars_hoax)
• НАСА (http://science.nasa.gov/science-news/science-at-nasa/2005/07jul_marshoax/)
• Вселенная сегодня (http://www. universetoday.com/11448/will-the-mars-look-as-big-as-the-moon-on-august-27-nope/)

Земля — ​​Марс — Сравнение Луны

Земля — ​​Марс — Сравнение Луны

	Земля	Марс	Luna (Луна)
Масса	5.98 x 10 24 кг	6,42 x 10 23 кг	7,35 x 10 22 кг
Сравнительная масса	1,00	0,107	0,0123
Диаметр	12756 км	6787 км	3476 км
Скорость убегания	4,03 x 10 4 км / ч	1. 80 x 10 4 км / ч	8,57 x 10 3 км / ч
Среднее расстояние от Солнца	1 AU (1.496 x 10 8 км)	1,524 AU (2,280 x 10 8 км)	3,84 x 10 5 км (от Земли)
Период вращения	23,93 ч.	24,66 ч.	27,32 сут
Период революции	365.26 дней	686.98 сут	27,32 сут
Средняя температура поверхности	286 К (13 С)	216 К (-57 С)	243 К (-30 С)
Компоненты атмосферы	78% азота 21% кислорода 1% аргона 0,035% двуокиси углерода	95% диоксид углерода 3% азот 1. 6% аргона 0,13% кислорода	незначительная
Атмосферное давление	101,3 кПа	0,7 кПа	0,0 кПа

Масса Марса составляет всего одну десятую массы Земли, его год почти вдвое длиннее, но его день почти такой же длины. Большая разница в среднем температура поверхности двух планет. Луна, луна Земли, всего лишь около одного восьмидесятая масса Земли.Поскольку у него нет атмосферы, у него экстремальная поверхность. колебания температуры, от +130 C в солнечное время суток до -170 C в темноте ночью.

Состав атмосферы Земли и Марса совсем не одинаков. Марс имеет очень маленькое атмосферное давление, всего около одной сотой земного, и его атмосфера почти полностью состоит из двуокиси углерода. Процентное количество углерода диоксида в земной атмосфере очень мало (так как он находится в равновесии, поддерживаемом его растворимость в воде и его использование зелеными растениями в фотосинтезе).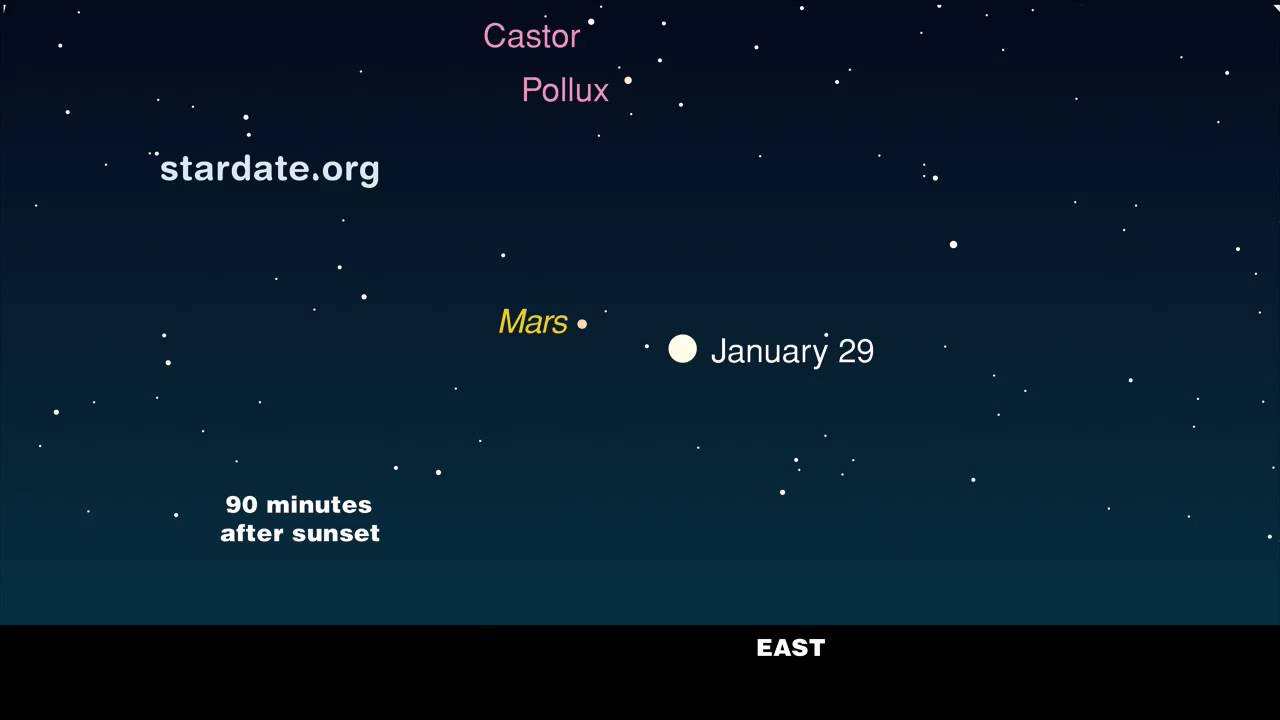 Луна вообще не имеет атмосферы, за исключением следов газов солнечного ветра, которые быстро уходят в Космос.

Сравнение орбит Марса и Земли показывает, что Марс гораздо более эксцентричен, чем орбиты Земли. Земли. Из-за этого, а также из-за разницы в сроках их жизни революции, расстояние между Землей и Марсом может сильно различаться.

На самом близком расстоянии Марс находится примерно в 50 миллионах км от Земли; на своем дальше всего — почти 402 миллиона км (когда Земля и Марс находятся по разные стороны от Солнца).Среднее расстояние между Землей и Марсом более чем в 200 раз больше, чем от Земля на Луну.

Деймос, спутник Марса — Солнечная система на море и небе

Колесница ужаса

Деймос [DEE-mos] — наиболее удаленный спутник от Марса и является меньшим из двух. Имея длину всего 9,9 миль (11 км), это также одна из самых маленьких известных лун в Солнечной системе .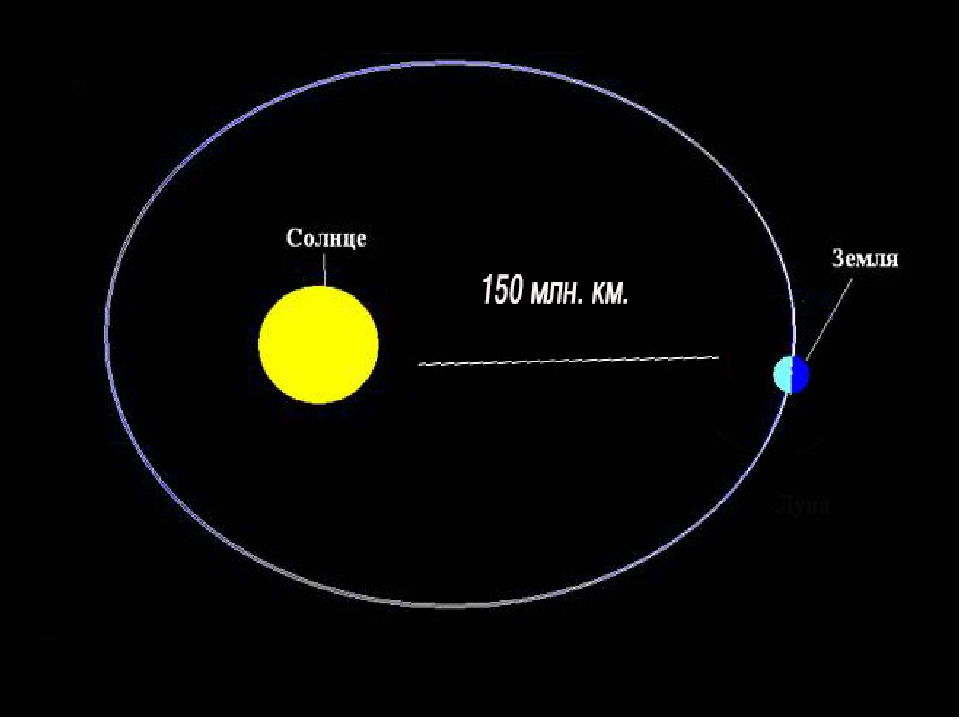 Деймос был назван в честь Ужаса, еще одного колесничего римского бога Марса. В греческой мифологии Деймос представляет страх и является одним из сыновей Ареса (Марса) и Афродиты (Венеры). Деймос был открыт 12 августа 1877 года американским астрономом Асафом Холлом во время наблюдения за Марсом в Военно-морской обсерватории США. Холл обнаружил Фобос в то же время, когда искал марсианские луны.

Изображение северного квартала Деймоса с космического корабля «Викинг» крупным планом (НАСА / Лаборатория реактивного движения)		Изображение Деймоса, сделанное викингом, на котором видна покрытая кратерами поверхность (NASA / JPL)		Космический корабль «Викинг», крупный план, изображение воронок от посева Деймоса (НАСА / Лаборатория реактивного движения)

Самая маленькая луна

Если бы мы думали, что Фобос был маленькой луной, Деймос еще меньше. При длине 9,9 миль (11 км) это немного больше, чем покрытый рябью кусок камня на орбите вокруг красной планеты. На расстоянии 14 573 миль (23 460 км) Деймос более чем в два раза дальше от Марса, чем Фобос. Это выглядит как не более чем умеренно яркое пятно на марсианском небе. Из-за большего расстояния Деймосу требуется более 30 часов, чтобы совершить один полный оборот вокруг Марса. Как и Фобос, его неправильная форма больше похожа на большие астероиды в поясе астероидов между Марсом и Юпитером.Исследования показывают, что Деймос состоит из многих из тех же материалов, что и объекты пояса астероидов. Возможно, когда-то это был астероид, но он был захвачен гравитацией Марса. Некоторые астрономы считают, что две марсианские луны могут быть остатками более крупного объекта, который был разрушен в результате столкновения. Возможно, мы никогда не узнаем наверняка.

Особенности Deimos

Как и Фобос, Деймос — довольно ничем не примечательный объект. Это тоже, по сути, просто большая скала с несколькими кратерами.У Деймоса гораздо более гладкий вид и меньше кратеров, чем у его кузена Фобоса. Самый большой из этих кратеров имеет диаметр 2 мили, что составляет около 1/5 размера самой Луны. В отличие от Фобоса, на Деймосе нет следов трещин на поверхности. Это может быть связано с тем, что он вдвое дальше от Марса, чем Фобос, и не подвержен таким же сильным гравитационным силам. Как и Фобос, Деймос, как полагают, состоит из смеси льда и богатой углеродом породы, подобной той, что обнаружена в астероидах C-типа во внешнем поясе астероидов.У Деймоса нет атмосферы и магнитного поля.

Другая судьба

Из-за того, что Деймос находится дальше от Марса, судьба его иная, чем его собрата. Ему не суждено врезаться в Марс, как Фобос. Скорее, Деймос медленно удаляется от Марса. Считается, что, как и луна Земли, Деймос в конечном итоге покинет орбиту своей родительской планеты и больше никогда его не увидит.

Как, когда и где увидеть, как Луна и Марс сияют вместе в эти выходные невооруженными глазами

В эти выходные Луна и Марс будут видны вместе… хотя, пожалуйста, не обращайте внимания на масштаб в этом … [+] ‘креативном’ макете!

Гетти

Этим летом вы видели три запуска космических кораблей к Марсу и читали о возможности существования там древней жизни.

Теперь посмотрите на «красную планету» собственными невооруженными глазами с яркой Луной на буксире, просто для хорошей меры.

В ближайшие выходные Луна выровняется с Марсом, хотя, когда именно она будет выглядеть ближе всего, зависит от того, где вы находитесь на планете.

Почему в эти выходные Луна выравнивается с Марсом?

Марс сейчас восходит сразу после наступления темноты на востоке, в то время как Луна будет освещена на 86%, что известно как «убывающая луна».

Солнечная система похожа на яичницу; планеты вращаются вокруг Солнца в одной плоскости, поэтому на нашем ночном небе есть линия, известная как эклиптика wikipedia.org/wiki/Ecliptic»> , по которой вращаются все планеты. Это также путь, по которому Солнце проходит по дневному небу. Эклиптика простирается на нашем небе с востока на запад, и в это время года она находится к югу от северного полушария; вы, вероятно, увидите планеты на востоке, юго-востоке, юге, юго-западе и западе. Никогда ищите планеты на севере!

Поскольку все планеты вращаются в одном направлении, но с разной скоростью, они догоняют и обгоняют друг друга, изменяя свое видимое положение в нашем ночном небе.

Так что насчет Луны?

БОЛЬШЕ ОТ FORBES Нет, 27 августа Марс не будет таким большим, как Луна. Вот когда и где их вместе увидеть Джейми Картер

Орбитальный путь Луны вокруг Земли лишь слегка наклонен к эклиптике, поэтому время от времени она проходит очень близко к планетам. Фактически, Луна и Марс тоже выровнялись в прошлом месяце.

Однако тогда Марс казался меньше и тусклее. Настоящая причина посмотреть на Луну и Марс в эти выходные — это то, что красная планета теперь становится впечатляюще большой и яркой.

Когда увидеть, как Луна и Марс сияют вместе

Убывающая луна, видимо, наиболее близко приблизится к «красной планете» в ночь на субботу 5 сентября 2020 года для Северной Америки (восточное небо) и ранним рассветным утром в воскресенье, 6 сентября 2020 года. для Европы (западное небо).

Вот удобная карта звездного неба для Северной Америки (если вы находитесь в Европе, она также будет работать, хотя самый близкий подход — примерно на пять часов позже, незадолго до восхода солнца, когда Марс и Луна будут на западе) .

5 сентября 2020 года Луна окажется близкой к Марсу.

Джейми Картер

Эти два объекта будут находиться на расстоянии около половины градуса друг от друга, хотя, если вы посмотрите в пятницу или воскресенье вечером, вы также заметите их довольно близко — около 4 ° , фактически .

Наблюдатели за небесами называют это соединение .

Будут ли Луна и Марс выглядеть одинакового размера?

Абсолютно нет! Не поддавайтесь на этот обман. Хотя Марс будет выглядеть относительно большим и ярким, Луна будет выглядеть намного больше.В конце концов, он намного ближе к нам, чем Марс.

В эти выходные Луна будет на расстоянии около 238 000 миль от Земли, а Марс будет на расстоянии около 47 миллионов миль. Чтобы он выглядел таким же большим, как Луна, Марс должен быть примерно в 476 000 миль от Земли — это почти вдвое больше, чем расстояние Земля-Луна.

Очевидно, этого не произойдет.

Почему Марс такой яркий?

Марс сейчас приближается к своей оппозиции в октябре, точке на своей орбите, когда он находится ближе всего к Земле.Это означает, что в нашем ночном небе оно становится больше и ярче. На самом деле, с каждой неделей он становится заметно больше и ярче.

Знание о противостоянии Марса также показывает, почему НАСА, Китай и ОАЭ только что начали свои миссии на Марс. Земле требуется 365 дней для обращения вокруг Солнца, а Марсу — 687 дней медленнее. Это 1,88 земных года, что делает Марс и Землю достаточно близкими к орбитальному резонансу 2: 1.

Земле требуется 365 дней для обращения вокруг Солнца, а Марсу — 687 дней медленнее.

Гетти

Итак, чуть более чем каждые два года Земля догоняет Марс, и планеты ненадолго выстраиваются в ряд. В этом случае они ближе всего друг к другу. Так что как раз перед этой точкой путешествие между двумя планетами занимает минимум времени. Каждые 2,2 года открывается окно запуска для эффективных и экономичных поездок между Землей и Марсом, и наоборот.

Пока вы ждете, когда три космических корабля достигнут Марса, взгляните на красную планету собственными глазами в эти выходные.Когда Луна рядом, будет невозможно пропустить — и это зрелище запомнится.

Примечание. Звездные карты приведены для 40º северной широты. Если вам нужна точная информация о том, где вы находитесь, обратитесь в онлайн-планетарий, например, com/planetarium»> The Sky Live .

Желаем вам ясного неба и широко раскрытых глаз.

фильмов НАСА показывают, как быстро свет распространяется от Земли до Луны, Марса

• Скорость света в вакууме составляет около 186 282 мили в секунду (299 792 километра в секунду).
• Ученый из НАСА показал, сколько времени требуется свету, чтобы путешествовать вокруг Земли, а также между планетой, ее луной и Марсом.
• Физические анимации показывают, насколько быстрым (и медленным) может быть ограничение скорости Вселенной.

Серия новых анимаций, созданных ученым НАСА, демонстрирует, насколько резкой — и при этом мучительно медленной — может быть скорость света.

Скорость света — это максимальная скорость, которую любой материальный объект может перемещать в космосе. Это, конечно, исключает существование теоретических коротких путей в ткани космоса, называемых червоточинами (и возможность пройти через них, не будучи разрушенными).

В совершенно пустом вакууме частица света, называемая фотоном, может двигаться 186 282 мили в секунду (299 792 километра в секунду), или около 670,6 миллиона миль в час (1,079 миллиарда километров в час).

Это невероятно быстро. Однако скорость света может быть удручающе медленной, если вы пытаетесь связаться с другими планетами или достичь их, особенно любых миров за пределами нашей солнечной системы.

Подробнее : Астрономы обнаружили «холодную суперземлю» менее чем в 6 световых годах от нас — и это может быть первая каменистая планета, которую мы сфотографируем за пределами Солнечной системы.

Чтобы изобразить ограничение скорости Космос таким образом, чтобы его мог понять любой, Джеймс О’Донохью, ученый-планетолог из Центра космических полетов имени Годдарда НАСА, взял на себя задачу оживить его.

«Мои анимации были сделаны так, чтобы максимально мгновенно показать весь контекст того, что я пытаюсь передать», — сказал О’Донохью Business Insider через Twitter. «Когда я делал поправки к экзаменам, я рисовал сложные концепции вручную, просто чтобы по-настоящему понять, так что я здесь и делаю».

О’Донохью сказал, что он только недавно научился создавать эти анимации — его первые сообщения были для пресс-релиза НАСА об исчезающих кольцах Сатурна. После этого он перешел к анимации других сложных для понимания космических концепций, включая видео, иллюстрирующее скорости вращения и размеры планет.Он сказал, что одно «собрало миллионы просмотров», когда он разместил его в Twitter.

В последней работе О’Донохью рассматриваются три различных сценария скорости света, чтобы показать, насколько быстрыми (и насколько болезненно медленными) могут быть фотоны.

Как быстро свет распространяется относительно Земли

Одна из первых анимаций О’Донохью показывает, насколько быстро свет движется относительно Земли.

Земля находится на расстоянии 24 901 мили от центра. Если бы в нашем мире не было атмосферы (воздух преломляет и немного замедляет свет), фотон, скользящий по его поверхности, мог бы пересечь экватор почти на 7 градусов. 5 раз в секунду.

На этом изображении скорость света кажется довольно высокой, хотя фильм также показывает, насколько она конечна.

Как быстро свет проходит между Землей и Луной

Вторая анимация О’Донохью делает большой шаг назад от Земли и включает в себя Луну.

В среднем, расстояние между нашей планетой и ее большим естественным спутником составляет около 238 855 миль (384 400 км).

Это означает, что весь лунный свет, который мы видим, имеет возраст 1,255 секунды, а путь туда и обратно между Землей и Луной со скоростью света занимает около 2 секунд.51 секунда.

Это время увеличивается с каждым днем, поскольку Луна удаляется от Земли со скоростью примерно 1,5 дюйма (3,8 см) в год. (Луна постоянно истощает энергию вращения Земли за счет океанских приливов, увеличивая свою орбиту на все большее и большее расстояние.)

Скорость движения света между Землей и Марсом

Третья анимация скорости света О’Донохью иллюстрирует проблему, с которой многие планетологи сталкиваются ежедневно.

Когда НАСА пытается поговорить или загрузить данные с космического корабля, такого как зонд InSight на Марсе, оно может сделать это только со скоростью света. Это слишком медленно, чтобы управлять космическим кораблем в «живом режиме», как с дистанционно управляемой машиной. Итак, команды должны быть тщательно продуманы, заранее упакованы и нацелены на точное место в пространстве в точное время, чтобы они не пропустили свою цель.

Подробнее : НАСА может слышать «преследующий» звук пыльных дьяволов, несущихся по Марсу с помощью своего нового посадочного модуля стоимостью 830 миллионов долларов

Самый быстрый разговор между Землей и Марсом — это когда планеты находятся на ближайшем расстоянии указывают друг на друга, событие, называемое ближайшим приближением, происходит примерно раз в два года.В среднем это расстояние в лучшем случае составляет около 33,9 миллиона миль (54,6 миллиона километров).

Как видно из 60-секундного клипа из полного фильма О’Донохью на YouTube, свету требуется 3 минуты 2 секунды, чтобы пройти между Землей и Марсом при самом близком приближении. Это шесть минут и четыре секунды для полета туда и обратно со скоростью света.

Но в среднем Марс находится примерно в 158 миллионах миль от Земли, так что средняя обратная связь занимает около 28 минут и 12 секунд.

Чем дальше вы идете, тем угнетающе становится скорость света

Иллюстрация «нанокрафта» Breakthrough Starshot, который направляется к звездной системе Альфа Центавра с помощью мощного лазерного луча.Фонд прорыва

Преодоление конечной скорости света становится еще более сложной задачей для таких космических аппаратов, как New Horizons, который сейчас находится на расстоянии более 4 миллиардов миль от Земли, и космических кораблей Voyager 1 и 2, каждый из которых достиг космического пространства между звездами.

Ситуация становится прямо-таки удручающей, когда вы начинаете смотреть за пределы солнечной системы. Ближайшая из известных экзопланет Проксима b находится на расстоянии около 4,2 световых лет от нас (расстояние около 24. 7 триллионов миль или 39,7 триллионов километров).

Тем не менее, самый быстрый из всех космических аппаратов — это солнечный зонд НАСА Parker Solar Probe со скоростью около 213 200 миль в час; с такой скоростью, чтобы достичь Проксимы b, потребуется 13 211 лет.

Проект Breakthrough Starshot российско-американского миллиардера предлагает способ решения этой проблемы со скоростью. План, рассчитанный на несколько десятилетий, состоит в том, чтобы построить и пролететь мимо таких экзопланет с помощью сверхмощных лазерных лучей и пролететь мимо таких экзопланет, в идеале с запланированной крейсерской скоростью 20% от скорости света.Тем не менее, вся концепция все еще является теоретической, может в конечном итоге не работать и будет работать на малой скорости света.

Пространство невозможно. Хотя возраст Вселенной составляет около 13,77 миллиарда лет, ее край находится на расстоянии 45,34 миллиарда световых лет в любом направлении и увеличивается из-за расширения.

Это слишком много, чтобы проиллюстрировать его простой анимацией. Однако одна иллюстрация подходит близко: это изображение, созданное музыкантом Пабло Карлосом Будасси, которое объединяет логарифмические карты Вселенной из Принстона и изображения из НАСА, чтобы запечатлеть все это на одном снимке.

Эта история обновлена.

Как далеко находится Марс, почему планета красная и сколько времени нужно, чтобы добраться туда?

Марс, четвертая планета от Солнца в нашей галактике, на протяжении веков восхищал звездочетов и назван в честь римского бога войны.

Зонд НАСА Insight приземлился на планету в попытке узнать больше о том, что находится на поверхности планеты.

2

Первая фотография, отправленная на Марс зондом НАСА InSight Фото: AP: Associated Press

Как далеко находится Марс?

Марсу, также известному как Красная планета, 33 года.9 миллионов миль (54,6 км) от Земли.

Это 141,6 м мили (227,9 м км) от Солнца.

У планеты есть две луны, Фобос и Деймос, маленькие и неправильной формы, которые могут даже быть астероидами, попавшими под действие гравитационного поля планеты.

Почему планета красная?

Его часто называют Красной планетой из-за его окраски, которая придает ей красноватый оттенок.

Это связано с большим количеством оксида железа (ржавчины) на его поверхности.

Поверхность Марса в основном состоит из толеитового базальта.

Период обращения Земли эквивалентен 687 земным суткам, а продолжительность марсианских суток — 24 часа 39 минут.

2

Изображение Марса, показывающее его основные географические особенности

Сколько времени нужно, чтобы добраться туда?

Согласно Space.com, при решении этой задачи необходимо учитывать ряд факторов, в том числе расстояние между Землей и Марсом, а также скорость вашего путешествия.

Хотя теоретически наибольшее расстояние между двумя планетами из-за их орбиты составляет 33,9 метра, это никогда не регистрировалось — самое близкое расстояние составляет 34,8 миллиона миль.

Максимальное расстояние, на которое они могут быть, составляет 250 м миль, что в среднем составляет 140 м миль.

Самым быстрым космическим кораблем, запущенным с Земли, была миссия НАСА New Horizons.

Зонд покинул Землю со скоростью 36 000 миль в час.

Live Blog

WAITING GAME

Live PS5 обновляется по мере падения консолей Playstation

DEAD COLD

Морозная погода может убить аккумулятор вашего iPhone и вызвать внезапное отключение

‘THEY BOIL MY BLOOD’

Человек обещает отправить плоскую Землю в космос, чтобы ДОКАЗАТЬ, что планета круглая

СКРЫТЫЕ ЦИФРЫ

На джойстике PS5 есть 40 000 СКРЫТЫХ логотипов PlayStation — вы можете их заметить?

ВЗРЫВ!

Первый космический запуск Великобритании должен стартовать в 2022 году с космодрома в Шотландии

GRAB IT! Уловка

Genius iPhone позволяет сделать снимок экрана ВСЕЙ страницы — вот как это сделать

Если подобный зонд оставит прямое направление к Марсу, то самое быстрое, что он сможет совершить, — это 39 дней, хотя самое быстрое, что было достигнуто до сих пор, — 41 день.

В среднем это займет 162 дня.

Это теория, но необходимо принимать во внимание другие факторы, например, две планеты постоянно движутся, поэтому, если зонд был отправлен по прямой линии, когда они были как можно ближе, к тому времени, когда зонд достигнет Марса, он бы переехали.

При расчетах необходимо учитывать, где будет планета, когда зонд достигнет Марса.

Другой фактор заключается в том, что зонд должен замедлиться при приближении к Марсу, иначе он просто врезался бы в планету.

Экономика также играет важную роль — чем быстрее космический корабль летит, тем больше топлива он сжигает, которое должно быть перенесено на борт, что сделает корабль тяжелее, и на самом деле может оказаться невозможным нести такое количество топлива, которое летит в космосе.

Диспетчерская НАСА в истерике, получив первое изображение, отправленное зондом InSight с Марса

Марс или Венера ближе к Земле?

Ответ на вопрос, находится ли Марс или Венера ближе к Земле: «Это зависит от обстоятельств». Марс и Венера — ближайшие соседи Земли в Солнечной системе.Однако все три планеты имеют почти круговые орбиты вокруг Солнца и движутся с разной скоростью. Итак, иногда Земля и Марс близки, а Венера находится по другую сторону от Солнца, иногда Венера уютно с Землей, а Марс — далекой.

TL; DR (слишком долго; не читал)

Венера становится ближе к Земле, чем Марс или любая другая планета: 38,2 миллиона километров (23,7 миллиона миль).

Расстояния между планетами

Ближайший к Марсу равен 55.7 миллионов километров (34,6 миллиона миль) от Земли, но только 38,2 миллиона километров (23,7 миллиона миль) разделяют Венеру и нашу планету. По отношению к Солнцу Венера находится на расстоянии 108 200 000 километров (67 232 400 миль), Земля — ​​149 600 000 километров (92 957 100 миль), а Марс — в 227 940 000 километров (141 635 000 миль) от Солнца. Для более удобного для восприятия сравнения размеров, если вы поместите солнце в одном углу комнаты, Венера будет в двух шагах от нее, Земля — ​​всего на полшага больше, а Марс — на полтора шага дальше — Плутон, вероятно, вас увезет. вне вашего дома, так как он находится в 100 шагах от солнца.

Факты о Венере

Венера вращается в направлении, противоположном Земле, и ее атмосфера разрушает космические зонды НАСА всего за несколько минут. Атмосфера в основном состоит из двуокиси углерода и азота. С точки зрения общих размеров Земля и Венера похожи, но в остальном Венера похожа на Землю, где глобальное потепление полностью взяло верх. Как самая горячая планета в Солнечной системе, поверхность Венеры составляет 462 градуса по Цельсию (864 градуса по Фаренгейту), и планета покрыта вулканами.

Факты о Марсе

Венера — это мир в огне, а Марс холодный — температура колеблется от -87 до -5 градусов по Цельсию (от -125 до 23 градусов по Фаренгейту). Марс размером примерно в половину Земли имеет пустынную поверхность, но очень тонкую атмосферу. Эта крошечная атмосфера состоит из углекислого газа и азота, как Венера, с добавлением аргона.