Презентация «Золотое сечение» (6 класс)

Описание презентации по отдельным слайдам:
1 слайд
ПРЕЗЕНТАЦИЯ К УРОКУ НА ТЕМУ «ЗОЛОТОЕ СЕЧЕНИЕ» для учащихся 6 класса (математика) ГБОУ Школа № 825 города Москвы Учитель Высоцкая Л. Р. Москва 2017
2 слайд Описание слайда:
Описание слайда:«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе — с драгоценным камнем…» Иоганн Кеплер
3 слайд Описание слайда:
Описание слайда:Основатели учения о золотом сечении Понятие золотого сечения «Золотые фигуры» Золотое сечение вокруг нас Содержание
4 слайд Описание слайда: 5 слайд
Описание слайда: 5 слайд 
Основатели учения о золотом сечении Пифагор Ввел понятие о золотом делении Леонардо да Винчи Ввел термин «золотое сечение»
6 слайд Описание слайда:
Описание слайда:Основная пропорция, свойственная нашему миру, выражается следующим образом: Отношение большей величины к средней равняется отношению средней к меньшей.
7 слайд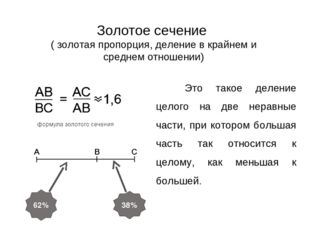 Описание слайда:
Описание слайда:Это такое деление целого на две неравные части, при котором большая часть так относится к целому, как меньшая к большей. 62% 38% Золотое сечение ( золотая пропорция, деление в крайнем и среднем отношении)
8 слайд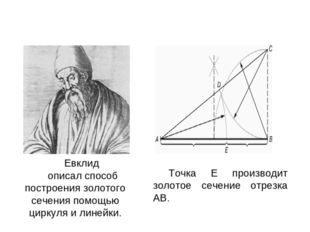
Евклид описал способ построения золотого сечения помощью циркуля и линейки. Точка Е производит золотое сечение отрезка АВ.
9 слайд Описание слайда:
Описание слайда:Монах Лука Пачоли описал свойства золотого сечения и золотых фигур
10 слайд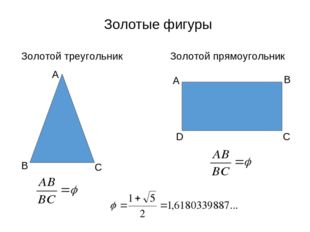 Описание слайда:
Описание слайда:Золотые фигуры Золотой треугольник Золотой прямоугольник А В С А В С D
11 слайд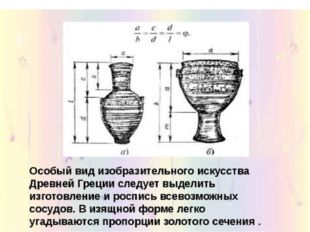 Описание слайда: 12 слайд
Описание слайда: 12 слайд 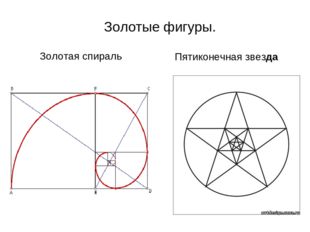
Золотая спираль Пятиконечная звезда Золотые фигуры.
13 слайд Описание слайда:
Описание слайда:Предметы , отношения сторон которых выбраны в золотом соотношении , вызывают ощущение гармонии и покоя
14 слайд Описание слайда: 15 слайд
Описание слайда: 15 слайд 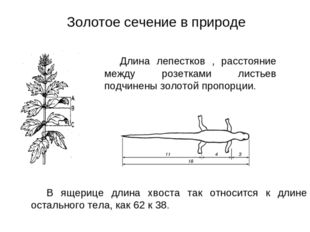 Описание слайда:
Описание слайда:Длина лепестков , расстояние между розетками листьев подчинены золотой пропорции. Золотое сечение в природе В ящерице длина хвоста так относится к длине остального тела, как 62 к 38.
16 слайд
 Описание слайда:
Описание слайда:Золотая спираль-это «кривая жизни»
18 слайд Описание слайда: 19 слайд
Описание слайда: 19 слайд  Описание слайда: 20 слайд
Описание слайда: 20 слайд  Описание слайда: 21 слайд
Описание слайда: 21 слайд  Описание слайда:
Описание слайда: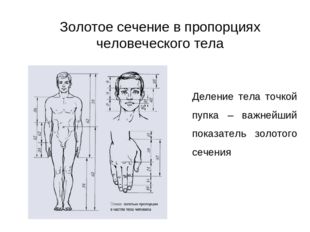 Описание слайда:
Описание слайда:Золотое сечение в пропорциях человеческого тела Деление тела точкой пупка – важнейший показатель золотого сечения
23 слайд Описание слайда:
Описание слайда:Золотое сечение в скульптуре Золотое сечение в архитектуре
24 слайд Описание слайда: 25 слайд
Описание слайда: 25 слайд  Описание слайда:
Описание слайда:ЗОЛОТОЕ СЕЧЕНИЕ ЭЙФЕЛЕВОЙ БАШНИ
26 слайд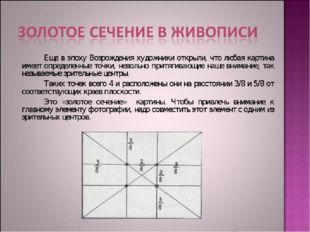 Описание слайда: 27 слайд
Описание слайда: 27 слайд  Описание слайда: 28 слайд
Описание слайда: 28 слайд  Описание слайда: 29 слайд
Описание слайда: 29 слайд  Описание слайда: 30 слайд
Описание слайда: 30 слайд  Описание слайда: 31 слайд
Описание слайда: 31 слайд  Описание слайда: 32 слайд
Описание слайда: 32 слайд  Описание слайда: 33 слайд
Описание слайда: 33 слайд  Описание слайда: 34 слайд
Описание слайда: 34 слайд  Описание слайда:
Описание слайда:Золотое сечение в живописи
35 слайд Описание слайда: 36 слайд
Описание слайда: 36 слайд  Описание слайда: 37 слайд
Описание слайда: 37 слайд  Описание слайда: 38 слайд
Описание слайда: 38 слайд  Описание слайда: 39 слайд
Описание слайда: 39 слайд  Описание слайда: 40 слайд
Описание слайда: 40 слайд  Описание слайда:
Описание слайда:Выводы: Человеческое представление о красивом сформировалось под влиянием знаний о золотой пропорции Золотое сечение – это один из основополагающих принципов природы

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-158585
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Урок математики «Золотое сечение» 6 класс
Выберите документ из архива для просмотра:
Выбранный для просмотра документ 6 УРОК МАТЕМАТИКИ.pptx

Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:09.04.2014 УРОК МАТЕМАТИКИ 6 класс
2 слайд Описание слайда:
Описание слайда:Что вы чувствуете?
3 слайд Описание слайда:
Описание слайда:Что такое гармония? ЕДИНСТВО порядок + = ГАРМОНИЯ ГАРМОНИЯ = красота красота = математика =
4 слайд Описание слайда:
Описание слайда:Тема урока: Золотое сечение
5 слайд Описание слайда:
Описание слайда:Цели: 1. Познакомиться с понятием «золотое сечение». 2. Узнать, где оно применяется. 3. Научиться использовать его в практической деятельности.
6 слайд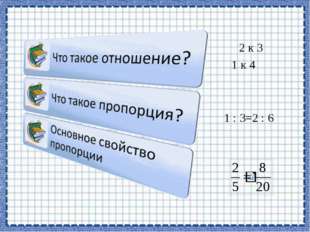 Описание слайда:
Описание слайда:1 : 3=2 : 6 2 к 3 1 к 4
7 слайд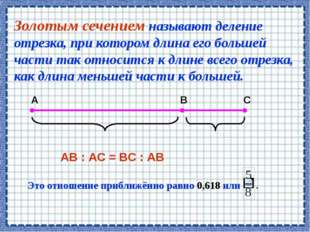 Описание слайда:
Описание слайда:Золотым сечением называют деление отрезка, при котором длина его большей части так относится к длине всего отрезка, как длина меньшей части к большей. АВ : АС = ВС : АВ Это отношение приближённо равно 0,618 или . А В С
8 слайд Описание слайда:
Описание слайда:ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ Парфенон Парфенон – один из самых величественных храмов Древней Греции. Отношение высоты здания к его длине равно 0,6!
9 слайд Описание слайда:
Описание слайда:ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ рисунок Леонардо Да Винчи
10 слайд Описание слайда:
Описание слайда:ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ схема к иконе А. Рублева «Троица»
11 слайд Описание слайда:
Описание слайда:ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ статуя Аполлона Бельведерского
12 слайд Описание слайда:
Описание слайда:Мотивы золотого сечения просматриваются в картинах И.И. Шишкина. Ярко освещенная солнцем сосна делит картину по золотому сечению. Справа – освещенный солнцем пригорок также делит картину по горизонтали по золотому сечению. ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ
13 слайд Описание слайда:
Описание слайда:ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ
14 слайд Описание слайда: 15 слайд
Описание слайда: 15 слайд 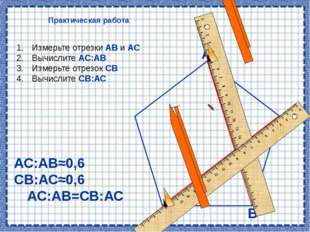 Описание слайда:
Описание слайда:Практическая работа В А С Измерьте отрезки АВ и АС Вычислите АС:АВ Измерьте отрезок СВ Вычислите СВ:АС АС:АВ≈0,6 СВ:АС≈0,6 АС:АВ=СВ:АС IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
16 слайд Описание слайда:
Описание слайда:Посмотрите вокруг и вы увидите множество примеров, подтверждающих это утверждение
17 слайд Описание слайда: 18 слайд
Описание слайда: 18 слайд  Описание слайда: 19 слайд
Описание слайда: 19 слайд  Описание слайда: 20 слайд
Описание слайда: 20 слайд  Описание слайда:
Описание слайда:Все они построены по законам золотого сечения
21 слайд Описание слайда:
Описание слайда:И ты, и он, и я — все мы созданы по законам божественной меры
22 слайд Описание слайда:
Описание слайда:РЕФЛЕКСИЯ: Сегодня я узнал….. Было интересно….. Было трудно… Теперь я могу…… Я научился…… У меня получилось….. Урок дал мне для жизни…. Мне захотелось…. Я понял, что…..
Выбранный для просмотра документ Задание 1.docx
Выбранный для просмотра документ Задание 2.docx
Выбранный для просмотра документ Задание 3.docx
Выбранный для просмотра документ Урок математики 6 класс.docx
Выбранный для просмотра документ карточка.docx

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: 171164
Похожие материалы
Оставьте свой комментарий
Проект по математике (6 класс): Презентация к уроку математики на тему «Пропорция — «Золотое сечение»
Слайд 1
Золотое сечение Разработчик проекта учитель математики ВКК МБОУ СОШ № 94 г. Воронеж Кухарева И.А 2018 год «Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине». Стахов А.П.Слайд 2
История «Золотого сечения» В Древнем Египте существовала «система правил гармонии», основанная на Золотом Сечении. В Древней Греции Золотое Сечение было своеобразным каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания. В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны. Согласно Пифагору гармония имеет численное выражение , то есть, она связана с концепцией числа. Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения. Теория гармонии Древних
Слайд 3
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или другими словами, меньший отрезок так относится к большему, как больший ко всему. В МАТЕМАТИКЕ a : b = b : c или с : b = b : а.
Слайд 4
Эта пропорция равна: Золотое сечение в процентах
Слайд 5
Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании . История понятия «Золотое сечение» В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования» .
Слайд 6
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.
Слайд 7
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC Из точки B восставляется перпендикуляр, равный половине AB. Полученная точка C соединяется линией с точкой A. На полученной линии откладывается отрезок BC, заканчивающийся точкой D. Отрезок AD переносится на прямую AB. Полученная при этом точка E делит отрезок AB в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618…, если AB принять за единицу, BE = 0,382… Для практических целей часто используют приближённые значения 0,62 и 0,38. Если отрезок AB принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения описываются уравнением: X² — X-1=0 X² — X-1=0
Слайд 8
Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении. Икосаэдр и додекаэдр
Слайд 9
Ряд Фибоначчи С историей золотого сечения связано имя итальянского математика Леонардо Фибоначчи. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи: Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления. Все исследователи золотого деления в растительном и в животном мире, искусстве, неизменно приходили к ряду Фибоначчи как арифметическому выражению закона золотого деления.
Слайд 10
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). Золотое сечение в архитектуре, скульптуре, живописи На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618…
Слайд 11
«Золотая Пропорция» — главный эстетический принцип эпохи Средневековья Эпоха Возрождения ассоциируется с именами таких «титанов», как Леонардо да Винчи, Микеланджело, Рафаэль, Николай Коперник, Альберт Дюрер, Лука Пачоли . Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение». « Витрувийский человек» — размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг. Рисунок и текст иногда называют каноническими пропорциями .
Слайд 12
Вклад Кеплера в теорию Золотого Сечения Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения, Платоновых тел и Пифагорейской доктрины о числовой гармонии Мироздания. Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией , доказав, что последовательность отношений соседних чисел Фибоначчи: 1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;… в пределе стремится к золотой пропорции
Слайд 13
Математическое понимание гармонии « Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия» — Большая Советская Энциклопедия Математическая гармония — это равенство или соразмерность частей с друг другом и части с целым. Понятие математической гармонии тесно связано с понятиями пропорции и симметрии .
Слайд 14
Дано: отрезок АВ. Построить: золотое сечение отрезка АВ, т.е. точку Е так, чтобы . Построение. Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= . Далее, соединим точки А и С, отложим отрезок CD = CB , и наконец AE = AD . Точка Е является искомой, она производит золотое сечение отрезка АВ. Деление отрезка в золотом отношении Золотое сечение в геометрии
Слайд 15
Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, получаем золотую логарифмическую спираль. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда. Золотая спираль
Слайд 16
Золотое сечение лист розы Величины отростков и лепестков цикория подчинены правилу золотой пропорции.
Слайд 17
Золотая пропорция в теле ящерицы – длина хвоста так относится к длине остального тела, как 62 к 38 Золотые пропорции в яйце птицы
Слайд 18
Золотое сечение в живописи и фотографии На живописном полотне существуют четыре точки повышенного внимания . Зрительные центры расположены на расстоянии 3/8 и 5/8 от краев любой картины и фотографии.
Слайд 19
Золотое сечение в картине Леонардо да Винчи «Джоконда» Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).
Слайд 20
Золотое сечение в архитектуре Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Пирамида Хеопса
Слайд 21
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери ( Нотр -дам де Пари) Золотое сечение в архитектуре, Золотая пропорция применялась многими античными скульпторами.
Слайд 22
Золотое соотношение мы можем увидеть и в здании Собора Парижской Богоматери Нотр — Дам де Пари
Слайд 23
Вечный Огонь Памятник Воинам Освободителям Золотая пропорция Памятника Воинам Освободителям. Отношение 1,68
Слайд 24
Скульптура «Ромео и Джульетта» также вписывается в золотой прямоугольник
Слайд 25
Золотое сечение скульптуры проходит перед девушкой, акцентируя внимание на нее взгляде, и усиливая впечатление, что она кого-то ожидает…
Слайд 26
Дизайн данной клумбы не отвечает пропорциям золотого сечения
Презентация для урока математики «Золотое сечение»(6 класс)

Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Работу выполнила учитель математики: Девнозашвили Наталья Ивановна
2 слайд Описание слайда:
Описание слайда:* * «…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…». Иоганн Кеплер
3 слайд Описание слайда:
Описание слайда:Как расположены листочки на стебле? Рассматривая расположение листьев на общем стебле многих растений, можно заметить, что между каждыми двумя парами листьев третья расположена в месте золотого сечения. Точка С делит отрезок АВ в золотом отношении, точка Е делит отрезок DA в золотом отношении.
4 слайд Описание слайда:
Описание слайда:Расположение семечек в корзине подсолнуха. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону у среднего подсолнуха закручено 13 спиралей, в другую – 21 . Отношение 13/21=0,619 – золотое сечение.
5 слайд Описание слайда:
Описание слайда:У большинства людей, верхняя точка уха делит высоту головы вместе с шеей в золотом отношении. Нижняя точка уха делит в золотом отношении расстояние от верхней части уха до основания шеи. Подбородок делит расстояние от нижней точки уха до основания шеи в золотом отношении.
6 слайд Описание слайда:
Описание слайда:Золотое сечение в строении человека. Линия талии делит высоту человека в золотом отношении. Основание шеи делит расстояние от макушки до линии талии в золотом отношении. Длина всех фаланг каждого пальца соотносятся друг к другу по правилу золотой пропорции.
7 слайд Описание слайда:
Описание слайда:Понятие о золотом сечении ввел в научный обиход Пифагор, древнегреческий математик и философ. Пифагор (580-500 г.г.до н.э.)
8 слайд Описание слайда:
Описание слайда:Впервые золотое деление упоминается в «Началах» Евклида. Евклид (около 365 — 300 годы до нашей эры)
9 слайд Описание слайда:
Описание слайда:Леонардо да Винчи (1452-1519 г.г.) Леонардо да Винчи вводит в широкое употребление название «золотое сечение», Композиционное построение картины «Джоконда» основано на двух «золотых» треугольниках, которые являются частями «пентаграммы».
10 слайд Описание слайда:
Описание слайда:Пропорция — равенство двух отношений a : b = c : d
11 слайд Описание слайда:
Описание слайда:Золотое сечение — деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. Это отношение приближенно равно 0,618 5/8.
12 слайд Описание слайда:
Описание слайда:Рассмотрим размеры статуи Апполона Бельведерского, которая является эталоном идеального мужчины.
13 слайд Описание слайда:
Описание слайда:Основание шеи делит расстояние от макушки до линии талии в золотом отношении. Линия талии делит высоту человека в золотом отношении.
14 слайд Описание слайда:
Описание слайда:Зевс Олимпийский и Афина Парфенос.
15 слайд Описание слайда:
Описание слайда:Парфенон Главной причиной красоты Парфенона является исключительная соразмерность его частей, основанная на золотом сечении.
16 слайд Описание слайда:
Описание слайда:Собор Василия Блаженного. Пропорции Покровского Собора на Красной площади в Москве определяются восемью членами ряда золотого сечения.

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-079267
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Проект по математике (6 класс): Золотое сечение
Муниципальное казенное общеобразовательное учреждение
«Тельмановская средняя общеобразовательная школа»
муниципального образования
Тосненский район Ленинградской области
ПОРТФОЛИО
исследовательской работы
«Эстетический эффект наличия золотого сечения
в предметах человеческого быта»
Работу выполнила: ученица 6А класса
Комкова Вероника
Руководитель: учитель математики
Ушакова Марина Анатольевна
п. Тельмана
2017-2018 уч. год.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
ПЛАН РАБОТЫ 4
ПОНЯТИЕ ЗОЛОТОГО СЕЧЕНИЯ 5
ЗОЛОТОЕ СЕЧЕНИЕ В ЧЕЛОВЕКЕ 5
ДРУГИЕ ПРИМЕРЫ ЗОЛОТОЙ ПРОПОРЦИИ В ПРИРОДЕ 6
ЗОЛОТОЕ СЕЧЕНИЕ В ОБЪЕКТАХ АРХИТЕКТУРЫ 7
ЭКСПЕРИМЕНТ С ЗОЛОТЫМ ПРЯМОУГОЛЬНИКОМ 9
ЗАКЛЮЧЕНИЕ 11
СПИСОК ЛИТЕРАТУРЫ 12
ВВЕДЕНИЕ
В повседневной жизни человек пользуется разными предметами, которые имеют определенную форму. Задумывается ли он о том, почему форма именная такая, а не иная. Например, пластиковые карты (банковские, скидочные), имеют прямоугольную форму определенного размера. Почему?
На уроке математики нами была рассмотрена тема «Золотое сечения», в ходе которого выяснили, что пропорции всех пластиковых карт соответствуют золотому сечению. Существует гипотеза, что наличие таких параметров производит эстетический эффект, т.е. является наиболее привлекательным для человеческого глаза. Было решено наиболее глубоко изучить данный вопрос в процессе исследовательской работы.
Цель работы: выявить наличие эстетического эффекта при использовании параметров золотого сечения в объектах, окружающих человека.
Задачи:
- Изучить понятие золотого сечения;
- Провести эксперимент, проверяющий выдвинутую гипотезу;
- Обработать полученные результаты;
- Подготовить презентацию.
В ходе изучения имеющейся информации по теме были использованы электронные (Интернет) и бумажные источники. В книгах золотое сечение рассматривается преимущественно с исторической точки зрения, рассказывается о его наличии в природе и объектах архитектуры. В Интернете можно найти примеры из повседневной жизни человека. А также было найдено много интересных роликов и один мультфильм по теме «Золотое сечение».
ПЛАН РАБОТЫ
- Собрать и изучить информацию по теме «Золотое сечение».
- Опытным путем проверить наличие золотого сечения в объектах архитектуры и параметрах человеческого тела.
- Подготовить материалы для проведения эксперимента с золотым прямоугольником.
- Провести эксперимент.
- Обработать результаты эксперимента.
- Подготовить презентацию и портфолио проведенного исследования.
ПОНЯТИЕ ЗОЛОТОГО СЕЧЕНИЯ
Золотое сечение — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ {\displaystyle \Phi } в честь древнегреческого скульптора и архитектора Фидия.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.
Для практических целей ограничиваются приблизительным значением Φ {\displaystyle \Phi } 1,618 или Φ {\displaystyle \Phi } 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 38 % к 62 % или 5 к 8.
ЗОЛОТОЕ СЕЧЕНИЕ В ЧЕЛОВЕКЕ
Кости продуманы природой тоже согласно пропорции 5/8.Большинство частей тела в соотношениях применяются к уравнению. Если все частички тела подчиняются Золотой формуле, тогда внешние данные будут весьма привлекательны и идеально сложены.
Отрезок от плеч до верха головы и ее размера = 1:1.618
Отрезок от пупа до верха головы и от плеч до верха головы =1:1.618
Отрезок от пупа до колен и от них до ступней ног =1:1.618
Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6.
Все расстояния лица общее представление об идеальных пропорциях, привлекающих взгляд. Пальцы, ладонь, тоже подчиняются закону. Необходимо еще отметить, что отрезок расставленных рук с туловищем равен росту человека. Даже все органы, кровь, молекулы соответствуют Золотой формуле.
Мы решили убедиться в этом самостоятельно и поэтому в классе провели эксперимент, в ходе которого с помощью портняцкого метра измеряли разные части тела своих одноклассников (например, расстояние от локтя до кончиков пальцев, расстояние от плеча до локтя, длину ладони) и результаты измерений делили друг на друга, чтобы определить, какие из полученных отношений близки к золотому сечению.
Результат:
- Отношение расстояния от макушки до кончиков пальцев к расстоянию от кончиков пальцев до пола: 93см : 56см = 1,66
- Отношение расстояния от макушки до пупка и от пупка до пола :
93см : 58см = 1,603
- Отношение расстояния от локтя до кончиков пальцев к расстоянию от плеча до локся: 45 см : 30 см = 1,5
ДРУГИЕ ПРИМЕРЫ ЗОЛОТОЙ ПРОПОРЦИИ В ПРИРОДЕ
Золотое сечение признано универсальным законом живых систем. Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.
Носители генетического кода — молекулы ДНК и РНК — имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.
Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.
В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Также можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.
ЗОЛОТОЕ СЕЧЕНИЕ В ОБЪЕКТАХ АРХИТЕКТУРЫ
Многие из построек, сохранившихся до сегодняшних дней, свидетельствуют, что архитекторы средневековья знали о существовании золотого сечения, и, конечно, при строительстве дома руководствовались своими примитивными расчетами и зависимостями, с помощью которых пытались добиться наибольшей прочности. Особенно проявлялось желание строить максимально красивые и гармоничные дома в постройках резиденций царствующих особ, церквей, ратуш и зданий.
Например, знаменитый собор Парижской богоматери в своих пропорциях имеет немало участков, соответствующих золотому сечению.
Другим известным и ярким примером применения золотого сечения в архитектуре является, Парфенон. Например, отношение длины здания Парфенона к его высоте равно числу «фи».
Используя схематичные изображения трех объектов архитектуры (Собор Парижской Богоматери, Храм Василия Блаженного и Парфенон), мы также в результате самостоятельных измерений и расчетов убедились в присутствии золотой пропорции в параметрах строений разных стран и эпох.
Результат измерений (на всех схемах сохранены пропорции реальных зданий):
- Отношение ширины фасада Парфенона к высоте: 17,6см : 11,2см = 1,57
- Отношение высоты Храма Василия Блаженного к ширине фасада:
14см : 8,5см = 1,647
- Отношение высоты нижнего этажа Собора Парижской Богоматери к высоте второго этажа: 4,5см : 2,8см = 1,607
ЭКСПЕРИМЕНТ С ЗОЛОТЫМ ПРЯМОУГОЛЬНИКОМ
Изучая понятие и примеры золотого сечения в природе и архитектуре, мы встретились с предположением, что объекты, в пропорциях которых встречается отношение, близкое к 1,618, воспринимаются человеком, как более красивые, приятные глазу, именно поэтому художники, скульпторы, архитекторы использовали это отношение в своих творениях. Чтобы проверить данную гипотезу, мы провели эксперимент, который показал, как золотое сечение влияет на выбор человека.
Для проведения эксперимента были подготовлены раздаточные материалы с изображением трех прямоугольников с разными пропорциями:
Прямоугольник №1 : длина — 8,5 см, ширина — 2,2 см
Прямоугольник №2 : длина — 6 см, ширина – 3,7 см
Прямоугольник №3 : длина – 3,6 см, ширина – 3,7 см
Параметры второго прямоугольника (6 : 3,7 = 1,649) близки к золотой пропорции.
В ходе опроса участникам предлагали (без объяснения теоретической части эксперимента) выбрать среди трех фигур ту, которая им больше нравиться.
№1
№2 №3
Результат:
В опросе приняли участие 35 человек разного возраста (школьники и их родители, учителя). Количество респондентов, выбравших каждую фигуру, распределилось так, как показано в таблице ниже.
Фигура | Выбрали фигуру, чел. |
Прямоугольник №1 | 11 |
Прямоугольник №2 (Золотой прямоугольник) | 19 |
Прямоугольник №3 | 5 |
Вывод:
Так как прямоугольник №2 (пропорции которого соответствуют золотому сечению) выбрало наибольшее количество человек, среди опрошенных, наше предположение подтвердилось. Действительно, геометрические фигуры, в размерах которых присутствует отношение 1:1,618 наиболее приятны человеческому глазу.
ЗАКЛЮЧЕНИЕ
Доверяя глазу больше, чем другим органам чувств, человек в первую очередь учился различать окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.
В ходе выполнения данной исследовательской работы мы убедились, что золотое сечение присутствует в пропорциях большинства объектов, окружающих человека, да и в самом человеке, что производит очевидный эстетический эффект. Человек, сам не осознавая этого, отдает предпочтение формам, в которых присутствует золотая пропорция. Именно этой идеей часто пользуются создатели разработчики предметов человеческого быта, например, создатели пластиковых скидочных и банковских карт.
СПИСОК ЛИТЕРАТУРЫ
- «Математика — Энциклопедия для детей» М.: Аванта +, 1998
- Журнал «Математика в школе», 1994, № 2; № 3.
- «Наука и техника» — электронная библиотека URL: http://n-t.ru/tp/iz/zs.htm (Дата обращения: 30.03.2018)
Проект по геометрии (6 класс) на тему: Золотое сечение
Слайд 1
Золотое сечение Или золотая пропорция. Быстрых Алексей. 6Б класс.Слайд 2
Введение Теперь более чем когда-либо все в нашем мире основано на числах. Некоторые из них даже имеют свои собственные имена – число пи, число e . Среди этих чисел одно является особенно интересным – 1,6180339887… Мы будем называть его «Золотым сечением». Оно обозначается буквой «Ф» (Фи) и играет в математике выдающуюся роль, обладая своими уникальными свойствами. Одним из уникальных свойств данного числа является его способность создавать изысканные формы: от треугольников, до двадцатигранных тел, называемых икосаэдрами. Оно также встречается и в повседневной жизни – кредитная карта была создана на основе данного числа. Это число часто присутствует в структуре зданий, на картинах и даже в настольных играх!
Слайд 3
Золотое сечение Как Вы думаете, что общего, между спиралью раковины улитки и формой Млечного пути? Ответом на этот вопрос является простое число, известное на протяжении многих веков. В разные эпохи его называли по разному – «божественное сечение», «золотое сечение», «золотое число»… Записать «Божественное сечение» практически невозможно, так как оно состоит из бесконечного ряда цифр, которые никогда не образуют повторяющуюся группу. Из-за этого нам придется использовать математическую формулу: Чувствам человека приятны объекты, обладающие правильными пропорциями Святой Фома Аквинский (1225 – 1274).
Слайд 4
Эксперимент Давайте попытаемся построить прямоугольник, одна сторона которого в 1,618 раз длиннее другой, получится такой прямоугольник:
Слайд 5
Эксперимент Этот прямоугольник называется золотым. Он входит в основу «Кредитных карт». Проведем еще один эксперимент. Положим одну кредитную карту вертикально, а вторую – горизонтально, так, чтобы нижние их стороны были на одинаковой высоте:
Слайд 6
Эксперимент Мы видим, что линия проходит в точности через правый верхний угол карты – приятная неожиданность! Многие предметы созданы с помощью формулы «Золотого сечения» – даже, вполне вероятно, — книги! Попробуйте проделать тот же эксперимент с книгами одинакового размера!
Слайд 7
Мона Лиза Леонардо Да Винчи также использовал «Золотое сечение» в своих работах. Давайте рассмотрим его, пожалуй, самую знаменитую картину: * (продолжение на сл. Слайде)
Слайд 8
Мона Лиза. Леонардо да Винчи
Слайд 9
Эксперимент Многие, наверняка, слышали об этой картине. Но никто не догадывался о её «Золотых» свойствах. Давайте же их рассмотрим:
Слайд 11
Разгадка Как показано в эксперименте, Леонардо да Винчи действительно использовал «Золотое сечение» в своих работах. Но только ли он придавал большое значение математике в своих шедеврах? Также золотое сечение можно заметить на картине Жоржа Сёра «Купальщики в Аньере »:
Слайд 12
Сечение в архитектуре Давайте рассмотрим Парфенон – шедевр Фидия:
Слайд 14
Эксперимент В нем также использован принцип «Золотого сечения»:
Слайд 16
Золотые пропорции в человеке:
Слайд 17
Золотое сечение в математике Но как же это золотое сечение построить? Просмотрим рисунок:
Слайд 18
Схема пропорциональных отрезков золотого сечения
Слайд 19
Хронология Золотое сечения, как мы уже знаем, использовалось и в искусстве, и в архитектуре. Составим хронологию использования «Золотого числа»:
Слайд 20
Кстати, греческая буква «Фи» — первая буква фамилии Фидиас , введенная для обозначения золотого сечения Марком Баром, вначале XX века. Заглавная буква обычно используется для обратного отношения: Ф = 1/Ф Фидиас ( Phidias ) (490–430 BC) создал статуи Парфенона , которые своими пропорциями воплощают золотое сечение . Платон (427–347 BC) в своем труде Timaeus описывает пять возможных правильных геометрических тел ( Платоновы тела : тетраэдр , куб , октаэдр , додекаэдр и икосаэдр ), часть из которых имеет отношение к золотому сечению . Евклид (325–265 BC) в своих Элементах дал первое письменное определение золотого сечения , которое в переводе было названо «деление в крайнем и среднем отношении ( extreme and mean ratio )» ( греч. α κροςκ αιμεσοςλογος). Фибоначчи ( Fibonacci ) (1170–1250) открыл числовой ряд, теперь называемый его именем, который тесно связан с золотым сечением . Фра Лука Пачоли ( Fra Luca Pacioli ) (1445–1517) совместно с Леонардо определил золотое сечение как «божественную пропорцию» в их труде «Божественная пропорция ( Divina Proportione )». Иоганн Кеплер ( Johannes Kepler ) (1571–1630) называет золотое сечение «драгоценным камнем»: «Геометрия обладает двумя великими сокровищами: теорема Пифагора и деление отрезка в крайнем и среднем отношении; первое можно сравнить с мерой золота, второе назвать драгоценным камнем».
Слайд 21
Кстати, греческая буква «Фи» — первая буква фамилии Фидиас , введенная для обозначения золотого сечения Марком Баром, вначале XX века. Заглавная буква обычно используется для обратного отношения: Ф = 1/Ф Чарльз Боне ( Charles Bonnet ) (1720–1793) указывает, что в спиралях растений, закрученных по и против часовой стрелки, часто обнаруживается ряд Фибоначчи. Мартин Ом ( Martin Ohm ) (1792–1872) был первым, кто систематически использовал слова золотое сечение для описания этого отношения. Эдвард Лукас ( Edouard Lucas ) (1842–1891) вводит числовую последовательность, теперь известную как последовательность Фибоначчи в её нынешнем виде. Марк Барр ( Mark Barr ) (20 в.) вводит «Ф» — первую греческую букву имени Фидиас для обозначения золотого сечения . Роджер Пенроуз ( Roger Penrose ) (р.1931) открывает симметрию, использующую золотое сечение в области «апериодических черепиц», которая привела к новым открытиям в квазикристаллах .
Слайд 22
Спасибо за просмотр!
Проект по математике «Золотое сечение» (5-7 класс)

Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Золотое сечение – гармоническая пропорция Над проектом работал ученик 6 класса Г МАОУ Лицея № 37 Ленинского района Коростин Максим Руководитель проекта Коростина Л.А.
2 слайд Описание слайда:
Описание слайда:Гипотеза: Золотое сечение является отображение окружающегося мира. Объект исследования: наличие Золотого сечения в искусстве, в окружающих предметах. Предметы исследования: предметы искусства, архитектуры, живописи, пропорции учебников, мебели, фигуры учеников. Цель проекта: изучение понятия пропорции.
3 слайд Описание слайда:
Описание слайда:Задачи Сформировать понятие пропорция, найти определение Золотого сечения, изучить литературу, связанную с Золотым сечением. Развивать чувство гармонии, прекрасного. Показать практическое применение этого понятия, провести эксперементы с элементами Золотого сечения. Учиться анализировать и делать выводы.
4 слайд Описание слайда:
Описание слайда:Определение Золотого сечения Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей a : b = b : c Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
5 слайд Описание слайда:
Описание слайда:История золотого сечения Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.
6 слайд Описание слайда:
Описание слайда:История золотого сечения В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-ой книге «Начал» дается геометрическое построение золотого деления.
7 слайд Описание слайда:
Описание слайда:Где мы встречаемся с Золотым сечением в жизни? Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках «упакованы» по логарифмическим спиралям, завивающимся навстречу друг другу. Причем числа «правых «и «левых » спиралей, всегда относятся друг к другу, как соседние числа Фибоначчи.
8 слайд Описание слайда:
Описание слайда:Где мы встречаемся с Золотым сечением в жизни? У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8.
9 слайд Описание слайда:
Описание слайда:Где мы встречаемся с Золотым сечением в жизни? Неудивительно, что стрекоза выглядит столь совершенной, ведь она создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
10 слайд Описание слайда:
Описание слайда:Золотое сечение в архитектуре и живописи Одним из красивейших произведений древнегреческой архитектуры является храм Парфенон (V в.до н.э.). В фасаде древнегреческого храма присутствуют золотые пропорции.
11 слайд Описание слайда:
Описание слайда:Золотое сечение в архитектуре и живописи Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
12 слайд Описание слайда:
Описание слайда:Как художники могут применять Золотое сечение? Художник и инженер Леонардо да Винчи изучавший и восхвалявший золотую пропорцию на протяжении всей своей жизни, назвал её «золотое сечение», он считал, что соразмерность, выражаемая отношением золотой пропорции наиболее приятна для глаза. В композиции своей знаменитой «Джоконды» Леонардо да Винчи использовал «золотой треугольник».
13 слайд Описание слайда:
Описание слайда:Как художники могут применять золотое сечение? Золотое сечение в картине И.И.Шишкина «Сосновая роща». На этой знаменитой картине с очевидностью просматриваются мотивы золотого сечения.
14 слайд Описание слайда:
Описание слайда:Как художники могут применять золотое сечение? Скульпторы утверждают, что талия делит совершенное человеческое тело отношении «золотого сечения»
15 слайд Описание слайда:
Описание слайда:Золотые пропорции в частях тела человека Немецкий исследователь золотого сечения профессор Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление точкой пупка – важнейший показатель золотого сечения
16 слайд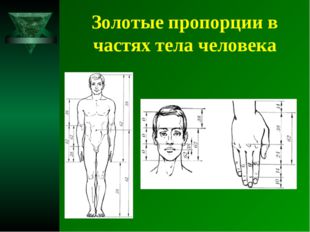 Описание слайда:
Описание слайда:Золотые пропорции в частях тела человека
17 слайд Описание слайда:
Описание слайда:Экспериментальная часть Учебник длина ширина отношение «Русский язык» 220 мм 141 мм 0,64 «Математика» 216 мм 170 мм 0,79 «Биология» 240 мм 168 мм 0,70 «История » 218 мм 167 мм 0,77
18 слайд Описание слайда:
Описание слайда:Экспериментальная часть «Золотое сечение» и 6 г класс В эксперименте приняли участие 23 человека. Измерили – рост (А), расстояние от пола до талии (В), и от талии до макушки головы (С). Нашли отношение В:А и С:В. Золотое сечение составляет 0,618. Результаты: у 82% в отношении присутствует 0,6….; у 23% отношение равно 0,61-0,62. Самые пропорциональные телосложения оказались у 4-х учеников (17%). Их имена:….
19 слайд Описание слайда:
Описание слайда:Заключение Общие выводы Золотое сечение – это один из основных основополагающих принципов природы; Закономерности Золотого сечения заложены в подсознании человека, использовались и используются архитекторами в своих работах; Золотое сечение является отображением окружающего мира; С возрастом увеличивается количество людей, выбирающих Золотую пропорцию; Золотое сечение имеет большое применение в нашей жизни.
20 слайд Описание слайда:
Описание слайда:Список ресурсов http://www.abc-people.com/idea/zolotsech/ http://n-t.ru/tp/iz/zs.htm http://tmn.fio.ru/works/04x/304/p3_4.htm http://www.arstudia.ru/kazakov/2.html http://e-project.redu.ru/mos/images/blds.htm

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-114797
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Стандарты общеобразовательной учебной программы Золотого сечения по математике
Добро пожаловать преподавателям, учителям, родителям и ученикам на страницу Академии Золотого сечения.
Золотое сечение встречается не только в природе и искусстве, но и в стандартах математики Common Core Curriculum. Эта страница предназначена для преподавателей, родителей и студентов, которые ищут самую лучшую и точную информацию о золотом сечении. Вы можете вернуться на эту страницу, просто перейдя по легко запоминающейся ссылке на Goldenratio.академия в вашем браузере.
Разделение математики и мифов: обучение золотому сечению фактам, а не вымыслам.
Много информации о золотом сечении доступно из различных источников, но удивительно, насколько она неверна. Это увековечивает как миф или городская легенда. Даже контент, подготовленный докторами математики и образовательными источниками, такими как Discovery Channel, содержит ошибки.
Моя цель — предоставить вам ресурсы, чтобы предоставить нашим студентам самую лучшую доступную информацию по этой увлекательной теме.В качестве фона я занимаюсь исследованием и написанием статей на эту тему на этом сайте с 1997 года. Я разработал программное обеспечение для проектирования и анализа с золотым сечением, доступное с 2004 года, которое используется для исследований на этом сайте пользователями более чем в 70 странах. Я переписывался с сотнями людей в самых разных областях, которые внесли свой вклад в более чем 100 страниц информации о золотом сечении на этом сайте.
Эта страница включает в себя ряд ресурсов по Золотому сечению, которые перечислены ниже.Ваши комментарии или предлагаемые ресурсы приветствуются.
GoldenNumber.net содержание сайта
Этот сайт включает в себя следующие категории:
- Phi — Основные понятия, история и другие интересные фоны на phi, 1.618, золотом сечении
- Дизайн — применение золотого сечения в искусстве, архитектуре и во всех видах дизайна
- Красота — Влияние золотого сечения на восприятие красоты лица человека
- Жизнь — проявления золотого сечения в физических измерениях людей, животных и растений
- Math — Уникальные математические свойства золотого сечения и множество способов его вычисления.
- Геометрия — Появление золотого сечения в геометрии и множество способов его построения
- Markets — Применение последовательности Фибоначчи и золотого сечения на фондовых рынках и обмене иностранной валюты
- Космос — проявления золотого сечения в солнечной системе и вселенной
- Богословие — Появление золотого сечения в Священных Писаниях и наблюдения за его значением Блог
- — Другие статьи общего интереса
- Карта сайта — полный список всего содержимого этого сайта.
Настоятельно рекомендуемые статьи
Темы Золотого сечения, которые часто рассматриваются в основных математических стандартах различных государственных учебных программ
Планы, задания и проекты уроков Золотого сечения
После просмотра десятков веб-сайтов в поисках хороших уроков и заданий мы рекомендуем следующие ресурсы:
Рекомендуемое программное обеспечение золотого сечения, датчики золотого сечения, штангенциркуль с золотой серединой и другие инструменты
- PhiMatrix — Программное обеспечение для проектирования и анализа золотого сечения для Windows и Mac.Предоставляет сетки, которые накладываются на любую другую программу или изображение на экране, чтобы легко найти или применить золотое сечение. Бесплатная двухнедельная пробная версия со скидкой 50% на странице загрузки. Штангенциркуль
- Golden Ratio — для общего использования при измерении золотого сечения. Доступен на Amazon в различных размерах
- Измерительные щупы «Золотая середина» — для более точного использования и применения в медицине / стоматологии
Онлайн-видео:
В Интернете очень мало видео с золотым сечением достаточно высокого качества, чтобы рекомендовать их в качестве учебных пособий.Некоторые показывают иллюстрации равноугольных / логарифмических спиралей, которые, хотя и распространены в природе, не основаны на золотом сечении или спиралях Фибоначчи. Некоторые стремятся опровергнуть золотое сечение, заявляя, что никаких доказательств не существует, игнорируя доказательства, которые действительно существуют, и не предъявляя никаких доказательств, подтверждающих свои утверждения. Некоторые утверждают, что это доказательство существования Бога, хотя для его многочисленных проявлений могут существовать как естественные, так и сверхъестественные причины. Следующие видео имеют хорошее качество и точность по содержанию:
Интернет-контент, который следует использовать с осторожностью или избегать:
- Дональд Дак в Mathmagic Land — классическое видео Диснея, которое включает в себя раздел о золотом сечении, который начинается на отметке 7:12 минуты видео.В этом видео рассказывается о некоторых чудесных принципах математики и геометрии и их применении в природе и искусстве. К сожалению, он также содержит некоторые чрезмерные упрощения применения золотого сечения, которые, несомненно, привели к некоторой путанице и противоречиям по этой теме. К ним относятся его содержимое на Парфеноне, Нотр-Даме, Штаб-квартире Организации Объединенных Наций, Моне Лизе и оболочке Наутилуса, где оно подразумевает точное отображение золотого сечения в тех случаях, когда фактические размеры только близко приближаются к золотому сечению, или используют его только в часть заявленных экземпляров.См. Ссылки на статьи в предыдущем предложении для получения дополнительных сведений по каждой теме.
- Discovery Education — Золотое сечение — на видео в 1:24 неверно указано, что золотой прямоугольник в 5 раз шире, чем высота (должен быть в 1,618 раза шире). Неправильная иллюстрация золотого прямоугольника на картине Да Винчи «Благовещение».
- Золотое сечение и числа Фибоначчи: факты против вымысла Стэнфордского университета и математические встречи — Фибоначчи и золотое сечение раскрыты — В постановке Стэнфордского университета есть хорошая информация о рядах Фибоначчи, но неверно категорически утверждается, что нет доказательств для многих из них. проявления золотого сечения в искусстве, архитектуре, человеческом теле и т. д.Доказательства вполне очевидны, если у вас есть подходящие инструменты и вы потратите время на изучение предмета, как это описано на этом сайте.
Справочная информация по математическим стандартам Common Core учебной программы для золотого сечения
Стандарты математики 7-го класса включают раздел «Соотношения и пропорциональные отношения». Стандарты требуют «Признавать и представлять пропорциональные отношения между величинами», а один из них требует «Определить константу пропорциональности (удельная ставка) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.”
В 2009 году лидеры различных штатов начали работу по разработке Общих основных государственных стандартов. Это было сделано в знак признания ценности последовательных реальных целей обучения, которые обеспечили бы подготовку всех выпускников средней школы к колледжу, карьере и жизни. К началу 2000-х годов в каждом штате были разработаны и приняты собственные стандарты обучения, определяющие, что должны уметь ученики 3–8 классов и старших классов. Это отсутствие стандартизации было одной из причин, по которой штаты решили разработать общие основные государственные стандарты.
В процессе разработки стандарты были разделены на две категории:
- Стандарты готовности к колледжу и карьере, которые касаются того, что учащиеся должны знать и понимать к моменту окончания средней школы.
- Стандарты K-12, отвечающие ожиданиям от начальной до средней школы
Разработаны стандарты английского языка по искусству и математике. Стандарты математики 7-го класса включают раздел «Соотношения и пропорциональные отношения».Стандарты требуют «Признавать и представлять пропорциональные отношения между величинами», и один из них требует «Определить константу пропорциональности (удельная ставка) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений».
,Открытие Фи: Золотое сечение — Задание
Открытие Фи: Золотое сечение — Задание — Обучение инженерииБыстрый просмотр
Уровень оценки: 7 (6-8)
Требуемое время: 1 час
Расходные материалы на группу: 5,00 долларов США
Кроме того, расходными материалами длительного пользования являются комплект LEGO® MINDSTORMS® EV3 стоимостью 300 долларов США для демонстрации для учителя; одного достаточно, и он очень многоразовый.
Размер группы: 2
Зависимость деятельности:
Тематические области: Алгебра, измерение, число и операции
Подпишитесь на нашу рассылку новостей


Резюме
Студенты открывают математическую константу фи, золотое сечение, в ходе практических занятий.Они измеряют размеры «природных объектов» — звезды, раковины наутилуса и костей человеческих рук — и вычисляют отношения измеренных величин, близкие к фи. Затем студенты изучают базовое определение математической последовательности, в частности последовательности Фибоначчи. Путем определения соотношений последовательных членов последовательности они находят числа, близкие к фи. Они решают головоломку с квадратами, которая создает приблизительную спираль Фибоначчи. Наконец, инструктор демонстрирует правило последовательности Фибоначчи с помощью робота LEGO® MINDSTORMS® EV3, оснащенного ручкой.Робот (уже созданный в рамках сопутствующего упражнения «Последовательность Фибоначчи и роботы») рисует спираль Фибоначчи, похожую на форму наутилуса.Инженерное соединение
Phi, возможно, одна из самых важных математических констант. От великих пирамид до Парфенона это число присутствует в формах и масштабах многих инженерных проектов и архитектурных достижений. В искусстве эта константа используется для количественной оценки эстетической красоты, например, в «Моне Лизе » да Винчи, или даже лица красивого человека.Это упражнение основано на вездесущности этого числа, чтобы познакомить студентов с дискретной математикой, и расширяет идею математической последовательности до базового программирования с использованием программного обеспечения EV3 MINDSTORMS.
Цели обучения
После этого занятия студенты должны уметь:
- Объясните общий термин последовательности Фибоначчи.
- Опишите примеры фи в природе.
- Определите фи как предел отношения членов последовательности Фибоначчи.
Образовательные стандарты Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными предметами K-12,
образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) ,
проект D2L (www.achievementstandards.org).
В ASN стандарты имеют иерархическую структуру: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика;
внутри типа по подтипу, затем по классу, и т. д. .
Общие основные государственные стандарты — математика
- Бегло делите многозначные числа по стандартному алгоритму.(Grade
6) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Бегло складывайте, вычитайте, умножайте и делите десятичные дроби, используя стандартный алгоритм для каждой операции.(Grade
6) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Используйте рассуждение о соотношении для преобразования единиц измерения; соответствующим образом манипулировать и преобразовывать единицы измерения при умножении или делении величин.(Grade
6) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Изучите закономерности ассоциации в двумерных данных.(Grade
8) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Помните, что последовательности — это функции, иногда определяемые рекурсивно, домен которых является подмножеством целых чисел.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ
Нью-Йорк — математика
- Используйте рассуждение о соотношении для преобразования единиц измерения; соответствующим образом манипулировать и преобразовывать единицы измерения при умножении или делении величин.(Grade
6) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Бегло делите многозначные числа по стандартному алгоритму.(Grade
6) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Бегло складывайте, вычитайте, умножайте и делите десятичные дроби, используя стандартный алгоритм для каждой операции.(Grade
6) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Изучите закономерности ассоциации в двумерных данных.(Grade
8) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
- Помните, что последовательности — это функции, иногда определяемые рекурсивно, домен которых является подмножеством целых чисел.(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом? Спасибо за ваш отзыв!
Какое альтернативное выравнивание вы предлагаете для этого контента?
Список материалов
Каждой группе необходимо:
Поделиться со всем классом:
- несколько ламинированных копий трехстраничного приложения Natural Pictures, достаточно, чтобы каждая группа могла иметь хотя бы одно изображение одновременно
Для демонстрации роботов-учителей:
Примечание: это упражнение также можно проводить с более старым (и больше не продается) комплектом LEGO MINDSTORMS NXT вместо EV3.
.Рабочие листы и приложения
Посетите [www.teachengineering.org/activities/view/nyu_phi_activity1], чтобы распечатать или загрузить.Больше подобной программы
Последовательность Фибоначчи и роботыИспользуя комплект робототехники LEGO® EV3, ученики конструируют и программируют роботов, чтобы проиллюстрировать и исследовать последовательность Фибоначчи. Разработав робота, который движется на основе последовательности чисел Фибоначчи, они могут лучше визуализировать, как быстро растут числа в последовательности.

Предварительные знания
Умение выполнять деление и понимание основной концепции функции.
Введение / Мотивация
Математическая константа фи изучалась по крайней мере с 300 г. до н. Э., Когда она была определена греческим математиком Евклидом.Формализация фи могла быть мотивирована его присутствием в пентаграмме, распространенном религиозном символе того времени. Он встречается повсюду в природе, от раковин улиток и головок семян цветов до многих растительных узоров, таких как ананасы, папоротники и шишки. И он играет ключевую роль в западной эстетике и архитектуре. Фи, как соотношение, занимает видное место в творчестве да Винчи и Дали. Кроме того, фи наблюдалась во многих областях математики, от геометрии, такой как регулярные пирамиды, до теории чисел, такой как аппроксимационная теорема Лагранжа.
 «Золотое сечение», фи, основанное на последовательности Фибоначчи, можно увидеть в природе в спирали раковин и в приятных пропорциях архитектурных узоров, таких как древний Парфенон в Афинах, Греция. Copyright
«Золотое сечение», фи, основанное на последовательности Фибоначчи, можно увидеть в природе в спирали раковин и в приятных пропорциях архитектурных узоров, таких как древний Парфенон в Афинах, Греция. Copyright
Copyright © (слева) 2004 Microsoft Corporation, One Microsoft Way, Redmond, WA 98052-6399 USA. (справа) Гленларсон, Википедия (США) http://en.wikipedia.org/wiki/File:Acropolis_of_Athens_01361.JPG
Во время сегодняшнего занятия вы «откроете» фи двумя способами: посредством моделирования и изучения конкретных математических объектов.
Математический источник фи, последовательность Фибоначчи, представляет собой последовательность, образованную добавлением двух последовательных членов, чтобы получить следующий член. (При необходимости используйте классную доску или проектор, чтобы показать студентам, как генерировать следующие термины.) Если я начну с 0 и 1, кто может сказать мне следующие несколько чисел в последовательности? (Ответ: 1, 2, 3, 5.)
В части этого упражнения, посвященной квадратам, вы можете решить эту головоломку множеством способов, создавая прямоугольники все большего размера с длинами сторон последовательности Фибоначчи.Далее вы подумаете, как эти прямоугольники соотносятся друг с другом. Оказывается, отношение последовательных членов последовательности Фибоначчи равно фи.
(Предполагая, что вы выполнили сопутствующее упражнение, Последовательность Фибоначчи и роботы …) Теперь давайте подумаем о роботах, которых мы запрограммировали с помощью последовательности Фибоначчи. Как робот следовал вашим приказам (программе) при выполнении последовательности Фибоначчи? Робот точно выполнил ваши приказы? Насколько точно вы должны были программировать робота? (Ожидайте, что учащиеся поймут, что робот делает только то, что ему говорят; например, он не может совершать ошибки сложения.) Этот тип точности необходим инженерам при программировании роботизированных технологий, таких как роботизированные манипуляторы, используемые в литейных цехах или хирургических отделениях. Сегодня мы также собираемся запрограммировать робота, чтобы он следил за соотношением фи и посмотрим, что произойдет.
Процедура
До начала деятельности
- Соберите материалы и сделайте копии Квадратов мозгового штурма и Рабочих листов для авантюристов по математике (по одному на каждых двух учеников).
- Распечатайте и ламинируйте достаточное количество копий трехстраничного документа Natural Pictures, чтобы каждая группа могла иметь хотя бы одно изображение в любой момент времени.
- Используя шаблон пазла «Квадраты», вырежьте и ламинируйте кусочки рекламного щита, отметив размер на каждом кусочке, чтобы получилось по одной головоломке на группу.
- Создайте и запрограммируйте робота LEGO EV3, как описано в упражнении «Последовательность Фибоначчи и роботы».
- Используйте скотч, чтобы прикрепить к полу большие листы бумаги для рисования робота.
- Используйте ленту, чтобы прикрепить маркер к роботу, чтобы маркер рисовал на полу при движении робота.
Со студентами
- Разделите класс на пары учеников.
- Раздайте каждой группе: линейку, калькулятор, лист с квадратами для мозгового штурма, рабочий лист, головоломку с квадратами и одну картинку.
- Начните с того, что команды выполнят задание «Квадраты мозгового штурма», следуя инструкциям на листе, как описано в разделе «Оценка».
- Введите понятие математической константы, в частности фи, как представлено в разделе «Введение / мотивация». Примечание. Студенты, возможно, уже знакомы с константой «пи», и это может быть хорошей отправной точкой для дальнейшего обсуждения констант.
 Рис. 1. Три «естественных изображения», которые студенты измеряют для вычисления золотого сечения, phi.copyright
Рис. 1. Три «естественных изображения», которые студенты измеряют для вычисления золотого сечения, phi.copyrightCopyright © 2010 Николь Абайд, AMPS, NYU-Poly
- Покажите все три «естественных изображения» всему классу и назовите каждое: человеческая рука, наутилус и пятиконечная звезда (см. Рисунок 1).Каждый из этих объектов может рассматриваться как хранящий золотое сечение, фи. Попросите студенческие команды заполнить часть 1 рабочих листов, выполнив следующие действия:
- Попросите каждую команду назначить замерщика и регистратора.
- Глядя на картинку, измеритель с помощью линейки измеряет длины A, B и C и передает эти числа на самописец.
- Регистратор записывает измерения в рабочий лист и использует калькулятор для определения соотношений измеренных длин, заполняя оставшуюся часть части 1 рабочего листа.
- Команды обмениваются картинками и повторяют это упражнение, пока все группы не рассмотрят все три картинки.
- Проведите обсуждение в классе, чтобы сравнить результаты. Спросите: Какова была тенденция соотношений, изображенных на фотографиях?
 Рис. 2. Завершенная головоломка с квадратами, которая представляет собой мозаику из квадратов, размеры сторон которых являются последовательными числами Фибоначчи. Диагональные линии, проходящие через каждый квадрат, приблизительно соответствуют форме золотой спирали. Авторское право
Рис. 2. Завершенная головоломка с квадратами, которая представляет собой мозаику из квадратов, размеры сторон которых являются последовательными числами Фибоначчи. Диагональные линии, проходящие через каждый квадрат, приблизительно соответствуют форме золотой спирали. Авторское правоCopyright © 2010 Николь Абайд, AMPS, NYU-Poly
- Ввести понятие математической последовательности, в частности последовательности Фибоначчи.
- Обратитесь к истории и информации, представленной в разделе Введение / Мотивация.
- Пройдите вместе с классом первые четыре или пять элементов последовательности и составьте первые две или три части головоломки с квадратами.
- Пусть пары вместе заполнят Часть 2 рабочего листа, найдя больше членов последовательности Фибоначчи, а также соотношения следующих друг за другом членов.
- Попросите учащихся собрать головоломку с квадратами (см. Рис. 2).
- Снова соберите класс для окончательного обсуждения ответов на листе и головоломки с квадратами. Свяжите присутствие фи в этом математическом объекте. Обсудите взаимосвязь длин сторон квадратов в головоломке и последовательности Фибоначчи.
 Рис. 3. Пример программирования LEGO MINDSTORMS для робота LEGO EV3, показывающий серию блоков программирования, в частности, блоки движения двигателя, соединенные через блоки последовательности. Эта конкретная программа предназначена для перемещения робота LEGO EV3 по спирали Фибоначчи.Блоки движения двигателя запрограммированы на использование расстояний в соответствии с последовательностью Фибоначчи. Авторское право
Рис. 3. Пример программирования LEGO MINDSTORMS для робота LEGO EV3, показывающий серию блоков программирования, в частности, блоки движения двигателя, соединенные через блоки последовательности. Эта конкретная программа предназначена для перемещения робота LEGO EV3 по спирали Фибоначчи.Блоки движения двигателя запрограммированы на использование расстояний в соответствии с последовательностью Фибоначчи. Авторское правоCopyright © LEGO MINDSTORMS
 Рис. 4. Робот LEGO EV3 с прикрепленной ручкой. Авторское право
Рис. 4. Робот LEGO EV3 с прикрепленной ручкой. Авторское право
Авторское право © Университет Колорадо в Боулдере
- Продемонстрируйте, как робот LEGO EV3 движется в соответствии с правилом последовательности Фибоначчи. Если возможно, отобразите измененный код MINDSTORMS из сопутствующего действия (Последовательность Фибоначчи и роботы), в котором робот проходит расстояния, продиктованные последовательностью Фибоначчи, вместе с поворотами под прямым углом, см. Рисунок 3.Если студенты не знакомы с программным обеспечением, объясните компоненты программы. Затем проведите демонстрацию:
- Установите робота на листах бумаги, приклеенных к полу, с прикрепленным маркером таким образом, чтобы при движении робота проводилась линия, см. Рис. 4.
- Попросите учащихся предсказать, какую форму нарисует робот.
- Запустить программу в соответствии с наблюдениями класса. (Робот должен нарисовать спираль Фибоначчи.)
- Обсудите, как с помощью робота мы можем визуально воспринимать фи, встроенные в последовательность Фибоначчи.
- Завершите выполнение действий по оценке, предложенных в разделе «Оценка».
Словарь / Определение
предел последовательности: число, к которому приближаются члены последовательности, когда человек проходит через порядок последовательности.
phi: математическая константа, равная приблизительно 1,61803, вычисленная как отношение между последовательными членами последовательности Фибоначчи.Чем выше вы поднимаетесь в последовательности Фибоначчи, тем точнее соотношение между двумя последовательными числами приближается к фи. Также называется «золотым сечением». (Произносится: «плата»)
последовательность (числовая): упорядоченный набор чисел, упорядоченный в соответствии с правилом.
термин: одно из чисел в последовательности.
оценка
Оценка перед началом деятельности
Квадраты для мозгового штурма : разделите класс на группы по два человека.Раздайте каждой группе по экземпляру квадратов для мозгового штурма и линейке. Попросите учащихся в паре найти математические модели в пределах размеров квадратов на спиральном рисунке в раздаточном материале. Дайте учащимся пять минут, чтобы они пришли к трем основанным на измерениях наблюдениям за тем, как квадраты соотносятся друг с другом. По истечении пяти минут попросите несколько групп поделиться с классом тем, что они узнали. Скажите классу, что к концу этого упражнения они будут точно знать, как эти квадраты соотносятся друг с другом!
Мероприятие Встроенная оценка
Рабочий лист : Попросите каждую пару учеников заполнить Рабочий лист «Математические приключения», произвести измерения и вычисления и ответить на вопросы.Просмотрите их ответы, чтобы оценить их понимание пройденного материала.
Прогноз : чтобы увидеть, следуют ли ученики, после объяснения программы робота, попросите учащихся предсказать форму, которую, по их мнению, робот будет рисовать.
Оценка после работы
Настройка последовательности : Предложите учащимся подумать о том, что произошло бы, если бы мы хотели, чтобы робот прошел другое начальное расстояние. Изменит ли это соотношение, которое раньше давало нам фи? (Ответ: Нет! Даже если отдельные числа изменятся, соотношения будут пропорционально такими же и все равно будут приближаться к фи.Помните, что phi определяется соотношением терминов и не зависит от начальных условий.)
Инженерное дело Phi : Предложите учащимся начать с размышлений о фи в природе, а затем провести мозговой штурм по инженерным проектам, имитирующим природу и золотое сечение как естественную природу (так называемая биомимикрия). Например, было обнаружено, что спиральные вентиляторы и насосы, имеющие ту же форму, что и наутилус, повышают эффективность использования энергии и зданий. В качестве примера см. «PaxFan: эффективный спиральный вентилятор» на веб-сайте компании Treehugger Discovery по адресу https: // www.treehugger.com/interior-design/paxfan-an-effective-spiral-fan.html
Советы по устранению неполадок
Протестируйте программу робота перед уроком и убедитесь, что лист бумаги достаточно велик, чтобы робот мог нарисовать хотя бы пару витков спирали.
Расширения деятельности
Перед этим упражнением проведите сопутствующее задание «Последовательность Фибоначчи и роботы», в котором студенческие команды программируют робота LEGO EV3 на движение на основе последовательности чисел Фибоначчи, помогая им визуализировать, как быстро растут числа в последовательности. ,
Золотое сечение — это в основном эстетика. Предложите учащимся выбрать одну конструкцию или технологию и представить, что они работают в инженерной фирме, которой было поручено каким-либо образом улучшить конструкцию. Попросите их написать абзацы о том, как они могли бы улучшить эстетику дизайна, в частности, используя фи.
Масштабирование активности
Для старших классов попросите учащихся построить и запрограммировать робота, как в упражнении «Последовательность Фибоначчи и роботы», используя концепцию переменных, разработанную в этом упражнении.Также обсудите, как фи появляется в соотношениях членов последовательности Фибоначчи независимо от начальных условий. Проиллюстрируйте это с помощью робота, изменив стартовые расстояния.
Ссылки
Ливио, Марио. Золотое сечение . Нью-Йорк, Нью-Йорк: Broadway Books, 2002.
Обара, Самуэль. «Золотое сечение в искусстве и архитектуре». Департамент математического образования.Университет Джорджии. Проверено 22 декабря 2011 г. (Большая история, пояснения и наглядные пособия для чая
.Золотое сечение — Люди читают это? Показывается 1-7 из 7
Люди это читают?
 Вау, это одна из причин, по которой я подписался, чтобы найти людей, которые читают эти материалы. Я думал, что я одинокий компьютерщик, но приятно видеть, что Гикдум — город, который живет и процветает. Вперед Geek Squad !!!!
Вау, это одна из причин, по которой я подписался, чтобы найти людей, которые читают эти материалы. Я думал, что я одинокий компьютерщик, но приятно видеть, что Гикдум — город, который живет и процветает. Вперед Geek Squad !!!!  Согласовано!!!!!! Это довольно интересная книга. Мне пришлось перечитать несколько страниц, но в книгах осталось много информативных тем.Отличное сочетание истории и математики.
Согласовано!!!!!! Это довольно интересная книга. Мне пришлось перечитать несколько страниц, но в книгах осталось много информативных тем.Отличное сочетание истории и математики.  Ах да, Джеффри, команда компьютерщиков сильна. На самом деле моя одинокая татуировка — это символ ФИ.
Ах да, Джеффри, команда компьютерщиков сильна. На самом деле моя одинокая татуировка — это символ ФИ.  Конечно, люди читают это. Я бы мог представить себе только супер-компьютерщиков;) Хорошее прочтение — это то, что есть. Книга о том, как появился 0 (ноль). Довольно интересно.
Конечно, люди читают это. Я бы мог представить себе только супер-компьютерщиков;) Хорошее прочтение — это то, что есть. Книга о том, как появился 0 (ноль). Довольно интересно.  Да, многие из нас читают этот материал. Я люблю естественные науки / математику. Я нашел эту книгу очень интересной — в конце концов, я выступил перед учеником 7-го класса моего сына по математике о золотом сечении (я банкир, а не математик).
Да, многие из нас читают этот материал. Я люблю естественные науки / математику. Я нашел эту книгу очень интересной — в конце концов, я выступил перед учеником 7-го класса моего сына по математике о золотом сечении (я банкир, а не математик). Обожаю эту книгу. Я несколько раз перечитывал его части. Еще мне нравится Zero: THe History of a Dangerous Idea.
Обожаю эту книгу. Я несколько раз перечитывал его части. Еще мне нравится Zero: THe History of a Dangerous Idea.  Хорошая книга, но не в Лиге истории PI или Zero: Биография опасной идеи. Чувствуется, что у автора есть несколько страниц, которые он обязан написать, и он прогоняет дохлую лошадь через многие главы.
Хорошая книга, но не в Лиге истории PI или Zero: Биография опасной идеи. Чувствуется, что у автора есть несколько страниц, которые он обязан написать, и он прогоняет дохлую лошадь через многие главы. вернуться наверх

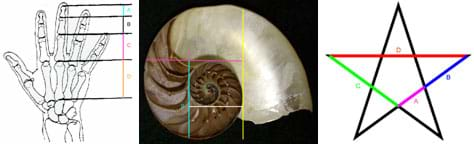 Рис. 1. Три «естественных изображения», которые студенты измеряют для вычисления золотого сечения, phi.copyright
Рис. 1. Три «естественных изображения», которые студенты измеряют для вычисления золотого сечения, phi.copyright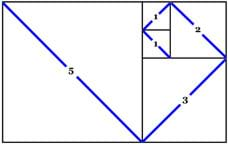 Рис. 2. Завершенная головоломка с квадратами, которая представляет собой мозаику из квадратов, размеры сторон которых являются последовательными числами Фибоначчи. Диагональные линии, проходящие через каждый квадрат, приблизительно соответствуют форме золотой спирали. Авторское право
Рис. 2. Завершенная головоломка с квадратами, которая представляет собой мозаику из квадратов, размеры сторон которых являются последовательными числами Фибоначчи. Диагональные линии, проходящие через каждый квадрат, приблизительно соответствуют форме золотой спирали. Авторское право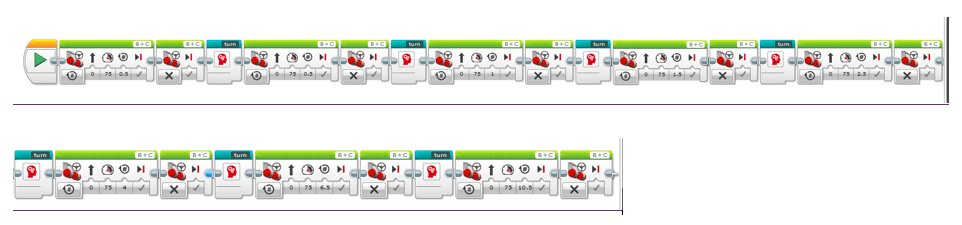 Рис. 3. Пример программирования LEGO MINDSTORMS для робота LEGO EV3, показывающий серию блоков программирования, в частности, блоки движения двигателя, соединенные через блоки последовательности. Эта конкретная программа предназначена для перемещения робота LEGO EV3 по спирали Фибоначчи.Блоки движения двигателя запрограммированы на использование расстояний в соответствии с последовательностью Фибоначчи. Авторское право
Рис. 3. Пример программирования LEGO MINDSTORMS для робота LEGO EV3, показывающий серию блоков программирования, в частности, блоки движения двигателя, соединенные через блоки последовательности. Эта конкретная программа предназначена для перемещения робота LEGO EV3 по спирали Фибоначчи.Блоки движения двигателя запрограммированы на использование расстояний в соответствии с последовательностью Фибоначчи. Авторское право