Срединный узел: Узел Австрийский проводник: схема, как вязать, видео

Узел Австрийский проводник: схема, как вязать, видео

В походных условиях без веревок не обойтись. Они широко используются в бытовых и страховочных целях. Навыки по завязыванию узлов пригодятся каждому, кто собирается в поход. Хоть туристические веревочные плетения и не самые простые, некоторые из них освоить достаточно легко.  Давайте подробно рассмотрим технику вязания узла проводник и его основные особенности.

Узел Австрийский проводник

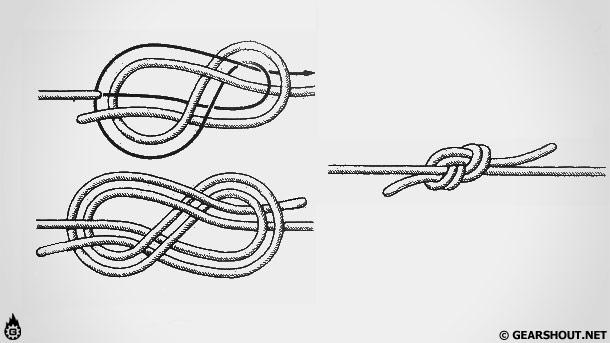
Самые крепкие и надежные — альпинистские, им смело можно доверять свою безопасность (Рисунок 1).

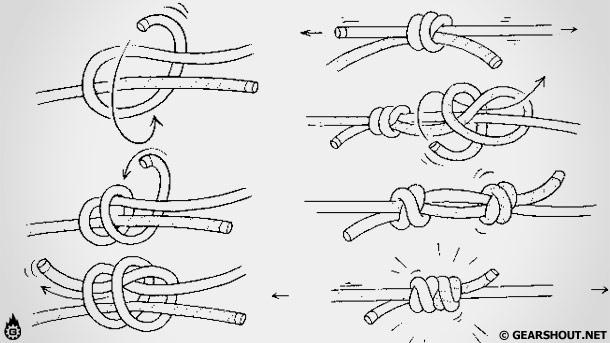
Рассмотрим, как вязать узел проводник, схема вязания и его ключевые особенности:

1. Он просто развязывается даже после снятия очень большой нагрузки;
2. Эффективен во всех направлениях и стабилен — не затягивается и не скользит;
3. Сохраняет запас прочности вашей веревки.

Рисунок 1. Узел Австрийский проводник

Есть у него и свои недостатки, которые, тем не менее, не мешают ему быть одной из универсальных страховочных бабочек:

1. Трудно завязывается, если свободна только одна рука и на вас надеты рукавицы;
2. Размеры готовой петли практически невозможно изменить;
3. Определить на глаз правильно ли удалось завязать тоже непросто;
4. Оба края веревок расходятся под углом, они не свисают параллельно.

Если предварительно потренироваться и освоить базовые принципы, то всех перечисленных проблем можно будет легко избежать.

История появления узла

По названию не сложно догадаться, что появился узелок именно в австрийских Альпах (Рисунок 2).

Рисунок 2. Австрийские Альпы — родина появления узла

Им организовывали крепежные точки по линии базовой веревки, закрепляли среднюю из них в общей связке.

Другие его наименования — бабочка и срединный.

Отличительной чертой от обычной восьмерки служила свободная затяжка в обе стороны и легкость в развязывании, отсутствие проскальзывания даже при сильном рывке одного из концов.

Где узел используется

Эта вязка имеет самое широкое применение (Рисунок 3):

• На фабриках и производствах;
• В морском и рыболовном деле;
• Альпинизме и туризме;
• Для бытовых нужд.

Рисунок 3. Сферы применения узла

УЗЛЫ (Пособие)

Узлы по ситуациям

1. Связать две верёвки одинакового диаметра (Встречный, встречная восьмёрка, грейпвайн, ткацкий, прямой)

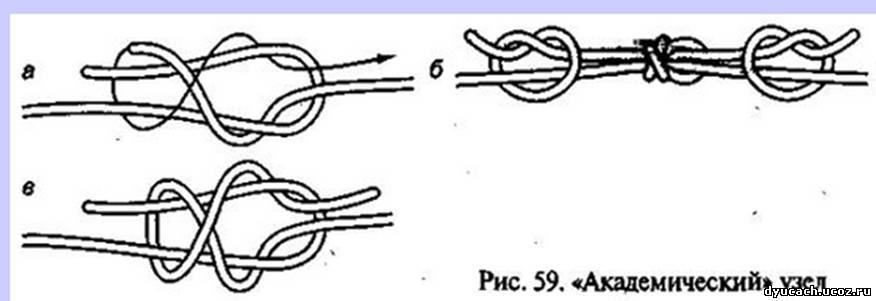
2. Связать две верёвки разного диаметра (Брамшкотовый, академический)

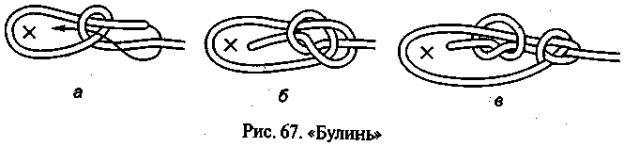
3. Завязать верёвку на опоре (Штык, булинь, стремя, карабинная удавка)

4. Узел на конце верёвки (Восьмёрка, проводник)

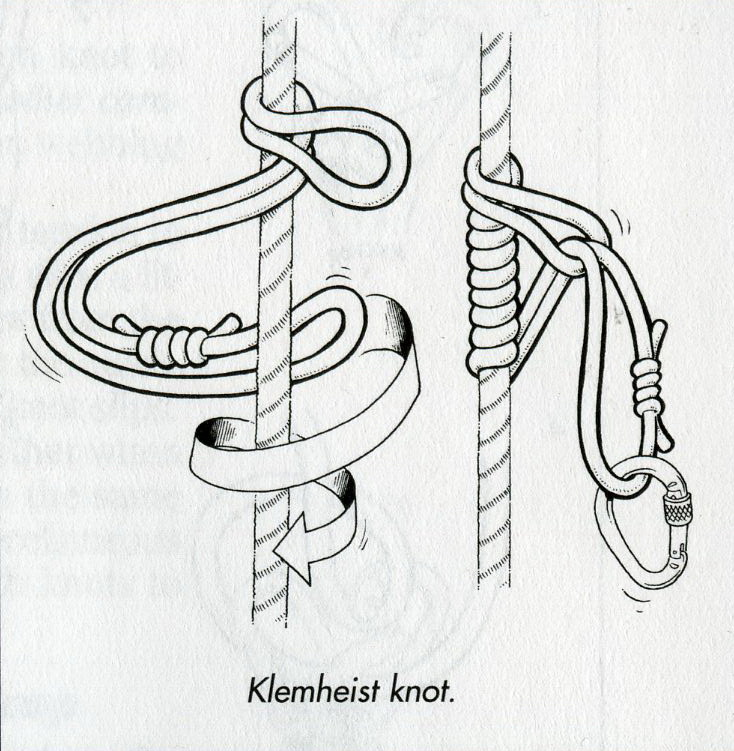
5. Завязать схватывающий узел (Прусик, автоблок, Бахмана)

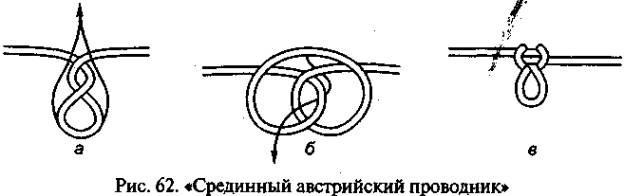
6. Завязать узел на середине верёвки (Серединный (австрийский) проводник)

7. Завязать двойной проводник (Двойную восьмёрку)

Узлы.

1). Встречный узел

2). Встречная восьмёрка

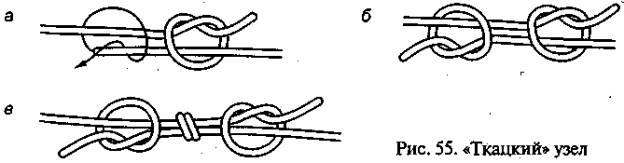
3). Ткацкий узел

4). Прямой узел

5). Грейпвайн

6). Брамшкотовый узел

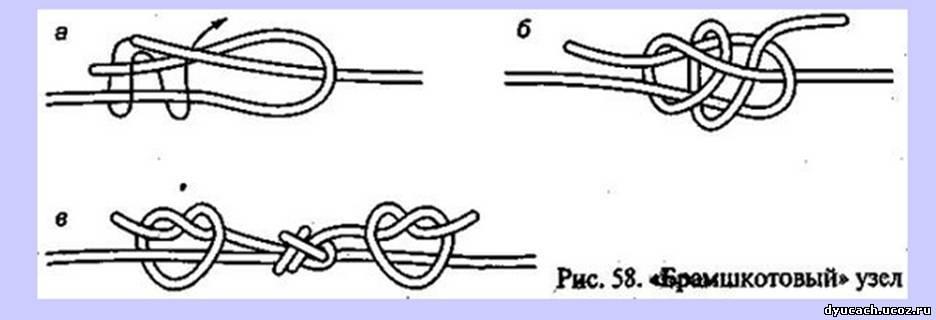
7). Академический узел

8). Узел Штык

9). Булинь

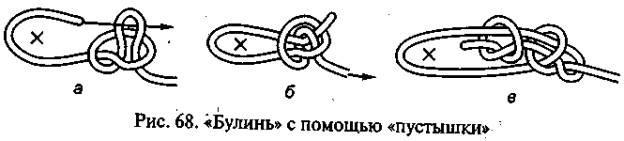
10). Карабинная удавка

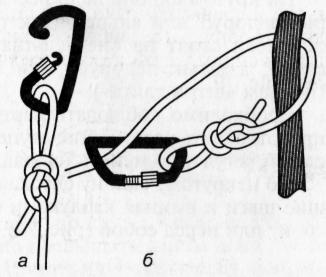
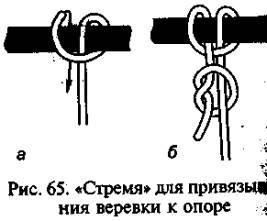
11). Стремя

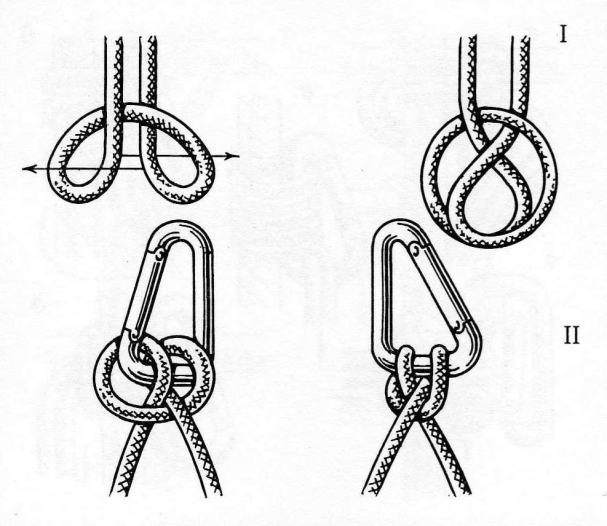
12). Проводник

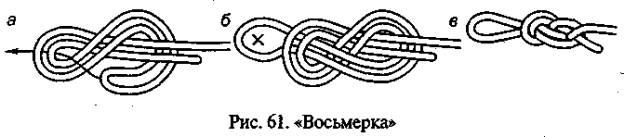
13). Восьмёрка

14). Схватывающий узел (

“Прусик”)

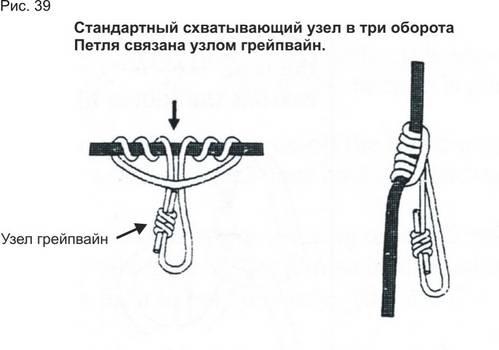
15). Узел “Бахмана” (Схватывающий)

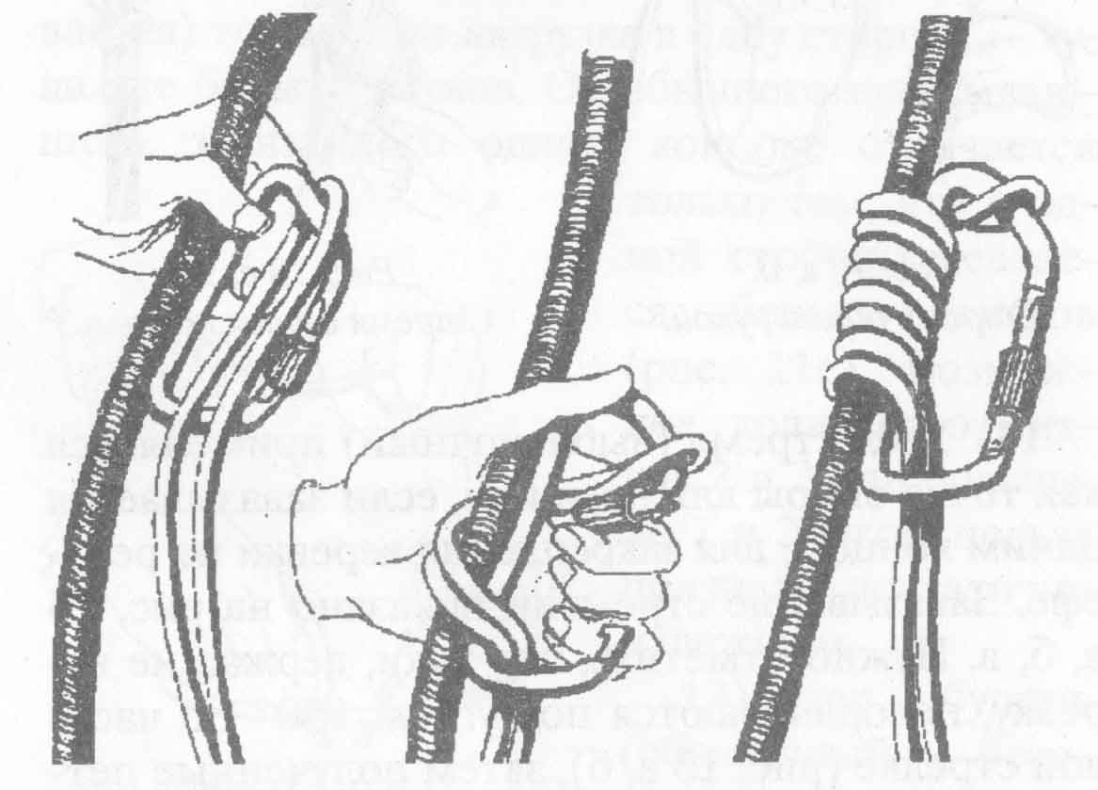
16). Узел “Автоблок” (Схватывающий)

17). Французский схватывающий (Узел “Машара”)

18). Серединный (австрийский) проводник

19). Двойной проводник

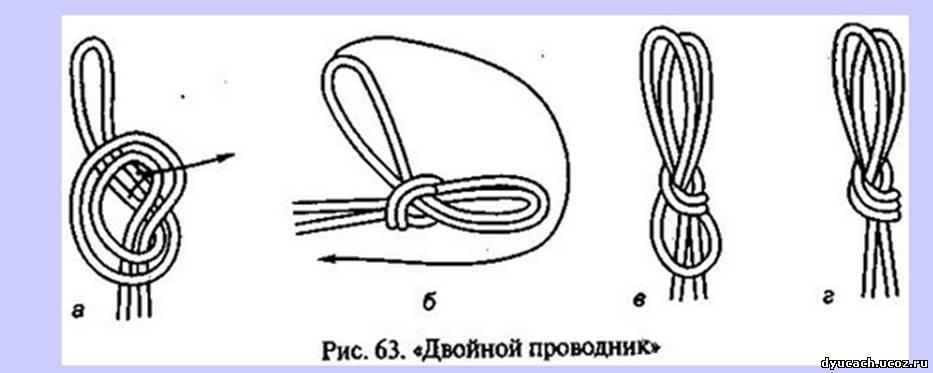
20). Двойная восьмёрка

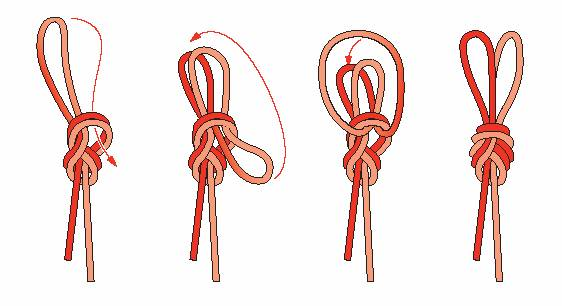
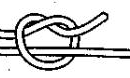
21). Контрольный узел.

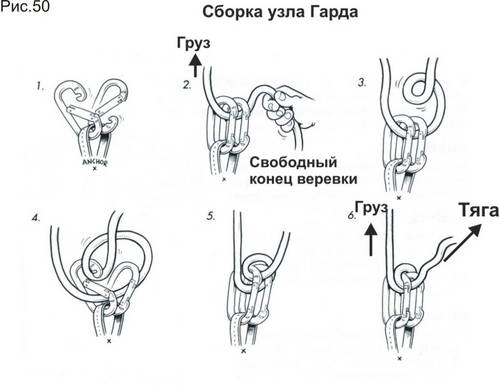
22). Узел “Гарда”. (Для подъёма по верёвке)

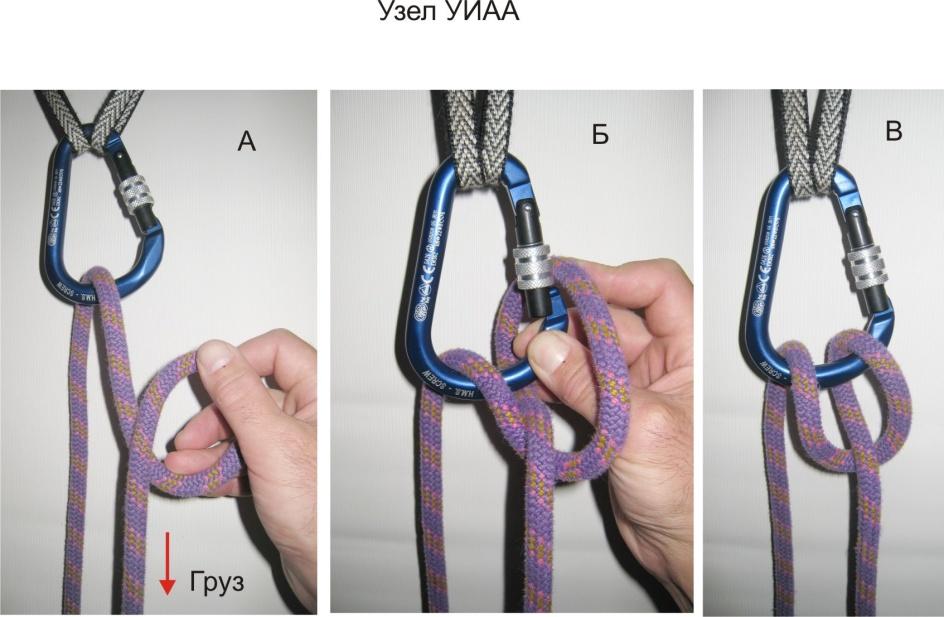
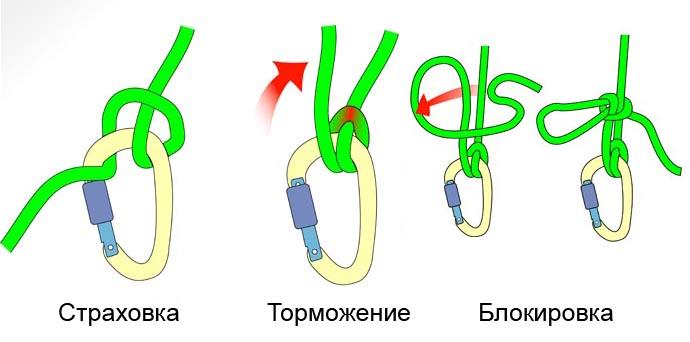
23). Узел УИАА (Для спуска по верёвке)

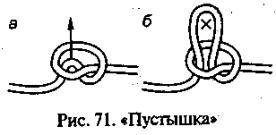
24). “Пустышка”

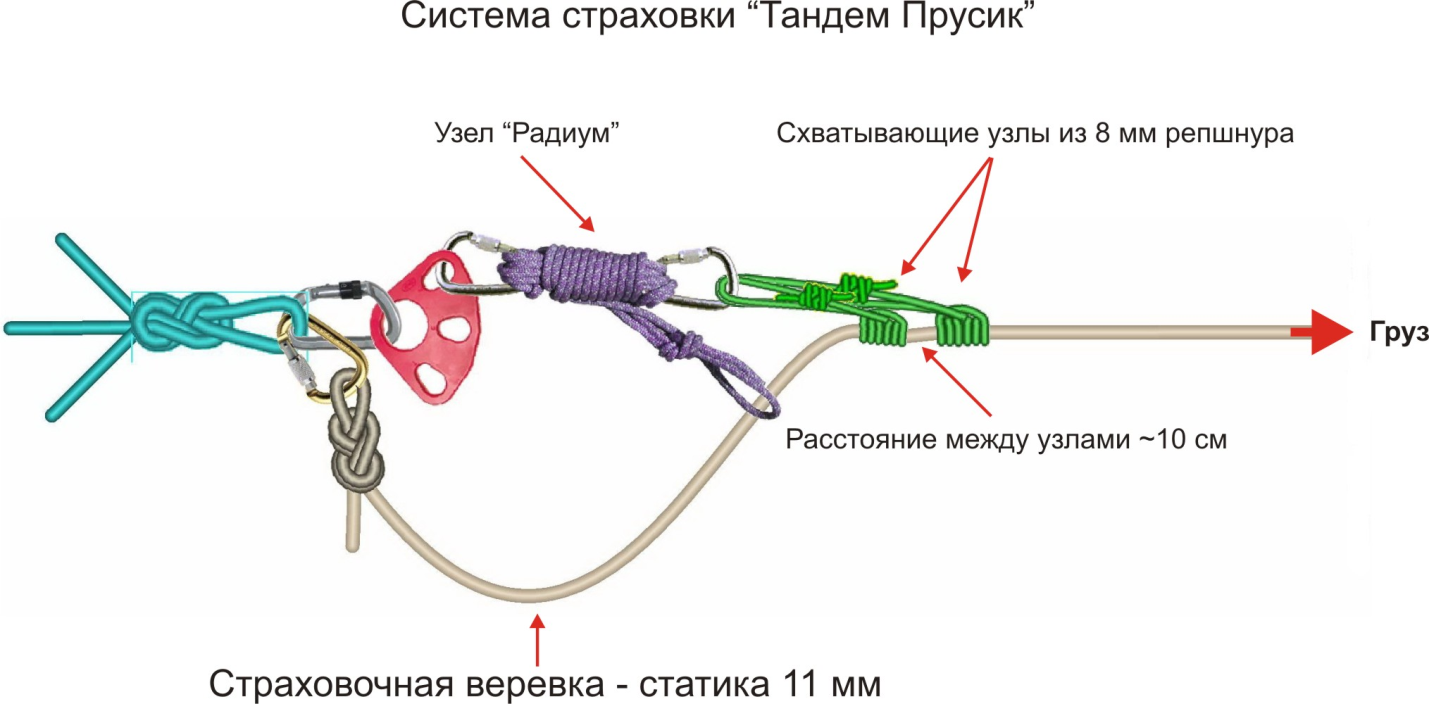
25). Узел ”Радиум

”

26). Система “Тандем Прусик” пример использования “радиума”.

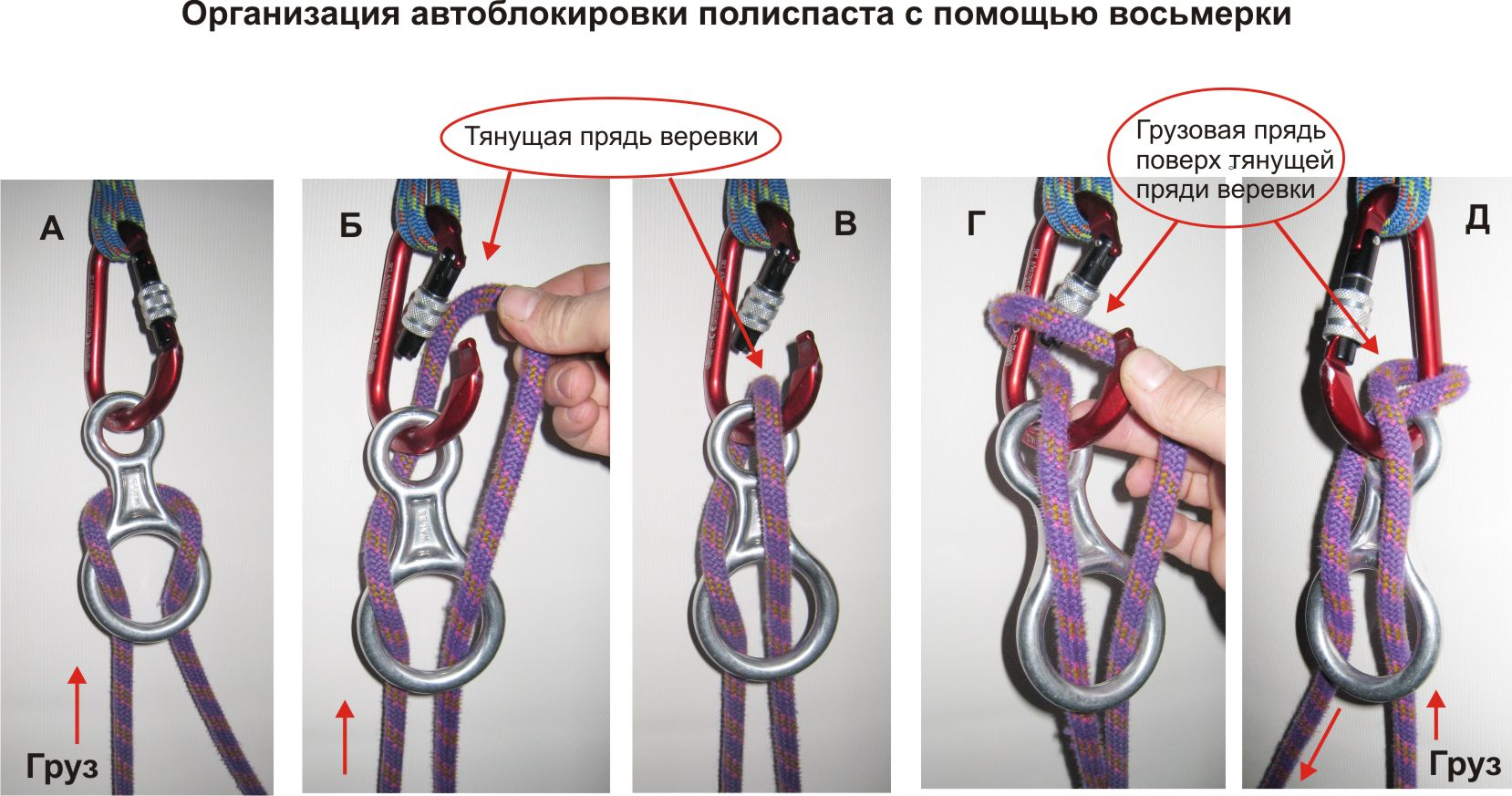
Узлы существую для разных целей и назначений

Узлы существую для разных целей и назначений, создание петель, которые затягиваются или нет, соединение веревок одинакового или различного диаметра, для привязывания веревки к различным объектам и т.д. Но чтобы правильно вязать узлы, нужна практика. И лучше отказаться от узла, и воспользоваться другим, если вы, хоть немного сомневаетесь в его вязке. Мы начнем с самых простых узлов и будем с каждым новым узлом приближаться к более сложным узлам.

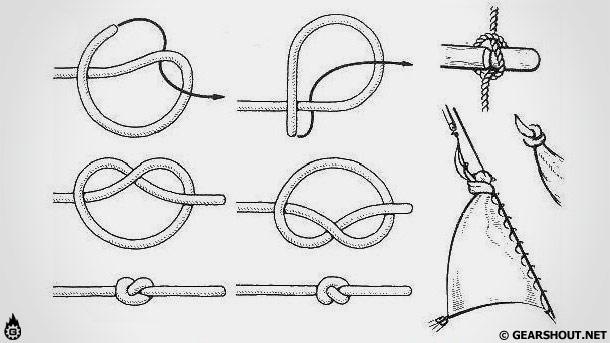
Простой узел

Простой узел, служит для соединения веревок и является составным элементом многих узлов, также его можно завязать на конце веревки, для предотвращения ее распускания. Пожалуй, это самый простейший из всех узлов и самый маленький. Но при натяжении троса узел сильно затягивается и порой его трудно развязать. Простой узел сильно изгибает веревку, что уменьшает прочность троса более чем в 2 раза. Но, тем не менее, это самый популярный узел.

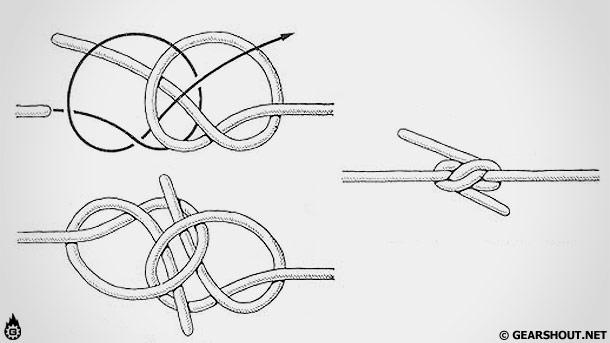
Прямой узел (Рифовый)

Прямой узел, служит для соединения веревок примерно одинакового диаметра. Связывать веревки разного диаметра этим узлом не безопасно, так как тонкий трос будет рвать более толстую веревку. Прямой узел был известен еще в пять тысяч лет до нашей эры в Египте. А древни греки и римляне, называли его Геракловым, потому что так мифический герой Геракл завязывал шкуру льва на своей груди. У прямого узла есть четыре варианта вязки, но достаточно знать и уметь вязать один из них. На коренных конца обязательны контрольные узлы.

Узел Хантера (Охотничий узел)

В 1968 году английский доктор Эдвард Хантер (Edward Hunter) случайно изобрел узел, который отлично держится на тросах и даже на синтетической леске. По существу это было удачное сплетение двух простых узлов завязанных на концах двух веревок. Это изобретение в определённых кругах вызвало сенсацию, а британекие патентоведы выдали Эдварду за это изобретение патент. Узел Хантера держится на всех веревка в особенности на мягких, а также на лентах и лесках. Автор книги «Морские узлы» Л. Н. Скрягин дал этому узлу другое название — «Охотничий узел» так как Фамилия Hunter с английского переводиться как охотник.

Встречная восьмерка

Еще один из древнейших узлов для связывания двух веревок. У этого узла есть и другое название «фламандский узел». Это надежный и прочный узел, он практически не уменьшает прочность веревки. Для начала на конце одной из веревки вяжут восьмерку, а затем ходовым концом второй веревки повторяют все изгибы восьмерки на первой веревке и пропускают его в сторону коренного конца. После этого затягивают. Встречную восьмерку сравнительно легко развязать.

Узел Грейпвайн

Грейпвайн является самым прочным из узлов предназначенных для связывания веревок одинакового диаметра. Этот узел имеет наименьший коэффициент ослабления веревок в 5%, таких показателей нет у других узлов. При вязке узла Грейпвайн можно обойтись без контрольных узлов, он всё равно остается довольно безопасным.

Узел Штык

Этот узел представляет собой незатягивающуюся петлю, которая может держать нагрузку, действующую почти в любом направлении. Еще один главный плюс этого узла в том, что его можно легко развязать даже под нагрузкой, что очень удобно. Сделайте полтора оборота веревки вокруг дерева, столба или даже камня. Ведите ходовой конец поверх коренного конца, заведите его вниз и пропустите из-под коренного конца в образовавшуюся петлю (так у вас получился шлаг). Затяните и сделайте еще один шлаг, а в конце обязательно завяжите контрольный узел.

Узел Быстроразвязывающиеся

Следующий узел может носить названия: пиратский узел, ведерный узел. Этот узел достаточно надежный, если правильно завязан, также его можно очень легко и быстро развязать, если потянуть за ходовой конец. Рекомендуется для временного крепления, где нужно быстро развязать узел. Либо можно использовать в ситуациях при спуске, где нужно вернуть веревку после спуска, дёрнув за ходовой конец.

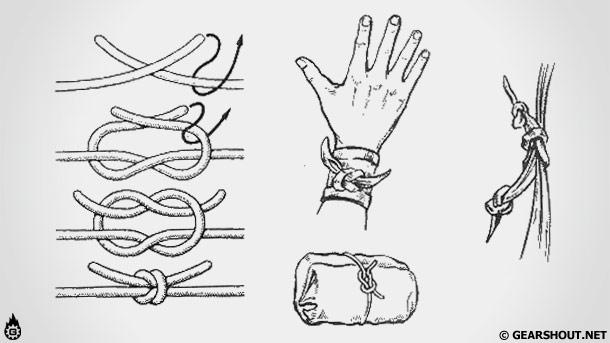
Схватывающий узел Прусика

Этот узел главным образом применяется в качестве страховки, при спуске или подъеме по веревке. В случае срыва человека во время спуска этот узел затягивается и предотвращает его падение. А при подъеме по веревке этот узел можно использовать как жумар. Подтягивая узел снизу вверх, при нагрузки узел затянется и будет держать человека. Узел был изобретен Карлом Прусиком президентом Австрийского Альпклуба в 1931 году и хорошо зарекомендовал себя в альпинизме и горном туризме. Но узел плохо работает на мокрой и обледенелой веревке.

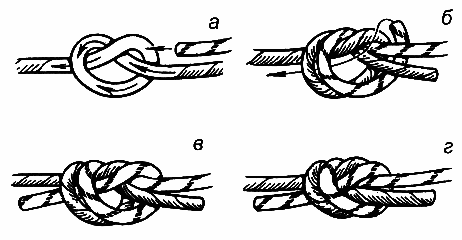
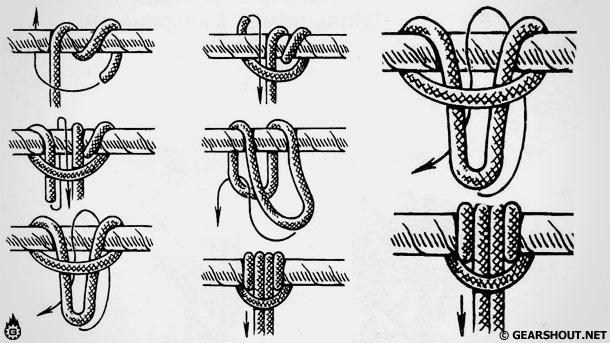
Австрийский проводник

Узел применяется в тех случаях, когда нужно сделать петлю на середине веревке, для создания точки крепления в случае страховки или если нужно отделить перетертый участок веревки. У этого узла есть также и другие названия: Альпийская бабочка, Узел среднего, Срединный проводник, Срединный проводник.

Узел Булинь (Беседочный узел)

Это один из самых старых и популярных узлов. Булинь можно с уверенностью назвать «королем узлов» за его простоту и надежность. Этот узел вяжется на конце веревки и является надежной не затягивающейся петлей. Беседочный узел применяется в морском деле, альпинизме и туризме. Также очень полезно будет уметь завязывать это узел одной рукой, что может пригодиться вам в экстремальной ситуации.

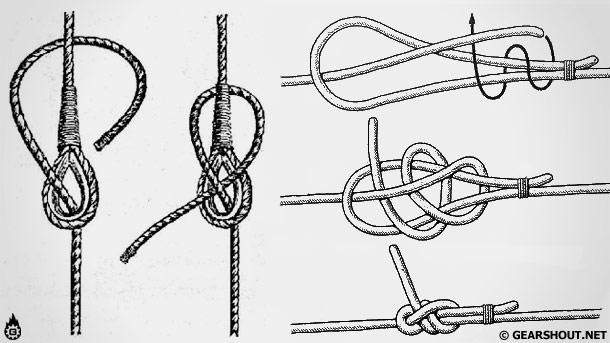
Шкотовый и Брамшкотовый узел

Эти узлы применяются для связывания веревок, как различного диаметра, так и одинакового. Узлы быстро и просто вяжутся. Также для этих узлов обязательны контрольные узлы.

Источник http://www.gearshout.net/verevochnyie-uzlyi-ih-vidyi-i-sposobyi-vyazki/#ixzz2mUtv6tWw

2.4. Линейные элементы и элементы высокого порядка

Библиотека элементов программы ANSYS включает два основных типа объемных и поверхностных элементов: линейные (с дополнительными формами или без) и квадратичные. Эти основные типы элементов схематично представлены на рис. 2.1.

(a) (b) (c)

Рис. 2.1. Основные типы элементов программы ANSYS

(a) Линейный изопараметрический

(b) Линейный изопараметрический с дополнительными формами

(c) Квадратичный

2.4.1. Линейные элементы (без срединных узлов)

В прочностном анализе элементы с расположенными в углах узлами и с дополнительными функциями формы обычно приводят к точному решению при разумных затратах компьютерного времени. Важно избегать вырожденных форм этих элементов в критических областях, т.е. не допускать появления двумерных линейных элементов треугольной формы и трехмерных линейных элементов клинообразной или пирамидальной формы в областях высокого градиента расчетных величин. Также следует избегать появления линейных элементов d чрезмерными искажениями. При проведении нелинейного анализа лучшая точность решения при меньших затратах времени чаще достигается при использовании мелкой сетки линейных элементов по сравнению с крупной сеткой квадратичных элементов (см. рис. 2.2).

(a) (b)

Рис. 2.2. «Сопоставимые» сетки:

(a) линейных элементов (b) сетки квадратичных элементов

При моделировании искривленных оболочек приходится выбирать между использованием искривленных (т.е. квадратичных) или плоских (т.е. линейных) оболочечных элементов. Каждый выбор имеет свои преимущества и недостатки. В большинстве случаев большинство задач может быть решено с высокой степенью точности за минимальное количество компьютерного времени при использовании плоских элементов. Однако нужно быть уверенным в том, что для моделирования соответствующей искривленной поверхности используется достаточное количество плоских элементов. Очевидно, чем меньше элемент, тем выше точность отображения геометрии. Рекомендуется, чтобы трехмерный плоский оболочечный элемент заменял собой дугу окружности не более 15°. Конические оболочечные (осесимметричные линейные) элементы должны быть ограничены дугой в 10° (или 5°, если находятся вблизи оси Y).

В большинстве других видов анализа (тепловой, магнитный и т.д.) линейные элементы работают почти также хорошо, как элементы более высокого порядка, и требуют меньших затрат времени. При этом даже вырожденные элементы (треугольной и тетраэдной форм) обычно приводят к точным результатам.

2.4.2. Квадратичные элементы (со срединными узлами)

В линейном прочностном анализе при наличии вырожденных форм конечного элемента (т.е. треугольных двумерных элементов и клинообразных или тетраэдных трехмерных элементов) использование квадратичных элементов обычно приводит к лучшим результатам при меньших затратах времени, чем использование линейных. Однако для правильного использования этих элементов необходимо знать их особенности.

• Распределенные нагрузки и давление не прикладываются к узлам элементов в соответствии со «здравым смыслом», т.е. так, как это происходит в случае линейных элементов (см. рис. 2.3). Силы реакции в срединных узлах также не соответствуют «интуитивным» представлениям.

• Трехмерные тепловые элементы со срединными узлами под действием конвективной нагрузки распределяют тепловой поток таким образом, что в срединном узле он имеет одно направление и обратное — в угловых узлах.

• Для элементов прочностного анализа температура, заданная в срединном узле и выпадающая из диапазона значений температуры в двух смежных угловых узлах, переопределяется как средняя температура этих узлов.

• Так как значение массы в срединных узлах больше, чем в угловых, то для проведения редуцированного анализа целесообразно выбирать ведущие степени свободы (мастер — степени) в срединных узлах.

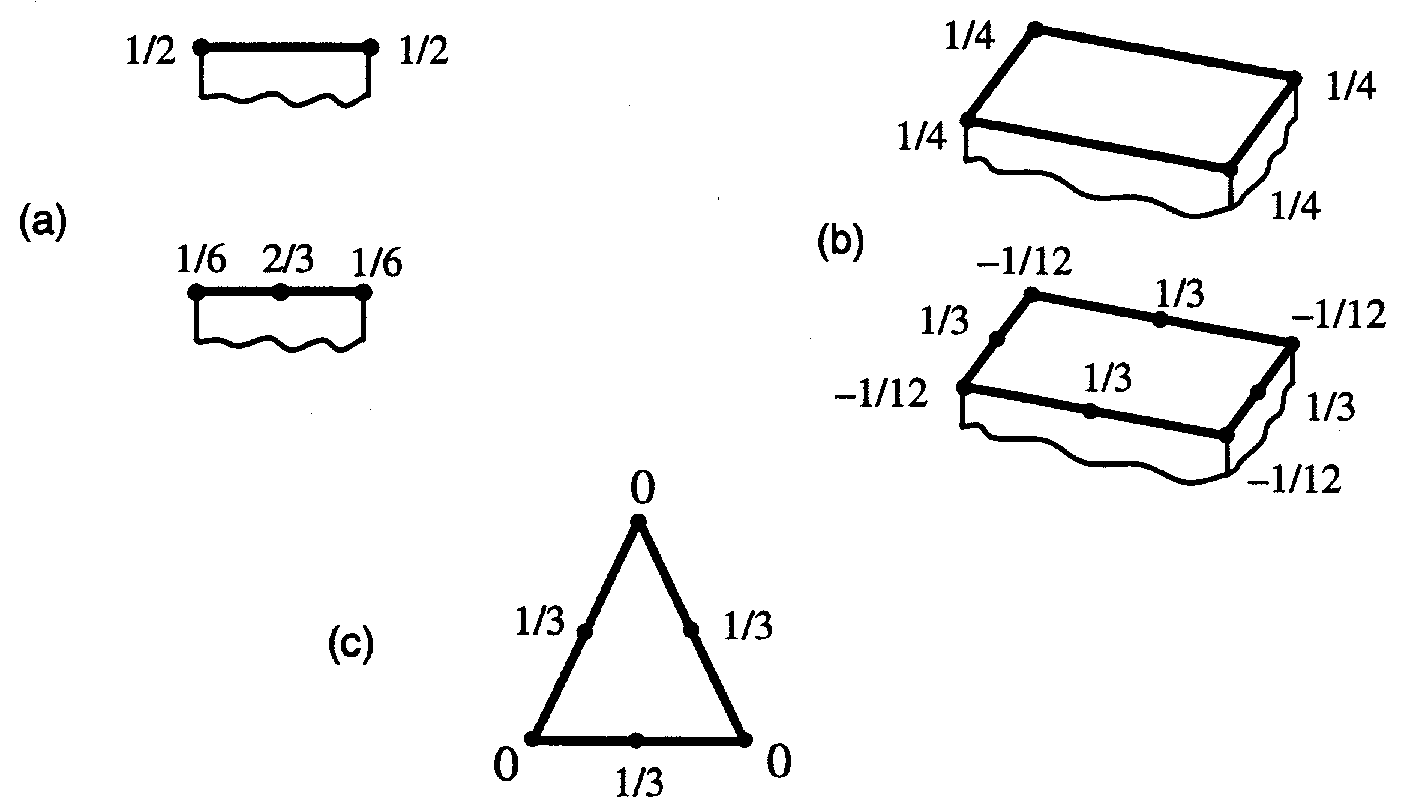
Рис. 2.3. Эквивалентное распределение единичной однородной поверхностной нагрузки по узлам:

(a) двумерного элемента; (b) трехмерного элемента;

(c) треугольного трехмерного элемента.

• В динамическом анализе, касающегося процессов распространения волн, срединные узлы не рекомендуется задавать из-за неоднородного распределения масс по узлам.

• Не следует присоединять контактные поверхности или элементы зазора к элементам модели со срединными узлами. Подобным же образом в тепловых задачах не рекомендуется прикладывать радиационные связи или нелинейные конвективные поверхности к границам элементов со срединными узлами. (Процедура построения сетки для твердотельных моделей предусматривает возможность исключения определенных срединных узлов.)

(Не рекомендуется) (Рекомендуется)

Рис. 2.4. Задание зазоров и поверхностей контакта

• При задании условий-ограничений для степеней свободы на краю или грани элемента должны ограничиваться все узлы, включая срединные.

• Угловой узел одного элемента должен быть связан только с угловым узлом другого, но не с его срединным узлом. Смежные элементы должны иметь связанные (или общие) срединные узлы.

(Не рекомендуется) (Рекомендуется)

Рис. 2.5. Соединение смежных элементов

• Элементы со срединными узлами должны иметь прямые края за исключением случаев, когда моделируется искривленные области геометрии или когда тонкие слои элементов «отслеживают» искривленную границу модели. Если центральный угол окружности, проходящий через узлы элемента, превышает 15°, то возможны локальные погрешности решения. Если угол превышает 45.2°, возможны глобальные погрешности. Ни в коем случае этот угол не должен превышать 106°.

• Предпочтительное положение срединных узлов — это точная середина границы элемента. Если по каким-то причинам нужно изменить положение узла, его следует поместить в пределах l/10 от точной середины границы элемента (здесь l — расстояние между угловыми узлами; см. рис. 2.6). Исключение составляют задачи с трещиной (см. ниже).

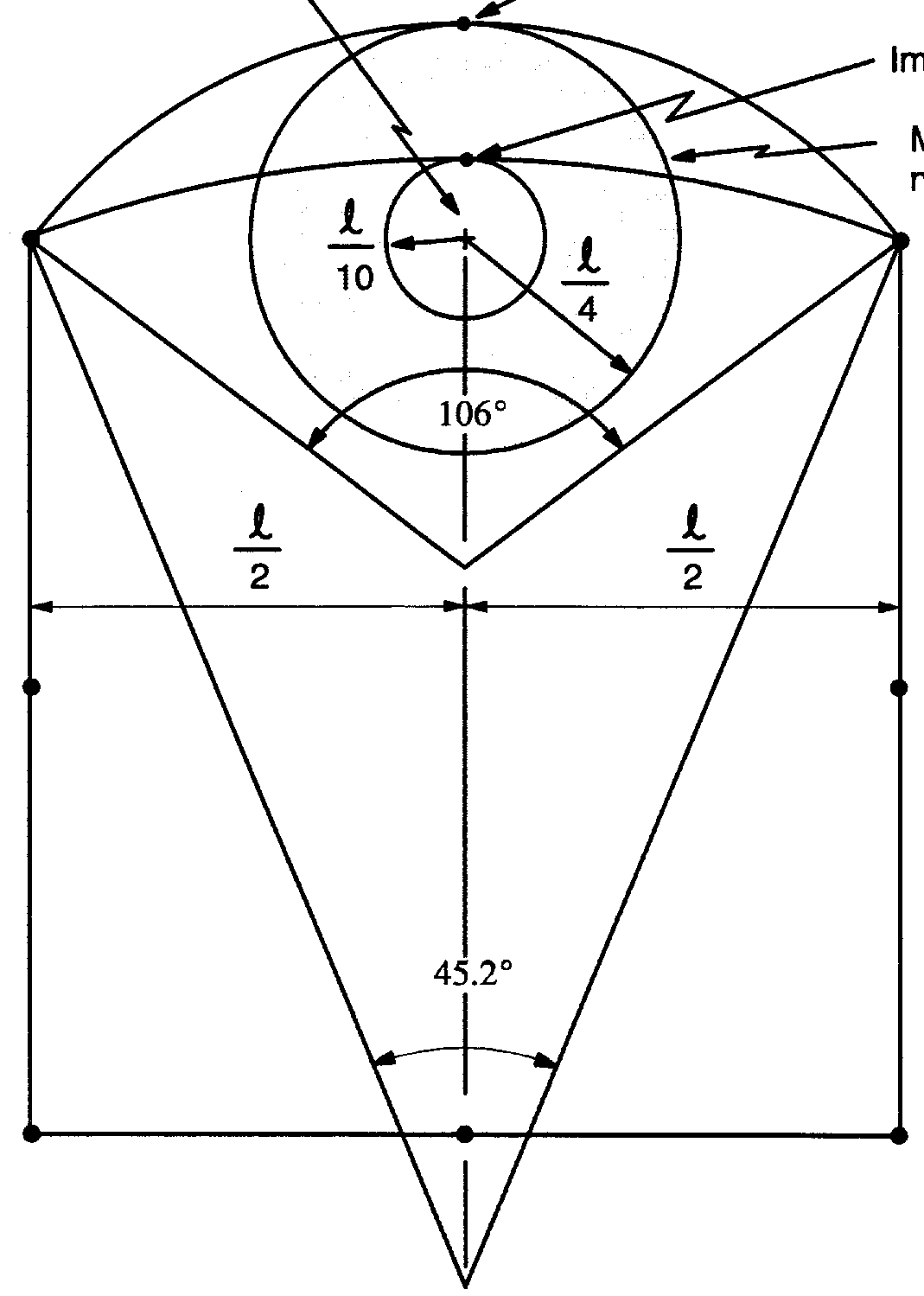
Рис. 2.6. Рекомендации по размещению срединных узлов

• Срединный узел, расположенный точно на расстоянии l/4 на линии, соединяющей два угловых узла, задает сингулярный элемент. Эта особенность, обычно используемая с треугольными элементами, часто оказывается полезной при моделировании трещин в задачах механики разрушения. (Для получения этого результата используется команда KSCON или маршрут меню Main Menu>Preprocessor>Shape & Size>Concentration KP.) Если используются совпадающие узлы, они должны быть размещены в вершине трещины.

• Если положение срединного узла не задано, программа автоматически поместит его между двумя угловыми узлами, используя линейную интерполяцию в декартовой системе координат. Узлы, размещенные таким способом, будут иметь систему узловых координат, также повернутую на угол, определяемый линейной интерполяцией.

• Связанные элементы должны иметь одинаковое число узлов на общей стороне. При смешивании разных типов элементов может оказаться необходимым удалить срединный узел. Например, при соединении четырехузлового элемента с восьмиузловым (рис. 2.7) узел N должен быть удален (или иметь нулевой номер при создании элемента [E]).

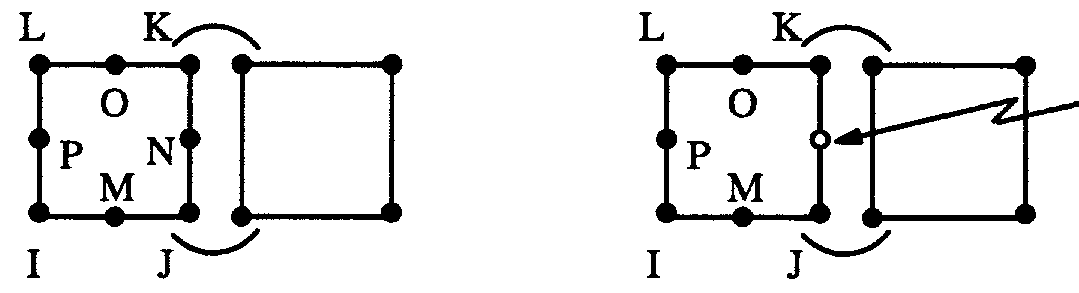
(Не рекомендуется) (Рекомендуется)

Рис. 2.7. Объединение элементов с разным числом узлов

Замечание — Программа автоматически удаляет срединные узлы на общей стороне линейных и квадратичных элементов в следующей ситуации: поверхность (или объем) имеет сетку из линейных элементов [AMESH, VMESH], затем на смежной поверхности (или объеме) строится сетка из квадратичных элементов. Срединные узлы не будут удалены, если используется опция SmartSizing [SMRTSIZE] или если порядок построения сетки обратный (квадратичные элементы предшествуют линейным).

• Удаление срединного узла предполагает, что граница элемента остается прямолинейной, что приводит к увеличению жесткости. Рекомендуется применять элементы с удаленными узлами только в зонах перехода от одного типа сетки к другому и в областях, в которых не используются линейные элементы с дополнительными функциями формы. При необходимости узлы могут быть добавлены или удалены после генерации элементов одним из следующих способов:

Команда: EMID

Маршрут: Main Menu>Preprocessor>Move / Modify>Add Mid Nodes

Main Menu>Preprocessor>Move / Modify>Remove Mid Nd

Команда: EMODIF

Маршрут: Main Menu>Preprocessor>Move / Modify>Modify Nodes

• Квадратичный элемент не может иметь больше точек интегрирования, чем линейный. По этой причине в нелинейном анализе предпочтительнее линейные элементы.

• Сетки, построенные из квадратичных элементов высшего порядка типа PLANE82 и SHELL93, могут давать сингулярные эффекты из-за нулевой энергии деформации.

• При постпроцессорной обработке для графического вывода сечений и невидимых линий используются только угловые узлы. Аналогично, для распечатки и выполнения процедур над результатами доступны только узловые напряжения в углах элемента.

• При графическом выводе элементы со срединными узлами, которые фактически имеют искривленные границы, выводятся на экран в виде прямолинейных отрезков (если только не используется модуль PowerGraphics). Модели, следовательно, будут выглядеть более «угловатыми», чем на самом деле.

Среднее значение, Медиана, Режим, Расчет диапазона

Для расчета укажите числа, разделенные запятыми.

Калькулятор связанной статистики | Калькулятор стандартного отклонения | Калькулятор объема выборки

Среднее значение

Слово mean, являющееся омонимом множества других слов в английском языке, также неоднозначно даже в области математики. В зависимости от контекста, математического или статистического, то, что подразумевается под «средним», меняется. В простейшем математическом определении наборов данных используемое среднее — это среднее арифметическое, также называемое математическим ожиданием или средним.В этой форме среднее значение относится к промежуточному значению между дискретным набором чисел, а именно к сумме всех значений в наборе данных, деленной на общее количество значений. Уравнение для расчета среднего арифметического практически идентично уравнению для расчета статистических концепций генеральной совокупности и выборочного среднего, с небольшими вариациями в используемых переменных:

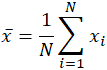
Среднее значение часто обозначается как x ̄ , произносится как «x bar», и даже в других случаях, когда переменная не равна x , обозначение столбца является обычным индикатором некоторой формы среднего.В конкретном случае среднего значения генеральной совокупности вместо использования переменной x ̄ используется греческий символ mu, или μ . Точно так же, или скорее сбивает с толку, выборочное среднее в статистике часто обозначается заглавной буквы X . Учитывая набор данных 10, 2, 38, 23, 38, 23, 21, применение суммирования выше дает:

10 + 2 + 38 + 23 + 38 + 23 + 21 7

=

= 22.143

Как упоминалось ранее, это одно из простейших определений среднего, некоторые другие включают взвешенное среднее арифметическое (которое отличается только тем, что одни значения в наборе данных вносят больший вклад, чем другие) и среднее геометрическое. Правильное понимание данных ситуаций и контекстов часто может дать человеку инструменты, необходимые для определения того, какой статистически значимый метод использовать. В целом, среднее значение, медиана, мода и диапазон в идеале должны быть вычислены и проанализированы для данной выборки или набора данных, поскольку они проливают свет на различные аспекты данных и, если их рассматривать отдельно, могут привести к искажению данных, что будет продемонстрировано в следующих разделах.

Медиана

Статистическая концепция медианы — это значение, которое делит выборку данных, совокупность или распределение вероятностей на две половины. Поиск медианы по существу включает в себя нахождение значения в выборке данных, физическое расположение которой находится между остальными числами. Обратите внимание, что при вычислении медианы конечного списка чисел важен порядок выборок данных. Обычно значения перечисляются в порядке возрастания, но нет реальной причины, по которой перечисление значений в порядке убывания дало бы разные результаты.В случае, когда общее количество значений в выборке данных нечетное, медиана — это просто число в середине списка всех значений. Когда выборка данных содержит четное количество значений, медиана является средним из двух средних значений. Хотя это может сбивать с толку, просто помните, что даже несмотря на то, что медиана иногда включает вычисление среднего, когда возникает этот случай, он будет включать только два средних значения, а среднее значение включает все значения в выборке данных. В нечетных случаях, когда есть только две выборки данных или есть четное количество выборок, где все значения одинаковы, среднее и медиана будут одинаковыми.Учитывая тот же набор данных, что и раньше, медиана будет получена следующим образом:

2,10,21, 23 , 23,38,38

После перечисления данных в порядке возрастания и определения нечетного числа значений становится ясно, что 23 — это медиана для данного случая. Если в набор данных было добавлено другое значение:

2,10,21, 23 , 23 , 38,38,1027892

Поскольку существует четное число значений, медиана будет средним из двух средних чисел, в данном случае 23 и 23, среднее из которых равно 23.Обратите внимание, что в этом конкретном наборе данных добавление выброса (значение, выходящее далеко за пределы ожидаемого диапазона значений), значение 1 027 892, не оказывает реального влияния на набор данных. Если, однако, вычислить среднее значение для этого набора данных, результатом будет 128 505,875. Это значение явно не является хорошим представлением семи других значений в наборе данных, которые намного меньше и ближе по значению, чем среднее значение и выброс. Это главное преимущество использования медианы при описании статистических данных по сравнению со средним значением.Хотя оба, а также другие статистические значения должны вычисляться при описании данных, если можно использовать только одно, медиана может обеспечить лучшую оценку типичного значения в данном наборе данных, когда между значениями очень большие различия.

Режим

В статистике режим — это значение в наборе данных, которое имеет наибольшее количество повторов. Набор данных может быть мультимодальным, то есть иметь более одного режима. Например:

2,10,21,23,23,38,38

И 23, и 38 появляются дважды каждый, что делает их режимом для указанного выше набора данных.

Подобно среднему значению и медиане, этот режим используется как способ выражения информации о случайных величинах и совокупностях. Однако, в отличие от среднего и медианного, этот режим представляет собой концепцию, которая может применяться к нечисловым значениям, таким как марка чипсов тортилья, которые чаще всего покупаются в продуктовом магазине. Например, при сравнении брендов Tostitos, Mission и XOCHiTL, если будет обнаружено, что в продаже чипсов из тортильи XOCHiTL является модным и продается в соотношении 3: 2: 1 по сравнению с чипами из тортильи Tostitos и Mission соответственно, это соотношение можно использовать для определения количества мешков каждой марки на складе.В случае, если в течение определенного периода было продано 24 пакета чипсов тортильи, в магазине будет храниться 12 пакетов чипсов XOCHiTL, 8 пакетов Tostitos и 4 пакета Mission при использовании режима. Если, однако, магазин просто использовал среднее значение и продавал по 8 пакетов каждого, он потенциально мог потерять 4 продажи, если бы покупатель захотел только чипы XOCHiTL, а не какой-либо другой бренд. Как видно из этого примера, важно принимать во внимание все виды статистических значений при попытке сделать выводы о любой выборке данных.

Диапазон

Диапазон набора данных в статистике — это разница между наибольшим и наименьшим значениями. Хотя диапазон действительно имеет разные значения в разных областях статистики и математики, это его самое основное определение, и именно оно используется предоставленным калькулятором. На том же примере:

2,10,21,23,23,38,38
38 — 2 = 36

Диапазон в этом примере равен 36. Подобно среднему значению, на диапазон могут существенно влиять очень большие или маленькие значения.Используя тот же пример, что и ранее:

2,10,21, 23 , 23 , 38,38,1027892

Диапазон в этом случае будет 1 027 890 по сравнению с 36 в предыдущем случае. Таким образом, важно тщательно анализировать наборы данных, чтобы обеспечить учет выбросов.

.

Среднее значение, медиана и мода от сгруппированных частот

Объяснение на трех примерах

Гонка и непослушный щенок

Это начинается с необработанных данных ( еще не сгруппированная частота ) …

В спринтерской гонке Алекс засчитал 21 человека, с точностью до секунды:

59, 65, 61, 62, 53, 55, 60, 70, 64, 56, 58, 58, 62, 62, 68, 65, 56, 59, 68, 61, 67

Чтобы найти среднее, Алекс складывает все числа, а затем делит их на количество:

Среднее значение = 59 + 65 + 61 + 62 + 53 + 55 + 60 + 70 + 64 + 56 + 58 + 58 + 62 + 62 + 68 + 65 + 56 + 59 + 68 + 61 + 67 21
Среднее = 61.38095 …

Чтобы найти медианное значение, Алекс расставляет числа в порядке значений и находит среднее число.

В данном случае медиана — это номер 11 ^th :

53, 55, 56, 56, 58, 58, 59, 59, 60, 61, 61, 62, 62, 62, 64, 65, 65, 67, 68, 68, 70

Медиана = 61

Чтобы найти режим, или модальное значение, Алекс размещает числа в порядке значений, затем подсчитывает, сколько каждого номера. Режим — это число, которое встречается чаще всего. (может быть более одного режима):

53, 55, 56, 56, 58, 58, 59, 59, 60, 61, 61, 62, 62, 62, 64, 65, 65, 67, 68, 68, 70

62 появляется трижды чаще, чем другие значения, поэтому Mode = 62

Таблица сгруппированных частот

Затем Алекс составляет сгруппированную таблицу частот:

Секунды	Частота
51–55	2
56-60	7
61–65	8
66 — 70	4

Итак, 2 бегунов заняли от 51 до 55 секунд, 7 — от 56 до 60 секунд и т. Д.

О нет!

Внезапно все исходные данные теряются (непослушный щенок!)

Сохранилась только таблица сгруппированных частот…

… можем ли мы помочь Алексу вычислить среднее значение, медианное значение и моду только по этой таблице?

Ответ … нет, не можем. Во всяком случае, не совсем точно. Но мы можем сделать оценки.

Оценка среднего по сгруппированным данным

Итак, у нас осталось:

Секунды	Частота
51–55	2
56-60	7
61–65	8
66 — 70	4

Группы (51-55, 56-60 и т. Д.), Также называемые интервалами классов, имеют ширину 5

Средние точки находятся в середине каждого класса: 53, 58, 63 и 68

Мы можем оценить среднее значение, используя средние точки .

Итак, как это работает?

Подумайте о 7 бегунах в группе 56-60 : все, что мы знаем, это то, что они пробежали где-то между 56 и 60 секундами:

• Может быть, все семеро отработали 56 секунд,
• Может быть, все семеро продержались 60 секунд,
• Но более вероятно, что существует разброс цифр: некоторые по 56, некоторые в 57 лет и т. д.

Итак, мы берем среднее значение и предполагаем, что все семь из них заняли 58 секунд.

Давайте теперь сделаем таблицу, используя средние точки:

Средняя точка	Частота
53	2
58	7
63	8
68	4

Мы думаем: «2 человека заняли 53 секунды, 7 человек — 58 секунд, 8 человек — 63 секунды и 4 — 68 секунд». Другими словами, мы, , представляем, что данные выглядят так:

53, 53, 58, 58, 58, 58, 58, 58, 58, 63, 63, 63, 63, 63, 63, 63, 63, 68, 68, 68, 68

Затем мы складываем их все и делим на 21.Самый быстрый способ сделать это — умножить каждую среднюю точку на каждую частоту:

Средняя точка x	Частота f	Средняя точка × Частота FX
53	2	106
58	7	406
63	8	504
68	4	272
Всего:	21	1288

И тогда наша оценка среднего времени для завершения гонки составляет:

Расчетное среднее = 1288 21 = 61.333 …

Очень близко к точному ответу, который мы получили ранее.

Оценка медианы на основе сгруппированных данных

Давайте еще раз посмотрим на наши данные:

Секунды	Частота
51–55	2
56-60	7
61–65	8
66 — 70	4

Медиана — это среднее значение, в нашем случае это 11 ^{-е значение} , которое находится в группе 61-65:

Можно сказать, что «медианная группа составляет 61–65″

Но если нам нужно приблизительное значение медианы , нам нужно более внимательно посмотреть на группу 61–65.

Мы называем это «61 — 65», но на самом деле он включает значения от 60,5 до (но не включая) 65,5.

Почему? Значения указаны в целых секундах, поэтому реальное время 60,5 измеряется как 61. Точно так же 65,4 измеряется как 65.

На 60,5 у нас уже будет 9 бегунов, а к следующей границе на 65,5 у нас будет 17 бегунов. Проведя прямую линию между ними, мы можем определить, где средняя частота бегунов n / 2 составляет:

И эта удобная формула выполняет расчет:

Расчетная медиана = L + (n / 2) — B G × w

где:

• L — нижняя граница класса группы, содержащей медианное значение
.
• n — общее количество значений
• B — совокупная частота групп перед средней группой
• G — частота медианной группы
• w — ширина группы

Для нашего примера:

• L = 60.5
• n = 21
• В = 2 + 7 = 9
• G = 8
• w = 5

Расчетная медиана = 60,5 + (21/2) — 9 8 × 5

= 60,5 + 0,9375

= 61,4375

Оценка режима на основе сгруппированных данных

Снова посмотрим на наши данные:

Секунды	Частота
51–55	2
56-60	7
61–65	8
66 — 70	4

Легко найти модальную группу (группу с самым высоким частота), что составляет 61-65

Можно сказать, что «модальная группа — это 61–65″

Но настоящий режим может даже не входить в эту группу! Или может быть более одного режима.Без необработанных данных мы ничего не знаем.

Но мы можем оценить режим по следующей формуле:

Расчетный режим = L + f _м — f _м-1 (f _м — f _м-1 ) + (f _м — f _{м + 1} ) × ш

где:

• L — нижняя граница класса модальной группы
• f _m-1 — частота группы перед модальной группой
• f _m — частота модальной группы
• f _{m + 1} — частота группы после модальной группы
• w — ширина группы

В этом примере:

• L = 60.5
• f _м-1 = 7
• f _м = 8
• f _{м + 1} = 4
• Вт = 5

Расчетный режим = 60,5 + 8–7 (8–7) + (8–4) × 5

= 60,5 + (1/5) × 5

= 61,5

Наш окончательный результат:

• Среднее расчетное: 61,333 …
• Расчетная медиана: 61,4375
• Расчетный режим: 61.5

(Сравните это с истинным Средним, Медианой и Модой 61,38 …, 61 и 62 , которые мы получили в самом начале.)

И вот как это делается.

Теперь давайте рассмотрим еще два примера и попутно попрактикуемся!

Молодая морковь, пример

Пример: вы вырастили пятьдесят молодых морковок на специальной почве. Вы выкапываете их, измеряете их длину (с точностью до миллиметра) и группируете результаты:

Длина (мм)	Частота
150–154	5
155–159	2
160–164	6
165–169	8
170–174	9
175–179	11
180–184	6
185–189	3

Среднее

Длина (мм)	Средняя точка x	Частота f	FX
150–154	152	5	760
155–159	157	2	314
160–164	162	6	972
165–169	167	8	1336
170–174	172	9	1548
175–179	177	11	1947
180–184	182	6	1092
185–189	187	3	561
	Всего:	50	8530

Расчетное среднее = 8530 50 = 170.6 мм

Медиана

Медиана — это среднее значение длины 25 ^-го и 26 ^-го , так же как и в группе 170–174 :

.

Среднее значение, медиана, режим Калькулятор

Использование калькулятора

Вычислить среднее значение, медианное значение, режим, а также минимум, максимум, диапазон, количество и сумму для набора данных.

Введите значения через запятую или пробел. Вы также можете копировать и вставлять строки данных из электронных таблиц или текстовых документов. См. Все допустимые форматы в таблице ниже.

Что такое средняя медиана и мода?

Среднее значение, медиана и мода — все это меры центральной тенденции в статистике. Каждый из них по-разному сообщает нам, какое значение в наборе данных является типичным или репрезентативным для набора данных.

Среднее значение совпадает со средним значением набора данных и находится с помощью вычислений. Сложите все числа и разделите их на количество чисел в наборе данных.

Медиана — это центральное число набора данных.Расположите точки данных от наименьшего к наибольшему и найдите центральное число. Это медиана. Если в середине два числа, то медиана — это среднее значение этих двух чисел.

Режим — это номер в наборе данных, который встречается наиболее часто. Подсчитайте, сколько раз каждое число встречается в наборе данных. Режим — это номер с наибольшим подсчетом. Ничего страшного, если есть более одного режима. И если все числа встречаются одинаковое количество раз, режима нет.

Как найти среднее значение

1. Сложите все значения данных, чтобы получить сумму
2. Подсчитайте количество значений в вашем наборе данных
3. Разделите сумму на количество

Среднее значение совпадает со средним значением в наборе данных.{n} x_i} {n} \]

Как найти медиану

Медиана \ (\ widetilde {x} \) — это значение данных, отделяющее верхнюю половину набора данных от нижней половины.

• Упорядочить значения данных от наименьшего к наибольшему значению
• Медиана — это значение данных в середине набора
• Если в середине есть 2 значения данных, медиана — это среднее значение этих 2 значений.

Пример медианы

Для набора данных 1, 1, 2, 5 , 6, 6, 9 медиана равна 5.

Для набора данных 1, 1, 2 , 6 , 6, 9 медиана равна 4. Возьмите среднее значение 2 и 6 или (2 + 6) / 2 = 4.

Медианная формула

Заказ набора данных x ₁ ≤ x ₂ ≤ x ₃ ≤ … ≤ x _n от наименьшего до наибольшего значения, медиана \ (\ widetilde {x} \) — это точка данных, разделяющая верхнюю половину значений данных из нижней половины.

Если размер набора данных n нечетный, медиана — это значение в позиции p , где

\ [p = \ dfrac {n + 1} {2} \] \ [\ widetilde {x} = x_p \]

Если n даже, медиана — это среднее значение в позициях p и п + 1 где

\ [p = \ dfrac {n} {2} \] \ [\ widetilde {x} = \ dfrac {x_ {p} + x_ {p + 1}} {2} \]

Как найти режим

Mode — это значение или значения в наборе данных, которые встречаются наиболее часто.

Для набора данных 1 , 1 , 2, 5, 6 , 6 , 9 режим 1, а также 6.

Межквартильный размах

IQR = Q ₃ — Q ₁

Выбросы

Потенциальные выбросы — это значения, которые лежат выше верхней границы или ниже нижней границы набора выборки.
Верхний забор = Q ₃ & plus; 1.5 × Межквартильный размах
Нижняя граница = Q ₁ — 1,5 × Межквартильный размах

Калькуляторы связанной статистики и анализа данных

Допустимые форматы данных

Колонна (новые строки)

42
54
65
47
59
40
53

42, 54, 65, 47, 59, 40, 53

через запятую

42,
54,
65,
47,
59,
40,
53,

или

42, 54, 65, 47, 59, 40, 53

42, 54, 65, 47, 59, 40, 53

Помещения

42 54
65 47
59 40
53

или

42 54 65 47 59 40 53

42, 54, 65, 47, 59, 40, 53

Смешанные разделители

42
54 65« 47« 59,
40 53

42, 54, 65, 47, 59, 40, 53

.

Среднее, Медиана и Мода

Мы используем статистику , такую ​​как среднее значение, медиана и мода, чтобы получить информацию о совокупности из нашего набора наблюдаемых значений.

Среднее значение

Среднее значение (или среднее значение) набора значений данных — это сумма всех значения данных, разделенные на количество значений данных. То есть:

Пример 1

Оценки семи учеников за тест по математике с максимально возможным оценка 20 приведены ниже:
15 13 18 16 14 17 12

Найдите среднее значение этого набора значений данных.

Решение:

Итак, средняя оценка 15.

Условно мы можем изложить решение следующим образом:

Итак, средний балл 15.

Медиана

Медиана набора значений данных — это среднее значение данных устанавливается, когда он был расположен в порядке возрастания.То есть из от наименьшего значения к наибольшему значению.

Пример 2

Оценки девяти учащихся на экзамене по географии с максимальным Возможная оценка 50 приведены ниже:
47 35 37 32 38 39 36 34 35

Найдите медиану этого набора значений данных.

Решение:

Расположите значения данных в порядке от наименьшего значения к наибольшему. значение:

32 34 35 35 36 37 38 39 47

Пятое значение данных, 36, является средним значением в этой компоновке.

Примечание:

Всего:

Если количество значений в наборе данных четное, то медиана равна среднее из двух средних значений.

Пример 3

Найдите медиану следующего набора данных:
12 18 16 21 10 13 17 19

Решение:

Расположите значения данных в порядке от наименьшего значения к наибольшему. значение:
10 12 13 16 17 18 19 21

Количество значений в наборе данных равно 8, что является четным.Так что Медиана — это среднее из двух средних значений.

Альтернативный способ:

В наборе данных 8 значений.

Четвертый и пятый баллы, 16 и 17, находятся посередине. То есть, не существует единой средней ценности.

Примечание:

• Половина значений в наборе данных лежит ниже медианы и половина лежат выше медианы.
• Медиана — это наиболее часто цитируемая цифра, используемая для измерить цены на недвижимость. Использование медианы позволяет избежать проблемы средняя цена недвижимости, на которую влияет несколько дорогих объектов недвижимости, не являются представителями общего рынка недвижимости.

Режим

Режим набора значений данных — это значения, которые встречаются чаще всего. довольно часто.

В режиме есть приложения в печати. Например, важно печатать больше самых популярных книг; потому что печать разных книг в равное количество может вызвать нехватку некоторых книг и переизбыток другие.

Аналогичным образом, режим имеет применение в производстве. Например, это важно производить больше самой популярной обуви; так как производство различной обуви в равных количествах вызовет нехватку одни туфли и избыток других.

Пример 4

Найдите режим следующего набора данных:

48 44 48 45 42 49 48

Решение:

Режим 48, т.к. встречается чаще всего.

Примечание:

• Набор значений данных может иметь более одного Режим.
• Если два значения данных встречаются наиболее часто, мы говорят, что набор значений данных — бимодальных .
• Если нет значения данных или значений данных, которые встречаются чаще всего часто мы говорим, что набор значений данных не имеет режима.

Анализ данных

Среднее значение, медиана и режим набора данных вместе известны как меры. центральной тенденции , поскольку эти три показателя сосредоточены на том, где находятся данные по центру или сгруппированы.Для анализа данных с использованием среднего, медианного и режима мы необходимо использовать наиболее подходящую меру центральной тенденции. Последующий Следует запомнить баллов:

• Среднее значение полезно для прогнозирования будущих результатов, когда нет экстремальные значения в наборе данных. Однако влияние экстремальных значений на среднее значение может быть важным, и его следует учитывать. Например. Воздействие крах фондового рынка по средней доходности инвестиций.
• Среднее значение может быть более полезным, чем среднее значение при экстремальных значений в наборе данных, поскольку на него не влияют экстремальные значения.
• Режим полезен, когда наиболее распространенный элемент, характеристика или значение набора данных не требуется.

Ключевые термины

статистика, среднее, среднее, медиана, режим, меры центральной тенденции

.