Золотое сечение. Золотой треугольник — SurWiki
Введение
Человек различает окружающие его предметы по цвету, вкусу, запаху, форме. Интерес к форме какого-либо предмета может быть вызван жизненной необходимостью, а может быть и красотой формы. Форма, в основе построения которой лежит принцип “золотого сечения”, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Классическими проявлениями золотого сечения являются предметы обихода, скульптура и архитектура, математика, музыка и эстетика. В предыдущем столетии с расширением области знаний человечества резко увеличилось количество сфер, где наблюдается феномен золотой пропорции. Это биология и зоология, экономика, психология, кибернетика, теория сложных систем, и даже геология и астрономия. Ежегодно издаются несколько книг, посвященных этой проблеме, постоянно расширяя область приложения золотого сечения. Авторы этих исследований связывают золотое сечение с такими несовместимыми, на первый взгляд понятиями, как красота, асимметрия, рекурсия, самоорганизация и пропорция. За последние годы появились интересные интернет-сайты, посвященные золотому сечению.
Цели и задачи:
Цель работы: изучить золотое сечение и золотые треугольники.
Задачи работы:
1.Изучить понятие о золотом сечении
2. Узнать о золотых треугольниках
3. Найти золотое сечение в выбранном фото и картине.
Определение Золотого сечения
Как известно, «золотая» пропорция создаёт зрительное ощущение гармонии и равновесия. Но помимо эстетических воздействий она обладает ещё интересными математическими свойствами. Существует бесконечное множество разбиений отрезка на две части. И лишь единственный способ разбиения такой, что отношение всего отрезка к его большей части равно отношению большей части к его меньшей части, т.е. с : b = b : а
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление величины (например, длины отрезка) на две части таким образом, при котором отношение большей части к меньшей равно отношению всей величины к её большей части. Или, если использовать вычисленную величину золотого сечения, — это деление величины на две части — 62 % и 38 % (процентные значения округлены). Число называется также золотым числом. Приблизительная величина золотого сечения равна 1,6180339887. Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется отрезком с точкой А. На отрезке AC от точки С откладывается отрезок, равный ВС, заканчивающийся точкой D. На отрезке AB от точки А откладываем отрезок АЕ, равный отрезку AD. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
История Золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле также заложены пропорции золотого деления. В дошедшей до нас античной литературе золотое деление впервые упоминается в “Началах” Евклида. Во 2-й книге “Начал” дается геометрическое построение золотого деления. В средневековой Европе с золотым делением познакомились по арабским переводам “Начал” Евклида. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи. «Пусть никто не будучи математиком, не посмеет читать мои труды.». Он, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась “О перспективе в живописи”. Его считают творцом начертательной геометрии.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя “Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности”.
Золотые треугольники
Существуют золотые прямоугольники треугольники пятиугольники и спирали. Рассмотрим золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618. В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками. Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
Для построения пентаграммы необходимо построить правильный пятиугольник. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения золотого прямоугольника.
Золотое сечение в архитектуре и живописи
Рассмотрим строения города Сургута. Во многих постройках присутствует золотое сечение, однако золотой треугольник не так часто встречается в архитектуре города. На фото представлена церковь Всех Святых. На этой фотографии соблюдаются пропорции золотого треугольника.
Медведева Олеся Анатольевна – югорская художница. Она живет и работает в городе Нижневартовск. Является участницей городских, областных, окружных, зональных, всероссийских, международных выставок. Одна из её картин показывает, что золотые треугольники встречаются также и в живописи.
Заключение
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Природа, понимаемая как весь мир в многообразии его форм, состоит как бы из двух частей: живая и неживая природа. Для творений неживой природы характерна высокая устойчивость, слабая изменчивость, если судить в масштабах человеческой жизни. Мир неживой природы — это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир природы — это прежде всего мир гармонии, в которой действует «закон золотого сечения». Повсюду мы встречаем золотое сечение, но лишь обратив на него свое пристальное внимание, мы сможем увидеть истинную красоту.
Список литературы
1. Азевич А.И. От золотой пропорции к ее «производным». // Квант – 1995. — № 3. – С. 55.
2. Хинн О.Г. под общ. Ред. ООО «Издательство АСТ-ЛТД» 2004 г. «Я познаю мир: математика».
3. Васютинский Н.А. Золотая пропорция. – М.: Молодая гвардия, 1990.
4. Виленкин Н.Я. и др. За страницами учебника математики, 10-11. – М.: Просвещение, 1996.
5. Волошинов А.В. Математика и искусство. – М.: Просвещение, 1992.
6. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов. – М.: Мнемозина, 2005
7. http://ru.wikipedia.org
8. http://n-t.ru
Дополнительные материалы
Золотой треугольник | Статья в журнале «Юный ученый»
Библиографическое описание:
Прямостанов, А. М. Золотой треугольник / А. М. Прямостанов, О. Е. Пароднова. — Текст : непосредственный // Юный ученый. — 2017. — № 2.2 (11.2). — С. 77-79. — URL: https://moluch.ru/young/archive/11/822/ (дата обращения: 18.08.2020).
В статье описывается дано определение золотого треугольника, способ построения и применение в различных задачах.
Ключевые слова: золотой треугольник, применение золотого треугольника.
Золотой треугольник— это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с основанием[1]. Нетрудно определить углы золотого треугольника (36°,72°,72°). Золотые треугольники можно увидеть в развёртках звёздчатых форм додекаэдра и икосаэдра, в вершинах пентаграммы, в десятиугольнике.
Построение золотого треугольника. Строим прямую АК. От точки А на прямой откладываем три раза отрезок произвольной величины (d), через полученную точку Р проводим перпендикуляр к линии АК, на перпендикуляре вправо и влево от точки Р откладываем отрезки длины d. Полученные точки D и D1 соединяем с точкой А. Отрезок DD1 откладываем на линию AD1, получая точку С. Точка С разделила линию AD1 в пропорции золотого сечения. Треугольник АDD1 – искомый.
При построении логарифмической спирали используется золотой треугольник. (Начиная с большого треугольника) делим угол при основании пополам, получаем следующую точку. Процесс деления может продолжаться бесконечно, создавая бесконечно много золотых треугольников. Логарифмическую спираль можно провести через полученные вершины. Эта спираль известна как равноугольная спираль. Термин предложил Рене Декарт: «Если провести прямую из полюса к любой точке на кривой, она пересечёт кривую всегда под одним и тем же углом» (рис. 1)
Золотой гномон, тупоугольный равнобедренный треугольник, в котором отношение длины боковых сторон к длине основания является обратным к золотому отношению. Золотой гномон является уникальным треугольником с пропорцией углов 1:1:3. Его острые углы составляют 36°, то же значение, что и у угла при вершине золотого треугольника.
Золотой треугольник может быть разрезан на золотой треугольник и золотой гномон. То же самое верно для золотого гномона. Золотой гномон и золотой треугольник с их равными сторонами (сторона гномона равна стороне треугольника) также являются тупым и острым треугольниками Робинсона. (рис. 2) Эти равнобедренные треугольники могут быть использованы для получения мозаик Пенроуза. Плитки Пенроуза состоят из «змеев» и «дротиков». «Змей» представляет собой золотой треугольник, а «дротик» состоит из двух гномонов.
Рис.1 | Рис.2 |
В планиметрических и стереометрических задачах золотой треугольник встречается в явном виде:
- Доказать, что биссектрисы при основании золотого треугольника равны основанию.
- Для золотого треугольника найти: медиану, проведенную к боковой стороне; высоту, проведенную к основанию; площадь.
- Найти радиусы описанной и вписанной окружностей золотого треугольника.
- Диагональ параллелограмма разбивает его на два золотых треугольника, в каждый из которых вписана окружность. Найти расстояние между центрами этих окружностей.
- Найти радиусы вневписанных окружностей золотого треугольника.
- Найти расстояния между скрещивающимися ребрами золотой пирамиды (Золотая пирамида, пирамида у которой каждая грань – золотой треугольник).
- Найти угол между скрещивающимися ребрами золотой пирамиды.
- Найти высоту золотой пирамиды.
- Найти объем золотой пирамиды.
- Найти двугранные углы золотой пирамиды.
- Для золотой пирамиды найти радиусы описанной и вписанной сфер.
И в неявном виде: золотой треугольник и его свойства применяются при решении задач:
- Найти длины диагоналей правильного 10-угольника со стороной, равной 1.
- Египетская пирамида Хеопса – правильная четырехугольная со стороной основания 233,16 м., угол наклона боковой грани к основанию равна 51°50´. Найти высоту пирамиды Хеопса и показать, что .
Литература:
- Каменева Т., Козлов А., Урмузов А. Золотой треугольник в задачах-М.:Чистые пруды, 2008.-32 с.
- Зубова С.П., Лысогорова Л.В. Некоторые аспекты структурирования курса математики в 10 классе. Развитие современного образования: теория, методика и практика. 2016. № 2 (8). С. 63-65.
- Лысогорова Л.В. Закономерности процесса обучения математике как основа реализации принципа быстрого продвижения обучающихся в развитии. Молодой ученый. 2016. № 5-6 (109). С. 68-70.
- Лысогорова Л.В., Кочетова Н.Г., Зубова С.П. Реализация принципа обучения математике на повышенном уровне трудности. В сборнике: Научные проблемы образования третьего тысячелетия VII Всероссийская научно-практическая конференция с международным участием. 2013. С. 109-114.
Основные термины (генерируются автоматически): золотой треугольник, золотая пирамида, золотой гномон, основание, треугольник, угол.
Ключевые слова
золотой треугольник, применение золотого треугольникаПохожие статьи
Золотой треугольник ипрямоугольник
Золотой прямоугольник — это прямоугольник, длины сторон которого находятся в золотой пропорции (Рис.2). Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на…
Интегрированный урок на тему «Треугольник и его виды»
Золотой треугольник— это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с основанием[1]. Нетрудно определить углы золотого треугольника (36°,72°,72°)… Комбинаторные приложения треугольника Паскаля.
Решение геометрических задач методом «Золотого сечения»
В живой природе«золотое сечение» встречается в некоторых видах морских звезд,раковинах моллюсков, рогах млекопитающих; в химиисечение
Кроме деления отрезка на неравные части (золотое сечение) рассматривают золотой треугольник и золотой прямоугольник [3]…
Теорема Стюарта и применение её для решения задач
Или другая формулировка: Произведение квадрата расстояния от точки, лежащей на стороне треугольника, до противоположной вершины на длину этой
Примеры решения задач. В равнобедренном треугольнике с боковой стороной 4 см, проведена медиана к боковой стороне.
К вопросу о золотом сечении в географических координатах…
На страницах журнала «Молодой учёный» мы неоднократно рассматривали тему золотого сечения. Как известно, золотое сечение связано с числами Фибоначчи (В дальнейшем ЧФ). Напоминаем, что числа Фибоначчи состоят из трёх рядов.
Организация учебного исследования в начальной школе…
Определение суммы углов треугольников. Работа с копилкой треугольников, которая
Дети в результате работы делают вывод, что если в основании пирамиды треугольник, то
Золотой треугольник— это равнобедренный треугольник, в котором две боковые (равные)…
Решение задач с применением метода геометрических…
А) треугольники ВСN и АСР подобны и ориентированы противоположно; В) треугольник АВМ равнобедренный с основанием АВ(или
Золотой треугольник— это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с…
«Золотое сечение» — божественная пропорция
«Золотое сечение» — божественная пропорция. Авторы : Хаустова Валентина Николаевна , Гладкова Наталья Анатольевна , Бондаренко Ирина Васильевна.
Библиографическое описание: Хаустова В. Н., Гладкова Н. А., Бондаренко И. В. «Золотое
Золотой треугольник.
Геометрические задачи в научных трудах Абу Али ибн Сины и их…
Золотой треугольник. От точки А на прямой откладываем три раза отрезок произвольной величины (d), через полученную точку Р проводим перпендикуляр к линии АК, на перпендикуляре вправо. (Начиная с большого треугольника) делим угол при основании пополам, получаем…
ЗОЛОТАЯ ПРОПОРЦИЯ. НОВЫЙ ВЗГЛЯД | Наука и жизнь
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Золотую пропорцию в школе не «проходят». И когда один из авторов предлагаемой ниже статьи (кандидат технических наук В. Белянин) рассказал о золотом сечении абитуриентке, собравшейся поступать в МАДИ, в процессе подготовки к экзаменам в институт, задача неожиданно вызвала живой интерес и массу вопросов, на которые «с ходу» не было ответов. Решили искать их вместе, и тогда обнаружились тонкости в золотой пропорции, ускользавшие от исследователей ранее. Совместное творчество привело к работе, которая лишний раз подтверждает созидательные возможности молодежи и вселяет надежду, что язык науки утерян не будет.
Узоры математики, как и узоры художника или узоры поэта, должны быть красивы;
идеи, как и краски или слова, должны сочетаться гармонически. Красота является первым критерием: в мире нет места для безобразной математики.
Дж. Х. Харди
Красота математической задачи служит одним из важнейших стимулов ее нескончаемого развития и причиной порождения многочисленных приложений. Порой проходят десятки, сотни, а иногда и тысячи лет, но люди вновь и вновь находят неожиданные повороты в хорошо известном решении и его интерпретации. Одной из таких долгоживущих и увлекательных задач оказалась задача о золотом сечении (ЗС), отражающая элементы изящества и гармонии окружающего нас мира. Нелишне напомнить, кстати, что, хотя сама пропорция была известна еще Евклиду, термин «золотое сечение» ввел Леонардо да Винчи (см. «Наука и жизнь» №1, 2003 г.).
Геометрически золотое сечение подразумевает деление отрезка на две неравные части так, чтобы большая часть была средним пропорциональным между всем отрезком и меньшей частью (рис. 1).
Алгебраически это выражается следующим образом:
, или ,
или (1)
Исследование этой пропорции еще до ее решения показывает, что между отрезками a и b существуют по крайней мере два удивительных соотношения. Например, из пропорции (1) легко получается выражение,
которое устанавливает пропорцию между отрезками a, b, их разностью и суммой. Поэтому о золотом сечении можно сказать иначе: два отрезка находятся в гармоничном соотношении, если их разность относится к меньшему отрезку так, как больший отрезок относится к их сумме.
Второе соотношение получается, если исходный отрезок принять равным единице: a + b = 1, что очень часто используется в математике. В таком случае
a2 — b2 = a — b = ab.
Из этих результатов следуют два удивительных соотношения между отрезками а и b:
a2 — b2 = a — b = ab,(2)
которые будут использованы в дальнейшем.
Перейдем теперь к решению пропорции (1). На практике используют две возможности.
1. Обозначим отношение a/b через . Тогда получим уравнение
x2 — x — 1 = 0, (3)
которое имеет иррациональные корни
Обычно рассматривают только положительный корень x1, дающий простое и наглядное деление отрезка в заданной пропорции. Действительно, если принять целый отрезок за единицу, то, используя значение этого корня x1, получим a ≈ 0,618, b ≈ 0,382.
Именно положительный корень x1 уравнения (3) наиболее часто называют золотой пропорцией или пропорцией золотого сечения. Соответствующее геометрическое деление отрезка называют золотым сечением (точка С на рис. 1).
Для удобства дальнейшего изложения обозначим x1 = D. Общепризнанного обозначения для золотого сечения до сих пор нет. Обусловлено это, видимо, тем, что под ним понимают иногда и другое число, о чем будет сказано ниже.
Оставляемый по обыкновению в стороне отрицательный корень x2 приводит к менее наглядному делению отрезка на две неравные части. Дело в том, что он дает делящую точку С, которая лежит вне отрезка (так называемое внешнее деление). Действительно, если a + b = 1, то, используя корень x2, получим a ≈ -1,618, b ≈ 2,618. Поэтому отрезок a необходимо откладывать в отрицательном направлении (рис. 2).
2. Второй вариант решения пропорции (1) принципиально не отличается от первого. Будем считать неизвестным отношение b/a и обозначим его через y. Тогда получим уравнение
y2 + y -1 = 0 , (4)
которое имеет иррациональные корни
Если a + b = 1, то, используя корень y1, получим a = y1 ≈ 0,618, b ≈ 0,382. Для корня y2 получим a ≈ -1,618, b ≈ 2,618. Геометрическое деление отрезка в пропорции золотого сечения с использованием корней y1 и y2 полностью идентично предыдущему варианту и соответствует рис. 1 и 2.
Положительный корень y1 непосредственно дает искомое решение задачи, и его также называют золотой пропорцией .
Для удобства обозначим значение корня y1 = d.
Таким образом, в литературе золотую пропорцию математически выражают числом D1,618 или числом d0,618, между которыми существуют две изумительные связи:
Dd = 1 и D — d = 1. (5)
Доказано, что другой подобной пары чисел, обладающих этими свойствами, не существует.
Используя оба обозначения для золотой пропорции, запишем решения уравнений (3) и (4) в симметричном виде: = D, = —d, = d, = —D.
Необычные свойства золотого сечения достаточно подробно описаны в литературе [1-4]. Они настолько удивительны, что покоряли разум многих выдающихся мыслителей и создали вокруг себя ореол таинственности.
Золотая пропорция встречается в конфигурации растений и минералов, строении частей Вселенной, музыкальном звукоряде. Она отражает глобальные принципы природы, пронизывая все уровни организации живых и неживых объектов. Ее используют в архитектуре, скульптуре, живописи, науке, вычислительной технике, при проектировании предметов быта. Творения, несущие в себе конфигурацию золотого сечения, представляются соразмерными и согласованными, всегда приятны взгляду, да и сам математический язык золотой пропорции не менее изящен и элегантен.
Кроме равенств (5) из соотношения (2) можно выделить три интересные соотношения, которые обладают определенным совершенством, выглядят вполне привлекательно и эстетично:
(6)
Величие и глубину природы можно ощущать не только, например, при созерцании звезд или горных вершин, но и вглядываясь в некоторые удивительные формулы, очень ценимые математиками за их красоту. К ним можно отнести изящные соотношения золотой пропорции, фантастическую формулу Эйлера eiπ = -1 (где i = √-1), формулу, определяющую знаменитое число Непера (основание натуральных логарифмов): e = lim(1 + 1/n)n = 2,718 при n → ∞, и многие другие.
После решения пропорции (1) ее идея кажется довольно простой, но, как это часто бывает со многими на первый взгляд простыми задачами, в ней скрыто немало тонкостей. Одной из таких замечательных тонкостей, мимо которой до сих пор проходили исследователи, является связь корней уравнений (3) и (4) с углами трех замечательных треугольников.
Чтобы убедиться в этом, рассмотрим, каким образом одномерный отрезок, разделенный в пропорции золотого сечения, может быть легко преобразован в двумерный образ в виде треугольника. Для этого, используя вначале рис. 1, отложим на отрезке АВ длину отрезка a дважды — от точки А в сторону точки В и, наоборот, от точки В в сторону А. Получим две точки С1 и С2, делящие отрезок АВ с разных концов в пропорции золотого сечения (рис. 3). Считая равные отрезки АС1 и ВС2 радиусами, а точки А и В центрами окружностей, проведем две дуги до их пересечения в верхней точке С. Соединив точки А и С, а также В и С, получим равнобедренный треугольник АВС со сторонами АВ = a + b = 1, АС = = ВС = a = d ≈ 0,618. Величину углов при вершинах А и В обозначим α, при вершине С — β. Вычислим эти углы.
По теореме косинусов
(АВ)2 = 2(АС)2(1 — cos β).
Подставив численные значения отрезков АВ и АС в эту формулу, получим
(7)
Аналогично получаем
(8)
Выход золотой пропорции на двумерный образ позволил связать корни уравнений (3) и (4) с углами треугольника АВС, который можно назвать первым треугольником золотой пропорции.
Выполним аналогичное построение, используя рис. 2. Если на продолжении отрезка АВ отложить от точки В вправо отрезок, равный по величине отрезку a, и повернуть вокруг центров А и В вверх оба отрезка как радиусы до их соприкосновения, то получим второй треугольник золотой пропорции (рис. 4). В этом равнобедренном треугольнике сторона АВ = a + b = 1, сторона АС = ВС = D ≈1,618, и поэтому по формуле теоремы косинусов получаем
(9)
Угол a при вершине С равен 36о и связан с золотой пропорцией соотношением (8). Как и в предыдущем случае, углы этого треугольника связаны с корнями уравнений (3) и (4).
Второй треугольник золотой пропорции служит основным составляющим элементом правильного выпуклого пятиугольника и задает пропорции правильного звездчатого пятиугольника (пентаграммы), свойства которых подробно рассмотрены в книге [3].
Звездчатый пятиугольник — фигура симметричная, и в то же время в соотношениях ее отрезков проявляется асимметрическая золотая пропорция. Подобное сочетание противоположностей всегда притягивает глубоким единством, познание которого позволяет проникнуть в скрытые законы природы и понять их исключительную глубину и гармонию. Пифагорейцы, покоренные созвучием отрезков в звездчатом пятиугольнике, выбрали его символом своего научного сообщества.
Со времен астронома И. Кеплера (XVII век) иногда высказываются различные точки зрения относительно того, что обладает большей фундаментальностью — теорема Пифагора или золотая пропорция. Теорема Пифагора лежит в основании математики, это один из ее краеугольных камней. Золотое сечение лежит в основании гармонии и красоты мироздания. На первый взгляд оно несложно для понимания и не обладает значительной основательностью. Тем не менее некоторые его неожиданные и глубокие свойства постигаются только в последнее время [1], что говорит о необходимости с почтением относиться к его скрытой тонкости и возможной универсальности. Теорема Пифагора и золотая пропорция в своем развитии тесно переплетаются одна с другой и геометрическими и алгебраическими свойствами. Между ними нет ни пропасти, ни принципиальных различий. Они не конкурируют, у них разные предназначения.
Вполне возможно, что обе точки зрения равноправны, так как существует прямоугольный треугольник, содержащий в себе разнообразные особенности золотой пропорции. Другими словами, существует геометрическая фигура, достаточно полно объединяющая два математических восхитительных факта — теорему Пифагора и золотую пропорцию.
Чтобы построить такой треугольник, достаточно продолжить сторону ВС треугольника АВС (рис. 4) до пересечения в точке Е с перпендикуляром, восстановленным в точке А к стороне АВ (рис. 5).
Во внутреннем равнобедренном треугольнике АСЕ угол φ (угол АСЕ) равен 144о, а угол ψ (углы ЕАС и АЕС) равен 18о. Сторона АС = СЕ = СВ = D. Используя теорему Пифагора, легко получить, что длина катета
Используя этот результат, легко приходим к соотношению(10)
Итак, найдена непосредственная связь корня y2 уравнения (4) — последнего из корней уравнений (3) и (4) — с углом 144о. В связи с этим треугольник АСЕ можно назвать третьим треугольником золотой пропорции.
Если в замечательном прямоугольном треугольнике АВЕ провести биссектрису угла САВ до пересечения со стороной ЕВ в точке F, то увидим, что вдоль стороны АВ располагаются четыре угла: 36о, 72о, 108о и 144о, с которыми корни уравнений золотой пропорции имеют непосредственную связь (соотношения (7) — (10)). Таким образом, в представленном прямоугольном треугольнике содержится вся плеяда равносторонних треугольников, обладающих особенностями золотого сечения. Кроме того, весьма примечательно то, что на гипотенузе любые два отрезка, ЕС = D и СF = 1,0 находятся в соотношении золотой пропорции с FВ = d. Угол ψ связан с корнями D и d уравнений (3) и (4) соотношениями
.
В основу представленных выше построений равнобедренных треугольников, углы которых связаны с корнями уравнений золотой пропорции, положены исходный отрезок АВ и его части a и b. Однако золотое сечение позволяет моделировать не только описанные выше треугольники, но и различные другие геометрические фигуры, несущие в себе элементы гармоничных отношений.
Приведем два примера подобных построений. В первом — рассмотрим отрезок АВ, представленный на рис. 1. Пусть точка С — центр окружности, отрезок b — радиус. Проведем радиусом b окружность и касательные к ней из точки А (рис. 6). Соединим точки касания E и F с точкой С. В результате получим асимметричный ромб АЕСF, в котором диагональ АС делит его на два равных прямоугольных треугольника АСЕ и АСF.
Обратим более пристальное внимание на один из них, например на треугольник АСЕ. В этом треугольнике угол АЕС — прямой, гипотенуза АС = a, катет СЕ = b и катет АЕ = √ab ≈ 0,486, что следует из соотношения (2). Следовательно, катет АЕ является средним геометрическим (пропорциональным) между отрезками a и b, то есть выражает геометрический центр симметрии между числами a ≈ 0,618 и b ≈ 0,382.
Найдем значения углов этого треугольника:
Как и в предыдущих случаях, углы δ и ε связаны через косинус с корнями уравнений (3) и (4).
Заметим, что асимметричный ромб, подобный ромбу AECF, получается при проведении касательных из точки В к окружности радиуса a и c центром в точке А.
Асимметричный ромб AECF получен иным путем в книге [1] при анализе формообразования и явлений роста в живой природе. Прямоугольный треугольник АЕС назван в этой работе «живым» треугольником, так как способен порождать наглядные образы, соответствующие различным структурным элементам природы, и служить ключом при построении геометрических схем начала развития некоторых живых организмов.
Второй пример связан с первым и третьим треугольниками золотого сечения. Образуем из двух равных первых треугольников золотой пропорции ромб с внутренними углами 72о и 108о. Аналогично объединим два равных третьих треугольника золотой пропорции в ромб с внутренними углами 36о и 144о. Если стороны этих ромбов равны между собой, то ими можно заполнить бесконечную плоскость без пустот и перекрытий. Соответствующий алгоритм заполнения плоскости разработал в конце 70-х годов ХХ века физик-теоретик из Оксфордского университета Р. Пенроуз. Причем выяснилось, что в получающейся мозаике невозможно выделить элементар ную ячейку с целым числом ромбов каждого вида, трансляция которой позволяла бы получить всю мозаику. Но самым замечательным оказалось то, что в бесконечной мозаике Пенроуза отношение числа «узких» ромбов к числу «широких» точно равно значению золотой пропорции d = 0,61803…!
В этом примере удивительным образом соединились все корни золотого сечения, выраженные через углы, с одним из случаев нетривиального заполнения бесконечной плоскости двумя элементарными фигурами — ромбами.
В заключение отметим, что приведенные выше разнообразные примеры связи корней уравнений золотой пропорции с углами треугольников иллюстрируют тот факт, что золотая пропорция более емкая задача, чем это представлялось ранее. Если прежде сферой приложения золотой пропорции считались в конечном итоге соотношения отрезков и различные последовательности, связанные с численными значениями ее корней (числа Фибоначчи), то теперь обнаруживается, что золотая пропорция может генерировать разнообразные геометрические объекты, а корни уравнений имеют явное тригонометрическое выражение.
Авторы отдают себе отчет, что высказанная выше точка зрения относительно изящества математических соотношений, связанных с золотой пропорцией, отражает личные эстетические переживания. В современной философской литературе понятия эстетики и красоты трактуются довольно широко и используются скорее на интуитивном уровне. Эти понятия отнесены главным образом к искусству. Содержание научного творчества в эстетическом плане в литературе практически не рассматривается. В первом приближении к эстетическим параметрам научных исследований можно отнести их сравнительную простоту, присущую им симметрию и способность порождать наглядные образы. Всем этим эстетическим параметрам отвечает задача, получившая название «золотая пропорция». В целом же проблемы эстетики в науке далеки от своего решения, хотя и представляют большой интерес.
Интуитивно чувствуется, что золотая пропорция все еще скрывает свои тайны. Некоторые из них, вполне возможно, лежат на поверхности, ожидая необычного взгляда своих новых исследователей. Знание свойств золотой пропорции может служить творческим людям хорошим фундаментом, придавать им уверенность и в науке и в жизни.
ЛИТЕРАТУРА
1. Шевелев И. Ш., Марутаев И. А., Шмелев И. П. Золотое сечение: Три взгляда на природу гармонии. — М.: Стройиздат, 1990. — 343 с.
2. Стахов А. П. Коды золотой пропорции. — М.: Радио и связь, 1984. — 152 с.
3. Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238 с.
4. Коробко В. И. Золотая пропорция: Некоторые философские аспекты гармонии. — М. — Орел: 2000. — 204 с.
5. Урманцев Ю. А. Золотое сечение // Природа, 1968, № 11.
6. Попков В. В., Шипицын Е. В. Золотое сечение в цикле Карно // УФН, 2000, т. 170, № 11.
7. Константинов И. Фантазии с додекаэдром // Наука и жизнь, 2001, № 2.
8. Шевелев И. Ш. Геометрическая гармония // Наука и жизнь, 1965, № 8.
9. Гарднер М. От мозаик Пенроуза к надежным шифрам. — М. : Мир, 1993.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Арифметика

Золотое отношение (золотое сечение)
Рассмотрим отрезок AB и точку C , расположенную внутри него.

Говорят, что точка C делит отрезок AB в золотом отношении (золотом сечении), если длина отрезка AB так относится к длине отрезка AC , как длина отрезка AC относится к длине отрезка CB . При этом самим золотым отношением (золотым сечением) называют отношение длины отрезка AB к длине отрезка AC .
Термин «золотое отношение» имеет ряд синонимов: золотое сечение, золотая пропорция, гармоническая пропорция, золотое число, деление отрезка в крайнем и среднем отношении.
Следуя исторической традиции, будем золотое отношение обозначать символом φ . Для того, чтобы найти значение φ , введем для длин отрезков AB и AC обозначения:
|AB| = x, |AC| = y .
Тогда длина отрезка CB будет выражена формулой:
|CB| = x – y ,
причем числа x и y будут удовлетворять неравенствам:
x > 0, y > 0, x – y > 0.
В случае, когда точка C делит отрезок AB в золотом отношении, числа x и y удовлетворяют уравнению:

где
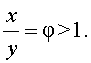
Выведем уравнение для переменной φ :

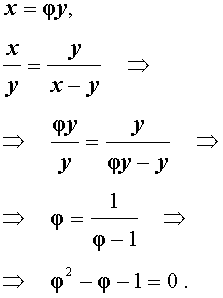
Следовательно,
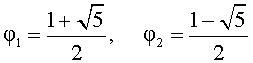
Поскольку φ > 1 , то второй корень должен быть отброшен.
Итак, золотое отношение
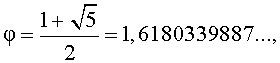
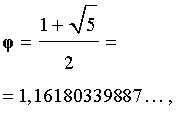
что и требовалось получить.
Правильный пятиугольник и его связь с золотым отношением
Золотое отношение (золотое сечение) встречается в различных областях человеческой деятельности: в скульптуре, архитектуре, живописи, музыке и т.д.
Приведем пример использования золотого отношения в планиметрии. Для этого рассмотрим правильный пятиугольник A1A2A3A4A5 , вписанный в окружность радиуса R с центром O .

Заметив, что длины всех диагоналей пятиугольника равны, обозначим длину стороны пятиугольника символом y , а длину диагоналей символом x .
Теперь рассмотрим треугольник A1A3A5 . Этот треугольник является равнобедренным треугольником с основанием A1A5 и боковыми сторонами A1A3 и A3A5, причем
A1A5 = y,
A1A3 = A3A5 = x .
Кроме того,

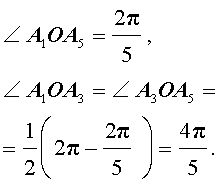
Следовательно,
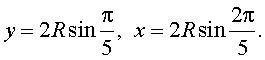

Теперь, воспользовавшись тем, что
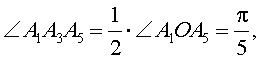

применим для треугольника A1A3A5 теорему косинусов:
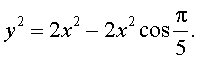
Разделив это равенство на y2, и заметив, что

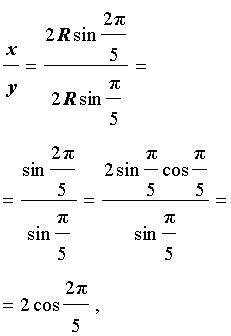
получим соотношение:
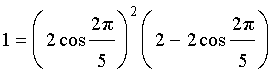

Если в этом соотношении ввести, для упрощения записи, переменную d по формуле
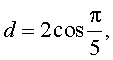
то возникает уравнение:
d 3 – 2d 2 + 1 = 0.
Для того, чтобы решить это уравнение, разложим его левую часть на множители:

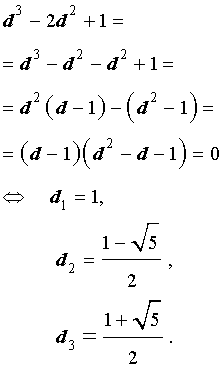
В силу того, что
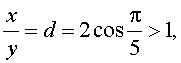
то первый и второй корни должны быть отброшены. Следовательно,
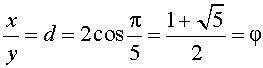

т.е. является золотым отношением.
В результате мы получили, что, во-первых, отношение диагонали правильного пятиугольника к стороне правильного пятиугольника равно золотому отношению, а, во-вторых, что для самого золотого отношения справедлива формула:
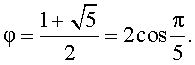

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Примеры золотого сечения в архитектуре, его применение
Примеры золотого сечения в архитектуре найти можно везде, когда умеешь его видеть. Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.
7+ примеров золотого сечения в архитектуре России
Санкт-Петербург
Здания исторического центра Санкт-Петербурга построены в разных архитектурных стилях, таких как барокко, классицизм, ампир, эклектика, необарокко, неоготика. Подчиняются ли они золотому правилу?
Исаакиевский собор
Придворный архитектор Александра I Огюст Монферран строил этот собор с 1819 по 1858 гг. Стиль позднего классицизма, в котором уже проявлены черты неоренессанса и эклектики. Елена задалась вопросом: «В чём же причина гармонии довольно громоздкого здания?»
Свой поиск она начала, как рекомендуется в методике профессора Московского архитектурного института Ю.Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.
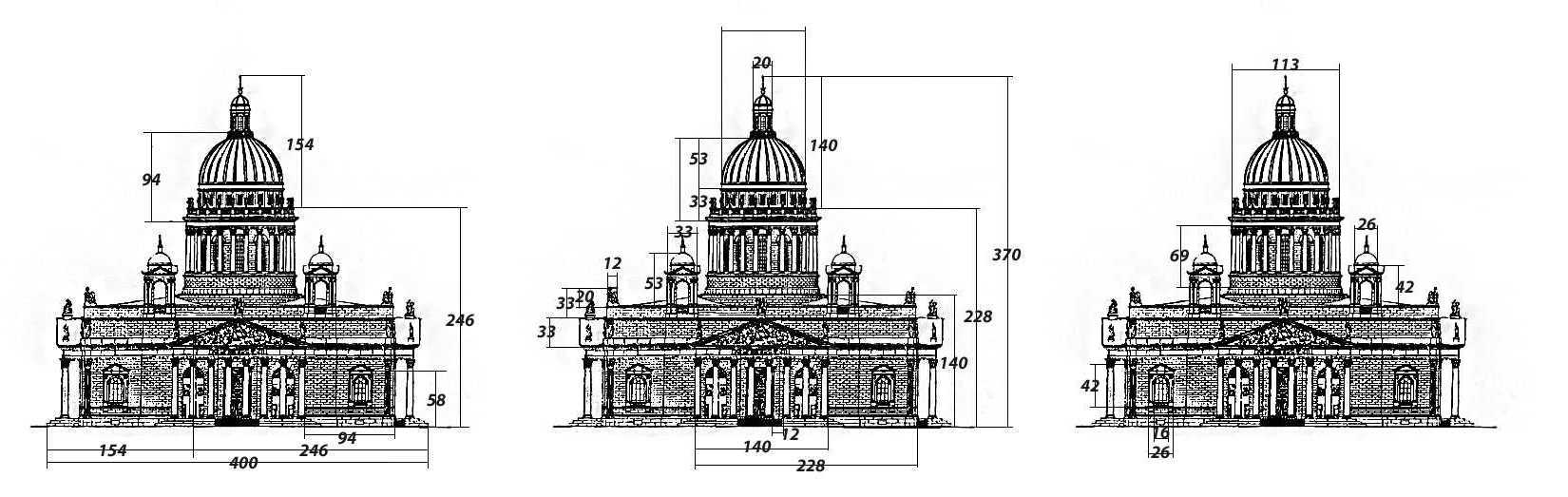
Первый ряд определён шириной здания, которая принята за 400 ед. и представляет такие цифры 400, 247, 153, 94, 58…
Если 400 разделим на число ≈1,618, то получим приблизительно 247; повторяем действие со следующим числом: 247: 1.618≈153.
И так находим все числа. Теперь смотрим на рисунок. Основная часть с колоннами вписывается в прямоугольник со сторонами 400 и 247. Поскольку стороны находятся в соотношении Ф≈1.618, то они образуют Золотой прямоугольник.
Следующий ряд представлен высотой здания: 370, 228, 140, 87, 53, 33, 20, 12. Эти размеры заложены в более мелкие детали. По вертикали Исаакиевский собор делится Золотым сечением у основания купола, что делает соотношение основной части и купола гармоничным.
Третий ряд размеров начинается со 113, и являет ширину основания главного купола: 113, 69, 42, 26, 16. Числа этого ряда встречаются в размерах окон, в высотах колонн и других деталей собора.
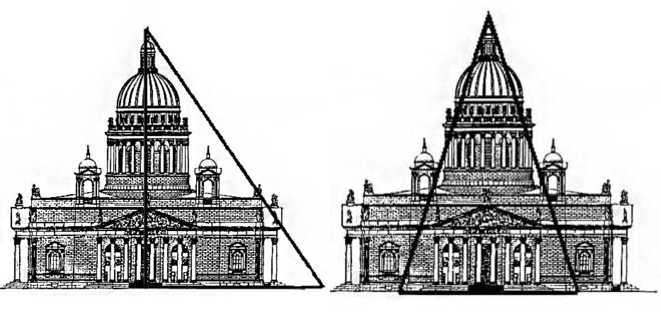
Золотые прямоугольный и равнобедренный треугольники имеют место в здании Исаакиевского собора, как видно из рисунка.
Кунсткамера
На Университетской набережной Васильевского острова стоит здание Кунсткамеры, заложенное в 1718 году под руководством немецкого архитектора Георга Маттарнови: Петровское барокко, два 3-этажных корпуса и сложная многоярусная купольная башня.
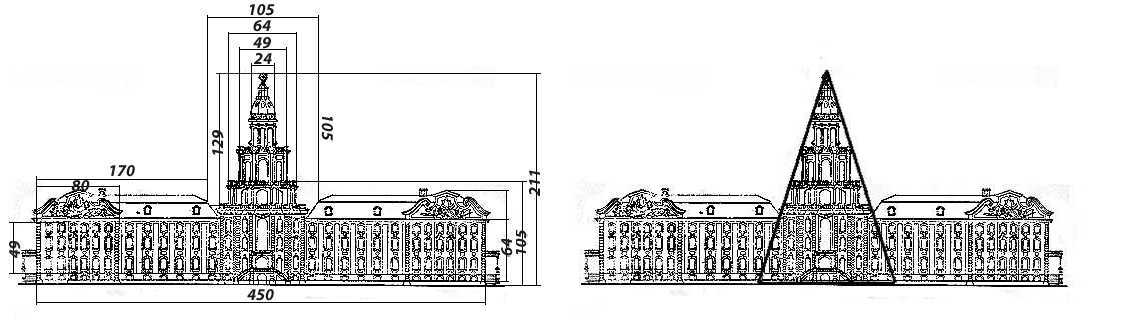
Исследование начинается с главных величин: высоты и длины здания, от которых строится золотой ряд. Длина — 450 ед., далее 277, 170, 105, 65, 40, 24. Такие размеры можно видеть в высоте и широте разных уровней башни, длине корпусов. Сама башенная часть вписана в золотой равнобедренный треугольник от основания до вершины. Золотое сечение просматривается в большей степени именно в этом главном элементе, что правильно с точки зрения архитектуры. Вывод: основа Кунсткамеры подчиняется золотому правилу и сохраняет композиционную гармоничность.
Новый золотой ряд начинает высота здания: 211, 130, 80, 49, 30. Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.
Торговый дом «Эсдерс и Схейфальс» на пересечении Мойки и Гороховой
Построено в 1907 году по проекту Владимира Александровича Липского и Константина Николаевича де Рошефора (Рошфора). В 1905 г. бельгиец С. Эсдерс и нидерландец Н. Схейфальс подали прошение о разрешении построить пятиэтажное здание с куполом и шпилем на угловой башне для их торгового дома вместо старого.
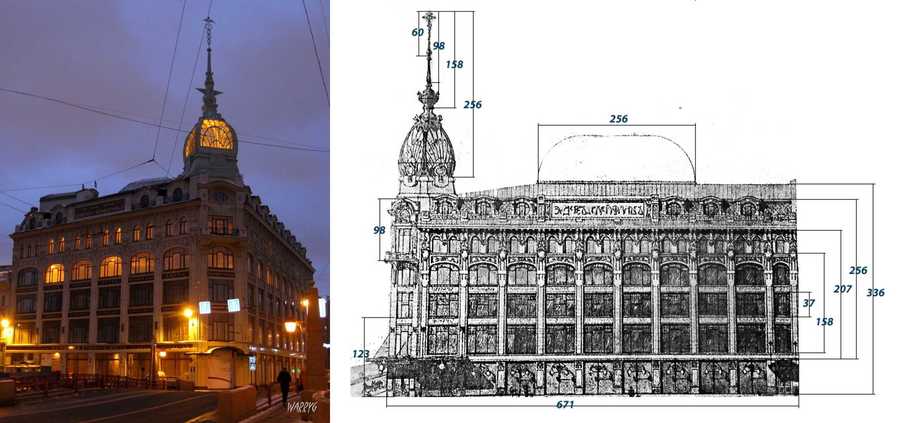
С длины здания в 671 ед. начинается ряд Золотого сечения, наблюдаемого в размерах: 671, 414, 256, 158, 98, 60, 37, 23. Обращаем внимание на основной элемент — шпиль. Убеждаемся, что композиционное решение завершено гармоничным сочетанием высотных величин.
Дом Советов на Московской площади
Построен в 1941г по проекту Ноя Абрамовича Троцкого. Здание советского периода рассматривают как творческую интерпретацию классики. Центральный портик с четырнадцатью колоннами завершает скульптурный ансамбль на тему строительства социализма и гербом Российской Советской Федеративной Социалистической Республики.

По бокам симметрично расположены пятиэтажные корпуса. Длина Дома достигает 1472 ед., из которого методом деления на число Ф получается ряд размеров элементов здания: 1472, 909, 562, 34, 214, 132, 81, 50 (Приложение 21): высоты сооружения, высоты входа и др.
Вершина Золотого равнобедренного треугольника совпадает с вершиной здания, а его стороны проходят через вехние точки главного входа. Прямоугольный золотой треугольник образован вершинами в верхушке здания и в конце внутренней части бокового крыла. Пропорциональность очевидна, хотя и не имеет большой композиционной значимости.

Москва
Московский Государственный Университет на Воробьёвых горах

Над его проектом работал коллектив под управлением Б.М.Иофана, которого позже сместили с должности главного архитектора. Образец послевоенной советской архитектуры выстроен с 1949 по 1953 годы.
Б.М.Иофан предложил композицию из пяти составляющих с центральной башней. В годы строительства это было самое высокое здание в Европе.
Длина здания равна 1472 ед. и начинает ряд: 909, 562, 347, 214, 132, 81, 50. Золотому сечению подчиняются, в основном высотные размеры. Из ширины башни проистекает другой ряд: 538, 332, 205, 126, который видим в широтных размерах.
Золотой прямоугольный треугольник гипотенузой проходит через угол здания и захватывает пристройки.
Таким образом, во всех исследуемых зданиях ученица обнаружила Золотое сечение, сохраняющее гармонию.
5 примеров дополнительно
Чтобы упростить задачу поиска ЗС, можно брать рациональные дроби 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; и так дальше. Закономерность ясна: 3+2 =5; 5+3=8; 8+5=13… Или ещё проще. Сделайте себе циркуль для определения пропорции по инструкции в видео. Времени уйдет минут 10. Как пользоваться этим циркулем для определения пропорциональности элементов тоже расскажут и покажут.
Применяя этот способ, находим золотую пропорцию русского зодчего Матвея Казакова в кремлёвском здании сената, да и во всех остальных работах: Пречистенском дворце в Москве, Благородном собрании, Голицынской больнице (им. Пирогова)…
Созданный другим великим архитектором Василием Ивановичем Баженовым дом Пашкова в Москве (Российская государственная библиотека) причисляют к образцам совершенных архитектурных памятников, в котором легко определить ЗС.

Ужасный символ Парижа и золотое сечение
 Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?
Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?
Она же наблюдается и самом знаменитом французском соборе Нотр-Дам-Де-Пари.
Вся правда о древних строителях
Интуитивно или сознательно великие архитекторы строили здания с учётом этих пропорций? Античные математики знали о золотом сечении со времён Пифагора. Находятся всё новые подтверждения его применения в архитектурных пропорциях. Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?
Может все выше приведённые исследования являются подгонкой под известный результат? Не так сложно выбрать из множества архитектурных элементов те, которые подтверждают гипотезу, т. к. абсолютной точности никто не требует. Логично задуматься над вопросом: «Что если греки НЕ применяли золотое сечение?»
Собственно говоря, и для Луки Пачоли, написавшего в 1509 году труд «Божественная пропорция», не столь важно было его прикладное значение. Важно было обосновать её мистическую природу. А применять его осознанно стали только с момента издания книги.
Тайна архитектуры Древней Греции
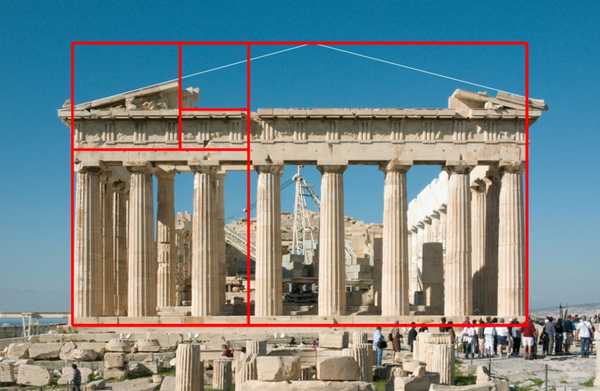
Красивые и гармоничные объекты всегда отвечают правилу ЗС, а при анализе величин определяется эта пропорциональность. Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?
Мифы и диковинные факты о пирамиде
Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?
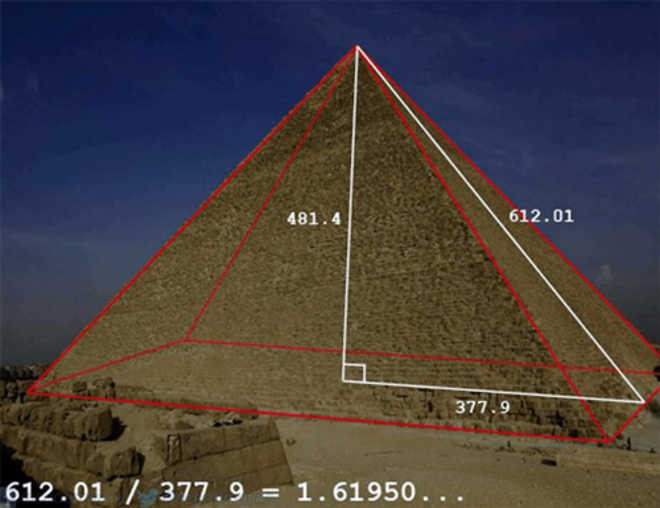
Но тогда возникает вопрос об уровне древнеегипетской математики. Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?
Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.
Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.
Как же всё-таки построить «Золотой» дом для себя?
Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия Золотого сечения. Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.
Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.
В природе подобная соразмерность встречается везде. Тот, кто чувствует гармонию пространства, создаст пропорциональное здание без специальных для этого усилий.
Например, наши предки строили хоромы соразмерные человеку. Мерили высоту и длину в саженях, локтях, аршинах, пядях. Никто не возражает, что в человеческом теле соблюдена золотая пропорция? Длина руки от кончиков пальцев до подмышки относится к расстоянию от той же точки до локтя как эта величина к размеру ладони.
Известный французский архитектор Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.
5 способов соблюдать правило в интерьере
- В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.
- Иногда достаточно переставить мебель или сделать дополнительную перегородку.
- Аналогичным образом меняется высота и длина окон и дверей.
- В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
- Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
О золотом сечении простыми словами
Что же это такое? Отрезки золотой пропорции выражаются бесконечной иррациональной дробью, десятичное значение которой равно приближённо числу Ф≈1,618 или Ф≈1,62. Другими словами: если берём целое и делим его на две части так, что одна из них составляет 62%, а другая — 38%, получаем Золотую пропорцию.
Золотой прямоугольник: когда длину большей стороны делим на длину меньшей и получаем число Ф. При делении меньшей на большую получается обратное значение φ ≈ 0,618.
Золотой равнобедренный треугольник: если отношение размера одной боковой стороны и размера основания составляет золотое число Ф; угол между равными сторонами равен 36°.
Золотой прямоугольный треугольник Кеплера объединяет в себе теорему Пифагора и ЗС: соотношение квадратов его сторон составляет 1,618.
Оцените полезность статьи, поделитесь с друзьями и добавьте в закладки, чтобы было легко найти.
Смотрите познавательное видео по теме
ОСНОВЫ КОМПОЗИЦИИ: Золотое сечение — PhotoDzen.com
- На главную
- Обучение
- Фото учебник
- Практикум
- МобиФото
- Форум
- Галерея
- Фотогалерея
- Фотографы
- Видеогалерея
- Статьи
- Интересно
- Камеры
- Обьективы
- Новости
- Конкурсы
- Архив конкурсов
- Предложения
- Фототур
- Регистрация
- Вход
- Главная
- / Обучение
Золотой треугольник
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.
Рис. 5. Построение правильного пятиугольника и пентаграммы
Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Рис. 6. Построение золотого треугольника
Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
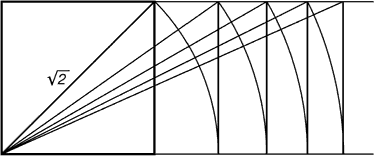
Рис. 7. Динамические прямоугольники
Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
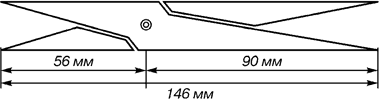
Рис. 8. Античный циркуль золотого сечения
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

Рис. 9. Построение шкалы отрезков золотой пропорции
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
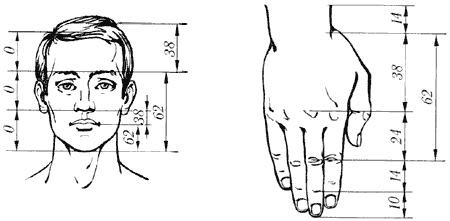
Рис. 10. Золотые пропорции в частях тела человека
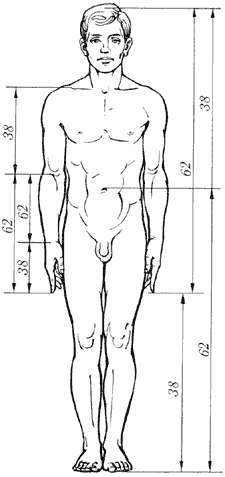
Рис. 11. Золотые пропорции в фигуре человека
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
Исследование Шри Янтры
Треугольники золотого сечения
Рисунок 1 Определение золотого сечения
Поскольку Шри Янтра состоит из треугольников, стоит потратить некоторое время на изучение треугольников, в частности, треугольников в контексте знаменитого золотого сечения.
Мы должны начать с золотого сечения, которое также известно как соотношение фи или золотое сечение . Это единственное соотношение, которое удовлетворяет определению a + b is to a as a to b , показанное на рисунке 1.Проще говоря, это означает, что a + b / a = a / b. Если мы сложим b над a, оно разделится в золотом сечении. Если мы возьмем меньшую часть и снова сложим ее, она снова и снова разделит линию в той же пропорции. Это идеальная пропорция самовложения, которая объясняет, почему большинство наших конечностей делятся в пропорции золотого сечения.
цифра 2. Золотой прямоугольник
Если это кажется слишком абстрактным, давайте посмотрим на это в двух измерениях. На рис. 2 показан простой золотой прямоугольник со сторонами 1 x φ.Если мы снова разделим этот прямоугольник, нарисовав линию, длина которой равна его более короткой стороне (длина 1), мы получим прямоугольник с золотым сечением меньшего размера (темно-серый). Мы можем повторить эту операцию с меньшим прямоугольником и снова получить меньший золотой прямоугольник и квадрат. Это показывает фрактал (самоподобие), и самовложенность, свойства годового отношения.
Рисунок 3 Маска красоты Золотое сечение
Наше восприятие красоты на самом деле определяется золотым сечением.Привлекательный человек привлекателен тем, что его пропорции ближе к золотому сечению. В природе числа Фибоначчи являются близким приближением к золотому сечению, поскольку дроби не всегда возможны в реальном мире.
Золотая пропорция — это 1.6180 .. также обозначается греческой буквой фи (φ). Обратное к фи (1 / φ) обозначается заглавной фи (Φ) и равно 0,6180 … Это одно из многих удивительных свойств золотого сечения: φ — 1 = 1 / φ.
В случае с золотым прямоугольником все просто.Вы рисуете прямоугольник со стороной 1 и 1.6180 … В Интернете (википидия) вы найдете множество методов, которые покажут вам, как точно нарисовать его с помощью линейки и циркуля.
Но поскольку Шри Янтра состоит из 9 взаимосвязанных треугольников, нас в основном интересуют треугольники. Есть только один способ нарисовать прямоугольник золотого сечения. Прямоугольник имеет только две степени свободы: ширину и высоту. Но у треугольника есть ширина, высота и длина наклонной стороны. Три степени свободы.Мы также увидим, что другие варианты также возможны, когда мы используем прямоугольный треугольник вместо равнобедренного.
Это дает начало множеству вариаций треугольников «золотого сечения». В этой статье мы рассмотрим семь разных моделей и их характеристики.
Король и королева
Начнем с Короля и Королевы треугольников золотого сечения. Эти двое настоящие. Эти два треугольника — это то, что обычно подразумевается под «треугольником золотого сечения».
Рисунок 4 Создание золотых треугольников из золотого прямоугольника
Эти два золотых треугольника можно легко создать из золотого прямоугольника, удалив одну из сторон и схватив две открытые стороны, пока они не встретятся в середине, как показано на рисунке 4. Интересно, что углы этих двух треугольников кратны 36.
Рисунок 5 Золотые треугольники в пятиугольнике
Другой способ создания золотых треугольников — нарисовать пятиугольник.Пентагон больше, чем любая другая фигура, связан с золотым сечением. При соединении пяти вершин пятиугольника мы получаем множество треугольников золотого сечения. Цветные области на рисунке 5 показывают два золотых треугольника двух разных размеров в пятиугольнике.
Рисунок 6 Золотой треугольник King
Давайте посмотрим на эти два треугольника более подробно и посмотрим, что делает их такими особенными. На изображении выше мы видим, что этот треугольник имеет два угла в 72 градуса и один угол в 36 градусов.Все углы кратны 36. Если длина основания равна 1, то наклонные стороны будут иметь длину 1,6180 .., что обозначается греческой буквой фи (φ). Вот почему его еще называют соотношением фи.
Если мы проведем линию, которая делит один из углов 72 градусов пополам (деление угла пополам), мы видим, что появляется еще один меньший треугольник золотого сечения. Это показывает самоподобное свойство золотого сечения в действии. Тот же эффект самовоспроизведения наблюдается и с золотым прямоугольником.
Рисунок 7 Королева золотого треугольника
Другой треугольник золотого сечения, очевидно, можно создать, сделав длину двух наклонных сторон равной 1 и длину основания 1,6180. В результате получается более плоский треугольник с одинаковыми углами 36 и 72 градуса. Здесь мы снова можем разделить этот треугольник (показанный пунктирной линией), на этот раз разделив угол 72 градуса на 1/3. У нас получается треугольник меньшего размера с такими же пропорциями с левой стороны. С правой стороны у нас есть треугольник, похожий на первый, который мы создали.Мы можем продолжать такое деление вечно, что создаст спираль золотого сечения. Еще один узор, широко используемый в природе.
Золотые кузены
Два треугольника, которые мы изучили в предыдущем разделе, являются настоящими треугольниками золотого сечения. Однако можно создать вариант, сделав треугольник с основанием единичной длины и высотой 1,6180 (вместо длины стороны). Он очень похож на первый треугольник, который мы рассматривали, но у него нет самовоспроизводящихся и фрактальных качеств, типичных для настоящих треугольников золотого сечения.
Рисунок 8
До сих пор мы использовали равнобедренные треугольники. Симметричные треугольники по вертикальной оси. Мы также можем использовать прямоугольные треугольники, что дает начало еще двум кузенам золотого сечения.
Рисунок 9 Золотой треугольник, использованный для пирамиды Гизы
Теперь, поскольку мы используем прямоугольный треугольник, у нас есть три стороны разной длины вместо двух, как в равнобедренном треугольнике. Это дает больше способов представить золотое сечение в треугольнике.
Первый можно увидеть на изображении выше. В этом треугольнике золотого сечения мы используем основание как единицу длины, а наклонную сторону — как длину фи. Это интересно приводит к высоте квадратного корня из фи. Еще один знак магии золотого сечения. Если мы создадим зеркальное отражение этого треугольника, мы получим равнобедренный треугольник с основанием 2, высотой квадратного корня из фи и сторонами длины фи. Это, кстати, действительно близко по форме к знаменитой великой пирамиде Гизы.
Рисунок 10
Второй вариант может быть получен, если задать треугольнику высоту фи и основание, равное единице. В результате получается треугольник, который немного выше предыдущего, поскольку угол составляет 58,3 градуса вместо 51,8 градуса. Теперь легко понять, почему первая была выбрана в качестве формы пирамиды в Гизе. Это делает пирамиду не слишком высокой и не слишком низкой, устойчивой и приятной на вид.
Дальние родственники
Также возможны два других варианта.Их можно было бы считать самым низшим типом, поскольку ни одна из их сторон не измеряет точно фи.
Рис. 11 Золотой треугольник — это подмножество треугольника ферзя.
В этом варианте используется высота phi / 2 и длина стороны 1. Мы видим, что этот треугольник на самом деле является подмножеством второго, на который мы смотрим. Вы можете видеть, что у нас одинаковые углы — 36 и 108 градусов. Это половина треугольника. Мы видим, что в этом треугольнике у нас есть углы, кратные 18, как и в первых двух треугольниках.
Рисунок 12
Этот последний треугольник завершает серию чисел, кратных 18. Мы видим, что соотношение фи и его сопряжение (заглавная фи) проявляются во всех трех длинах. Теперь у нас есть треугольники с меньшим углом 18, 36, 54, 72 градусов, которые все кратны 18.
Семейное воссоединение
Рисунок 13 Золотые треугольники внутри золотого прямоугольника.
На этом рисунке показаны все треугольники золотого сечения, помещенные внутри золотого прямоугольника.Мы могли разделить золотое сечение на три семьи. Сначала у нас есть треугольники с четными углами, кратными 18. Их можно разделить на две группы. Король и Королева треугольников золотого сечения — первые два, которые мы создали, свернув стороны золотого прямоугольника. Стороны этих двух треугольников имеют длину 1 или φ. Третья группа будет включать треугольники с иррациональными углами: 51,82 …, 58,28 …, 72,82 …
Равносторонний треугольник
Рисунок 14 Равносторонний треугольник
Мы также должны упомянуть равносторонний треугольник как главный игрок на арене треугольников.У него нет золотых пропорций, но он является основным компонентом природы из-за его идеальной симметрии и простоты. Мы замечаем, что это проявляется во многих платоновых телах, которые являются строительным блоком трехмерной геометрии. Например, все формы кристаллов могут быть получены из платоновых тел.
Рисунок 15 Платоновы тела
Как мы видим на этом рисунке, это строительный блок 3 из 5 платоновых тел. Равносторонний треугольник — простейшая геометрическая поверхность, потому что у него минимальное количество сторон.Любое изображение или фигура можно представить в виде группы треугольников (триангуляция). Также интересно отметить, что число 3 считается священным во многих религиях. На ум приходит святая троица, а также многие троицы ведического знания (Вишну, Шива, Брахман), (Риши, Дэвата, Чанда), (Саттва, Раджас, Тамас), (Вата, Питта, Капха) и т. Д.
.Фи и Фибоначчи в треугольниках Кеплера и золотых
Создание треугольника на основе Фи (или Пифагор встречает Фибоначчи):
Пифагор обнаружил, что прямоугольный треугольник со сторонами длиной a и b и гипотенузой длины c имеет следующее соотношение:
a² + b² = c²
Основополагающее равенство фи имеет аналогичную структуру:
1 + Phi = Phi 2
(1+ 1,618… = 2,618…)
Взяв квадратный корень из каждого члена в этом равенстве, мы получим размеры треугольника, известного как треугольник Кеплера, прямоугольного треугольника, основанного на этом равенстве фи, где:
| Сторона | Длина в квадрате по выше | Длина, или квадратный корень | Длину, деленную на на фи, поэтому c = 1 |
| a | 1 | 1 | 1 / Phi |
| б | Phi | √ Фи | 1 / √ Фи |
| в | Фи 2 | Phi | 1 |
Этот треугольник показан ниже.Он имеет угол 51,83 ° (или 51 ° 50 ‘), что соответствует косинусу 0,618 или фи.
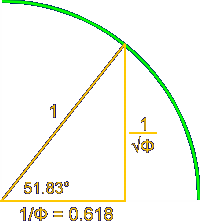
Треугольник Пифагора 3-4-5 — единственный прямоугольный треугольник, стороны которого находятся в арифметической прогрессии. 3 + 1 = 4 и 4 плюс 1 = 5. Треугольник Кеплера — единственный прямоугольный треугольник, стороны которого находятся в геометрической прогрессии: квадратный корень из фи, умноженного на Φ = 1 и 1, умноженного на Φ = Φ.
Хотя этот угол трудно доказать с уверенностью из-за разрушения с течением времени, некоторые считают, что этот угол использовался древними египтянами при строительстве Великой пирамиды Хеопса.
Другие треугольники с пропорциями золотого сечения могут быть созданы с помощью отношения Фи (1,618 0339…) к 1 основания и сторон треугольников:
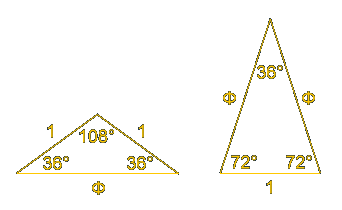
Равнобедренный треугольник вверху справа с основанием, равным 1 двум равным сторонам Фи, известен как Золотой треугольник. Эти знакомые треугольники воплощены в пентаграммах и плитках Пенроуза.
| |
Создание треугольника на основе чисел Фибоначчи
Никакие три последовательных числа в ряду Фибоначчи не могут быть использованы для создания прямоугольного треугольника.Марти Стэндж, однако, внес следующую взаимосвязь в январе 2007 года: каждую последующую серию из четырех чисел Фибоначчи можно использовать для создания прямоугольного треугольника, в котором основание и гипотенуза определяются вторым и третьим числами, а другая сторона — квадратом. корень произведения первого и четвертого чисел. В таблице ниже показано, как работает эта взаимосвязь:
| | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, для иллюстрации, выделенной золотом, в «Трактате о треугольниках Фибоначчи» Штанге показано, что треугольник со сторонами 5 и квадратным корнем из 39 (т.е.g., 3 x 13) даст прямоугольный треугольник с гипотенузой 8.
По мере того, как используются большие числа в серии, треугольник приближается к пропорциям треугольника Кеплера, основанного на фи выше, с отношением гипотенузы к основанию числа Фи, или 1,618…
,Как использовать золотой треугольник в композиции фотографии
В фотографии существует довольно много правил композиции. Вы наверняка слышали о таких вещах, как направляющие линии, золотое сечение и правило третей. В сегодняшней статье вы узнаете, как применить фотографию золотого треугольника к своей работе.
 На этой фотографии используется правило третей, но есть также диагонали, проходящие через рамку, образованные линиями, образованными камнями.
На этой фотографии используется правило третей, но есть также диагонали, проходящие через рамку, образованные линиями, образованными камнями.  Правило третей — классика композиции.На этом фото видно, насколько сильным может быть этот тип композиции.
Правило третей — классика композиции.На этом фото видно, насколько сильным может быть этот тип композиции. 

Зачем использовать композицию «Золотой треугольник» в фотографии?
Вы не ошибетесь, если ограничитесь основным предметом, используя простой фон, состоящий из правила третей. Но через какое-то время эта формула может немного повторяться, как вы можете ее разбить? Один из подходов — рассмотреть вариант правила третей — золотой треугольник.
С этим типом композиции вы теперь будете использовать диагонали на фотографии.Это придаст вашей фотографии более динамичный вид.
Как образуется композиция «Золотой треугольник»?
Правило третей помещает важные элементы в кадр на линиях, образующих правило третей. Эти линии образуются из девяти прямоугольников одинакового размера по всему кадру.
Что касается золотого треугольника, вы теперь будете использовать треугольники вместо прямоугольников. Это создаст диагонали в вашей композиции.
Представьте свою рамку и проведите диагональную линию из верхнего левого угла, а затем проведите ее вниз к правому нижнему углу.Неважно, в каких углах вам нужна диагональная линия, проходящая через рамку.
Теперь из нижнего левого угла проведите линию до диагональной линии, которая пересекает ее под прямым углом. Если хотите, можете завершить эту линию до края рамки. Сделайте то же самое с линией из правого верхнего угла, которая также пересекает исходную линию под прямым углом.
Теперь у вас будут треугольники, которые образуют фотографическую композицию, известную как золотой треугольник. Эта композиция также может быть образована вертикальным или горизонтальным прямоугольником.
 На этом фото интересны солнечные лучи, пробивающиеся через фасад. Он находится на одной из пересекающихся линий.
На этом фото интересны солнечные лучи, пробивающиеся через фасад. Он находится на одной из пересекающихся линий.Как составить фото для золотого треугольника?
После того, как вы настроите сетку для композиции золотого треугольника, вы заметите две точки пересечения.
Один слева и один справа от вашей композиции. Как и в случае с правилом третей, вы стремитесь разместить интересующую вас точку над этой точкой пересечения.
Фотографии, как правило, содержат интересные места и ведущие линии, проходящие через них.Вот как с ними обращаться для золотого треугольника.
- Достопримечательности — Это главный объект вашей фотографии. На портрете доминирующий глаз должен опираться на одну из этих точек, скорее всего, на ту, которая находится в верхней части кадра. Пейзажные объекты, такие как одинокие деревья или дом, будут располагаться в точке пересечения.
- Ведущие линии — Теперь важна линия, ведущая к теме. Это то, что делает вашу фотографию композицией золотого треугольника в отличие от правила третей.Итак, вы ищете диагональную линию, ведущую к вашему основному объекту. Опять же, это могло быть множество вещей. В пейзажной фотографии идеально подойдет дорога, которая по диагонали пересекает кадр к главному объекту.
 Интересное расположение лодок на этой фотографии создает сильную композицию с красивыми треугольными формами.
Интересное расположение лодок на этой фотографии создает сильную композицию с красивыми треугольными формами.Какие предметы лучше всего подходят для этой композиции?
Есть места, где композиция золотого треугольника возможна только с голландскими углами.Голландские ракурсы — далеко не все хорошее фото.
Итак, какие фотографии подходят для этого типа фотографий? Ниже приведены несколько идей для вас, хотя, как и в случае с любым другим видом искусства, в конце концов, вам придется использовать собственное суждение.
- Портреты — Стандартный портрет, вероятно, здесь не подойдет. У вас будет слишком много прямых линий. Вместо этого посмотрите на портреты, на которых модель сидит или лежит. Вы можете играть с углами, создавая диагонали. Вы также должны использовать руки и ноги для создания диагоналей, образующих золотые треугольники.
- Горы — Когда линия горизонта не плоская, у вас есть больше возможностей для формирования композиции золотого треугольника. Используйте диагональную линию горизонта, ведущую к вашему основному объекту. Вам не обязательно использовать горы, вы также можете использовать песчаные дюны точно так же.
- Дорога — Вы можете использовать дорогу, которая прорезает рамку по диагонали, чтобы создать композицию золотого треугольника. Стоять на обочине дороги — это один из способов заставить дорогу проходить сквозь кадр по диагонали.Если вы можете подняться над дорогой и удалить линию горизонта, это также может помочь в композиции.
 Общие вопросы о композиции фотографии.
Общие вопросы о композиции фотографии.
Что означает золотой треугольник?
Золотой треугольник — это правило композиции. Это правило чем-то похоже на правило третей. Однако способ разделения фото немного отличается.
Вместо прямых, серия диагональных линий, что для
.{\ circ}}. Углы основания 72 ° каждый.
Золотой гномон.
Золотой треугольник , также называемый возвышенным треугольником , [1] — это равнобедренный треугольник, в котором дублированная сторона находится в золотом сечении φ {\ displaystyle \ varphi} со стороной основания:
- ab = φ = 1 + 52≈1,618 034. {\ Displaystyle {a \ over b} = \ varphi = {1 + {\ sqrt {5}} \ over 2} \ приблизительно 1,618 ~ 034 ~.}
Энциклопедия YouTube
✪ ЗОЛОТОЕ СООТНОШЕНИЕ (Золотой треугольник — это равнобедренный треугольник с углом при вершине 36 градусов).{\ circ}.}
- Золотой треугольник однозначно идентифицируется как единственный треугольник с тремя углами в пропорции 1: 2: 2 (36 °, 72 °, 72 °). [3]
Прочие геометрические фигуры
- Золотые треугольники можно найти в шипах правильных пентаграмм.
- Золотые треугольники также можно найти в правильном десятиугольнике, равностороннем и равностороннем десятиугольном многоугольнике, соединив любые две смежные вершины с центром. Это потому, что: 180 (10-2) / 10 = 144 ° — это внутренний угол, а деление его пополам через вершину к центру: 144/2 = 72 °. [1]
- Также золотые треугольники встречаются в сетях нескольких звёздчатых додекаэдров и икосаэдров.
Логарифмическая спираль
Золотой треугольник используется для образования некоторых точек логарифмической спирали. Разделив пополам один из основных углов, создается новая точка, которая, в свою очередь, образует еще один золотой треугольник. [4] Процесс деления пополам можно продолжать бесконечно, создавая бесконечное количество золотых треугольников. Через вершины можно провести логарифмическую спираль.Эта спираль также известна как равноугольная спираль, термин, придуманный Рене Декартом. «Если провести прямую линию от полюса к любой точке кривой, она срежет кривую точно под таким же углом», следовательно, равноугольный . [5]
Золотой гномон
Золотой треугольник, разделенный пополам в треугольниках Робинсона: золотой треугольник и золотой гномон.
 Правильная пентаграмма. Каждый угол — золотой треугольник. Фигура также содержит пять «больших» золотых гномонов, образованных соединением с «маленьким» центральным пятиугольником двух углов, которые не примыкают друг к другу.Если нарисовать пять сторон «большого» пятиугольника вокруг пентаграммы, получится пять «маленьких» золотых гномонов.
Правильная пентаграмма. Каждый угол — золотой треугольник. Фигура также содержит пять «больших» золотых гномонов, образованных соединением с «маленьким» центральным пятиугольником двух углов, которые не примыкают друг к другу.Если нарисовать пять сторон «большого» пятиугольника вокруг пентаграммы, получится пять «маленьких» золотых гномонов.Тесно связан с золотым треугольником золотой гномон, равнобедренный треугольник, в котором отношение равных длин сторон к длине основания является обратной величиной 1φ {\ displaystyle {1 \ over \ varphi}} золотого сечения φ {\ displaystyle \ varphi}.
«Золотой треугольник имеет отношение длины основания к длине стороны, равное золотому сечению φ, тогда как золотой гномон имеет отношение длины стороны к длине основания, равное золотому сечению φ.{\ circ}.}
- Золотой гномон однозначно идентифицируется как треугольник с тремя углами в пропорциях 1: 1: 3 (36 °, 36 °, 108 °). Его базовые углы составляют 36 ° каждый, что совпадает с вершиной золотого треугольника.
Деление пополам
- Разделив один из углов основания на 2 равных угла, золотой треугольник можно разделить пополам на золотой треугольник и золотой гномон.
- Разрезав угол при вершине на 2 угла, один из которых является двойным, золотой гномон можно разделить пополам на золотой треугольник и золотой гномон.
- Золотой гномон и золотой треугольник, равные стороны которых совпадают по длине, также называются тупым и острым треугольниками Робинсона. [3]
Плитка
- Золотой треугольник и два золотых гномона образуют правильный пятиугольник. [7]
- Эти равнобедренные треугольники можно использовать для построения мозаик Пенроуза. Плитки Пенроуза делают из воздушных змеев и дротиков. Воздушный змей сделан из двух золотых треугольников, а дротик — из двух гномонов.
См. Также
Список литературы
Внешние ссылки
 Эта страница последний раз была отредактирована 8 мая 2020 в 22:36
,
Эта страница последний раз была отредактирована 8 мая 2020 в 22:36
,


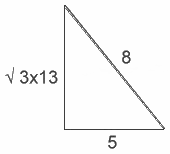
 Общие вопросы о композиции фотографии.
Общие вопросы о композиции фотографии.  Правильная пентаграмма. Каждый угол — золотой треугольник. Фигура также содержит пять «больших» золотых гномонов, образованных соединением с «маленьким» центральным пятиугольником двух углов, которые не примыкают друг к другу.Если нарисовать пять сторон «большого» пятиугольника вокруг пентаграммы, получится пять «маленьких» золотых гномонов.
Правильная пентаграмма. Каждый угол — золотой треугольник. Фигура также содержит пять «больших» золотых гномонов, образованных соединением с «маленьким» центральным пятиугольником двух углов, которые не примыкают друг к другу.Если нарисовать пять сторон «большого» пятиугольника вокруг пентаграммы, получится пять «маленьких» золотых гномонов. Эта страница последний раз была отредактирована 8 мая 2020 в 22:36
,
Эта страница последний раз была отредактирована 8 мая 2020 в 22:36
,