Что такое золотое сечение? | Вечные вопросы | Вопрос-Ответ
«Золотое сечение — это пропорциональное деление отрезка на две неравные части, при котором меньший отрезок так относится к большему, как больший ко всему», — указывает Научно-технический энциклопедический словарь. Это выражается формулой AC/BC = BC/AВ, где АС — меньший отрезок, а ВС — больший.
Считается, что эта пропорция является проявлением гармонии и порядка мирового устройства, идеальной моделью Вселенной. Монах Лука Пачоли в книге «Божественная пропорция» писал, что в золотом сечении проявляется божественное триединство: малый отрезок олицетворяет Сына, большой — Отца, а целое — Святой дух.
В чём еще проявляется золотое сечение?
Существует концепция, согласно которой, золотое сечение является универсальным правилом, воплощается во всём, что окружает человека. Немецкий исследователь золотого сечения, профессор Адольф Цейзинг считал, что части растений и пропорции человеческого тела подчинены правилу золотого сечения. Обмерив около двух тысяч людей, он пришёл к выводу, что части человеческого тела относятся друг к другу примерно в одинаковом отношении. Свои наблюдения он проверил на античных статуях, где эта закономерность подтвердилась, что означало осведомлённость древних о законе золотого сечения.
Исследователи природы находят «идеальную пропорцию» в строении различных живых систем. Самый известный пример — это структура спирали, которая подчиняется математическому закону золотого сечения и находит воплощение, например, в форме рогов горных козлов или раковинах моллюсков.
Золотое сечение в раковине моллюска. Фото: Shutterstock.comПринципы золотого сечения можно найти в архитектуре древних людей, например, египтян или вавилонян. После измерения пропорций пирамиды Хеопса, храмов и барельефов из гробницы Тутанхамона стало известно, что древние архитекторы основывали расчеты на этой закономерности.
В эпоху Возрождения принцип золотого сечения начинают намеренно использовать художники и скульпторы, отдавая таким образом дань античным традициям. Одним из последователей этого правила считается Леонардо да Винчи, которому, кстати, часто предписывают появление самого термина «золотое сечение». Искусствоведы находят проявление золотого сечения на многих его картинах, в частности, в композиции «Тайной вечери» и в пропорции частей тела «Витрувианского человека».
В математике, помимо основного закона, касающегося соотношения отрезков, примером золотого сечения является Ряд Фибоначчи. Это такая последовательность чисел, при которой каждое последующее число равно сумме двух предыдущих чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. При этом отношение смежных чисел ряда приближается к отношению золотого сечения. Считается, что эта последовательность возникла в качестве ответа на загадку: «Сколько пар кроликов в один год от одной пары родится?»
Что такое числа Фибоначчи и почему их выделили в отдельную группу чисел?
Числа Фибоначчи в Европе популяризовал Леонардо Пизанский (по прозвищу Фибоначчи – сын Боначчи), в задаче о кроликах:
Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.
Оказывается, число кроликов по месяцам описывается последовательностью
1, 2, 3, 5, 8, 13,…
В ней каждое число равно сумме двух предыдущих. Условия задачи все равно нереалистичны, так что можно не стесняться: предположить, что кролики бессмертны, и продолжить последовательность до бесконечности:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ….
Есть свидетельства, что последовательность задолго до Леонардо была известна в Индии, и что в честь Фибоначчи ее назвал Эдуард Люка.
Про экспоненциальный рост
Как мы видим, последовательность очень быстро растет (экспоненциально, как последовательность степеней). Примерно как 1, 2, 4, 8, 16, 32, … или 1, 10, 100, 1000, … (тоже экспоненциальный рост.) Экспоненциальный рост вообще встречается в природе и в приложениях: так растут популяции, капиталы в банке, число радиоактивных атомов и число зерен на шахматной доске (Вы же помните легенду про жадного султана и бедного изобретателя шахмат ;))
В природе экспоненциальный рост имеет место лишь приблизительно и только в некоторых пределах.
Красивые фотографии
Последовательности в природе, напоминающие Фибоначчи, тоже похожи на Фибоначчи только приблизительно и в некоторых пределах. Широко известны примеры из мира растений: семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса. Видимо, здесь задействован один механизм (я скопировала первую попавшуюся картинку из интернета):
Отчасти популярность чисел Фибоначчи связана с такими красивыми картинками. В интернете их полным-полно.
А вот скажем, закон радиоактивного распада не менее поразителен, история его открытия драматична, человечество поставило его себе на службу… но он не так популярен в СМИ. Нет для него таких красивых картинок, да и описывается он дифференциальным уравнением, а любителей дифференциальных уравнений меньше, чем любителей красивых картинок.
В математике
В математике бывают объекты, которые задаются очень просто, но показывают удивительно сложные и многогранные связи между своими компонентами. Например: треугольник в планиметрии, конические сечения, треугольник Паскаля, простые числа, … Они завораживают нас как картинки в калейдоскопе. Чуть повернешь – и открываются новые узоры, новые свойства. Числа Фибоначчи –один из таких объектов. Каждый математик на пути в науку их обязательно встречал.
Чтобы перечислить все их удивительные свойства, нужна отдельная книга (и кстати, выходит журнал с таким названием, посвященный одним только числам Фибоначчи). Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.
Почему же математики выделили числа Фибоначчи в отдельную группу чисел
Потому что любят все классифицировать и раскладывать по полочкам. Раз есть объект – надо дать ему название. На сайте https://oeis.org/A000045 , где собраны большинство последовательностей чисел, встречающихся в математике, последовательность Фибоначчи идет под номером 45. Она вовсе не такая уж исключительная, кроме неё на этом сайте собрано около трети миллиона последовательностей. Каждая из них тоже представляет собой «отдельную группу чисел».
Специалист по теории чисел Леопольд Кронекер считал, что только одна из них создана Богом (и это вовсе не последовательность Фибоначчи, а другая, на сайте ее номер 27), а остальные – дело рук человеческих.
В целом журналисты несколько преувеличивают значимость чисел Фибоначчи: они, безусловно, прекрасны, но стоят в одном ряду с многими другими не менее прекрасными и полезными математическими объектами.
Ваше «золотое» число — как рассчитать в классической нумерологии
Итак мы уже много о себе узнали. Сегодня будем рассчитывать Ваше “золотое” число. Называют его так по аналогии с самым главным процессом в Алхимии – получение, а точнее превращение из нескольких элементов, золота.
Золото в Алхимии – элемент Силы. Поэтому и “золотое” число еще называют число Силы. Что же оно нам дает? Это одно из самых важных чисел человека. Оно показывает смысл вашего существования, Мотивацию или причину Вашего воплощения. Само число рассчитывается очень просто. А вот его значения – достаточно объемные. Поэтому давайте приступим к делу.
“Золотое” число – это сумма чисел даты рождения и числа имени, приведенных к элементарному.
Например: Число даты рождения – 7, а число имени – 5. Сумма – 12. Приводим к элементарному числу 1+2=3.
Итак, число пути или “Золотое” число равно – трем.
[warning]Хочу обратить внимание на то, что при расчете числа имени – надо считать то имя, которым Вас чаще всего называют. Если Вы не можете определить, то используйте имя, указанное в Вашем паспорте или Свидетельстве о рождении.[/warning]А теперь давайте обсудим каждую цифру, обозначающую мотивацию воплощения. Сначала предлагаю вдуматься в значение числа. Вибрация этого числа очень сильна. Даже человек, который абсолютно незнаком с нумерологией очень часто, скажем так, не совсем понимает свои поступки. Часто делает выбор, который кажется в данный момент не оправданным.
Каждый из нас знает такое понятие, как внутренний голос или как его еще называют – интуицию. Это влияние вибрации числа силы. Еще говорят – это исполнение “Божественного плана”, того предназначения, которое дано вам как задание для исполнения в этой жизни. А еще считают, что это число вашей Кармы.
Если человек понимает свое предназначение, то ему не понадобится делать “лишние” движения в этой жизни. Он не будет терять время на пустые действия. Он быстрее выполнит свою задачу.
Очень надеюсь, что смогла донести до Вас важность знания своего числа Силы или Пути.
Единица – Лидерство.
Этот человек лидер. Ему суждено руководить. Он требователен и успешен, как в бизнесе, так и в роли руководителя любого предприятия. Они быстро мыслят и предлагают не стандартные решения. Если у них возникла какая-то идея, они не задумываясь принимаются ее воплощать.
Но у этого числа есть и обратная сторона – деспотичность. Он может увлечься своей удачей и возможностями и просто стать диктатором.Задача этого человека – незамедлительно исправлять свои отрицательные качества. Иначе он может встретить свою старость в одиночестве.
Двойка – Сотрудничество.
Это популярные и очень приятные люди. Их задача – научиться работать с окружающими. Это часто люди искусства, музейные работники, замечательные и очень грамотные библиотекари. Если они угадали со своим предназначением и выбрали соответствующую профессию, то она им будет доставлять удовольствие. В противном случае – эти люди будут чувствовать себя не на своем месте, обделенными и не понятыми.
Для двоек, ключевым словом является – сотрудничество.Главной и критической ошибкой для них может стать выбор одиночества. Они должны суметь побороть свою стеснительность, иначе она может просто перейти в депрессию. Окружающие должны понимать, что таким людям нужна забота, любовь и внимание. Этот момент я хочу донести до родителей. Если у Вас ребенок – двойка, то в его первой половине жизни это замечательный домашний ребенок. А вот при переходе к самостоятельной жизни – возможны серьезные проблемы. И еще – здесь надо обратить внимание на выбор профессии. Двойки – это дети не технари. И если Вы будете давить на такого ребенка при выборе профессии – то можете сломать ему жизнь…
Тройка – Самовыражение.
Это люди с отличным воображение: ораторы, актеры, литераторы… Это люди – созидатели. В детстве, в связи с их воображением, могут быть серьезные проблемы. Они даже могут заболеть, прочувствовав болезнь близкого и “вообразив” себя больным. Но если они смогут преодолеть все трудности, то превратятся в оптимистичных, радостных и удачливых людей.Это отзывчивые и контактные люди. Такие люди любят быть в центре внимания. Но настроение у них часто развивается по синусоиде: радость может быстро переходить в безразличие.
Эти люди добьются успеха, если не будут разбрасываться своими талантами.Очень любят красивые вещи, цветы, музыку, отличные друзья.
Отрицательные качества, с которыми надо быть осторожными – нетерпеливость, чувствительность, экстравагантность, застенчивость. Конечно, если они гипертрофированы.
Четверка – Трудолюбие.
Люди труда, это те люди. которые воплощают мечту в жизнь. Они строят прочный фундамент, независимо от того в какой сфере работают. Это может быть и религия, и наука и искусство и бизнес. Это очень разносторонние люди. Они умеют конкретизировать размытые идеи. очень требовательны к рациональному использованию времени. Точны и внимательны к деталям. Обучаемы. Они симпатичны, честны, добры, имеют твердые убеждения, полны энергии.
Из отрицательных проявлений – взаимоотношения в семье. Не смотря на то, что к семье они относятся очень ответственно, работа у них на первом месте. Отсюда и возникают проблемы…
Еще один момент, на который надо обратить внимание – замкнутость. Четверки имеют очень мало друзей, и выбирает он их по сходным интересам.
Что бы преуспеть в жизни, им надо воплощать свои идеи, а не чужие.
На этом я. пожалуй, сегодня закончу. Остальные числа опубликую завтра.
Поделиться ссылкой:
Золотое число — это… Что такое Золотое число?
- Золотое число
«Золотое число» – условная количественная характеристика защитного действия на золи различных высокомолекулярных соединений : количество миллиграммов, которое необходимо добавить к 10 мл красного золотого золя для предотвращения его коагуляции при введении в систему 1 мл раствора хлорида натрия с массовой долей 10%.
Общая химия : учебник / А. В. Жолнин [1]
Общая химия : учебник . А. В. Жолнин ; под ред. В. А. Попкова, А. В. Жолнина.. 2012.
Смотреть что такое «Золотое число» в других словарях:
ЗОЛОТОЕ ЧИСЛО — число одного года в метоническом цикле, в который входит 235 новолуний и который эквивалентен 6939 дням 16 часам 31 минуте, что приблизительно составляет 19 лет. Золотое число использовали для определения Пасхального Воскресения. Цикл начинается… … Астрологическая энциклопедия
ЗОЛОТОЕ ЧИСЛО — ЗОЛОТОЕ ЧИСЛО, величина, характеризующая защитное действие эмульсионного коллоида. Окраска коллоидальных растворов, в частности гидрозолей металлов, очень часто зависит не от хим. природы коллоида или его дисперсионной среды, а от степени… … Большая медицинская энциклопедия
золотое число — aukso skaičius statusas T sritis Standartizacija ir metrologija apibrėžtis Stambiamolekulės medžiagos antikoaguliacinės gebos rodiklis, kuriam nustatyti vartojamas aukso zolis. atitikmenys: angl. gold number vok. Goldzahl, f rus. золотое число, n … Penkiakalbis aiškinamasis metrologijos terminų žodynas
золотое число — aukso skaičius statusas T sritis chemija apibrėžtis Stambiamolekulės medžiagos antikoaguliacinės gebos rodiklis, kuriam nustatyti vartojamas aukso zolis. atitikmenys: angl. gold number rus. золотое число … Chemijos terminų aiškinamasis žodynas
Золотое оружие «За храбрость» — наградное оружие в Российской империи, причисленное к статусу государственного ордена с 1807 по 1917 годы.В знак особых отличий, за проявленную личную храбрость и самоотверженность производилось награждение Золотым холодным оружием шпагой,… … Википедия
Число зверя — … Википедия
Золотое оружие — ЗОЛОТОЕ ОРУЖІЕ, принадлежитъ къ числу почет. боев. наградъ. Историч. прошлое З. ор., какъ награды, утрачено. Даже въ спец. изслѣд ніи О регаліяхъ и знакахъ отличія рус. арміи приводится лишь слѣд. кратк. указаніе: При Екатеринѣ II въ награду за… … Военная энциклопедия
Число Зверя — особое число, упоминаемое в Библии, под которым скрыто имя апокалиптического зверя; нумерологическое воплощение ставленника сатаны. Число зверя равно 666. Число 666 очень часто используемый элемент сатанинской атрибутики, наряду с перевёрнутым… … Википедия
Число дьявола — Число зверя особое число, упоминаемое в Библии, под которым скрыто имя апокалиптического зверя; нумерологическое воплощение ставленника сатаны. Число зверя равно 666. Число 666 очень часто используемый элемент сатанинской атрибутики, наряду с… … Википедия
Число Грэма — (Грехема, англ. Graham s number) большое число, которое является верхней границей для решения определённой проблемы в теории Рамсея. Названо в честь Рональда Грэма (англ.). Оно стало известно широкой публике после того, как Мартин … Википедия
Книги
- Золотое сечение, Зельцер Ефим Абрамович. В 6-м издании книги были рассмотрены фундаментальные постоянные Природы — золотое сечение, мировая постоянная, строительный элемент балка с числом пи и компактность. Показано, что золотое… Подробнее Купить за 389 руб
- Нина и Золотое Число Книга пятая, Витчер М.. Приключения нашей знакомой мадридской школьницы Нины Де Нобили продолжаются!. Казалось, прекрасная планета Ксоракс, Шестая Луна, спасена — ее злейший враг князь Каркон повержен. Но не тут-то… Подробнее Купить за 304 руб
- Нина и Золотое Число, Витчер М.. Муни Витчер – Лунная волшебница – псевдоним итальянской писательницы, создавшей серию книг о девочке Нине и ее друзьях, в которых переплетается удивительный мир реальности и сказочного… Подробнее Купить за 286 руб
«КОСМИЧЕСКИЙ ГОСТ». Часть II. ЗОЛОТАЯ СЕРЕДИНА
В числах содержится больше реальности, чем в реальных вещах.Пифагор
Число есть мысль Бога.
Св. Августин
Начало в Части I
Когда рыцари-тамплиеры в 1128 году вернулись во Францию из первого похода в Иерусалим, они, по легенде, привезли с собой тайное знание о Божественных мерах и весах. Как утверждают, в числе привезенного было знание о пропорции золотого сечения. Знание это не было новым для Европы, поскольку его применяли при постройке храмов еще в Древней Греции (Парфенон), но к 12-му веку знание было утеряно или забыто, поэтому пришлось его реимпортировать с Востока.
О пропорции золотого сечения сейчас не пишет разве что ленивый. Это иррациональное число 1.618….., которое обозначают буквой ф (в честь Фидия, построившего Парфенон), похоже, поистине универсально и неотделимо от жизни во всех проявлениях. Аналогичным образом, другое таинственное иррациональное число — е неразрывно связано с фунциями роста, а третье – π – с волновыми процессами и «квадратурой круга». Двум другим числам уделяется далеко не так много внимания в литературе о сакральной геометрии, как золотому числу, хотя они тоже важны. Но о них как-нибудь в другой раз.
Цивилизация допескового Египта, создавшая великие пирамиды, обладала знаниями о важности священных констант и почитала их в образе Нетеров – божественных сил, действующих в материи. Нетеры – не боги, но орудия Верховного Существа — одухотворенные математические константы. Так сказать, блюстители «кода матрицы»…
Золотая пропорция встречается в соотношении частей тела живых организмов, орбит и размеров небесных тел, элементарных частиц и прочая, и прочая…. проще говоря, во всем, что движется и эманирует волны.
Примеров очень много, и они замечательно иллюстрированы и объяснены, поэтому я не буду на них останавливаться — просто по ходу рассказа приведу ссылки на некоторые ресурсы. Собеседникам, впервые сталкивающимся с темой золотого сечения, предлагаю вначале прочитать базовые сведения.
Если вам прямо сейчас захочется увидеть пример пропорции золотого сечения, можете загнуть пальцы на руке по очереди, начиная с мизинца. Паттерн, который получается при таком движении, является золотосеченной спиралью. Соотношение длин фаланг ваших пальцев, длины пальцев к кисти, а всего предплечья к плечу тоже будет близко к золотому сечению. Золотая пропорция сейчас используется в дизайне множества предметов – длина и ширина вашей кредитной карты, например, имеет это соотношение. Я нашла пропорцию золотого сечения в размерах холодильника, стеклянной бутылки из-под кока-колы, авторучек, велосипедов и многих, многих других вещей…
Среди великих произведений архитектуры пропорция золотого сечения была, например, использована в Великой Пирамиде в Гизе (у нас в школах ее называли пирамидой Хеопса, хотя построил ее далеко не Хеопс), в Запретном Городе в Пекине, в византийской Софии Константинопольской, в индийском мавзолее Тадж-Махал, в Нотр-Дам де Пари, в мозаиках исламских мечетей, в Соборе Василия Блаженного в Москве…. Если кто-то заинтересуется, много хороших примеров вот на этом сайте
Я, конечно, не смогу перечислить их все. А в своем сообщении просто попытаюсь сделать чуть-чуть более понятным то, почему золотое сечение было выбрано Великим Геометром в качестве одного из важных компонентов «космического ГОСТа».
Золотое сечение в пропорциях Храма Василия Блаженного
«В НАЧАЛЕ БЫЛ ЛОГОС…»
Так начинается Евангелие от Иоанна: «В начале было Слово, и Слово было у Бога, и Слово было Бог» (Ин, 1:1). В греческом оригинале это звучало так: «В начале был Логос, и Логос был с Богом, и Логос был Бог». Греческое слово «логос», помимо прочих, имеет также значение «пропорция». Единственная пропорция во Вселенной, которая позволяет чему-то быть Одним и одновременно вместе с Одним — это пропорция золотого сечения!
Сейчас мы это попробуем увидеть.
Представьте, что вас назначили творцом-демиургом одной отдельно взятой маленькой вселенной. Она существует только на листе бумаги и имеет всего одно измерение, потому что ее форма – отрезок.
Вот такой:
1
I—————————————
ц е л о е
Это весь ваш универсум, от альфы до омеги. Он представляет из себя Единство, Целое, поэтому мы обозначим его единицей. Все, что вы сотворите как демиург, должно помещаться в этом отрезке. Поэтому вы пойдете единственным возможным путем — делением отрезка на все меньшие и меньшие части. Теоретически, деление может продолжаться бесконечно, поэтому ваша вселенная может быть весьма густо населена….
Согласно Первому Правилу начинающих демиургов, «Omnia in omnibus» — «Все во всем», а также Второму Правилу начинающих демиургов, «Как вверху, так и внизу», условием вашего творения должно быть подобие частей целому. Как бы вы не делили отрезок 1, соотношение между целым и частью должно оставаться точно таким же, как и у последующих частей между собой.
Такое подобие в науке называют фрактальностью – когда каждая часть является уменьшенной копией целого. (Представьте для наглядности русскую матрешку – все меньшие матрешки как две капли воды похожи как на «маму», так и друг на друга, только размер разный).
Поскольку ваше творение может идти только путем деления отрезка на меньшие части, вы должны найти «золотую середину» деления. Как ее найти? Сразу приходит в голову просто поделить отрезок на две равные части.
1
½ ½
I—————————I————
ц е л о е
Но что при этом получится? Соотношение между частями будет равно 1:1, а между Целым и меньшей частью –1:½ . Принцип подобия не соблюдается… придется продолжать поиски «золотой середины». Если вы продвинутый демиург, владеющий алгеброй, то будете искать ваше неизвестное число, решая уравнение 1/х = х/(1-х). Ну, а если алгебры вы не знаете, то придется просто сказать: «По щучьему велению, по моему хотению…» И вот что получится:
0.618 1
Малая часть Большая часть
I———————I——————
ц е л о е
Соотношение между Целым и Большой частью равно 1/0.618 = 1.618.
Соотношение между Большой и Малой частями также составляет 0.618/(1 – 0.618) = 1.618.
Принцип подобия удовлетворен, и вы тоже. Таким образом, «золотой серединой» оказалось совсем не деление пополам, а деление по золотому сечению!
Можно продолжить творение, деля отрезок на все меньшие и меньшие части, сохраняя найденное соотношение:
Боль
Малая часть
Еще
меньше
Совсем
крохотная
…
..
.
0.618 1
0.618 1
0 .618 1
….
I-I—I——I————-I—————
ц е л о е
Все части новой вселенной будут идеально соответствовать друг к другу. Вы можете вкладывать их друг в друга, как матрешки, и они отлично сгармонизируются. Представьте, что получилось бы, если хотя бы одна из матрешек не подходила под стандарт? Сбился бы весь ряд…
Дальше вы выходите на крыльцо и говорите: «Мамки-няньки Нетеры, вот вам Число демиурга — собирайтесь-снаряжайтесь и к завтрему устройте всю мою вселенную по этому Числу». Вы можете, если захотите, даже назвать отрезок «Лучом Творения», Большую Часть – Миром Галактик, Малую часть – Миром Солнц, Еще Меньшую Часть – Миром Планет, и так далее, вплоть до микрокосмов.
Вы спросите, какое отношение эта игровая ситуация имеет к нашей реальности? Ну, некоторые современные физики, например, рассматривают Вселенную как ряд фрактальных золотосеченных тороидов-бубликов, «вложенных» друг в друга, как матрешки. Одна из множества существующих теорий, конечно, потому что на самом деле никто не знает, как устроена Вселенная, но….что-то в этой теории есть.
****
Теперь усложним задачу и предположим, что творцом-демиургом вас назначили не в одномерной вселенной отрезка, а в более сложном варианте трехмерной вселенной (похожей на нашу). Она состоит из волн. Волны встречаются и взаимодействуют друг с другом (это называется интерференция). Если волны находятся в правильном отношении друг к другу, то взаимодействие будет полезным для каждой из них, а результатом – волна с большей амплитудой. Такая интерференция называется конструктивной. В противном случае волны взаимно погашают друг друга, вплоть до нуля. Такая интерференция называется деструктивной.
Иллюстрация конструктивной и деструктивной интерференции – красная волна + синяя волна = зеленая волна. В первом случае порождается волна с бОльшей амплитудой, во втором — волны взаимно уничтожаются:
При взаимодействии волны могут не только складыва
«Золотое» (действительное) число. Нумерология. Все числа вашей судьбы
«Золотое» (действительное) число
«Золотое» число (его называют так по аналогии с символом алхимического превращения; кроме того, оно известно как действительное число, или число силы) – одно из самых важных чисел в жизни человека. Оно определяет смысл всего нашего существования, показывает мотивацию нашего жизненного воплощения.
Это число как бы приоткрывает Божественный план, и если попытаться жить в соответствии с ним, то жизнь наполнится смыслом, станет полезной и счастливой. Даже если человек и не подозревает о существовании «золотого» (действительного) числа, оно все равно оказывает влияние на нашу жизнь. Люди часто недоумевают, почему они делают тот или иной выбор в жизни, что заставляет их поступать определенным образом. Каждому знакомо понятие так называемого внутреннего голоса. Этот голос и есть вибрация «золотого» числа. Наша цель – научиться правильно определять его и в соответствии, и в антипатии.
Вибрации действительного числа ощущаются на протяжении всей жизни. Если вы живете в соответствии с ними, то вы просто экономите свое время, в вашей жизни не будет бесполезных дней, ваше время и жизненные силы не будут тратиться понапрасну.
«Золотое» число – ключ, раскрывающий для нас жизненную цель. Помните о его постоянном присутствии, и тогда вы реализуете себя и добьетесь успеха.
«Золотое» число – это источник энергии самого высокого порядка. Даже если на всех нижних уровнях (число имени, число отчества, число фамилии) энергия разрушительна, энергия планеты, соответствующей «золотому» числу, будет для нас защитой и поддержкой. Это магический символ нашей жизни. С ним связана карма человека.
Предположим, «золотым» числом является число 7 (соответствующая ему планета – Сатурн). В этом случае высшая цель жизни связана с познанием, искусством трансмутации (преобразования, преображения) и с магией слова (особенно молитвой).
Для того чтобы найти «золотое» число, надо сложить число даты рождения с числом полного имени и сократить полученное двузначное число до простого (до одной цифры).
В нашем примере (Иван Александрович Петров) надо прибавить 6 к 7 – получается 13. Сокращаем эту сумму: 13 = 1 + 3 = 4 – это и есть «золотое» число.
Заполните приведенную ниже форму собственными значениями:
Число даты рождения __________
Число полного имени __________
Перекрестная сумма ___________
Полученная перекрестная сумма и есть ваше «золотое» (Действительное) число. Если оно окажется равным 11 или 22, то подумайте, не целесообразнее ли его сократить до 2 или 4 соответственно, так как истинные вибрации чисел 11 и 22 доступны далеко не всем людям.
Данный текст является ознакомительным фрагментом.Читать книгу целиком
Поделитесь на страничкеЗолотое сечение — Википедия. Что такое Золотое сечение
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
- 1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
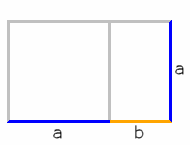Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
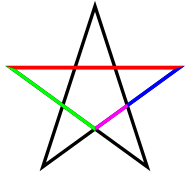Золотое сечение в пятиконечной звезде- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
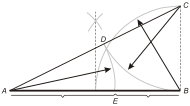Построение золотого сечения- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны[18].
- ∑n=1∞(−1)n+1n2(2nn)=2ln2φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 992 дня]
Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.
Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3360 дней].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 585 дней].
Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
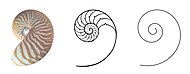Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В. Лаврус, Золотое сечение
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ Системы счисления.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
Ссылки
О GoldenNumber.net
Наша миссия — обучение, применение и Excel:
Этот сайт существует для того, чтобы помочь вам оценить невероятную красоту и дизайн в окружающем вас мире и преуспеть в том, что вы делаете, применяя те же принципы дизайна в своих творческих работах. Следуйте за мыслями многих великих умов до вас, от древних цивилизаций до эпохи Возрождения и до лучших представителей всех областей современного искусства и дизайна.
Мы стремимся предоставить вам лучшую информацию и инструменты по этому золотому числу, известному как Фи, золотое сечение, золотое сечение, золотая пропорция, золотое сечение или божественная пропорция, и его математическому родственнику — последовательности Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21…)
Наша цель — представить широкий выбор тем, связанных с фи, в визуально привлекательном и легком для понимания формате, чтобы создать онлайн-сообщество, в котором можно будет делиться и обсуждать новые открытия о фи, а также предлагать инструменты и услуги (см. панель справа), чтобы помочь вам понять и применить фи и золотое сечение в вашей работе, увлечениях или хобби.
Делитесь своими мыслями с другими на странице «Обсуждение и комментарии» или в любых сообщениях по конкретным темам, перечисленным выше или справа.
Об авторе:
Для тех, кто задается вопросом, кто создал этот сайт и почему, вот небольшая справочная информация.
Вдохновением для создания сайта послужило все более глубокое осознание и понимание красоты и дизайна в жизни. Чем больше я исследовал, тем больше обнаруживал, что число, называемое Фи, или 1,6180339…, выступает в качестве постоянной константы дизайна во многих аспектах нашего существования.Те, что представлены на этом сайте, — это только начало, и я хотел бы поблагодарить всех участников, которые предоставили контент для сайта.
Могут ли некоторые проявления фи быть естественными? Безусловно. Даже в этом случае мы должны спросить, как физические законы Вселенной, которые мы считаем «естественными», так точно настроены для поддержания жизни, не так ли? Может ли повсеместное появление Фи свидетельствовать о более широком плане дизайна? Это то, что каждый из нас должен изучить, испытать, обдумать и решить для себя.
Этот сайт не связан с какой-либо научной, религиозной или исследовательской организацией. Мои полномочия по этой теме разнообразны, что было полезным в этой работе, поскольку применения золотого сечения также весьма разнообразны. Я всю жизнь люблю математику, естественные науки и природу. Личностные тесты показывают, что я аналитик, архитектор и изобретатель. Когда я был подростком, я построил телескоп, использовал его для наблюдения за всеми объектами Мессье, основал астрономический клуб в своей средней школе и участвовал в астрономических исследованиях с Астрономическим клубом Аргоннской национальной лаборатории.В колледже я прошел курсы высшего уровня по математике, статистике и химии, прежде чем переключить свое внимание на бизнес, чтобы получить диплом CPA и бакалавра бухгалтерского учета в Университете Иллинойса, лучшей школе в стране в то время. Я получил степень MBA в области финансов и маркетинга в другой ведущей бизнес-школе, Чикагском университете, и сделал успешную карьеру в бизнесе. Я начал с публичной бухгалтерии «большой восьмерки», а затем занимал должности финансового директора и директора по информационным технологиям в операционных подразделениях шести компаний из списка Fortune 1000 и одной технологической компании, поддерживаемой частным капиталом.В целом, я продемонстрировал страсть к аналитике и творческому решению проблем и руководил как новатор в использовании технологий для достижения стратегических и операционных преимуществ. Я изучал музыку, играю на нескольких инструментах и пишу песни. Как технолог и предприниматель, я создаю веб-сайты с 1997 года и изучил предметно-ориентированное программирование для конкретной цели разработки PhiMatrix, моего приложения для проектирования и анализа золотого сечения. С тех пор он был продан тысячам очень отзывчивых клиентов в более чем семидесяти странах.На этом сайте я проводил независимые исследования и писал статьи по Фи, серии Фибоначчи и связанным темам. У меня также была возможность вести переписку с тысячами людей по всему миру по самым разным аспектам этой темы. Я имел удовольствие помогать им, включая их вклад на сайт и установление дружеских отношений со многими из них. Возможно, когда-нибудь я получу докторскую степень по философии, чтобы пополнить мои фонды исследованиями, писать статьи и вносить свой вклад в эту работу.
Основная цель сайта — просто поделиться фи и опытом увидеть математику дизайна и красоты, которая проявляется повсюду вокруг нас и внутри нас, и более глубоко обдумать значения, которые можно найти в этом.Я надеюсь, что этот сайт выведет вас за пределы интереса к пониманию и вдохновению, и что с его помощью вы придете к поиску собственных ответов относительно происхождения и цели жизни. Вы можете найти другие сайты, которые я разработал для тех же целей, в PhiMatrix и Snapshots of God.
Гэри Б. Мейснер, MBA
, он же «Пхи-Гай»
Автор / редактор, Phi 1.618: Золотой номер
Разработчик «Золотой линейки ™» и «Золотой сетки ™».
Разработчик, программное обеспечение для проектирования и анализа золотого сечения PhiMatrix
Миф о золотом сечении, математика и недоразумения (для разоблачителей)
Существует много неправильных представлений и искажений относительно золотого сечения. Некоторые слишком страстно ищут закономерности и говорят, что они существуют, хотя на самом деле их нет. Некоторые, чья цель — развенчать миф о золотом сечении, говорят, что его не существует там, где он есть на самом деле, упуская из виду очевидное и часто не указывая, какие пропорции появляются вместо этого. Люди с обеих сторон часто просто повторяют то, что они слышали, вместо того, чтобы лично проводить анализ, необходимый для подтверждения своих выводов.Интеллект и образование не всегда являются факторами, помогающими понять истину, поскольку даже доктора математических наук иногда ошибаются. Как автор этого сайта с 1997 года, я изменил свои взгляды и информацию на этом сайте. Давайте рассмотрим некоторые общие моменты путаницы и споров, касающиеся красоты, Парфенона, здания Секретариата ООН, Великой пирамиды, раковины Наутилуса, использования известными художниками (да Винчи, Боттичелли, Сёра и т. Д.) И других тем. Я дам объективные ответы с дополнительными доказательствами во вспомогательных статьях по каждой теме.Я также приветствую любые доказательства в поддержку противоположных взглядов.
Золотое сечение: пропорции зубов / губ и носа по отношению к
расстоянию от зрачков до нижней части подбородка.
Не все согласятся, но есть много доказательств, подтверждающих, что ответ — «Да». Есть доля правды в пословицах «красота в глазах смотрящего» и «красота — это всего лишь кожа», но нельзя отрицать, что существует почти всеобщее согласие, когда их просят различать очень привлекательное и очень непривлекательное лицо.Давайте признаем, что каждое человеческое лицо имеет множество уникальных размеров и пропорций. В результате нельзя сказать, что ни одна мера применима ко всем аспектам каждого лица. Настоящий вопрос заключается в том, представляет ли золотое сечение среднее или идеальное для человеческих размеров лица. Еще более интересный вопрос заключается в том, влияет ли золотое сечение черт лица на наше восприятие привлекательности и красоты. Разоблачители укажут на вариации и, возможно, предположат, что те, кто находит золотые отношения в красивом лице, сделали это, потому что искали их.Однако рассмотрим следующие исследования, которые демонстрируют, что связь с красотой основана на гораздо большем, чем поиск данных для достижения желаемого результата:
Да, но только частично, а не так, как вы часто слышите. Передний фасад Парфенона часто изображают с золотым прямоугольником, обрамляющим его, чтобы проиллюстрировать пропорции золотого сечения. К сожалению, точный золотой прямоугольник нужно было бы начинать на второй из четырех ступеней приближения к Парфенону, а не к основанию его колонн.Затем золотой прямоугольник заканчивался бы на вершине Парфенона, точку, которую необходимо оценить, потому что структура находится в руинах. Даже для энтузиастов золотого сечения это довольно произвольное и неубедительное свидетельство. Это близко к золотому прямоугольнику, но недостаточно близко, чтобы сделать вывод, что он использовался в его дизайне. Однако это не конец истории.
- Когда этот золотой прямоугольник помещаются как только что описано, в нижней части опорной балки в верхней части колонны находится в золотой пропорции его высоты.
- В верхней части опорной структуры пучка через столбцы имеют размеры, которые кажутся очень близко к золотой пропорции его основания до вершины крыши.
- Что еще интереснее, четырнадцать прямоугольников поперек горизонтального луча кажутся разделенными точно в точке своего золотого сечения, насколько это можно определить по фотографиям.
Эти золотые отношения могли быть включены или не включены намеренно среди всех других чисел и соотношений, представленных в Парфеноне.Первое письменное упоминание о золотом сечении было сделано Евклидом почти через 100 лет после его постройки, поэтому архитекторы Парфенона не узнали о нем от него. Платон родился вскоре после постройки и принял пятиугольную звезду в качестве символа для своей группы последователей, так что это предполагает, что в ту эпоху могло быть известно об особых геометрических формах, использующих золотое сечение. Парфенон имеет сложную конструкцию, в которой воплощено множество чисел и математических соотношений. Вовсе не разумно, что золотое сечение было среди представленных.
Может, но не так, как вы часто слышите. Традиционная «золотая спираль» состоит из ряда смежных золотых прямоугольников. Это создает спираль, размер которой увеличивается по золотому сечению с каждым поворотом спирали на 90 градусов. Спираль раковины Наутилуса не соответствует этой золотой спирали, которая является источником путаницы в этом вопросе. Однако существует более одного способа создать спираль с пропорциями золотого сечения. Например, вы можете создать спираль, которая расширяется по золотому сечению с каждым поворотом спирали на 180 градусов.Эта спираль больше подходит для спиралей многих раковин Наутилуса, особенно при первых нескольких оборотах спирали. Еще более близкое совпадение обнаруживается при измерении спиралей на противоположных сторонах центральной точки.
Да. Разоблачители часто считают это совершенно неподдерживаемым. Одна часто цитируемая статья доктора философии в математике указывает, что нет упоминания о золотом сечении в двух биографиях, написанных о да Винчи. Не лучше ли измерить картины, чем прочитать биографию? Другой разоблачитель, также имеющий докторскую степень.D. в области математики утверждает, что «нет доказательств» того, что да Винчи использовал золотое сечение, но в его презентации показаны только простые наброски да Винчи, а не его шедевры на религиозные темы. К сожалению, большинство комментариев об использовании да Винчи золотого сечения в его картинах основаны на «Моне Лизе», в которой очень мало линейных элементов композиции, по которым можно окончательно измерить золотое сечение. Золотые сечения действительно довольно легко увидеть, если у вас есть подходящие инструменты.
Как заметил автор «Цивилизация» Кеннет Кларк: « Этот союз искусства и математики далек от нашего собственного мышления, но он был фундаментальным для эпохи Возрождения.”
Некоторые есть, но большинство — нет. Спирали, которые чаще всего встречаются в природе, представляют собой равноугловые (также известные как логарифмические) спирали. Это просто означает, что спираль расширяется с постоянной скоростью. Это происходит потому, что он создает равномерный поток энергии или распределение напряжения. Это не имеет ничего общего с золотым сечением. Соответственно, все иллюстрации спиральных рукавов галактик, кривых океанских волн, спиралевидных ураганов и т. Д., Которые ошибочно определены как «золотое сечение» или «золотая спираль», должны быть переименованы или удалены, чтобы избежать дальнейшей путаницы при сохранении этого золотого сечения. миф.Есть еще один тип спирали, связанный с золотым сечением, однако он очень часто встречается в природе. Спирали, которые появляются в сосновых шишках, ананасах, семенных стручках и подобных структурах растений, обычно основаны на двух последовательных числах последовательности Фибоначчи. Например, если есть восемь спиралей, вращающихся по часовой стрелке, вы обнаружите, что тринадцать спиралей идут против часовой стрелки. Ни одна из этих спиралей сама по себе не обязательно является спиралью «золотого сечения», но соотношение этих последовательных чисел Фибоначчи приблизительно соответствует золотому сечению.
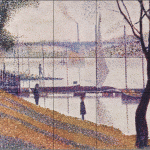Да. Один искусствовед утверждал, что Жорж Сёра «атаковал каждое полотно золотым сечением». По крайней мере, один опровергатель говорит, что это просто «миф, который необходимо развеять». Истина где-то посередине.
Итак, правильный ответ состоит в том, что Сёра часто использовал золотое сечение в своих художественных композициях, но, вероятно, не атаковал им все холсты.
Возможно, но неизвестно. Это также является предметом обсуждения и интерпретации, и на этот вопрос нет однозначного ответа.В существующих исторических записях египтян нет упоминания о золотом сечении. Внешняя оболочка пирамиды из известняка в настоящее время отсутствует, поэтому ее точные первоначальные размеры подлежат некоторой оценке. Тем не менее, внешняя оболочка сверху остается неповрежденной и, таким образом, дает хорошее представление о первоначальной форме. Что мы действительно знаем, так это:
- Приблизительные первоначальные размеры Великой пирамиды в Википедии показывают пирамиду со средним размером основания 230,4 метра и высотой 146 метров.5 метров.
- Эта высота отличается от треугольника, основанного на фи, всего на 0,0367 метра, отклонение всего 0,025%.
- Существует еще одна школа мысли, согласно которой пропорции пирамиды основаны на дуге круга, окружность которого равна периметру основания пирамиды.
- Если это правда, то расчетная высота отличается всего на 0,177 метра), то есть отклонение составляет 0,1%.
Также возможны другие геометрические формы, одна основанная на площадях поверхности, а другая на градиентах с использованием египетских единиц измерения.Есть также свидетельства того, что относительные размеры и положение пирамид на территории Гизы воплощают пропорции золотого сечения. На самом деле мы многого не знаем об этих пирамидах или их конструкции, поэтому размеры могут быть основаны на любом из этих методов и геометрии. Великая пирамида явно была построена с учетом определенной геометрии и с высокой точностью, поэтому мы можем разумно предположить, что ее архитекторы не случайно создали пирамиду с такой особенной и уникальной геометрией.По-прежнему остается очень интересный вопрос: даже если пирамида не была спроектирована сознательно с учетом фи, почему они выбрали геометрию Великой пирамиды, которая так близко воплощает золотое сечение, единственное число, которое повсеместно присутствует в геометрии. , а что связано с природой и красотой?
Нет. В исследовании 2009 года утверждалось, что оно опровергло связь золотого сечения с красотой, и заявлено, что были обнаружены два измерения «нового золотого сечения», определяющих привлекательность.Однако лица, признанные наиболее привлекательными, имели более десятка золотых сечений в размерах основных черт лица. Исследователи, очевидно, не осознавали, что эти золотые сечения существуют, и разработали свои собственные альтернативные точки измерения. Должно быть очевидно, что человеческая красота лица не может быть сведена к одному измерению по вертикали и по горизонтали, и довольно легко доказать это с помощью нескольких простых примеров непривлекательных лиц, которые все же соответствуют этим двум измерениям.
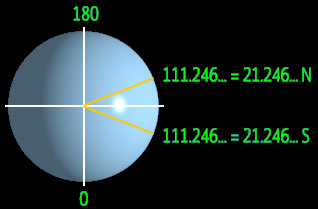Нет, по крайней мере, не совсем. Между полюсами Земли есть две точки золотого сечения по широте, по одной в каждом полушарии. Мекка находится примерно в 12 милях от широты золотого сечения в северном полушарии. Золотое сечение долготы определить непросто, поскольку нет естественной точки отсчета, такой как полюс вращения. Заявление о Мекке было основано на проекции Меркатора Земли, которая простирается от точки разделения между США и Россией. Исходя из этого, Мекка находится в 938 километрах от точки золотого сечения долготы.Используя другие отправные точки в качестве основы, на Земле есть много других точек долготы золотого сечения.
Да. Это предположительно было «опровергнуто» в статье доктора Джорджа Марковски, доктора философии из Гарварда. по математике, который вычислил простое отношение высоты здания к ширине. Он отметил, что это соотношение было 1,76, а не 1,618, пришел к своему выводу и упустил многие исторические и математические факты. Один из ведущих архитекторов, Ле Корбюзье, создал систему дизайна, основанную на золотом сечении, всего за несколько лет до своего участия в проекте ООН.Известный образовательный фильм Диснея, отмеченный наградами, показывает, что соотношение золотого сечения основано на трех горизонтальных золотых прямоугольниках, сложенных вертикально, а не на их высоте и ширине. Золотые отношения появляются в визуальных разделительных точках на фасаде здания, и их легко измерить и рассчитать. Другие очень четкие золотые соотношения присутствуют в размерах навесной стены, окон и парадного входа.
Это определенно особый номер с уникальными свойствами, он встречается в природе в некоторых довольно неожиданных местах.Даже те, кто стремится развенчать миф о золотом сечении, согласятся, что золотое сечение обладает свойствами, которые делают его уникальным в математике и геометрии. Это число заинтриговало и вдохновило бесчисленное количество людей на протяжении всей истории человечества и заслужило особое место в их сердцах и умах. Вероятно, именно по этой причине некоторые люди приняли это за рамки фактов, превратившись в фантастику и мистику. Это, в свою очередь, побудило других отказаться от него с таким же рвением. Обе крайности ошибочны и мешают нам узнать правду и применить ее.
Является ли золотое сечение универсальной константой дизайна в природе? Нет. Должны ли все черты лица соответствовать идеальной пропорции золотого сечения, чтобы быть красивым? Нет. Может ли это помочь нам лучше понять и оценить красоту природы и применить ее в нашей жизни? Да.
Требуется ли золотое сечение для создания великого искусства? Нет. Может ли это помочь лучше оценить великое искусство и создать лучшую композицию и дизайн? Да. Он используется для этой цели в искусстве, кадрировании и композиции фотографий, дизайне логотипов, дизайне продуктов и других областях дизайна.
Как и многие другие вещи в жизни, он дает нам понимание природы вещей, возможность лучше их ценить и способность использовать их с пользой. При всей существующей дезинформации и заблуждениях лучше всего сохранять непредвзятость и не принимать заявления, сделанные без исследования доказательств с обеих сторон, собственных экспериментов и собственных выводов.
Ссылки на статьи:
Миф, который никуда не денется, Кит Девлин
Заблуждения о золотом сечении Джорджа Марковского
Разоблаченные легенды о золотом сечении Джулии и Джесси Галеф
«Путешествие сквозь математику» Фил Кинан, Ph.Д.
Герни, серия «Путешествие: Разрушение мифов, золотая середина» Джеймса Герни
Другие статьи GoldenNumber.net о понимании улик и опровержении разоблачителей:
Доктор Джордж Марковски о «Заблуждениях о золотом сечении»
Доктор Кейт Девлин о «Формуле, которая должна« доказать красоту », в корне неверна».
Fastco Design на тему «Золотое сечение: величайший миф о дизайне. Золотое сечение — это полная чепуха в дизайне».”
Google Shortcode Ссылка на эту статью: http://goo.gl/QSNZRB
,Phi до 20 000 мест и миллион мест
Просто не можете насытиться Phi? Вот несколько способов получить столько, сколько кому-либо понадобится.
Есть миллионы мест, где можно найти фи, но вот кое-что поможет найти фи в миллионе мест. Вы можете скачать PhiCalculator, программу, которую бесплатно предоставляет Алиреза Шафай. Он вычислит phi до указанного вами количества десятичных знаков, до 1 миллиона и, возможно, больше, и выведет результаты в текстовый файл.Он также предоставил исходный код C ++ и текстовый файл Phi для 100 000 мест.
Примечание. PhiCalculator был просканирован с помощью McAfee 29 марта 2008 г. и не содержит вирусов, но пользователь принимает на себя все риски, связанные с его использованием.
Для тех, у кого мало аппетита, здесь 20 000 мест:
| 1,61803398874989484820458683436563811772030917980576286213544862270526046281890 244970720720418939113748475408807538689175212663386222353693179318006076672635 44333890865959395829056383226613199282 88067520876689250171169620703222104 321626954862629631361443814975870122034080588795445474924618569536486444924104 432077134494704956584678850987433944221254487706647809158846074998871240076521 705751797883416625624940758906970400028121042762177111777805315317141011704666 599146697987317613560067087480710131795236894275219484353056783002287856997829 778347845878228911097625003026961561700250464338243776486102838312683303724292 675263116533924731671112115881863851331620384005222165791286675294654906811317 159934323597349498509040947621322298101726107059611645629909816290555208524790 352406020172799747175342777592778625619432082750513121815628551222480939471234 1451702237358057727861600868838295230 45926478780178899219 | 7769038953219681
Вы нашли то, что искали?
,Формат | Жанр
| Стиль
| Купить музыку | Продам музыку |