Золотое сечение — Википедия
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам [10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
- 1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
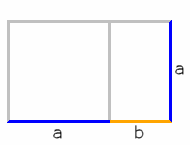 Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения
Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
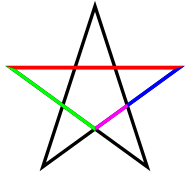 Золотое сечение в пятиконечной звезде
Золотое сечение в пятиконечной звезде- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
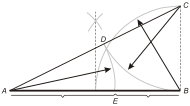 Построение золотого сечения
Построение золотого сечения- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны[18].
- ∑n=1∞(−1)n+1n2(2nn)=2ln2φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]
Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.
Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3378 дней].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 603 дня].
Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
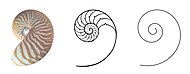 Золотое сечение в природе
Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В. Лаврус, Золотое сечение
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ Системы счисления.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
Ссылки
Золотое сечение — Википедия. Что такое Золотое сечение
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Число Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку [8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
- 1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
 Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения
Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
 Золотое сечение в пятиконечной звезде
Золотое сечение в пятиконечной звезде- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
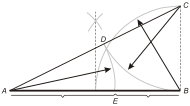 Построение золотого сечения
Построение золотого сечения- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны[18].
- ∑n=1∞(−1)n+1n2(2nn)=2ln2φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]
Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.
Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3378 дней].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 603 дня].
Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
 Золотое сечение в природе
Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В. Лаврус, Золотое сечение
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ Системы счисления.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
Ссылки
Золотое сечение — Википедия. Что такое Золотое сечение
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
- 1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
 Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения
Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
 Золотое сечение в пятиконечной звезде
Золотое сечение в пятиконечной звезде- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
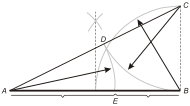 Построение золотого сечения
Построение золотого сечения- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны[18].
- ∑n=1∞(−1)n+1n2(2nn)=2ln2φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]
Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.
Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3378 дней].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 603 дня].
Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
 Золотое сечение в природе
Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В. Лаврус, Золотое сечение
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ Системы счисления.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
Ссылки
Золотое сечение Википедия
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин a{\displaystyle a} и b{\displaystyle b}, при котором бо́льшая величина относится к меньшей так же как сумма величин к бо́льшей, то есть: ab=a+ba.{\displaystyle {\frac {a}{b}}={\frac {a+b}{a}}.} Исторически изначально в древнегреческой математике золотым сечением именовалось деление отрезка AB{\displaystyle AB} точкой C{\displaystyle C} на две части так, что бо́льшая часть относится к меньшей, как весь отрезок к большей: BCAC=ABBC{\displaystyle {\frac {BC}{AC}}={\frac {AB}{BC}}}. Позже это понятие было распространено на произвольные величины.
Число, равное отношению a/b{\displaystyle a/b}, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi } (фи), в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }.
Из исходного равенства (например, представляя a или даже a/b независимой переменной и решая выводимое из исходного равенства квадратное уравнение) нетрудно получить, что число
- Φ=5+12{\displaystyle \Phi ={\frac {{\sqrt {5}}+1}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=5−12≈0.61803{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {{\sqrt {5}}-1}{2}}\approx 0.61803}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Число Φ{\displaystyle \Phi } называется также золотым числом.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Иллюстрация к определениюЗолотое сечение имеет множество замечательных свойств (например, произведение 1,6180339… × 1,6180339… = 2,6180339…) но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
- 1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны[18].
- ∑n=1∞(−1)n+1n2(2nn)=2ln2φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1663 дня]
Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке, имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматриваются в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.
Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 4031 день].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 1256 дней].
Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.
Золотое сечение в биологии и медицине
Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits Архивная копия от 6 марта 2015 на Wayback Machine
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В. Лаврус, Золотое сечение
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. (англ.)русск.. A History of Mathematics (неопр.). — Second Edition. — John Wiley & Sons, Inc., 1991. — С. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77—6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ Системы счисления (неопр.).
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Золотое сечение, или Божественная пропорция // Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Приемы гармонизации пространства в классической архитектуре // Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
Ссылки
- В. С. Белнин, «Владел ли Платон кодом золотой пропорции? Анализ мифа»
- А. В. Радзюкевич, К вопросу о научном изучении пропорций в архитектуре и искусстве.
- А. В. Радзюкевич, Критический анализ Адольфа Цейзинга — основоположника гипотезы «золотого сечения».
- Шевелев И. Ш., Марутаев М. А., Шмелев И. П. Золотое сечение: Три взгляда на природу гармонии. — М.: Стройиздат, 1990. — 343 с., ил.
- Статья о золотом сечении в изобразительном искусстве, Золотое сечение в изобразительном искусстве
- J. J. O’Connor, E. F. Robertson. Golden ratio (неопр.). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland.
- Функция Фибоначчи в Wolfram alpha
Золотое сечение — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин a и b, b > a, когда справедливо b/a = (a+b)/b. Число, равное отношению b/a, обычно обозначается прописной греческой буквой <math>\Phi</math> в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой <math>\tau</math>. Из исходного равенства нетрудно получить, что число
- <math>\Phi=\frac{1+\sqrt5}2</math>
Обратное число, обозначаемое строчной буквой <math>\varphi</math>[2],
- <math>\varphi=\frac1\Phi=\frac{-1+\sqrt5}2</math>
Отсюда следует, что
- <math>\varphi = \Phi-1</math>.
Для практических целей ограничиваются приблизительным значением <math>\Phi</math> = 1,618 или <math>\Phi</math> = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что большая часть отрезка составляет такую же долю в целом отрезке, какую меньшая часть отрезка составляет в его большей части. Позже это было распространено на произвольные величины.
Число <math>\Phi</math> называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию своей книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14] Марио Ливио</span>ruen считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространен вскоре после Ома в немецкой математической литературе.[16]
Математические свойства
- <math>\frac 1\Phi = \varphi = \operatorname{tg} \left ( \frac {\operatorname{arctg}(2)}{2} \right ) = \frac {2}{1+\sqrt{1+2^2}} = \frac {2}{1+\sqrt5} = \frac {\sqrt5-1}{2}.</math>
- <math>\Phi</math> представляется в виде бесконечной цепочки квадратных корней:
- <math>\Phi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \dots}}}}.</math>
- <math>\Phi\;</math> представляется в виде бесконечной цепной дроби
- <math>\Phi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1+\dots}}},</math>
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи <math>\frac{F_{n+1}}{F_n}</math>. Таким образом,
- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон <math>\Phi = a/b </math>, что и у исходного прямоугльника <math>\Phi = (a+b)/a </math>.
- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны <math>\Phi</math>. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно <math>\Phi</math>.
- Геометрическое построение. Золотое сечение отрезка <math>AB</math> можно построить следующим образом: в точке <math>B</math> восстанавливают перпендикуляр к <math>AB</math>, откладывают на нём отрезок <math>BC</math>, равный половине <math>AB</math>, на отрезке <math>AC</math> откладывают отрезок <math>CD</math>, равный <math>BC</math>, и наконец, на отрезке <math>AB</math> откладывают отрезок <math>AE</math>, равный <math>AD</math>. Тогда
- <math>\Phi=\frac{|AB|}{|AE|}=\frac{|AE|}{|BE|}.</math>
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=<math>\frac{\sqrt5}2</math>. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной <math>\Phi</math>. Так как DH=EH-ED, другим результатом будет отрезок DH длиной <math>\varphi</math>[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для <math>\Phi</math>, <math>\frac1\Phi</math> и <math>\Phi^2</math> в любой системе счисления будут равны[18].
- <math>\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^2 \binom{2n}{n}}=2\ln^2\varphi</math>
Тогда как <math>\sum_{n=1}^\infty \frac{1}{n^2 \binom{2n}{n}}=\frac{\pi^2}{18}</math>К:Википедия:Статьи без источников (тип: не указан)[источник не указан 1665 дней]
Золотое сечение и гармония в искусстве
Под «правилом золотого сечения» в архитектуре и искусстве обычно понимаются композиции, содержащие пропорции, близкие к золотому сечению <math>3/8</math> и <math>5/8</math>К:Википедия:Статьи без источников (тип: не указан)[источник не указан 1648 дней].
Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»К:Википедия:Статьи без источников (тип: не указан)[источник не указан 4033 дня].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий Жолтовский использовал золотое сечение в своих проектах[19]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте).
Геометрия плана гробницы фараона Древнего Египта Менеса построена с использованием пропорции, которую мы сейчас связываем с золотым сечением[20].
Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[21] и др.
См. также
Напишите отзыв о статье «Золотое сечение»
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 [www.cs.arizona.edu/icon/oddsends/phi.htm Golden ratio 1000 digits]
- ↑ 1 2 Савин А. [kvant.mccme.ru/pdf/1997/06/kv0697kaleid.pdf Число Фидия — золотое сечение] (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ [www.sibdesign.ru/index.php?text=1&razdel=stat&textnew=20030615041954 Радзюкевич А. В. Красивая сказка о «золотом сечении»]
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, [web.archive.org/web/20070523075937/www.maa.org/devlin/devlin_05_07.html The Myth That Will Not Go Away]
- ↑ [www.n-t.ru/tp/iz/zs.htm В. Лаврус, Золотое сечение]
- ↑ François Lasserre. [books.google.com/books?id=c9_uAAAAMAAJ The birth of mathematics in the age of Plato]. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. [books.google.com/books?id=KS3yAAAAMAAJ Die reine Elementar-Mathematik]. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. [www.trinitas.ru/rus/doc/0232/009a/02321196.htm Знак-символ золотого сечения] // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. [books.google.com/books?id=Iq41AAAAcAAJ Die reine Elementar-Mathematik]. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. [books.google.com/books?id=fLEwBQAAQBAJ Математика: 50 идей, о которых нужно знать] = [books.google.com/books?id=XfYSKAAACAAJ 50 Mathematical Ideas you really need to know]. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ [numsys.ru/ Системы счисления].
- ↑ [www.architektor.ru/ai/2004_1/kordo.htm Золотой запас зодчества]
- ↑ Стеликов Н. Е. «Гармония древнеегипетской архитектуры.» Горки: БГСХА. 2009, 108 с.
- ↑ [314159.ru/tsvetkov/tsvetkov2.htm Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.]
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. [kvant.mccme.ru/1973/08/zolotoe_sechenie.htm Золотое сечение] «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Mario Livio. [books.google.com/books?id=bUARfgWRh24C The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number]. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. [books.google.com/books?id=t9lICAAAQBAJ φ – Число Бога. Золотое сечение – формула мироздания]. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
- Roger Herz-Fischler. [books.google.com/books?id=aYjXZJwLARQC A Mathematical History of the Golden Number]. — Courier Corporation, 2013. — 228 с. — ISBN 9780486152325.
Ссылки
- В. С. Белнин, [www.a3d.ru/architecture/stat/182 «Владел ли Платон кодом золотой пропорции? Анализ мифа»]
- А. В. Радзюкевич, [elib.altstu.ru/elib/books/Files/pv2014_01/pdf/159radzukevich.pdf К вопросу о научном изучении пропорций в архитектуре и искусстве].
- А. В. Радзюкевич, [marhi.ru/AMIT/2014/4kvart14/radzukevich/radzukevich.pdf Критический анализ Адольфа Цейзинга — основоположника гипотезы «золотого сечнения».]
- Статья о золотом сечении в изобразительном искусстве, [www.linteum.ru/article44.html Золотое сечение в изобразительном искусстве]
- J. J. O’Connor, E. F. Robertson. [www-history.mcs.st-andrews.ac.uk/history/HistTopics/Golden_ratio.html Golden ratio]. MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland.
- [www.wolframalpha.com/input/?i=fibonacci+&a=*C.fibonacci-_*Function- Функция Фибоначчи] в Wolfram alpha
Отрывок, характеризующий Золотое сечение
Есть у нас Багратионы,Будут все враги у ног» и т.д.
Только что кончили певчие, как последовали новые и новые тосты, при которых всё больше и больше расчувствовался граф Илья Андреич, и еще больше билось посуды, и еще больше кричалось. Пили за здоровье Беклешова, Нарышкина, Уварова, Долгорукова, Апраксина, Валуева, за здоровье старшин, за здоровье распорядителя, за здоровье всех членов клуба, за здоровье всех гостей клуба и наконец отдельно за здоровье учредителя обеда графа Ильи Андреича. При этом тосте граф вынул платок и, закрыв им лицо, совершенно расплакался.
Пьер сидел против Долохова и Николая Ростова. Он много и жадно ел и много пил, как и всегда. Но те, которые его знали коротко, видели, что в нем произошла в нынешний день какая то большая перемена. Он молчал всё время обеда и, щурясь и морщась, глядел кругом себя или остановив глаза, с видом совершенной рассеянности, потирал пальцем переносицу. Лицо его было уныло и мрачно. Он, казалось, не видел и не слышал ничего, происходящего вокруг него, и думал о чем то одном, тяжелом и неразрешенном.
Этот неразрешенный, мучивший его вопрос, были намеки княжны в Москве на близость Долохова к его жене и в нынешнее утро полученное им анонимное письмо, в котором было сказано с той подлой шутливостью, которая свойственна всем анонимным письмам, что он плохо видит сквозь свои очки, и что связь его жены с Долоховым есть тайна только для одного него. Пьер решительно не поверил ни намекам княжны, ни письму, но ему страшно было теперь смотреть на Долохова, сидевшего перед ним. Всякий раз, как нечаянно взгляд его встречался с прекрасными, наглыми глазами Долохова, Пьер чувствовал, как что то ужасное, безобразное поднималось в его душе, и он скорее отворачивался. Невольно вспоминая всё прошедшее своей жены и ее отношения с Долоховым, Пьер видел ясно, что то, что сказано было в письме, могло быть правда, могло по крайней мере казаться правдой, ежели бы это касалось не его жены. Пьер вспоминал невольно, как Долохов, которому было возвращено всё после кампании, вернулся в Петербург и приехал к нему. Пользуясь своими кутежными отношениями дружбы с Пьером, Долохов прямо приехал к нему в дом, и Пьер поместил его и дал ему взаймы денег. Пьер вспоминал, как Элен улыбаясь выражала свое неудовольствие за то, что Долохов живет в их доме, и как Долохов цинически хвалил ему красоту его жены, и как он с того времени до приезда в Москву ни на минуту не разлучался с ними.
«Да, он очень красив, думал Пьер, я знаю его. Для него была бы особенная прелесть в том, чтобы осрамить мое имя и посмеяться надо мной, именно потому, что я хлопотал за него и призрел его, помог ему. Я знаю, я понимаю, какую соль это в его глазах должно бы придавать его обману, ежели бы это была правда. Да, ежели бы это была правда; но я не верю, не имею права и не могу верить». Он вспоминал то выражение, которое принимало лицо Долохова, когда на него находили минуты жестокости, как те, в которые он связывал квартального с медведем и пускал его на воду, или когда он вызывал без всякой причины на дуэль человека, или убивал из пистолета лошадь ямщика. Это выражение часто было на лице Долохова, когда он смотрел на него. «Да, он бретёр, думал Пьер, ему ничего не значит убить человека, ему должно казаться, что все боятся его, ему должно быть приятно это. Он должен думать, что и я боюсь его. И действительно я боюсь его», думал Пьер, и опять при этих мыслях он чувствовал, как что то страшное и безобразное поднималось в его душе. Долохов, Денисов и Ростов сидели теперь против Пьера и казались очень веселы. Ростов весело переговаривался с своими двумя приятелями, из которых один был лихой гусар, другой известный бретёр и повеса, и изредка насмешливо поглядывал на Пьера, который на этом обеде поражал своей сосредоточенной, рассеянной, массивной фигурой. Ростов недоброжелательно смотрел на Пьера, во первых, потому, что Пьер в его гусарских глазах был штатский богач, муж красавицы, вообще баба; во вторых, потому, что Пьер в сосредоточенности и рассеянности своего настроения не узнал Ростова и не ответил на его поклон. Когда стали пить здоровье государя, Пьер задумавшись не встал и не взял бокала.
– Что ж вы? – закричал ему Ростов, восторженно озлобленными глазами глядя на него. – Разве вы не слышите; здоровье государя императора! – Пьер, вздохнув, покорно встал, выпил свой бокал и, дождавшись, когда все сели, с своей доброй улыбкой обратился к Ростову.
– А я вас и не узнал, – сказал он. – Но Ростову было не до этого, он кричал ура!
– Что ж ты не возобновишь знакомство, – сказал Долохов Ростову.
– Бог с ним, дурак, – сказал Ростов.
– Надо лелеять мужей хорошеньких женщин, – сказал Денисов. Пьер не слышал, что они говорили, но знал, что говорят про него. Он покраснел и отвернулся.
– Ну, теперь за здоровье красивых женщин, – сказал Долохов, и с серьезным выражением, но с улыбающимся в углах ртом, с бокалом обратился к Пьеру.
– За здоровье красивых женщин, Петруша, и их любовников, – сказал он.
Пьер, опустив глаза, пил из своего бокала, не глядя на Долохова и не отвечая ему. Лакей, раздававший кантату Кутузова, положил листок Пьеру, как более почетному гостю. Он хотел взять его, но Долохов перегнулся, выхватил листок из его руки и стал читать. Пьер взглянул на Долохова, зрачки его опустились: что то страшное и безобразное, мутившее его во всё время обеда, поднялось и овладело им. Он нагнулся всем тучным телом через стол: – Не смейте брать! – крикнул он.
Услыхав этот крик и увидав, к кому он относился, Несвицкий и сосед с правой стороны испуганно и поспешно обратились к Безухову.
– Полноте, полно, что вы? – шептали испуганные голоса. Долохов посмотрел на Пьера светлыми, веселыми, жестокими глазами, с той же улыбкой, как будто он говорил: «А вот это я люблю». – Не дам, – проговорил он отчетливо.
Бледный, с трясущейся губой, Пьер рванул лист. – Вы… вы… негодяй!.. я вас вызываю, – проговорил он, и двинув стул, встал из за стола. В ту самую секунду, как Пьер сделал это и произнес эти слова, он почувствовал, что вопрос о виновности его жены, мучивший его эти последние сутки, был окончательно и несомненно решен утвердительно. Он ненавидел ее и навсегда был разорван с нею. Несмотря на просьбы Денисова, чтобы Ростов не вмешивался в это дело, Ростов согласился быть секундантом Долохова, и после стола переговорил с Несвицким, секундантом Безухова, об условиях дуэли. Пьер уехал домой, а Ростов с Долоховым и Денисовым до позднего вечера просидели в клубе, слушая цыган и песенников.
– Так до завтра, в Сокольниках, – сказал Долохов, прощаясь с Ростовым на крыльце клуба.
– И ты спокоен? – спросил Ростов…
Долохов остановился. – Вот видишь ли, я тебе в двух словах открою всю тайну дуэли. Ежели ты идешь на дуэль и пишешь завещания да нежные письма родителям, ежели ты думаешь о том, что тебя могут убить, ты – дурак и наверно пропал; а ты иди с твердым намерением его убить, как можно поскорее и повернее, тогда всё исправно. Как мне говаривал наш костромской медвежатник: медведя то, говорит, как не бояться? да как увидишь его, и страх прошел, как бы только не ушел! Ну так то и я. A demain, mon cher! [До завтра, мой милый!]
На другой день, в 8 часов утра, Пьер с Несвицким приехали в Сокольницкий лес и нашли там уже Долохова, Денисова и Ростова. Пьер имел вид человека, занятого какими то соображениями, вовсе не касающимися до предстоящего дела. Осунувшееся лицо его было желто. Он видимо не спал ту ночь. Он рассеянно оглядывался вокруг себя и морщился, как будто от яркого солнца. Два соображения исключительно занимали его: виновность его жены, в которой после бессонной ночи уже не оставалось ни малейшего сомнения, и невинность Долохова, не имевшего никакой причины беречь честь чужого для него человека. «Может быть, я бы то же самое сделал бы на его месте, думал Пьер. Даже наверное я бы сделал то же самое; к чему же эта дуэль, это убийство? Или я убью его, или он попадет мне в голову, в локоть, в коленку. Уйти отсюда, бежать, зарыться куда нибудь», приходило ему в голову. Но именно в те минуты, когда ему приходили такие мысли. он с особенно спокойным и рассеянным видом, внушавшим уважение смотревшим на него, спрашивал: «Скоро ли, и готово ли?»
Когда всё было готово, сабли воткнуты в снег, означая барьер, до которого следовало сходиться, и пистолеты заряжены, Несвицкий подошел к Пьеру.
– Я бы не исполнил своей обязанности, граф, – сказал он робким голосом, – и не оправдал бы того доверия и чести, которые вы мне сделали, выбрав меня своим секундантом, ежели бы я в эту важную минуту, очень важную минуту, не сказал вам всю правду. Я полагаю, что дело это не имеет достаточно причин, и что не стоит того, чтобы за него проливать кровь… Вы были неправы, не совсем правы, вы погорячились…
– Ах да, ужасно глупо… – сказал Пьер.
– Так позвольте мне передать ваше сожаление, и я уверен, что наши противники согласятся принять ваше извинение, – сказал Несвицкий (так же как и другие участники дела и как и все в подобных делах, не веря еще, чтобы дело дошло до действительной дуэли). – Вы знаете, граф, гораздо благороднее сознать свою ошибку, чем довести дело до непоправимого. Обиды ни с одной стороны не было. Позвольте мне переговорить…
– Нет, об чем же говорить! – сказал Пьер, – всё равно… Так готово? – прибавил он. – Вы мне скажите только, как куда ходить, и стрелять куда? – сказал он, неестественно кротко улыбаясь. – Он взял в руки пистолет, стал расспрашивать о способе спуска, так как он до сих пор не держал в руках пистолета, в чем он не хотел сознаваться. – Ах да, вот так, я знаю, я забыл только, – говорил он.
– Никаких извинений, ничего решительно, – говорил Долохов Денисову, который с своей стороны тоже сделал попытку примирения, и тоже подошел к назначенному месту.
Место для поединка было выбрано шагах в 80 ти от дороги, на которой остались сани, на небольшой полянке соснового леса, покрытой истаявшим от стоявших последние дни оттепелей снегом. Противники стояли шагах в 40 ка друг от друга, у краев поляны. Секунданты, размеряя шаги, проложили, отпечатавшиеся по мокрому, глубокому снегу, следы от того места, где они стояли, до сабель Несвицкого и Денисова, означавших барьер и воткнутых в 10 ти шагах друг от друга. Оттепель и туман продолжались; за 40 шагов ничего не было видно. Минуты три всё было уже готово, и всё таки медлили начинать, все молчали.
– Ну, начинать! – сказал Долохов.
– Что же, – сказал Пьер, всё так же улыбаясь. – Становилось страшно. Очевидно было, что дело, начавшееся так легко, уже ничем не могло быть предотвращено, что оно шло само собою, уже независимо от воли людей, и должно было совершиться. Денисов первый вышел вперед до барьера и провозгласил:
– Так как п’отивники отказались от п’ими’ения, то не угодно ли начинать: взять пистолеты и по слову т’и начинать сходиться.
– Г…’аз! Два! Т’и!… – сердито прокричал Денисов и отошел в сторону. Оба пошли по протоптанным дорожкам всё ближе и ближе, в тумане узнавая друг друга. Противники имели право, сходясь до барьера, стрелять, когда кто захочет. Долохов шел медленно, не поднимая пистолета, вглядываясь своими светлыми, блестящими, голубыми глазами в лицо своего противника. Рот его, как и всегда, имел на себе подобие улыбки.
– Так когда хочу – могу стрелять! – сказал Пьер, при слове три быстрыми шагами пошел вперед, сбиваясь с протоптанной дорожки и шагая по цельному снегу. Пьер держал пистолет, вытянув вперед правую руку, видимо боясь как бы из этого пистолета не убить самого себя. Левую руку он старательно отставлял назад, потому что ему хотелось поддержать ею правую руку, а он знал, что этого нельзя было. Пройдя шагов шесть и сбившись с дорожки в снег, Пьер оглянулся под ноги, опять быстро взглянул на Долохова, и потянув пальцем, как его учили, выстрелил. Никак не ожидая такого сильного звука, Пьер вздрогнул от своего выстрела, потом улыбнулся сам своему впечатлению и остановился. Дым, особенно густой от тумана, помешал ему видеть в первое мгновение; но другого выстрела, которого он ждал, не последовало. Только слышны были торопливые шаги Долохова, и из за дыма показалась его фигура. Одной рукой он держался за левый бок, другой сжимал опущенный пистолет. Лицо его было бледно. Ростов подбежал и что то сказал ему.
– Не…е…т, – проговорил сквозь зубы Долохов, – нет, не кончено, – и сделав еще несколько падающих, ковыляющих шагов до самой сабли, упал на снег подле нее. Левая рука его была в крови, он обтер ее о сюртук и оперся ею. Лицо его было бледно, нахмуренно и дрожало.
– Пожалу… – начал Долохов, но не мог сразу выговорить… – пожалуйте, договорил он с усилием. Пьер, едва удерживая рыдания, побежал к Долохову, и хотел уже перейти пространство, отделяющее барьеры, как Долохов крикнул: – к барьеру! – и Пьер, поняв в чем дело, остановился у своей сабли. Только 10 шагов разделяло их. Долохов опустился головой к снегу, жадно укусил снег, опять поднял голову, поправился, подобрал ноги и сел, отыскивая прочный центр тяжести. Он глотал холодный снег и сосал его; губы его дрожали, но всё улыбаясь; глаза блестели усилием и злобой последних собранных сил. Он поднял пистолет и стал целиться.
– Боком, закройтесь пистолетом, – проговорил Несвицкий.
– 3ак’ойтесь! – не выдержав, крикнул даже Денисов своему противнику.
Пьер с кроткой улыбкой сожаления и раскаяния, беспомощно расставив ноги и руки, прямо своей широкой грудью стоял перед Долоховым и грустно смотрел на него. Денисов, Ростов и Несвицкий зажмурились. В одно и то же время они услыхали выстрел и злой крик Долохова.
– Мимо! – крикнул Долохов и бессильно лег на снег лицом книзу. Пьер схватился за голову и, повернувшись назад, пошел в лес, шагая целиком по снегу и вслух приговаривая непонятные слова:
– Глупо… глупо! Смерть… ложь… – твердил он морщась. Несвицкий остановил его и повез домой.
Ростов с Денисовым повезли раненого Долохова.
Долохов, молча, с закрытыми глазами, лежал в санях и ни слова не отвечал на вопросы, которые ему делали; но, въехав в Москву, он вдруг очнулся и, с трудом приподняв голову, взял за руку сидевшего подле себя Ростова. Ростова поразило совершенно изменившееся и неожиданно восторженно нежное выражение лица Долохова.
– Ну, что? как ты чувствуешь себя? – спросил Ростов.
– Скверно! но не в том дело. Друг мой, – сказал Долохов прерывающимся голосом, – где мы? Мы в Москве, я знаю. Я ничего, но я убил ее, убил… Она не перенесет этого. Она не перенесет…
– Кто? – спросил Ростов.
Золотое сечение — это… Что такое Золотое сечение?
Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Иллюстрация к определению.Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью
и, наоборот, отношение меньшей части к большей
Число называется также золотым числом.
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.
Золотое сечение имеет множество замечательных свойств, но ещё больше свойств вымышленных[1][2][3].
Математические свойства
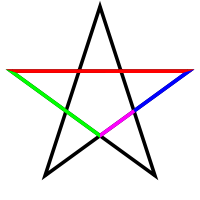 Золотое сечение в пятиконечной звезде
Золотое сечение в пятиконечной звезде 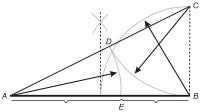 Построение золотого сечения
Построение золотого сечения- представляется в виде бесконечной цепочки квадратных корней:
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи . Таким образом,
- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны ).
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
Золотое сечение и гармония в искусстве
Под «правилом золотого сечения» в архитектуре и искусстве обычно понимаются асимметричные композиции, не обязательно содержащие золотое сечение математически.
Есть основание считать, что значимость золотого сечения в искусстве преувеличена и основывается на ошибочных расчётах. Некоторые из таких утверждений:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.
При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 3:4 или 9:16) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 1237 дней].
Примеры сознательного использования
Золотое сечение и зрительные центры
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий Жолтовский также использовал золотое сечение в своих проектах[4].
- Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам золотого сечения, разбив ленту на пять частей (в первых трёх действие развивается на корабле, в двух последних — в Одессе), где переход в город происходит точно в точке золотого сечения.[источник?]
- Предполагается, что, возможно, при возведении Пирамиды Хеопса также использован принцип «золотого сечения».
См. также
Примечания
Литература
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973.
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
Ссылки
Золотое сечение — Вікіпедія
Ця стаття про аукціонний дім. Про відповідний математичний термін див. Золотий перетин.«Золото́е сече́ние» («Золотий перетин», Golden Section)[1] — український аукціонний дім. Заснований 19 листопада 2004 Михайлом та Олексієм Василенками. Один із провідних учасників українського арт-ринку[2]. Основні напрямки: класичний живопис ХІХ-ХХ ст., альтернативні течії (авангард, нонконформізм, андеґраунд), сучасне мистецтво та іконопис. Крім того, художня фотографія, предметний дизайн, раритетні автомобілі, книги[3]. Компанія перша в Україні почала проводити аукціони сучасного мистецтва, дизайну і фотографії[4].
За рейтингом журналу «Фокус» співзасновники «Золотого сечения» Михайло та Олексій Василенки посіли 4 та 5 місця серед 25 найбільш впливових діячів вітчизняного арт-ринку[5]. Вони виступають експертами при аналізі тенденцій вітчизняного і світового ринків мистецтва[6].
Події[ред. | ред. код]
У березні 2005 компанія провела перший аукціон «Радянське мистецтво». Він визначив сегмент арт-ринку на подальші 4 роки.
2009 аукціонний дім провів перший в Україні аукціон сучасного мистецтва (англ. contemporary art). Окрім живопису, серед лотів вперше у країні представляли інсталяції, об’єкти, відео, фотороботи, стріт-арт (англ. street art) та цифрове мистецтво (англ. digital art). У 2009—2010 завдяки активній діяльності аукціоннного дому сучасне мистецтво зайняло помітне місце в уподобаннях вітчизняних колекціонерів. За компанією закріпився статус основного учасника у сегменті ринку сучасного мистецтва[7].
У 2010 відбувся перший в Україні аукціон предметного дизайну. До нього увійшли арт-об’єкти та інтер’єрні інсталяції, а також авторські концептуальні меблі, освітлювальні прилади, кераміка, гутне скло. Були представлені українські дизайнери Володимир Бондаренко, Юрій Ринтовт, Ілля Чичкан, Сергій Махно, художники скла і кераміки — Тарас Левків, Іван Зарицький, Олександр Шевченко, Андрій Бокотей[8].
У 2010—2011 організовано 12 аукціонів. Більшість торгів 2011 завершилася продажем 30-50 % лотів[9].
Початок аукціонної діяльності у регіонах покладено в 2011—2012, двічі відбулися виїзні торги у Донецьку[10].
2011 відділ аукціонного дому «Дизайн» був розширений розділом «Фотографія».
Аукціон «Classic. Contemporary. Design» (2012) заявлений як найбільший і найрізноманітніший в історії України. Були виставлені три великі блоки ТОП-лотів — класичне українське та російське мистецтво ХІХ-ХХ ст., твори сучасного мистецтва і колекційні зразки предметного дизайну[11].
2013 започатковано триденні виставки-продажі творів класичного та сучасного мистецтва нового формату «Three days sale»[12]. У 2013—2014 відбулися два закриті камерні заходи — виставка творів Давида Бурлюка та експозиція «47 artworks private sales».
«Post war & contemporary art» (2014) зацікавив нових колекціонерів. Реалізовано 50 % лотів[13]. Спільно з FedorivHub проведено «Christmas art weekend». Це одноденна виставка, завершена аукціоном, та арт-ярмарок наступного дня[14]. Продажі склали 40 %[15].
17 березня 2015 проведено перший в Україні великий аукціон класичного та сучасного мистецтва за останні три роки. За даними журналу «Forbes Україна», захід виявився успішним[16].
Аукціонні твори[ред. | ред. код]
Серед топових імен художників: класика українського живопису — Сергій Світославський, Петро Нілус, Микола Бурачек, Сергій Васильківський, Іван Труш, Микола Кричевський, Михайло Ткаченко, Микола Мурашко; авангард — Василь Кандінський, Давид Бурлюк, Василь Єрмилов, Борис Косарєв; радянський період — Микола Глущенко, Віктор Зарецький, Сергій Шишко, Адальберт Ерделі, Валентина Цвєткова, Тетяна Яблонська, Роман Сельський, Андрій Коцка, Йосип Бокшай; сучасне мистецтво — Олександр Гнилицький, Марко Гейко, Анатолій Криволап, Олександр Ройтбурд, Тіберій Сільваші, Олег Тістол, Роман Жук, Артем Волокітін, Микита Кравцов, Назар Білик, Олександр Животков, Роман Мінін, Михайло Деяк[17][18].
Найдорожчі роботи, котрі були продані на торгах — «Зловісне море» Миколи Глущенка ($165 тис., 2008), «Хризантеми» Сергія Шишка ($61,6 тис., 2006) і «Серпень» Віктора Зарецького ($55 тис., 2011)[19]. Також «Львів. Площа Ринок» Йосипа Бокшая ($44 тис., 2006), «Веснянки» Володимира Сингаївського ($20,8 тис., 2008) і «Улісс» Олександра Гнилицького ($44 тис., 2011)[20].
На аукціоні «Авангард» (2010) була представлена композиція Василя Кандінського, яка вважається одним з перших у світі творів абстракціонізму[21].
- Відділ «Класичне мистецтво» (з 2005). Аукціони відділу проводяться двічі на рік (березень, вересень).
- Відділ «Актуальне мистецтво» (з 2009), аукціони двічі на рік у квітні й жовтні.
- Відділ «Ікони» (з 2009).
- Відділ «Дизайн і фото» (з 2010), торги у листопаді[22].
Ознайомитися з колекцією можна на передаукціонному показі, в друкованому каталозі або на офіційному сайті компанії. З 2010 відкрито онлайн-участь у торгах (у режимі реального часу).
«Золотое сечение» надає 4 категорії послуг, які охоплюють основні аспекти арт-ринку: приватні продажі, арт-банкінг, експертиза та оцінка, формування колекцій.
Упродовж існування аукціонний дім оформив понад 1000 колекцій з різних напрямків, починаючи з класичного українського й російського мистецтва до сучасного. Твори надходять з приватних збірок і галерей пострадянських країн і Європи[23].
Компанія організовує великі художні виставки. Проведені дві масштабні експозиції російської ікони — «Російська ікона XVII — початку XX ст. з приватних збірок» (2009) і «Чистота душевна. Російська ікона XVI—XX ст. у приватних зібраннях» (2014). Основна виставкова мета — продемонструвати різноманітність шкіл і стилів у російському іконописі Нового часу, виокремлюючи рідкісні сюжети ікон.
Також відбулися ретроспективні виставки художників — Якова Басова (2006), Миколи Глущенка (2012) та Віктора Зарецького (2012). Виставка графіки Віктора Зарецького стала найбільшою персональною експозицією митця[24].
Всі п’ять виставкових проектів отримали каталоги.
Видання «Золотого сечения»[ред. | ред. код]
З 2005 вийшло друком 35 видань — 26 каталогів аукціонів, 5 каталогів художніх виставок, 3 каталоги виставок-продажів, 1 дайджест. Під егідою Національного музею «Київська картинна галерея» вийшов каталог російської ікони XVII — початку XX ст. (2009) та «Графіка М. Глущенка 1930—1970 років» (2012). Опубліковано каталог виставки Якова Басова (2006), альбом графіки Віктора Зарецького (2012)[25].
Видавався дайджест аукціонного дому — «Digest» (2012). Головний редактор Олексій Василенко, шеф-редактор Михайло Василенко, серед авторів Дмитро Горбачов, Володимир Петрашик, Ліза Герман, Ольга Балашова. Повноколірне глянцеве видання. Мова російська, наклад 5000 примірників. Тематика: арт-ринок, антикварні автомобілі, колекційні вина[26].
- ↑ Назва у статуті компанії: укр. Золотое сечение, рос. Золотое сечение, англ. Golden Section.
- ↑ Сандуляк, А. Торг доречний: класики і сучасники. Cultprostir розповідає про перший великий київський арт-аукціон воєнного часу Архівовано 15 квітня 2015 у Wayback Machine.. Cultprostir. 16 березня 2015.
- ↑ В ЦСМ «М17» пройде перший комерційний аукціон з продажу предметів мистецтва. Art Ukraine. 19 вересня 2014. (рос.)
- ↑ Панафидина, Н. Украинские оформители вернулись на родину Архівовано 15 квітень 2015 у Wayback Machine. // Экономические известия. — 2011. — № 206. (рос.)
- ↑ 25 самых влиятельных деятелей украинского арт-рынка // Фокус. — 2012. — № 51. (рос.)
- ↑ На Sotheby’s Contemporary East третину продажів посіли роботи українських митців. Дело. 26 листопада 2014. (рос.)
- ↑ Хрущак, М. Українські тенденції: зберігайте гроші в сучасному мистецтві. Українська правда. 24 листопада 2010. (рос.)
- ↑ #Каталоги аукціонів.
- ↑ Рейтинг молодих підприємців: Михайло і Олексій Василенки. Деньги. 24 травня 2012. (рос.)
- ↑ Голова, Л. Ексклюзивна розмова зі співвласником аукціонного дому «Золотое сечение» Михайлом Василенком Архівовано 15 квітень 2015 у Wayback Machine.. АртДонбас. Березень 2012. (рос.)
- ↑ Найбільш крупний і різноманітний аукціон в історії України. Інтерфакс-Україна. 6 листопада 2012. (рос.)
- ↑ Виставка-продаж «Three days sale» від аукціонного дому «Золотое сечение». Art Ukraine. 11 березня 2013. (рос.)
- ↑ Куприна, Ю. Аукционный дом «Золотое сечение» провел торги современным искусством. Судя по итогам, отечественный арт-рынок скорее жив[недоступне посилання з липень 2019] // Капитал. — 2014. — № 153. — С. 16. (рос.)
- ↑ У Києві картина Чичкана пішла з молотка за 3,6 тисячі доларів. Главред. 23 грудня 2014. (рос.)
- ↑ Під час Art Weekend продано 40 % робіт сучасних українських авторів Архівовано 15 квітень 2015 у Wayback Machine.. Экономические известия. 24 грудня 2014. (рос.)
- ↑ На торгах «Золотого сечения» натюрморт Давида Бурлюка проданий за $11000. Forbes Україна. 18 березня 2015. (рос.)
- ↑ Совладелец аукционного дома «Золотое сечение» Алексей Василенко объясняет, зачем покупать искусство во время кризиса[недоступне посилання з липень 2019] / беседовала Ю. Куприна // Капитал. — 2014. — № 141. — С. 15. (рос.)
- ↑ Іванова, А. Чи варто інвестувати в українське мистецтво. UBR. 18 вересня 2014. (рос.)
- ↑ Ложко, М. Украинское искусство как рынок // Equipage. — 2014. — № 1. — С. 86. (рос.)
- ↑ Корусь, Е. Факты и комментарии. Обзор киевских аукционов 2011 года // Антиквар. — 2012. — № 1-2. — С. 78-85. (рос.)
- ↑ Гладських, О. Картини Кандинського, Шемякіна, Заливахи на предаукціонній виставці «Золотое сечение. Авангард» оцінені від $15 тисяч до $150 тисяч. Дело. 9 грудня 2010. (рос.)
- ↑ Відділи аукціонного дому «Золотое сечение».
- ↑ Перший аукціон у 2014 році в Києві. Итоги. 27 вересня 2014. (рос.)
- ↑ Віктор Зарецький — перша масштабна виставка графіки Архівовано 9 березня 2016 у Wayback Machine.. Український бізнес портал. 6 вересня 2012. (рос.)
- ↑ Виктор Зарецкий в центре современного искусства «М17» // Коммерсантъ Weekend. — 2012. — № 136. — С. 14. (рос.)
- ↑ #Каталоги виставок, дайджест.
Каталоги виставок, дайджест[ред. | ред. код]
- Басов Яков Александрович (1914—2004). — К., 2006. — 76 с. (рос.)
- Русская икона XVII — начала XX вв. из частных собраний: каталог выставки. — К., 2009. — 152 с. (рос.)
- Digest: информационное издание аукционного дома «Золотое сечение». — 2012. — № 1. — 132 с. (рос.)
- Графіка В. Зарецького 1940-1980-х рр. : альбом. — К., 2012. — 296 с. (укр.) (англ.)
- Графіка М. Глущенка 1930—1970 років: каталог виставки. — К., 2012. — 128 с. (укр.) (англ.)
- Three days sale. Класичне мистецтво. Contemporary art. Виставка-продаж. 15-17 березня 2013. — К., 2013. — [40] с.
- Three days sale. Класичне мистецтво. Contemporary art. Виставка-продаж. 27-29 вересня 2013. — К., 2013. — [60] с.
- Contemporary art. Аукціон. 19 грудня 2014. — [К., 2014]. — [48] с.
- Чистота душевная. Русская икона XVI—XX вв. в частных собраниях. — К., 2014. — 322 с. — ISBN 978-966-1568-91-3. (рос.) (англ.)
Каталоги аукціонів[ред. | ред. код]
- Радянський живопис ХХ століття. Аукціон № 1. 5 березня 2005. — К., 2005. — 52 с.
- Український та російський живопис ХІХ-ХХ ст. Аукціон № 2. 12 листопада 2005. — К., 2005. — 68 с.
- Український та російський живопис ХІХ-ХХ ст. Аукціон № 3. 4 листопада 2006. — К., 2006. — 100 с.
- Український живопис ХХ-ХХІ ст. Аукціон № 4. 21 квітня 2007. — К., 2007. — 88 с.
- Український живопис та графіка ХХ-ХХІ ст. Аукціон № 5. 16 березня 2008. — К., 2008. — 132 с.
- Український живопис та графіка ХХ-ХХІ ст. Аукціон № 6. 12 жовтня 2008. — К., 2008. — 128 с.
- Український живопис та графіка ХХ-ХХІ ст. Російська ікона. Аукціон № 7. 12 квітня 2009. — К., 2009. — 94 с.
- Український живопис та графіка ХХ-ХХІ ст. Російська ікона. Аукціон № 8. [26 вересня 2009]. — К., 2009. — 212 с.
- Українське актуальне мистецтво. Аукціон. 24 жовтня 2009, Київ. — [К., 2009]. — [214] с.
- Українське, російське мистецтво ХХ-ХХІ ст. Аукціон № 10. [18 квітня 2010, Київ]. — К., 2010. — 152 с.
- Українське молоде актуальне мистецтво. Аукціон. 22 травня 2010, Київ. — [К., 2010]. — 72 с.
- Українське, російське мистецтво ХІХ-ХХІ ст. Аукціон № 12. [25 вересня 2010, Київ]. — К., 2010. — 128 с.
- Дизайн. Аукціон № 13. [30 жовтня 2010, Київ]. — К., 2010. — [120] с.
- Contemporary art. Аукціон № 14. [27 листопада 2010, Київ]. — К., 2010. — [160] с.
- Авангард. Аукціон № 15. [18 грудня 2010, Київ]. — К., 2010. — [112] с.
- Український класичний живопис та графіка ХХ ст. Аукціон № 16. [5 березня 2011, Київ]. — К., 2011. — 120 с.
- Contemporary art. Аукціон № 17. [9 квітня 2011, Київ]. — К., 2011. — [160] с.
- Українське — російське класичне мистецтво. Аукціон № 18. 17 вересня 2011. — К., 2011. — 184 с.
- Contemporary art. Аукціон № 19. 29 жовтня 2011. — К., 2011. — [200] с.
- Дизайн і фото. Аукціон № 20. 26 листопада 2011. — К., 2011. — [200] с.
- Contemporary art. Аукцион № 21. 17 декабря 2011. — Донецк, 2011. — [176] с. (рос.)
- Классическое искусство. Аукцион № 22. 17 марта 2012. — Донецк, 2012. — [176] с. (рос.)
- Contemporary art. Аукціон № 23. 28 квітня 2012. — К., 2012. — [192] с.
- Classic. Contemporary. Design. Аукціон № 24. 10 листопада 2012. — К., 2012. — [272] с.
- Post war & contemporary art. Аукціон. 25 вересня 2014. — К., 2014. — 16 с.
- Classic & contemporary art. Аукціон. 17 березня 2015. — К., 2015. — 112 с.
Золотое сечение — Википедия, свободная энциклопедия
Википедия todavía no tiene una página llamada «Золотое сечение».
Busca Золотое сечение en otros proyectos hermanos de Wikipedia:
 | Wikcionario (diccionario) |
 | Wikilibros (обучающие / руководства) |
 | Викицитатник (цитаты) |
 | Wikisource (biblioteca) |
 | Викинотики (noticias) |
 | Wikiversidad (Contenido académico) |
 | Commons (изображения и мультимедиа) |
 | Wikiviajes (viajes) |
 | Викиданные (данные) |
 | Викивиды (особые) |
-
 Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla.
Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla. -
 Busca «Золотое сечение» en el texto de otras páginas de Wikipedia que ya existen.
Busca «Золотое сечение» en el texto de otras páginas de Wikipedia que ya existen. -
 Проконсультируйтесь по списку произведений искусства на тему «Золотое сечение».
Проконсультируйтесь по списку произведений искусства на тему «Золотое сечение». -
 Busca las páginas de Wikipedia que tienen объединяет «золотое сечение».
Busca las páginas de Wikipedia que tienen объединяет «золотое сечение». -
 Si ya habías creado la página con este nombre, limpia la caché de tu navegador.
Si ya habías creado la página con este nombre, limpia la caché de tu navegador. -
 También puede que la página que buscas haya sido borrada.
También puede que la página que buscas haya sido borrada.
Si el artículo incluso así no existe:
-
 Crea el artículo utilizando nuestro asistente o solicita su creación.
Crea el artículo utilizando nuestro asistente o solicita su creación. -
 Puedes traducir este artículo de otras Wikipedias.
Puedes traducir este artículo de otras Wikipedias. -
 En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatible con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.
En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatible con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия. -
 Ten en cuenta también que:
Ten en cuenta también que:- Artículos vacíos o con información minima serán borrados —véase «Википедия: Esbozo» -.
- Artículos de publicidad y autopromoción serán borrados —véase «Википедия: Lo que Wikipedia no es» -.
Золотое сечение | Знай своего мема
О
Золотое сечение , иногда обозначаемое как , Золотая спираль , Золотое сечение или Божественная пропорция — это особое число, которое в математике можно найти, разделив линию на две части так, чтобы более длинная часть, разделенная на меньшую, также равна всей длине, разделенной на более длинную часть. Изображение изгибающейся, падающей спирали, которое часто используется для представления золотого сечения в искусстве и дизайне, часто накладывается на меметические изображения как демонстрация их естественного баланса или эстетики.
Происхождение
Происхождение математической концепции золотого сечения неизвестно, но восходит к временам греческого математика Евклида. Выражение уравнения в виде спирали внутри разделяющего прямоугольника происходит с того времени, когда писались начальные правила геометрии. Однако позже спираль часто называлась спиралью Фибоначчи по имени математика, который определил серию постоянно увеличивающихся чисел, которые приближались к золотому сечению, но никогда официально не встречали его.
Со времен эпохи Просвещения изображение золотой спирали использовалось как часть классического художественного образования, особенно для преподавания работ Леонардо да Винчи, который использовал это соотношение для создания своих композиций, таких как Мона Лиза. Это также известно как «правило третей» в искусстве и композиции.
Разворот
Online спиральное изображение часто накладывается на меметические изображения, чтобы продемонстрировать (иронично или нет), что эти вирусные изображения так же приятны, как и классическая композиция.На Tumblr и «золотая спираль», и «золотое сечение» вызывают эти типы изображений. Многие популярные сюжеты покрыты золотой спиралью; Например, 15 декабря 2015 года фотография (внизу слева) Дональда Трампа, на которой направление его волос было сформировано золотой спиралью, была загружена в / r / pics и получила 4 133 балла (87% голосов). Еще один популярный оверлей с золотой спиралью для лица был создан российским графическим дизайнером Игорем К. в январе 2014 года, который создал изображения, которые изменили расположение лиц таких знаменитостей, как Николас Кейдж, в соответствии с пропорциями (внизу справа).
Среди других популярных объектов оверлея — ёжик Соник, шипы которого расположены по спирали, и Владимир Путин, которого на фотографиях без рубашки часто изображают со спиралью, сфокусированной на соске. Кроме того, популярный веб-комикс xkcd поддерживает несвязанную страницу под названием «Спираль», которая содержит случайные фотографии, наложенные на золотую спираль.
Манчестер Новогоднее фото
Манчестерское новогоднее фото — это фотошоп-мем, основанный на фотографии, сделанной во время новогоднего разгула 2016 года в Манчестере, Англия.Позже в тот же день старший продюсер новостей BBC Роланд Хьюз опубликовал фотографию в Твиттере, сравнив высокий уровень драматизма с прекрасной картиной. По состоянию на 5 января 2015 года твит получил более 25 600 ретвитов и 29 600 добавленных в избранное. Из-за того, что Хьюз упомянул рисование на изображении, многие респонденты твита начали изменять изображение, чтобы получить результаты, похожие на рисование. Одним из первых, кто сделал это вскоре после первоначального твита Хьюза, был пользователь GroenMNG, который подробно описал способ в котором фотография отражала золотое сечение.

 Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla.
Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla. Busca «Золотое сечение» en el texto de otras páginas de Wikipedia que ya existen.
Busca «Золотое сечение» en el texto de otras páginas de Wikipedia que ya existen. Проконсультируйтесь по списку произведений искусства на тему «Золотое сечение».
Проконсультируйтесь по списку произведений искусства на тему «Золотое сечение». Busca las páginas de Wikipedia que tienen объединяет «золотое сечение».
Busca las páginas de Wikipedia que tienen объединяет «золотое сечение». Si ya habías creado la página con este nombre, limpia la caché de tu navegador.
Si ya habías creado la página con este nombre, limpia la caché de tu navegador. También puede que la página que buscas haya sido borrada.
También puede que la página que buscas haya sido borrada. Crea el artículo utilizando nuestro asistente o solicita su creación.
Crea el artículo utilizando nuestro asistente o solicita su creación. Puedes traducir este artículo de otras Wikipedias.
Puedes traducir este artículo de otras Wikipedias. En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatible con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.
En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatible con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.  Ten en cuenta también que:
Ten en cuenta también que: