Мир математики. Золотое сечение. Выпуск 1
 Добавить
Добавить- Читаю
- Хочу прочитать
- Прочитал
Оцените книгу
1 планируeт, 1 прочитал и 2 читают
Скачать книгу (полная версия)
1638 скачиваний
О книге «Мир математики. Золотое сечение. Выпуск 1»
Можно ли выразить красоту с помощью формул и уравнений? Существует ли в мире единый стандарт прекрасного? Возможно ли измерить гармонию с помощью циркуля и линейки? Математика дает на все эти вопросы утвердительный ответ. Золотое сечение — ключ к пониманию секретов совершенства в природе и искусстве.
Одним из чудесных свойств золотого сечения является его неисчерпаемая способность порождать изысканные формы: от треугольников до двадцатигранных тел, называемых икосаэдрами. Но несмотря на почетное имя, это число встречается даже в повседневных геометрических объектах, таких как кредитные карты и пятиконечная звезда. Форма кредитных карт представляет собой пример так называемого золотого прямоугольника, стороны которого находятся в золотом отношении.
Именно соблюдение «божественной пропорции» — помогает художникам достигать эстетического идеала. Книга «Золотое сечение. Математический язык красоты» открывает серию «Мир математики» — уникальный проект, позволяющий читателю прикоснуться к тайнам этой удивительной науки.
Произведение относится к жанру Наука. Оно было опубликовано в 2014 году издательством Де Агостини. Книга входит в серию «Мир математики». На нашем сайте можно скачать бесплатно книгу «Мир математики. Золотое сечение. Выпуск 1» в формате pdf или читать онлайн. Рейтинг книги составляет 3.46 из 5. Здесь так же можно перед прочтением обратиться к отзывам читателей, уже знакомых с книгой, и узнать их мнение. В интернет-магазине нашего партнера вы можете купить и прочитать книгу в бумажном варианте.Отзывы читателей
Подборки книг
Похожие книги
Другие книги автора
Информация обновлена:
Читать книгу φ – Число Бога. Золотое сечение – формула мироздания Марио Ливио : онлайн чтение
Марио Ливио
φ – Число Бога. Золотое сечение – формула мироздания
Памяти моего отца Робина Ливио
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.
Права на перевод получены соглашением между Broadway Books (Crown Publishing Group, Random House LLC, a Penguin Random House Company) и литературным агентством «Синопсис»
Mario Livio
THE GOLDEN RATIO: The Story of PHI, the World’s Most Astonishing Number
© Mario Livio, 2002
© Бродоцкая А., перевод на русский язык, 2014
© ООО «Издательство АСТ», 2015
Секрет гармонии во всем
Являются ли некоторые числа более значимыми, чем другие? Конечно же, да! Если уж у простых людей, далеких от науки или мистики, есть свои любимые и нелюбимые числа, что же говорить про математиков и физиков? Число – такой же важный компонент культуры, как слово. Нет человека, которому бы ни о чем не говорили числа 7, 13 или 666. Но есть числа, которые влияют на нашу жизнь, даже если мы о них не знаем. Таково число фи, в котором кроется секрет гармонии во всем. Марио Ливио написал эту книгу, чтобы мы не были так слепы и не думали, что нумерология – это предрассудки.
Тимоти Хью, Коннектикут
Из чего складывается красота
Книга Марио Ливио полна увлекательнейших цифровых трюков, но, чтобы понять их, вовсе не нужно иметь математический склад ума. Все мы сталкиваемся с тем, что называют красотой. Но кто скажет, из чего складывается красота? Почему нам так нравится смотреть на картины старых мастеров, любоваться спиральными галактиками или разглядывать сосновую шишку? В своей книге Ливио раскрывает секреты красоты и уводит читателя в увлекательный мир математики – науки, которая объясняет все.
Элис Хоул, Лос-Анджелес
Потрясающее исследование
Я даю этой книге пять звезд из пяти! Эта книга – и для математиков, и для тех, кто не дружит с цифрами. Если вы любите науку, вас захватит потрясающее исследование, которое автор предпринимает в своем труде, если вы любитель беллетристики – эта книга станет для вас тем же, что и хороший детектив.
Рэндом Уэсли, Сан-Франциско
Формула вселенской гармонии
Марио Ливио написал прекрасную работу, в которой дается подробный исторический обзор того, как на протяжении веков люди старались открыть универсальную формулу вселенской гармонии. Оказалось, что все гораздо проще – все сводится к одному-единственному числу, известному как золотое сечение, или число Бога. Вы можете быть математиком или всего лишь человеком, которого чуть-чуть интересует мистика. Если вам интересен окружающий мир, книга приведет вас в восторг!
Кристофер Паркер, Кембридж
Хорошая литература
«Золотое сечение» – это настоящий шедевр талантливого автора. Я был впечатлен той четкой и захватывающей манерой, которая делает научный труд книгой не только для ума, но и для отдыха. В этой книге Марио Ливио одновременно отвечает на самые актуальные вопросы современной науки и рассказывает удивительную историю, увлечься которой способен каждый. Это хорошая литература во всех отношениях.
Мишель Тернер, Колд Спринг Харбор
Предисловие
«Золотое сечение» – это книга об одном-единственном числе, однако число это совершенно особое. Это число – 1,61803… – встречается и в лекциях по истории искусств, и в перечнях «любимых чисел», которые составляют математики. Не менее поразительно, что оно было предметом множества экспериментов по психологии.
Так называемое «золотое сечение» заинтересовало меня пятнадцать лет назад, когда я готовился к лекции об эстетике в физике (представьте себе, это отнюдь не оксюморон), и с тех пор оно не идет у меня из головы.
В создании этой книги прямо и косвенно поучаствовало столько моих коллег, друзей и учеников, что всех и не перечислишь. Здесь я хотел бы выразить особую благодарность Иву-Алену Буа, Митчу Фейгенбауму, Гиллелю Гаухману, Теду Хиллу, Рону Лифшицу, Роджеру Пенроузу, Джоанне Постма, Полу Стейнхардту, Пат Тиль, Анне ван дер Хельм, Дивакару Вишванату и Стивену Вольфраму – за бесценные сведения и крайне продуктивные споры.
Я благодарен своим коллегам Даниэле Кальцетти, Стефано Казертано и Массимо Стиавелли за помощь с переводами с латыни и итальянского, Клаусу Лейтереру и Эрмине Ландт за помощь с переводами с немецкого, а Патрику Годону – за помощь с переводами с французского. Сара Стивенс-Рейберн, Элизабет Фрэзер и Нэнси Хэнкс очень посодействовали мне во всем, что касалось лингвистики и библиографии. Особенно я благодарен Шэрон Тулан за содействие в подготовке рукописи.
Искренне благодарю своего литературного агента Сьюзен Рабинер за то, что она не давала мне опустить руки до начала и во время работы над книгой. Я в огромном долгу перед Джеральдом Ховардом, моим редактором из издательства «Doubleday Broadway», за то, что он так тщательно вычитывал рукопись и делал такие точные, глубокие замечания. Также я благодарен Ребекке Холланд, выпускающему редактору в «Doubleday Broadway», за постоянное содействие в то время, пока книга была в печати.
И, наконец, эта книга вообще была написана исключительно благодаря постоянной помощи, терпению и поддержке Софи Ливио.
Прелюдия к числу
Много есть чудес на свете.
Софокл (495–405 гг. до н. э.) (Пер. С. Шервинского, Н. Познякова)
Знаменитый английский физик лорд Кельвин (Уильям Томпсон, 1824–1907), в честь которого назван градус абсолютной температурной шкалы, во время одной своей лекции сказал: «Если знание невозможно выразить численно, значит, оно поверхностно и недостаточно». Разумеется, Кельвин имел в виду то знание, которое необходимо для научного прогресса. Однако числа и математика удивительным образом предрасположены к тому, чтобы способствовать пониманию даже того, что крайне далеко от науки – или, по крайней мере, представляется таким на первый взгляд. В «Тайне Мари Роже» Эдгара Аллана По знаменитый детектив Огюст Дюпен замечает: «Мы превращаем случайность в предмет точных исчислений. Мы подчиняем непредвиденное и невообразимое научным математическим формулам» ( пер. И. Гуровой). Можно пояснить это и на более простом примере. Представьте себе, что вы готовитесь к приему гостей и столкнулись со следующей задачей: у вас есть шоколадка, состоящая из двенадцати долек – сколько раз нужно ее разломить, чтобы разделить все части? Ответ куда проще, чем вы думали, и почти не требует вычислений. Каждый раз, когда вы ломаете шоколадку, у вас получается на один кусок больше, чем раньше. Следовательно, если вам нужно получить двенадцать кусков, придется ломать шоколадку одиннадцать раз (убедитесь сами). А если обобщить, то количество разломов всегда будет на один меньше, чем требуемое количество кусков, независимо от того, из скольких частей состоит шоколадка.
Даже если вы не слишком любите шоколад, то все равно понимаете, что этот пример демонстрирует простой математический закон, который можно применить и во многих других случаях. Однако математические свойства, формулы и законы (многие из которых не задерживаются у нас в памяти) – это далеко не все; существуют еще и особые числа, которые настолько вездесущи, что не устают нас изумлять. Самое прославленное из них – число π (пи), отношение длины окружности к ее диаметру. Значение π – 3,14159… – завораживало много поколений математиков. Хотя изначально число π было определено в геометрии, оно очень часто и неожиданно всплывает при вычислении вероятности. Знаменитый пример – так называемая игла Бюффона, названная в честь французского математика Жоржа-Луи Леклерка, графа де Бюффона (1707–1788), который поставил и решил эту вероятностную задачу в 1777 году. Леклерк задал следующий вопрос: представьте себе, что у вас на полу лежит большой лист бумаги, разлинованный параллельными линиями через равные заданные промежутки. На лист совершенно случайным образом бросают иглу, длина которой в точности равна промежутку между линиями. Какова вероятность, что игла упадет так, что пересечет одну из линий (то есть как на рис. 1)? Как ни странно, ответ, оказывается, 2/π. То есть в принципе возможно даже вычислить π, если повторить этот эксперимент много раз и понаблюдать, какая доля бросков заканчивается пересечением иглы с линией (правда, есть и другие методы вычисления π, не такие скучные). Словосочетание «число π» настолько вошло в обиходный лексикон, что кинорежиссер Даррен Аронофски в 1998 году даже снял психологический триллер под таким названием.
Рис. 1
Менее знаменито другое число – φ (фи), а между тем, во многих отношениях оно даже интереснее. Вот, скажем, представьте себе, что я спрашиваю у вас, что общего у изумительного расположения лепестков алой розы, композиции знаменитой картины Сальвадора Дали «Тайная вечеря», чудесного рисунка спиральной раковины и статистики размножения кроликов? Трудно поверить, что у столь разнородных явлений действительно есть нечто общее – и это некое число или геометрическая пропорция, известная человечеству еще со времен античности, число, которому в XIX веке дали почетное называние «золотое число» или «золотое сечение». А в начале XVI века в Италии вышла книга, в которой это число называлось «Божественной пропорцией» – не более и не менее.
В повседневной жизни мы применяем слово «пропорция» для обозначения соотношения между частями целого по размеру или количеству – или когда хотим подчеркнуть гармоничные отношения между разными частями. В математике термин «пропорция» применяется для описания равенства следующего типа: девять относится к трем, как шесть к двум. Как мы увидим, золотое сечение дарит нам чарующее сочетание этих определений: хотя определяется оно строго математически, однако считается, что оно обладает свойствами, обеспечивающими приятную гармонию.
Первое четкое определение соотношения, которое впоследствии станет известно как золотое сечение, дал примерно в 300 году до н. э. Евклид Александрийский, основатель геометрии как формальной дедуктивной системы. К Евклиду и его фантастическим достижениям мы еще вернемся в главе 4, а пока позвольте отметить, что Евклид вызывает столь сильное восхищение, что поэтесса Эдна Сент-Винсент Миллей в 1923 году даже посвятила ему стихотворение под названием «На обнаженность красоты Евклид взглянул» (пер. Л. Мальцевой). Эдна даже сохранила свою школьную тетрадь по евклидовой геометрии. Евклид определил пропорцию, выведенную из простого деления линии (отрезка), по его выражению, «в крайнем и среднем отношении»: «Прямая линия называется рассеченною в крайнем и среднем отношении, когда как целая прямая к большему отрезку, так больший к меньшему» (пер. Ф. Петрушевского) (рис. 2).
Рис. 2
Иначе говоря, если мы посмотрим на рис. 2, то увидим, что отрезок АВ определенно длиннее отрезка АС, в то же время АС длиннее СВ. Если отношение длины АС к длине СВ такое же, как отношение длины АВ к длине АС, значит, отрезок поделен «в крайнем и среднем отношении» – или в золотом сечении.
Кто бы мог подумать, что такое на первый взгляд невинное разделение отрезка, которое Евклид определил в чисто геометрических целях, окажет влияние на самые разные разделы знания – от положения листьев в ботанике до структуры галактик, состоящих из миллиардов звезд, от математики до искусства? Следовательно, золотое сечение – прекрасный пример того самого крайнего изумления и восторга, которые так высоко ценил великий физик Альберт Эйнштейн (1879–1955). Вот как он об этом писал: «Самое прекрасное, что только может выпасть нам на долю, – это тайна. Стремление разгадать ее стоит у колыбели подлинного искусства и подлинной науки. Тот, кто не знает этого чувства, утратил любопытство, не способен больше удивляться, – все равно что мертвый, все равно что задутая свеча».
Как мы еще увидим, когда проследим на страницах этой книги все необходимые вычисления, точное значение золотого сечения (то есть отношение АС к СВ на рис. 2) – бесконечное непериодическое число 1,6180339887…, а такие бесконечные неповторяющиеся числа интересовали людей со времен античности. Рассказывают, что когда греческий математик Гиппас из Метапонта в V веке до н. э. обнаружил, что золотое сечение – это и не целое число (подобное нашим добрым знакомым 1, 2, 5 и т. д.), и даже не отношение двух целых чисел (подобное дробям вроде 1/2, 2/3, 3/4, которые в совокупности называются рациональными числами), это привело остальных пифагорейцев – то есть последователей знаменитого математика Пифагора – в полнейшее смятение. Предметом поклонения для пифагорейского мировоззрения (о котором мы подробно поговорим в главе 2) был arithmos – то есть имманентные качества целых чисел и их отношений и их предполагаемая роль в мироздании. А открытие, что существуют числа вроде золотого сечения, которые все тянутся и тянутся вечно и при этом в них нет никаких следов повторяемости, никакой закономерности, вызвало самый настоящий философский кризис. Легенда даже утверждает, будто пифагорейцы, совершенно потрясенные этим открытием колоссальной важности, устроили гекатомбу – пожертвовали сто быков, – хотя это вряд ли, учитывая, что пифагорейцы были строгими вегетарианцами. Тут я вынужден подчеркнуть, что большинство подобных историй основаны на недостоверном историческом материале. Так или иначе, мы даже приблизительно не знаем, когда именно были открыты числа, которые не являются ни целыми, ни дробями – так называемые иррациональные числа. Однако некоторые ученые датируют это открытие V веком до н. э., что, по крайней мере, соответствует только что рассказанным легендам. Очевидно одно: пифагорейцы в общем и целом считали, что существование подобных чисел так ужасно, что это, должно быть, своего рода ошибка мироздания, которую надо замолчать и держать в тайне.
Тот факт, что золотое сечение невозможно выразить в виде дроби (как рациональное число), попросту означает, что нельзя выразить в виде дроби соотношение длин АС и СВ на рис. 2. Иначе говоря, как бы мы ни трудились, мы не найдем единицы измерения, которая, скажем, укладывалась бы 51 раз в АС и 19 раз в СВ. Две длины, у которых нет подобной единицы измерения, называются несоизмеримыми. В своем труде «Жизнь Пифагора» (ок. 300 г. н. э.) философ и историк Ямвлих из аристократического сирийского семейства так описывает бурную реакцию на это открытие: будто бы тот, кто открыл эту тайну непосвященным, «вызвал, как говорят, такую ненависть, что его не только изгнали из общины и отлучили от пифагорейского образа жизни, но и соорудили ему надгробие, как будто действительно ушел из жизни тот, кто некогда был их товарищем» (пер. И. Ю. Мельниковой).
В профессиональной математической литературе золотое сечение принято обозначать греческой буквой τ (тау) – от греческого слова τομή (читается «томэ»), которое означает «сечение» или «разрез». Однако в начале ХХ века американский математик Марк Барр предложил обозначать золотое сечение буквой φ – по первой букве имени великого древнегреческого скульптора Фидия, жившего примерно в 490–430 гг. до н. э. Величайшие шедевры Фидия – Афина Партенос в Афинах и Зевс в Олимпии. Кроме того, полагают, что он отвечал и за другие скульптуры в Парфеноне, хотя весьма вероятно, что их создали его ученики и помощники. Барр решил, что надо почтить память скульптора, поскольку многие искусствоведы полагают, что Фидий часто и весьма точно применял золотое сечение в своих творениях (эту и подобные гипотезы мы очень дотошно разберем в нашей книге). Я буду называть его и золотым сечением, и числом φ, поскольку именно такие обозначения чаще всего встречаются в популярной математической литературе.
Величайшие математические умы в истории – и древнегреческие мудрецы Пифагор и Евклид, и средневековый итальянский ученый Леонардо Пизанский по прозвищу Фибоначчи, и астроном эпохи Возрождения Иоганн Кеплер, и современные научные светила, например, физик из Оксфорда Роджер Пенроуз, немало часов провели в размышлениях над этим простым соотношением и его свойствами. Однако золотое сечение чарует отнюдь не только математиков. Биологи, художники, историки, музыканты, архитекторы, психологи и даже мистики – все они размышляли над тем, почему это число столь вездесуще и в чем его притягательность. По сути дела, можно, пожалуй, сказать, что золотое сечение вдохновляло мыслителей из всех отраслей знания – и в этом с ним не в силах сравниться никакое другое число в истории математики.
Даже простому вопросу о происхождении названия «золотое сечение» посвящено огромное количество исследований, а особенно глубоко этим интересовался канадский математик и писатель Роджер Герц-Фишлер, о чем и рассказано в его превосходной книге «A Mathematical History of the Golden Number» («Математическая история золотого сечения»). Учитывая, какой пристальный интерес вызывало это число еще со времен античности, можно было бы подумать, что и название это античного происхождения. И в самом деле, некоторые авторитетные труды по истории математики, например, «Рождение математики во времена Платона» Франсуа Ласерре (François Lasserre. «The Birth of Mathematics in the Age of Plato») и «История математики» Карла Б. Бойера (Carl B. Boyer. «History of Mathematics»), возводят это название, соответственно, к XVI и XVII векам. Однако дело, скорее всего, не в этом. Насколько я могу судить по обширным источниковедческим данным, впервые это словосочетание применил в 1835 году немецкий математик Мартин Ом (брат знаменитого физика Георга Симона Ома, в честь которого назван закон Ома в электромагнетизме) во втором издании своей книги «Чистая элементарная математика» (Martin Ohm. «Die Reine Elementar-Mathematik»). В одной сноске Ом пишет: «Подобное разделение произвольного отрезка на две части принято также называть золотым сечением». Формулировка Ома однако создает впечатление, что он не сам придумал этот термин, а скорее привел уже принятое название. Тем не менее, в первом издании книги, опубликованном в 1826 году, Ом этого названия не приводит, а это заставляет сделать по крайней мере тот вывод, что выражение «золотое сечение» (нем. «der Goldene Schnitt») завоевало популярность лишь к 1835 году. Вероятно, ранее это было лишь разговорное выражение, применявшееся преимущественно в математических кругах. Однако нет никаких сомнений, что после книги Ома термин «золотое сечение» стал часто повторяться в немецкой литературе по математике и искусствоведению. А в англоязычной печати это выражение, по всей видимости, дебютировало в статье Джеймса Салли (James Sully) по эстетике, которая появилась в девятом издании Британской энциклопедии в 1875 году. Салли описывает «интересное экспериментальное исследование… проведенное Густавом Теодором Фехнером (известным немецким физиком и первопроходцем в области психологии, жившим в XIX веке) о том, что «золотое сечение» первоначально было именно зримой пропорцией» (об экспериментах Фехнера мы подробно поговорим в главе 7). В математическом контексте этот термин впервые встретился в англоязычной литературе, по всей видимости, в статье Э. Эккерманна, которая так и называлась «Золотое сечение» (E. Ackermann. «The Golden Section») и была напечатана в журнале «American Mathematical Monthly» в 1895 году, а также – примерно в это же время, в 1898 году – в книге «Введение в алгебру» известного преподавателя и писателя Дж. Кристала (1851–1911). Позвольте мне отметить любопытства ради, что единственное определение «золотого числа», появившееся в издании французской энциклопедии «Nouveau Larousse Illustré» 1900 года, гласит: «Число, определяющее каждый год лунного цикла». Это относится к положению календарного года в пределах 19-летнего цикла, после которого фазы луны снова приходятся на те же даты. Очевидно, во французскую математическую номенклатуру «золотое число» и тем более «золотое сечение» проникало гораздо дольше.
Однако почему это вообще так важно? Из-за чего, собственно, это число или геометрическая пропорция так сильно нас интересуют? Привлекательность золотого сечения в первую очередь коренится в том факте, что оно обладает прямо-таки пугающим свойством вылезать там, где его никак не ожидаешь.
Возьмем, к примеру, самое обычное яблоко – фрукт, который часто и, вероятно, ошибочно ассоциируется с древом познания, играющим столь заметную роль в библейском рассказе о грехопадении – и разрежем его поперек. И мы увидим, что яблочные семечки образуют пятиконечную звезду – она же пентаграмма (рис. 3). Каждый из пяти равнобедренных треугольников, составляющих лучи пентаграммы, обладает таким свойством, что соотношение длины его длинной стороны к короткой, то есть к основанию, равно золотому сечению – 1,618… Правда, вы, вероятно, решите, что это не так уж и удивительно. В конце концов, золотое сечение и определяется в первую очередь как геометрическая пропорция, так что, вероятно, не надо так уж поражаться, если эта пропорция встречается в некоторых геометрических фигурах.
Рис. 3
Однако это лишь верхушка айсберга. Согласно буддистской традиции, Будда во время одной своей проповеди не проронил ни слова, а всего-навсего показал слушателям цветок. Чему может научить нас цветок? Скажем, роза часто служит примером природной симметрии, гармонии, любви и хрупкости. Индийский поэт Рабиндранат Тагор (1861–1941) в своей «Религии человека» пишет: «Нам почему-то кажется, что роза – это язык, который нашла любовь, чтобы достичь наших сердец». Предположим, вам нужно качественно оценить симметричное устройство розы. Возьмите розу и препарируйте ее, чтобы разобраться, каким образом ее внешние лепестки накладываются на внутренние. Как я показываю в главе 5, вы обнаружите, что лепестки расположены в соответствии с математическим законом, основанном на золотом сечении.
Рис. 4
Теперь обратимся к царству животных: все мы хорошо знакомы с чарующе прекрасными спиральными структурами многих раковин моллюсков, например, вида Nautilus pompilius (рис. 4). Между прочим, такую раковину держит в руке танцующий Шива из индийских легенд – это символ одного из орудий творения. Кроме того, структура этих раковин вдохновляла и многих зодчих. Например, американский архитектор Фрэнк Ллойд Райт (1869–1959) положил эту структуру в основу здания музея Гуггенхайма в Нью-Йорке. Попав в музей, посетители поднимаются по спиральному пандусу, насыщая воображение созерцанием произведений искусства – точно так же, как моллюск выстраивает новые спиральные камеры, заполняя свое физическое пространство. В главе 5 мы увидим, что рост спиральных раковин также подчиняется правилу, основанному на золотом сечении.
Рис. 5
Пожалуй, не нужно быть особым поклонником нумерологии – мистики чисел, чтобы уже сейчас почувствовать некоторый душевный трепет: столь поразительна способность золотого сечения проявляться в самых разных ситуациях, в самых разных феноменах, казалось бы, совершенно не связанных друг с другом. Более того, как я уже отметил в начале главы, золотое сечение обнаруживается не только в природных явлениях, но и в самых разных рукотворных предметах и произведениях искусства. Например, на рис. 5 мы видим картину Сальвадора Дали «Тайная вечеря», написанную в 1955 году (она хранится в Национальной галерее в Вашингтоне): соотношение сторон этой картины – ее размеры 167 на 268 см – приблизительно равно золотому сечению. Более того, над столом, словно охватывая композицию, парит фрагмент огромного додекаэдра – правильного двенадцатигранника, каждая грань которого представляет собой правильный пятиугольник. Как мы увидим в главе 4, правильные многогранники, например, куб, которые можно вписать в сферу (т. е. сделать так, чтобы все их углы лежали на сфере), а особенно додекаэдр, тесно связаны с золотым сечением. Почему Дали решил так явно подчеркнуть золотое сечение в своей картине? Художник отмечал, что «Композиция Тайной Вечери должна быть симметричной» – но это лишь начало ответа на наш вопрос. Как я показываю в главе 7, золотое сечение появляется – или по крайней мере, должно появляться по замыслу создателя – в работах многих других художников, архитекторов, дизайнеров и даже в знаменитых музыкальных произведениях. Говоря обобщенно, золотое сечение применяется в некоторых произведениях искусства с целью достичь определенного зрительного или слухового эффекта. Подобный эффект вызывается, в частности, особым соотношением размеров отдельных частей и целого, особыми пропорциями. История искусств показывает, что в результате долгих поисков неуловимого канона «совершенных» пропорций – такого, чтобы любое произведение искусства при его применении автоматически становилось эстетичным и приятным – выяснилось, что этим требованиям лучше всего удовлетворяет именно золотое сечение. Но почему?
Если подробнее рассмотреть примеры из мира природы и из мира искусства, окажется, что они заставляют задаваться вопросами на трех уровнях глубины. Прежде всего, это непосредственные вопросы: (а) все ли случаи появления числа φ в природе и искусстве, описанные в литературе, действительно имеют место или некоторые из них – всего лишь результаты неверных интерпретаций и всякого рода натяжек? (б) Если число φ и правда появляется в этих и других обстоятельствах, можем ли мы как-то это объяснить? Далее, если учесть, что мы придерживаемся определения «красоты», подобного, скажем, тому, которое дано в словаре Уэбстера: «Качество, которое делает объект приятным или приносит определенное удовлетворение» – возникает вопрос: есть ли у математики эстетическая составляющая? Если да, какова сущность этой составляющей? Это серьезный вопрос, поскольку, как заметил однажды американский архитектор, математик и инженер Ричард Бакминстер Фуллер (l895–l983): «Когда я работаю над какой-то задачей, то никогда не думаю о красоте. Думаю я только о том, как решить эту задачу. Но если я решу ее и решение окажется некрасивым, я буду знать, что ошибся». И, наконец, самый интересный вопрос звучит так: почему, собственно, математика столь могущественна и столь вездесуща? Благодаря чему математика и численные константы вроде золотого сечения играют столь важную роль во всем на свете – от фундаментальных теорий происхождения Вселенной до рынка ценных бумаг? Существует ли математика и ее принципы независимо от людей, которые ее открыли или обнаружили? Математична ли Вселенная по своей природе? Последний вопрос можно задать, переформулировав известный афоризм английского физика сэра Джеймса Джинса (1847–1946): может быть, и сам Бог – математик?
В этой книге я постараюсь обсудить все эти вопросы более или менее подробно с точки зрения увлекательной истории числа φ. История этой константы, временами запутанная, насчитывает тысячелетия и разворачивается на всех материках. Но при этом я надеюсь рассказать вам еще и интересную историю о человеческой психологии. Наш сюжет отчасти повествует о тех временах, когда физиками и математиками называли себя люди, которых попросту интересовали различные вопросы, разжигавшие в них любознательность. Зачастую подобные люди трудились и умирали, не зная, удастся ли результатам их трудов изменить ход научной мысли или они просто канут в Лету, не оставив и следа.
Однако прежде чем пуститься в этот путь, нам придется поближе познакомиться с числами вообще и с золотым сечением в частности. Откуда, в сущности, появилась сама идея золотого сечения? Что именно заставило Евклида задуматься о том, чтобы разделить отрезок именно в таком соотношении? Моя цель – помочь вам заглянуть в подлинные истоки, так сказать, «золотого исчисления». Для этого мы и предпримем краткую ознакомительную экскурсию во времена зарождения математики.
Внеклассное мероприятие по математике «Золотое сечение»
В работе любого учителя внеклассная работа по предмету является наиболее эффективной, т.к. именно она повышает мотивацию при обучении, активизирует учебные коммуникативные умения и навыки учащихся, расширяет базовые знания учащихся о мире. Ребята с удовольствием принимают участие в таких внеклассных мероприятиях. Данная разработка внеклассного мероприятия для учащихся 9-11-х классов будет полезна учителям математики в проведении предметной недели, а также может быть использована учителями других предметов.
“…Геометрия владеет двумя сокровищами
– теоремой Пифагора
и золотым сечением, и если первое из них можно
сравнить с мерой золота,
то второе – с драгоценным камнем”.
(Иоганн Кеплер)
“Там, где красота, там действуют законы математики”. (Г.Харди)
Цели урока:
1. Образовательные:
- Дать представление о золотом сечение в математике, архитектуре, живописи, скульптуре, природе, анатомии.
2. Развивающие:
- Активизировать самостоятельную деятельность.
- Развивать познавательную активность и мировоззренческие представления о единстве красоты природы.
- Учить обобщать и систематизировать полученную информацию.
3. Воспитательные:
- Расширить кругозор учащихся, способствовать развитию познавательного интереса.
- Способствовать познанию законов красоты и гармонии окружающего мира.
- Воспитывать гармонически развитую личность.
Содержание:
- Основатели учения о золотом сечении.
- Понятие золотого сечения.
- Золотое сечение в математике.
- Золотое сечение в архитектуре.
- Золотое сечение в живописи.
- Золотое сечение в скульптуре.
- Золотое сечение в природе.
- Золотое сечение в анатомии.
Ход урока
Золотая пропорция возникает в расцвет античной культуры в трудах греческих философов: Пифагора, Платона, Эвклида. Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.).(Слайд 3) Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создания.
Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
После Пифагора, в III веке до нашей эры золотое сечение упоминается Эвклидом в его “Началах”, еще через 100 лет его изучает некий геометр Гипсикл, а еще через 500 лет — математик Папп.
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, 1202 г вышел в свет его математический труд “Книга об абаке” (счетной доске).
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. (Слайд 4) Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3= 5; 3 + 5= 8; 5 + 8= 13, 8 + 13= 21; 13 + 21= 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.
В 1509 г. в Венеции была издана книга Луки Пачоли “Божественная пропорция” с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи.. (Слайд 5) Книга была восторженным гимном золотой пропорции.. Он снабжает золотое сечение эпитетами: сам этот термин “Золотое сечение” Так оно и держится до сих пор как самое популярное. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее “божественную суть” как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого). Художник Леонардо да Винчи много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении..
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии.. (Слайд 6) Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя “Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности”.
Вновь “открыто” золотое сечение было в середине XIX в. (Слайд 7) В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд “Эстетические исследования”. Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название “Золотое деление как основной морфологический закон в природе и искусстве”. В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга.
ЗОЛОТОЕ СЕЧЕНИЕ В МАТЕМАТИКЕ. (Слайд 8,9)
Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты. Красота многогранна и многолика. Красота помогает с радостью воспринимать окружающий мир, математика даёт возможность осознать явления и упрочить знания о гармонии всего мира. Усилием математиков золотая пропорция была объяснена, изучена и глубоко проанализирована, Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей a : b = b : c или с : b = b : а. “Золотое сечение”– это иррациональное число, приблизительно равно 1,618.
На этой пропорции базируются основные геометрические фигуры.
Окружающие нас предметы дают примеры золотого прямоугольника: обложки многих книг, журналов, тетрадей, открытки, картины, крышки столов, экраны телевизоров и т.д. близки по размерам к золотому прямоугольнику.
Разумеется есть и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1.618.
ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ. (Слайд 11,12)
Далее перенесемся в эпоху классической Греции. На протяжении многих столетий человек в своем творчестве учился у природы, постигая законы её гармонии, её красоту. Мерой соотношения симметрии и асимметрии выступала у древних греков пропорция. Замечательные произведения архитектуры не стареют. Древние сооружения с их гармоническими пропорциями дарят современным людям такое же эстетическое удовлетворение как и их далеким предкам. Великолепные памятники архитектуры оставили нам зодчие древней Греции и среди них первое место по праву принадлежит Парфенону при построении которого, великий скульптор и архитектор Фидий использовал золотую пропорцию, поэтому она была обозначена буквой (фи) – первой буквой его имени.
Парфенон и сейчас, несмотря на то, что со времени его постройки прошло более 2,5 тысячелетий, производит огромное впечатление. Некогда белоснежный мрамор стал от времени золотисто-розовым. Величественное здание, стоящее на холме из известняка, возвышается над Афинами и их окрестностями. Но поражает оно не своими размерами, а гармоническим совершенством пропорций. Здание не вдавливается своей тяжестью в землю, а как бы парит над нею, кажется очень лёгким. Многие искусствоведы стремились раскрыть секрет того могучего эмоционального воздействия, которое это здание оказывает на зрителя. Разгадку они увидели в том, что в соотношениях многих частей храма присутствует золотая пропорция Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора.. Отношение высоты здания к его длине равно 0,618..
ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ. (Слайд 13,14)
В наиболее известной картине Леонардо да Винча, портрете Моны Лизы (около 1503, Лувр) образ богатой горожанки предстает таинственным олицетворением природы как таковой, не теряя при этом чисто женского лукавства; внутреннюю значительность композиции придает космически-величавый и в то же время тревожно-отчужденный пейзаж, тающий в холодной дымке. Ее композиция основана на золотых треугольниках.
В картине Сальвадора Дали “Тайняя вечерня” в которой заложен глубокий религиозный смысл, также использован принцип золотого сечения.
ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕ (Слайд 15)
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Древнегреческий скульптор Фидий часто использовал “ золотое сечение” в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос. Знаменитая статуя Аполлона Бельведерского тоже состоит из частей делящихся по золотым отношениям.
ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ. (Слайд 16,17)
“Великая книга природы написана на языке математики”. Галилео Галилей. Корни золотой пропорции в живой природе уходят также глубоко, как и корни самой жизни.
Золотое сечение – это один из основных основополагающих принципов природы.
Мир природы – это, прежде всего, мир гармонии, в которой действует «закон золотого сечения». Золотое сечение – божественная мера красоты, сотворенная в природе. В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Пропорцию можно увидеть в изгибах морской раковины, в формах цветов, в теле человека. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции. И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Все живое и красивое подчиняется божественному закону – золотому сечению.
Представление о золотом сечении будет неполным, если не сказать о спирали. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение е
Исследовательская работа по математике «Золотое сечение»
Слайд 1 Здравствуйте Уважаемые члены жюри, мы представляем вашему вниманию исследовательскую работу на тему : «Золотое сечение». И хотим мы начать с замечательной фразы Святого Фомы Аквинского: «Чувствам человека приятны объекты, обладающие правильными пропорциями.»
Слайд 2 Цель нашей работа: Выявить что же такое «Золотое сечение», исследовать принцип «золотого сечения – красоты и гармонии» в окружающем мире. Основная задача стоящая перед нами: Изучить красоту окружающих предметов с математической точки зрения
Слайд 3 Теперь более чем когда-либо все в нашем мире основано на числах. Некоторые из них имеют даже свои имена (число π). Среди всех замечательных чисел есть одно особенно интересное: 1,6180339887…
С особым благоговением относились к этому числу: золотое число, божественное число, божественное сечение… Мы назовем его золотым сечением. Оно обозначается греческой буквой Ф (фи) и играет в математике выдающуюся роль, обладая удивительными свойствами и неожиданными связями с творениями природы и человека.
Слайд 4 Золотое сечение – это иррациональное число. Оно было открыто древними греками, и его документированная история начинается с одной из самых известных книг всех времен и народов «Начал» Евклида, написанной около 300 г. до н.э. «Начала» состоят из 13 книг, а именно 6 книга содержит текст, с которого началась история золотого сечения:
«Разделить прямую линию в крайнем и среднем отношении значит разделить ее на два таких отрезка, чтобы отношение всей линии к большему отрезку равнялось отношению большего отрезка к меньшему». Иными словами «Целое относится к большей части, как большая часть к меньшей»
Слайд 5 Для записи золотого сечения используют математическую формулу:
(1+√5)/2=1,6180339887
Как мы видим это число чуть больше единицы, состоит из бесконечного ряда цифр, которые никогда не образуют повторяющуюся группу.
Чтобы подойти к золотому сечению геометрически, можно построить прямоугольник, у которого одна сторона в 1,618 раз длиннее другой
Слайд 6 На слайде представлено более точное значение числа Фи
Слайд 7 Мы решили провести эксперимент: Взяли две кредитные карты. Одну разместили горизонтально, а другую вертикально так, чтобы нижние стороны находились на одной линии.
Если в горизонтальной карте мы проведем диагональную линию и продолжим ее, то увидим, что она пройдет в точности через правый верхний угол вертикальной карты – приятная неожиданность.
Слайд 8 Еще мы провели небольшое исследование по методу немецкого экспериментального психолога Густава Теодора Фехнера. В 1876 году он провел исследование с людьми не имеющими отношение к искусству. Им было необходимо из прямоугольников, включая квадрат, выбрать один, который наиболее приятен глазу. Подавляющее большинство выбрали прямоугольник с «золотым » соотношением сторон. Мы предлагаем вам тоже выбрать прямоугольник который наиболее вам приятен.
Слайд 9 А теперь мы посмотрим что-же представляет собой каждый прямоугольник. ( показать прямоугольники на слайде и прочитать что они обозначают)
Слайд 10 Мы повторили этот эксперимент в 6-7 классах. И отметили одну особенность, дети которые выбрали «золотой прямоугольник», либо хорошо рисуют, либо занимаются в художественной школе, т.е. все же имеют отношение к искусству.
Слайд 11 Далее мы приступаем к изучению красоты окружающих предметов с математической точки зрения. Начнем мы с идеальных пропорций. На слайде представлена статуя Апполона, который являлся примером тех самых идеальных пропорций. Рост человека= размаху рук (расстоянию между кончиками пальцев разведенных в стороны рук) = 8 ладоням = 6 ступням = 8 лицам = 1,618, умноженному на высоту пупка ( расстоянию от пупка до земли. Мы добрались до соотношения 1,618, что является приблизительным значением числа Фи. При проверке этих пропорций в наших телах мы, несомненно, расстроимся. Ведь идеалу соответствовать трудно.
Слайд 12 Золотое сечение встречается и в живописи. Композиционные элементы картины Леонардо «Тайная вечеря» содержат золотые пропорции. Хотя прямых доказательств этого нет. Но «золотые прямоугольники» определяют как размеры картины, так и положение Христа и его учеников. Стены и окна на заднем плане следуют правилу золотого сечения.
Слайд 13 Даже портрет Моны Лизы построен на золотом сечении. Ее лицо и в целом, и в деталях обрамлено элегантной последовательностью «золотых» прямоугольников разных размеров.
Слайд 14 Символ пентаграммы, который по утверждению Пифагора скрывает в себе золотое сечение, помогал в определении пространства картины, в расположении человеческих фигур. «Святое семейство» Микеланджело служит тому примером.
Слайд 15 Золотое сечение в архитектуре. В других цивилизациях, далеких от классической културы, тоже ценили золотое сечение. Рядом с озером Титикака, недалеко от столицы Боливии, находятся Врата Солнца – каменная арка доинковской эпохи с пропорциями, которые полностью диктуются золотым сечением. Врата разрушены, время постройки датируется примерно 1500 г до н.э.
Слайд 16 Врата Солнца в виде «золотых прямоугольников»
Слайд 17 Фасад Университета Саламанки содержит большой «золотой прямоугольник». Испания 1218 г.
Слайд 18 Музей Гуггенхайма в Нью-Йорке. Вид снаружи похож на золотую спираль. А золотая спираль – это в геометрии логарифмическая спираль, скорость роста которой равна Фи, золотой пропорции. И опять мы пришли к золотому числу.
Слайд 19 На слайде представлен вид сверху на школу им. Хайнца Галински. Идея навеяна расположением лепестков. В то время как архитектор подражает природе, расположение лепестков тесно связано с числом Фи.
Слайд 20 Золотое сечение в дизайне. Логотип Toyota использует соотношение a и b, формируя сетку, в которой образуются три кольца. Обратите внимание, как этот логотип использует прямоугольники вместо кругов для создания золотого сечения. Компания Apple видимо использовала золотую спираль, ведь она так отлично вписывается в логотип компании.
Слайд 21 Золотое сечение в природе. Рассмотрим листья шершавого вяза и фигового дерева. Они имеют форму в соответствии с золотой пропорцией.
Слайд 22 Рассмотрим обычное куриное яйцо. В его изображение отлично вписывается золотая (логарифмическая спираль)
Слайд 23 А задумывались ли вы о пропорциях ящерицы? В ящерице с первого взглядя улавливается приятная для нашего глаза пропорция. Длина ее хвоста так относится к длине остального тела как 62:38. Разделим 62 на 38 получим 1,631… что близко к числу Фи.
Слайд 24 Мир золотого сечения глубок и сложен, мы лишь едва коснулись его. Роль Фи вовсе не ограничивается тем, что мы видели. Но самое интересное заключается в том, что это древнее и прославленное число, появившееся в математике более 20 веков назад, до сих пор встречается в новых областях современной науки. «Божественное» число вовсе не является отслужившей своей игрушкой, оно и сегодня продолжает играть важную роль.
Слайд 25 На слайде список использованной литературы и источников в сети Интернет. Спасибо за внимание.
Золотое сечение вокруг нас | Проекты
Содержание исследовательской работы:
- ВВЕДЕНИЕ.
- Актуальность
- История золотого сечения
- Ряд Фибоначчи и золотое сечение
- Тело человека и золотое сечение
- Золотое сечение в природе
- Платоновы тела
- Мажорное и минорное золото
- Золотое сечение в скульптуре и живописи
- Золотое сечение в фотографии
- Золотое сечение в современной науке
- Золотое сечение в архитектуре
- Золотое сечение в архитектуре г. Волгограда
- Заключение
ВВЕДЕНИЕ.
Актуальность
В современной науке и различных видах искусства используется принцип «золотого сечения». Вся Вселенная построена по одному принципу. Однако в науке он не нашёл практической ценности. Возникает проблема определения смысла пропорциональности в науке
Золотое сечение (гармоническое деление, деление в крайнем и среднем отношении) — деление отрезка на две части таким образом, что большая его часть является средней пропорциональной между всем отрезком и меньшей его частью.
Принципы «золотого сечения» используются в математике, физике, биологии, астрономии и др. науках, в архитектуре и др. искусствах. Они лежат в основе архитектурных пропорций многих замечательных произведений мирового зодчества, главным образом античности и Возрождения.
«В геометрии существует два сокровища — теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем». Эти слова сказал четыре столетия назад немецкий астроном и математик Иоганн Кеплер, они являются эпиграфом практически ко всем трудам, посвященным «золотому сечению». Гениальный ученый поставил пропорцию «золотого сечения» на один уровень с самой знаменитой геометрической теоремой.
Однако «золотому сечению» повезло меньше, чем теореме Пифагора — «классическая» наука и педагогика его игнорируют, а «официальная» математика не признаёт.
Цель данной работы провести краткий обзор истории и математической сущности золотого сечения, и попытаться осмыслить его роль в современной математике.
- Познание математических закономерностей в мире, определение значения математики в мировой культуре и дополнение системы знаний представлениями о «Золотом Сечении» как гармонии окружающего мира.
- Формирование навыков самостоятельной исследовательской деятельности.
- Формирование навыков решения ключевой проблемы в процессе сотрудничества и создания продукта, полезного обществу.
- Обучение работе с информацией и медиасредствами для расширения кругозора и развития творческих способностей.
Проблема
определение смысла пропорциональности в науке
Объект исследования:
применение пропорциональности в искусстве и научной деятельности.
Предмет исследования
«золотое сечение» как один из видов пропорциональности
Цель исследования:
Выявить принципы применения «золотого сечения» в искусстве и различных областях науки.
Гипотеза исследования заключается в том, что «золотое сечение» вокруг нас повсеместно.
Новизна результатов исследования
Состоит в том, что были выявлены способы применения «золотого сечения» в различных сферах нашей жизни и научной деятельности.
Практическая ценность работы состоит в выявлении способов применения «золотого сечения» в окружающем мире.
- История золотого сечения
В математике принцип «золотого сечения» впервые был сформулирован в «Началах» Эвклида, самом известном математическом сочинении античной науки, написанном в III веке до н.э. Переводчик Дж. Kампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
Если упростить задачу Эвклида, то отрезок линии АВ будет считаться разделенным точкой С (которая ближе к точке А) в «золотой пропорции», если отношение большей части СВ к меньшей АВ равно отношению всего отрезка АВ к большей части СВ, т.е. СВ:АС=АВ:СВ. Результатом решения этой задачи является иррациональное число, приблизительно равняющееся 1,618, которое и называют золотым сечением, золотым числом или золотой пропорцией.
После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.
В целом все первые геометрические системы — эвклидова геометрия, теорема Пифагора — свидетельствуют о том, насколько волновали древних греков проблемы гармонии, поиск идеальных пропорций и форм. Однако есть предположение, что первыми к принципу золотого сечения пришли все же египтяне. Наиболее известная пирамида Хеопса построена с использованием т.н. золотого треугольника, в котором соотношение гипотенузы к меньшему катету равно золотому сечению. Храмы, барельефы, предметы быта и украшения из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого сечения.
Эстетическим каноном древнегреческой культуры этот принцип стал благодаря Пифагору, который изучал в стране пирамид тайные науки египетских жрецов. Их результат воплощен в фасаде древнегреческого храма Парфенона, где присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления. Также с использованием золотого сечения созданы Афродита Праксителя и театр Диониса в Афинах.
Платон (427-347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
Во времена средневекового Ренессанса гениальный итальянский математик Лука Пачоли написал первую книгу о золотом сечении, назвав ее «Божественной пропорцией». По его мнению, даже Бог использовал принцип золотого сечения для создания Вселенной. Эта идея была позже использована Кеплером, последняя книга которого так и называлась — «Гармония Вселенной». Пачоли считают творцом начертательной геометрии.
В то же самое время Леонардо да Винчи, другом которого был Пачоли, использовал для композиционного построения своей знаменитой Джоконды т.н. «золотой равнобедренный треугольник», в котором отношение бедра к основе равно золотому сечению.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название «золотое сечение». Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил «золотому сечению». Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т.д. Известен пропорциональный циркуль Дюрера.
Систематизировать знания по золотому сечению и придать им четкую арифметическую форму фундаментальной пропорции мироздания удалось уже только в наше время. Большая роль в исследовании золотого сечения принадлежит украинскому учёному Алексею Стахову, в 80-х годах прошлого века обосновавшему базис нового учения о гармонии систем, должного стать, по его мнению, основной интегрирующей наукой XXI века. Книги винницкого ученого «Введение к алгоритмической теории измерения», «Коды золотой пропорции», «Компьютерная арифметика на числах Фибоначчи и золотом сечении», «Новый тип элементарной математики и компьютерной науки на основе золотого сечения» изданы за рубежом и не остались без внимания западных производителей информационных и компьютерных технологий. Канадский университет Торонто признал автора «мыслителем XXI века». Весной 2003 г. российский физик-теоретик Юрий Владимиров открыл принцип золотого сечения в структуре атома. Ощутимый прорыв в современных представлениях о природе формообразования биологических объектов сделал в начале 90-х годов украинский ученый Олег Боднар, создавший новую геометрическую теорию филлотаксиса.
Ряд Фибоначчи и золотое сечение
Существует математическая прогрессия, известная как ряд Фибоначчи, и она имеет особое отношение к числу фи и пирамидам в Гизе. Принципы этого ряда впервые изложил средневековый математик Леонардо Фибоначчи. Этот ряд использовали для описания роста растений. Вот эта последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее. Для того, чтобы получить каждое следующее число в этом ряду, надо сложить два предыдущих: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и так далее.
У этой последовательности очень интересное соотношение с числом фи: если разделить каждый член этого ряда на предыдущий, полученные результаты будут стремиться к трансцендентному числу 1,6180339+. (Я не заставлю вас проводить эти расчеты. Просто смотрите…)
1/1=1, 2/1=2, 3/2=1.5, 5/3=1.66, 13/8=1.625, 21/13=1.615, 34/21=1.619, 55/34=1.617, 89/55=1.6181, Чем дальше вы будете продолжать считать, тем ближе будете подходить к числу фи. Конечно, вы никогда не дойдете до него, потому что у него нет арифметического решения, но вы будете бесконечно приближаться к нему. Эту последовательность можно изобразить графически, в виде так называемой спирали Фибоначчи.
Эта спираль почти идентична логарифмической спирали фи, известной как спираль золотого сечения. Разница заключается в том, что спираль Фибоначчи – это интерпретация (при помощи целых чисел) арифметически невозможной спирали золотого сечения, у которой нет ни конца, ни начала. У спирали Фибоначчи есть определенное начало.
Тело человека и золотое сечение
Все кости человека выдержаны в пропорции золотого сечения.
Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными.
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.
Расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618
Расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618
Расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618
Расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618
Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.
Расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618
Расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618
Высота лица / ширина лица
Центральная точка соединения губ до основания носа / длина носа.
Высота лица / расстояние от кончика подбородка до центральной точки соединения губ
Ширина рта / ширина носа
Ширина носа / расстояние между ноздрями
Расстояние между зрачками / расстояние между бровями
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения.
Каждый палец нашей руки состоит из трех фаланг.Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).
Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения
У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.
Также следует отметить тот факт, что у большинства людей расстояние между концами расставленных рук равно росту.
Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.
Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях.
Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.
Во внутреннем ухе человека имеется орган Cochlea («Улитка»), который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и также сотворена в форме улитки, содержащую в себе стабильную логарифмическую форму спирали = 73? 43’.
Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке сердца в момент его сжатия (систолы). В артериях во время систолы желудочков сердца кровяное давление достигает максимальной величины, равной 115-125 мм ртутного столбца у молодого, здорового человека. В момент расслабления сердечной мышцы (диастола) давление уменьшается до 70-80 мм рт.ст. Отношение максимального (систолического) к минимальному (диастолическому) давлению равно в среднем 1,6, то есть близко к золотой пропорции.
Если взять за единицу среднее давление крови в аорте, то систолическое давление крови в аорте составляет 0,382, а диастолическое — 0,618, то есть их отношение соответствует золотой пропорции. Это означает, что работа сердца в отношении временных циклов и изменения давления крови оптимизированы по одному и тому же принципу — закону золотой пропорции.
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.
Золотое сечение в природе
Изучая конструкции раковин, ученые обратили внимание на целесообразность форм и поверхностей раковин: внутренняя поверхность гладкая, наружная — рифленая. Внутри покоится тело моллюска — внутренняя поверхность должна быть гладкой. Наружные ребра увеличивают жесткость раковины и, таким образом, повышают ее прочность. Форма раковин поражает своим совершенством и экономичностью средств, затраченных на ее создание. Идея спирали в раковинах выражена не приближенно, а в совершенной геометрической форме, в удивительно красивой, «отточенной» конструкции
У большинства улиток, которые обладают раковинами, раковина растет в форме логарифмической спирали, которая точно соответствуют «золотой пропорции»
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.
Это цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции.
Большой интерес представляет исследование форм птичьих яиц. Их всевозможные формы колеблются между двумя крайними типами: один из них может быть вписан в прямоугольник золотого сечения, другой — в прямоугольник с модулем 1,272 (корень золотой пропорции)
Такие формы птичьих яиц не являются случайными, поскольку в настоящее время установлено, что форме яиц, описываемых отношением золотого сечения, отвечают более высокие прочностные характеристики оболочки яйца.
Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.
Спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестков роз и т.д.
В живой природе широко распространены формы, основанные на «пентагональной» симметрии (морские звезды, морские ежи, цветы). Пяти-лепестковыми являются
Цветы кувшинки, шиповника, боярышника, гвоздики, груши, черемухи, яблони, земляники и многих других.
Справа показано цветок китайской розы с ярко выраженной «пентагональной» симметрией
Также можно встретить золотую пропорцию в разрезе яблока (пентаграмма).
Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).
Так вот 21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.
Очень совершенна форма стрекозы, которая создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
Многие насекомые (например, бабочки, стрекозы) в горизонтальном разрезе имеют простые асимметричные формы, основанные на золотом сечении.
Паук плетет паутину спиралеобразно
Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом.
Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору.
Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.
Оказывается, что расположение листьев на стеблях также носит строгий математический характер и это явление называется в ботанике «филлотаксисом».
Суть филлотаксиса состоит в винтовом расположении листьев на стебле растений (ветвей на деревьях, лепестков в соцветьях и т.д.).
В явлении филлотаксиса используются более сложные понятия симметрии, в частности понятие «винтовая ось симметрии». Рассмотрим, например, расположение листьев на стебле растения ( слева). Мы видим, что листья находятся на различных высотах стебля вдоль винтовой линии, обвивающейся вокруг его поверхности. Для того чтобы перейти от нижележащего листа к следующему, приходится мысленно повернуть лист на некоторый угол вокруг вертикальной оси стебля, а затем поднять его на определенный отрезок вверх. В этом и состоит суть «винтовой симметрии
А теперь рассмотрим характерные „винтовые оси“, которые возникают на стеблях растений (Рис слева). На Рисунке изображен стебель растения с винтовой осью симметрии третьего порядка. Проследим линию листорасположения на этом рисунке. Для того, чтобы перейти от листа 1 к листу 2, следует повернуть первый вокруг оси стебля на 120° против часовой стрелки (если смотреть снизу) и затем передвинуть листок 1 вдоль стебля по вертикали до тех пор, пока он не совместится с листком 2. Повторяя подобную операцию, перейдем от листа 2 к листу 3, а затем к листу 4. Обратим внимание на то, что листок 4 лежит над листком 1 (как бы повторяет его, но этажом выше) и что, идя от листа 1 к листу 4, мы трижды совершили поворот на угол 120°, т.е. осуществили полный оборот вокруг оси стебля (120° х 3 = 360°).
Угол поворота винтовой оси у ботаников называется „углом расхождения листьев“. Вертикальная прямая, соединяющая два листа, расположенные друг над другом на стебле, именуется „ортостихой“. Отрезок 1-4 ортостихи соответствует полной трансляции винтовой оси. Число оборотов вокруг оси стебля для перехода от нижнего листа к вышележащему, расположенному в точности над нижним (по ортостихе), может равняться не только единице, но и двум, трем и т.д. Это число оборотов называется „листовым циклом“. В ботанике принято характеризовать винтовое листорасположение с помощью дроби, числителем которой является число оборотов в листовом цикле, а знаменателем — число листьев в этом цикле. В рассмотренном нами случае мы имеем винтовую ось типа 1/3.
Заметим, что существуют и более замысловатые оси, например, типа 3/8, 5/13 и т.д.
Какими могут быть числа a и b, характеризующие винтовую ось типа a/b. Дробь 1/2 свойственна злакам, березе, винограду; 1/3 — осоке, тюльпану, ольхе; 2/5 — груше, смородине, сливе; 3/8 — капусте, редьке, льну; 5/13 — ели, жасмину и т.д.
Ботаники утверждают, что дроби, характеризующие винтовые оси растений, образуют строгую математическую последовательность, состоящую из отношений соседних чисел Фибоначчи, то есть:
1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34,…
Вспомним, что ряд Фибоначчи есть следующая последовательность чисел:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
Какова же „физическая“ причина, лежащая в основе „законов филлотаксиса“?
Ответ очень прост. Оказывается, что именно при таком расположении листьев достигается максимум притока солнечной энергии к растению.
Практически все соцветья и плотно упакованные ботанические структуры (сосновые и кедровые шишки, ананасы, кактусы, головки подсолнечников и многие другие) также строго следуют числам Фибоначчи (Семечки в головке подсолнуха располагаются по спиралям, при этом отношение числа левых и правых спиралей равно отношению соседних чисел Фибоначчи).
В биологическом и растительном мире вступает в действие принцип экономии материи, который не действует в неорганическом мире.
Ярким примером этому служит стремление живых организмов к экономии костной субстанции при распределении материи, дающее максимум прочности во всех нужных направлениях.
Кроме этого, живые организмы проявляют лишь одним им свойственный феномен — феномен роста. Неорганические кристаллы увеличиваются путем присоединения идентичных элементов; живой организм растет путем „всасывания“, идущего изнутри и направляющегося наружу.
Отвечая на вопрос: „Где граница между живой и мертвой природой?“ многие известные специалисты в области симметрии и кристаллографии обращают внимание на то, что это различие состоит в использовании в живых организмах так называемой „пятерной“ или „пентагональной“ симметрией, связанной с золотым сечением.
ПЛАТОНОВЫ ТЕЛА
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники приписывают честь их открытия Пифагору В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику.
Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал.
В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками.
МАЖОРНОЕ И МИНОРНОЕ ЗОЛОТО
Известно, что построить пропорцию золотого сечения можно с помощью линейки и циркуля. Разделим квадрат по горизонтали пополам. Проведем диагональ полуквадрата и, приняв ее за радиус, перенесем на вертикаль. Полученный прямоугольник будет прямоугольником золотого сечения
В прямоугольнике со сторонами 1 и 2 (его называют или полуквадратом, или двойным квадратом) диагональ равна √5. Если к этой величине прибавить единицу и полученный отрезок разделить пополам, то мы получим мажорное золото. Если же единицу отнять и остаток разделить на два, то золото будет минорным.
При этом надо помнить, что: Части относятся друг к другу по удвоенному минорному золоту, когда они получены путем разделения целого на √5.
Золотое сечение в искусстве
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.
Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину «Джоконда». Портрет Моны Лизы (Джоконда) привлекает тем, что композиция рисунка построена на „золотых треугольниках“, точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника. Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами золотого треугольника делят их в пропорции Золотого сечения.
Таким образом, Леонардо Да Винчи использовал в своей картине не только принцип симметрии, но и Золотое сечение Пропорции Золотого сечения в произведении Леонардо Да Винчи — «Тайной вечере» Соответствующие прямоугольники в картине — »золотые».Было так же определено, что больше всего внимания смотря на прямоугольный рисунок придается центральной части, образованной точками которые делят этот рисунок в золотой пропорции.
Одним из высших достижений классического греческого искусства может служить статуя Дорифора, изваянная Поликтетом в V веке до н.э. Эта статуя считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с Золотым сечение. М=0,618…Венера Милосская, статуя богини Афродиты и эталон женской красоты, является одним из лучших памятников греческого скульптурного искусства — также построена на пропорциях золотого сечения
Золотое сечение в фотографии
Золотое сечение является основой в построении геометрических пропорций гармоничных изображений, чертежей, написании картин, архитектуре и фотографии. Теоретическое и практическое знание правил золотого сечения, и использование его даёт преимущество фотографу, так как правильно построенное (скомпонованное) изображение более естественно и понятно. Впервые упоминание деления отрезка в крайнем и среднем отношении встречается в «Началах Евклида» (ок. 300 лет до н. э.), и использовалось в построении правильного пятиугольника. Леонардо да Винчи так же использовал золотое сечение в чертежах своих работ и набросках для будущих картин, а его современник Лука Пачоли называл это отношение «божественной пропорцией». Правила золотого сечения на столько естественны, что многие историки ищут его проявления во всей древней архитектуре и художественных произведениях, но есть мнение, что значимость золотого сечения в искусстве преувеличено. При этом, руководствуясь именно пропорциями (отношениями) размеров золотого сечения известные художники выбирали холсты для написания своих работ.
Золотое сечение – это деление отрезка AC на две части таким образом, что большая его часть AB относится к меньшей BC так, как весь отрезок AC относится к AB (т.е. AB:BC = AC:AB). Это отношение равно 5:8 и близко к стандарту кадра (24х36 мм = 5:7,5 = 2:3).
Золотое сечение в фотографии имеет свои правила, которые заключаются в использовании центральных точек пересечения прямых, воображаемые прямые делят фотографию на три горизонтальные и вертикальные части. Как оказалось, математические правила могут быть применимы к таким субъективным и творческим материям как фотография. И это хорошо работает, если соблюдать правила золотого сечения, фотографии получатся более гармоничными. Нужно лиши помнить о золотом сечении во время фотосъёмки, взять эти правила за основу фотографии и постоянно тренировать свой вкус. Но если во время съёмки не удалось добиться оптимального результата, можнокадрировать изображение по сетке золотого сечения. В качестве примера возьму не совсем удачную фотографию в композиционном плане. Котэ слишком быстро двигался и особо не хотел позировать, так что о правилах золотого сечения некогда было думать, именно по этому кадр получился таким скомканным.
Золотое сечение в современной науке
В каждой науке есть т.н. «метафизические» знания, без которых невозможно существование самой науки. Например, если исключить из математики понятия натурального и иррационального чисел или аксиомы геометрии, математика сразу же перестанет существовать. С таким же правом к разряду «метафизических» знаний может быть отнесено и «золотое сечение», которое считалось «каноном» античной культуры, а затем и эпохи Возрождения. Однако, как это ни парадоксально, в современной теоретической физике и математике «золотая пропорция» никак не отражена. Ныне делаются попытки показать, что «золотое сечение» является одной из важнейших «метафизических» идей, без которой трудно представить дальнейшее развитие науки, в частности, теоретической физики и математики.Анализ современных программ образования в таких странах, как США, Канада, Россия и Украина, показывает, что в большинстве из них нет даже упоминания о «золотом сечении». То есть, имеет место сознательное игнорирование одного из важнейших открытий античной математики. Возможно, причину следует искать в негативном отношении современной «материалистической» науки и «материалистического» образования к астрологии и так называемым «эзотерическим» наукам. В них «золотое сечение» и связанные с ним геометрические фигуры – «пентаграмма», «Платоновы тела», «куб Метатрона» – широко используются в качестве основных «сакральных» символов. И «материалистическое» образование не нашло ничего более разумного, как выбросить золотое сечение на свалку «сомнительных научных концепций» вместе с астрологией и «эзотерическими» науками. В результат большинство т.н. «образованных» людей хорошо знают «теорему Пифагора», но имеют весьма смутное представление о «золотом сечении».В настоящее время исследуются математические теории связанные с принципами «золотого сечения»: новая теория гиперболических функций, новая теория чисел, новая теория измерения, теория матриц Фибоначчи и так называемых «золотых» матриц, новые компьютерные арифметики, новая теорию кодирования и новая теория криптографии. Суть новой науки, в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора, что, естественно, повлечет в теории новые и наверняка очень интересные математические результаты. В практическом отношении – «золотую» компьютеризацию. А поскольку «математика гармонии» существенно дополнит классическую математику, вполне возможно придется пересмотреть и всю систему современного математического образования.
Золотое сечение в архитектуре
В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.
Другим примером из архитектуры древности является Пантеон.Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”.Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. 5).
Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.
Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.
При восстановлении здание приобрело более массивные формы. Не сохранилась и внутренняя планировка здания, о которой дают представления только чертеж нижнего этажа.
Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания… К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок”.
Золотое сечение в архитектуре г. Волгограда
С момента приобретения статуса города-героя внешне город сильно изменился. Архитекторы и строители, работающие в городе создают здания, архитектурные ансамбли, которые прекрасно гармонируют с современным дизайном города.
И Именно принцип – параллельное и гармоничное соединение привычных нам образов… — и составляет основу эстетической архитектуры и уникальности нового Волгограда”
Я позволю изложить концепцию столичного градостроительства Волгограда в оригинале, устами автора проекта: “ Эстетическая ценность композиции городского центра зависит от художественных качеств и приёмов размещения архитектурных форм с точки зрения их восприятия в ракурсе человеческих глаз “.
Опорными элементами данного восприятия будут служить четыре объёмно – пространственных композиции: Администрация города, здание Педагогического университета, звезда Вечного огня, здание государственного педуниверситета.
Ещё в эпоху Возрождения художники открыли что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, как формат имеет картина – горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.
Данное открытие у художника того времени получило название «Золотое сечение» картины. Поэтому, для того чтобы привлечь внимание главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров.
Заключение
В заключении можно привести некоторые научные факты которые были открыты благодаря «золотому сечению»
- пояс астероидов между Марсом и Юпитером- по пропорции там должна
находится ещё она планета;
- Возбуждение струны в точке, делящей её в отношении «золотого деления» , не вызовет колебаний струны, то есть это точка компенсации;
- на летательных аппаратах с электромагнитными источниками энергии создают прямоугольные ячейки с пропорцией «золотого сечения»
Проанализировав применение «золотого сечения» в искусстве, а также различные научные открытия о существовании «золотой» пропорции в различных областях нашей жизни можно предположить, что:
- При анализе и возможных численных выводах о чем-либо в живой природе сначала необходимо рассматривать «золотую» пропорцию первоначальных параметров;
- «золотое сечение» является основной пропорциональностью мира.
Список использованной литературы.
- Математический энциклопедический словарь – М.: Советская энциклопедия, 1988.
- Атанасян Л.С. Геометрия 7-9. — М.: «Просвещение», 1992.
- Волошинов В.А. Пифагор. — М.: Просвещение, 1993.
- Воробьев Н.Н. Числа Фибоначчи. — М.: Наука, 1978.
- Васютинский Н. Золотая пропорция. — М.: Молодая гвардия, 1990.
- Ковалев Ф.В. Золотое сечение в живописи – К: Высшая школа, 1989.
- Азевич А.И. Двадцать уроков гармонии: гуманитарно-математический курс. – М.: Школа-пресс, 1998.
- Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
- «Математика. Я познаю мир». – М.: Аванта, 1998
Список ресурсов
http://www.abc-people.com/idea/zolotsech/
http://n-t.ru/tp/iz/zs.htm
http://tmn.fio.ru/works/04x/304/p3_4.htm
http://www.arstudia.ru/kazakov/2.html
http://e-project.redu.ru/mos/images/blds.htm
математических мифов: золотое сечение
Большинство из вас слышали о числе золотого сечения . Он появляется, например, в книге / фильме Код да Винчи , а также во многих статьях, книгах и школьных проектах, целью которых является показать, насколько важна математика в реальном мире. Многие авторы (включая автора Кода да Винчи) описывают его как основу всех прекрасных узоров в природе, и иногда его называют божественной пропорцией .Утверждается, что большая часть произведений искусства и архитектуры содержит особенности в пропорциях, заданных золотым сечением. Например, утверждается, что и Парфенон, и пирамиды находятся в этой пропорции. Также утверждалось, что золотое сечение проявляется в человеческом теле, например, как отношение роста взрослого человека к высоте его пупка или длины предплечья к длине руки.
Тем не менее, за всю мою карьеру применения математики в реальном мире я встречал золотое сечение ровно дважды.Да дважды! Итак, верны ли какие-либо из этих великих заявлений о золотом сечении?
Какое опять золотое сечение?
Начнем с того, что быстро вспомним, что такое золотое сечение. Это было определено древнегреческим математиком Евклидом следующим образом. Представьте, что у вас есть отрезок линии, который вы хотите разделить на две части. Вы хотите разделить его таким образом, чтобы соотношение между целым сегментом и более длинным из двух кусков было таким же, как соотношение между более длинным из двух кусков и более коротким.Каким должно быть это соотношение?

Мы хотели бы выбрать A и B так, чтобы ( A + B ) / A = A / B .
Немного математики (см. Здесь) покажет, что соотношение должно быть
![\[ \phi = \frac{1+\sqrt {5}}{2}\approx 1.618. \]](/800/600/https/plus.maths.org/MI/bec836b6d6beb601263198e8affc4444/images/img-0001.png) |
Тот факт, что  определяется как соотношение между двумя длинами, означает, что вы можете искать его всякий раз, когда смотрите на что-то, на котором есть сегменты линий — будь то лицо или здание.
определяется как соотношение между двумя длинами, означает, что вы можете искать его всякий раз, когда смотрите на что-то, на котором есть сегменты линий — будь то лицо или здание.
Золотое сечение в человеческом теле
Предполагается, что золотое сечение лежит в основе многих пропорций человеческого тела. К ним относятся форма идеального лица, а также отношение высоты пупка к высоте тела. Действительно, утверждается, что почти каждая пропорция идеального человеческого лица связана с золотым сечением (см. Эту статью, чтобы узнать больше о таких утверждениях).
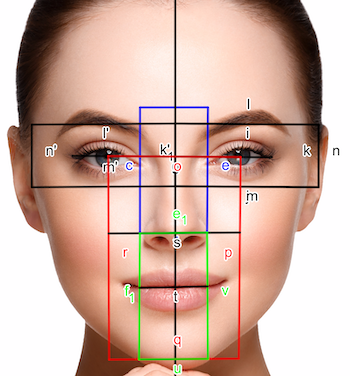
Вы можете наложить всевозможные прямоугольники на красивое лицо, а затем заявить, что красота проистекает из пропорций прямоугольника.
Однако все это неправда, даже отдаленно. У тела есть много возможных соотношений, многие из которых лежат где-то между 1 и 2. Если вы рассмотрите их достаточно, то обязательно получите числа, близкие к значению золотого сечения (около 1,618). Это особенно верно, если объекты, которые вы измеряете, не очень четко определены (как на рисунке слева), и можно изменить определение таким образом, чтобы получить пропорции, которые вы хотите найти.
Если вы присмотритесь, вы также обнаружите, что пропорции человеческого тела близки к 1,6, 5/3, 3/2, квадратному корню из 2, 42/26 и т. Д. И т. Д. В действительности большинство чисел от 1 до 2 будут иметь две части тела, приближающие их в соотношении. Подобные ложные закономерности также наблюдаются в солнечной системе (которая также имеет множество различных соотношений, из которых вы можете выбирать). Также помните, что поскольку золотое сечение — это иррациональное число (см. Ниже), вы никогда не увидите его точно ни при каких измерениях.
Все это пример того, как человеческий мозг находит ложные корреляции. Действительно, при наличии достаточного количества данных можно найти закономерности, согласующиеся практически с любой гипотезой. Хороший способ убедиться в этом — выйти в ясный солнечный день на улицу и посмотреть на облака. Рано или поздно вы найдете облако, которое соответствует какому-то новому образцу. В качестве примера посмотрите эту статью BBC News, в которой рассказывается о «королеве-воине», наблюдаемой в облачной структуре.
Это явление на самом деле может быть довольно опасным, когда в данных обнаруживаются ложные корреляции, подтверждающие точку зрения.Например, они могут привести к ложным обвинениям и даже к ложным обвинениям. Много примеров ложных корреляций можно найти на этом сайте.
Спирали золотые и прочие
Если взять линию, разделенную на два сегмента 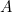 и
и 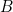 , так что
, так что 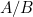 является золотым сечением, а затем сформировать прямоугольник со сторонами
является золотым сечением, а затем сформировать прямоугольник со сторонами 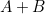 и
и 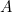 , то этот прямоугольник называется золотым прямоугольником .
, то этот прямоугольник называется золотым прямоугольником .
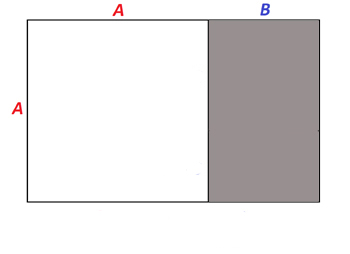
Золотой прямоугольник состоит из квадрата (белого) и меньшего прямоугольника (серого).Меньший прямоугольник также является золотым.
Золотой прямоугольник, который мы только что сформировали, состоит из квадрата и меньшего прямоугольника, который сам по себе является золотым прямоугольником (см. Здесь, чтобы узнать больше). Этот золотой прямоугольник снова состоит из квадрата и меньшего прямоугольника, который сам по себе является золотым прямоугольником. И так далее.
Используя последовательность все меньших и меньших золотых прямоугольников, мы можем сформировать нечто похожее на спираль. Просто нарисуйте четверть круга в каждом квадрате, который появляется в золотых прямоугольниках.
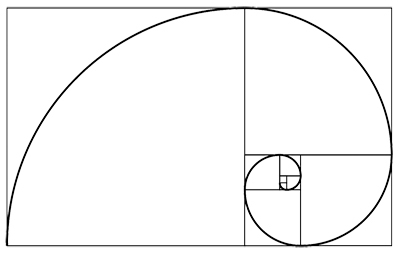
Спиральная форма, построенная из золотого прямоугольника.
Часто утверждают, что эту спиралевидную форму можно найти во многих местах в природе и искусстве. Например, по форме раковины наутилуса, по форме галактики, по форме урагана или даже волны.
Здесь две проблемы. Во-первых, это не спираль. Это последовательность дуг окружности. При переходе от одной дуги к другой кривизна спирали скачет. Вряд ли в каком-либо природном явлении мы увидим такие скачки.Фактически, форма — это только приближение к истинной спирали. Форма спирали, которую он аппроксимирует, является примером логарифмической спирали . Такие спирали очень распространены в природе. У них есть полярное уравнение
![\[ r =a e^{b\theta }, \]](/800/600/https/plus.maths.org/MI/ab5c7eed4c794ae3d2257d88acab2fe7/images/img-0001.png) |
 — основание натурального логарифма. В природе мы видим такие спирали везде, с разными значениями
— основание натурального логарифма. В природе мы видим такие спирали везде, с разными значениями  и
и 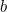 в зависимости от контекста.Причина, по которой эти спирали настолько распространены, заключается в том, что они обладают свойством самоподобия . Это означает, что если вы повернете спираль на любой фиксированный угол, вы получите спираль, которая является масштабированием оригинала.
в зависимости от контекста.Причина, по которой эти спирали настолько распространены, заключается в том, что они обладают свойством самоподобия . Это означает, что если вы повернете спираль на любой фиксированный угол, вы получите спираль, которая является масштабированием оригинала. Так называемая золотая спираль имеет частное значение 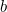 ,
,
![\[ b=\frac{\ln {\phi }}{(\pi /2)}=0.3063489... \]](/800/600/https/plus.maths.org/MI/9cf89760c1bbf8c13c7dea9304ac15c2/images/img-0001.png) |
, где 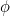 — золотое сечение (а углы измеряются в радианах).
— золотое сечение (а углы измеряются в радианах).
Нет никаких причин, по которым этот номер является каким-либо особенным. Оболочка наутилуса представляет собой логарифмическую спираль, потому что свойство самоподобия позволяет оболочке расти без изменения формы. Значения 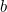 , наблюдаемые для раковины наутилуса, не имеют никакого отношения к приведенному выше значению, при этом значение
, наблюдаемые для раковины наутилуса, не имеют никакого отношения к приведенному выше значению, при этом значение 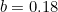 наиболее часто встречается в реальных раковинах.
наиболее часто встречается в реальных раковинах.
Искусство и архитектура
Здесь надо быть осторожными. Несомненно, некоторые художники, такие как Ле Корбюзье (в его системе Модулора), сознательно использовали золотое сечение в своих произведениях искусства.Это потому, что было заявлено, что пропорции золотого прямоугольника особенно приятны для человеческого глаза, и что с эстетической точки зрения мы предпочитаем золотой прямоугольник всем другим прямоугольникам. Таким образом, имеет смысл использовать их в художественных произведениях. Затем утверждается, что золотое сечение можно увидеть практически в любом другом произведении искусства и архитектуры.
Доказательств того, что золотой прямоугольник особенно хорош, довольно мало. Психологические исследования, показывающие разные прямоугольники группам людей, по-видимому, указывают на широкий диапазон предпочтений, причем отношение квадратного корня из двух к одному часто оказывается предпочтительнее других.Проверьте себя на прямоугольниках ниже, чтобы выбрать, какой из них вам больше нравится.

Согласно книге Кейта Девлина Взгляд Девлина: миф, который не исчезнет , идея о том, что золотое сечение вообще имеет какое-либо отношение к эстетике, исходит в основном от двух людей, один из которых был неправильно процитирован, а другой прибегнул к изобретение. Неправильно процитированным автором был Лука Пачоли, который написал книгу под названием De Divina Proportione еще в 1509 году. Книга была названа в честь золотого сечения, но не выступала в поддержку теории эстетики, основанной на золотом сечении, или о том, что она должна применяться к искусству и архитектуре.Такой взгляд был ошибочно приписан Пачоли в 1799 году.
Пачоли был близким другом Леонардо да Винчи, и часто утверждают, что Леонардо сам использовал золотое сечение в своих картинах. Прямых доказательств этому нет. Возможно, самым известным из этих примеров является витрувианский человек . Однако пропорции на этой картине не соответствуют золотому сечению. Действительно, Леонардо упоминал в своих работах только отношения целых чисел. Предполагаемые примеры золотого сечения, появляющиеся на его картинах, относятся к тому же классу, что и те, которые находят это соотношение в природе.
Девлин приписывает «популяризацию» золотого сечения Адольфу Цайзингу, немецкому психологу 19-го века, который утверждал, что золотое сечение было универсальным законом, описывающим «красоту и завершенность в сферах как природы, так и искусства […], которые пронизывает как высший духовный идеал все структуры, формы и пропорции, космические или индивидуальные, органические или неорганические, акустические или оптические ». Это был просто пример (как указано выше) выявления ложных паттернов. Однако работы Цейзинга повлияли на многих других и заложили основы для большей части современного мифа.

Так называемая золотая спираль, наложенная на Парфенон. Нет никаких доказательств того, что золотое сечение сыграло роль в дизайне этого здания. Основное изображение Парфенона: Ойвинд Солстад, CC BY 2.0.
Еще одним примером этого мифа является утверждение, что золотое сечение проявляется в пропорциях Парфенона, части Акрополя в Афинах.
Нет никаких свидетельств этого в греческой науке, и идея о том, что Парфенон имеет пропорции, определяемые золотым сечением, восходит только к 1850-м годам.Более того, фактические размеры Парфенона не дают пропорций, особенно близких к золотому сечению, если вы не будете осторожны с выбором прямоугольников. Фактически, Парфенон обретает свой гармоничный вид благодаря продуманному расположению линий, которые выглядят параллельными, но на самом деле сходятся или изгибаются, поэтому практически невозможно проводить измерения с достаточной точностью, чтобы получить точные соотношения. Поскольку пропорции Парфенона меняются в зависимости от его высоты, просто невозможно найти общую пропорцию, соответствующую золотому сечению.
То же самое относится и к остальной греческой архитектуре: нет никаких доказательств того, что греки считали золотое сечение эстетически приятным или вообще использовали его в своем искусстве и архитектуре.
Это касается и музыки. Утверждается, что золотое сечение играет важную роль в музыкальной композиции. Об этом мало свидетельств. Однако в композиции важна гамма, а гамма очень тесно связана с корнем двенадцатой степени из 2. Именно это последнее число лежит в основе музыки, а не золотое сечение [ссылка].
В этих упорных мифах о золотом сечении есть реальная опасность. Школьников и многих других обманывают, вводя в заблуждение ложную реальность о том, как работает математика. Рано или поздно они обнаружат, что эта реальность неверна, и потеряют веру в вполне реальную способность математики объяснять мир.
Великая реальность
Относясь к золотому сечению довольно пренебрежительно, я хотел бы завершить этот раздел, подчеркнув, насколько удивительным является золотое сечение — ему действительно не нужны все эти ложные утверждения, чтобы сделать его особенным.
Сначала обратимся к явлениям природы, которые действительно связаны с золотым сечением. Золотое сечение тесно связано со знаменитой последовательностью Фибоначчи
![\[ 1,1,2,3,5,8,13,21,... \]](/800/600/https/plus.maths.org/MI/bfa464bc3f1681e856b96d3b13a0cc3b/images/img-0001.png) |
Подробнее об этой ссылке можно узнать здесь. Последовательность Фибоначчи, безусловно, появляется в природе, поскольку она связана как с тем, как растет население, так и со способом сочетания форм.Например, последовательность можно увидеть в спиралях на подсолнечных цветках, которые должны соответствовать друг другу упорядоченным образом, и в листьях некоторых растений, которые необходимо расположить так, чтобы улавливать больше солнечного света. В результате можно наблюдать соотношения, близкие к золотому сечению, возникающие в определенных природных явлениях (подробнее здесь).
Эти явления включают распространение трутней среди самок пчел в улье, что связано с тем, как пчелы размножаются на протяжении многих поколений (подробнее см. Здесь).Итак, действительно возможно увидеть золотое сечение в саду, и для этого есть очень веские математические причины.

Фибоначчи подумал о своей последовательности, рассматривая рост популяции идеализированных кроликов. См. Эту статью, чтобы узнать больше.
Но, возможно, еще более интересны многие увлекательные математические свойства золотого сечения. Они рассматриваются в различных статьях Plus , но я хотел бы указать на одну, которая особенно интересна и которая действительно отличает золотое сечение от других чисел: его крайняя иррациональность.
Иррациональные числа — это числа, которые не могут быть представлены дробями, и которые имеют бесконечное десятичное расширение, которое не заканчивается повторяющимся блоком. Именно это означает, что иррациональные числа трудно наблюдать в природе. Золотое сечение обладает удивительным свойством быть самым иррациональным числом из всех. Это означает, что это не только невозможно точно представить в виде дроби, но и невозможно легко аппроксимировать дробью. См. Эту статью для математических подробностей.
Сложность аппроксимации золотого сечения дробью делает его очень полезным числом для математиков и ученых, изучающих процесс синхронизации . Это происходит, когда система с собственной частотой форсируется одной из другой частоты и принимает частоту форсирования. Одним из примеров является синхронизация человеческого тела с дневной частотой солнечного света. Второй пример — климат Земли, который синхронизируется с естественными циклами обращения вокруг Солнца.
Однако синхронизация сама по себе может быть проблемой, приводящей к нежелательным резонансам в системе (например, висячий мост сильно вибрирует, если по нему проходит марширующий оркестр). Выбирая две частоты в соотношении 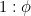 , мы можем избежать синхронизации из-за крайней иррациональности золотого сечения. Это очень полезное свойство, по-видимому, используется мозгом и насекомыми, а также учеными-климатологами и даже людьми, производящими самолеты.
, мы можем избежать синхронизации из-за крайней иррациональности золотого сечения. Это очень полезное свойство, по-видимому, используется мозгом и насекомыми, а также учеными-климатологами и даже людьми, производящими самолеты.
Итак, золотое сечение играет главную роль, но не ту, о которой вы часто читаете в связанной с ним мифологии.Какая жалость! Это прекрасный парадокс, но самое интересное в золотом сечении заключается в том, что это не соотношение.
Об авторе
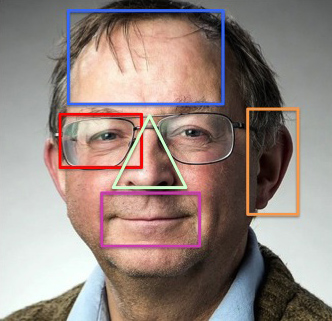
Крис Бадд.
Эта статья основана на выступлении Бадда в продолжающемся Gresham Серия лекций колледжа (см. Видео выше). Вы можете увидеть другие статьи по итогам беседы здесь.
Крис Бадд OBE — профессор прикладной математики Университета Бата, вице-президент Института математики и ее приложений, заведующий кафедрой математики Королевского института и почетный член Британской научной ассоциации.Он особенно заинтересован в применении математики в реальном мире и продвижении понимания математики в обществе.
Он является соавтором популярной книги по математике Mathematics Galore! , опубликованный издательством Oxford University Press совместно с К. Сангвином, и представлен в книге 50 Visions of Mathematics ed. Сэм Парк.
.Металлические числа: за пределами золотого сечения
Вы слышали о золотом сечении . В фильмах и литературе это изображается как альтернативный ответ жизни, Вселенной и всему остальному. И действительно, это повсюду: от узоров из семечек подсолнечника до раковин аммонитов и, предположительно, «идеального» соотношения для эстетичных лиц и тел. Таким образом, он имеет тенденцию затмевать своего младшего брата, о котором вы, возможно, еще не слышали, — соотношение серебра .
Вспомните золотое сечение
Прежде чем говорить о серебряном сечении, мы напомним, что такое золотое сечение.Перефразируя древнегреческого математика Евклида:
Прямая линия разрезается в соответствии с золотым сечением, когда отношение всей линии к более длинному отрезку такое же, как отношение более длинного отрезка к более короткому отрезку.
Мы видим, как это выглядит на следующей диаграмме:

Здесь отношение длины участка A к длине участка B такое же, как отношение длины всей линии к длине участка A.Это соотношение, называемое золотым сечением и обозначаемое греческой буквой 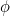 , составляет приблизительно 1,618 числового значения.
, составляет приблизительно 1,618 числового значения.
Мы можем найти это значение, сначала выразив определение Евклида алгебраически:
Умножение последнего выражения на 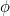 дает нам квадратное уравнение
дает нам квадратное уравнение
![\[ \phi ^2=\phi +1, \]](/800/600/https/plus.maths.org/MI/b58c145cb897e8abcec6b938eaaf67de/images/img-0007.png) |
, который имеет решения
![\[ \phi =\frac{1\pm {\sqrt {5}}}{2}. \]](/800/600/https/plus.maths.org/MI/b58c145cb897e8abcec6b938eaaf67de/images/img-0008.png) |
Поскольку мы имеем дело с положительными длинами, мы игнорируем отрицательное решение, оставляя нам
![\[ \phi =\frac{1+\sqrt {5}}{2}=1.618033... \]](/800/600/https/plus.maths.org/MI/b58c145cb897e8abcec6b938eaaf67de/images/img-0009.png) |
Соотношение серебра
Теперь давайте разрежем линию на три сегмента: два более длинных сегмента равной длины и один меньший сегмент, так чтобы отношение всей линии к одному из более длинных сегментов было таким же, как отношение одного более длинного сегмента к меньшему.Затем эта линия обрезается в соответствии с соотношением серебра, которое мы обозначим греческой буквой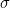 . Числовое значение отношения серебра составляет приблизительно 2,414.
. Числовое значение отношения серебра составляет приблизительно 2,414. 
И снова мы можем вывести это алгебраически:
, дающее квадратное уравнение
![\[ \sigma ^2=2\sigma +1. \]](/800/600/https/plus.maths.org/MI/2fd76bc99b2390409f12b64d1fe95349/images/img-0006.png) |
Имеет положительное решение
![\[ \sigma =\frac{2 +\sqrt {8}}{2}=\frac{2+2\sqrt {2}}{2}=1+\sqrt {2}=2.414213... \]](/800/600/https/plus.maths.org/MI/2fd76bc99b2390409f12b64d1fe95349/images/img-0007.png) |
Напомним, золотое сечение предполагает деление линии на два сегмента, а серебряное сечение предполагает разрезание ее на три сегмента, два из которых имеют одинаковую длину.Это предполагает возможность дальнейшего обобщения …
Познакомьтесь с семьей
Предположим, мы делим нашу линию на 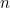 сегментов равной длины, которые мы называем
сегментов равной длины, которые мы называем 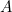 , и один меньший сегмент длиной
, и один меньший сегмент длиной 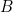 . Если мы требуем, чтобы соотношение между
. Если мы требуем, чтобы соотношение между 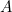 и
и 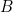 было таким же, как соотношение между всей линией и одним из сегментов длиной
было таким же, как соотношение между всей линией и одним из сегментов длиной 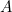 , мы имеем
, мы имеем
![\[ A/B=(nA+B)/A. \]](/800/600/https/plus.maths.org/MI/d75151ea107f242c8c76f47a26ade61b/images/img-0004.png) |
Запись 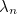 для этого отношения означает, что
для этого отношения означает, что
![\[ \lambda _ n=A/B=n+B/A, \]](/800/600/https/plus.maths.org/MI/d75151ea107f242c8c76f47a26ade61b/images/img-0006.png) |
, поэтому по аналогии с нашими расчетами выше мы имеем
![\[ \lambda _ n=n+1/\lambda _ n, \]](/800/600/https/plus.maths.org/MI/d75151ea107f242c8c76f47a26ade61b/images/img-0007.png) |
, что дает квадратное уравнение
![\[ \lambda _ n^2=n \lambda _ n +1. \]](/800/600/https/plus.maths.org/MI/d75151ea107f242c8c76f47a26ade61b/images/img-0008.png) |
Положительные решения этого уравнения:
![\[ \lambda _ n=\frac{n+\sqrt {n^2+4}}{2}. \]](/800/600/https/plus.maths.org/MI/d75151ea107f242c8c76f47a26ade61b/images/img-0009.png) |
Числа 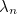 , по одному на каждое значение
, по одному на каждое значение 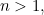 , называются металлическими отношениями или металлическими средствами .Для
, называются металлическими отношениями или металлическими средствами .Для  мы получаем золотое сечение, а для
мы получаем золотое сечение, а для  — серебряное.
— серебряное.
Металлические отношения имеют много общих свойств: они связаны с бесконечными последовательностями, напоминающими знаменитую последовательность Фибоначчи, с очень специальными прямоугольниками и логарифмическими спиралями. Мы рассмотрим их во второй части статьи.
Об авторах
Гокул Раджив и Йонг Чжэн Ю — двое бывших старшеклассников из Сингапура, которым довелось исследовать идею металлических средств в одном проекте, и они нашли его достаточно интересным, чтобы поделиться им.
 .
.Точка золотого сечения Земли
 Есть ли у Земли точка золотого сечения?
Есть ли у Земли точка золотого сечения?
Было заявлено, что золотое сечение Земли находится в Мекке. (См. Заархивированный веб-сайт или видео на Vimeo или YouTube.) Это правда?
Широта
Давайте сначала посмотрим на широты. Phi на 15 мест — 1.6180339887499. Между Северным и Южным полюсами 180 градусов, поэтому 180, деленное на Фи, равно 111,2461179749810. Поскольку широта выражается в градусах и расстоянии от экватора, мы вычитаем 90 градусов и конвертируем их в широту 21 градус, 14 минут и 46.02 секунды, север или юг.
Широта Мекки, согласно Google Earth, составляет 21 градус 25 минут и 38,56 секунды. Таким образом, он находится всего в 10 минутах 52,54 секунды к северу от точной северной широты золотого сечения Земли. Это отклонение составляет менее 1/10 процента, примерно в 12 милях или 20 километрах к северу от точной точки широты золотого сечения.
Долгота
Широта имеет четкую исходную точку отсчета, которая определяется полюсами, определяемыми осью вращения Земли.Выбор исходной точки долготы не так ясен, поскольку нет единой окончательной точки отсчета. Те, кто заявляет, что Мекка является золотым сечением точки долготы Земли, основывают это на проекции Земли Меркатора, на которую наложено золотое сечение с помощью программного обеспечения PhiMatrix, доступного на этом сайте:
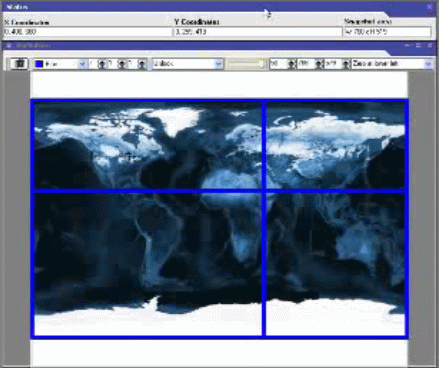


Можно начать с любой долготы, чтобы добраться до любого места, но использование проекции мира — разумный подход.Однако проблема в том, что существуют сотни различных интерпретаций прогнозов мира, которые значительно различаются. Вот пример других, которые дают аналогичные результаты:
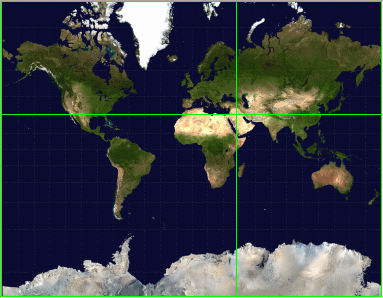
Верхнее изображение — знакомая проекция Меркатора. Нижнее изображение — это проекция Петерса, которая устраняет смещение Меркатора, чтобы выделить Северное полушарие.
Вместо использования изображения, подлежащего интерпретации, для определения золотого сечения широты, возможно, лучше использовать фактические измерения долготы.
Если вы примете предпосылку, что карта мира, разделяющая Восток и Запад, является правильным основанием, наиболее точной начальной точкой отсчета по долготе будет средняя точка между Аляской и Россией под углом 168 градусов, 52 минуты и 42 секунды, найденная на спутнике. фото ниже. Используя это в качестве отправной точки, точка золотого сечения падает на 31 градус, 22 минуты и 16,05 секунды, что в 938 км к западу от Мекки, что, согласно Google Earth, находится на 39 градусах, 48 минутах и 53.42 второй восток. Если мы используем собственный меридиан человечества под углом 180 градусов в качестве точки отсчета, точка золотого сечения находится на 42 градусе, 29 минутах и 32,05 секунды, что в 298 км к востоку от Мекки.
На изображении ниже показана середина между Аляской и Россией.
На изображении ниже показаны полученные точки золотого сечения долготы от средней точки слева, а также от меридиана 180 градусов. Щелкните любое изображение, чтобы увеличить его.
Другой способ приблизиться к этому — начать с долготы Мекки и переместиться по золотому сечению на 360 градусов (222 градуса, 29 минут и 32.05 секунд), чтобы увидеть, где вы приземлитесь. Эта точка находится на 117 градусах, 19 минутах и 21,37 секунды к западу, что внутри границы с Россией, как показано ниже. Нажмите на картинку, чтобы увеличить.
Находится ли Мекка в точке золотого сечения Земли? Ответ подлежит интерпретации. Однако как верующий в Бога автор говорит следующее:
Если Бог существует (а я твердо верю, что Он существует) и хотел сделать Свое существование известным с абсолютной уверенностью, Он мог бы сделать это разными способами.Бог, которого я познал, хотя Иисус Христос дает нам выбор принять Его из Его любви к нам. Он дает нам все признаки и доказательства, которые нам нужны, чтобы ощутить Его любовь и присутствие, но всегда оставляет достаточно места для сомнений, чтобы мы пришли к Нему по собственному выбору веры и любви, а не потому, что нет другой альтернативы, кроме как делать. так. Он любит нас и желает нашей любви, но настоящая любовь требует истинного выбора. Он говорит с нами разными способами, но иногда мы решаем не улавливать и не принимать послание, как отмечено в этих отрывках из Священных Писаний:
«Небеса возвещают славу Божью; небеса провозглашают дело его рук.День за днем они изливают речь; ночь за ночью они показывают знание. Нет речи или языка, на котором не слышен их голос. Их голос разносится по всей земле, их слова — до концов света ». Псалом 19: 1-4
«Хотя видят, но не видят; хотя они слышат, они не слышат и не понимают. В них исполнилось пророчество Исаии: «Вы всегда будете слышать, но никогда не понимаете; вы всегда будете видеть, но никогда не будете воспринимать. Сердце этого народа стало мозолистым; они почти не слышат ушами и закрыли глаза.Иначе они могли бы видеть своими глазами, слышать своими ушами, понимать своим сердцем и обращаться, и я исцелил бы их ». Но благословенны ваши глаза, потому что они видят, и ваши уши, потому что они слышат». Слова Иисуса Христа в Матфея 13: 13-16
Итак, будь то видение фи в красоте человеческого облика или местонахождение своего святого места, пусть наши глаза, уши, сердце и разум будут открыты посланию нашего Создателя и Бога. Где бы ни находилась точка золотого сечения Земли, эти отрывки указывают на более глубокий смысл, но в поиске места, где наш Бог приведет нас к поклонению Ему:
«Сэр, — сказала женщина, — я вижу, что вы пророк.Наши отцы поклонялись на этой горе, но вы, евреи, утверждаете, что место, где мы должны поклоняться, находится в Иерусалиме ». Иисус заявил: «Поверь мне, женщина, наступит время, когда ты не будешь поклоняться Отцу ни на этой горе, ни в Иерусалиме. Вы, самаритяне, поклоняетесь тому, чего не знаете; мы поклоняемся тому, что знаем, потому что спасение от евреев. Тем не менее, наступает время, и уже настало время, когда истинные поклонники будут поклоняться Отцу в духе и истине, поскольку они являются теми поклонниками, которых ищет Отец.Бог есть дух, и его поклонники должны поклоняться в духе и истине ». Женщина сказала: «Я знаю, что Мессия» (называемый Христом) «грядет. Когда он придет, он все нам объяснит ». Тогда Иисус объявил: «Я, говорящий с вами, есть он». Иоанна 4: 19-26
Однажды, когда фарисеи спросили, когда придет Царство Божье, Иисус ответил: «Царство Божье не придет с вашим внимательным наблюдением, и люди не будут говорить:« Вот оно »или« Вот оно ». , потому что Царство Божье внутри вас.”Луки 17: 20-21
Артикулы:
Сайт HolyMysteries.com в архиве (Сайт больше не активен.)
Видео Holy Mysteries на Vimeo или YouTube.
.форматов бумаги и золотое сечение

Профессор Джон Д. Барроу FRS был профессором математических наук в Кембриджском университете с 1999 года, проводя исследования в области математической физики с особым интересом к космологии, гравитации, физике элементарных частиц и связанной с ней прикладной математике.
С момента его создания в 1999 году Джон Барроу был директором математического проекта тысячелетия, цель которого — улучшить понимание и понимание математики и ее приложений среди молодежи и широкой общественности.Это принесло свои плоды: в 2005 году Проект получил Юбилейную премию Королевы за достижения в области образования. Кроме того, он получил множество наград и премий за свои собственные исследования в области математики и астрономии, в том числе приз Локера в области астрономии и приз Темплтона 2006 года.
Он является автором более 420 статей и 19 книг, переведенных на 28 языков, исследующих более широкие исторические, философские и культурные разветвления развития математики, физики и астрономии.Он также читал лекции в, возможно, уникальном сочетании мест, включая Даунинг-стрит, 10, Виндзорский замок, Ватиканский дворец и Венецианский кинофестиваль. Он также является автором (на итальянском языке) Infinities , получившего итальянскую премию Premi Ubu за лучшую пьесу в итальянском театре в 2002 году.
Назначение профессора Бэрроу на кафедру геометрии в Gresham College повторяет только подвиг. предыдущий был достигнут в 1652 году членом-основателем Королевского общества Лоуренсом Рук.Будучи очень популярным профессором астрономии в период с 2003 по 2007 год, профессор Барроу является лишь вторым профессором за четырехвековую историю Грешем-колледжа, который был назначен на две отдельные кафедры.
Лекции профессора Барроу по геометрии дополняют темы, изучаемые его предшественниками на кафедре профессора геометрии, фокусируясь на применении математики к знакомым вещам. Его цель — показать, как математика повсюду вокруг нас, и рассказать нам много вещей о мире, которые мы не могли бы изучить никаким другим способом.Ежедневные математические задачи, которые он будет решать, раскрывают важность увлекательных элементов простой математики.
Все предыдущие лекции профессора Барроу доступны здесь.
Читать далее
Читать меньше
.
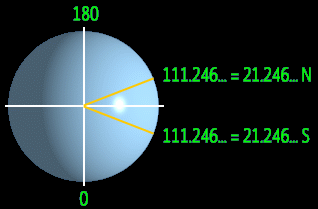 Есть ли у Земли точка золотого сечения?
Есть ли у Земли точка золотого сечения?