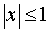Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.
Правило 1 (производная от произведения числа на функцию). Справедливо равенство
(c f (x))’ = c f ‘ (x) ,
где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле
(f (x) + g (x))’ = f ‘ (x) + g’ (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле
(f (x) – g (x))’ = f ‘ (x) – g’ (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле
(f (x) g (x))’ =
= f ‘ (x) g (x) + f (x) g’ (x),
Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
Правило 5 (производная частного двух функций). Производная от дроби (частного двух функций) вычисляется по формуле

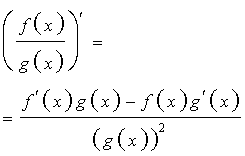
Определение. Рассмотрим функции f (x) и g (x) . Сложной функцией или «функцией от функции» называют функцию вида
f (g (x))
При этом функцию f (x) называют внешней функцией, а функцию g (x) – внутренней функцией.
Правило 6 (производная сложной функции). Производная сложной функции вычисляется по формуле
[ f (g (x))]’ = f ‘ (g (x)) g’ (x)
Другими словами, для того, чтобы найти производную от сложной функции f (g (x)) в точке x нужно умножить производную внешней функции, вычисленную в точке g (x) , на производную внутренней функции, вычисленную в точке x .
Таблица производных часто встречающихся функций
В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
| Функция | Формула для производной | Название формулы |
y = c , где c – любое число | y’ = 0 | Производная от постоянной функции |
y = x c , где c – любое число | y’ = c xc – 1 | Производная степенной функции |
| y = e x | y’ = e x | Производная от экспоненты (показательной функции с основанием e) |
y = a x где a – любое положительное число, не равное 1 | y’ = a x ln a | Производная от показательной функции с основанием a |
| y = ln x , x > 0 | 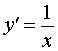 , x > 0 , x > 0 | Производная от натурального логарифма |
y = log a x , x > 0 где a – любое положительное число, не равное 1 | 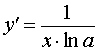 , x > 0 , x > 0 | Производная от логарифма по основанию a |
| y = sin x | y’ = cos x | Производная синуса |
| y = cos x | y’ = – sin x | Производная косинуса |
y = tg x ,
|  , , 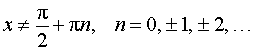 | Производная тангенса |
y = ctg x ,
| 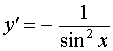 , , 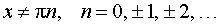 | Производная котангенса |
y = arcsin x , | 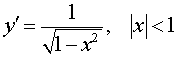 | Производная арксинуса |
y = arccos x , | 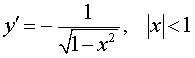 | Производная арккосинуса |
| y = arctg x | 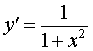 | Производная арктангенса |
| y = arcctg x |  | Производная арккотангенса |
| Производная от постоянной функции |
Функция: y = c , где c – любое число Формула для производной: y’ = 0 |
| Производная степенной функции |
Функция: y = x c , где c – любое число Формула для производной: y’ = c xc – 1 |
| Производная от экспоненты (показательной функции с основанием e) |
Функция: y = e x Формула для производной: y’ = e x |
| Производная от показательной функции с основанием a |
Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a |
| Производная от натурального логарифма |
Функция: y = ln x , x > 0 Формула для производной: 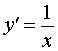 , x > 0 , x > 0 |
| Производная от логарифма по основанию a |
Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной: 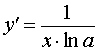 , x > 0 , x > 0 |
| Производная синуса |
Функция: y = sin x Формула для производной: y’ = cos x |
| Производная косинуса |
Функция: y = cos x Формула для производной: y’ = – sin x |
| Производная тангенса |
Функция: y = tg x , где 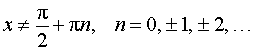 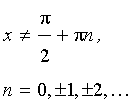 Формула для производной:  , ,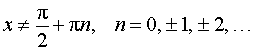 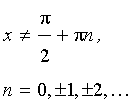 |
| Производная котангенса |
Функция: y = ctg x , где 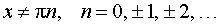 Формула для производной: 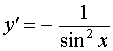 , ,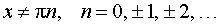 |
| Производная арксинуса |
Функция: y = arcsin x , Формула для производной: 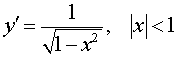 |
| Производная арккосинуса |
Функция: y = arccos x , Формула для производной: 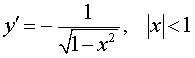 |
| Производная арктангенса |
Функция: y = arctg x Формула для производной: 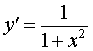 |
| Производная арккотангенса |
Функция: y = arcctg x Формула для производной:  |
Таблица производных сложных функций
В следующей таблице приведены формулы для производных сложных функций.
В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx + b , где k и b – любые числа, 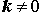 .
.
| Функция | Формула для производной |
y = (kx + b) c , где c – любое число. | y’ = kc (kx + b) c – 1 , |
y = ( f (x)) c , где c – любое число. | 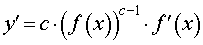 |
| y = ekx + b | y = kekx + b |
| y = e f (x) | 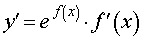 |
y = akx + b где a – любое положительное число, не равное 1 | 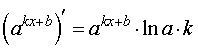 |
y = a f (x) где a – любое положительное число, не равное 1 | 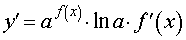 |
| y = ln (kx + b) , kx + b > 0 | 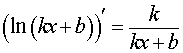 , ,kx + b > 0 |
| y = ln ( f (x)) , f (x) > 0 | 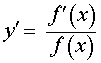 , ,f (x) > 0 |
y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 | 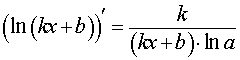 , kx + b > 0 , kx + b > 0 |
y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 |  , f (x) > 0 , f (x) > 0 |
| y = sin (kx + b) | y’ = k cos (kx + b) |
| y = sin ( f (x)) | 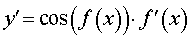 |
| y = cos (kx + b) | y’ = – k sin (kx + b) |
| y = cos ( f (x)) | 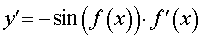 |
y = tg (kx + b), где | 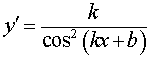 , ,  |
y = tg ( f (x)), где |  , , 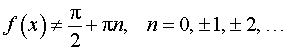 |
y = ctg (kx + b), где | 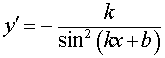 , ,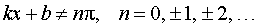 |
y = ctg ( f (x)), где | 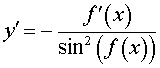 , ,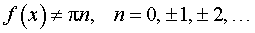 |
y = arcsin (kx + b), 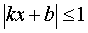 | 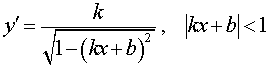 |
y = arcsin ( f (x)), 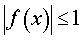 | 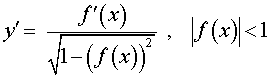 |
y = arccos (kx + b), 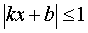 |  |
y = arccos ( f (x)), 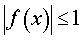 |  |
| y = arctg (kx + b) | 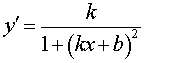 |
| y = arctg ( f (x)) | 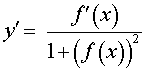 |
| y = arcctg (kx + b) | 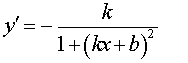 |
| y = arcctg ( f (x)) |  |
Функция: y = (kx + b) c , где c – любое число. Формула для производной: y’ = kc (kx + b) c – 1 , |
Функция: y = ( f (x)) c , где c – любое число. Формула для производной: 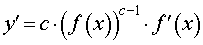 |
Функция: y = ekx + b Формула для производной: y = kekx + b |
Функция: y = e f (x) Формула для производной: 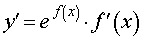 |
Функция: y = akx + b где a – любое положительное число, не равное 1 Формула для производной: 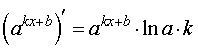 |
Функция: y = a f (x) где a – любое положительное число, не равное 1 Формула для производной: 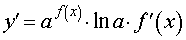 |
Функция: y = ln (kx + b) , kx + b > 0 Формула для производной:
|
Функция: y = ln ( f (x)) , f (x) > 0 Формула для производной:
|
Функция: y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 Формула для производной: 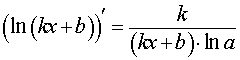 , kx + b > 0 , kx + b > 0 |
Функция: y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 Формула для производной:  , f (x) > 0 , f (x) > 0 |
Функция: y = sin (kx + b) Формула для производной: y’ = k cos (kx + b) |
Функция: y = sin ( f (x)) Формула для производной: 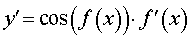 |
Функция: y = cos (kx + b) Формула для производной: y’ = – k sin (kx + b) |
Функция: y = cos ( f (x)) Формула для производной: 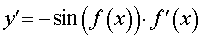 |
Функция: y = tg (kx + b), где Формула для производной: 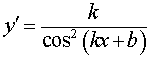 , ,  |
Функция: y = tg ( f (x)), где Формула для производной:  , , 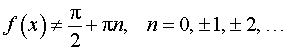 |
Функция: y = ctg (kx + b), где Формула для производной: 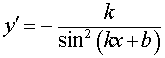 , , 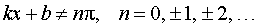 |
Функция: y = ctg ( f (x)), где Формула для производной: 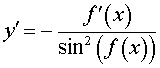 , , 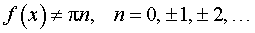 |
Функция: y = arcsin (kx + b), Формула для производной: 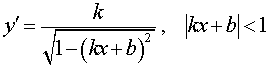 |
Функция: y = arcsin ( f (x)), Формула для производной: 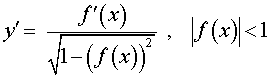 |
Функция: y = arccos (kx + b), Формула для производной:  |
Функция: y = arccos ( f (x)), Формула для производной:  |
Функция: y = arctg (kx + b) Формула для производной: 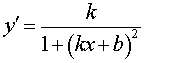 |
Функция: y = arctg ( f (x)) Формула для производной: 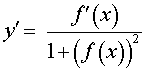 |
Функция: y = arcctg (kx + b) Формула для производной: 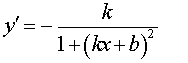 |
Функция: y = arcctg ( f (x)) Формула для производной:  |

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Калькулятор онлайн — Найти (с решением) производную функции
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Примеры подробного решения >>
Введите выражение функции
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Сообщение отправлено. Спасибо.
Определение производной
Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \). Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение \( \frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$
Для обозначения производной часто используют символ y’. Отметим, что y’ = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x).
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
Поскольку \( k = tg(a) \), то верно равенство \( f'(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \( y = f(x) \) имеет
производную в конкретной точке \( x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x) $$
Это означает, что около точки х выполняется приближенное равенство \( \frac{\Delta y}{\Delta x} \approx f'(x) \), т.е.
\( \Delta y \approx f'(x) \cdot \Delta x \).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х.
Например, для функции \( y = x^2 \) справедливо приближенное равенство \( \Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \( x \), найти \( f(x) \)
2. Дать аргументу \( x \) приращение \( \Delta x \), перейти в новую точку \( x+ \Delta x \), найти \( f(x+ \Delta x) \)
3. Найти приращение функции: \( \Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \( \frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f'(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция \( y=\sqrt[3]{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \( f'(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием.
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
$$ f’_x(g(x)) = f’_g \cdot g’_x $$
Таблица производных некоторых функций
$$ \left( \frac{1}{x} \right) ‘ = -\frac{1}{x^2} $$ $$ ( \sqrt{x} ) ‘ = \frac{1}{2\sqrt{x}} $$ $$ \left( x^a \right) ‘ = a x^{a-1} $$ $$ \left( a^x \right) ‘ = a^x \cdot \ln a $$ $$ \left( e^x \right) ‘ = e^x $$ $$ ( \ln x )’ = \frac{1}{x} $$ $$ ( \log_a x )’ = \frac{1}{x\ln a} $$ $$ ( \sin x )’ = \cos x $$ $$ ( \cos x )’ = -\sin x $$ $$ ( \text{tg} x )’ = \frac{1}{\cos^2 x} $$ $$ ( \text{ctg} x )’ = -\frac{1}{\sin^2 x} $$ $$ ( \arcsin x )’ = \frac{1}{\sqrt{1-x^2}} $$ $$ ( \arccos x )’ = \frac{-1}{\sqrt{1-x^2}} $$ $$ ( \text{arctg} x )’ = \frac{1}{1+x^2} $$ $$ ( \text{arcctg} x )’ = \frac{-1}{1+x^2} $$| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | cos((5pi)/12) | |
| 3 | Найти точное значение | arctan(-1) | |
| 4 | Найти точное значение | sin(75) | |
| 5 | Найти точное значение | arcsin(-1) | |
| 6 | Найти точное значение | sin(60 град. ) | |
| 7 | Найти точное значение | sin(pi/3) | |
| 8 | Найти точное значение | arctan(- квадратный корень 3) | |
| 9 | Найти точное значение | cos(pi/3) | |
| 10 | Найти точное значение | sin(0) | |
| 11 | Найти точное значение | cos(pi/12) | |
| 12 | Найти точное значение | sin(30 град. ) | |
| 13 | Найти точное значение | cos(60 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | sin((2pi)/3) | |
| 16 | Найти точное значение | arcsin(1) | |
| 17 | Найти точное значение | sin(pi/2) | |
| 18 | График | f(x)=x^2 | |
| 19 | Найти точное значение | sin(45 град. ) | |
| 20 | Найти точное значение | sin(15) | |
| 21 | Упростить | квадратный корень x^2 | |
| 22 | Найти точное значение | arccos(-1) | |
| 23 | Найти точное значение | tan(60 град. ) | |
| 24 | Найти точное значение | cos(45 град. ) | |
| 25 | Вычислить | логарифм по основанию 2 от 8 | |
| 26 | Упростить | квадратный корень x^3 | |
| 27 | Найти точное значение | arcsin(-1/2) | |
| 28 | Найти точное значение | cos(45) | |
| 29 | Найти точное значение | tan(30 град. ) | |
| 30 | Найти точное значение | tan(30) | |
| 31 | Найти точное значение | arcsin(1) | |
| 32 | Найти точное значение | arctan( квадратный корень 3) | |
| 33 | Найти точное значение | sin(45) | |
| 34 | Найти точное значение | cos(0) | |
| 35 | Найти точное значение | tan(45 град. ) | |
| 36 | Найти точное значение | arctan(0) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | График | y=x^2 | |
| 39 | Вычислить | натуральный логарифм 1 | |
| 40 | Вычислить | логарифм по основанию 3 от 81 | |
| 41 | Найти точное значение | cos(15) | |
| 42 | Вычислить | логарифм по основанию 5 от 125 | |
| 43 | Упростить | кубический корень из квадратного корня 64x^6 | |
| 44 | Вычислить | логарифм по основанию 3 от 81 | |
| 45 | Вычислить | логарифм по основанию 2 от 8 | |
| 46 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 47 | Найти точное значение | cos(75) | |
| 48 | Найти точное значение | sin((3pi)/4) | |
| 49 | Упростить | (1/( квадратный корень x+h)-1/( квадратный корень x))/h | |
| 50 | Упростить | кубический корень x^3 | |
| 51 | Найти точное значение | sin((5pi)/12) | |
| 52 | Найти точное значение | arcsin(-1/2) | |
| 53 | Найти точное значение | sin(30) | |
| 54 | Найти точное значение | sin(105) | |
| 55 | Найти точное значение | tan((3pi)/4) | |
| 56 | Упростить | квадратный корень s квадратный корень s^7 | |
| 57 | Упростить | корень четвертой степени x^4y^2z^2 | |
| 58 | Найти точное значение | sin(60) | |
| 59 | Найти точное значение | arccos(-( квадратный корень 2)/2) | |
| 60 | Найти точное значение | tan(0) | |
| 61 | Найти точное значение | sin((3pi)/2) | |
| 62 | Вычислить | логарифм по основанию 4 от 64 | |
| 63 | Упростить | корень шестой степени 64a^6b^7 | |
| 64 | Вычислить | квадратный корень 2 | |
| 65 | Найти точное значение | arccos(1) | |
| 66 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 67 | График | f(x)=2^x | |
| 68 | Найти точное значение | sin((3pi)/4) | |
| 69 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 70 | Вычислить | логарифм по основанию 5 от 25 | |
| 71 | Найти точное значение | tan(pi/2) | |
| 72 | Найти точное значение | cos((7pi)/12) | |
| 73 | Упростить | 1/( кубический корень от x^4) | |
| 74 | Найти точное значение | sin((5pi)/6) | |
| 75 | Преобразовать из градусов в радианы | 150 | |
| 76 | Найти точное значение | tan(pi/2) | |
| 77 | Множитель | x^3-8 | |
| 78 | Упростить | корень пятой степени 1/(x^3) | |
| 79 | Упростить | корень пятой степени 1/(x^3) | |
| 80 | Найти точное значение | sin(135) | |
| 81 | Преобразовать из градусов в радианы | 30 | |
| 82 | Преобразовать из градусов в радианы | 60 | |
| 83 | Найти точное значение | sin(120) | |
| 84 | Найти точное значение | tan((2pi)/3) | |
| 85 | Вычислить | -2^2 | |
| 86 | Найти точное значение | tan(15) | |
| 87 | Найти точное значение | tan((7pi)/6) | |
| 88 | Найти точное значение | arcsin(( квадратный корень 3)/2) | |
| 89 | Найти точное значение | sin(pi/2) | |
| 90 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 91 | Упростить | кубический корень 8x^7y^9z^3 | |
| 92 | Упростить | arccos(( квадратный корень 3)/2) | |
| 93 | Упростить | i^2 | |
| 94 | Вычислить | кубический корень 24 кубический корень 18 | |
| 95 | Упростить | квадратный корень 4x^2 | |
| 96 | Найти точное значение | sin((3pi)/4) | |
| 97 | Найти точное значение | tan((7pi)/6) | |
| 98 | Найти точное значение | tan((3pi)/4) | |
| 99 | Найти точное значение | arccos(-1/2) | |
| 100 | Упростить | корень четвертой степени x^4 |
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Производная функции. Понятие производной. Геометрический смысл производной. Физический смысл производной. Правила дифференцирования. Производная сложной функции. Достаточное условие монотонности функции. Необходимое и достаточное условия экстремума. Поделиться:
| |||||||||||||||||||||||||||||||||
операций с функциями | Purplemath
Purplemath
Сначала вы узнали (еще в средней школе), что можно складывать, вычитать, умножать и делить числа. Затем вы узнали, что можно складывать, вычитать, умножать и делить многочлены. Теперь вы узнаете, что вы также можете складывать, вычитать, умножать и делить функции. Выполнение этих операций над функциями не сложнее, чем сама запись.Например, когда они дают вам формулы для двух функций и говорят, что нужно найти сумму, все, что они говорят вам сделать, это добавить две формулы. В этой теме нет ничего больше, кроме, возможно, некоторого упрощения используемых выражений.
MathHelp.com

Дано f ( x ) = 3 x + 2 и g ( x ) = 4-5 x , найдите ( f + g ) ( x ), ( f — г ) ( x ), ( f x г ) ( x ) и ( f / г ) ( x ).
Чтобы найти ответы, все, что мне нужно сделать, это применить операции (плюс, минус, умножение и деление), которые они мне говорят, в том порядке, в котором они мне говорят.
( f + г ) ( x ) = f ( x ) + г ( x )
= [3 x
= 3 x + 2 + 4-5 x
= 3 x -5 x + 2 + 4
= –2 x + 6
( f — г ) ( x ) = f ( x ) — г ( x )
= [3 x + 2] — [4–5 x ]
= 3 x + 2-4 + 5 x
= 3 x + 5 x + 2 — 4
= 8 x — 2
( f × г ) ( x ) = [ f ( x )] [ г ( x )]
= (3 x + 2) (4-5 x )
= 12 x + 8-15 x
2 -10 x= –15 x 2 + 2 x + 8
Мой ответ — аккуратный список всех моих результатов, с четким указанием, что есть что.
( f + g ) ( x ) = –2 x + 6
( f — г ) ( x ) = 8 x — 2
( f × г ) ( x ) = –15 x 2 + 2 x + 8
( f / g ) ( x ) = (3 x + 2) / (4-5 x )Дано f ( x ) = 2 x , g ( x ) = x + 4 и h ( x ) = 5 — x 3 , найти ( f + g ) (2), ( h — g ) (2), ( f × h ) (2) и ( h / g ) (2).
Это упражнение отличается от предыдущего тем, что мне нужно не только выполнять операции с функциями, но и выполнять оценку с определенным значением
f (2) = 2 (2) = 4
г (2) = (2) + 4 = 6
ч (2) = 5 — (2) 3 = 5 — 8 = –3
Теперь я могу оценить перечисленные выражения:
( f + г ) (2) = f (2) + г (2)
( ч — г ) (2) = ч (2) — г (2)
( f × h ) (2) = f (2) × h (2)
( ч / г ) (2) = ч (2) ÷ г (2)
Тогда мой ответ:
( f + g ) (2) = 10, ( h — g ) (2) = –9, ( f × h ) (2) = –12, ( h / г ) (2) = –0.5
Если вы сначала работаете символически, а значение x вставляете только в конце, вы все равно получите те же результаты. В любом случае будет работать. Обычно легче сначала оценить, но выбор за вами.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в работе с функциями. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Решить», чтобы сравнить свой ответ с ответом Mathway.(Или пропустите виджет и продолжите урок.)
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления .)
Дано f ( x ) = 3 x 2 — x + 4, найдите упрощенную форму следующего выражения и вычислите значение h = 0:
На самом деле это не вопрос функций-операций, но что-то подобное часто возникает в контексте операций-функций.Это выглядит намного хуже, чем есть на самом деле, если я не тороплюсь и буду осторожен.
Самый простой способ продолжить это упражнение — работать по частям, упрощая по мере продвижения; затем я все соберу и упростлю в конце.
Для первой части числителя мне нужно вставить выражение « x + h » для каждого « x
» в формуле функции, используя то, что я узнал о нотации функций, и затем упростите:f ( x + h )
= 3 ( x + h ) 2 — ( x + h ) + 4
= 3 ( x 2 + 2 xh + h 2 ) — x — h + 4
= 3 x 2 + 6 xh + 3 h 2 — x — h + 4
Выражением для второй части числителя является сама функция:
Теперь вычтю и упросту:
Остается разделить на знаменатель; факторинг позволяет упростить:
Теперь я должен оценивать
6 x + 3 (0) — 1 = 6 x — 1
упрощенная форма: 6 x + 3 h — 1
значение при ч = 0: 6 x — 1
Это почти все, что касается «операций над функциями», пока вы не дойдете до композиции функций.Пусть вас не беспокоят обозначения этой темы; это означает не что иное, как то, что он говорит: сложить, вычесть, умножить или разделить; затем упростите и оцените по мере необходимости. Не зацикливайтесь на этом. Это действительно так просто.
А, и последний пример? Они поместили это туда, чтобы вы могли «попрактиковаться» в том, что вы будете делать в математике. Вы, вероятно, не вспомните этого к тому времени, когда фактически перейдете к исчислению, но вы будете следовать очень похожему процессу для поиска чего-то, что называется «производными».
URL: https://www.purplemath.com/modules/fcnops.htm
. Состав
Функций: Разделы: Составление функции, которые являются наборами точек, Составление функций в точках, Составление функции с другими функциями, проблемы Word с использованием композиции, обратных функций и композиции  Предположим, вам дали две функции f ( x ) = 2 x + 3 и г ( x ) = x 2 + 5.Состав означает, что вы можете подключить г ( x ) в ф ( х ). Это записывается как «( f o г ) ( x ) «, произносится как « f -compose- g » размером x дюймов. И «( f o g ) ( x )» означает «» f ( г ( x )) «.То есть вы что-то подключаете для x , затем вы вставляете это значение в g , упростите, а затем вставьте результат в f . Процесс здесь такой же, как и на предыдущей странице, за исключением что теперь мы будем использовать формулы для поиска значений, а не просто читать значения из списков баллов.
Когда я работаю с функцией композицию, которую я обычно конвертирую »( f o г ) ( x ) » на более интуитивно понятный « f ( g ( x ))» форма. Это не обязательно, но я считаю это полезным. В этом случай, получаю: Это означает, что, работая справа налево (или изнутри) подключаю х = 1 в f ( x ), оценка f ( x ), а затем вставляем результат в g ( x ).Я могу делать расчеты по крупицам, вот так: f (1) = 2 (1) + 3 = 2 + 3 = 5, а с г (5) = (5) 2 + 5 = 25 + 5 = 20, затем ( g o f ) (1) = г ( f (1)) = г (5) = 20. Выполнение всех расчетов (что будет полезно позже, когда мы делаем вещи символически), это выглядит так: ( г о f ) (1) = g ( f (1)) Обратите внимание, как я написал каждый правила функции четко, оставляя открытыми круглые скобки для того, где ввод ( х или что-то еще) пойдет.Это полезный прием. Какой бы метод вы используете (побитовое или все-в-одном), ответ: Я только что вычислил ( г o ф ) (1); в композиция может работать и в другом порядке:
Сначала я конвертирую это в более интуитивно понятную форму, а затем я упрощу: Работает побитно, т.к. г (1) = (1) 2 + 5 = 1 + 5 = 4, а с f (4) = 2 (4) + 3 = 8 + 3 = 11, затем ( f o г ) (1) = г ( г (1)) = ж (4) = 11.С другой рука, работающая как все в одном (справа налево или изнутри), я получить это: ( ф о г ) (1) = г ( г (1)) В любом случае, ответ это: Авторское право Элизабет Стапель 2002-2011 Все права защищены Устное примечание: « f о г «- это , а не . произносится как «fogg» и « g » о f «есть , а не произносится как «гофф».Они произносятся как « f -compose- g ». и « г -компоновать- ф «соответственно. Не показывайте себя невежественным, произнося это неправильно! Как вы видели выше, вы можете подключить одну функцию к другой. Вы также можете подключить функцию к сам:
( г о г ) (1) = г ( г (1)) В каждом из этих случаев Я тщательно выписал шаги, используя круглые скобки, чтобы указать, где ввод производился по формуле. Если это поможет вам сделать шагов по отдельности, затем рассчитайте г (1) вне другого г ( x ) как отдельный шаг.То есть проводите вычисления побитно, сначала находя г (1) = 4, а затем вставка 4 в г ( x ) получить г (4) = 11. << Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | Возвращение к указателю Вперед >>
|
Состав
функций: Разделы: Составление функции, которые являются наборами точек, Составление функции в точках, Составление функций с другими функциями, Word задачи с использованием композиции, обратные функции и состав  Иногда нужно осторожно с областью и диапазоном составной функции.
С f ( x ) включает квадратный корень, входные данные должны быть неотрицательными.Это означает, что домен (набор значений x ) для f ( x ) равно «все х > 0 «. Затем в ( г о f ) ( x ), куда воткну х первый в f ( x ) = sqrt ( x ), домен ограничен как минимум «все x > 0 «.Посмотрим как выглядят две композиции: Домен для квадрата root — это все входные данные, которые делают « x 2 «неотрицательный. То есть все x такое, что x 2 > 0. Решение этой проблемы для х , Я понимаю, что домен ( f o г ) ( x ) есть «все x > 2 дюйма. Теперь займемся другим составом: ( г о f ) ( x ) = g ( f ( x )) Домен для этого все входные данные, определяющие квадратный корень.Поскольку есть только « x » внутри квадратного корня, тогда: Если ваши начальные функции просто старые полиномы, тогда их области «все x «, и так будет домен композиции. Это в значительной степени, только если вы имеете дело со знаменателями (где нельзя делить на ноль) или квадратом корни (где у вас не может быть отрицательного), что домен когда-либо становится вопрос. Обычно состав используется для объединения двух функций. Но иногда вас просят вернуться назад. То есть вам дадут функцию, а вас попросят подойти с двумя исходными функциями, которые они составили. Например: Авторские права Элизабет Стапель 2002-2011 Все права защищены.
Это просит вас замечать закономерности и выяснять, что «внутри» чего-то еще. В данном случае это похоже на квадратичный x 2 + 2 х 3, за исключением того, что вместо квадрата x , они возводят в квадрат x + 1. Другими словами, это квадратичная, в которую они подключили x + 1.Итак, давайте сделаем г ( x ) = x + 1, и затем подключите эту функцию к f ( x ) = x 2 + 2 x 3: ( ф о г ) ( x ) = г ( г ( x )) Затем h ( x ) может быть обозначен как состав f ( x ) = x 2 + 2 x 3 и g ( x ) = x + 1.
Поскольку квадратный корень находится «на» (или «около») «4 x + 1 «, затем 4 x + 1 равно положить внутрь квадратный корень.Мне нужно взять х , do «4 x +1 к нему, а затем извлеките квадратный корень из результата: г ( x ) = 4 x + 1, f ( x ) = sqrt ( x ) и h ( x ) = ( f o г ) ( х ). << Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | Возвращение к указателю Вперед >>
|