Информация о золотом сечении: Attention Required! | Cloudflare

Эффективные сайты с золотым сечением — DEADSIGN

Золотое сечение применяется в графических макетах любых типов, главным образом чтобы сбалансировать контент, в котором много текста. Оно помогает дизайнерам выстраивать иерархию и привлекать внимание пользователя к нужным областям экрана. Следующие примеры сайтов помогут понять, как дизайнеры пользуются этим приемом!

Что такое золотое сечение?

Золотое сечение — это математическая пропорция. Она часто встречается в природе и применяется по классической теории дизайна для создания сбалансированной композиции, приблизительно равна 1,6180, также известна как «золотая середина» или «гармоническое деление» и обычно обозначается греческой буквой Фи «ϕ».

Ещё есть «золотой прямоугольник» — прямоугольник, длина которого пропорциональна ширине в соотношении 1,6180. Например, блок <div> с шириной 300рх и длиной, равной 300 * 1,6180 ≈ 485px, можно назвать золотым прямоугольником.

Если вы отрежете от золотого прямоугольника идеальный квадрат, останется ещё один золотой прямоугольник.

То же самое можно сделать с меньшим прямоугольником, и опять по новой до бесконечности, пока вы не получите знакомое изображение:

Последовательность Фибоначчи

Последовательность Фибоначчи чем то похожа на золотое сечение. Это ряд цифр, в котором каждая следующая цифра является суммой двух предыдущих. Например: 0, 1, 1, 2, 3, 5, 8, 13, 21

Если к идеальному квадрату добавить такой же, получается прямоугольник.

Продолжайте добавлять квадраты к длине получающихся прямоугольников.

Затем мы добавляем другой квадрат со стороной, равной длине прямоугольника из двух маленьких квадратов:

И потом повторяем это снова и снова:

Это может продолжаться бесконечно. Получается эффект как и у золотого прямоугольника, но на этот раз мы выстраиваем фигуру, а не режем ее. Пропорции золотого сечения и последовательности Фибоначчи получаются одинаково привлекательными.

Теперь давайте проанализируем несколько сайтов, где применяются эти пропорции.

Пример #1: YStudio

yourlocalstudio.dk

О чём этот сайт?

«Your Local Studio» — студия дизайна и разработки из Копенгагена. Они разрабатывают визуальные концепции дизайна сайтов для создания общего впечатления, улучшающего восприятие.

Как здесь применяется золотое сечение

На сайте «золотая середина» применяется на двух страницах из трёх. Главная страница — это концептуальный обзор ключевых работ. Страница «studio» совмещает более традиционный подход к верстке с формами золотого прямоугольника.

Почему это эффективно

Хотите выделиться из толпы? Yourlocalstudio (YLS) это удалось благодаря золотому сечению в дизайне сайта. Дизайн выглядит прогрессивно и при этом имеет чёткую сетку. Вы могли бы поспорить, что в настоящее время всё выглядит как bootstrap. Присмотритесь, ведь всё больше и больше сайтов стараются привлекать к себе внимание более структурными и динамичными макетами.

Пример #2: Mashable

mashable.com

О чём этот сайт?

Mashable — это новостной сайт, источник информации, знаний и материалов для современных людей.

Как здесь применяется золотое сечение

Я использовал тест золотого сечения с сайта UX Triggers, чтобы показать вам, как Mashable применяет последовательность Фибоначчи в макете. Расположение контента гибкое, заголовки поставлены слева, а ссылки на другие новости справа. Блоки отделены друг от друга сетками.

Почему это эффективно

Золотое сечение в данном случае эффективно, поскольку позволяет контенту сайта с большим количеством текста дышать свободнее. Похожие сайты могут показаться более плотно забитыми материалом, если используют традиционную сетку в макетах. Mashable является примером того, как золотое сечение может быть эффективным даже оставаясь незаметным.

Пример #3: Jackson & Kent

www. jandk.fr

О чём этот сайт?

Jackson & Kent — это агентство веб-продакшн из Франции. Они специализируются на цифровых сервисах типа HTML5, CSS3, Drupal, WordPress, PHP/MySQL, Flash и прочих.

Как здесь применяется золотое сечение

На скриншоте сверху показано, что макет в основном состоит из готовых работ агентства. Страница также содержит блок информации о самом агентстве и панель навигации в центре экрана. Как показано ниже, подраздел «Контакты» подчиняется общей сетке золотого сечения, но контент в нем организован по своему.

Почему это эффективно

Данный пример заставляет вас просматривать сайт и контент горизонтально. Сетка из блоков разного размера делает контент визаульно интереснее. Поскольку пользователи предпочитают смотреть контент на десктопах (кстати, на планшетах тоже), на горизонтальной панели навигации есть пагинатор из цифр. Получился новаторский подход к подаче контента, также как и UI в целом.

Заключение

Золотое сечение естественным образом обращает внимание пользователя на определенные точки в интерфейсе. Как концепт, оно может помочь вам задуматься о расположении контента и эффективном использовании иерархии. Союз верстки, типографики, цвета и других ключевых принципов дизайна поможет поднять ваши работы в дизайне на новый уровень.

Информация о золотом сечении

Золотое сечение (или пропорция Фидия), по мнению многих исследователей, является наиболее приятной для человеческого глаза. Этим можно объяснить ее многогранное применение человеком, например такие сферы как архитектура, живопись, фотография и ландшафтный дизайн широко используют эту пропорцию и связанные с ней свойства. Это пропорция была в почете у умнейших людей, таких как Леонардо Да Винчи и Ле Корьбюзье. Художник и архитектор Леонардо Да Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с золотым сечением. Архитектор Ле Корьбюзье руководствовался им во множестве своих работ.

Мне же хотелось получить первоначальные знания по этой теме.

В эпоху Возрождения золотое сечение было очень популярно например было принято брать размеры картины такими, чтобы отношение ширины к высоте было равно числу Фидия. Форму золотого сечения придавали не только картинам, но и книгам, столам, открыткам. Поэтому мне бы хотелось подробнее рассмотреть применение золотого сечения в различные эпохи от древности, эпохи Возрождения до XlX века. Для этого нужно прочитать и изучить литературу, связанную с этой темой, найти наиболее интересные факты и изложить их в своем реферате.

Цель данной работы заключается в том, чтобы представить информацию наглядно и интересно. Для достижения цели поставлены следующие задачи

1. дать определение понятий симметрии и ассиметрии, золотое сечение.

2. описать золотые фигуры и построить некоторые из них

3. рассказать о применении и использовании божественной пропорции человеком

Золотое сечение

Самым известным примером гармонии ассиметрии является золотое сечение. Есть слова, принадлежащие Иоганну Кеплеру: «Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое – деление отрезка в среднем и крайнем отношении». Великий ученый пол словами «деление отрезка в среднем и крайнем отношении» имеет ввиду известную пропорцию – золотое сечение. Именно эта пропорция является темой моего реферата. В следующих главах я расскажу о применении золотого сечения, а ниже дам определение этого понятия и способы его получения.

Деление отрезка в среднем и крайнем отношении называют золотым сечением. Другое название – «золотая пропорция».[5]

с : b = b : а.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.

a=c-b

b:c= (c-b):а

В пропорции произведение крайних членов равно произведению средних

b ² + cb – c² =0

Длина отрезка выражается положительным числом, поэтому после преобразований

b= −(c+√5с² )∕2 или b=(√5−1)∕2∙с

Число (√5−1)∕2 обозначается буквой в честь древнегреческого скульптора Фидия, в творениях которого это число встречается многократно.

Число — иррациональное. В практике его используют округляя до тысячных 0,618 или сотых 0,62 или десятых 0,6.

Части золотого сечения приблизительно составляют 62% и 38% всего отрезка.

Древние математики обнаружили, что золотое сечение можно получить при помощи геометрии, и потом применять в любом масштабе, даже для строительства пирамид.

Я предлагаю рассмотреть один из многих способов, как это можно сделать.

1. Построим отрезок AB, восстановим в точке B перпендикуляр к AB, на нем отложим точку E таким образом, чтобы BE=0,5AB

2. Далее соединив точки A и E, отложим ED=BE, и AC=AD. Точка С является искомой, она производит «золотое сечение» отрезка AB.

Заметим, что по теореме Пифагора

(AD + DE)² =AB² + BD² ,

а по построению AD=AC, DE=BE=0,5AB

Из этих равенств следует, что AC² + AC∙AB=AB² , а отсюда можно получить равенство

AC:AB=CB:AC

Золотые фигуры

На основе идеи золотого сечения существуют различные фигуры, содержащие эту пропорцию. Аналогично названию пропорции, их называют «золотые фигуры». Каждая такая фигура обязательно содержит пропорцию Фидия.

1. Золотой прямоугольник

Золотой прямоугольник – прямоугольник, у которого отношение смежных сторон дает пропорцию Фидия. А форму «золотого сечения» придавали книгам, столам и т.д. «Золотой прямоугольник» обладает интересным свойством: если от него отрезать квадрат, то останется вновь «золотой прямоугольник». Так можно продолжать до бесконечности. Если провести диагонали первого и второго прямоугольников, то точка О их пересечения принадлежит всем получаемым «золотым прямоугольникам»

Произведения в искусстве значительно улучшены с использованием знания Золотого прямоугольника. Притягательность его ценности и употребления были особенно сильны в древнем Египте и Греции и во времена Ренессанса, т.е. во всех важных периодах цивилизации. Леонардо да Винчи ( Leonardo da Vinci ) придавал огромное значение Золотой пропорции. Он также находил ее приятной в своих соотношениях и говорил: Если предмет не имеет правильного облика, он не работает. Многие из его картин обладают правильным обликом, потому что он использовал Золотое сечение для того, чтобы усилить их привлекательность.

2.

Золотой треугольник

Золотой треугольник представляет собой равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется числу Фидия. Одним из его свойств является то что, длины биссектрис его углов при основании равны длине самого основания. Остальные свойства «вытекают» из свойств пентаграммы, которую мы рассмотрим позже.

Стороны золотого треугольника образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Одним из свойств золотого треугольника является то что, длины биссектрис его углов при основании равны длине самого основания. Остальные свойства вытекают из свойств пентаграммы, которую мы рассмотрим позже.

Пентаграмма

Пятиконечная звезда, пожалуй, является одной из самых известных фигур. Она постоянно привлекала внимание людей своим совершенством. Пифагорейцы – ученики Пифагора выбрали ее в качестве символа своего союза именно эту звезду. Ее же считали амулетом здоровья. Сейчас звезда используются на многих флагах и гербах многих стран. Почему же она так привлекает, притягивает взгляд? Дело в том, что в этой звезде есть удивительное постоянство отношений составляющих ее отрезков.

Нужно построить ее, чтобы в этом убедиться.

Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения. Описание построения золотого треугольника написано выше.

Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.

Построения золотых пятиугольника и пентаграммы содержатся уже в «Началах» Евклида, написанных за 300 лет до нашей эры. Процесс построения циркулем и линейкой описан еще в первой главе.

Пентаграмма из церкви Святого Петра .

Структура яблока в разрезе.

Если разрезать поперёк яблоко или грушу, то мы увидим вот такую структуру расположения семян . Цветы этих деревьев так же имеют структуру пятиугольника.

Пятиконечная звезда – это вторая пространственная структура вокруг которой гнездятся мистика и в разное время у разных народов пятиконечная звезда означала разное.

У пифагорейцев — символ здоровья и совершенства, опознавательный знак общины.

В христианской символике пентаграмма символизирует пять ран Иисуса или, в числовом толковании, сумму Троицы (Отец, Сын и Дух Святой) и двойственной природы Христа (божественной и человеческой).

На фото приведена деталь отделки северного фасада Амьенского собора. Амьенский собор (фр. Cathédrale Notre-Dame d’Amiens) — самый большой из французских соборов по своему объему (200 000 м³).

Перевёрнутая пентаграмма, пятиконечная звезда с тремя лучами, направленными вниз, в начале истории христианства перевёрнутая пентаграмма трактовалась как символ Преображения Христа.

Различают также “мужскую” и “женскую” пентаграммы (женская в с двумя лучами кверху). Иногда (особенно в Алхимии) упоминается как защитный знак, так как вызванный демон не мог переступить её линий. Например, в “Фаусте” Гёте сам Мефистофель не мог покинуть комнату, пока на выходе была нарисованна пентаграмма. Тамплиеры считали Пентаграмму символом Священного Женского Начала, а в Индии пентаграмма — символ Венеры (богини Кали).[10]

Применение золотого сечения и его фигур

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Kорбюзье нашел, что в рельефе из храма фараонa Cети I в Абидосе и в рельефе, изображающем фараона Pамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Kвадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе)

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.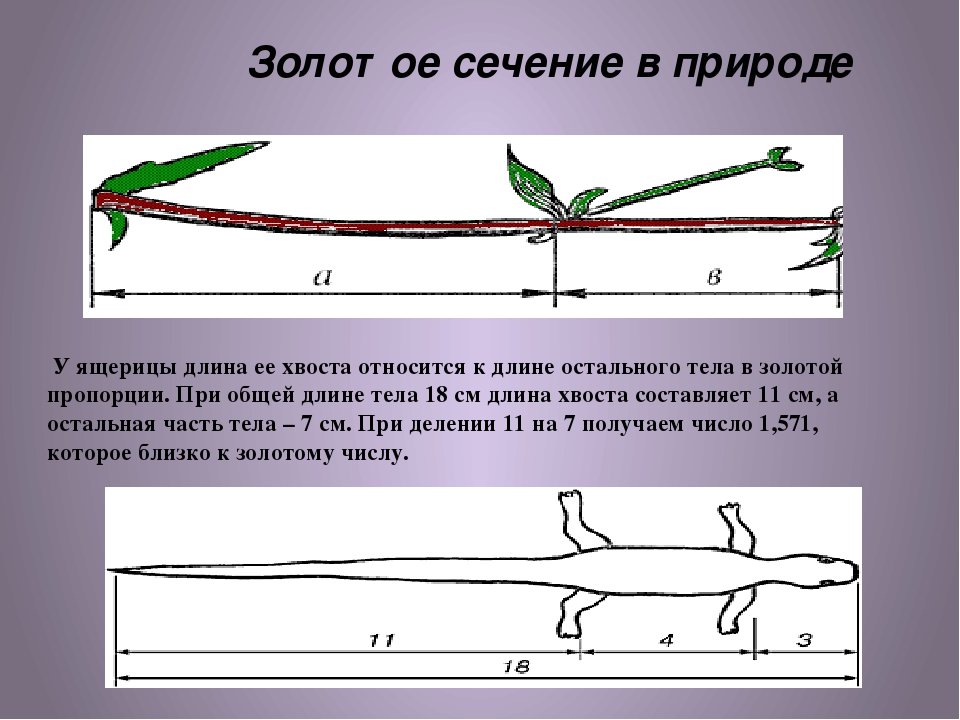 Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Великий астроном XVI в. Иоган Kеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой». [12]

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах.

Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.

Золотое сечение в архитектуре

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). [15]

На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618…

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Что касается пирамид, то не только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у Мексикансих пирамид.[16]

Золотое сечение в изобразительном искусстве

На картине И.И. Шишкина «Сосновая роща» просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины приблизительно в золотом сечении. Справа от сосны — освещенный солнцем пригорок. Он делит в золотом сечении правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины в пропорциях золотого сечения.

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Посмотрим внимательно на картину «Джоконда». Композиция портрета построена на»золотых треугольниках».

Портрет Моны Лизы (Джоконда) привлекает тем, что композиция рисунка построена на «золотых треугольниках», точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника. Зрачок левого глаза, через который проходит вертикальная ось полотна, находится на пересечении двух биссектрис верхнего золотого треугольника, которые с одной стороны, делят пополам углы при основании золотого треугольника, а с другой стороны, в точках пересечения с бедрами золотого треугольника делят их в пропорции Золотого сечения.

Таким образом, Леонардо Да Винчи использовал в своей картине не только принцип симметрии, но и Золотое сечение

Картина «Святое семейство» Микеланджело признана одним из шедевров западноевропейского искусства эпохи Возрождения. Гармонический анализ показал, что композиция картины основана на пентакле.

В. И. Суриков «Боярыня Морозова».

Роли ее отведена средняя часть картины. Она окована точкой высшего взлёта и точкой низшего спадания сюжета картины.

1) Это — взлёт руки Морозовой с двуперстным крестным знамением как высшая точка.

2) Это — беспомощно протянутая к той же боярыне рука, но на этот раз — рука старухи — нищей странницы, рука, из-под которой вместе с последней надеждой на спасение выскальзывает конец розвальней.

А как обстоит дело с «высшей точкой»? На первый взгляд имеем кажущееся противоречие: ведь сечение А1В1, отстоящее на 0,618… от правого края картины, проходит не через руку, не даже через голову или глаз боярыни, а оказывается где-то перед ртом боярыни!

Золотое сечение режет здесь действительно по самому главному.

В нём, и именно в нём, — величайшая сила Морозовой.

Заключение

В 13 веке от Рождества Христова известный итальянский математик известный по имени Фиббоначи, наблюдая за различными явлениями живой природы, открыл золотую пропорцию – бесконечную последовательность чисел, где каждое последующее число является сумой двух предыдущих; разделив каждое предыдущее на последующее мы всегда будем получать приблизительно 0,618 (например 987/1597=0,618034). Леонардо Да Винчи, создавая свои картины, использовал особый способ структурного совершенства: он называл его Золотым Сечением, при котором отношение всего отрезка к большей части равно отношению большей части к меньшей и приблизительно равно 0,618. До этого в 6 веке нашей эры греческий философ и математик Пифагор находит это соотношение в геометрии. А в 3 веке нашей эры упоминание о нем можно найти и у древних египтян, которые называли его божественной сутью. Возможно, им было дано знание о существовании особых законов гармонии, которые являются основой всего совершенного в этом мире. Теперь о воде. В обычной воде угол между водородными связями равен 104, а у талой 108 и соотношение длин водородных связей 0,618. Некоторые ученые предполагают, что замерзая и оттаивая, вода неизменно сохраняет одну базовую программу жизни, именно по этой программе и создавалось все совершенное.

Реферат по математике на тему: Золотое сечение читать

Главная>Рефераты по математике

Золотое сечение

Человечество с древних времен интересовал вопрос о том, какую роль играет такая наука как математика в искусстве и эстетике. На первый взгляд может показаться, что эти дисциплины очень далеки друг от друга, но это вовсе не так, и рассмотрение такого феномена как золотое сечение способно это доказать.

Ещё Иоган Кеплер утверждал, что геометрия обладает двумя непревзойденными сокровищами человечества: теоремой Пифагора и Золотым сечением. Конечно, теорема Пифагора известна практически каждому, чего нельзя сказать о золотом сечении.

Итак, чем же является золотое сечение. Сначала рассмотрим на простейшем примере отрезка. Предположим, что дан отрезок AB. Точка С, лежащая на отрезке будет пересекать его в соответствии с золотым сечением в том случае если она разделит его в таком отношении, чтобы: AC : AB = CB : AC. Отсюда делаем вывод, что:

Золотое сечение – это деление целого, на две не равные части таким образом, чтобы отношение большей части к целом равнялось отношению меньшей части к большей.

Пусть длина отрезка равняется а. Примем большую часть данного отрезка за х. Тогда вторая часть будет равняться а-х. Исходя из теоремы о золотом сечении, получим следующую пропорцию, из которой следует, что большая часть данной отрезка является средним геометрическим его длины и­ меньшей части

Кроме того, существует несложный способ построить золотое сечение геометрически. Для это к отрезку АВ проведем перпендикуляр ВD так, чтобы BD=12 AB. Затем соединим точку A c точкой D и получим прямоугольный треугольник. Следующим действием необходимо отложить точку Е на отрезке AD так, чтобы DE=DB, и точку С на АВ так, чтобы АЕ=АС. В результате получаем точку С, которая и является золотым сечением отрезка АВ.

Математики подсчитали, что разделив отрезок в соответствии с золотым сечением, мы получаем две неравные части, каждая из которых составляет приблизительно 62% и 38%. В действительности же эти значения округлены. Таким образом величина золотого сечения соответствует числу 1,6180339887…

Впервые упоминания о данной пропорции встречаются ещё в работах древнегреческого математика Евклида. Но сам термит «золотое сечение» первым употребил и ввел Мартин Ом в IXX веке.

Нет смысла отрицать, что человечество во все времена завораживала тема золотого сечения. Многие художники целенаправленно старались соблюсти в своих работах эту пропорцию, будучи убежденными в том, что она является идеальной и божественной. Зачастую люди наделяли феномен несвойственными ему качествами и свойствами. Но так или иначе следует признать, что теперь, как и много лет тому назад «Золотое сечение» рассматривается человечество не только как математический аспект, но и как культурный.

см. также:
Все рефераты по математике

что такое золотое сечение простыми словами. Тайны мироздания в числах. Золотое сечение морской раковины

Когда смотрим на красивый пейзаж, мы охватываемых все вокруг. Потом уделяем внимание деталям. Речке журчащей или дереву величественному. Видим поле зеленое. Замечаем, как ветер его обнимает нежно и журя шатает со стороны в сторону траву. Можем почувствовать аромат природы и услышать пение птиц…Все гармонично, все взаимосвязано и даёт чувство умиротворения, чувство прекрасного. Восприятие идёт поэтапно чуть меньшими долями.Куда вы сядете на скамье: на край, на середину или в любое место? Большинство ответит, что чуть дальше от середины. Приблизительное число в пропорции скамьи от вашего тела до края будет 1,62. Так и в кинотеатре, в библиотеке,- везде. Инстинктивно создаём гармонию красоту, которую во всем мире называю “Золотым сечением”.

Золотое сечение в математике

Вы задумывались, можно ли определить меру красоте? Оказывается, с математической точки зрения возможно. Простая арифметика даёт понятие об абсолютной гармонии, которая и отображается в безупречной красоте, благодаря принципу Золотого сечения. Архитектурные сооружения др. Египта и Вавилона первыми начали соответствовать данному принципу. Но сформулировал принцип первым Пифагор. В математике это деление отрезка чуть больше половины, а точнее 1,628. Данное соотношение представляется как φ =0,618= 5/8. Маленький отрезок = 0,382 = 3/8, а полностью отрезок принимаем за единицу.

А:B=B:C и C:B=B:A

От принципа золотого сечения отталкивались и великие писатели, архитекторы, скульпторы, музыканты, – люди искусства, и христиане, рисующие пиктограммы (пятиконечные звезды и т.д.) с его элементами в храмах, спасаясь от нечисти, и люди, изучающие точные науки, решающая проблемы кибернетики.

Золотое сечение в природе и явлениях.

Все на земле приобретая форму растет вверх, в сторону или по спирали. Последнему пристально уделил внимание Архимед, составив уравнение. По ряду Фибоначчи устроена шишка, ракушка, ананас, подсолнух, ураган, паутина, молекула ДНК, яйцо, стрекоза, ящерица…

Тицириус доказал, что вся наша Вселенная, космос, галактическое пространство, – все спланировано исходя из Золотого принципа. Абсолютно во всем живом и не живом можно прочесть высшую красоту.

Золотое сечение в человеке.

Кости продуманы природой тоже согласно пропорции 5 /8 . Это и исключает оговорки людей про “кости широкие “. Большинство частей тела в соотношениях применяются к уравнению . Если все частички тела подчиняются Золотой формуле , тогда внешние данные будут весьма привлекательны и идеально сложены .

Отрезок от плеч до верха головы и ее размера = 1 :1 .618
Отрезок от пупа до верха головы и от плеч до верха головы = 1 :1 .618
Отрезок от пупа до коленок и от них до ступней ног = 1 :1 . 618
Отрезок от подбородка до крайней точки верхней губы и от неё до носа = 1 :1 .618

Все расстояния лица дают общее представление об идеальных пропорциях , привлекающих взгляд .
Пальцы , ладонь , тоже подчиняются закону . Необходимо ещё отметить , что отрезок расставленных рук с туловищем равен росту человека . Да что там , все органы , кровь , молекулы , соответствуют Золотой формуле . Истинная гармония внутри и снаружи нашего пространства .

Параметры с физической стороны окружающих факторов.

Громкость звука. Высшая точка звука, вызывающая не комфортное ощущение и боль в ушной раковине = 130 децибелам. Это число можно разделить пропорцией 1,618, тогда выходит, что звук человеческого крика будет = 80 децибел.
Тем же методом двигаясь дальше получаем 50 децибел, что характерно для нормальной громкости речи человека. И последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Простая арифметика гармонии заложена во всем нашем окружении.

Золотое сечение в искусстве.

В архитектуре самые известные здания и сооружения: египетские пирамиды, пирамиды Майя в Мексике, Нотр-дам де Пари, Парфенон греческий, Петровский дворец, и другие.

В музыке: Аренский, Бетховен, Гаван, Моцарт, Шопен, Шуберт, и другие.

В живописи: почти все картины знаменитых художников написаны согласно сечению: разносторонний Леонардо да Винчи и неподражаемый Микеланджело, такие родные в писании Шишкин с Суриковым, идеал чистейшего художества – испанец Рафаэль, и подаривший идеал женской красоты – итальянец Боттичелли, и многие-многие другие.

В поэзии: упорядоченная речь Александра Сергеевича Пушкина, в особенности “Евгений Онегин” и стихотворение “Сапожник”, поэзия замечательных Шота Руставели и Лермонтова, и многих других великих мастеров слова.

В скульптуре: статуя Аполлона Бельведерского, Зевса Олимпийского, прекрасной Афины и грациозной Нефертити, и другие скульптуры и статуи.

В фотографии используется “правило третьей”. Принцип такой: композиция делится на 3 равные части по вертикали и по горизонтали, ключевые моменты располагаются либо на линиях пересечения (горизонт), либо в точках пересечений (объекте). Таким образом пропорции равны 3/8 и 5/8.
В согласно Золотого сечения имеется много уловок, которые стоит разобрать детально. Их опишу подробно в следующей .

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах — рост вверх или расстилание по поверхности земли и закручивание по спирали. Лежащее в основе строения спирали правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях.

Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Среди придорожных трав растет ничем не примечательное растение — цикорий. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

Самые наглядные примеры — спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, строении лепестков роз и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке, семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.

Представление о золотом сечении в природе будет неполным, если не сказать о спирали. Раковина закручена по спирали Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Архимед изучал ее и вывел уравнение логарифмической спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

Пауки всегда плетут свои паутины в виде логарифмической спирали.Испуганное стадо северных оленей разбегается по спирали. В ящерице- длина ее хвоста так относится к длине остального тела, как 62 к 38. Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Золотые пропорции в строении молекулы ДНК. Все сведения о физиологических особенностях живых существ, хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра). 21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.

Тело человека и золотое сечение

Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону золотой пропорции.

Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы.

Первый пример золотого сечения в строении тела человека: если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1,618. Есть еще несколько основных золотых пропорций нашего тела (1:1,618): расстояние от кончиков пальцев до запястья и от запястья до локтя равно расстоянию от уровня плеча до макушки головы и размера головы; расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы; расстояние точки пупа до коленей и от коленей до ступней; расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей; расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки; расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки.

Золотое сечение в чертах лица человека, является критерием совершенной красоты. В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Приведем несколько таких соотношений: высота лица / ширина лица; центральная точка соединения губ до основания носа / длина носа; высота лица / расстояние от кончика подбородка до центральной точки соединения губ; ширина рта / ширина носа; ширина носа / расстояние между ноздрями; расстояние между зрачками / расстояние между бровями.

Золотая пропорция в руках человека. У человека две руки, пальцы на каждой руке состоят из трех фаланг (за исключением большого пальца). Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения. На каждой руке имеется по пять пальцев, но за исключением двух двухфаланговых больших пальцев, только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.

Золотая пропорция в строении легких человека. Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение. Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче. Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.

Золотое сечение присутствует в строении уха человека. Во внутреннем ухе человека имеется орган Cochlea («Улитка»), который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и сотворена в форме улитки, содержащую в себе стабильную логарифмическую форму спирали.

Любое тело, предмет, вещь, геометрическая фигура, соотношение которых соответствует «золотому сечению», отличаются строгой пропорциональностью и производят наиболее приятное зрительное впечатление.

Таким образом, строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле.

Золотое сечение в неживой природе

Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.

Спиралью закручивается ураган. Гете называл спираль “кривой жизни”.

Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.

Золотое сечение в искусстве и архитектуре

Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, это главные правила эстетики.

Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина — горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости. Данное открытие у художников того времени получило название «золотое сечение» картины. Поэтому, для того чтобы привлечь внимание к главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров.

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность — одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в. Золотое сечение присутствует в картине Леонардо да Винчи «Джоконда» . Портрет Монны Лизы долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.

На знаменитой картине И. И. Шишкина «Сосновая роща» с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен — при желании можно с успехом продолжить деление картины по золотому сечению и дальше.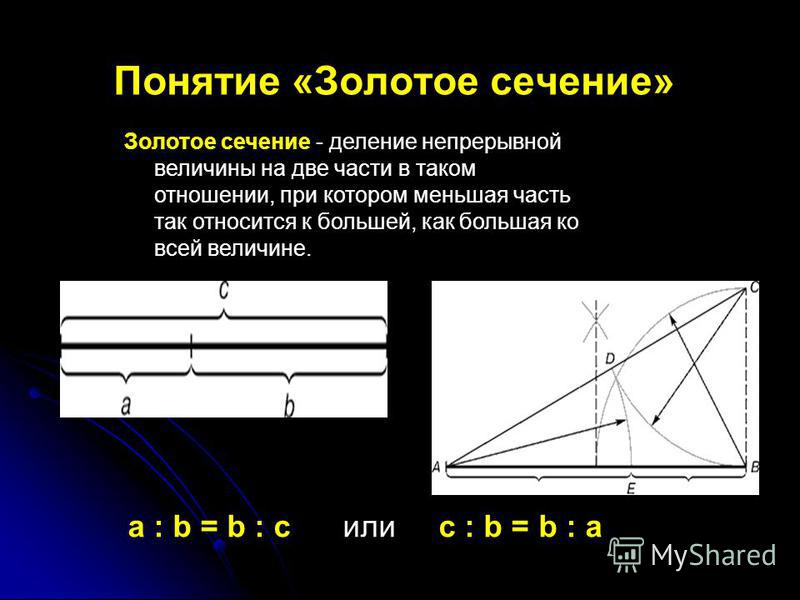

Наличие в любой картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.

В отличие от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре — золотой спирали.

Многофигурная композиция Рафаэля «Избиение младенцев», выполненная в 1509 — 1510 годах Рафаэлем, содержит золотую спираль.Эта картина, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру «Избиение младенцев».

На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции — точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, — вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мячом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то получается…золотая спираль! Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции «Избиение младенцев» или только » чувствовал» ее. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел.

Художник Александр Панкин исследуя, циркулем и линейкой, законы красоты… на знаменитых квадратах Казимира Малевича, заметил, что картины Малевича удивительно гармоничны. Здесь нет ни одного случайного элемента. Взяв единственный отрезок, размер холста или сторону квадрата, можно по одной формуле выстроить всю картину. Есть квадраты, все элементы которых соотносятся в пропорции “золотого сечения”, а знаменитый “Черный квадрат” нарисован в пропорции квадратного корня из двух. Александр Панкин обнаружил, удивительную закономерность: чем меньше стремления самовыразиться, тем больше творчества…Важен канон. Не случайно в иконописи он так строго соблюдается.

Золотое сечение в скульптуре

«Необходимо прекрасному зданию быть построенным подобно хорошо сложенному человеку» (Павел Флоренский)

Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.

Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.

Золотое сечение в архитектуре

В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). В фасаде Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) заложены золотые пропорции.

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.

Другим примером из архитектуры древности является Пантеон.

Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”. Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. 5).

Еще один архитектурный шедевр Москвы — дом Пашкова — является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 году. При восстановлении здание приобрело более массивные формы.

Итак, с уверенностью можно сказать, что золотая пропорция — это та основа формообразования, применение которой обеспечивает многообразие композиционных форм во всех видах искусства и дает основание создать научную теорию композиции и единую теорию пластических искусств.

Древних греков, художников эпохи Возрождения, астрономов XVII века и архитекторов XXI века объединяло то, что все они использовали золотое сечение , иначе известное как золотая пропорция .

Это число Phi — 1.61803399 — обладает действительно уникальными математическими свойствами, проявляется повсюду в природе, благодаря его использованию художники могут создать идеальные по композиции произведения.

Согласно астрофизику Марио Ливи, некоторые из величайших математиков всех эпох: Пифагор и Евклид в Древней Греции, итальянский математик Леонардо Пизанский в Средневековье и астроном Иоганн Кеплер в эпоху Ренессанса, а также современный учёный, физик Роджер Пенроуз из Оксфорда, провели бесконечно много времени, размышляя над этим особым числом и изучая его свойства. Не только математики увлекались золотым сечением.

Биологи, художники, музыканты, историки, архитекторы, психологи и даже мистики обсуждают причину его вездесущности и привлекательности. Можно с уверенностью сказать, что золотое сечение вдохновило мыслителей всех дисциплин, как никакое другое число в истории математики.

В математике и искусстве золотая пропорция проявляется тогда, когда отношение суммы двух величин к большей из них равно отношению большей величины к меньшей. Когда Золотое сечение осмысляется в двух измерениях, оно, как правило, представлено в виде спирали, которая определяется с помощью серии квадратов и дуг, образующих «золотые прямоугольники».

Спиральная форма выражает динамику роста растений и других природных объектов, золотая пропорция проявляется и в строении человеческого тела. Таким образом, это особое соотношение простых спиралей и прямоугольников свидетельствует о присутствии универсального порядка, лежащего в основе мира, поэтому оно было названо золотым или божественным.

Золотое сечение в истории

Золотое сечение очаровывало западных интеллектуалов, по крайней мере, 2400 лет. Самые ранние известные памятники — статуи и храм Парфенона в Греции (490-430 гг. до н.э.) были построены в соответствии с золотой пропорцией.

Тем не менее, многие утверждают, что она была известна гораздо раньше и что египтяне хорошо разбирались в свойствах этого уникального числа.

По мнению некоторых историков, египтяне считали золотое сечение священным. Они использовали золотое сечение при создании храмов и мест захоронения. Кроме того, египтяне обнаружили, что всё, соответствующее золотому сечению, приятно для глаз. Они использовали его в своей системе письменности и проектировании.

Греческий математик Евклид (ок. 365 — 300 до н. э.), описал то, что он назвал «уникальной средней пропорцией». Тем не менее, золотое сечение стало популярным только в XV веке, когда эстетика стала жизненно важным компонентом жизни в эпоху Возрождения, а искусство и геометрия служили и практическим, и символическим целям.

Известный математик, астроном, астролог Иоганн Кеплер (1571 — 1630 гг.) писал: «В геометрии существуют два сокровища: теорема Пифагора и среднее соотношение; первую мы можем сравнить с мерой золота, второе можно назвать драгоценным камнем».

Золотое сечение в архитектуре

Многие художники и архитекторы создавали свои творения в соответствии с золотой пропорцией в надежде получить лучшие результаты с точки зрения эстетики. Используя любое из золотых соотношений, архитектор может создать дверную ручку, соответствующую двери, которая в свою очередь имеет аналогичное соотношение со стенами и всем помещением в целом, и так далее.

Но более всего золотое сечение проявлено в фасаде зданий-шедевров архитектуры: от Парфенона до Великой мечети Кайруана, от Сиднейского оперного театра до Национальной галереи в Лондоне.

Золотое сечение в природе

Самым удивительным в золотом сечении является то, что оно может рассматриваться как естественное явление в природе. Золотое сечение выражается в расположении ветвей вдоль стволов деревьев, прожилок в листьях. Его можно увидеть в строении скелетов животных и людей, в разветвлении их вен и нервов.

Оно даже может быть замечено в пропорции химических соединений и геометрии кристаллов. По сути, оно вокруг и внутри нас, и по этой причине немецкий психолог Адольф Цейзинг (1810 — 1876 гг.) назвал его «универсальным законом, в котором содержится основной принцип формирования всего, стремление к красоте и полноте в природе и искусстве, который пронизывает, как первостепенный духовный идеал, все структуры, формы и пропорции, будь то космические или индивидуальные, органические или неорганические, акустические или оптические; который полностью реализован в теле человека».

Благодаря уникальным свойствам золотого сечения многие считают его священным или божественным, позволяющим обрести более глубокое понимание красоты и духовности в жизни, увидеть скрытую гармонию и связность во всём, что нас окружает.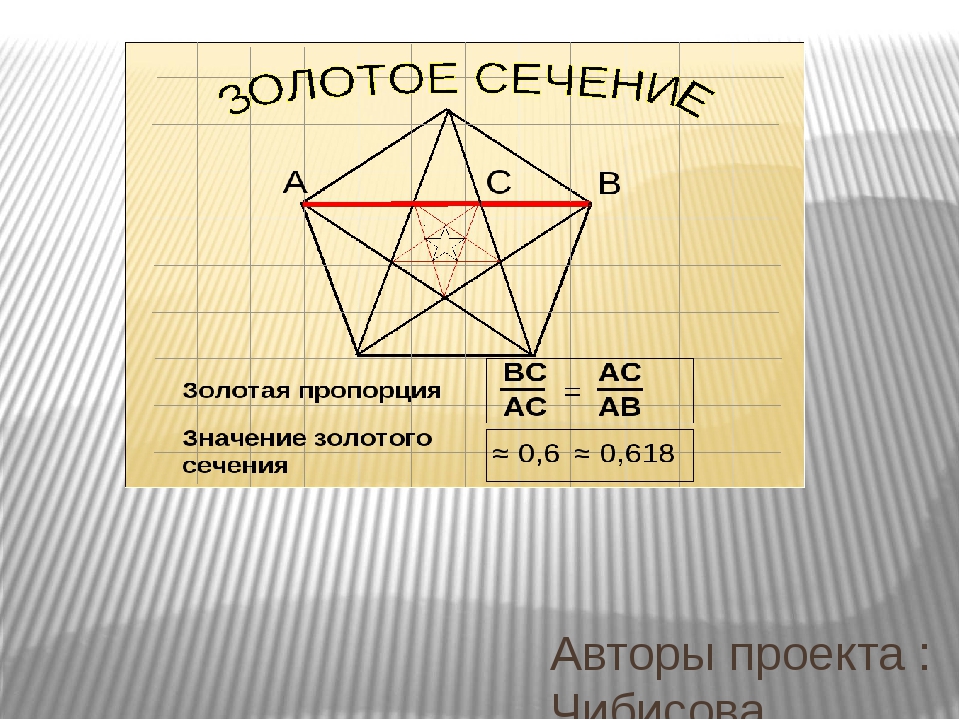

Яковлева Алёна

Цель работы – изучить понятие Золотое сечение, рассмотреть, как Золотое сечение используется природой.

В реферате подробно рассматриваются понятия Золотого сечения, Золотого прямоугольника, Золотой спирали и их применение в природе. Описываются исследования, проведенные в классе.

Скачать:

Предварительный просмотр:

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №48»

ГОРОДСКАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ

Секция: математика, биология

«Золотое сечение в природе».

МОУ г.Кургана «СОШ №48»,

8 «Б» класс.

Научные руководители: Якущенко

Татьяна Александровна

Учитель биологии,

МОУ г.Кургана «СОШ №48»,

Баева Лилия Николаевна,

МОУ г.Кургана «СОШ №48»,

Учитель математики.

Курган,

2010 г.

1. Введение стр. 3
2. Понятие Золотого сечения стр.5
3. История Золотого сечения стр. 5
4. Золотой прямоугольник стр.7
5. Золотая спираль стр.8
6. Золотые спирали в живой природе стр.9
7. Вездесущий филлотаксис стр.10
8. Золотое сечение в природе стр.11
9. Золотые пропорции в теле человека стр.12
10. Мои исследования стр.13
11. Заключение стр.13
12. Приложение стр. 16
13. Список литературы стр.15

Введение. О живой и неживой природе.

Природа, понимаемая как весь мир в многообразии его форм, состоит как бы из двух частей: живая и неживая природа. В чем различие между ними? Для творений неживой природы характерна высокая устойчивость, слабая изменчивость, если судить в масштабах человеческой жизни. Человек рождается, живет, стареет, умирает, а гранитные горы (прил. 1) остаются такими же и планеты вращаются вокруг Солнца так же, как и во времена Пифагора.

Мир живой природы предстает перед нами совсем иным — подвижным, изменчивым и удивительно разнообразным. Жизнь демонстрирует нам фантастический карнавал разнообразия и неповторимости творческих комбинаций!(прил. 2) Мир неживой природы — это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир живой природы — это прежде всего мир гармонии, в которой действует закон Золотого сечения.

Цель моей работы – изучить понятие Золотое сечение, рассмотреть как Золотое сечение используется природой.

Из цели вытекают задачи:

Изучить литературу по данной теме;

Изучить понятие Золотое сечение», рассмотреть как «Золотое сечение» используется природой;

Источниками исследования явились:

1. библиотечные фонды;
2. интернет;
3. библиотека моего научного руководителя.

Методы исследования:

1. изучение материалов по теме;
2. работа с классом;

Понятие Золотого сечения

Золото́е сече́ние (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление, φ) — деление отрезка на части в таком соотношении, при котором меньшая часть относится к большей, как большая ко всему в целом. Например, деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ (т. е. |АВ| / |ВС| = |АС| / |АВ|). (прил.3) Эту пропорцию принято обозначать греческой буквой, φ и она равна: 1.618 (прил.4)

Отрезки золотой пропорции выражаются иррациональной бесконечной дробью 0,618…, если c принять за единицу, a = 0,382. Числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи. На этой пропорции базируются основные геометрические фигуры.

Если вы подходите к пустой скамейке и садитесь на неё, то вы сядете не посередине скамейки (как-то нескромно, хотя встречаются и такие, ярко выраженные характеры) и, конечно, не на самый край. Если вы незаметно замерите длины, на которые своим телом разделили скамейку, то обнаружите, что отношение большего отрезка к меньшему равно отношению всей длины к большему отрезку и равно примерно 1,62. Это число, называемое Золотым сечением, входит в тройку самых известных иррациональных чисел, то есть таких чисел, десятичные представления которых бесконечны и непериодичны.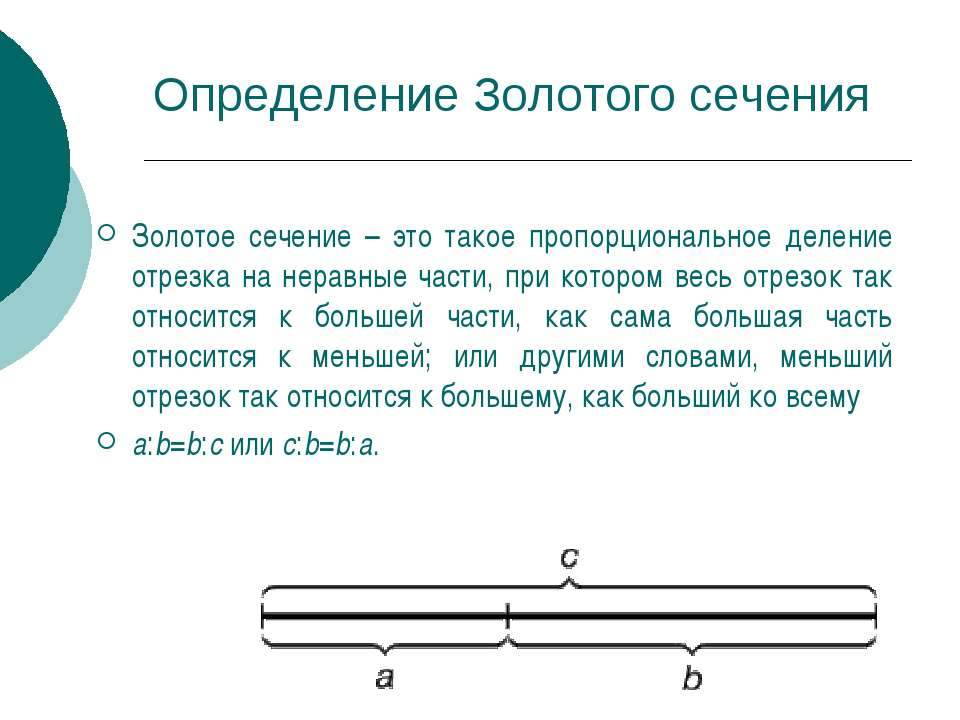

История Золотого сечения.

Принято считать, что понятие о Золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Kвадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.
Платон (прил.5) (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида (прил.6) Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж.Kампано из Наварры (III в.) сделал к переводу комментарии. Cекреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре.
Лука Пачоли (прил.7) прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи (прил.8). В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Kнига была восторженным гимном Золотой пропорции. Cреди многих достоинств Золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына)

Золотой прямоугольник

Золотое сечение очень широко используется в геометрии. Мы начнем наше путешествие по геометрическим свойствам Золотого сечения с Золотого прямоугольника, которые имеет следующее геометрическое определение. Золотым прямоугольником называется такой прямоугольник, в котором отношение большей стороны к меньшей равно золотой пропорции (прил.9) Рассмотрим случай простейшего Золотого прямоугольника, когда AB = и BC = 1.(прил.10)

Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим Золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие Золотые прямоугольники. Причем располагаться они будут по логарифмической спирали (прил.11), имеющей важное значение в математических моделях природных объектов (например, раковинах улиток). Полюс спирали лежит на пересечении диагоналей начального прямоугольника BD и первого отрезаемого вертикального AC. Причем, диагонали всех последующих уменьшающихся Золотых прямоугольников лежат на этих диагоналях (прил.12)

Золотое сечение было известно древним грекам. Вряд ли можно сомневаться в том, что некоторые древнегреческие архитекторы и скульпторы сознательно использовали его в своих творениях. Примером может служить хотя бы Парфенон. Именно это обстоятельство и имел в виду американский математик Марк Барр, когда предложил называть отношение двух отрезков, образующих золотое сечение, числом. Буква (фи) — первая буква в имени великого Фидия.

В то время как Золотое сечение и Золотой прямоугольник представляют статические формы естественной и сотворенной человеком красоты и деятельности, представление эстетически привлекательного динамизма, организованного движения роста и развития может быть выполнено только самой прекрасной формой во Вселенной — Золотой спиралью.

Золотая Спираль

Золотой прямоугольник можно использовать для построения Золотой спирали. Любой Золотой прямоугольник, можно разделить на квадрат и меньший Золотой прямоугольник.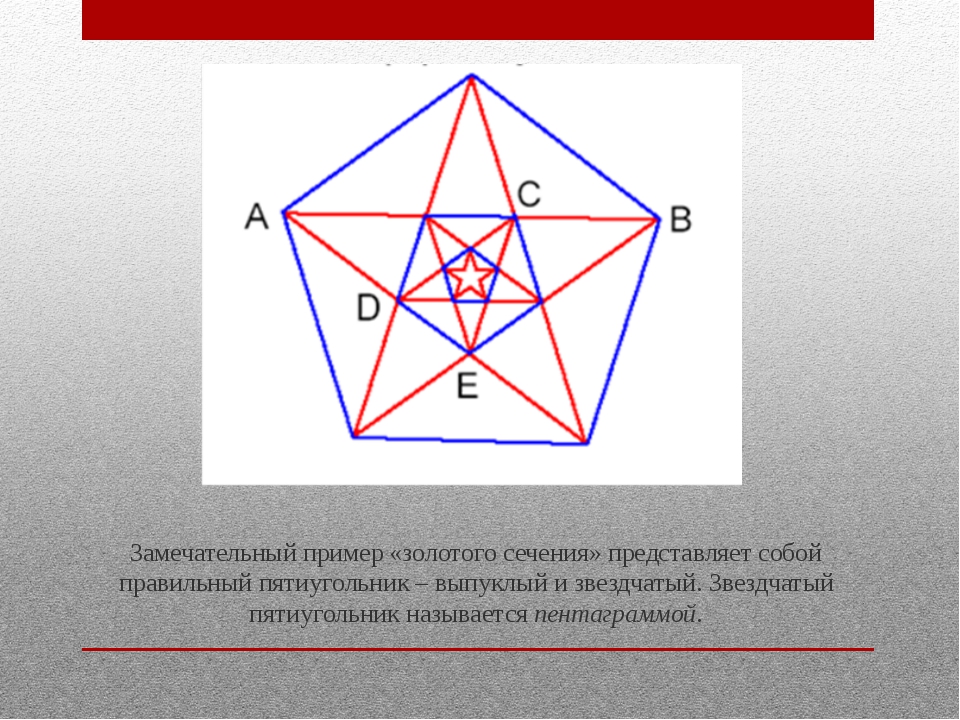 Этот процесс теоретически можно продолжать до бесконечности. Эти получающиеся прямоугольники, которые мы нарисовали и которые, как оказалось, скручиваются внутрь, промаркированы A, B, C, D, E, F и G (прил.13) Пунктирные линии, которые сами находятся в золотом соотношении одна к другой, рассекают прямоугольники по диагонали и точно обозначают теоретический центр, скручивающихся квадратов. Приблизительно из центральной точки мы можем начертить спираль (прил.14), соединяя точки пересечения каждого скручивающегося квадрата в порядке возрастания размера. Так как квадраты скручиваются внутрь и наружу, их точки соединения выписывают Золотую спираль. Для построения Золотой спирали может применяться такой же процесс, но с использованием скручивающихся треугольников.

В любой точке развития Золотой спирали, отношение длины дуги к ее диаметру равно 1.618. Диаметр и радиус в свою очередь соотносятся с диаметром и радиусом, отстоящих на угол в 90 градусов, с коэффициентом 1.618 (прил.15), Золотая спираль, которая является разновидностью логарифмической или изогональной спирали, не имеет границ и является

постоянной по форме. Из любой точки спирали можно двигаться бесконечно или в направлении внутрь, или наружу. Центральная часть логарифмической спирали, рассмотренная через микроскоп, имела бы тот же облик, что и самая широкая видимая ее часть на удалении многих световых лет.

Золотые спирали в живой природе

Золотые спирали широко распространены в биологическом мире. Как отмечалось выше, рога животных растут лишь с одного конца. Этот рост осуществляется по логарифмической спирали. В книге «Кривые линии в жизни» Т. Кук исследует различные виды спиралей, проявляющихся в рогах (прил.16) баранов, коз, антилоп и других рогатых животных. Среди множества спиралей он выбирает Золотую спираль (кривую гармонического возрастания) и рассматривает ее как символ эволюции и возрастания.

Спирали широко проявляют себя в живой природе. Спирально закручиваются усики растений (прил.17), по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровне.

Спиралевидную форму имеют большинство раковин (прил.18-19). Изучая конструкции раковин, ученые обратили внимание на целесообразность форм и поверхностей раковин: внутренняя поверхность гладкая, наружная — рифленая. Внутри покоится тело моллюска — внутренняя поверхность должна быть гладкой. Наружные ребра увеличивают жесткость раковины и, таким образом, повышают ее прочность. Форма раковин поражает своим совершенством и экономичностью средств, затраченных на ее создание. Идея спирали в раковинах выражена не приближенно, а в совершенной геометрической форме, в удивительно красивой, «отточенной» конструкции.

Русский ученый С.В. Петухов, изучая схемы строения опорно-двигательного аппарата у различных позвоночных животных, пришел к выводу о том, что построение их конечностей происходило под воздействием двух факторов: законов Золотой пропорции и приспособление организма к образу жизни:

«Законы Золотой пропорции определили основной план, основную идею конструкции конечностей, а конкретные условия существования каждого животного обусловили отклонения — флуктуации от этого плана все многообразие строения существующих форм».

Вездесущий филлотаксис .

Характерной чертой строения растений и их развития является

спиральность. Еще Гете, который был не только великим поэтом, но и

естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений, по спирали происходит рост ткани в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровнях.

Нет сомнений, что наследственная спиральность является одним из

основных свойств организмов, она отражает один из существенных признаков живого. На первый взгляд кажется, что в кристаллах неорганических веществ спиральность или винтовая структура отсутствуют. Однако более глубокие исследования показали, что винтовое расположение атомов наблюдается и в некоторых кристаллах и выражается в образовании так называемых винтовых дислокаций. Такие кристаллы состоят из единственной винтообразной изогнутой атомной плоскости. При каждом обороте вокруг оси эта плоскость поднимается

на один шаг винта, равный межатомному расстоянию. Следует добавить, что кристаллы с такой винтовой структурой обладают сверхпрочностью. От винтовой структуры молекул ДНК до закручивания усиков растений – таковы формы проявления спиральности на различных уровнях организации растений.

Отчетливо проявляется эта особенность организации растений в

закономерностях листорасположения.

Существует несколько способов листорасположения. В первом листья

побега располагаются строго один под другим, образуя вертикальные ряды – ортостихи. Условная спираль, соединяющая места расположения листьев на побеге, называется генетической, или основной спиралью, точнее, винтовой линией и делится на ряд листовых циклов. Генетическим этот винт называется потому, что расположение листьев в нем отвечает порядку появления в нем листьев. Проекция на плоскость листорасположения позволяет в долях окружности выразить угол расхождения листьев.

Рассмотренную закономерность расположения листьев, чешуек, семян

называют филлотаксисом. Установлено, что при расположении

листьев под идеальным углом ни один лист не будет располагаться точно над другим, чем создаются лучшие условия для фотосинтеза

Золотое сечение в природе.

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах — рост вверх или расстилание по поверхности земли и закручивание по спирали.

Среди придорожных трав растет ничем не примечательное растение — цикорий (прил.20). Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т.д. Длина лепестков тоже подчинена Золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции Золотого сечения.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38 (прил.21).

Золотые пропорции в теле человека.

В 1855 г. немецкий исследователь Золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию Золотого сечения, объявив ее универсальной для всех явлений природы и искусства.

У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что Золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к Золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6. У новорожденного пропорция составляет отношение 1: 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции Золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т.д. (прил.22).

Мои исследования.

Я рассмотрела комнатные цветы в школе и дома и выделила те, которые растут по законам Золотого сечения (Приложения 23 — 29) и те, которые растут по законам Золотой спирали (Приложения 30 — 34).

В классе я провела следующее исследование – предложила ребятам сесть на скамейку. Все данные сведены в таблицу (Приложение 35), проведены расчеты отношений длины скамейки к большей части и большей части к меньшей. Получилось примерно 1,6. Это число и есть Золотое сечение.

Заключение.

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и Золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип Золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе .

Список литературы

1. Н. Васютинский “Золотая пропорция” –М.,”Молодая гвардия”, 1990
2. А. Азевич “Двадцать уроков гармонии” –М., “Школа-Пресс”, 1998
3. М. Гарднер “Математические головоломки и развлечения” –М., “Мир”, 1971
4. Д. Пидоу “Геометрия и искусство” – М., “Мир”, 1989
5. Энциклопедический словарь юного математика –М.,1989
6. Журнал “Квант”, 1973, № 8
7. Журнал “Математика в школе”, 1994, № 2, № 3

В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Можно отметить два вида проявлений золотого сечения в живой природе: иррациональные отношения по Пифагору — 1.62 и целочисленные, дискретные — по Фибоначчи.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи. Хорошо известна «золотая» пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода — молекулы ДНК и РНК — имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Еще Гете подчеркивал тенденцию природы к спиральности. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни». Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках «упакованы» по логарифмическим («золотым») спиралям, завивающимся навстречу друг другу, причем числа «правых «и «левых» спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.

Приглядимся внимательно к побегу цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.

Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого

Великий Гете, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввел в научный обиход термин морфология.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Золотое сечение

Любому человеку, которому хотя бы косвенно приходилось сталкиваться с геометрией пространственных объектов в интерьерном дизайне и архитектуре, наверняка хорошо известен принцип золотого сечения. Еще недавно, несколько десятков лет назад, популярность золотого сечения была настолько высокой, что многочисленные сторонники мистических теорий и устройства мира его называют универсальным гармоническим правилом.

Сущность универсальной пропорции

Удивительно другое. Причиной предвзятого, почти мистического отношения к столь простой числовой зависимости послужило несколько необычных свойств:

• Большое количество объектов живого мира, от вируса до человека, имеют основные пропорции тела или конечностей, очень близкие к значению золотого сечения;
• Зависимость 0,63 или 1,62 характерна только для биологических существ и некоторых разновидностей кристаллов, неживые объекты, от минералов до элементов ландшафта, обладают геометрией золотого сечения крайне редко;
• Золотые пропорции в строении тела оказались наиболее оптимальными для выживания реальных биологических объектов.

Сегодня золотое сечение находят в строении тела животных, панцирей и раковин моллюсков, пропорций листьев, веток, стволов и корневых систем у достаточно большого числа кустарников и трав.

Многими последователями теории универсальности золотого сечения неоднократно предпринимались попытки доказать тот факт, что его пропорции являются наиболее оптимальными для биологических организмов в условиях их существования.

Обычно в качестве примера приводится устройство раковины Astreae Heliotropium, одного из морских моллюсков. Панцирь представляет собой свернутую спиралью кальцитовую оболочку с геометрией, практически совпадающей с пропорциями золотого сечения.

Более понятным и очевидным примером является обычное куриное яйцо.

Соотношение основных параметров, а именно, большого и малого фокуса, или расстояний от равноудаленных точек поверхности до центра тяжести, будет также соответствовать золотому сечению. При этом форма скорлупы птичьего яйца является наиболее оптимальной для выживания птицы, как биологического вида. При этом прочность скорлупы играет далеко не главную роль.

Происхождение универсальной пропорции

О золотой пропорции сечения знали древнегреческие математики Евклид и Пифагор. В одном из памятников древней архитектуры — пирамиде Хеопса соотношение сторон и основания, отдельные элементы и настенные барельефы выполнены в соответствии с универсальной пропорцией.

Методика золотого сечения широко использовалась в средние века художниками и архитекторами, при этом суть универсальной пропорции считалась одной из тайн вселенной и тщательно скрывалась от простого обывателя. Композиция многих картин, скульптур и зданий выстраивалась строго в соответствии с пропорциями золотого сечения.

Впервые суть универсальной пропорции документально была сформулирована в 1509 г монахом-францисканцем Лукой Пачоли, обладавшим блестящими математическими способностями. Но настоящее признание состоялось после проведения немецким ученым Цейзингом всестороннего изучения пропорций и геометрии человеческого тела, древних скульптур, произведений искусства, животных и растений.

У большинства живых объектов некоторые размеры тела подчиняются одним и тем же пропорциям. В 1855 г ученым был сделан вывод о том, что пропорции золотого сечения являются своеобразным стандартом гармонии тела и формы. Речь идет, прежде всего, о живых существах, для мертвой природы золотое сечение встречается значительно реже.

Как получили золотое сечение

Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.

Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.

На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.

Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:

• Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
  
  Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
• Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
• В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.

Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.

Главный секрет золотого сечения

Если природные проявления универсального сечения в пропорциях тел животных и человека, стеблевой основы растений еще можно объяснить эволюцией и приспосабливаемостью к влиянию внешней среды, то открытие золотого сечения в строительстве домов XII-XIX века стало определенной неожиданностью. Мало того, знаменитый древнегреческий Парфенон был построен с соблюдением универсальной пропорции, многие дома и замки состоятельных вельмож и зажиточных людей в средние века строились сознательно с параметрами, очень близкими к золотому сечению.

Золотое сечение в архитектуре

Многие из построек, сохранившихся до сегодняшних дней, свидетельствуют, что архитекторы средневековья знали о существовании золотого сечения, и, конечно, при строительстве дома руководствовались своими примитивными расчетами и зависимостями, с помощью которых пытались добиться максимальной прочности. Особенно проявлялось желание строить максимально красивые и гармоничные дома в постройках резиденций царствующих особ, церквей, ратуш и зданий, имеющих особое социальное значение в обществе.

Например, знаменитый собор Парижской богоматери в своих пропорциях имеет немало участков и размерных цепей, соответствующих золотому сечению.

Еще до публикации своих исследований в 1855 году профессором Цейзингом, в конце XVIII века были построены знаменитые архитектурные комплексы Голицынской больницы и здания сената в Санкт-Петербурге, дома Пашкова и Петровского дворца в Москве с использованием пропорций золотого сечения.

Разумеется, дома с точным соблюдением правила золотого сечения строили и ранее. Стоит упомянуть памятник древней архитектуры церкви Покрова на Нерли, изображенный на схеме.

Всех их объединяет не только гармоничное сочетание форм и высокое качество строительства, но и, в первую очередь, наличие золотого сечения в пропорциях здания. Удивительная красота постройки становится еще более загадочной, если принять во внимание возраст, здание церкви Покрова датируется XIII веком, но современный архитектурный облик постройка получила на рубеже XVII века в результате реставрации и перестройки.

Особенность золотого сечения для человека

Старинная архитектура зданий и домов средневековья остается притягательной и интересной для современного человека по многим причинам:

• Индивидуальный художественный стиль в оформлении фасадов позволяет избежать современного штампа и серости, каждое здание представляет собой произведение искусства;
• Массовое использование для декорирования и украшения статуй, скульптур, лепнины, необычных сочетаний строительных решений разных эпох;
• Пропорции и композиции здания притягивают взор к наиболее важным элементам постройки.

Важно! При проектировании дома и разработке внешнего вида средневековые архитекторы применяли правило золотого сечения, неосознанно используя особенности восприятия подсознания человека.

Современные психологи экспериментально доказали, что золотое сечение является проявлением неосознанного желания или реакции человека на гармоничное сочетание или пропорцию в размерах, формах и даже цветах. Был проведен эксперимент, в ходе которого группе людей, незнакомых между собой, не имеющих общих интересов, разных профессий и возрастных категорий, предложили ряд тестов, среди которых была задача согнуть лист бумаги в наиболее оптимальной пропорции сторон. По результатам тестирования было установлено, что в 85 случаях из 100 лист сгибался испытуемыми практически точно по золотому сечению.

Поэтому современная наука считает, что феномен универсальной пропорции является психологическим явлением, а не действием каких-либо метафизических сил.

Использование фактора универсального сечения в современном дизайне и архитектуре

Принципы применения золотой пропорции в последние несколько лет стали необыкновенно популярны в строительстве частных домов. На смену экологии и безопасности строительных материалов пришли гармоничность конструкции и правильное распределение энергии внутри дома.

Современная интерпретация правила всеобщей гармонии давно распространилась за пределы привычной геометрии и формы объекта. Сегодня правилу подчиняются не только размерные цепи длины портика и фронтона, отдельных элементов фасада и высоты здания, но и площадь комнат, оконных и дверных проемов, и даже цветовая гамма внутреннего интерьера помещения.

Проще всего построить гармоничный дом на модульной основе. В этом случае большинство отделений и комнат изготавливаются в виде самостоятельных блоков или модулей, спроектированных с соблюдением правила золотого сечения. Построить здание в виде набора гармоничных модулей значительно проще, чем строить одну коробку, в которой большая часть фасада и внутренних помещений должна быть в жестких рамках пропорций золотого сечения.

Немало строительных фирм, выполняющих проектирование частных домовладений, используют принципы и понятия золотого сечения для увеличения сметы и создания у клиентов впечатления глубокой проработки конструкции дома. Как правило, такой дом декларируется, как очень удобный и гармоничный в пользовании. Правильно подобранное соотношение площадей комнат гарантирует душевный комфорт и отменное здоровье хозяев.

Если дом был построен без учета оптимальных соотношений золотого сечения, можно выполнить перепланировку комнат так, чтобы пропорции помещения соответствовали соотношению стен в пропорции 1:1,61. Для этого может перемещаться мебель или устанавливаться дополнительные перегородки внутри комнат. Аналогичным образом меняются размеры оконных и дверных проемов так, чтобы ширина проема была меньше высоты дверного полотна в 1,61 раза. Таким же способом выполняется планирование мебели, бытовой техники, отделки стен и пола.

Сложнее выбрать цветовое оформление. В этом случае вместо привычного соотношения 63:37 последователями золотого правила принята упрощенная трактовка – 2/3. То есть основной цветовой фон должен занимать 60% пространства помещения, оттеняющему цвету отдают не более 30%, и остальное отводится под различные родственные тона, призванные усилить восприятие цветового решения.

Внутренние стены помещения делятся горизонтальным поясом или бордюром на высоте 70 см, установленная мебель должна соизмеряться с высотой потолков по соотношению золотого сечения. То же правило касается распределения длин, например, размер дивана не должен превышать 2/3 длины простенка, а общая площадь, занимаемая мебелью, относится к площади комнаты, как 1:1,61.

Золотую пропорцию сложно в массовом порядке применять на практике из-за всего лишь одного значения сечения, поэтому при проектировании гармоничных зданий нередко прибегают к ряду чисел Фибоначчи. Это позволяет расширить количество возможных вариантов пропорций и геометрических форм основных элементов дома. В этом случае ряд чисел Фибоначчи, связанных между собой четкой математической зависимостью, называют гармоническим или золотым.

В современной методике проектирования жилья на основе принципа золотого сечения, кроме ряда Фибоначчи, широко используется принцип, предложенный известным французским архитектором Ле Корбюзье. В этом случае в качестве отправной единицы измерения, по которой рассчитываются все параметры здания и внутреннего интерьера, выбирается рост будущего владельца или средняя высота человека. Такой подход позволяет спроектировать дом не только гармоничный, но и по-настоящему индивидуальный.

Заключение

На практике, по отзывам тех, кто решился на строительство дома по правилу золотого сечения, качественно построенное здание действительно оказывается достаточно удобным для проживания. Но стоимость строения из-за индивидуального проектирования и применения стройматериалов нестандартных размеров возрастает на 60-70%. И в этом подходе нет ничего нового, так как большинство зданий прошлого века строилось именно под индивидуальные особенности будущих хозяев.

О золотом сечении

1. Понятие гармонии Вот как пишет о гармонии Алексей Петрович Стахов, доктор технических наук (1972 г.), профессор (1974 г.), академик Академии инженерных наук Украины (www.goldenmuseum.com). «С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель — служить хранилищем воды, оружием на охоте и т. д., демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции изучение сущности красоты, прекрасного, сформировалось в самостоятельную ветвь науки — эстетику, которая у античных философов была неотделима от космологии. Тогда же родилось представление о том, что основой прекрасного является гармония. Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый — красоту в истине. Красота скульптуры, красота храма, красота картины, симфонии, поэмы… Что между ними общего? Разве можно сравнивать красоту храма с красотой ноктюрна? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов — от цветка ромашки до красоты обнаженного человеческого тела…». Известный итальянский теоретик архитектуры Леон-Баттиста Альберти, написавший много книг о зодчестве, говорил о гармонии следующее: «Есть нечто большее, слагающееся из сочетания и связи трех вещей (числа, ограничения и размещения), нечто, чем чудесно озаряется весь лик красоты. Это мы называем гармонией, которая, без сомнения, источник всякой прелести и красоты. Ведь назначение и цель гармонии — упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту… Она охватывает всю жизнь человеческую, пронизывает всю природу вещей. Ибо все, что производит природа, все это соизмеряется законом гармонии. И нет у природы большей заботы, чем та, чтобы произведенное ею было совершенным. Этого никак не достичь без гармонии, ибо без нее распадается высшее согласие частей». В Большой Советской Энциклопедии дается следующее определение понятия «гармония»: «Гармония — соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия». «Формул красоты» уже известно немало. Уже давно в своих творениях люди предпочитают правильные геометрические формы — квадрат, круг, равнобедренный треугольник, пирамиду и т. д. В пропорциях сооружений отдаются предпочтение целочисленным соотношениям. Из многих пропорций, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Эту пропорцию называли по разному — «золотой», «божественной», «золотым сечением», «золотым числом», «золотой серединой». рис. 1 «Золотая пропорция» — это понятие математическое и ее изучение — это прежде всего задача науки. Но она же является критерием гармонии и красоты, а это уже категория искусства и эстетики. И наш Музей, который посвящен изучению этого уникального феномена, является, несомненно, научным музеем, посвященным изучению гармонии и красоты с математической точки зрения». На сайте А. П. Стахова (www.goldenmuseum.com) приводится много интересной и поучительной информации о замечательных свойствах золотого сечения. И это не удивительно. С понятием «золотое сечение» связывают гармонию Природы. При этом с гармонией, как правило, связывают принципы симметрии в живой и неживой Природе. Поэтому всеобщностью проявления принципа золотого сечения сегодня уже никого не удивишь. И каждое новое открытие в сфере выявления еще одной золотой пропорции уже никого не поражает, разве что самого автора такого открытия. Всеобщность этого принципа ни у кого не вызывает сомнения. В различных справочниках приводятся сотни формул, связывающих ряд Фибоначчи с золотым сечением, в том числе и ряд формул, отражающих взаимодействия в мире элементарных частиц [92]. Среди этих формул хочется отметить одну- бином Ньютона для золотой пропорции где -число перестановок. А бином Ньютона, как известно, отражает степенную функцию двойственного отношения. Данная формула привязывает бином золотого отношения к Единице. Без этого принципа, по сути дела, нельзя рассмотреть ни одной фундаментальной проблемы. В милогии эта пропорция обоснована как принцип самодостаточности. И все же несмотря на всеобщность золотая пропорция на практике используется далеко не всегда, и не везде. 2. МОНАДА И ЗОЛОТОЕ СЕЧЕНИЕ Принципы симметрии лежат в основе теории относительности, квантовой механики, физики твердого тела, атомной и ядерной физики, физики элементарных частиц. Выше было показано, что симметрия — это одна из форм проявления двойственности. Поэтому нет ничего удивительного в том, что эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. В [1,2] показано, что симметрия и асимметрия не просто взаимосвязаны друг с другом, а они являются разными формами проявления закономерности двойственности. Закономерность двойственности является одним из основных механизмов эволюции живой и неживой материи. Действительно, способность к размножению у живых организмов можно естественно объяснить только тем, что в процессе своего развития организм полностью достраивает свою оболочку и попытка дальнейшего усложнения структуры приводит, в силу закономерности об ограниченности и замкнутости, к трансформации из организма с внутренней двойственностью в организм с внешней двойственностью, т. е. удвоению, которое осуществляется путем деления оригинала. Затем процесс повторяется. Закономерность двойственности является ответственной за создание дублирующих органов в живом организме. Это дублирование не является следствием эволюции живых организмов. В основе золотого сечения лежит простая пропорция, которая хорошо видна на рисунке золотой спирали: Правила золотого сечения были известны еще в Вавилонии и древнем Египте. Пропорции пирамиды Хеопса, предметов из гробницы Тутанхамона, других произведений древнего искусства красноречиво об этом свидетельствуют, а сам термин «золотое сечение» принадлежит Леонардо да Винчи. С тех пор многие шедевры искусства, архитектуры и музыки выполняются при неукоснительном соблюдении золотой пропорции, несомненно отражающей строение наших сенсорных оболочек — глаз и ушей, головного мозга — анализатора геометрических, цветовых, световых, звуковых и других образов. Золотое сечение обладает еще одной тайной. Оно скрывает в себе свойство самонормирования. Академик Толкачев В. К. в своей книге „Роскошь системного мышления“ так пишет об этом важном свойстве золотого сечения: „Когда-то Клавдий Птолемей разделил равномерно рост человека на 21 отрезок и выделил две основные части: большую (мажор), состоящую из 13-и отрезков, и меньшую (минор) — из 8-и. При этом оказалось, что отношение длины всей фигуры человека к длине ее большей части равно отношению большей части к меньшей… Проиллюстрировать золотое отношение можно следующим образом. Если единичный отрезок разделить на две неравные части (мажор и минор) так, что длина всего отрезка (т.е. мажор + минор = 1) относится к мажору точно так же, как мажор относится к минору: (мажор + минор) / мажор = мажор / минор = Ф, то такая задача имеет решение в виде корней уравнения х2 — х — 1 =0, численное значение которых: х1 = — 0,618033989…, х2 = 1,618033989…, Первый корень обозначается буквой „Ф“, а второй „- Ф“, но мы будем пользоваться иными обозначениями: Ф=1,618033989…, а Ф-1= 0,618033989… Это — единственное число, которое обладает свойством быть ровно на единицу больше своего обратного отношения“. Отметим, что другое уравнение х2 — y- 1 =xy превращается в тождество при следующих значениях х1 = + 0,618033989…, y1 =- 1,618033989…, x2 = -1,618033989…, y2= 0,618033989…, Может быть в совокупности эти корни и порождают животворящий крест— крест золотого сечения? Уравнение золотого сечения Ф2-Ф=1 где Ф1 = -Ф-1= — 0,618033989…, и Ф2 = Ф1=1,618033989…, удовлетворяют свойству самонормирования, позволяющее строить более сложные „конструкции“ по „образу и подобию“. Подставляя корни в уравнение х (х-1)=1, мы получим Ф1(Ф1-1)= 1,618.*1,618.-1,618.=2,618.-1,618.=1 Ф-2-(-Ф-1)=0,382…+0,6181=1. Таким образом, данное уравнение отражает не только принцип самонормирования, вытекающего из Единого закона эволюции двойственного отношения (монады), но и связь золотого сечения с биномом Ньютона (с монадой). Нетрудно показать, что будут справедливы следующие тождества Ф-2=0,382…; Ф-1=0,618…; Ф1=1,618…; Ф2=2,618…; Откуда непосредственно можно увидеть, что корни уравнения Ф2-Ф=1 обладают еще и другим и замечательными свойствами Ф1Ф-1=Ф0 =1 и Ф-1(Ф1-1)= 1-Ф-1; Ф1(Ф-1-1)=1-Ф1=1; Оно характеризует инвариантность одной математической монады в другую, путем умножения её на обратную величину, т. е. можно сказать, что корни уравнения золотого сечения сами формируют золотую, самонормированную монаду <Ф-1, Ф1>. Поэтому данное уравнение по праву можно назвать уравнением золотого сечения. Дополнительные свойства этого уравнения может узнать каждый, используя бином Ньютона и производящие функции (Преемственность). Нетрудно понять, что процесс все более сложных „золотых монад“ будет осуществляться „по образу и подобию“, т. е. этот процесс будет периодически повторяющимся, а все результаты оказываются как бы замкнутыми в рамки золотого сечения. Но, пожалуй, самые замечательные свойства золотого сечения связаны, в первую очередь, с уравнением золотого сечения, приведенным выше. Это уравнение является двойственным х2 + х — 1 =0. Корни этого уравнения численно равны: х1 = + 0,618033989…, х2 = -1,618033989…, Это значит, что уравнения золотого сечения формируют крест золотого сечения с перекладинами рис. 2 Вот он, поистине золотой крест, лежащий в основе мироздания! На правом рисунке непосредственно видно, что значения выражения в полюсах вертикальной перекладины равны 1. Из креста на левом рисунке видно также, что при каждом переходе с одной перекладины на вторую осуществляются самонормировки. Самонормировка происходит как при сложении, так и при умножении. Разница получается только в знаке. И это не случайно. При движении по перекладинам мы получаем еще четыре значения при сложении: 0 и 0, при умножении: -0,382., и -2,618. Нетрудно показать, что будут справедливы следующие тождества Ф-2=0,382…; Ф-1=0,618…; Ф1=1,618…; Ф2=2,618…; Используя ряд этих значений, и совершая обход по кресту мы получим еще один золотосеченный крест. рис. 3 Нетрудно показать, как из этих крестов, сформировать двойной крест, порождающий закон Куба. рис. 4 Ниже мы покажем, что шесть полученных значений полностью вписываются в рамки сложного отношения — уникальной закономерности, известной из проективной геометрии. А сейчас мы приведем еще один рисунок, который непосредственно говорит о связи золотого сечения и Куба Закона. рис. 5 Сравните этот рисунок, нарисованный еще Леонардо да Винчи, с предыдущим. Увидели? Поэтому гимн золотому сечению можно продолжать до бесконечности. Так итальянский математик Лука Пачолли в своем труде „Божественная пропорция“ приводит 13 свойств золотого сечения, снабжая каждое из них эпитетами — исключительное, несказанное, замечательнейшее, сверхъестественное, и т. д. Трудно сказать, связаны ли эти свойства с числом 13 или нет. Но вот хроматическая гамма связана и с числом 13, и с числом 8. Так, пропорцию 13/8 можно представить как 8/8+5/8. С этими пропорциями связываются и многие духовные знания (Путь к себе). 3. РЯДЫ ЗОЛОТОГО СЕЧЕНИЯ Из вышеприведенных свойств золотого сечения следует вывод, что ряд …; Ф-2=0,382…; Ф-1=0,618…; Ф0; Ф1=1,618…; Ф2=2,618…; …; может быть продолжен как вправо, так и влево. Более того, умножение это ряда на Ф+n или Ф-nпорождает новый ряд, сдвинутый соответственно вправо или влево от исходного. Коэффициенты Ф+n или Ф-n можно считать коэффициентами подобия золотосеченных рядов. Золотосеченные ряды могут формировать натуральный ряд целых чисел. Посмотрите, эти числа имеют удивительные свойства. Они формируют не только Великие Пределы двойственных»золотых монад». Они формируют Великие Пределы триад (числа 5, 8,.). Они формируют и крест (число 9). Но существуют и другие, более фундаментальные золотосеченные ряды. В первую очередь следует привести формулу «золотого» бинома Ньютона. Бином Ньютона уже изначально свидетельствует о существовании монады (двойственного отношения) и его свойства лежат в основе биномиальных рядов (арифметический треугольник и др.). Теперь можно сказать и о том, что все биномиальные ряды могут быть выражены через золотую пропорцию. Золотая монада бинома Ньютона отражает еще одно важнейшее свойство мироздания. Она является нормированной (единичной). В [140] приводится следующая схема эволюции монады 1=(0,62+0,38)m. рис. 6 Видите, на каждом уровне иерархии каждое золотое число раскладывается, по образу и подобию. Из этих отношений нетрудно увидеть, как формируется золотой арифметический треугольник. рис. 7 И вот мы уже непосредственно выходим на схему эволюции Великого Предела ТАЙ-ЦЗИ (Книга перемен). рис. 8 Видите, как эволюция Великого предела ТАЙ-ЦЗИ, производящих функций арифметического треугольника и золотого бинома Ньютона сливаются в одну схему, порождаемую природными операционными механизмами Единого закона эволюции двойственного отношения. 4. ЗОЛОТОЕ СЕЧЕНИЕ И ПРИНЦИПЫ САМООРГАНИЗАЦИИ 4.1. САМОДОСТАТОЧНОСТЬ Принципы саморганизации (самодостаточность, саморегулирование, самовоспроизведение, саморазвитие и самонормирование) очень тесно связаны с золотым сечением. Рассматривая принципы самоорганизации и принципы нового мышления (О новом мышлении, О глобалистике) был обоснован вывод о том, что понятие самодостаточность определяет долю вклада собственных целевых функций в общую целевую функцию того или иного объекта окружающего мира. Если собственная доля вклада в общую целевую функцию объект будет не ниже 2/3, то такой объект будет иметь «контрольный пакет акций» целевой функции объекта и, следовательно, будет являться самодостаточным, не «марионеточным» объектом. Но 2/3=0, 66…, а золотая пропорция равна 0,618… Очень близкое совпадение, или.? Вот именно ИЛИ! Поэтому более точной количественное оценкой самодостаточности можно считать пропорцию золотого сечения. Однако для практического использования мерой самодостаточности, определяющей качественное состояние объекта, живет он в гармонии с окружающим миром, или нет, оценка 2/3 является даже предпочтительнее. Глубокая взаимосвязь этого принципа с золотым сечением показана на рис. 4, на котором рукой великого мастера -Леонардо да Винчи были приведены самые замечательные свойства золотого сечения и их взаимосвязь с ЕДИНЫМ ЗАКОНОМ. И очень жаль, что ЭТОГО НЕ ПОНИМАЮТ ЕЩЕ МНОГИЕ УЧЕНЫЕ ДАЖЕ СЕГОДНЯ. ПОЗОР!!! 4.2. САМОВОСПРОИЗВЕДЕНИЕ. САМОРАЗВИТИЕ Из принципов построения универсальной логики (подробнее) следует, что бесконечномерная логика в рамках эволюции одного и того же семейства, формирует бинарную спираль. рис. 9 В этой схеме узловые точки характеризует нисходящую спираль эволюции логического семейства бинарной спирали (правый винт). По индукции можно определить, что левый винт будет определять восходящую спираль этого семейства. Эта эволюционная бинарная спираль характеризует самовоспроизведение и саморазвитие логического семейства. Пусть мы имеем начальную логику <-i,-1>. Тогда, изображая оси комплексной системы отсчета в соответствии с правилом обхода тетраэдра по кресту. рис. 10 Из схемы видно, что при каждом переходе от одной логики к другой, по направлению стрелок, происходит зеркальное самокопирование логики. И когда мы завершим «круг эволюции», то последняя и первая логики окажутся противоположными друг к другу. Следующая попытка приводит уже к логике бинарного удвоения, т. к. клетка оказывается занятой. В результате рождается логика, отличающаяся от первой масштабностью, вместо <-i,-1> рождается пара <-2i,-2>. Отметим, что последовательное зеркальное копирование логик приводит к их зеркальной инверсии по диагоналям. Так, по диагонали -i,+1 мы имеем логики <-i,-1> <+1,+i>. Из правил обхода вершин тетраэдра по кресту мы получаем, что эти логики образуют крест в тетраэдре, если соответствующие ребра спроектировать на плоскость. По диагонали -1,+i мы получили взаимодополнительную пару логик <-1,-i> <+i,+1>, также образующую крест. На рис. 14, стороны квадратов ориентированы по направлению крещения. Поэтому противоположные стороны этого квадрата являются перекладинами креста. Отметим, что в тетраэдре существует еще и третий крест, образованной ребрами <+i,-i> и <-1,+1>. Но этот крест несет другие функции, о которых будет сказано в другом месте. Но схема на рис. 6 обосновывает только простое самовоспризводство логик. Оно может порождать многомерный мир «черно-белых» копий, которые могут характеризоваться только разными «оттенками». В соответствии с принципами самоорганизации логики должны иметь возможность к саморазвитию. И такая возможность реализуется. рис. 11 Здесь в квадрате II вначале происходит самокопирование исходной логики, а в третьем квадрате, происходит процесс саморазвития. Здесь вначале первый и второй квадрат складываются со сдвигом, а затем воспроизводятся в квадрате III. Затем полученная цепочка зеркально копируется в квадрат IV, где происходит «замыкание» цепочки. В результате рождается тетраэдр, с четырьмя вершинами, т. е. рождается комплексная логика. Так из пары <1,1> рождается пара <2,2>. Так рождается Первый период Периодической системы логических элементов. Возьмем теперь вторую пару, состоящую из двух логических соседних подоболочек —<1,2>. расписывая эволюцию этой пары по квадратам в соответствии с вышеприведенными правилами, мы получим пару <3,3>. Присоединяя ее к начальной цепочке <1,1,2>, мы получим <1,1,2,3>/ Тогда эволюция пары <2,3> произведет пару <5,5> и, соответственно, цепочку <1,1,3,5,>. Нетрудно увидеть, что рождается ряд Фибоначчи, являющийся основой золотого сечения. И этот ряд рождается естественным образом, в основе его лежит Единый Периодический закон эволюции и вытекающие из него принципы самоорганизации (самодостаточность, саморегуляция, самовоспроизведение, саморазвитие, самонормирование). 5. О СЛОЖНОМ ОТНОШЕНИИ Рассмотренные выше свойства золотого сечения и ряда Фибоначчи и их взаимосвязь, позволяют высказать предположение о связи с Единым законом эволюции двойственного отношения еще одного замечательного отношения, которое в проективной геометрии известно как сложное отношение точек ABCD. Рис. 12 Это число обладает тем свойством, что оно в точности одно и то же как. для изображения, так и для оригинала. Если вам нужно вычислить х, то не играет роли, измеряете ли вы расстояние на изображении или на самом участке. Фотокамера может обмануть. Она обманывает, когда выдает равные длины за неравные и прямые углы за непрямые. Единственное, что она не искажает, — это выражение Значение этого выражения может быть найдено прямо из фотографии. И все, что можно с уверенностью утверждать, пользуясь свидетельством фотографии, может быть выражено в терминах таких величин. Обычно, в качестве сокращенной записи сложного отношения используется символ ABCD. Перерисуем теперь схему сложного отношения в пространственном виде Рис. 13 Известно, что золотое сечение выражается пропорцией где числитель является меньшим числом, а знаменатель-большим. Применительно к рисунку золотая пропорция будет отражаться в треугольнике ABC, например, векторной суммой AB=BC+CA. Если углы между катетами будут равны нулю, то получим деление отрезка пополам. Если угол равен π/2, то получим прямоугольный треугольник со сторонами 1, Ф, Ф0,5; Следовательно, мы имеем исходное уравнение Ф2-Ф=1, записанное в векторной форме -гипотенуза является единицей, а катеты являются ортогональными друг к другу, что и отражается в уравнении золотого сечения. При любом другом угле описываются некие замкнутые пространства. Сравнение рисунков 16 и 17 показывает также, что прямая линия (рис.16), порождающая сложное отношение, трансформируется в ломаную, и сложное отношение порождается процессом « обхода по кресту». При этом Последняя вершина ломаной линии замыкается на Первую. В результате мы получаем уже известное из животворящего креста рис. 14 правило рычага-«выигрываешь в силе, проигрываешь в расстоянии»: — умножение перекладин креста и деление на длину плеч, определяющих переход с одной перекладины на другую. При построении этих более сложных отношений необходимо учитывать, что в формировании сложного отношения, точно также, как и в ряде Фибоначчи, участвуют только две соседних вершины ломаной линии. Это правило рычага, с использованием золотого сечения можно записать в следующем виде . А теперь мы можем построить сложное отношение на тетраэдре, учитывая, что расстояния от всех вершин пирамиды до точки О одинаково. Рис. 15 Из последних рисунков можно понять и принципы построения более сложных отношений, для пространств с большей мерностью, т. е. можно сказать, что n-мерное сложное отношение отражает процесс формирования монадного кристалла n-мерности и потому «упражнения» по формированию более сложных отношений могут иметь самостоятельный интерес (Сложное отношение). Но все значения сложного отношения х, (1/х), (х-1)/х, х/(х-1), 1/(1-х), (1-х), х,… являются частями уравнения золотого сечения х2 — х — 1 =0 или х (х -1) =1. 6. ЗАКОН СОХРАНЕНИЯ ЗОЛОТОГО СЕЧЕНИЯ Рассмотренные выше свойства золотого сечения и, в первую очередь, свойства сложного отношения позволяют говорить о том, что золотое сечение формирует главный закон мироздания, отражающий в себе главный закон сохранения- закон сохранения золотого сечения. Соотношения x=0,618…, 1/x=1,618, 1−1/x=-0,618…, 1/(1−1/x)=-1,618,… образуют бесконечный ряд, в котором первые четыре значения образуют крест золотого сечения. При этом всякий раз, когда получается величина, большая значения золотого сечения, то происходит нормировка ОБЪЕКТа. От него вычленяется единица и процесс эволюции продолжается! Однако для пятого и шестого значений мы получаем значения «-2,616» и «-0,382», после чего процесс начинается с начала. Полученный бесконечный ряд значений 0,618 и 1,618 является причиной, по которой золотое сечение лежит в основе гармонии мира. Закон сохранения (Законы сохранения) золотого сечения можно продемонстрировать во вращающемся кресте (свастике). рис. 16 Ниже, на странице, вскрывающей тайны информации (Информация, О времени) будут показано, что золотое сечение, генная память лежат в основе самого понятия информации, о природных механизмах эволюции монады «ОБРАЗ-ПОДОБИЕ» во ВРЕМЕНИ. Таким образом, сущность нормирования сводится к получению пропорций золотого сечения, т. е. все чудесные свойства сложного отношения четырех точек определяются свойствами животворящего креста, что сложное отношение тесно взаимосвязано с золотым сечением, формируя закон сохранения золотого сечения. 7. ГАРМОНИЯ ЗОЛОТОГО СЕЧЕНИЯ И ДИСГАРМОНИЯ РЫЧАЖНЫХ ВЕСОВ Сегодня о чудесных свойствах золотого сечения не говорят разве что ленивые. Возникли даже научные дисциплины («золотая математика», «числонавтика», «триалектика» и др.), которые в той или иной мере связаны с этой замечательной пропорцией. Число подобных дисциплин, видимо, будет непрерывно расти. Сегодня все ученые дружно убеждают и доказывают друг другу всеобщность и уникальность свойств этой золотой пропорции. Но это «сладкоголосное пение» подобно пению сирен (греческие мифы). В фундаменте этого «сладкого пения» лежит старая парадигма Познания: «Все возникает из Пустоты». И золотая пропорция -яркий этому пример. Откуда она возникла? Откуда возник ряд Фибоначчи и ряд Люка, формирующие, в пределе, численное значение этой замечательной пропорции? Это напоминает ситуацию, которая возникла вокруг категории «информация». Число научных дисциплин, которые «употребляют» данную категорию непрерывно растет. Более того, непрерывно растет и число чисто информационных наук (информатика, техническая информатика, фундаментальная информатика,…). Все бы хорошо, но при этом как оказывается само понятие «информация» не определено. Его просто не существует. Есть лишь отдельные малосвязные трактовки этого понятия применительно к конкретному приложению. Нечто подобное возникает и вокруг «золотого сечения». Ниже предлагается новая гипотеза, которая объясняет причины появления на свет божий этой замечательной пропорции. Рассмотрим взаимосвязь между рычажными весами Единого закона сохранения двойственного отношения «а-b» и золотым сечением. Выше мы уже приводили определение золотой пропорции: «Меньшее так относится к большему, как большее к сумме меньшего и большего» Заметим, что в этом отношении сумма отрезков нормирована, т. е. все отношения определяются в долях от единицы. Таким свойством обладают все двойственные отношения. Они всегда нормированы. Это позволяет очень наглядно представлять их взаимоотношения:«Что от одного тела убудет, то присовокупится к другому». Эта пропорция очень похожа на рычажные весы, но не является ими. Однако подобное отношение проявляется не при всех значениях «а» и «b». Рассмотрим свойства этого отношения более подробно. Запишем формально данную пропорцию в виде рычажных весов Из этих весов непосредственно видно, что имеет место нарушение закона сохранения двойственного отношения. Так, в этих рычажных весах перекладина Меры («b-b») имеет равные плечи, а перекладина двойственного отношения имеет избыточное «эволюционное накопление». Она отражает «дефект» рычажных весов. Гармония золотого сечения как оказывается порождается дисгармонией рычажных весов. Но как? Предположим, что «дефектное накопление» уравновешивает существующие рычажные весы путем формирования собственных рычажных весов, которые формируются по образу и подобию. Попытаемся взвесить на рычажных весах четыре отрезка, формирующих сложное отношение (Сложное отношение) Если составить последовательные отношения, то мы получим следующую цепочку «рычажных весов» сложного отношения Но каждые рычажные весы оказываются несбалансированными (числитель левой части в каждых весах количественно не равен знаменателю в правой части. И с целью уравновешивания начинают формироваться следующие рычажные весы, в которых неуравновешенный член уравновешивается соответствующим членом весов смежного уровня иерархии. Однако Природа умеет устранять подобный дисбаланс. В качестве рабочей гипотезы можно рассмотреть следующую. Если предположить, что каждое число в рычажных весах является вектором, и предполагая, что каждый последующий вектор в базисе рычажных весов ортогонален к предыдущему, то четыре базисных вектора образуют замкнутый контур. И если пятый «дефектный» вектор вынести из этого замкнутого контура путем его поворота в перпендикулярную плоскость, то в результате все весы оказываются уравновешенными путем поворота векторов «дефектного накопления» на 90 градусов. В результате, мы получаем, например из первых рычажных весов, что в двойственном отношении «х»-«(х-1)/х» вектор «(х-1)/х» заменяется на сумму двух векторов «1/x» +«1/(х-1)». Данную гипотезу можно усилить, если предположить, что каждые два смежных базисных вектора рычажных весов ортогональны друг другу и лежат в одной плоскости, но третий вектор по отношению к двум предыдущим векторам лежит в ортогональной плоскости, то мы получим Единый механизм формирования рычажных весов на всех уровнях иерархии. И эта гипотеза подтверждается Единым законом эволюции двойственного отношения. рис. 17 Данный рисунок отражает проекцию шести вершин куба на плоскость. Эта проекция проявляется в «Звезде Давида». Но «Звезду Давида» можно насаживать на что угодно, на любой «жизненный стержень», вокруг которого она и будет вращаться, ибо у нее нет «жизненного стержня». Ей не хватает двух центральных вершин куба, образующих ось вращения, вокруг которой вращаются все остальные вершины. Таким образом, сложное отношение отражает свойства «порочного круга». Но в этом порочном круге содержится нечто, которое может способствовать выходу за пределы этого круга. Если взять в сложном отношении в качестве параметра «х» золотую пропорцию, то мы получим следующую цепочку рычажных весов Из этой цепочки видно, что форма рычажных весов изменяется после того, как в цепочке четвертый член становится равен первому члену, но с обратным знаком. А далее идет модификация отношения. Числитель уменьшается (1-(1/Ф)), а знаменатель увеличивается (1+Ф), т. е.числитель раздваивается, а знаменатель удваивается, как бы закладывая фундамент для формирования бинарного ряда (бинарной производящей функции двойственного отношения «х»-«1/х»). Затем это отношение переворачивается. Затем перевернутое отношение трансформируется: из числителя и знаменателя вычитается единица и начинается следующий цикл эволюции сложного золотого отношения, но первый член сложного отношения будет со знаком «-«. Мы получили очень важный результат-фундамент «точки бифуркации». Последние два члена данной цепочки формируют весы «точек бифуркации» сложного отношения. Если эти весы будут уравновешены. то эволюция следующего цикла будет происходить без изменений, порождая принцип «порочного круга». В противном случае, в случае нарушения баланса в точке бифуркации, происходит «скачок» сложного отношения к другим значениям «х» и «1/х», при этом исходное значение х удваивается, или раздваивается. Таким образом, сложное отношение содержит в себе самую сокровенную тайну происхождения «точек бифуркации» (точек раздвоения или удвоения). Рычажные весы точки бифуркации (два последних члена цепочки) формируют «базисный крест» эволюции двойственного отношения. Теперь для сложного отношения мы можем записать следующую цепочку рычажных весов Здесь красным цветом в квадратных скобках в правой части выделены «дефектные накопления». Объединим теперь эти весы в единую цепочку. Из этой цепочки вложенных друг в друга рычажных весов мы видим, что последний «дефект» замыкается на первый, порождая итерационный процесс уравновешивания. Видимо не менее интересный результат мы можем получить теперь, представляя члены рядов Фибоначчи и Люка в виде вложенных друг в друга членов. Известно, что ряд Фибоначчи формирует следующую последовательность чисел 1, 1, 2, 3, 5, 8, 13,.. Выстраивая из этой последовательности цепочку рычажных весов, мы получаем Из совокупности этих рычажных весов мы уже изначально делаем вывод том, что отношения любых смежных членов ряда Фибоначчи соответствует определению золотой пропорции, но порождают ее путем последовательных итераций. Таким образом, сходимость ряда Фибоначчи к своему пределу — золотой пропорции, объясняется очень просто. Дисгармония «золотых » рычажных весов, порождает итерационный процесс уравновешивания. И этот процесс приводит в конечном итоге, к гармонии проявленного золотого сечения. Двойственность, которая проявляется в точках бифуркации сложного отношения, порождает бинарную функцию, Свойства рычажных весов в сложном отношении порождают золотосеченную функцию. Эти две функции становятся производящими функциями, формирующими двойственные числа Русской матрицы. Но числа ряда Фибоначчи в общем случае являются векторами, каждый из которых имеет собственное. выделенное в пространстве -времени направление. Так связывая каждую триграмму (Книга перемен) с 3-х мерным пространством, мы получим следующее их в пространстве Куба Единого Закона. рис. 18 Продемонстрируем теперь принципы формирования золотосечнного триграммного ряда. рис. 26 Определение золотого сечения не через пропорцию а через рычажные весы дает важные преимущества. Во-первых, «золотосеченные» рычажные весы связывают ряд Фибоначчи с природными операциоными механизмами Единого закона эволюции двойственного отношения. Во-вторых, эти рычажные весы наглядно демонстрируют КАК из одного двойственного отношения (левая часть рычажных весов) порождается новое уникальное двойственное отношение, демонстрируя тем самым принцип природного саморазвития, который является одним из важнейших принципов самоорганизации (Cамоорганизация). В-третьих, золотосеченные рычажные весы, по сравнению с золотой пропорцией, могут не только разворачивать ряд Фибоначчи, но и сворачивать его. Если известно отношение в правой части весов, то мы можем легко вычислить и левую часть рычажных ввесов В этих рычажных весах мы видим проявление закона сохранения двойственного отношения «Что от одного отношения убудет, то присовокупится к другому» Это значит, что золотое сечение может сворачиваться в Единицу (Великий предел). В-четвертных, золотосеченые рычажные весы могут порождать и другой принцип самоорганицации (принцип саморегулирования). Здесь на процесс саморегулирования накладываются ограничения, эти процессы протекают в рамках от «1» до «-1», т. е. «1» и «-1» выполняют роль верхнего и нижнего ограничений на значение членов ряда. В данных рычажных весах в явном виде проявляются принцип оптимальности (максимин). В левой части весов идет раскручивание ряда (n->max), а в правой -его скручивание (n-min). Данные рычажные весы отражают уравновешенность всех соответствующих членов ряда и всего ряда в целом. В числителе левой части идет разворачивание ряда от Единицы до n членов, а в правой части, наоборот, сворачивание всех членов пока не будет достигнуто единичное значение. При этом «промаха» никогда не будет, ибо «Единица» является Истоком и Стоком эволюционного сворачивания и разворачивания рядов, формируемых золотосеченными рычажными весами. Таким образом, нетрудно убедится в том, что золотосеченные рычажные весы ВСЕ связали в Единое, Целое. Единица, золотое сечение, рычажные весы Единого закона эволюции двойственного отношения, принципы самоорганизации (самодостаточность, саморегуляция, саморазвитие, и др.,). 8. РЫЧАЖНЫЕ ВЕСЫ. ЗОЛОТОЕ СЕЧЕНИЕ. ПРИНЦИП САМОДВИЖЕНИЯ. 8.1. О ПРЕРЫВНОСТИ И НЕПРЕРЫВНОСТИ ЗОЛОТОГО СЕЧЕНИЯ Золотое сечение обладает и многими иными, поистине замечательными свойствами. Оно может формироваться как прерывным, так и непрерывным путем. Если в рычажных весах золотой пропорции Заменить символ «b» на «1», а символ «а» на «х», несущей смысл переменной в n-мерной производящей функции, то мы получим следующую золотосеченные рычажные весы. нетрудно видеть, что золотая пропорция в рычажных весах стала характеризовать взаимоотношения двух производящих функций, которые известны в математике как бином Ньютона. Коэффициенты биномиальных рядом обладают многими замечательными свойствами. Поэтому уже никого не волнует, когда кто-нибудь открывает какую-либо новую закономерность, связанную с биномиальными коэффициентами (кроме самого автора). Анализируя свойства бинома в левой и правой частях мы видим, что в левой части производящая имеет конечное число членов ряда, в правой же части производящая функция характеризуется непрерывностью. На странице «Преемственность-1» мы подробно рассматривали свойства биномиальных производящих функций. Были рассмотрены два класса производящих функций:P (x) и Q(x).Так вот, оказалось, что даже непрерывные производящие функции обладают свойством прерывности, причем на одном и том же уровне иерархии, отражая синхронное и сфазированное протекание процессов. рис. 18 рис. 19 Из этих рисунков непосредственно следует, что имеют место следующие рычажные весы Видите, в левой части непрерывная производящая функция имеет знакочередующиеся члены, т. е. имеет место нарушение монотонности производящей функции, в то время как в правой части производящая функция является монотонно возрастающей. 8.2. О ЕДИНСТВЕ ПРЕРЫВНОГО И НЕПРЕРЫВНОГО Исходя их вышеизложенного мы впервые можем высказать гипотезу о причинах самодвижения материи, которые раскрывают последние золотосеченные рычажные весы. Когда-то, когда в науке господствовала механистическая картина мира, в основе которой лежала механика И. Ньютона, считалось, что Мироздание подобно часовому механизму, который будучи запущен однажды, позволяет спрогнозировать все События и Перемены (если известны начальные условия) Сегодня наука перешла на совершенно противоположную точку зрения. Квантово-механические подходы привели к тому, что что в физике доминирует сегодня «принцип квантовой запутанности». Рассмотрим суть такого подхода, используя принцип рычажных весов. Последовательность Событий характеризуется прерывностью (дискретностью), в то время как Перемены характеризуются как непрерывный процесс. Единство прерывности и непрерывности в физике микромира известно как корпускулярно-волновое единство, в макромире оно проявляется как структурно-функциональное единство, в мегамире оно характеризует свойства Материи, которая существует в единстве Вещества и Поля. Квантовая запутанность возникает тогда, когда учитываются только Состояния векторов, участвующих во взаимодействии, но не учитывается степень уравновешенности состояний относительно внешних систем. Если эту ситуацию можно изобразить в следующей форме Можно ли в этих условиях говорить о квантовой определенности? Такая определенность возникнет только тогда, когда рычажные весы состояний двух взаимодействующих векторов будут отнормированы и приведены к «нормальному бою», т. е. взаимодействие будет в явном виде учитывать Меру, отражающую степень неуравновешенности состояний взаимодействующих векторов, как в статике, так и динамике. А между тем Природа умеет строить такую Меру, ибо она знает Единый закон, а люди, точнее те, кто когда-то были людьми, эту Меру не знают и знать не желают. На странице «Преемственность-1» мы рассмотрели и взаимодополнительную бинарную производящую функцию G (x). Взаимосвязь этих функций была показана на следующем рисунке рис. 20 По сути этот рисунок отражает собой декартовую систему координат. в которой существует еще одно двойственное измерение, отражающее Меру, характеризующую «жизненный стержень», вокруг которого вращаются все члены биномиальных производящих функций Поэтому не будет ничего удивительного в том, что все числа в этом биномиальном пространстве-времени могут быть представлены в матричном виде. В этой матрице главная диагональ будет отражать свойства системообразующих чисел, определяющих Меру для всех остальных чисел. 8.3. ЗОЛОТОЕ СЕЧЕНИЕ. РЫЧАЖНЫЕ ВЕСЫ. ПЕРИОДИЧЕСКАЯ СИСТЕМА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ Принципы эволюции отношений взаимодополнительности между протонами и электронами в атомах, можно записать в виде следующих рычажных весов. Здесь -постоянная Планка. Эти рычажные весы по форме полностью соответствуют определению золотого сечения. А если мы теперь произведем нормирование, то мы получим Мы видим, что данные золотосеченные рычажные весы исповедуют рычажные закон сохранения Единицы (протона). Поскольку у данных рычажных весов существуют и взаимодополнительные, то закон сохранения (формирования) золотой пропорции может быть записан в виде следующих рычажных весов. Эти рычажные весы отражают принципы оптимального саморегулирования. При этом единичная перекладина Меры несет в себе нормировочный аспект уравновешивания рычажных весов на всех уровнях иерархии. Например, на самом элементарном уровне иерархии нашего мироздания в качестве перекладины меры, в последних рычажных весах может служить фотон. Из последних рычажных весов также можно сделать вывод о том, что спираль производящей «рычажной» функции, стоящая в числителе левой части будет раскручивающейся, а спираль «рычажной» функции, стоящей в правой части, в знаменателе, будет раскручивающейся. На странице «Атом-3» приведен следующий рисунок, отражающий принципы построения Периодической системы химических элементов. В классификации Периодической таблицы лежит «институт Меры» рычажных весов. рис. 21 Этот рисунок отражает взаимоотношения производящих функций Периодической системы (P (x) и G (x)), свойства которых отображено на рисунках выше. Из этого рисунка можно непосредственно увидеть каким образом на каждом уровне иерархии формируются собственная Мера, характеризующая закон сохранения двойственного отношения на данном уровне иерархии. При этом закон сохранения проявляется через механизмы саморегулирования, в которых собственная определяет верхнюю и нижнюю границы саморегулирования. РЕЗЮМЕ 1. Ни у кого уже не возникает сомнений, что золотое сечение лежит в основе гармонии мироздания, а ряд Фибоначчи порождает эту замечательную пропорцию. Дополнительную информацию о свойствах золотого сечения любознательные читатели могут получить на сайте www.goldenmuseum.com. Эта поистине золотая пропорция имеет такое множество замечательных свойств, что открытие новых свойств уже ни у кого не вызывает удивления. 2. Но парадокс заключается в том, что именно золотая пропорция является источником дисгармонии, порождая бинарную и золотосеченную производящие функции Русской матрицы, о числах которой можно сказать «ВСЕ ЕСТЬ ЧИСЛО РУССКОЙ МАТРИЦЫ» 3. Следует отметить, что золотая пропорция в «чистом» виде проявляется в свойствах смежных чисел рядов Фибоначчи. При этом, поскольку все члены ряда непосредственно связаны между собой золотой пропорцией в чистом виде, то этот факт не может не находить своего отражения в свойствах предельного значения всех членов этого ряда. Да иначе и не может быть, ибо формирование всех членов ряда производится по образу и подобию на все новые и новые рычажные весы высших уровней иерархии. 4. Хочется надеяться, что осознание тривиального факта порождения золотого сечения природными операционными механизмами Единого закона эволюции двойственного отношения, которые проявляется в свойствах рычажных весов, наконец повернет мышление людей от воспевания чудесных свойств золотой пропорции к ее практическому использованию во всех сферах жизнедеятельности современной цивилизации. Не надо более доказывать друг другу и восхвалять золотое сечение. Надо его использовать, ибо оно позволяет измерять и соизмерять все События и Перемены в их многомерности. 5. И, наконец, пришла пора раскрыть самую сокровенную тайну золотого сечения. Из рычажных весов, лежащих в основе определения золотой пропорции мы можем по аналогии написать другие рычажные весы Эти рычажные весы определяют золотую пропорцию для двойственного отношения «ян-инь». Но из китайской Книги Перемен известно, что (ян+инь) есть Великий предел двойственного отношения. Таким образом, золотая пропорция определяет условия синтеза для двойственного отношения, а золотосеченное рычажное уравнение формирует Периодические системы эволюции двойственного отношения «а-в», при этом «a+b=1», демонстрируя принцип самодвижения, в основе которого лежит принцип оптимального саморегулирования, с использование принципов максимина и (или) минимакса. e-mail: [email protected] С благодарностью приму все ваши замечания, предложения, с признательностью отвечу на ваши вопросы

Правило золотого сечения в архитектуре, пропорции яйца

Исследовательская работа: Золотое сечение в архитектуре храмов

Золотое сечение в архитектуре

Закон золотого сечения часто проявляется в архитектуре. Архитектурные пропорции- это важное и надежное средство зодчего для достижения сбалансированного равновесия между целым и его частями, имя которому – гармония.

По сравнению с композитором или скульптором архитектор находится в более сложном положении, так как на пути к гармонии он должен заботиться не только о «красоте», но также и о «пользе» и «прочности» и «долговечности».

Пропорции различных частей храмов составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то строение здания считается идеальным и долговечным. Принцип расчета золотой меры в строениях храмов Н/h=1,618.

Рассмотрим шедевр античного зодчества – Парфенон. Он был и остается совершеннейшим из архитектурных сооружений. Отношение всех его частей являются числом «золотого сечения».

Рассмотрим кратко пропорции церкви Покрова на Нерли. Этот архитектурный шедевр для русского человека значит столько же, сколько Парфенон для грека. Закону золотого сечения подчинены прежде всего главные вертикали храма, определяющие его силуэт: высота основания, равная высоте тонких колонок четверика, и высота барабана. Диаметр барабана относится к его высоте также в золотой пропорции. Эти пропорции видны с любых точек зрения.

Исследование золотого сечения в архитектуре

Чтобы проверить правильность нашей гипотезы мы исследовали фотоснимки 4-х церквей.

Мы рассмотрели:

Храм Преподобного Сергия Радонежского, храм Александра Невского, храм Рождества Христова и церковь Феодора Стратилата.

По фотографиям мы измеряли высоту церкви, нижний ярус, расстояние от основания купола до креста, основание купола.

Далее мы вычисляли:

• отношение высоты церкви к нижнему ярусу;
• «золотой треугольник»: отношение расстояния от основания купола до креста к диаметру основания.

Результаты расчетов мы занесли в таблицу и представили наглядно.

На основании наших вычислений мы сделали следующие выводы: почти у всех храмов вышеописанные измерения очень близки к числу золотого сечения — 1,618.

Наша гипотеза о том, что пропорции различных частей храмов составляют число, очень близкое к золотому сечению подтвердилась.

Для проверки второй части гипотезы мы решили исследовать макеты храмов, созданные ранее учащимися нашей школы. Мы выполняли те же измерения на трех макетах. Результаты также представили наглядно.

В результате измерений макетов храмов мы сделали вывод, что и они также пропорциональны, значит, человек может без дополнительных измерений определить правильные пропорции. Это еще раз доказывает, что «золотое сечение» присутствует везде — даже в подсознании человека. В этой части наша гипотеза также подтвердилась.

Заключение

В результате исследовательской работы мы познакомились с понятием «золотого сечения», применением его в искусстве, живописи, природе, архитектуре. Приобрели навыки исследовательской работы, опыт работы в поисковой системе Интернет. Также мы научились работать с электронной таблицей: выполнять расчеты строить и анализировать диаграммы.

Законам «золотого сечения» подчиняются не только творения природы, но и продукты его деятельности. Строение храмов также подчинены закону «золотого сечения».

Человек во всем старается достичь гармонии. Так как все основывается и стремится к правилу «золотого сечения».

В данной работе мы проверили нашу гипотезу. На конкретных примерах наша гипотеза полностью нашла свое подтверждение. С нашей работой мы познакомили одноклассников. Данный материал стал пособием для работы учителей математики, информатики, изобразительного искусства.

Исследование математических зависимостей в архитектуре, музыке, природе, человеке очень интересны и мы в дальнейшем продолжим свою работу.

Литература

Приложение 1

Процесс исследования

Приложение 2

Основные измерения

Приложение 3

Результаты измерений

Приложение 4

Результаты измерений

Перейти к содержанию
Исследовательской работы «Золотое сечение в архитектуре храмов»

Любому человеку, которому хотя бы косвенно приходилось сталкиваться с геометрией пространственных объектов в интерьерном дизайне и архитектуре, наверняка хорошо известен принцип золотого сечения. Еще недавно, несколько десятков лет назад, популярность золотого сечения была настолько высокой, что многочисленные сторонники мистических теорий и устройства мира его называют универсальным гармоническим правилом.

СУЩНОСТЬ УНИВЕРСАЛЬНОЙ ПРОПОРЦИИ

Удивительно другое. Причиной предвзятого, почти мистического отношения к столь простой числовой зависимости послужило несколько необычных свойств:

Большое количество объектов живого мира, от вируса до человека, имеют основные пропорции тела или конечностей, очень близкие к значению золотого сечения;

Зависимость 0,63 или 1,62 характерна только для биологических существ и некоторых разновидностей кристаллов, неживые объекты, от минералов до элементов ландшафта, обладают геометрией золотого сечения крайне редко;

Золотые пропорции в строении тела оказались наиболее оптимальными для выживания реальных биологических объектов.

Сегодня золотое сечение находят в строении тела животных, панцирей и раковин моллюсков, пропорций листьев, веток, стволов и корневых систем у достаточно большого числа кустарников и трав.

Многими последователями теории универсальности золотого сечения неоднократно предпринимались попытки доказать тот факт, что его пропорции являются наиболее оптимальными для биологических организмов в условиях их существования.

Обычно в качестве примера приводится устройство раковины Astreae Heliotropium, одного из морских моллюсков. Панцирь представляет собой свернутую спиралью кальцитовую оболочку с геометрией, практически совпадающей с пропорциями золотого сечения.

Более понятным и очевидным примером является обычное куриное яйцо.

Соотношение основных параметров, а именно, большого и малого фокуса, или расстояний от равноудаленных точек поверхности до центра тяжести, будет также соответствовать золотому сечению. При этом форма скорлупы птичьего яйца является наиболее оптимальной для выживания птицы, как биологического вида. При этом прочность скорлупы играет далеко не главную роль.

К сведению! Золотое сечение, называемое еще универсальной пропорцией геометрии, было получено в результате огромного количества практических измерений и сравнений размеров реальных растений, птиц, животных.

ПРОИСХОЖДЕНИЕ УНИВЕРСАЛЬНОЙ ПРОПОРЦИИ

О золотой пропорции сечения знали древнегреческие математики Евклид и Пифагор. В одном из памятников древней архитектуры — пирамиде Хеопса соотношение сторон и основания, отдельные элементы и настенные барельефы выполнены в соответствии с универсальной пропорцией.

Методика золотого сечения широко использовалась в средние века художниками и архитекторами, при этом суть универсальной пропорции считалась одной из тайн вселенной и тщательно скрывалась от простого обывателя. Композиция многих картин, скульптур и зданий выстраивалась строго в соответствии с пропорциями золотого сечения.

Впервые суть универсальной пропорции документально была сформулирована в 1509 г монахом-францисканцем Лукой Пачоли, обладавшим блестящими математическими способностями. Но настоящее признание состоялось после проведения немецким ученым Цейзингом всестороннего изучения пропорций и геометрии человеческого тела, древних скульптур, произведений искусства, животных и растений.

У большинства живых объектов некоторые размеры тела подчиняются одним и тем же пропорциям. В 1855 г ученым был сделан вывод о том, что пропорции золотого сечения являются своеобразным стандартом гармонии тела и формы. Речь идет, прежде всего, о живых существах, для мертвой природы золотое сечение встречается значительно реже.

КАК ПОЛУЧИЛИ ЗОЛОТОЕ СЕЧЕНИЕ

Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.

Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.

На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.

Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:

Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.

Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;

Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;

В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.

К сведению! В отличие от классического золотого соотношения, архитектурная версия подразумевает соотношение сторон отрезка в пропорции 44:56.

Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.

ГЛАВНЫЙ СЕКРЕТ ЗОЛОТОГО СЕЧЕНИЯ

Если природные проявления универсального сечения в пропорциях тел животных и человека, стеблевой основы растений еще можно объяснить эволюцией и приспосабливаемостью к влиянию внешней среды, то открытие золотого сечения в строительстве домов XII-XIX века стало определенной неожиданностью. Мало того, знаменитый древнегреческий Парфенон был построен с соблюдением универсальной пропорции, многие дома и замки состоятельных вельмож и зажиточных людей в средние века строились сознательно с параметрами, очень близкими к золотому сечению.

ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ

Многие из построек, сохранившихся до сегодняшних дней, свидетельствуют, что архитекторы средневековья знали о существовании золотого сечения, и, конечно, при строительстве дома руководствовались своими примитивными расчетами и зависимостями, с помощью которых пытались добиться максимальной прочности. Особенно проявлялось желание строить максимально красивые и гармоничные дома в постройках резиденций царствующих особ, церквей, ратуш и зданий, имеющих особое социальное значение в обществе.

Например, знаменитый собор Парижской богоматери в своих пропорциях имеет немало участков и размерных цепей, соответствующих золотому сечению.

Еще до публикации своих исследований в 1855 году профессором Цейзингом, в конце XVIII века были построены знаменитые архитектурные комплексы Голицынской больницы и здания сената в Санкт-Петербурге, дома Пашкова и Петровского дворца в Москве с использованием пропорций золотого сечения.

Разумеется, дома с точным соблюдением правила золотого сечения строили и ранее. Стоит упомянуть памятник древней архитектуры церкви Покрова на Нерли, изображенный на схеме.

Всех их объединяет не только гармоничное сочетание форм и высокое качество строительства, но и, в первую очередь, наличие золотого сечения в пропорциях здания. Удивительная красота постройки становится еще более загадочной, если принять во внимание возраст, здание церкви Покрова датируется XIII веком, но современный архитектурный облик постройка получила на рубеже XVII века в результате реставрации и перестройки.

ОСОБЕННОСТЬ ЗОЛОТОГО СЕЧЕНИЯ ДЛЯ ЧЕЛОВЕКА

Старинная архитектура зданий и домов средневековья остается притягательной и интересной для современного человека по многим причинам:

Индивидуальный художественный стиль в оформлении фасадов позволяет избежать современного штампа и серости, каждое здание представляет собой произведение искусства;

Массовое использование для декорирования и украшения статуй, скульптур, лепнины, необычных сочетаний строительных решений разных эпох;

Пропорции и композиции здания притягивают взор к наиболее важным элементам постройки.

Важно! При проектировании дома и разработке внешнего вида средневековые архитекторы применяли правило золотого сечения, неосознанно используя особенности восприятия подсознания человека.

Современные психологи экспериментально доказали, что золотое сечение является проявлением неосознанного желания или реакции человека на гармоничное сочетание или пропорцию в размерах, формах и даже цветах. Был проведен эксперимент, в ходе которого группе людей, незнакомых между собой, не имеющих общих интересов, разных профессий и возрастных категорий, предложили ряд тестов, среди которых была задача согнуть лист бумаги в наиболее оптимальной пропорции сторон. По результатам тестирования было установлено, что в 85 случаях из 100 лист сгибался испытуемыми практически точно по золотому сечению.

Поэтому современная наука считает, что феномен универсальной пропорции является психологическим явлением, а не действием каких-либо метафизических сил.

ИСПОЛЬЗОВАНИЕ ФАКТОРА УНИВЕРСАЛЬНОГО СЕЧЕНИЯ В СОВРЕМЕННОМ ДИЗАЙНЕ И АРХИТЕКТУРЕ

Принципы применения золотой пропорции в последние несколько лет стали необыкновенно популярны в строительстве частных домов. На смену экологии и безопасности строительных материалов пришли гармоничность конструкции и правильное распределение энергии внутри дома.

Современная интерпретация правила всеобщей гармонии давно распространилась за пределы привычной геометрии и формы объекта. Сегодня правилу подчиняются не только размерные цепи длины портика и фронтона, отдельных элементов фасада и высоты здания, но и площадь комнат, оконных и дверных проемов, и даже цветовая гамма внутреннего интерьера помещения.

Проще всего построить гармоничный дом на модульной основе. В этом случае большинство отделений и комнат изготавливаются в виде самостоятельных блоков или модулей, спроектированных с соблюдением правила золотого сечения. Построить здание в виде набора гармоничных модулей значительно проще, чем строить одну коробку, в которой большая часть фасада и внутренних помещений должна быть в жестких рамках пропорций золотого сечения.

Немало строительных фирм, выполняющих проектирование частных домовладений, используют принципы и понятия золотого сечения для увеличения сметы и создания у клиентов впечатления глубокой проработки конструкции дома. Как правило, такой дом декларируется, как очень удобный и гармоничный в пользовании. Правильно подобранное соотношение площадей комнат гарантирует душевный комфорт и отменное здоровье хозяев.

Если дом был построен без учета оптимальных соотношений золотого сечения, можно выполнить перепланировку комнат так, чтобы пропорции помещения соответствовали соотношению стен в пропорции 1:1,61. Для этого может перемещаться мебель или устанавливаться дополнительные перегородки внутри комнат. Аналогичным образом меняются размеры оконных и дверных проемов так, чтобы ширина проема была меньше высоты дверного полотна в 1,61 раза. Таким же способом выполняется планирование мебели, бытовой техники, отделки стен и пола.

Сложнее выбрать цветовое оформление. В этом случае вместо привычного соотношения 63:37 последователями золотого правила принята упрощенная трактовка – 2/3. То есть основной цветовой фон должен занимать 60% пространства помещения, оттеняющему цвету отдают не более 30%, и остальное отводится под различные родственные тона, призванные усилить восприятие цветового решения.

Внутренние стены помещения делятся горизонтальным поясом или бордюром на высоте 70 см, установленная мебель должна соизмеряться с высотой потолков по соотношению золотого сечения. То же правило касается распределения длин, например, размер дивана не должен превышать 2/3 длины простенка, а общая площадь, занимаемая мебелью, относится к площади комнаты, как 1:1,61.

Золотую пропорцию сложно в массовом порядке применять на практике из-за всего лишь одного значения сечения, поэтому при проектировании гармоничных зданий нередко прибегают к ряду чисел Фибоначчи. Это позволяет расширить количество возможных вариантов пропорций и геометрических форм основных элементов дома. В этом случае ряд чисел Фибоначчи, связанных между собой четкой математической зависимостью, называют гармоническим или золотым.

В современной методике проектирования жилья на основе принципа золотого сечения, кроме ряда Фибоначчи, широко используется принцип, предложенный известным французским архитектором Ле Корбюзье. В этом случае в качестве отправной единицы измерения, по которой рассчитываются все параметры здания и внутреннего интерьера, выбирается рост будущего владельца или средняя высота человека. Такой подход позволяет спроектировать дом не только гармоничный, но и по-настоящему индивидуальный.

А ТЕПЕРЬ простым и понятным языком

На практике, по отзывам тех, кто решился на строительство дома по правилу золотого сечения, качественно построенное здание действительно оказывается достаточно удобным для проживания. Но стоимость строения из-за индивидуального проектирования и применения стройматериалов нестандартных размеров возрастает на 60-70%. И в этом подходе нет ничего нового, так как большинство зданий прошлого века строилось именно под индивидуальные особенности будущих хозяев.

Почему яйцо является символом Золотого сечения?

ПОЧЕМУ ЯЙЦО ЯВЛЯЕТСЯ СИМВОЛОМ ЗОЛОТОГО СЕЧЕНИЯ?

В живой природе встречается очень часто явление, когда живые организмы и растения сами создают вокруг себя зоны комфортной для себя энергетики, тем самым частично или полностью нейтрализуя вредное воздействие различных негативных факторов: таких, например, как геопатогенные зоны.

Примерами подобных «живых» конструкций являются яйца птиц, раковины, пчелиные соты, осиные гнезда, яблоки, цветы и многие другие.

Все они построены по закону Золотого сечения, называемого законом гармонии и являющимся законом формообразования в Живой природе. На основе этого закона построены музыкальные и цветовые ряды, гениальные произведения живописи и архитектуры, музыки и поэзии.

Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.

Такие формы птичьих яиц не являются случайными, поскольку в настоящее время установлено, что форме яиц, описываемых отношением золотого сечения, отвечают более высокие прочностные характеристики оболочки яйца.

Получается, что форма птичьего яйца является идеальной. Наверное, поэтому не случайно, что яйцо является одним из символов Золотого сечения.

Начало в Части 1, Части 2, Части 3, Части 4, Части 5.
Посмотрите на яйцо. Оно ниспровергает все богословские школы и религиозные учения на свете. (Дидро)
Интерес к этой теме возник у меня во время турецкого каравана, пять лет тому назад. Тогда в нескольких стамбульских мечетях, а также в мавзолеях суфийских святых мы с друзьями заметили большие яйцеобразные предметы, свешивающиеся на цепочке из центральной точки купола или помещенные в арках вдоль стен. Рассмотрев странные артефакты, мы пришли к выводу, что часть из них были похожи на страусиные яйца, вставленные в металлическую оправу, а часть были просто имитациями, сделанными из мрамора, оникса или металла.
Страусиное яйцо в металлической оправе в Голубой Мечети, Стамбул
Впоследствии aналогичные предметы нам встречались в теккиях боснийских дервишей – иногда яйца были окрашены в тот цвет, с которым ассоциировала себя данная суфийская община (как страусиное яйцо голубого цвета на фотографии внизу справа, которую мы сделали в боснийской теккии).
Ни в первом, ни во втором случае никто так и не смог нам объяснить, для чего они служат. Ответы «для красоты» или «от мышей и пауков» не показались мне убедительными, а аргумент «так было всегда» породил вопрос: a почему?
И я решила разобраться.
…Дело в том, что увидев странные артефакты, я тут же вспомнила одну интересную вещицу, которую ее изобретатель, часто упоминаемый мной Дэн Винтер (Dan Winter), называл биоконденсатором (накопителем энергии). Этот прибор был сделан из белой керамики и выглядел как большое яйцо, за исключением того, что изнутри был покрыт тонким слоем золота. С помощью этого приспособления Дэн измерял ни много ни мало – жизненную энергию различных субстанций или объектов! Согласно его утверждению, эти слабые и обычно с трудом регистрируемые токи можно значительно усилить и сделать различимыми для приборов типа вольтметра, помещая их в натуральное страусиное яйцо или имитирующий его форму керамический «биоконденсатор».
Так выглядел «биоконденсатор» Дэна. На фото запечатлен
опыт с измерением жизненной энергии, содержащейся в обычном курином яйце
Но все по порядку…
Мое исследование вопроса – были ли яйцевидные предметы неизвестного назначения уникальными для мусульманской и суфийской Традиции – дали однозначный ответ: нет, не были. Оказывается, их использование – очень древняя традиция.
Самые ранние сосуды для питья, сделанные из половинок страусиных яиц, были найдены в захоронении 3-го тысячелетия до н.э. на территории современного Бахрейна. В качестве чашек, ритуальных ритонов, контейнеров для хранения жидкостей или своеобразных консервных банок яйца страуса или их имитации из благородных металлов и керамики использовались минойской, микенской и эгейской цивилизациями Средиземноморья 3-2 тысячелетий до н.э, а также на Ближнем Востоке вплоть до исламского средневековья.
Ритуальный сосуд из страусиного яйца,
минойская цивилизация, Крит, около 1500 до н.э.
В Египте времен фараонов в них хранили духи и благовония. По-видимому, уже оттуда знание о свойствах страусиных яиц попало к коптам в Эфиопии и другим ранним христианским общинам восточного Средиземноморья, которые использовали их в качестве культовых предметов. До сих пор в коптских церквях можно встретить яйца страуса, подвешенные у сводов, в нефах или над мощами святых. Также распространенной практикой было помешать страусиные яйца на концах креста, венчавшего купол эфиопской церкви. (Источники: D.A.Agius. Egypt and Syria in the Fatimid, Ayyubid and Mamluk eras; N.Green. Ostrich Eggs and Peacock Feathers: Sacred Objects as Cultural Exchange between Christianity and Islam)
На картине Мастера Традиции Альбрехта Дюрера «Поклонение волхвов» (1504) один из приносящих дары, Бальтазар (Валтасар), изображен мавром в одеянии, напоминающем двухцветный костюм-домино странствующих суфиев-трубадуров. В качестве дара он подносит младенцу Иисусу страусиное яйцо в золотой оправе.
Исследователи объясняют использование яйца в убранстве раннехристианских храмов его значением как символа жизни и возрождения, связью с пасхальной мистерией. И все бы хорошо, но чем объяснить аналогичный феномен в исламской культуре? Что символизировало яйцо в мусульманском храме османского времени, и откуда взялась традиция подвешивать их к куполу мечети или устанавливать на вершинах минаретов?
Два страусиных яйца на вершине минарета Великой Мечети, Нионо, Мали
Зачем страусиные яйца прикрепляли, иногда по нескольку штук, на цепи над могилами суфийских святых? Неужели исключительно в качестве украшения?
Почему все вышеперечисленные цивилизации, независимо от вероисповедания и местоположения, с такой охотой использовали яйцо в качестве культового предмета?
Возможно, все дело в форме яйца… точнее, в его геометрии. Чтобы разобраться с этим, мы вернемся к Дэну Винтеру и его пояснениям:
Жизнь появляется, когда биологическая структура концентрируeт заряд, втягивая, как в воронку, волны различной длины. Живые формы организуются по принципам фрактальной геометрии («как вверху, так и внизу»), основанной на Золотой Пропорции. Это единственный предлагаемый Вселенной способ для создания в одной точке «места встречи» всевозможных вибраций таким образом, чтобы они не разрушали друг друга.
Золотая Пропорция в яйце: a : b = (a + b) / a = 1,618
(источник иллюстрации)
Таким образом, мы можем определить жизненную силу как способность привлекать и удерживать заряд. Принцип прост – чем больше волн, несущих заряд силы, может собрать в одном месте биологический объект, тем более он жизнеспособен, тем он ЖИВЕЕ. Это называется имплозией – втяжением заряда.
Яйцо представляет из себя биологический конденсатор большой емкости — накопитель заряда. Если притронуться к противоположным концам свежего яйца, можно почувствовать слабый разряд, результат напряжения от 4 до 12 вольт. Биология не может объяснить, откуда берется это напряжение. А ответ прост – вольты, генерируемые яйцом, называются «жизнь». Потенциал, создаваемый репродуктивным материалом – яйцом или сосновой шишкой – источник его самодостаточности, способности поддерживать себя энергетически.
Действительно, яйцо или шишка — настоящие природные «батарейки», так устроенные геометрически и структурно, чтобы вызревающая в них отдельно от материнского существа жизнь притягивала достаточно жизненной силы извне. Извне — это откуда? Дэн считает — из всего многообразия пространственных волн, включая гравитационное поле Земли. Замечательно то, что эти свойства сохраняются даже после того, как функция яйца или шишки в качестве вместилищ генетического материала прекращается (благодаря этим свойствам их и использовали древние).
Яйца птиц и рептилий, и шишки разных растений значительно отличаются по форме, но у всех них, как правило, есть более острая верхушка — апекс. Такого рода геометрия позволяет создавать точку имплозии — горлышко воронки, место сортировки пространственных волн на те, что можно приспособить для жизни (они втягиваются по принципу подобия) и все остальные, которые отсеиваются. Kак показано на этой иллюстрации Дэна, внутрь яйца или шишки впускаются только те волны, которые прошли контроль на соответствие Космическому ГОСТУ – Золотой Пропорции 1,618.
Cледует заметить, что сам по себе термин «имплозия» не принадлежит Дэну. Его в середине прошлого века ввел немецкий изобретатель-визионер Виктор Шаубергер (Viktor Schauberger), создания рук которого, связанные с использованием силы воды и имевшие естественную геометрию природных объектов, действовали на принципах, до сих пор так и не понятых человечеством. Шаубергер видел все процессы в наблюдаемом мире как проявления невидимого Единства, суть которого была в спиральном, вихревом движении. Там, где есть завихрения или воронки — появляется жизнь, и наоборот.
Форма яйца была одной из его излюбленных. Шаубергер считал, что Природа не случайно выбрала ее для генерирования энергии творения. Яйцеобразная форма, математически получаемая как разрез гиперболической воронки, также является наиболее совершенным вместилищем для своей собственной внутренней воронки. Это единственная герметичная форма, естественным образом генерирующая вихреобразное движение.
Именно по этой причине свой первый аппарат по обогащению воды Виктор Шаубергер сделал в форме яйца. Поскольку он полагал воду живым организмом (а мы уже однажды убедились, что вода действительно может быть живой), то считал, что она должна находиться в непрерывном движении, чтобы оставаться таковой. Единственная форма контейнера, обеспечивающая постоянное внутреннее спиралевидное движение – яйцеобразная.
Как мы видели выше, цивилизации прошлого прекрасно об этом знали, приспосабливая яйца для хранения жидкостей. Древние греки не случайно придавали яйцевидную форму глиняным амфорам для хранения воды, вина и зерна. Зерно двухтысячелетней давности из одной подобной амфоры, найденной археологами, не только прекрасно сохранилось, но и дало всходы – такова эффективность геометрии яйца, сохраняющего жизненную силу через века.
Интуитивно нам больше нравятся посуда и бытовые предметы, имеющие форму яйца или половинки яйца (кувшины, вазы, чайные чашки и т.д) — жидкости в них остаются более живыми. (Кстати, по той же причине растения лучше растут в горшках, напоминающих по форме половинку яйца. Шаубергер даже изобрел форму яйцевидной компостной кучи, которая очень нравилась растениям).
Еще одну интересную особенность также заметил Шаубергер — яйцевидные тела создают вихревой паттерн не только внутри себя, но и снаружи, порождая волны правильной геометрии в воде или воздухе. Благодаря этому окружение, в котором они находятся, становится более живым.
Схематический разрез участка русла реки, показывающий,
как яйцеобразная конструкция завихривает движущийся на нее поток воды.
*****
Я помню, во времена моего детства люди часто держали дома в качестве сувенира нераскрывшиеся кедровые шишки. Они, конечно, были очень красивые, но, оказывается, могли иметь и другую роль — действовать как маленький биологический конденсатор и гармонизатор пространства. Как и страусиные яйца в храмах разных времен и народов, с которых мы начали эту заметку…
С такой же целью, возможно, не осознаваемой, принято сохранять пасхальные яйца, не портящиеся годами. Мама как-то подарила нам пару таких сваренных и окрашенных яиц, для которых она связала специальные сеточки, и мы подвесили их на домашнее растение. Висят уже года три без каких-либо признаков разложения. В общем, хотя страусов в наших краях нет, тоже гармонизируем помаленьку, чем Бог послал 🙂

Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.

Винтовая лестница построена по принципу золотого сечения

Просто о сложном: что это такое – правило золотого сечения

Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.

Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.

Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

• практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
• данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
• именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.

Идеальный пример ЗС в природе — раковина морского моллюска

Экскурс в историю: кто придумал золотое сечение

Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:

• маленький отрезок – это сын;
• большой – отец;
• весь отрезок – это святой дух.

Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.

Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.

Золотое сечение в божественной пропорции

Принцип расчета и построения золотого сечения

Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.

Как определить число золотого сечения

С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:

Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.

Ряд Фибоначчи в церкви Покрова на Нерли

Как рассчитать золотое сечение на простейшем примере

Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.

Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.

Простой пример золотого сечения в курином яйце

Как построить золотое сечение на примере прямоугольника и спирали

Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:

• нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
• над ними разместить квадрат со стороной 2;
• слева гармонично помещается квадрат с гранью 3;
• ниже – квадрат со стороной 5;
• справа пространство займет квадрат с гранью 8;
• площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
• если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
• если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.

Принцип золотого сечения в прямоугольникеПостроение золотой спирали из прямоугольника

На видео можно более подробно узнать про магию чисел Фибоначчи:

Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства

Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.

Тайны древнеегипетской архитектуры

В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.

Это интересно! Форма пирамиды имеет ещё одно неоспоримое свойство. В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.

Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.

Идеальная пропорция золотого сечения в пирамиде

Идеальные пропорции в древней Греции

Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.

Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.

Принцип идеальной пропорции в древнегреческом Парфеноне:

Памятники архитектуры средневековья

Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.

В здании очень заметно желание архитектора соблюсти гармонию и целостностьАнализируя строение, принцип ЗС можно видеть на нескольких участках

Архитектура России

Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.

Разметчик Фибоначчи построен по правилу золотого сеченияИспользовать циркуль можно практически на любом архитектурном сооруженииЧтобы исследовать большие объекты, нужно отойти на некоторое расстояние и приложить циркуль

Золотое сечение в архитектуре Москвы

Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.

В МГУ золотому сечению подчиняются высоты

Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова.

Кремлевское здание сенатаПречистенский дворецГолицынская больницаДом союзов — благородное собрание

Использовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам

Дом Пашкова

Архитектура в Санкт-Петербурге

Живым примером золотого сечения является Исаакиевский собор.

ЗС в Исаакиевском соборе

В первую очередь можно проанализировать его ширину, равную 400 единицам:

• при делении числа 400 на значение золотого сечения получим приблизительно 248;
• при дальнейшем делении 248/1,618=153;
• основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248.

По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.

На фото чётко прослеживаются золотой треугольник и прямоугольник в Исаакиевском соборе

Приведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.

Кунсткамера

Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.

В башне по всей высоте четко прослеживается равнобедренный треугольник, а это значит, что Кунсткамера построена по общему принципу ЗС

Торговый дом Эсдерс и Схейфальс

ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:

• 671, 414, 256, 98, 60, 37 и 23.

Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.

Основной элемент здания — шпиль

Дом Советов

Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:

• 1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.

Анализ длин и высот Дома Советов

Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.

Очевидная пропорциональность Дома Советов

Примеры золотого сечения в современной архитектуре

В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.

Правило золотого сечения при строительстве частного дома

Многие архитекторы, которые разрабатывают проекты частных домов, используют правило золотого сечения. У клиентов создается ощущение, что все детали проработаны для максимально комфортного проживания. При грамотном выборе площадей жильцы на психологическом уровне ощущают умиротворение и успокоение.

Что нужно знать при проектировании фасада

В современном строительстве при проектировании домов кроме ряда Фибоначчи используют ещё один метод, основоположником которого был архитектор из Франции Ле Корбюзье. Он принимал за основу рост будущих владельцев усадьбы и, исходя их этого, рассчитывал параметры строения и комнат. Благодаря такому подходу дом получался не только гармоничный, но и максимально комфортный с индивидуальными чертами хозяев.

Идеальные пропорции частного дома

Золотое сечение в оформлении интерьера

Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.

Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило:

• 60% — основная палитра;
• 30% — дополнительный оттенок;
• 10% — близкий тон, который усиливает восприятие основного и дополнительного.

Правило 1/1,62 в интерьере должно сопровождаться во всем: в соотношении мебели к общей площади, в ее высоте по отношению к параметрам комнаты.

Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.

Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.

Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:

Тайны золотого сечения, объясненные математикой и подсолнухами

Золотое сечение — это почти мифическое число, о котором вы, возможно, слышали в различных областях архитектуры и дизайна. Например, многие утверждают, что древнегреческий Парфенон имеет множество примеров золотого сечения в своем дизайне. Другие говорят, что самые красивые люди — это те, чьи черты соответствуют золотому сечению.

Эти утверждения в лучшем случае являются приблизительными приближениями к золотому сечению, а в худшем — к псевдонауке.Правда намного круче.

Замечательный канал на YouTube Numberphile недавно поговорил с Беном Спарксом, математиком, работающим в Университете Бата, чтобы раскрыть истинную природу золотого сечения: 1 плюс квадратный корень из 5 из 2, или приблизительно 1,62, представленное в математике греческая буква фи . В геометрии это число дает завораживающие узоры, например золотой прямоугольник. (Если вы возьмете золотой прямоугольник меньшей длины и создадите квадрат этой длины, а затем удалите площадь этого квадрата из золотого прямоугольника, у вас останется другой, золотой прямоугольник меньшего размера.)

Как поясняется в видео ниже, золотое сечение также можно считать «самым иррациональным» из всех иррациональных чисел. Иррациональное число — это число, которое не может быть выражено дробью целых чисел или целыми числами. Пи, например, — иррациональное число. Это почти 22/7, но не совсем.

Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

Математический метод исследования иррациональных чисел — это своего рода игра.Идея в том, что у вас есть цветок, и вы пытаетесь разместить семена на лицевой стороне цветка таким образом, чтобы вы могли уместить как можно больше. Если вы поместите семя, а затем поверните лицевую сторону цветка на определенную величину и поместите еще одно семя, а затем повторите этот процесс, какое значение будет идеальным для поворота лицевой стороны цветка?

Например, если вы поместите семя, поверните цветок на 1/2 оборота, поместите другое семя и повторите, тогда вы получите две части цветка со всеми семенами. Если вы сделаете 1/3 оборота, вы получите 3 строки семян, а если вы сделаете 1/10 оборота, вы получите 10 строк.

Лучшее число для поворота цветка для оптимального размещения семян — это золотое сечение, когда все лицо покрывается более или менее равномерно, без скопления семян в одном месте. Как демонстрирует видео, это связано с тем, что золотое сечение — очень иррациональное число, то есть оно не очень хорошо аппроксимируется каким-либо целым числом или даже какой-либо дробью целых чисел.

Оказывается, когда вы наносите семена подсолнечника на лицевую сторону цветка, это как если бы цветок играл в эту самую игру, помещая семена почти с математической точностью.Обязательно посмотрите видео, чтобы увидеть наглядное объяснение и дополнительную информацию об удивительной силе золотого сечения и о том, почему это самое иррациональное из чисел.

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.

Руководство для дизайнера по золотому сечению [с 14 примерами]

Что общего у раковин улиток, ураганов, Парфенона и Моны Лизы?

Все они следуют золотому сечению.

Дело в том, что независимо от того, являетесь ли вы дизайнером или нет, исследования показали, что ваш мозг, скорее всего, запрограммирован на то, чтобы предпочитать природу и произведения искусства, соответствующие золотому сечению. На самом деле искусство, которое следует золотому сечению, часто считается самым красивым. Так что, даже если вы не знаете, что это такое, вы, несомненно, видели это в некоторых из ваших любимых дизайнов и архитектур.

В математике (предмет, в котором я никогда не был так хорош), золотое сечение существует, когда линия делится на две части, и более длинная часть (a), деленная на меньшую часть (b), равна сумме обеих частей. (a) + (b), деленное на (a).Он должен составлять примерно 1,618.

Понял? И я нет. Но для наших целей мы собираемся сконцентрироваться на золотом узоре, как он существует в искусстве — например, в древнеримской архитектуре или картинах Леонардо да Винчи.

Изображение предоставлено Музей науки .

Если золотое сечение действительно является предпосылкой для создания захватывающего искусства, понятно, что вы, как человек, занимающийся дизайнерским проектом, должны знать о нем все. Здесь мы разберем примеры золотого сечения в природе, дизайне и даже человеческом лице, чтобы вы могли подумать, как включить золотое сечение в свои собственные маркетинговые проекты.

Что такое золотое сечение в дизайне?

Золотое сечение, также известное как Золотое Сечение, Золотое Сечение или Фи, представляет собой математическое соотношение, которое можно использовать для создания некоторых из самых красивых произведений искусства и архитектуры, таких как Мона Лиза или Парфенон. Наш мозг запрограммирован на то, чтобы предпочитать визуальные эффекты, соответствующие золотому сечению, которое можно найти во многих элементах в природе, и даже в человеческом лице, и поэтому он выглядит чистым и органичным.

Золотое сечение в природе

Золотое сечение проявляется во многих заметных и очевидных объектах природы, включая деревья, сосновые шишки и семена клубники.

Однако его можно увидеть и в в значительной степени абстрактных местах, например, в точке в черной дыре, где температура меняется с положительной на отрицательную. Его постоянное присутствие может обозначать золотое сечение как фундаментальную константу природы, что может объяснить, почему наш мозг, кажется, настроен лучше реагировать на визуальные эффекты, соответствующие золотому сечению.

Здесь мы рассмотрим лишь несколько примеров золотого сечения в природе:

1. Лепестки цветов

2.Ураганы

3. Спиральные галактики

4. Корпуса Nautilus

5. Семена цветов

6. Шишки сосновые

Значение золотого сечения для человеческого лица

Теперь, когда мы изучили, как природа следует золотому сечению, давайте посмотрим на золотое сечение, как оно существует на человеческом лице.

Предположительно, голова образует золотой прямоугольник с глазами в качестве середины, а рот и нос представляют собой золотые части расстояния между глазами и подбородком.Золотое сечение можно найти даже в наших зубах и профиле, когда мы поворачиваем голову в сторону.

Исследования показали, что лица, наиболее близкие к золотому сечению, считаются самыми красивыми.

Доктор Стивен Р. Марквардт, получивший докторскую степень в Калифорнийском университете в Лос-Анджелесе и проводящий исследования привлекательности человека, считает, что золотое сечение — это математическая формула, описывающая красоту лица.

Примеры золотого сечения

1. «Мона Лиза» Леонардо да Винчи
2. Парфенон
3. Раковины улиток
4. Ураганы
5. Высевные головки
6. Лепестки цветов
7. Шишки
8. «Тайная вечеря» Леонардо да Винчи
9. Ветви деревьев
10. Человеческое лицо
11. Спиральная галактика
12. «Сотворение Адама» Микеланджело
13. молекул ДНК
14. «Таинство Тайной вечери» Сальвадора Дали

Следующий курс был разработан совместно с Институтом цифрового маркетинга:

Золотое сечение в фотографии: что это такое и как его использовать.

Это материал следующего уровня.

Правило третей. ведущие линии. Все это важно, но они не так бросаются в глаза, как золотое сечение.

Если вы готовы пройти мимо, просто поместив объект в третью строку и назвав его композицией, читайте дальше. Если нет, даже не думайте читать дальше.

Я говорю это в шутку, надеюсь, вы знаете, но суть в том, что это композиционное правило может быть трудным для понимания и даже сложнее добавить в ваши изображения.Однако, если вы можете, качество и привлекательность ваших изображений вырастут в геометрической прогрессии.

Для начала поймите, что золотое сечение применяется к вашим изображениям по-разному и известно под разными именами. Некоторые из имен, с которыми вы, возможно, знакомы: золотая середина, фи, спираль Фибоначчи или божественная пропорция. Возможно, вы знакомы с одним или несколькими из этих терминов, но не запутайтесь.

Каждый из них использует золотое сечение по-разному для создания искусства, изображений и архитектуры, приятных для человеческого глаза.

Золотое сечение — это соотношение примерно 1,618: 1. Художники веками использовали это соотношение для создания произведений искусства, от картин до архитектуры. Бетховен использует его в своей знаменитой пятой симфонии. Это действительно повсюду вокруг нас, в том числе в наших собственных телах.

Чтобы увидеть и понять золотое сечение, давайте разделим линию на две части. Если следовать золотому сечению, это будет выглядеть, как на изображении ниже, где A — длинная сторона (1,618), а B — более короткая сторона (1).

Проще всего увидеть это на теле человека на руке, хотя есть много других частей человеческого тела, которые следуют золотому сечению.

Для художников сила золотого сечения начинается тогда, когда это соотношение применяется к другим формам. Давайте сначала построим так называемый золотой прямоугольник. Мы делаем это, беря длинную сторону линии, которую мы пометили A, и согласовывая эту длину, чтобы сформировать более короткие стороны прямоугольника.

Эта форма часто используется как в современной, так и в древней архитектуре, самой известной из которых является Парфенон.

Подробнее о золотом сечении в архитектуре.

Некоторые называют правило третей упрощенной версией золотого сечения, и если вы задумаетесь, то поймете почему. Добавив еще одну вертикальную линию к золотому прямоугольнику, вы получите очень точную копию правила третей.

Последовательность Фибоначчи

В 1200 году нашей эры математик Леонардо Фибоначчи открыл то, что сейчас известно как последовательность Фибоначчи, которая помогла продвинуть золотое сечение еще дальше.Он взял числа 0 и 1 и сложил их, получив 1.

Затем он продолжил брать два предыдущих ответа и сложил их вместе, чтобы сформировать цепочку чисел, которую вы видите ниже.

Красота этой цепочки чисел заключается в том, что вы берете любые две суммы рядом друг с другом и делите большую на меньшую. Когда вы это сделаете, вы получите число, очень близкое к золотому сечению. Смотри ниже.

5 + 18 = 13 и 8 + 13 = 21 находятся рядом друг с другом в последовательности Фибоначчи.Возьмите обе их суммы, 13 и 21, и разделите наибольшее на наименьшее, и вы получите число, очень близкое к 1,618.

Сделайте это с любой из сумм в последовательности Фибоначчи, и вы обнаружите то же самое.

Останьтесь со мной сейчас, потому что мы не собираемся больше углубляться в математику, так что не прекращайте читать обо мне!

Оглядываясь назад на золотой прямоугольник, когда я начинаю добавлять меньшие золотые прямоугольники внутри больших, происходит кое-что удивительное.

Площадь каждого из вновь образованных квадратов является суммой уравнения в последовательности Фибоначчи, и отсюда мы получаем спираль Фибоначчи, которую многие художники используют сегодня в качестве своей основной композиционной техники.

Спираль Фибоначчи

Спираль создается путем рисования дуг окружности из противоположных углов каждого квадрата. Посмотрите на рисунок ниже, чтобы увидеть спираль внутри золотого прямоугольника. Эта спираль широко распространена в природе, особенно в раковине наутилуса.

Посмотрите это видео, это прекрасная иллюстрация золотого сечения, встречающегося в природе.

Обратите внимание, и вы увидите золотое сечение и спираль Фибоначчи повсюду, от продуктов, которые вы покупаете, до логотипов компаний и архитектуры.

Это хорошо известно маркетологам, которые понимают, что следуя золотому сечению, люди с большей вероятностью будут рассматривать свои продукты как благоприятные. Мы можем использовать это в своих интересах и в наших изображениях.

Использование золотого сечения в фотографии

Ниже приведена диаграмма, на которой подробно описана спираль Фибоначчи с основными линиями 1: 1.618. Спираль Фибоначчи — один из основных способов использования золотого сечения в фотографии для фотографов.

Многие известные фотографы используют золотое сечение в фотографии.Ансель Адамс часто использовал его в своих пейзажных портретах.

© Ансель Адамс

Анри Картье-Брессон, один из моих любимых фотографов, использовал его, чтобы запечатлеть жизнь такой, какая она есть. Картье-Брессон всю свою карьеру использовал объектив с фокусным расстоянием 50 мм, уделяя меньше внимания оборудованию и больше композиции. Ниже представлен автопортрет, сделанный им с использованием спирали Фибоначчи в качестве композиционной техники.

Анри Картье-Брессон

Посмотрите на эти изображения и постарайтесь увидеть в них красоту.Это изображения повседневной жизни, но сделанные в интересной и вдохновляющей манере. У него был мощный способ использования золотого сечения в фотографии, чтобы оживить обыденное.

Изображения выше, © Анри Картье-Брессон

На мой взгляд, это и есть фотография. Не о том, сколько оборудования мы можем купить или какой объектив самый большой. Речь идет о рассказе истории, которая происходит прямо у нас на глазах.

«Для меня фотография — это одновременное признание значимости события за доли секунды».
-Анри Картье-Брессон

Создание с использованием спирали Фибоначчи в фотографии

Спираль Фибоначчи сложнее понять, чем, скажем, баланс или правило третей. Эти композиционные правила проще понять и использовать.

Это причина того, что многие фотографы никогда не слышали о спирали Фибоначчи или золотом сечении в фотографии.Чтобы использовать это в своих фотографиях, требуется больше практики и внимания. Позвольте мне рассказать о некоторых способах включения спирали Фибоначчи в ваше изображение, чтобы облегчить композицию ваших изображений.

Самый простой способ начать использовать спираль Фибоначчи — снимать сцены с неподвижными объектами и размещать их так, чтобы они образовывали плавное число девять, а ваш объект находится в круге девяти. Изображение справа — хороший тому пример.

Другой способ творить со спиралью Фибоначчи — использовать открытое пространство или пространство, яркость которого отличается от яркости объекта.

На этом изображении ниже, взгляд направлен на объект человеком в тени в нижнем левом углу и человеком в тени справа. Светлые тона неба помогают привлечь внимание зрителя к изображению, а затем подталкивают взгляд к объекту.

Это изображение серферов — еще один пример.

Используя серфера внизу, чтобы провести взгляд по изображению, зритель оказывается у серфера на волне. Вы можете сказать себе: «Это просто правило третей.«Вы правы, правило третей является частью этого образа.

Однако серфер в нижнем левом углу не следует правилу третей, но добавляет баланс, глубину и помогает направить взгляд на объект. Серфер в нижнем левом углу демонстрирует все это, потому что он находится в месте, где можно использовать спираль Фибоначчи. Взгляните на изображения ниже.

Что вы предпочитаете?

Эти тонкие различия могут превратить ваши изображения из хороших в отличные.

Создание с использованием золотого сечения в фотографии

Создание изображений с использованием соотношения сторон может быть невероятно трудным.Что еще хуже, каждый прямоугольник можно также превратить в более мелкие золотые прямоугольники. Взгляните на изображения ниже. Это беспорядок из строк!

Чтобы еще больше усложнить ситуацию, линии золотого сечения также могут быть диагональными. На изображении ниже показано, как диагональные линии могут составлять золотое сечение, и снова внутри каждого набора линий могут быть добавлены дополнительные линии, соответствующие золотому сечению. В бесконечность.

Чтобы помочь решить эту путаницу, позвольте мне дать несколько простых советов, когда вы начнете использовать золотое сечение в фотографии.

СОВЕТ ПЕРВЫЙ: РАЗМЕСТИТЕ ТЕМУ НА ПЕРЕСЕЧЕНИИ ЛИНИЙ

Как и в случае с правилом третей, размещение объекта на пересечении линий поможет создать более приятное изображение для зрителя. Поступая так, вы уйдете или вырежете что-то из изображения, которое вы не сделали бы иначе. Сам факт этого поможет изменить то, как вы снимаете изображения.

СОВЕТ ВТОРОЙ: РАЗМЕСТИТЕ СИЛЬНЫЕ ЛИНИИ НА ЛИНИЯХ ЗОЛОТОГО СООТНОШЕНИЯ

Этот совет особенно полезен при фотографировании архитектуры с четкими линиями.Поместите эти четкие линии на линии золотого сечения, чтобы создать больше интереса к изображению.

На изображении здания линия между темной и светлой частями здания проводится по линии золотого сечения, а также по верхним углам.

На фотографии моста линии перил совпадают с линиями золотого сечения, помогая создать изображение, которое привлекает внимание зрителей и добавляет интереса.

Энни Либовиц

Вы когда-нибудь видели групповое фото от Энни Либовиц? Она далека от правила третей.В большинстве групповых фото используется золотое сечение.

© Энни Либовиц

Заключение

Это может сбивать с толку, когда вы начинаете включать золотое сечение в свои изображения, потому что есть чертовски много способов! Я бы посоветовал взять один или два метода и поработать над ними, прежде чем вводить другие.

Сделав это, вы привыкнете к использованию этого метода, и по мере того, как вы привыкнете к одному или двум методам, начнете добавлять другие.

Отказ от правила третей и использование более продвинутых композиционных приемов действительно поможет вам стать фотографом с яркими изображениями.

Супер-классный бесплатный курс по освещению.

Готовы узнать об освещении?

Независимо от того, снимаете ли вы в помещении, мой бесплатный онлайн-курс по освещению для вас. Просто нажмите «Зарегистрируйтесь» ниже и введите свое имя и адрес электронной почты.

Поднимите свои навыки освещения на новый уровень!

Успех !! Я так рада, что ты здесь! Вы найдете ссылку на курс в своем электронном письме.

Золотое сечение, наблюдаемое в человеческих черепах

Золотое сечение, описанное Леонардо да Винчи и Лукой Пачоли как Божественная пропорция, представляет собой бесконечное число, которое часто встречается в природе, искусстве и математике. Это узор в сосновых шишках, ракушках, галактиках и ураганах.

В новом исследовании, посвященном изучению того, соответствует ли форма черепа золотому сечению (1,618…), исследователи Джона Хопкинса сравнили 100 человеческих черепов с 70 черепами шести других животных и обнаружили, что размеры человеческого черепа соответствуют золотому сечению.Однако черепа менее родственных видов, таких как собаки, два вида обезьян, кролики, львы и тигры, расходились с этим соотношением.

«У других обследованных нами млекопитающих действительно уникальные соотношения, приближающиеся к золотому сечению с увеличением видовой сложности», — говорит Рафаэль Тамарго, доктор медицины, профессор нейрохирургии Медицинской школы Университета Джонса Хопкинса. «Мы считаем, что это открытие может иметь важные антропологические и эволюционные последствия.

Исследователи опубликовали свои выводы в сентябрьском номере журнала The Journal of Craniofacial Surgery .

Золотое сечение можно вычислить, разделив линию на две неравные части, причем длина более длинной части, разделенная на более короткую, будет равна всей длине, разделенной на более длинную часть. Интерес Тамарго к истории и анатомии побудил его в 2010 году опубликовать статью об обнаружении человеческого мозга и спинного мозга в изображении Бога на картине Микеланджело Сикстинской капеллы.

Джонатан Пиндрик, ныне детский нейрохирург в Национальной детской больнице в Огайо, также внес свой вклад в исследование.

Витрувианский человек Леонардо с выделенными золотыми пропорциями Кредит: Изменено Рафаэлем Тамарго

---

В сети:

Как использовать золотое сечение в дизайне

Вы ищете способы вывести свою дизайнерскую работу на новый уровень? Иногда лучшее, что вы можете сделать, — это вернуться к классике.Вы слышали о золотом сечении? Что ж, этот простой древний принцип — отличный трюк, который вы можете использовать для улучшения своих дизайнов. Читайте дальше, чтобы узнать, что такое золотое сечение и как вы можете использовать золотое сечение в дизайне, выводя свое онлайн-портфолио дизайна на новый уровень. Но сначала…

Что такое золотое сечение?

Древние греки первыми открыли красоту, присущую асимметрии природы, и выразили это явление золотого сечения греческой буквой «ϕ» (фи).Художники и архитекторы использовали фи в качестве секретного оружия в своем творческом арсенале, создавая произведения, которые имеют чувство гармонии и пропорции, созвучные естественному порядку.

Золотое сечение образовано линией, разделенной на две части. Затем более длинная часть делится на меньшую, равную сумме (a) + (b), деленной на (a), которые оба равны 1,618.

Это тебе еще не сломало? Нет? Отлично.

Золотое сечение тесно связано с последовательностью Фибоначчи.Он был назван в честь Леонардо Пизанского, который позже стал известен как Фибоначчи. Эта последовательность была впервые использована для выяснения особенностей размножения популяций кроликов.

По сути, числа Фибоначчи следуют последовательности, в которой каждое число является суммой двух предыдущих, начиная с 0 и 1. Вот простой пример: 0, 1, 1, 2, 3, 5, 8, 13 и т. Д.

Если вы сложите два последовательных числа в последовательности вместе, вы получите золотые сечения — до бесконечности .

Где я видел примеры золотого сечения в действии?

Скорее всего, вы видели золотое сечение в природе бесчисленное количество раз и никогда не осознавали этого.Точно так же вы встречали бесчисленное количество классических картин и никогда не осознавали последовательность Фибоначчи, скрывающуюся под их поверхностью.

Природа

Золотое сечение похоже на лежащую в основе универсальную сетку, которую можно найти повсюду в природе. Например, знаете ли вы, что камеры раковины наутилуса на самом деле придерживаются логарифмической спирали последовательности Фибоначчи?

Как золотое сечение проявляется в природе

Вселенная может быть хаотичной и непредсказуемой, но это также высокоорганизованный физический мир, связанный законами математики.Один из самых фундаментальных (и поразительно красивых) способов проявления этих законов — это золотое сечение.

Нетрудно найти примеры этого логарифмического явления в природе — будь то простое комнатное растение (например, растение алоэ выше) или обширная спиральная галактика (например, спиральная галактика Мессье 83, показанная ниже), все они происходят из одной и той же математической модели. концепции.

Мессье 83, спиральная галактика, расположенная в 15 миллионах световых лет от Земли. (Фото: НАСА, ЕКА и группа «Наследие Хаббла» (STScI / AURA) / Благодарность: Уильям Блэр, Университет Джона Хопкинса)

Золотое сечение (часто обозначаемое греческой буквой φ) напрямую связано с числовым шаблоном, известным как последовательность Фибоначчи, который представляет собой список, состоящий из чисел, являющихся суммой двух предыдущих чисел в последовательности.Последовательность Фибоначчи, которую часто называют естественной системой нумерации космоса, начинается просто (0 + 1 = 1 , 1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5 , 3 + 5 = 8 …), но вскоре вы обнаружите, что складываете числа в тысячи и миллионы (10946 + 17711 = 28657 , 17711 + 28657 = 46368 , 28657 + 46368 = 75025 …) и так будет продолжаться вечно.

Когда число Фибоначчи делится на предшествующее ему число Фибоначчи, оно приближается к золотому сечению, которое является иррациональным числом, начинающимся с 1.6180339887 … и, опять же, продолжается вечно.

Когда золотое сечение применяется в качестве фактора роста (как показано ниже), вы получаете тип логарифмической спирали, известный как золотая спираль.

Узнайте больше о последовательности Фибоначчи и естественных спиралях в этой увлекательной серии видео, созданной математиком Ви Харт, которая говорит быстро, но интересна и напомнит вам о том, как ваш мозг когда-то прыгал от предмета к предмету:

Как объясняет Харт, примеры приблизительных золотых спиралей можно найти в природе, особенно в морских ракушках, океанских волнах, паутинах и даже в хвостах хамелеонов! Продолжайте читать ниже, чтобы увидеть лишь некоторые из способов, которыми эти спирали проявляются в природе.

Хвосты хамелеона

Хвост хамелеона славится своей плотной спиралевидной формой. (Фото: Райан М. Болтон / Shutterstock)

Ракушки

Морская ракушка — один из самых известных примеров спирали золотого сечения в природе. (Фото: Tramont_ana / Shutterstock)

Папоротник для скрипки

Свернувшиеся вверх листья молодого папоротника известны как головастые. (Фото: Zamada / Shutterstock)

Океанские волны

Несмотря на свою бурную природу, океанские волны — еще один пример проявления золотого сечения в природе.(Фото: irabel8 / Shutterstock)

Бутоны цветов

Когда цветок еще не распустился, легко увидеть свидетельство золотого сечения. (Фото: Романцова Ольга / Shutterstock)

Раковины улиток

Раковины улиток — прекрасный пример золотого сечения в природе. (Фото: vvoronov / Shutterstock)

Романеско брокколи

Фрактальные спирали брокколи Романеско (Brassica oleracea). (Фото: Сергей Склезнев / Shutterstock)

Водовороты

Водоворот, показывающий спираль золотого сечения.(Фото: Элейн Дэвис / Shutterstock)

Цветы окопника

Вы можете увидеть спираль стебля этого цветка окопника. (Фото: Михаил Мельников / Shutterstock)

Шишки сосновые

Спирали золотого сечения, если смотреть со дна шишки. (Фото: bzanchi / Shutterstock)

Кочан для подсолнечника

Золотое сечение роста подсолнечника. (Фото: Portogas D Ace / Shutterstock)

Ураган Изабель (2003)

Спираль урагана Изабель в 2003 году. (Фото: Майк Тренчард / НАСА)

Каллы

Спиральное цветение каллы.(Фото: Линн Уотсон / Shutterstock)

Раковины

Колючая раковина со спиралью золотого сечения. (Фото: Fontana / Shutterstock)

Спираль алоэ

Спиральное растение алоэ сидит в садовом горшке. (Фото: PhotoSky / Shutterstock)

Паутина

Эта паутина имеет спиралевидную форму. (Фото: mycteria / Shutterstock)

Лепестки цветов

Среди этих фигурных лепестков цветов много золотых пропорций. (Фото: Ян Грейнджер / Shutterstock)

Золотое сечение. Факты для детей

Для одного числа a и другого меньшего числа b соотношение этих двух чисел находится путем их деления.Их соотношение составляет a / b . Другое соотношение получается путем сложения двух чисел и деления их на большее число a . Новое соотношение: ( a + b ) / a . Если эти два отношения равны одному и тому же числу, то это число называется золотым сечением . Греческая буква (фи) обычно используется в качестве названия золотого сечения.

Например, если b = 1 и a / b =, то a =.Тогда будет второе соотношение ( a + b ) / a . Поскольку эти два соотношения равны, это правда:

Один из способов написать это число —

похоже на любое число, которое при умножении на само себя дает 5 (или какое число умножается):.

Золотое сечение — это иррациональное число. Если человек попытается написать это, он никогда не остановится и никогда не создаст узор, но он начнется так: 1.6180339887 … В этом числе важно то, что человек может вычесть из него 1 или разделить на него 1. В любом случае, число будет продолжаться и никогда не прекратится.

Золотой прямоугольник

Большой прямоугольник BA — золотой прямоугольник; то есть пропорция b: a равна 1 :. Для любого такого прямоугольника и только для прямоугольников этой конкретной пропорции, если мы удалим квадрат B , то, что останется, A , будет другим золотым прямоугольником; то есть с теми же пропорциями, что и исходный прямоугольник.

Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник является «золотым прямоугольником». Если квадрат отрезан от одного конца золотого прямоугольника, то другой конец будет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) — это золотой прямоугольник, потому что. Синяя часть (B) — это квадрат, а розовая часть (A) — это еще один золотой прямоугольник, потому что. Большой прямоугольник и розовый прямоугольники имеют одинаковую форму, но розовый прямоугольник меньше и повернут.

Числа Фибоначчи

Числа Фибоначчи — это список чисел. Человек может найти следующий номер в списке, сложив два последних числа вместе. Если человек делит число в списке на число, которое было перед ним, это соотношение все ближе и ближе к золотому сечению.

Число Фибоначчи	делится на число до	соотношение
1
1	1/1	= 1.0000
2	1/2	= 2,0000
3	3/2	= 1,5000
5	5/3	= 1,6667
8	8/5	= 1,6000
13	13/8	= 1,6250
21	21/13	= 1,6154 …
34	34/21	= 1.6190 …
55	55/34	= 1,6177 …
89	89/55	= 1,6182 …
…	…	…
		= 1,6180 …

Золотое сечение в природе

Использование золотого угла позволит оптимально использовать солнечный свет. Это вид сверху.

В природе золотое сечение часто используется для расположения листьев или цветов.В них используется золотой угол приблизительно 137,5 градусов. Листья или цветы, расположенные под таким углом, лучше всего используют солнечный свет.

Связанные страницы

Образы для детей

• Майкл Маэстлин, первый, кто написал десятичную аппроксимацию отношения

• Вид на минарет со двора Большой мечети Кайруана

• Иллюстрация Леонардо с додекаэдром из пропорции Дивины Пачоли (1509)

• Фрагмент блюдца, Aeonium tabuliforme , демонстрирующий множественное спиральное расположение (парастихи)

• Аппроксимация обратного золотого сечения конечными цепными дробями или отношениями чисел Фибоначчи

• Раковины наутилуса часто ошибочно называют золотыми пропорциями.