Определение высоты объекта на местности: % способов определения высоты предметов

% способов определения высоты предметов

Определение высоты некоторых предметов

Рекомендуем несколько способов, при помощи которых можно определить высоту предметов.

1. По тени. В солнечный день можно определить высоту предмета по его тени, руководствуясь следующим правилом: высота измеряемого предмета во столько раз больше высоты известного вам предмета (палки, удочки), во сколько раз  тень от измеряемого предмета больше тени от палки, удоччки.

Если при измерении окажется, что тень от палки или удочки в 2 раза больше длины палки или удочки, то высота измеряемого предмета будет в 2 раза меньше длины его тени, а если тень от палки или удочки будет равна их длине, высота измеряемого предмета также равна высоте своей тени.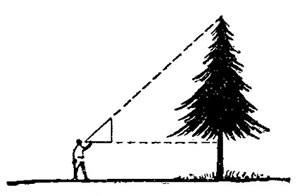

 

2. При помощи равнобедренного треугольника. Приближаясь к предмету (например, к дереву) или удаляясь от него, установить треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с линией визирования на вершину дерева. Высота дерева будет равняться расстоянию до дерева (в шагах) плюс высота до глаз наблюдателя.

 

3. По шесту. Взять шест, равный своему росту, и установить его на таком расстоянии от предмета (дерева), чтобы лёжа можно было видеть верхушку дерева на одной прямой с верхней точкой шеста.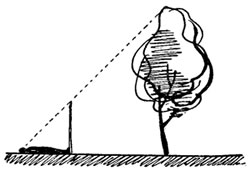

Высота дерева будет равна расстоянию от головы наблюдателя до основания дерева.

 

4. При помощи высотомера со стрелкой. Изготовив прибор по данному чертежу, можно приступить к определению высоты  какого-либо предмета. Находясь на различном расстоянии от предмета, надо следить, чтобы при визировании вершины дерева показания стрелки не выходили за пределы шкалы.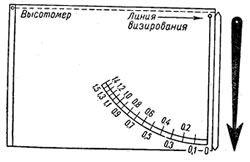

При визировании следует приложить глаз к отверстию сбоку прибора и, наклонив прибор, добиться, чтобы вторая визирная точка (угол на другом конце прибора) совпала с вершиной визируемого предмета. Стрелка укажет число, на которое следует умножить расстояние до предмета, чтобы получить его высоту. К этому прибавляется выста прибора во время визирования.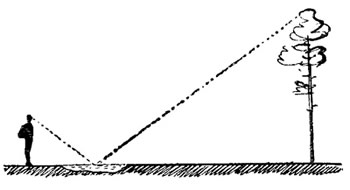

 

5. При помощи лужи. Если недалеко от дерева находится лужа, надо стать так, чтобы она помещалась между вами и предметом, а затем при помощи горизонтально положенного зеркальца найти в воде отражение вершины деерва. Высота дерева будет во столько раз больше роста человека, во сколько раз расстояние от него до лужи больше, чем расстояние от лужи до наблюдателя.

Как определить высоту недоступного объекта

Григорию Владимировичу понадобилось определить высоту дерева, находящегося на приусадебном участке. Дерево подверглось нападению жука типографа и его нужно срочно спилить. При этом нужно выбрать, в какую сторону оно должно упасть в результате спиливания, чтобы не повредить строения и насаждения на участке. Дерево было очень высокое, и он никак не мог найти возможность измерить его известными ему методами.

Ему на помощь пришла его дочь Ангелина, которая рассказала о том, что в курсе школьной программы они изучали тему «Подобие треугольников» и учитель объяснила всем ребятам, как можно измерить высоту предмета подручными средствами, с использованием знаний по математике и физике. Григорий Владимирович был очень удивлён, когда Ангелина сказала, что для проведения расчётов им понадобятся небольшое зеркало, рулетка и шнур.

Вооружившись всем необходимым, отец и дочь приступили к работе. Они проложили шнур от дерева по поверхности земли. На некотором удалении от дерева, на линии шнура, положили зеркало. После этого Ангелина встала на линии шнура так, чтобы верхушка дерева была ей видна в зеркале. «Папа, здесь «включается» физика: угол падения луча света равен углу отражения луча света.

Наличие двух равных углов в двух прямоугольных треугольниках позволяет говорить нам о подобии этих треугольников», – сказала Ангелина.

Затем Ангелина попросила отца произвести три замера:

1. расстояние от дерева до зеркала

2. расстояние от зеркала до того места, где стоит Ангелина

3. рост самой Ангелины.

Отец произвёл измерения. Расстояние от дерева до зеркала составило 10,3 м, от зеркала до Ангелины – 1,4 м, а рост Ангелины составил 1,65 м.

«А теперь, папа, всё очень просто! – воскликнула Ангелина. – Мне необходимо произвести несложные вычисления, и мы узнаем высоту нашего дерева».

В соответствии с построенным чертежом, Ангелина записала следующее:

AC = 1,4 м

CD = 10,3 м

AB = 1,65 м

KD = 1,65*10,3:1,4 = 12,139… м ≈ 12 м.

Статья на тему «определение высоты предмета»

Определение высоты предмета

Предположим, что нам нужно определить высоту какого-нибудь предмета, например высоту телеграфного столба А1С1. Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А1 столба. Отметим на поверхности земли точку В, в которой прямая А1А пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников

Определение высоты предмета (продолжение)

Из подобия треугольников следует:

Измерив расстояния ВС1 и ВС и зная длину АС шеста, по полученной формуле определяем высоту А1С1 телеграфного столба. Если, например, ВС1=6,3 м, ВС=2,1 м, АС=1,7м, то

Определение расстояния до недоступной точки

Предположим, что нам нужно найти расстояние от пункта А до недоступного пункта В. Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябии измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник А1В1С1, у которого и измеряем длины сторон А1В1 и АС1 этого треугольника. Так как треугольник АВС пропорционален треугольнику А1В1С1, то

По известным расстояниям АС, А1С1 и А1В1 находим расстояние АВ. Для упрощения вычислений удобно построить треугольник А1В1С1 так, чтобы А1С1:АС=1:1000. Например, если АС=130м, то расстояние А1С1 возьмём равным 130 мм. В этом случае

Определение расстояния до недоступной точки(продолжение)

поэтому, измерив расстояние А1В1 в миллиметрах, мы сразу получаем расстояние АВ в метрах.

ПРИМЕР. Пусть

Строим треугольник А1В1С1 так, чтобы

Измеряем отрезок А1В1. Он равен 153 мм, поэтому искомое расстояние равно 153 м.

Почему летом теплее, чем зимой?

Все дело в наклоне земной оси по отношению к плоскости земной орбиты ( рис.)

Зимой в умеренных широтах солнце невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом в моменты наивысшего подъёма над горизонтом солнце приближается к зениту, его лучи падают почти отвесно на те же участки земного шара.

ПОТОК ЭНЕРГИИ, ИДУЩЕЙ ОТ Солнца, одинаков во все времена года. Но в зависимости от наклона солнечных лучей она по-разному распределяется по земной поверхности. Больше всего её приходится на заданный участок поверхности при отвесном падении света. Чем меньше угол, который образуют лучи с поверхностью, тем меньше их приходится на тот же участок.

Именно эту зависимость применяет курортник, загорающий под солнцем юга, когда он поворачивает свой топчан так, чтобы солнечные лучи как можно менее отклонялись от перпендикуляра к плоскости топчана.

Попытаемся определить: какая доля солнечной энергии, приходящейся на некоторый участок плоскости при отвесном падении лучей, приходится на него при наклонном падении лучей под тем или иным углом?

На поставленный вопрос можно ответить, проследив эволюцию прямоугольного треугольника на приведенных чертежах. Гипотенуза, на которую падают солнечные лучи,- всюду одна и та же. Катет, через который входят падающие на нее лучи,- меняются по длине уменьшаясь вместе с углом, который образует с гипотенузой падающие на него лучи .

Интересующая нас доля энергии равна отношению указанного катета к гипотенузе. Если задан угол, под которым солнечные лучи встречаются с освещаемой поверхностью, нужно отложить его на круговой диаграмме, из точки пересечения его наклонной стороны с окружностью опустить перпендикуляр на горизонтальный диаметр и взять отношение противолежащего катета к гипотенузе. Полученное число и укажет интересующую нас долю солнечной энергии. Число, определённое таким образом и поставленное в соответствие углу, для которого оно определялось , называется синусом угла.

Полезные советы туристам. Как определить расстояние по звуку и глазомером. Измерение дальности.

В походе, особенно по неизвестной местности и с не очень подробной картой зачастую возникает потребность в ориентировании и определении дальности до каких либо предметов или объектов. И даже GPS-приемник навигатор тут не выручит, так как к нему должна еще прилагаться и карта. А с ними (на территории России) весьма туго. Привязка же координат с туристической карте весьма условная (+- километр).

Возможно, вам помогут простые советы наработанные многолетним туристическим опытом предшественников.

1. На открытой местности населенные пункты видны с 10-12 км.

2. Многоэтажные строения — 8-10 км.

3. Отдельные одноэтажные (частные) дома – 5-6 км.

4. Окна в домах различимы с 4 км.

5. Трубы печей на крышах — 3 км.

6. Отдельные деревья различимы с 2 км.

7. Люди (в виде точек) – 1,5 – 2 км.

8. Движение рук и ног человека — 700 метров.

9. Переплеты оконных рам – 500 метров.

10. Голова человека – 400 м.

11. Цвет и части одежды — 250-300 м.

12. Листья на деревьях – 200 м.

13. Черты лица и кисти рук – 100 м.

14. Глаза в виде точек – 60-80 м.

В ночное время:

1. Горящий костер (обычных размеров) виден на расстоянии 6-8 км.

2.

 Свет электрического фонарика (обычного) – 1,5 – 2 км.

3. Горящая спичка — 1-1,5 км.

4. Огонь сигареты – 400-500 м.

Определение расстояние по звуку сильно зависит от плотности воздуха и в еще большей степени от его влажности. Чем выше давление и выше влажность, тем дальше разносятся звуки. Это необходимо учитывать. Для тихого места и при нормальной влажности:

1. Шум железной дороги (идущего поезда) слышен за 5-10 км.

2. Выстрел из ружья — 2-4 км.

3. Гудок автомобиля, треск пускача трактора, громкий свисток — 2-3 км.

4. Лай собак — 1-2 км.

5. Движение автомобилей по шоссе — 1-2 км.

6. Человеческий крик неразборчиво — 1 – 1,5 км.

7. Звук газующего мотора легкового автомобиля – 0,5 – 1 км.

8. Шум падающего дерева (треск) — 800 – 1000 метров.

9. Стук топора, стук по металлическим предметам — 300-500 метров.

10. Спокойный разговор людей – 200 метров.

11. Негромкая речь, кашель — 50 – 100 метров.

Психологические поправки, которые надо учитывать:

1. Чем дальше предмет, тем он кажется более низким и узким. Поэтому крупные объекты кажутся более близкими (особенно горы), чем есть на самом деле. Лежащие предметы кажутся длиннее, чем стоящие.

2. Расстояние на «гладкой» поверхности (снег, вода, ровное поле) кажется меньше действительного. Ширина реки с пологого берега больше, чем с обрыва.

3. При взгляде снизу вверх склон кажется менее крутым, а расстояние до объектов меньше действительного.

4. Ночь любой свет кажется значительно (!) ближе реального расстояния. Днем светлые предметы так же кажутся более близкими.

5. Обнаженные склоны кажутся более крутыми, чем покрытые растительностью.

6. Обратная дорога кажется более короткой. Ровная дорога кажется короче пересеченной.

Простой способ определения расстояния до предметов методом подобных треугольников.

Этот метод основан на простом математическом соотношении сторон треугольников и знании пары величин, как то: 1) Длина большого пальца человека равна примерно 6 см (60 мм) и 2) Расстояние от большого пальца до глаз человека при вытянутой руке равно примерно 60 см. (Разумеется, вы можете точно измерить свои собственные параметры и внести соответствующие поправки в формулу. Кстати, вместо большого пальца удобнее использовать обычную спичку (длина 45 мм)).

Для того, что бы достаточно точно определить расстояние до объекта, необходимо еще знать его размеры, высоту, в частности.

Например, нам нужно определить расстояние до деревни. Средняя высота стен дома – ок. 3-х метров. Столько же имеет в высоту и крыша. Т.е. высота дома – около 6 метров. Вытягиваем руку, выставив вверх большой палец и оцениваем, в какую часть пальца «укладывается» дом. Допустим, это примерно 1/3 пальца, т.е. 2 см.

В подобных треугольниках истинная высота будет так же соотноситься с истинным расстоянием, как и «проекция» высоты с расстоянием до этой проекции из точки обзора. (или наоборот).

Т.е. 6 метров высоты / Х метров (расстояние) = 2 см/60 см, или

Х метров / 6 = 60/2

Отсюда получаем Что Х = 6 х 30, т.е. до дома 180 метров.

Если знать высоту объекта и иметь при себе линейку (рулетку) то вычислять расстояния можно весьма точно (с достаточной для туристических целей точностью).

Если высота объекта неизвестна даже приблизительно, то предстоит решить немного более сложную задачку, которая позволит вычислить и расстояние до объекта и его высоту. Для этого потребуется сделать два замера проекции высоты объекта с двух разных точек. После первого замера надо приблизиться к объекту на какое то расстояние (и это расстояние запомнить, обозначим его «L», первую проекцию «h2», а вторую «h3»).

Не буду утомлять математическими выкладками, а сразу приведу формулу:

Х = (L x h2) / (h3 – h2) (h3 будет больше, если вы приближались к объекту).

Ну а теперь зная расстояние до объекта несложно вычислить и его высоту (H) :

H (м) = X x h3 / 0.6

Вот такие незамысловатые формулы позволят вам весьма точно ориентироваться на местности и определять расстояния не имея дальномера.

Автор: Константин Тимошенко.

ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ — ПОСТРОЕНИЕМ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ

При определении расстояния до недоступных предметов используют различные приемы, связанные с построением подобных треугольников.

Определение расстояния по линейным размерам предметов. Для измерения расстояния турист, держа линейку на вытянутой руке, направляет ее на предмет {рис. 56), высота (длина) которого ему примерно известна. Так, рост человека в метрах равен 1,7, колесо велосипеда имеет высоту 0,75, деревянный столб линии связи —5—7, одноэтажный дом с крышей — 7—8, средневозрастной лес — 18—20; легковой автомобиль имеет длину в 4—4,5, грузовой автомобиль — 5—6, железнодорожный пассажирский вагон — 24—25; расстояние между столбами линий связи в среднем составляет 50—60 м и т. д.Допустим, надо определить расстояние до столба линии связи. Нл линейке его изображение заняло 20 мм. Принимая длину руки взрослого человека приблизительно за 60 см, составляем пропорцию: 

длина рукти/расстояние до столба=величина изображения на линейке/высота столба 

или 

0,6/х=0,02/6 

откуда

х=(0,6*6)/0,02=180 

Таким образом — до столба 180 м. 

ри определении расстояния до недоступных предметов используют различные приемы, связанные с построением подобных треугольников.
 

Определение расстояния по линейным размерам предметов. Для измерения расстояния турист, держа линейку на вытянутой руке, направляет ее на предмет {рис. 56), высота (длина) которого ему примерно известна. Так, рост человека в метрах равен 1,7, колесо велосипеда имеет высоту 0,75, деревянный столб линии связи —5—7, одноэтажный дом с крышей — 7—8, средневозрастной лес — 18—20; легковой автомобиль имеет длину в 4—4,5, грузовой автомобиль — 5—6, железнодорожный пассажирский вагон — 24—25; расстояние между столбами линий связи в среднем составляет 50—60 м и т. д.Допустим, надо определить расстояние до столба линии связи. Нл линейке его изображение заняло 20 мм. Принимая длину руки взрослого человека приблизительно за 60 см, составляем пропорцию: 

 

длина рукти/расстояние до столба=величина изображения на линейке/высота столба  

 

или

 

0,6/х=0,02/6

 

откуда

 

х=(0,6*6)/0,02=180 

 

Таким образом — до сто0 м. 

 

 

 

Походные эталоны. Для измерений на маршруте с помощью построения подобных треугольников туристам полезно знать некоторые другие походные эталоны.
Длина «четверти», то есть расстояние между концами расставленых большого пальца и мизинца у взрослого человека составляет при-мерно 18—22 см. Длина указательного пальца от основания большого пальца 11—13 см, от основания среднего — 7—8 см. Наибольшее расстояние между концами большого и указательного пальцев 16—18 см, между концами указательного и среднего пальцев — 8—10 см. Расстояние от глаз до поднятого большого пальца вытянутой руки — 60— 70 см. Ширина указательного пальца около 2 см, ширина его ногтя 1 см. Ширина четырех пальцев ладони 7—8 см.
Конкретную длину этих и других эталонов каждый турист определяет самостоятельно и записывает в свою походную записную книжку.

При определении расстояния до отдаленных или недоступных предметов, можно использовать следующий прием.

На обычную спичку надо нанести чернилами или карандашом двухмиллиметровые деления.

Также необходимо знать примерную высоту предмета, до которого определяется расстояние.

Так, рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник — 2,2 м, телеграфный столб — 6 м, одноэтажный дом без крыши — 2,5-4 м.

Допустим, надо определить расстояние до столба. Направляем на него спичку на вытянутой руке, длина которой приблизительно равна 60 см, предположим, высота столба выглядит равной двум делениям спички, т.е. 4 мм. Имея такие данные можно составить пропорцию:

длина руки / расстояние до столба = отрезок спички / высота столба

0,6/х = 0,004/6,0; х=(0,6*6)/0,004=900.

Таким образом, до столба 900 м.

Измерительные работы на местности в курсе геометрии основной школы

В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. Практические работы на местности являются одной из наиболее активных форм связи обучения с жизнью, теории с практикой. Учащиеся учатся пользоваться справочниками, применять необходимые формулы, овладевают практическими приёмами геометрических измерений и построений.

Практические работы с использованием измерительных инструментов повышают интерес учащихся к математике, а решение задач на измерение ширины реки, высоты предмета и определение расстояния до недоступной точки позволяют применить их в практической деятельности, увидеть масштаб применения математики в жизни человека.

По мере изучения материала способы решения этих задач изменяются, одну и ту же задачу можно решить многими способами. При этом используются следующие вопросы геометрии: равенство и подобие треугольников, соотношения в прямоугольном треугольнике, теорема синусов и теорема косинусов, теорема Пифагора, свойства прямоугольных треугольников и т.д.

Цели проведения уроков “Измерение на местности”:

• практическое применение теоретических знаний учащихся;
• активизация познавательной деятельности учащихся;

Задачи:

• расширение кругозора учащихся;
• повышение интереса к предмету;
• развитие смекалки, любознательности, логического и творческого мышления;
• формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.

При отборе содержания каждого урока по данной теме и форм деятельности учащихся используются принципы:

• взаимосвязи теории с практикой;
• научности;
• наглядности;
• учёта возрастных и индивидуальных особенностей учащихся;
• сочетания коллективной и индивидуальной деятельности участников;
• дифференцированного подхода;

Критерии оценки достижения ожидаемых результатов:

• активность учащихся;
• самостоятельность учащихся в выполнении заданий;
• практические применения математических знаний;
• уровень творческих способностей участников.

Подготовка и проведение таких уроков позволяют в результате:

• подключить, пробудить и развить потенциальные способности учащихся;
• выявить наиболее активных и способных участников;
• воспитывать нравственные качества личности: трудолюбие, упорство в достижении цели, ответственность и самостоятельность.
• научить применять математические знания в повседневной практической жизни.

 Одной из наиболее активных форм связи обучения с жизнью, теории с практикой является выполнение учащимися на уроках геометрии практических работ, связанных с измерением, построением, изображением. В курсе изучения геометрии основной школы рассматриваются задачи, связанные с практическим применением изученных знаний: измерительные работы на местности, измерительные инструменты. На уроках математики параллельно с изучением теоретического материала учащиеся должны научиться производить измерения, пользоваться справочниками и таблицами, свободно владеть чертёжными и измерительными инструментами. Работа проводится как на местности, так и решение задач в классе различными способами на нахождение высоты предмета и определение расстояния до недоступной точки. По программе в курсе геометрии рассматриваются следующие вопросы:

7 класс

• “Провешивание прямой на местности” (п.2),
• “Измерительные инструменты” (п.8),
• “Измерение углов на местности” (п.10),
• “Построение прямых углов на местности” (п.13),
• “Задачи на построение. Окружность” (п.21),
• “Практические способы построения параллельных прямых” (п.26),
• “Уголковый отражатель” (п.36),
• “Расстояние между параллельными прямыми” (п.37 – рейсмус),
• “Построение треугольника по трём элементам” (п.38)

8 класс.

• “Практические приложения подобия треугольников” (п.64 – определение высоты предмета, определение расстояния до недоступной точки)

9 класс.

• “Измерительные работы” (п.100 – измерение высоты предмета, измерение расстояния до недоступной точки).

Практические работы на уроках геометрии позволяют решать педагогические задачи: ставить перед учащимися познавательную математическую проблему, актуализировать их знания и готовить к усвоению нового материала, формировать практически умения и навыки в обращении с различными приборами, инструментами, вычислительной техникой, справочниками и таблицами.. Они позволяют реализовать в обучении важнейшие принципы взаимосвязи теории и практики: практика выступает в качестве исходного звена развития теории и служит важнейшим стимулом её изучения учащимися, она является средством проверки теории и областью её применения.

Система проведения уроков “Измерение на местности” ставит цели:

• практическое применение теоретических знаний учащихся;
• активизация познавательной деятельности учащихся;

Предусматривает выполнение следующих задач:

• расширение кругозора учащихся;
• повышение интереса к предмету;
• развитие смекалки, любознательности, логического и творческого мышления;
• формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.

При отборе содержания каждого урока по данной теме и форм деятельности учащихся используются принципы:

• взаимосвязи теории с практикой;
• научности;
• наглядности;
• учёта возрастных и индивидуальных особенностей учащихся;
• сочетания коллективной и индивидуальной деятельности участников;
• дифференцированного подхода;

Критерии оценки достижения ожидаемых результатов:

• активность учащихся;
• самостоятельность учащихся в выполнении заданий;
• практические применения математических знаний;
• уровень творческих способностей участников.

Подготовка и проведение таких уроков позволяют в результате:

• подключить, пробудить и развить потенциальные способности учащихся;
• выявить наиболее активных и способных участников;
• воспитывать нравственные качества личности: трудолюбие, упорство в достижении цели, ответственность и самостоятельность.
• научить применять математические знания в повседневной практической жизни;
• обращаться с различными приборами, инструментами, вычислительной техникой, справочниками и таблицами.

Измерительные инструменты, используемые при измерении на местности:

• Рулетка – лента, с нанесёнными на ней делениями, предназначена для измерения расстояния на местности.
• Экер – прибор для построения прямых углов на местности.
• Астролябия – прибор для измерения углов на местности.
• Вехи (вешки) – колья, которые вбивают в землю.
• Землемерный циркуль ( полевой циркуль – сажень) – инструмент в виде буквы А высотой 1,37 м и шириной 2 м. для измерения расстояния на местности, для учащихся удобнее расстояние между ножками взять 1 метр.

Экер

Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны.

Экер

Астролябия

Устройство: астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.

астролябия

Практические работы

1. Построение прямой на местности (провешивание прямой линии)

Отрезки на местности обозначают с помощью вех. Чтобы вешка стояла прямо, применяют отвес (какой – либо грузик, подвешенный на нитке). Ряд вбитых в землю вех и обозначает отрезок прямой линии на местности. В выбранном направлении ставят две вехи на расстоянии друг от друга, между ними другие вехи, так, чтобы глядя через одну, другие прикрывались друг другом.

Практическая работа: построение прямой на местности.

Задание: отметьте на ней отрезок в 20 м, 36 м, 42 м.

2. Измерение средней длины шага.

Считается некоторое число шагов (например, 50), измеряется данное расстояние и вычисляется средняя длина шага. Опыт удобнее провести несколько раз и сосчитать среднее арифметическое.

Практическая работа: измерение средней длины шага.

Задание: зная среднюю длину шага, отложите на местности отрезок 20 м, проверьте с помощью рулетки.

3. Построение прямых углов на местности.

Чтобы построить на местности прямой угол АОВ с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (ОВ).

Практическая работа: построение прямого угла на местности, прямоугольника, квадрата.

Задание: измерьте периметр и площадь прямоугольника, квадрата.

4. Построение и измерение углов с помощью астролябии.

Астролябию устанавливают в вершине измерительного угла так, чтобы лимб её был расположен в горизонтальной плоскости, а отвес, подвешенный под центром лимба, проектировался бы в точку, принимаемую за вершину угла на поверхности земли. Затем визируют алидадой по направлению одной стороны измеряемого угла и отсчитывают на лимбе градусные деления против метки предметного диоптра. Повёртывают алидаду по ходу часовой стрелки в направлении второй стороны угла и делают второй отсчёт. Искомый угол равен разности показаний при втором и первом отсчётах.

Практическая работа:

• измерение заданных углов,
• построение углов заданной градусной меры,
• построение треугольника по трём элементам – по стороне и двум прилежащим к ней углам, по двум сторонам и углу между ними.

Задание: измерить градусные меры заданных углов.

5. Построение окружности на местности.

На местности устанавливается колышек, к которому привязывается верёвка. Держась за свободный конец верёвки, двигаясь вокруг колышка, можно описать окружность.

Практическая работа: построение окружности.

Задание: измерение радиуса, диаметра; вычисление площади круга, длины окружности.

6. Определение высоты предмета.

а) С помощью вращающейся планки.

Предположим, что нам нужно определить высоту какого – нибудь предмета, например высоту столба А₁С₁ (задача № 579). Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку С₁ столба. Отметим на поверхности земли точку В, в которой прямая А₁А пересекается с поверхностью земли. Прямоугольные треугольники А₁С₁В и АСВ подобны по первому признаку подобия треугольников ( угол А₁ = углу А = 90^о, угол В – общий). Из подобия треугольников следует;

Измерив расстояния ВА₁ и ВА (расстояние от точки В до основания столба и расстояние до шеста с вращающейся планкой), зная длину АС шеста, по полученной формуле определяем высоту А₁С₁ столба.

б) С помощью тени.

Измерение следует проводить в солнечную погоду. Измерим длину тени дерева и длину тени человека. Построим два прямоугольных треугольника, они подобны. Используя подобие треугольников составим пропорцию (отношение соответственных сторон), из которой и найдём высоту дерева (задача №580). Можно таким образом определить высоту дерева и в 6 кл, используя построение прямоугольных треугольников в выбранном масштабе.

в) С помощью зеркала.

Для определения высоты предмета можно использовать зеркало, расположенное на земле горизонтально (задача №581). Луч света, отражаясь от зеркала попадает в глаз человека. Используя подобие треугольников можно найти высоту предмета, зная рост человека (до глаз), расстояние от глаз до макушки человека и измеряя расстояние от человека до зеркала, расстояние от зеркала до предмета (учитывая, что угол падения луча равен углу отражения).

г) С помощью чертёжного прямоугольного треугольника.

На уровне глаз расположим прямоугольный треугольник, направив один катет горизонтально поверхности земли, другой катет направив на предмет, высоту которого измеряем. Отходим от предмета на такое расстояние, чтобы второй катет “прикрыл” дерево. Если треугольник ещё и равнобедренный, то высота предмета равна расстоянию от человека до основания предмета (прибавив рост человека). Если треугольник не равнобедренный, то используется снова подобие треугольников, измеряя катеты треугольника и расстояние от человека до предмета (используется и построение прямоугольных треугольников в выбранном масштабе). Если треугольник имеет угол в 30⁰, то используется свойство прямоугольного треугольника: против угла в 30⁰ лежит катет вдвое меньше гипотенузы.

д) Во время игры “ Зарница” учащимся не разрешается использовать измерительные приборы, поэтому можно предложить следующий способ:

один ложится на землю и направляет глаза на макушку другого, находящегося от него на расстоянии своего роста, так чтобы прямая проходила через макушку товарища и верхушку предмета. Тогда треугольник п

Определение высоты объекта

Передача отметки на дно котлована и на монтажный горизонт

Решением задачи предусматривается передача отметки с одного горизонта на другой, когда разность высот превышает длину рейки. В этом случае применяют остальные рулетки или ленты с подвешенным грузом.

На краю котлована подвешивают рулетку с помощью кронштейна, внизу к рулетке прикрепляют груз (рис.).

Рейки устанавливают на репере и на колышке, забитом в точке С на дне котлована. Нивелирование выполняют, как правило, двумя нивелирами, один из которых устанавливают на дне котлована, а другой – на исходном горизонте. Отсчеты по рулетке берутся по нивелирам одновременно двумя наблюдателями. Рулетка во время снятия отсчетов должна быть неподвижна. Если в распоряжении имеется только один нивелир, необходимо производить измерения несколько раз (не менее трех), обеспечивая неподвижность рулетки на протяжении всего цикла измерений.

Вычисляется отметка точки С на дне котлована:

Н _С= Н _RP+a-b₁+b₂–c. (**)

Передача отметки на монтажный горизонт осуществляется аналогично (рис.).

Вычисление отметки точки С производится по формуле (**)

1. Определение высоты объекта

В случае, если высоту объекта невозможно измерить непосредственно, ее можно определить косвенным способом (рис.).

Для этого на местности устанавливают теодолит, определяют горизонтальное расстояние от теодолита до объекта L, измеряют вертикальные углы: на верх объекта_, и низ объекта_. Вычисляется высота объекта:

h

(***)

=L(tg_tg_;

Где значения вертикальных углов _и_берут со знаком «+».

Затем теодолит устанавливают в другую точку (по возможности в перпендикулярном положении) и высота объекта определяется повторно.

Д

опустимое расхождение между полученными высотами не должно превышать величины.

1. Определение расстояния до недоступного объекта

В случае, когда невозможно измерить расстояние между точками непосредственно, его можно определить косвенным способом (рис.)

На местности разбивают базис b₁и измеряют его несколькими приемами в точках А и В устанавливают теодолит и измеряют горизонтальные углы_и₂одним полным приемом. Затем вычисляют горизонтальные расстоянияL₁иL₂:

(****)

(*****)

Для контроля на местности можно разбить базис b₂и аналогично определить расстоянияL₂иL₃:

1. Определение высоты недоступного объекта

Для решения этой задачи необходимо вначале определить расстояние от прибора до объекта, а затем найти высоту самого объекта. С этой целью на местности разбивают базис b₁ (рис.) и измеряют его несколькими приемами. В точках А и В последовательно устанавливают теодолит и измеряют горизонтальные углы_и₂(рис.) – одним полным приемом. Одновременно с этим измеряют вертикальные углы_и_(рис.) в начале точки А, затем в точке В. По формулам (****) и (*****) вычисляются расстоянияL₁иL₂(рис.). Допустимое расхождение между полученными высотами не должно превышать величины

.

1. Пров

19.8 Определение высоты сооружения

Для определения высоты сооружения, например, здания (рисунок 66, а) в точке А, расположенной вблизи здания, устанавливают теодолит и измеряют углы наклона ν₁ и ν₂ , визируя на верхнюю и нижнюю точку здания. Измеряют расстояние АВ = d и определяют высоту здания

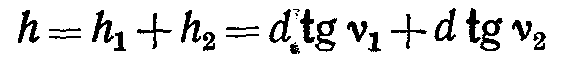
или (66)

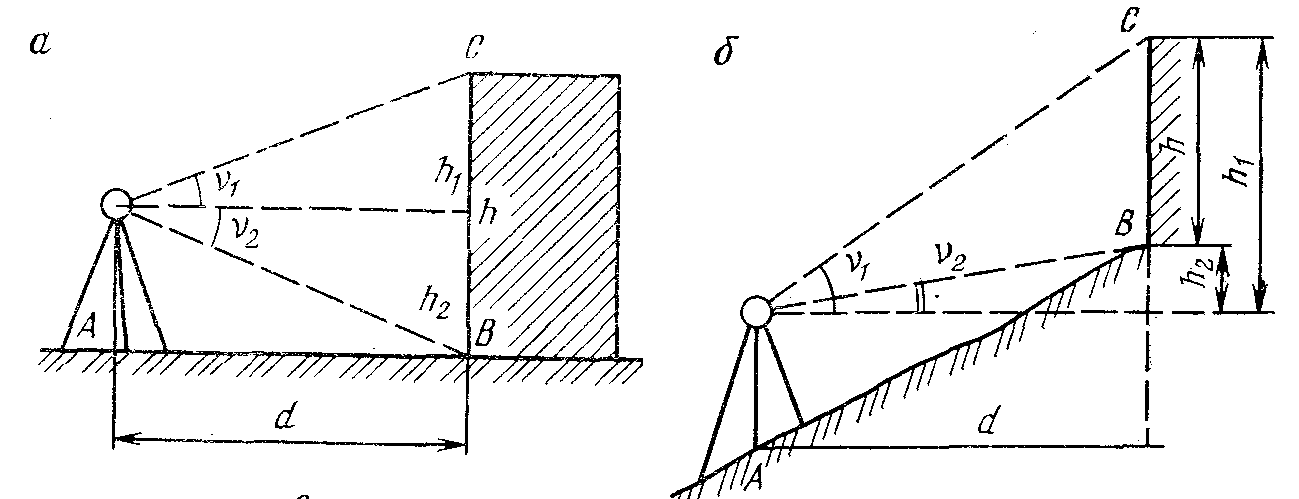
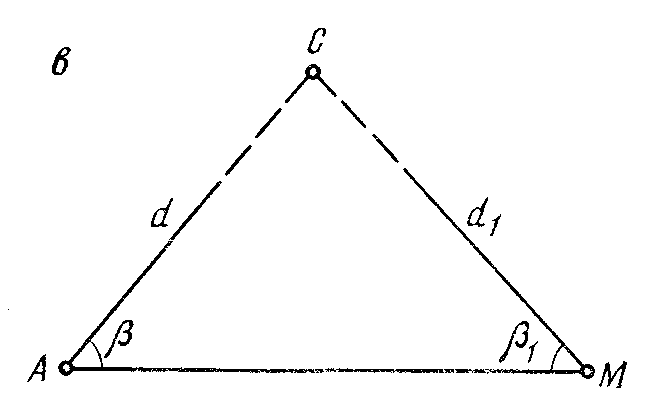
Рисунок 66- Схемы определения высоты сооружения

Если линия местности АВ наклонна (рисунок 66, б), то нужно измерить ее наклон и вычислить горизонтальное проложение d.

Из рисунка 66, б следует, что высота здания равна

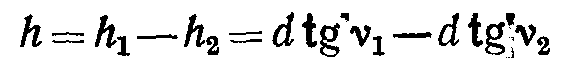
или 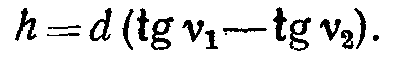(67)

В формуле (67) углы наклона ν₁ и ν₂ положительные.

Если в формуле (66) учесть знак минус угла наклона (рисунок 66,а), то формула (66) будет иметь вид (67) и будет универсальной.

В том случае, когда измерить расстояние от теодолита до сооружения нельзя, его определяют как неприступное расстояние, для чего в стороне от сооружения разбивают базис АМ (рисунок 66, в).

Теодолитом измеряют горизонтальные углы β и β₁ и вычисляют длины линий

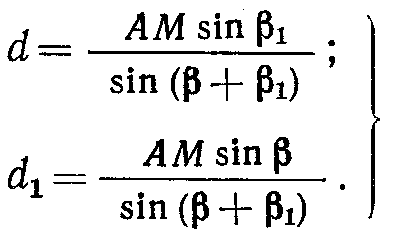(68)

В точках А и М измеряют вертикальные углы соответственно ν₁ , ν₂ и ν₃, ν₄. Высоту сооружения вычисляют дважды

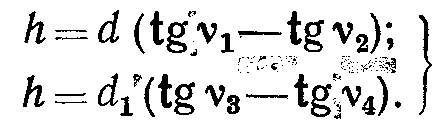(69)

В формулах (69) следует учитывать знак угла наклона; за окончательное значение h берут среднее, если расхождение не более 1: 300 высоты измеряемого сооружения.

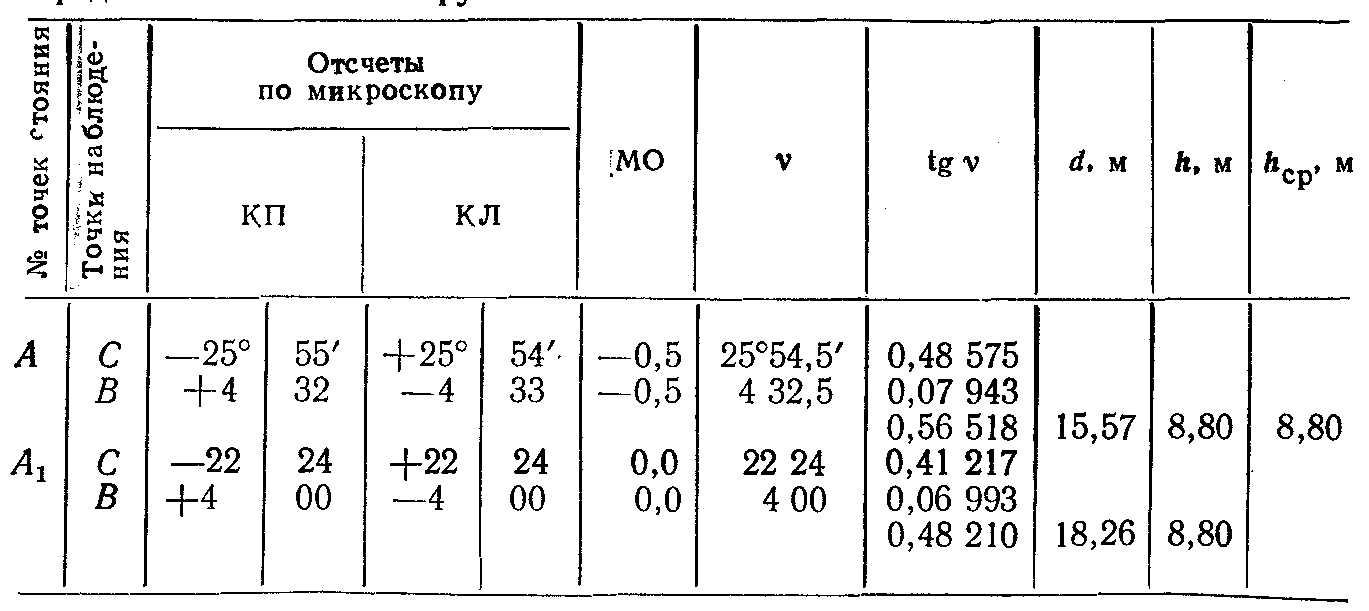
Пример определения высоты сооружения приведен в таблице 22. Углы наклона измерялись теодолитом 2Т30.

Таблица 22 — Определение высоты сооружения

ЛЕКЦИЯ 20

20.1 Геодезические работы в процессе строительства. Детальная

разбивка зданий и сооружений

Детальная разбивка выполняется после вынесения на мест­ность основных осей зданий или сооружений. Основными ви­дами геодезических работ при детальной разбивке являются следующие:

1. Разбивка котлованов и траншей для проведения земля­ных работ.

2. Разбивка осей для возведения фундаментов.

3. Разбивка осей для монтажа строительных конструкций и геодезический контроль за установкой конструкций в проект­ное положение.

Точность выполнения геодезических работ при детальной разбивке зависит от типа сооружения, этажности, высоты со­оружения, материала возведения, технологических особенностей производства и регламентируется строительными нормами и правилами СНиП 3.01.03—84 «Геодезические работы в строи­тельстве», а также ГОСТами «Система обеспечения точности геометрических параметров в строительстве». Вследствие того, что оси детальной разбивки определяют взаимное положение различных конструкций, к точности их разбивки предъявляют более высокие требования, чем к разбивке основных осей, оп­ределяющих положение всего здания или сооружения на мест­ности. В зависимости от требуемой точности выбираются при­боры и способы геодезических разбивочных работ.

Исследовательская работа «Определение высоты дерева различными физическими способами»

Инфоурок › Физика ›Другие методич. материалы›Исследовательская работа «Определение высоты дерева различными физическими способами»

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: 305580

Похожие материалы

Оставьте свой комментарий

Определение угла естественного откоса грунта

Определение угла естественного откоса грунта

Угол естественного откоса φ, град. — угол, при котором несвязанный откос песчаного грунта сохраняет равновесие или угол наклона поверхности свободно насыпанного грунта к горизонтальной плоскости.

Определение угла естественного откоса важно при проектировании грунтовых сооружений: насыпей и насыпей, насыпей дорог, насыпей, хвостохранилищ, а также для оценки устойчивости естественных откосов и проведения мероприятий, но для их укрепления.

В тех случаях, когда сопротивление перемещению частиц определяется только силами трения. угол естественного откоса совпадает с углом внутреннего трения (φ = φο ). Однако в реальных грунтах сопротивление сдвигу зависит не только от сил трения, но также от взаимодействия частиц и других факторов, влияющих на φ, , т.е.

.

, где φ p, — составляющая, обусловленная трением; φ L — то же, за счет зацепления; φ с — то же, за счет разрезания частиц.

Составляющая φ T зависит от минерального состава частиц, наличия поверхностных пленок и т. Д., φ L — от шероховатости поверхности и плотности упаковки частиц, а φ от — от округлости и формы. частиц почвы. Поэтому значения φ и φ о обычно разные, особенно для плотных и неоднородных песков. Однако угол естественный от

Оплетка φ о — легко определяемая и удобная характеристика прочности разъединенных грунтов.Метод используется только для приближения величины внутреннего трения рыхлых грунтов — чистых песков. В чистых песках приблизительное значение угла внутреннего трения соответствует углу естественного откоса, т. Е. Углу, при котором несвязанный откос песчаного грунта устойчив [50].

Угол естественного откоса определяется на установке ультрапастеризации (рис. 8.44), которая состоит из металлического поддона, клетки и резервуара. Поддон установлен на трех опорах и перфорирован с отверстиями 0.Диаметр 8 … 1,0 мм для водонасыщения песка. Шкала, укрепленная в центре стола поддонов, имеет деление от 5 ° до 45 °, по которому определяется угол наклона.

Рис. 8.44. Устройство для определения угла естественного откоса песчаных грунтов: схема устройства: 1 резервуар: 2 крышка резервуара: 3 зажима: 4 стол: 5 перфорированное днище: 6 — масштаб: 7 — опора: б — общий вид инструменты

Определение угла естественного откоса в воздушно-сухом состоянии .На стол устанавливают клетку, в которую через воронку насыпают песок до тех пор, пока она не наполнится, слегка постукивая по зажиму. Осторожно, стараясь не рассыпать песок, поднимите клетку вертикально и вверху образовавшегося песочного конуса проведите обратный отсчет на шкале.

Эксперимент повторяется 3 раза и вычисляется среднее арифметическое. Расхождение между повторными определениями не должно превышать 1 градус.

Определение угла естественного откоса песка под водой .После заполнения корпуса песком резервуар заполняется водой и после полного насыщения образца определяется угол естественного откоса.

При предварительном назначении откосов котлованов и карьеров рекомендуется ориентироваться на значения углов, близких к углам естественного откоса грунта (таблица 8.61).

Таблица 8.61

Угол естественного откоса рыхлых грунтов

Название почвы	Угол естественного откоса Fa, градусов.
	Сухая	мокрый	мокрый
Органический	40	35	25
Сэнди	28	35	25
Гравийно-песчаный	45	40	35
Суглинок	45… 50	35 … 40	25 … 30
Глина	45 … 60	35	15 … 20
Скалистый грунт	45	40	40

На величину угла естественного откоса (#>) разобщенных почв влияет однородность их гранулометрического состава: монодисперсные почвы имеют большее значение φ0,, чем полидисперсные почвы того же минерального состава.Это связано с тем, что в смеси мелкие частицы заполняют пространства между крупными частицами, что облегчает их перемешивание по поверхности склона.

Наличие в грунте жидкостей, наличие которых снижает φ. , оказывает большое влияние на трение между частицами несвязанного грунта. В рыхлых песчаных грунтах влага существенно влияет на угол внутреннего трения. При увеличении влажности песка до максимальной молекулярной влагоемкости величина φ o естественно уменьшается из-за постепенного уменьшения трения и достигает минимума при максимальной молекулярной влагоемкости.Дальнейшее увеличение влажности песка приводит к формату

.

Влияние гравитации на боковое движение, Рон Куртус

SfC Home> Физика> Гравитация>

Рона Куртуса (редакция 5 февраля 2018 г.)

Когда объект движется вбок , горизонтально или параллельно поверхности Земли с постоянной скоростью, влияние силы тяжести на объект не зависит от бокового движения объекта.

Другими словами, объект, движущийся вбок, будет падать с той же скоростью, что и просто брошенный.Вы можете вывести уравнение смещения объекта до того, как он ударится о землю, из уравнений гравитации для падающих объектов. Исключение составляют случаи, когда объект перемещается так далеко, что кривизна Земли вступает в игру во время ее падения на землю.

Вопросы, которые могут у вас возникнуть:

• Как гравитация влияет на боковое движение?
• С какой скоростью падают объекты, движущиеся вбок и неподвижно?
• Когда происходит стрельба из ружья параллельно земле?

Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц

---

---

Гравитация не влияет на боковое движение

Сила тяжести действует на объекты в направлении, перпендикулярном ровной поверхности.

Примечание : Поскольку Земля представляет собой сферу с окружностью приблизительно 40 000 км или 25 000 миль, земля может считаться ровной или плоской (не считая холмов и долин) для кратковременных перемещений в несколько километров или несколько миль.

Это означает, что если объект движется параллельно земле, сила тяжести тянет объект только вниз.На силу не влияет боковое движение, она просто тянет объект вниз с такой же скоростью, как если бы он был неподвижен.

Это правило подробно объясняется в Горизонтальное движение, не подверженное гравитации .

Сила тяжести вниз одинакова для движущихся и неподвижных объектов

Объекты одновременно ударились о землю

Если вы спроецируете или бросите объект точно параллельно поверхности Земли, то боковое движение объекта не повлияет на то, как на него действует гравитация.Другими словами, объект будет падать с той же скоростью, что и объект, падающий с такой же высоты. Время, за которое любой объект упадет на землю, будет одинаковым.

Мяч, брошенный вбок, падает с той же скоростью, что и брошенный мяч

Простой эксперимент

Вы можете попробовать простой эксперимент, чтобы проверить это явление. Поместите монету на край стола или стола и держите другую монету на той же высоте. Одной рукой подбросьте монету по столу через комнату.В то же время бросьте другую монету. Вы услышите, что они падают на пол примерно в одно и то же время.

Вывод уравнения перемещения

Вы можете найти смещение объекта, спроецированного вбок, из следующего вывода. Сначала рассмотрим стандартное уравнение скорости смещения:

x = v _с т

где

• x — горизонтальное смещение в футах (футах) или метрах (м)
• v _с — начальная боковая или горизонтальная скорость в фут / с или м / с
• t — время до падения объекта на землю в секундах (с)

Уравнение для определения времени падения объекта:

t = √ (2y / г)

где

• y — это смещение, при котором объект упал с начальной точки. м или фут
• g — ускорение свободного падения (32 фут / с ² или 9.8 м / с ² )

( Для получения информации об уравнении см. Уравнения времени гравитации для падающих объектов.)

Таким образом, перемещение объекта в зависимости от начальной скорости и высоты составляет:

x = v _с √ (2y / g)

Ход по параболической кривой

Вы можете увидеть, что объект движется по параболической траектории, возведя в квадрат обе части уравнения, с x в качестве вертикальной оси и y в качестве горизонтальной оси:

x ² = (2v _s ² / g) y

Это приводит к уравнению параболы, где постоянная k = 2v _h ² / g :

x ² = ky

Стрельба и сброс пули

Если вы выстрелите из пистолета точно параллельно поверхности Земли, движение пули не повлияет на то, как гравитация действует на пулю.Другими словами, пуля будет падать с той же скоростью, что и неподвижный объект.

Упавшая пуля и выстреленная пуля одновременно ударились о землю

Многие люди не верят, что если вы держите винтовку или пистолет параллельно земле и в то же время вы стреляете пулей, вы уронили другую пулю с той же высоты, обе пули упадут на землю одновременно. Однако это факт.

Исключение

Исключением из этого явления было бы, если бы пуля или объект могли пройти столько миль или километров, что кривизна Земли вступила в игру.В такой ситуации пуле потребуется немного больше времени, чтобы ударить по земле, потому что смещение относительно земли было больше из-за кривизны Земли.

Пример

Если вы выстрелите пулей со скоростью 900 м / с из винтовки, находящейся на высоте 1,5 м над землей, как далеко пролетит пуля, пока не упадет на землю? Уменьшите сопротивление воздуха и предположите, что винтовка параллельна земле.

Решение

x = v _с √ (2y / g)

x = (900 м / с) √ [2 * (1.5 м) / (9,8 м / с ² )]

x = (900 м / с) √ (0,306 с ² )

x = (900 м / с) (0,553 с)

x = 498 м или 1634 фута

Сводка

Объект, движущийся вбок или параллельно поверхности Земли, упадет с той же скоростью, что и просто упавший. Уравнение смещения объекта до того, как он упадет на землю, может быть получено из уравнений гравитации для падающих объектов.Исключение составляют случаи, когда объект движется так быстро или далеко, что кривизна Земли вступает в игру во время ее падения на землю.

---

Интересуйтесь окружающим миром

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайты

Независимость перпендикулярных компонентов движения — PhysicsClassroon.com

Гравитационные ресурсы

Книги

Книги с самым высоким рейтингом по простой науке о гравитации

Книги с самым высоким рейтингом по продвинутой физике гравитации

---

Вопросы и комментарии

Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_sideways_motion.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

Гравитационные темы

Влияние силы тяжести на боковое движение

---

.

Геометрия | математика | Britannica

Самые ранние известные однозначные примеры письменных записей — датируемые Египтом и Месопотамией около 3100 г. до н.э. — демонстрируют, что древние народы уже начали разрабатывать математические правила и методы, полезные для съемки земельных участков, строительства зданий и измерения контейнеров для хранения. Начиная примерно с VI века до нашей эры, греки собрали и расширили эти практические знания и на их основе обобщили абстрактный предмет, ныне известный как геометрия, из сочетания греческих слов geo («Земля») и metron («мера»). ) для измерения Земли.

В дополнение к описанию некоторых достижений древних греков, в частности, логического развития геометрии Евклидом в Elements , в этой статье исследуются некоторые применения геометрии в астрономии, картографии и живописи от классической Греции до средневекового ислама и Европы эпохи Возрождения. , Он завершается кратким обсуждением расширений неевклидовой и многомерной геометрии в современную эпоху.

Древняя геометрия: практическая и эмпирическая

Происхождение геометрии лежит в повседневной жизни.Традиционный отчет, сохраненный в книге Геродота История (V век до нашей эры), приписывает египтянам создание геодезических изысканий для восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекает из необходимости оценивать дань, хранить нефть и зерно и строить плотины и пирамиды. Даже три сложные геометрические задачи древних времен — удвоение куба, разрезание угла и квадрат круга, которые будут обсуждаться позже, — вероятно, возникли из практических вопросов, из религиозных ритуалов, хронометража и строительства, соответственно, в догреческие общества Средиземноморья.И главный предмет поздней греческой геометрии, теория конических сечений, обязана своим общим значением, а, возможно, и своим происхождением, своим приложением к оптике и астрономии.

В то время как многие древние люди, известные и неизвестные, внесли свой вклад в эту тему, ни один из них не сравнится с влиянием Евклида и его Элементов геометрии, книги, которой сейчас 2300 лет и которая является объектом столь же болезненного и кропотливого изучения, как Библия. Однако об Евклиде известно гораздо меньше, чем о Моисее.Фактически, единственное, что известно с достаточной степенью уверенности, — это то, что Евклид преподавал в Александрийской библиотеке во время правления Птолемея I (323–285 / 283 гг. До н. Э.). Евклид писал не только по геометрии, но также по астрономии и оптике, а также, возможно, по механике и музыке. Только Elements , который был широко скопирован и переведен, уцелел.

Элементов Евклида был настолько полным и ясно написан, что буквально перечеркнул работу его предшественников.То, что известно о греческой геометрии до него, происходит главным образом из отрывков, цитируемых Платоном и Аристотелем, а также более поздними математиками и комментаторами. Среди других ценных вещей, которые они сохранили, — некоторые результаты и общий подход Пифагора ( ок. 580– ок. 500 до н. Э.) И его последователей. Пифагорейцы убедили себя, что все вещи являются числами или обязаны своим отношением к ним. Доктрина придавала математике первостепенное значение в исследовании и понимании мира.Платон развивал аналогичную точку зрения, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключе к интерпретации Вселенной. Таким образом, древняя геометрия приобрела ассоциацию с возвышенным, чтобы дополнить ее земное происхождение и репутацию образца точного рассуждения.

Нахождение прямого угла

Древним строителям и геодезистам нужно было уметь строить прямые углы в поле по запросу. Метод, применявшийся египтянами, принес им в Греции прозвище «съемники каната», по-видимому, потому, что они использовали веревку для составления инструкций по строительству.Один из способов, которым они могли использовать веревку для построения прямоугольных треугольников, состоял в том, чтобы пометить веревку с петлей с узлами, чтобы веревка, удерживая ее за узлы и сильно натянув, должна образовывать прямоугольный треугольник. Самый простой способ выполнить трюк — взять веревку длиной 12 единиц, завязать узел на 3 единицы с одного конца и еще на 5 единиц с другого конца, а затем связать концы вместе, чтобы сформировать петлю, как показано на анимация. Однако египетские писцы не оставили нам инструкций по этим процедурам, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой напротив прямого угла равен сумме квадратов на двух других. стороны.Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Необходимые прямые углы были сделаны веревками, отмеченными для получения триад (3, 4, 5) и (5, 12, 13).

В вавилонских глиняных табличках ( ок. 1700–1500 гг. До н. Э.) Современные историки обнаружили проблемы, решения которых указывают на то, что теорема Пифагора и некоторые особые триады были известны более чем за тысячу лет до Евклида.Однако у прямоугольного треугольника, созданного наугад, очень маловероятно, что все его стороны будут измеряться одной и той же единицей измерения, то есть, каждая сторона будет целым числом, кратным некоторой общей единице измерения. Этот факт, который был шокирован пифагорейцами, привел к возникновению концепции и теории несоизмеримости.

Обнаружение недоступного

Согласно древней традиции, Фалес Милетский, живший до Пифагора в VI веке до нашей эры, изобрел способ измерения недоступных высот, таких как египетские пирамиды.Хотя ни одно из его сочинений не сохранилось, Фалес, возможно, хорошо знал о вавилонском наблюдении, что для подобных треугольников (треугольников, имеющих одинаковую форму, но не обязательно одинаковый размер) длина каждой соответствующей стороны увеличивается (или уменьшается) на одно и то же число. Определение высоты башни с помощью подобных треугольников показано на рисунке. Древние китайцы достигли измерения недоступных высот и расстояний другим путем, используя «дополнительные» прямоугольники, как показано на следующем рисунке, который, как можно показать, дает результаты, эквивалентные результатам греческого метода с использованием треугольников.

Сравнение китайской и греческой геометрических теорем На рисунке показана эквивалентность китайской теоремы о дополнительных прямоугольниках и греческой теоремы о подобных треугольниках. Encyclopædia Britannica, Inc.

Оценка состояния

Вавилонская клинопись, написанная около 3500 лет назад, посвящена проблемам плотин, колодцев, водяных часов и раскопок. В нем также есть упражнение на круглых ограждениях с предполагаемым значением π = 3. Подрядчик плавательного бассейна царя Соломона, который сделал пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение.Однако евреям следовало взять π у египтян до того, как пересечь Красное море, так как папирус Ринда ( ок. 2000 до н. Э .; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.

Знание площади круга имело практическую ценность для чиновников, следивших за дани фараона, а также для строителей алтарей и бассейнов. Ахмес, писец, который скопировал и комментировал папирус Райнда ( ок. 1650 г. до н. Э.), Много говорит о цилиндрических зернохранилищах и пирамидах, целых и усеченных.Он мог вычислить их объемы и, как следует из его египетского секед , горизонтального расстояния, связанного с вертикальным подъемом на один локоть, в качестве определяющей величины для наклона пирамиды, он кое-что знал о подобных треугольниках.

.