Pagerank висячий узел: Внутренний PageRank от А до Я

Содержание

как правильно оптимизировать ваш сайт

Зачем нужен внутренний аудит? Ваш сайт скрывает много неиспользуемых возможностей. Важно их найти и задействовать, чтобы подняться в поисковой выдаче. Это в свою очередь повысит трафик и конверсию. Поэтому не спешите закупаться ссылками, сперва определите состояние вашего сайта.

Desktop vs. SaaS — что выбрать?

Когда речь заходит о внутреннем аудите своими руками, вам не обойтись без хорошего ПО. Выбор лежит между SaaS и desktop продуктом. Конкретно под внутреннюю оптимизацию лучше заточены десктопы в силу своей скорости и детальности анализа. Их сейчас немало, но отличия существенны: начиная от места обработки информации (только на операционке, только на жёстком диске или на операционке и жёстком — это напрямую влияет на скорость аудита), заканчивая адекватным юзабилити. В этой статье мы рассмотрим внутренний аудит с помощью одного из десктопов — Netpeak Spider.

Структура страниц

Сперва рекомендуем провести мониторинг архитектуры сайта:

Расстояние между главной и основными страницами должно исчисляться 1 кликом.

Глубина сайта должна быть продумана (пользователь не проходит квесты в поиске нужной страницы). Волшебной формулы расчёта нет. Просто постарайтесь максимально упростить задачу пользователя в поиске информации.

Программное исполнение

Код ответа сервера: 200, 301/302, 4xx, 5xx. Очень часто случается, что склейку страницы проводят с помощью 302 редиректа — не надо так. Постоянное перенаправление проводим с помощью 301-го, временное — 302-го. Совсем «не ок», когда внутренние ссылки на вашем сайте ведут к несуществующей странице с 404-й ошибкой.
Дубли. Даже самый качественный контент можно убить, не проставив на частично похожих или повторяющихся страницах canonical. В таком случае вас ожидает ухудшение индексации, выявление нерелевантной страницы роботом (он выбирает на своё усмотрение), утрата доли естественных ссылок (пользователи ссылаются на дублированную страницу).

Sitemap. Поисковому роботу нередко тяжело проиндексировать весь сайт (в особенности, если у вас крупный интернет-магазин). В таком случае направьте его, указав с помощью sitemap, что именно нужно индексировать.

Robots.txt. Неверно прописанный robots.txt может закрыть доступ к целым тематическим категориям. И тогда вам не поможет ни уникальный контент, ни правильная разметка — всё это тщетно, если страницы скрыты от поисковых роботов.

Висячие узлы. Внутренние ссылки позволяют пользователю ориентироваться в структуре сайта, направляют по его страницам. Висячими узлами называют ссылки на такие страницы, которые сами никуда не ведут. В итоге вы теряете ссылочный вес и повышаете вероятность потери пользователей, которые просто уйдут на другие сайты.

Внутренний PageRank. Вам нужно знать, как распределяется ссылочный вес в пределах вашего сайта. Так вы пойметес, какие страницы, являясь неважными, напрасно получают избыточный вес. Грамотная схема перелинковки внутри сайта может сэкономить приличный бюджет.

Проверить PageRank можно так:

Контент

Заголовки h2-h6. Здесь важно избегать дублирования заголовков, наличия нескольких сразу или полного их отсутствия.

Это не критические ошибки, но ваш контент наверняка направлен на информирование и привлечение пользователей. Скорее всего, не видя заголовка и не понимая, о чём статья, юзер просто закроет страницу. О спам-заголовках и вовсе промолчим. Здесь и так всё понятно: ни в коем случае.

Оформление текста. Даже если у вас уникальный и крутой контент, это не гарантирует, что пользователь его прочтёт. Ему может просто не понравиться оформление текста. Так что структурируйте его, выделяйте заголовки, подзаголовки, прикрепляйте изображения. Помните: вы пишете для людей.

Заспамленность. Проводя «сео-оптимизацию своего сайта бесплатно за 2 минуты», помните, что «сео-оптимизация сайта бесплатно за 2 минуты» должна обходиться без избытка ключевых слов.

Изображения. Отсутствие атрибута ALT (подписи к изображению), непроработанные километровые инфографики без сжатия, замедляющие загрузку страницы, — это не понравится ни вашим пользователям, ни поисковикам.

Подытожим. Проводя внутренний аудит, обязательно проверяйте:

структуру сайта, глубину ключевых для продвижения страниц;
дубли, коды ответа сервера, robots.txt, sitemap, висячие узлы;
оформление и заспамленность контента;
распределение ссылочного веса с помощью внутреннего PageRank.

Не забывайте, что внутренний аудит следует проводить регулярно. Проверяйте изменения в перелинковке сайта, возможном дублировании страниц и их canonical — всё это непосредственно влияет на место вашего сайта в поисковой выдаче. В этой статье мы рассмотрели некоторые важные параметры, однако внутри программы Netpeak Spider их больше 60-ти. Изучайте их, экспериментируйте, применяйте.

А как считаете вы, какие параметры аудита заслуживают первостепенного внимания?

No birds: Развитие PageRank

С того момента, когда PageRank был впервые представлен в 1998 году, было потрачено немало усилий, чтобы улучшить его качество и скорость вычисления. В этой обзорной и достаточно популярной статье я опишу основные направления исследований вокруг PageRank и варианты алгоритма.

Я разрабатываю систему оценки важности web-страниц на основе входящих и исходящих ссылок в компании Нигма, поэтому смотрю на PageRank с математической стороны, со стороны разработчика а не seo.

Я не буду пересказывать здесь многократно описанные основы PageRank. Предполагается, что читатель знает, что это вообще такое. Если же нет, то для начала могу порекомендовать статью Растолкованный PageRank.

На следующей картинке схематически представлены основные направления исследований, окруживших PageRank. Каждому овалу на схеме будет соответствовать отдельная глава статьи.

PageRank с математической стороны

PageRank основан на математической модели случайного блуждания «пользователя» в сети интернет. В некоторый момент он находится на одной странице, затем случайным образом выбирает одну из ссылок и переходит по ней на другую. «Пользователь» произвольно выбирает ссылки, не отдавая предпочтение каким-либо из них.

PageRank страницы – это вероятность того, что блуждающий «пользователь» находится на данной странице.

Сделаем небольшой набросок того, как рассчитать эту вероятность.

Пронумеруем web-страницы целыми числами от 1 до N.

Сформируем матрицу переходов P, содержащую вероятность перехода «пользователя» с одной страницы на другую. Пусть deg(i) – количество исходящих ссылок на странице i. В таком случае, вероятность перехода со страницы i на страницу j равна:

P[i, j] = 1 / deg(i), если i ссылается на j
P[i, j] = 0, если i не ссылается на j

Пусть p^(k) – это вектор, содержащий для каждой страницы вероятность того, что в момент k на ней находится «пользователь». Этот вектор – распределение вероятностей местоположения «пользователя».

Предположим, что «пользователь» может начать своё бесцельное блуждание с любой страницы. То есть, начальное распределение вероятностей равномерно.

Зная распределение вероятностей в момент k, мы можем узнать распределение вероятностей в момент k+1 по следующей формуле:

В основе этой формулы не более чем правила сложения и умножения вероятностей.

Математически мы пришли к цепи Маркова с матрицей переходов P, где каждая web-страница представляет собой одно из состояний цепи.

Но нам нужно знать вероятность нахождения «пользователя» на странице независимо от того, сколько шагов k он сделал от точки начала блуждания.

Мы берём начальное распределение вероятностей p⁽⁰⁾. Считаем по представленной выше формуле распределение p⁽¹⁾. Затем по той же формуле считаем p⁽²⁾, затем p⁽³⁾ и т.д. до тех пор, пока некие p^(k-1) и p^(k) не будут отличаться лишь незначительно (полное равенство будет достигнуто при k стремящемся к бесконечности).

Таким образом, последовательность p⁽¹⁾, p⁽²⁾, p⁽³⁾ … сойдётся к некому вектору p = p^(k). Интересно, что вектор p на самом деле не зависит от начального распределения (т.е. от того, с какой страницы начал своё блуждание воображаемый «пользователь»).

Вектор p таков, что в любой момент (начиная с некоторого момента k), вероятность того, что «пользователь» находится на странице i, равна p[i]. Это и есть искомый PageRank.

Этот алгоритм называется методом степеней (power method). Он сойдётся только в том случае, если выполняются два условия: граф страниц должен быть сильно связным и апериодическим. Как достигается выполнение первого условия, будет рассмотрено далее. Второе же без дополнительных усилий справедливо для структуры web.

Примечание

При выполнении условий сильной связности и апериодичности, согласно эргодической теореме, цепь Маркова с матрицей перехода P имеет единственное стационарное распределение p:

PageRank и является стационарным распределением цепи Маркова.

Также это выражение представляет собой собственную систему, а вектор p — собственный вектор матрицы A. Поэтому и применяется метод степеней — численный метод для поиска собственных векторов.

Висячие узлы (dangling nodes)

Висячие узлы – это страницы, которые не имеют исходящих ссылок. Страница может не иметь исходящих ссылок просто потому, что у неё их нет, либо потому, что она не была прокраулена (crawled) – т.е. страница попала в базу, т.к. на неё ссылаются другие прокрауленные страницы, но сама прокраулена не была, и о её исходящих ссылках ничего не известно.

Для вычисления PageRank в графе страниц не должно быть висячих узлов. Сумма каждого ряда матрицы переходов должна быть равна единице (row-stochastic), для висячих же узлов она окажется равной 0 – входные данные алгоритма будут некорректными.

По статистике, даже если поисковая система имеет достаточно большой индекс, 60% страниц оказывается висячими. Поэтому то, как с ними поступать, оказывает большое влияние на ранжирование.

Метод удаления

Изначальный подход, предложенный Пэйджем, заключается в том, чтобы удалить висячие узлы перед вычислением PageRank. В качестве обоснования предлагается то, что висячие узлы не оказывают влияния на другие страницы. Но это не совсем так – удаляя их, мы уменьшаем количество исходящих ссылок страниц, которые на них ссылаются. Тем самым мы увеличиваем значение PageRank, которое эти страницы передают через свои ссылки.

Кроме того, удаление висячих узлов, может создать новые висячие узлы. Таким образом, требуется проделать несколько итераций удаления (обычно 5 или что-то около того).

В качестве развития этого подхода, было предложено после вычисления PageRank возвращать удалённые узлы назад в граф и проделывать ещё столько же итераций алгоритма PageRank, сколько было проделано итераций удаления. Это позволяет получить значение PageRank и для висячих узлов.

Считать связанными со всеми другими страницами

Наиболее популярный трюк заключается в том, чтобы считать висячие узлы связанными со всеми другими страницами. В модели случайного блуждания данный метод находит подходящее объяснение: попав на страницу без исходящих ссылок, «пользователь» перескакивает на любую другую страницу сети случайным образом.

Можно считать вероятность попадания «пользователя» на страницу из висячего узла в результате такого перескока распределённой равномерно среди всех страниц сети. Но можно и не считать её таковой. Например, можно исключить попадание из висячего узла на другой висячий узел. Или распределить вероятность между страницами по аналогии с аристократическим вектором телепортации, о котором будет рассказано ниже в главе Телепортация.

Матрица переходов модифицируется следующим образом:

d[i] = 1, если i – висячий узел, и 0 в противном случае
v[j] – вероятность попадания «пользователя» на страницу j из висячего узла

Шаг назад (step back)

Проблему висячих узлов можно решить, добавив каждому такому узлу обратные ссылки на страницы, которые на него ссылаются. В модели блуждания это соответствует нажатию кнопки назад в браузере «пользователем», попавшим на страницу без исходящих ссылок. Этот метод критикуют за то, что он поощряет страницы с большим количеством ссылок на висячие узлы. Однако в некоторых моих экспериментах такой подход давал лучшее ранжирование.

Петля (self-link)

Упомяну кратко ещё один способ. Каждому висячему узлу можно добавить ссылку на самого себя – это приведёт в порядок матрицу переходов. Но после вычисления PageRank, результат придётся определённым образом скорректировать. Подробности описаны в G. Jeh and J.Widom “Scaling Personalized Web Search.”

Телепортация

Решение проблемы висячих узлов ещё не даёт сильную связность графа. Поэтому вводится телепортация.

В модели случайного блуждания это выглядит так: «пользователь», находясь на некоторой странице, с вероятностью c переходит по одной из её ссылок и с вероятностью (1 – c) * v[j] перескакивает (телепортируется) на страницу j. Стохастический вектор v описывает вероятность телепортации на ту или иную страницу и называется вектором телепортации.

c как правило выбирается в диапазоне 0.85 – 0.9. Большие значения дают более точные результаты, но более медленную сходимость. Меньшие значения – быструю сходимость, но менее точные результаты.

Плюс ко всему, чем меньше значение с, тем больше возможностей для поискового спама – достаточно создать на сайте огромное количество страниц и они будут, как зонтик, собирать значительный PageRank, получаемый за счёт телепортации.

Существует два способа выбора вектора телепортации: демократический и аристократический. Демократический вектор содержит одинаковые значения вероятности для всех страниц. Это стандартный вариант. Аристократический содержит низкую вероятность для обычных страниц и более высокую для избранных достоверно качественных неспамерских страниц. Последний способ явно поощряет избранные страницы в ущерб остальным, зато более устойчив к поисковому спаму.

В одной из статей предлагалось делать более высокую вероятность телепортации для главных страниц сайтов, но мне не известно, каковы были результаты.

Значение v[j] не должно быть равно 0. Иначе может оказаться, что j недосягаема из некой другой страницы, что означает нарушение сильной связности.

Телепортация модифицирует матрицу переходов следующим образом:

v – вектор телепортации

Мы ещё вернёмся к вектору телепортации, когда будем обсуждать персонализацию PageRank.

Ускорение метода степеней

Многие исследователи пытались ускорить сходимость метода степеней. Посмотрим на самые удачные способы.

Для удобства повторю формулу, которую мы используем на каждой итерации. Назовём её формулой А:

Метод Гаусса-Зейделя (Gauss-Seidel method)

На каждой итерации в методе степеней мы используем значения элементов вектора p^(k) чтобы рассчитать вектор p^(k+1). Отличие метода Гаусса-Зейделя в том, что мы сразу используем значения вычисленных элементов вектора p^(k+1) для вычисления его остальных элементов.

В методе Гаусса-Зейделя мы последовательно элемент за элементом вычисляем вектор p^(k+1). При это там где, согласно формуле А, нам нужно использовать значение p^(k)[i] мы используем p^(k+1)[i], если этот элемент вектора уже был вычислен.

Согласно экспериментам этот метод способен сократить необходимое количество итераций на 40%. Его недостаток в том, что его достаточно сложно вычислять параллельно.

Методы экстраполяции (Extrapolation methods)

В этой группе методов мы проделываем некоторое количество d обычных итераций метода степеней. Затем на основе результатов этих итераций строим аппроксимацию решения и используем её вместо p^(k) для следующей итерации. Через следующие d итераций повторяем трюк. И так далее пока алгоритм не сойдётся.

Исследователям удавалось достичь сокращения необходимого количества итераций на 30%.

Адаптивный метод (Adaptive method)

Этот метод основан на наблюдении, что значительная часть элементов вектора p сходится гораздо быстрее остальных и затем почти не меняется. Ускорение в этом методе достигается за счёт того, что мы не пересчитываем значения таких элементов.

Если в какой-то момент k для некоторого элемента i обнаруживается что p^(k+1)[i] — p^(k)[i] меньше определённого порога, мы считаем, что значение PageRank для страницы i найдено и более не пересчитываем i-тый элемент вектора p.

Исследователям удавалось достичь сокращения времени работы метода степеней на 20% при помощи этого трюка.

Однако данный метод требует периодически переупорядочивать данные, чтобы избежать вычисления тех элементов, значения которых считаются уже найденными. Поэтому адаптивный метод плохо подходит для больших графов – переупорядочить огромный объём данных становится слишком дорогой задачей.

Метод блочной структуры (Block Structure Method)

Web имеет блочную структуру. Это открытие столь интересно, что я намерен посвятить ему отдельный пост. Там же и обсудим этот метод.

UPD: пост о блочной структуре web.

Численные методы

Вычисляя значение PageRank, мы ищем такой вектор p, что

Это выражение является так называемой собственной системой, а p – собственный вектор матрицы A. Задача поиска собственного вектора может быть представлена системой линейных уравнений. В нашем случае это будет огромная, но всё же обычная система, которая может быть решена при помощи численных методов линейной алгебры.

Тем не менее, вычисление PageRank численными методами ещё находится в экспериментальной области. Каковы будут характеристики и свойства этих методов на реальных графах web пока не понятно.

Стоит отметить, что существуют уже готовые решения для параллельного вычисления крупных линейных систем.

Параллелизация

Вычисление PageRank параллельно на нескольких машинах позволяет существенно ускорить работу.

По сути методы параллелизации можно разделит на два типа.

Первые разделяют граф страниц на плотно связные компоненты – группы страниц плотно связанных ссылками между собой и имеющие относительно немного ссылок на страницы вне группы. PageRank для каждой такой группы вычисляется параллельно. Процессы/потоки периодически обмениваются информацией, когда дело доходит до ссылок между страницами разных групп.

Ко второму типу относятся методы, использующие блочную структуру web. О них мы поговорим в уже обещанном выше посте о блочной структуре.

UPD: пост о блочной структуре web.

Оптимизация ввода-вывода

Это довольно интересная тема, которую я приберегу для одного из следующих постов. Я представлю три алгоритма, которые будут интересны не только с точки зрения вычисления PageRank, но и вообще с точки зрения обработки больших объёмов информации.

Эволюция графа

Довольно естественной кажется идея не пересчитывать PageRank для всех страниц целиком, а найти способ обновлять его по мере эволюции графа страниц (по мере эволюции web).

В «Incremental Page Rank Computation on Evolving Graphs» Prasanna Desikan и др. предлагают следующий способ.

Сперва выделить часть графа, состоящую из страниц, до которых не существует путей от новых страниц, исчезнувших страниц, либо страниц, ссылки которых были изменены. Удалить эту часть графа, оставив только граничные узлы (т.к. они влияют на PageRank оставшихся страниц). Посчитать PageRank для оставшегося графа. Затем отмасштабировать значения PageRank с учётом общего количества страниц – т.к. количество страниц влияет на часть PageRank, получаемую за счёт телепортации.

Замечу, что полученный в результате PageRank не является точным, а всё же некой аппроксимацией.

По различным данным от 25% до 40% ссылок между web-страницами меняются в интернет в течение недели. Такая скорость изменения, на мой взгляд, оправдывает полный пересчёт PageRank всех страниц.

Персонализация

Представление о важности той или ной страницы во многом субъективно. То, что покажется одному отбросом, другой сочтёт изумрудом. Пусть есть очень качественная страница об игре керлинг, но я совершенно не хочу, чтобы она вылезала лично мне в топ. Чтобы учитывать в ранжировании интересы конкретного человека был придуман персонализированный PageRank.

Выбирается какое-то количество категорий, по которым можно классифицировать тематику тех или иных страниц (или сайтов). Например: культура, спорт, политика и т.п.

Пусть T[j] – множество страниц, принадлежащих к категории j (или расположенных на сайте, принадлежащем к данной категории).

Для каждой категории формируется особый вектор телепортации v (см. главу Телепортация).

v[i] очень мало, если страница i не принадлежит T[j], и значительно больше если принадлежит.

Для каждого тематического вектора телепортации вычисляется тематический PageRank p_j. Вычислить сто тематических PageRank для ста категорий вполне реально.

Допустим, у нас есть вектор k, сумма элементов которого равна единице. Значение k[j] отражает степень заинтересованности пользователя (реального, а не того из модели блуждания) в категории j.

Степень заинтересованности пользователя может быть указана явно, или она может быть сохранена в его профиле. Или она может быть выведена исходя из того, какие слова входят в запрос. Например, если запрос содержит слово fairtrade то можно вывести, что пользователь заинтересован на 0.4 в теме общество, на 0.4 в теме экономика и на 0.2 в теме политика.

Во время ранжирования результатов запроса пользователя для страниц используется следующее итоговое значение PageRank:

k[0] * p₀ + k[1] * p₁ + … + k[n] * p_n , где n – количество категорий

Таким образом, рейтинг страницы будет зависеть от того, что реально интересно пользователю.

Темы, которые будут рассмотрены в следующих постах

Оптимизация ввода-вывода

Siterank

UPD: Эта тема освещена в посте о блочной структуре web.

Технический аудит сайта программой Netpeak Spider

Обзор программы Netpeak Spider начну с банального: главное для продвижения сайта – seo-оптимизация. Только когда техническое состояние, контент, скорость загрузки и другие составляющие доведены до нормального уровня, можно вступать в борьбу за позиции с конкурентами. В противном случае не помогут никакие инструменты (читайте: ухищрения) в виде закупки ссылок, добавления в каталоги, краунд-маркетинга и прочего. Технический аудит сайту требуется не меньше, чем человеку профилактические осмотры врачей. Чем раньше выявляются и устраняются ошибки, тем быстрее ресурс завоюет доверие поисковиков и получит стабильность в ранжировании.

Массив информации сложно обработать без ПО. Созданы онлайн сервисы и программы, которые помогают в проведении диагностики сайтов, бесплатных и платных. Каждый из таких инструментов полезен оптимизаторам, вебмастерам или владельцам сайтов, которые самостоятельно поддерживают жизнеспособность блога, интернет-магазина, электронной витрины и проч. Netpeak Spider – программа платная, но с двухнедельным периодом тестирования, причем, функционал полный. Тарифы предлагаются разные, зависимо от срока использования. Лицензией можно обзавестись и на год, и на месяц, и это хорошо, потому что есть программы только с годовой подпиской и ценами, что не каждому по карману.

Параметров, включенных во внутренний технический аудит, более 60-ти. Опущу описание процесса авторизации и установки (у разработчиков прекрасная презентация https://netpeaksoftware.com/spider), но не спешите уходить — поделюсь впечатлением.

Настройка Netpeak Spider

Первое, с чего следует начать работу с программой по внутреннему аудиту, это с внимательного изучения настроек и выставлению их по своим потребностям – оставить только те характеристики или области, которые нужно проверить. Например, требуется получить информацию о внешних ссылках – запускаем проверку только внешних ссылок. Обратите внимание, есть параметры обязательные, есть использующиеся по умолчанию. Выставляем тип контента и вид урлов (изображения кликабельны).

Задаем количество потоков во вкладке «Скорость». Если к серверу будет много запросов, он ответит кодом 429. Ставим галочку в чекбокс – и проверка в таком случае приостановится, но сервера Beget, на котором расположено большинство моих сайтов, превышение нагрузки от ботов Netpeak Spider не испытали.

Как Netpeak Spider отображает информацию о скорости

Начну с того, что сам Netpeak Spider сканирует сайты быстро даже на минимальном количестве потоков практически со всеми включенными параметрами. Обратила внимание, что дольше проверяются сайты, загружающиеся медленно и в браузере пользователя, и по результатам сервисов проверки скорости загрузки. Но в отличие от, например, гугловского PageSpeed, в Netpeak Spider видно время загрузки и ответа сервера по каждой странице, а это шанс поработать над ускорением конкретной.

Скорость — исключительно серьезная характеристика сайта, и большую роль играют изображения. Картинки часто грузят сервер, не считая скриптов и стилей, хотя проблема легко устраняется на большинстве CMS простой заменой файла на сжатый. Благодаря Netpeak Spider обнаружила на одном проверенном-перепроверенном много раз сайте пяток картинок, которые очевидно загружались в оригинальном виде. Но что характерно для программы, она показывает и те изображения, которые не подгружаются с сервера. Например, загрузили на WordPress изображение размерами 4000*3000 пикселей, вывели на страницу 400*300 (к сожалению, такое часто встречается в работе с клиентскими сайтами) и дали ссылку, чтобы медиафайл открывался в полном размере. Netpeak Spider нашел эту большую и тяжеловесную картинку (изображения были сжаты пакетно, но, вероятно, файл не перезаписался). После замены одной картинки диск на сервере освободился на полтора мегабайта. А иногда речь идет о ГБ.

Проверка заголовков, мета-тегов, альтов

Параметры относятся к оптимизации контента, поэтому объединила заголовки, тайтлы, дескрипшены и альты вместе. В результатах проверки отображается количество пустых тегов, дублей, наличие нескольких заголовков h2. Соотношение text/html покажет страницы, где контента недостаточно. Из сводного отчета можно переключаться на детальный. Программа показывает и объем мета-тегов, и выгружает содержимое. Для этих целей использовала таблицы Гугла (мета-теги парсились с помощью заданных формул, но у Диска Гугл есть минус – в ячейках случается error, что тормозит работу).

Висячий узел – фишка Netpeak Spider

Внутренняя перелинковка – проверенный работающий метод продвижения сайта. В зависимости от структуры страниц и элементов на них, ссылки идут из меню, сайдбаров, футеров, виджетов, выведенных похожих записей. Плюс ручками добавляем ссылки в статьи. В итоге оптимизатор может сам затеряться в этой паутине, не заметив наступившего ссылочного дисбаланса. Netpeak Spider определяет внутренний PageRank урлов, обнаруживает и указывает на висячие узлы, когда со страницы линки идут, а сама страница не получает ничего. Правда, если программа просканировала URL изображений, то и эти страницы показывает проблемными. Но, как подсказали разработчики, в таких случаях устанавливается фильтр, чтобы сведения в отчете игнорировались.

Работа с техническими параметрами

Код 404, редиректы, канонические адреса, корректность файла robots.txt — под контролем желательно держать все. Бывает, страницы нет в поиске, а на нее просто установлен запрет для поисковых ботов. Но встречаются и другие случайные ошибки, когда стоит 301 перенаправление или canonical на удаленную страницу. Отследить вручную эти недочеты проблематично, а наличие таких косяков на web-ресурсе нежелательно. Паучок глазастый все обнаруживает и предоставляет в отчете.

Заключение

Статья содержит краткий обзор программы. Большего не требуется. Юзабилити продумано до мелочей. Всплывают подсказки. Во вкладке «Все результаты» отражено количество просканированных адресов (в первой, после нумерации, колонке отчета). Ссылки, при необходимости, открываются в браузере с помощью правой клавиши мыши. Напротив каждого URL проверенные параметры разбиты также по колонкам, в том числе и количество ошибок. Справа сгруппированные ошибки, и оттуда можно извлечь часть отчета.

Результаты как сохраняются, так и экспортируются в форматах CSV и Ecxel для работы. Нужно быть внимательными при экспорте: если нужно экспортировать весь отчет, а до этого мы просматривали детали, нужно вернуться на вкладку «Все результаты». Иначе будет выгружена только та часть данных, находясь на которой, мы затребовали экспорт.

Функционала Netpeak Spider достаточно, чтобы привести в порядок даже запущенный сайт и поддерживать его в отличном состоянии, если проверки проводить регулярно и оперативно принимать меры к исправлению новых ошибок.

Две техники SEO, которые дадут рост трафика уже через месяц. Читайте на Cossa.ru

Показываем, как с помощью рассчитанной на основе алгоритма PageRank перелинковки и рассчитанных на основе алгоритма BM25 текстов повысить позиции сайта по ключевым словам и привлечь больше трафика.

Техника 1. Перелинковка сайта на основе PageRank

Перед перелинковкой мы внимательно изучили статью Александра Садовского «Растолкованный PageRank» и решили применить знания на сайте клиента.

Внутренняя перелинковка — это метод внутренней оптимизации сайта, выполняемый для перераспределения ссылочного веса сайта на продвигаемые страницы. Статический вес сайта всегда равен 100%. Когда одна страница ссылается на другую, она передает некоторую часть своего веса, так называемый ссылочный сок. Таким образом, чем больше ссылочного сока передается страницам, тем более важными они считаются и для посетителей, и для поисковых систем.

Проще говоря, перелинковка выполняет две задачи.

Внутренние ссылки передают вес с одной страницы на другую.
Направляют посетителей на важные и ценные страницы.

Алгоритм перелинковки сайта

Рассмотрим алгоритм перелинковки на примере сайта производителя плитки ПВХ для промышленных и спортивных помещений.

1. Выбираем страницы, которые хотим видеть в топе поисковых систем.

В нашем случае это:

главная;
полы ПВХ для цеха, склада, производства;
плитка ПВХ для тренажерного зала;
полы для гаража, автосервиса и паркинга;
полы для бассейна, душевой, ванной комнаты;
плитка ПВХ для офиса;
полы для кафе и ресторанов;
полы для ледовых дворцов;
полы для магазинов и супермаркетов;
плитка ПВХ для автосервиса;
полы для технических этажей.

2. Далее узнаём по каждой странице, какие ссылки ведут на страницу и со страницы.

Для этого можно использовать различные сервисы, например: сервис saitreport.ru или программы Xenu1 и PageWeight. Не забываем, что нам нужны только открытые для индексации ссылки, никаких тегов nofollow и noindex там быть не должно. Закрытые ссылки не участвуют в передаче внутреннего веса и нужны исключительно для удобства пользователя, помогая найти нужный раздел, склонить к прочтению дополнительной информации и уменьшить количество отказов.

3. Теперь рассчитываем текущее распределение веса по всему сайту.

Берём отчёт по внутренним ссылкам, которые мы получили в Xenu1 или PageWeight, и вносим данные в таблицу. Мы использовали отчёт по ссылкам в Saitereport.

Так выглядит отчёт по внутренним ссылкам в Excel с Saitereport.

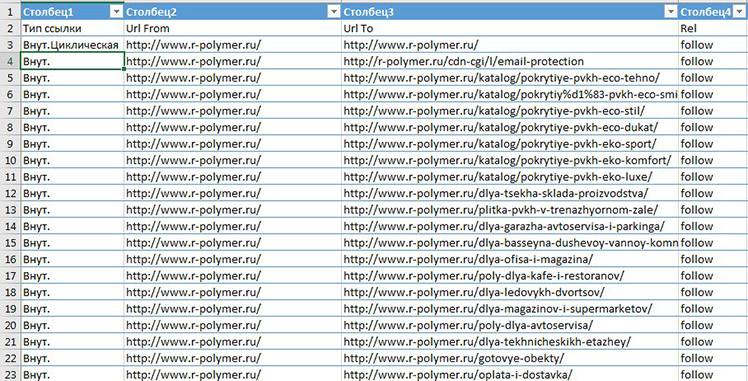
Отчёт по внутренним ссылкам

Для этого используем Excel. Открываем калькулятор, по горизонтали и вертикали вносим все страницы, которые есть на сайте. Для удобства это можно сделать по определённой иерархии. Таких страниц 45 с каждой стороны.

Текущее распределение ссылочного веса по сайту

Заполнили таблицу и получили PageRank для каждой страницы. Квадратики с заливкой показывают, что на определённую страницу ссылаются отдельные страницы. На скриншоте видно, что вес всех страниц практически одинаковый, все страницы ссылаются друг на друга в приблизительно одинаковом количестве, а некоторые не продвигаемые страницы имеют непомерно высокий вес.

Наша задача — сделать такую перелинковку на сайте, чтобы вес был самым высоким на продвигаемых страницах.

Выполнять нужную перелинковку нам поможет та же таблица в Excel.

Запомним, каких ссылок быть не должно:

Висячих узлов: страниц без исходящих ссылок.
Зацикливающих страниц: ссылающихся на самих себя.
Дублирующих ссылок.
Ссылок на не продвигаемые и страницы с ответом 404.
Несвязных узлов: страницы без входящих ссылок.

После нескольких итераций у нас получилось такое распределение веса: главная и продвигаемые страницы получили в среднем 7,6% ссылочного веса, в сумме — почти 84% всего PageRank сайта. Остальные страницы сайта получили около 0,5%. То есть модель перелинковки, согласно теории PageRank, сделана правильно. Вес сосредоточен на продвигаемых страницах!

Готовая модель перелинковки

Техника 2. Подготовка текстов на основе алгоритма семантического анализа

Следующий этап — это проведение оптимизации текстов по вхождению ключевых слов.

Для этого мы выполнили семантический анализ всех текстов: определили соответствие поискового запроса документу как на продвигаемых, так и на служебных страницах. Мы применили метод оценки релевантности TF-IDF.

Метод заключается в следующем: чем больше частота запроса в документе, тем значимей будет данный текст по отношению к запросу. То есть вероятность показа этого текста по запросу возрастает. Например:

Предложения в тексте	Всего слов	Плитка	ПВХ	Покрытие
Текстура плитки ПВХ ЭКО-ТЕХНО имеет выступающие прямоугольники	7	1	1
Плитка обеспечивает сцепление для транспортных средств и для пешеходов	9	1
ПВХ-покрытия не взаимодействуют с кислотами, щёлочами, маслами, бензином и другой активной «химией»	11		1	1
Плитка ПВХ легко режется	4	1	1
Итого	31	3	3	1

Например, из этой таблицы мы понимаем, что запрос «покрытие» используется 1 раз, в то время как «плитка» и «ПВХ» используется по 3 раза. Мы можем заменить вхождение слова «плитка» на слово «покрытие». В таком случае не будет заспамленности, и эту страницу можно будет продвигать по двум запросам — «плитка ПВХ» и «покрытие ПВХ».

В текстах мы выявили чрезмерную заспамленность по ключевым словам. Чтобы уменьшить вхождение фраз, а также расширить его, мы воспользовались подбором ключевых слов Yandex.Wordstat, выделили нужные ключевые запросы и внедрили их в тексты, а чрезмерное количество одинаковых ключевиков — уменьшили. Затем написали подробное техническое задание копирайтеру. Полное ТЗ находится в GoogleDocs. Не все ключевые слова были использованы копирайтером в тексте, так как текст был бы слишком ими перенасыщен. А тексты в первую очередь должны быть написаны для людей.

Результат

В среднем трафик с поисковых систем увеличился на 16% в июне по сравнению с апрелем. Сравнивали с апрелем, потому что в апреле такое же количество дней, как в июне, и столько же праздников. К тому же, в мае и происходили все действия, которые могли повлиять на точность данных. В итоге грамотная внутренняя перелинковка и написанные для людей уникальные тексты, ранжирование которых можно улучшить при помощи TF-IDF, дают прирост органического трафика.

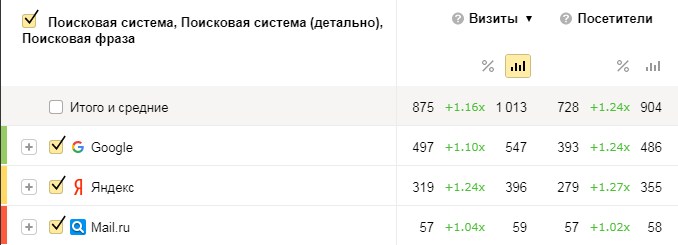
Сравнение поискового трафика

Также выросли позиции по основным ключевым словам. Многие запросы стали видны в топ-100.

Зелёный цвет — позиции выросли.
Красный — снизились.
Без заливки — остались неизменными.

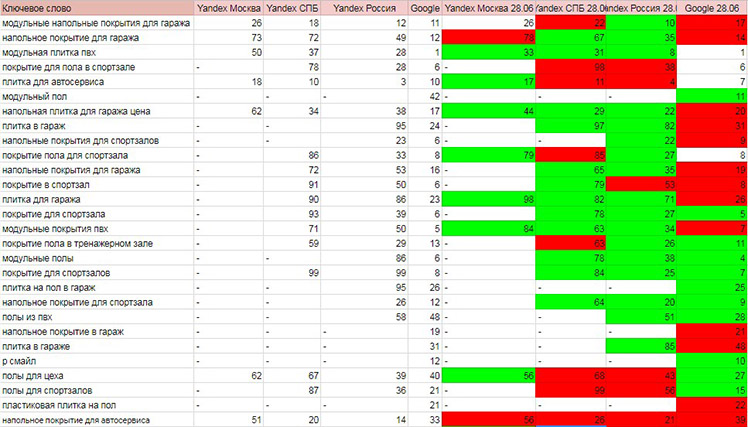
Позиции в поисковой системе

Вывод

Даже если у вас на сайте выполнена базовая внутренняя оптимизация сайта: прописаны title и description, написаны уникальные тексты, грамотная перелинковка сайта всё равно может быть полезна. Она принесёт увеличение органического трафика уже при первой полной переиндексации сайта. Главное помнить, что перелинковка должна быть удобной и пользователям и не создаваться исключительно для перераспределения веса.

Что касается текстов — пишите их в первую очередь для людей и только потом, применяя метод TF-IDF, отрабатывайте их для поисковых систем. Такой подход точно даст результат, так как тексты будут читабельными и поисковый робот будет их правильно трактовать.

Читайте также: 11 советов SEO-шнику, которому попался сложный клиент

Мнение редакции может не совпадать с мнением автора. Ваши статьи присылайте нам на [email protected]. А наши требования к ним — вот тут.

Анализ сайта на ошибки: онлайн программа Netpeak Spider

Привет, друзья! В 2017 году я делала обзор программы Netpeak Spider, который позволяет проводить аудит сайтов на ошибки. Если у вас есть желание сделать комплексную проверку сайта, в этом вам поможет Netpeak Spider. Этим сервисом могут пользоваться интернет-маркетологи, специалисты по SEO, специалисты по настройке контекстной рекламы, вебмастера и т.д.

Уникальность данного инструмента в том, что он позволяет делать анализы больших сайтов, имеет гиперскорость сканирования и понятную SEO-аналитику, в результатах которой разберется даже новичок.

Разработчики этого проекта не стоят на месте, и уже в этом году они презентовали крутое обновление Netpeak Spider 3.1., в которое вошло более 300 изменений. О том, что новенького появилось в программе, и пойдет речь в моей статье.

Содержание статьи
Высокая скорость сканирования сайтов

Я не могла не обратить внимания на скорость анализа своего сайта. Для того, чтобы просканировать мой блог, Netpeak Spider понадобилось около 10 секунд! Да, мой сайт на данный момент включает в себя всего 2 856 страниц (из аналитики Netpeak Spider), тем не менее, я видела, насколько быстро прошла обработка.

Именно на этом моменте акцентируют свое внимание специалисты данного сервиса. Они добились того, что время на анализ сайта до 10 000 страниц сократилось в 8 раз, а для сайтов более 100 000 страниц практически в 30 раз.

Также они смогли снизить потребление оперативной памяти до 235 Мб и потребление памяти на жестком диске до 30 Мб.

Кстати, теперь при анализе сайта происходит мониторинг лимита памяти для сохранения данных. Если памяти не хватает, программа останавливает свою работу и выдает соответствующее сообщение. В этом случае вы можете сохранить проект, выгрузить его, а затем продолжить далее.

Остановить работу программы вы можете и самостоятельно, т.е. возможно частичное сканирование сайта с сохранением результата. Следующее сканирование возобновится с этого момента.

Обновление таблицы после исправления ошибок и удаление URL

В обновленной версии Netpeak Spider теперь появилась возможность пересканировать таблицу с URL, которые содержат ту или иную ошибку.

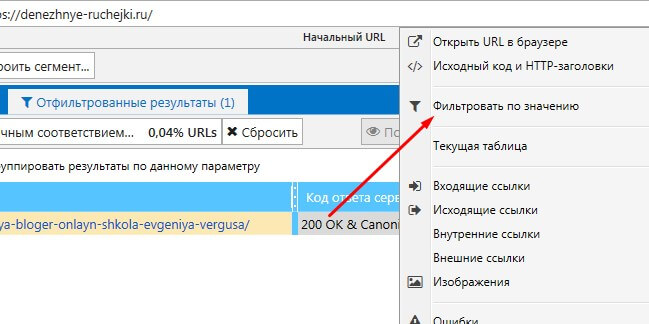
Пример. Сервис показал, что на вашем сайте присутствуют битые ссылки, как у меня.

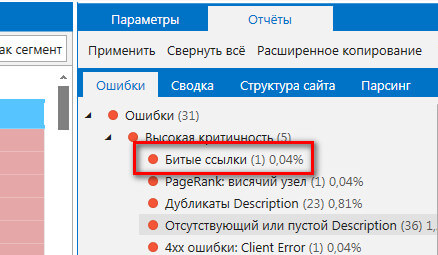
Если кликнуть по этому параметру, в левой части окна программы вы увидите URL, где спряталась эта битая ссылка. Удалив ее с сайта, вам не нужно пересканировать весь блог снова. Достаточно в программе выделить эту ссылку правой кнопкой мыши, выбрать команду Текущая таблица – Пересканировать таблицу.

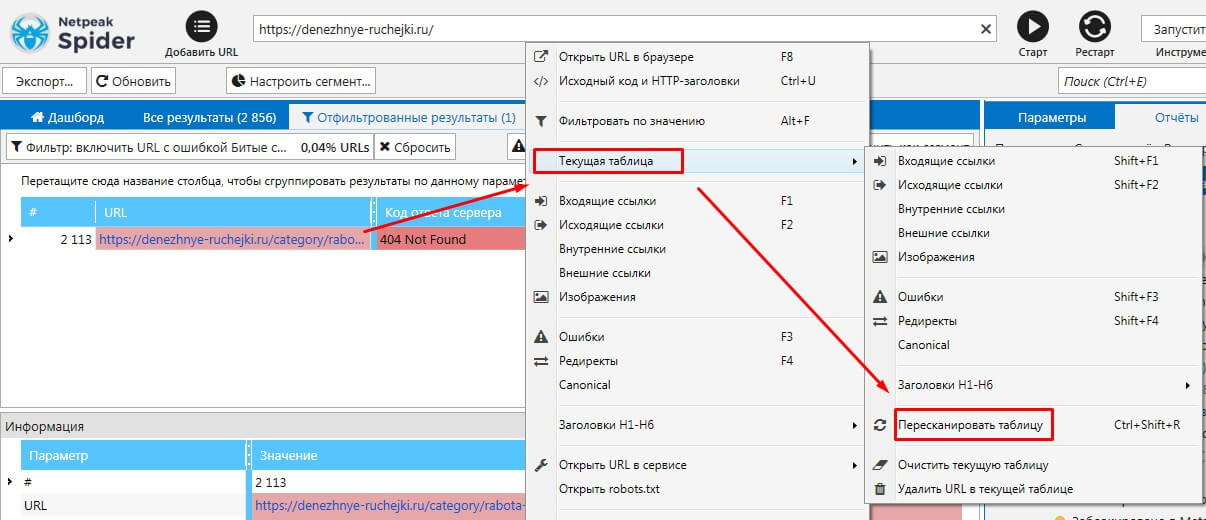
Если в списке ошибок вы нашли URL и знаете, что на этих страницах сайта все правильно, эти URL из таблицы можно удалить. Для этого по адресу страницы кликните правой кнопкой мыши и выберите функцию Удалить URL.

Новая вкладка Параметры

Обратите внимание, что из настроек Netpeak Spider параметры переместились в правую часть рабочего окна программы. Именно здесь вы можете выбрать те параметры, по которым хотите проанализировать свой сайт на ошибки.

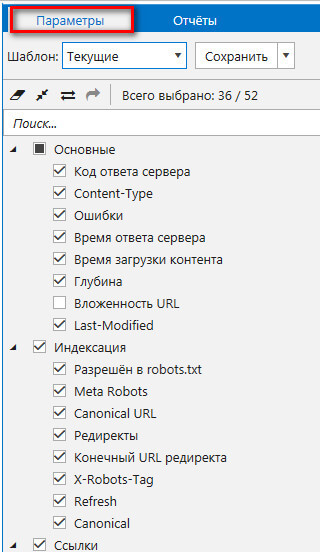
Любой параметр можно добавить и во время сканирования сайта. Для этого необходимо сканирование остановить и поставить галочку у нужного параметра. Конечно, та часть сайта, которая уже просканировалась, останется без этого показателя. Но далее после возобновления сканирования этот параметр будет учтен. Также работает и обратный вариант: любую галочку из параметров можно удалить.

Клик по любому параметру выбирает в таблице ошибок столбец с этим параметром. В данном случае не нужно двигать ползунком влево-вправо, чтобы найти этот самый показатель.

В последнем обновлении появилась возможность синхронизации таблицы с параметрами. Если вы хотите выгрузить таблицу с определенными параметрами, а остальные отключить, для этого просто снимите галочки с параметров в правой панели сервиса.

Сегментация и дашборд

Дашборд – это новая функция, которая позволяет анализировать показатели сканирования сайта в виде диаграмм.

Здесь вы можете ознакомиться со следующими показателями:

Количество просканированных URL
URL с важными ошибками
Индексируемые URL
Внутренние URL
Индексируемость URL
Критичность ошибок
Причины неиндексируемости URL
Время ответа сервера
Код ответа сервера
Глубина URL
Инструкции по индексации
Тип контента

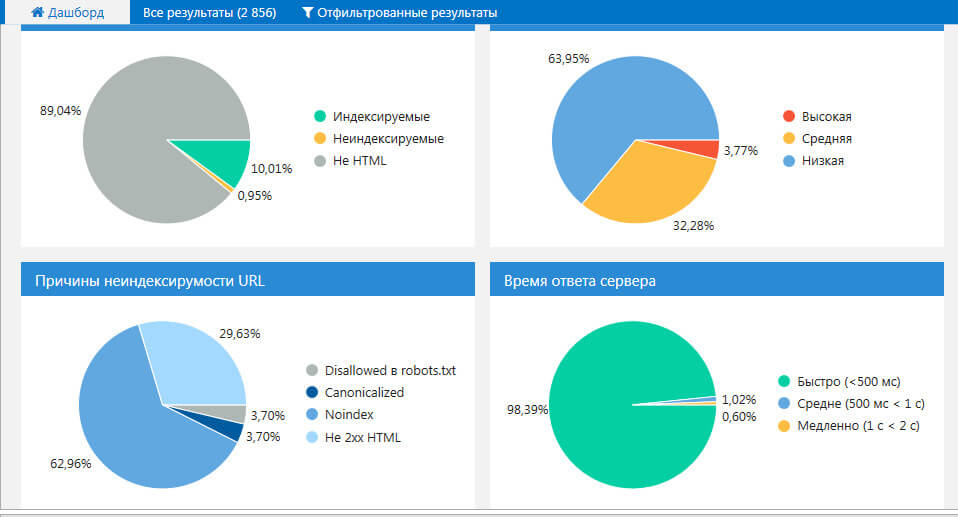
Если вы обратите внимание на 1-й показатель Индексируемость URL по моему сайту, то нельзя не заметить, что индексируется у меня всего 10% информации. Не стоит пугаться, т.к. остальная часть – это скриншоты (картинки) – не HTML.

Это, кстати, видно по нижнему графику, который отвечает за тип контента.

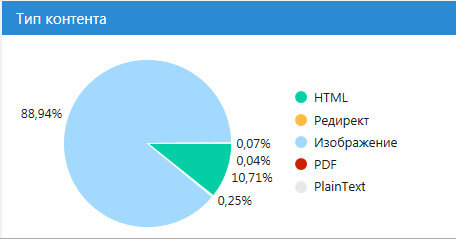
Очень удобно, что каждый сегмент графика кликабельный.

Например, меня заинтересовал сегмент графика с высокой критичностью ошибок.

Чтобы посмотреть список ошибок, мне достаточно кликнуть мышкой по этому сегменту. И передо мной откроется таблица со списком этих ошибок.

Но это еще не все! Теперь у вас появилась возможность самостоятельно любую ошибку представить в виде сегмента. Допустим, в программе вас заинтересовал раздел ошибок со средней критичностью. Для этого вы должны выделить эту ошибку и кликнуть по кнопке Применить как сегмент.

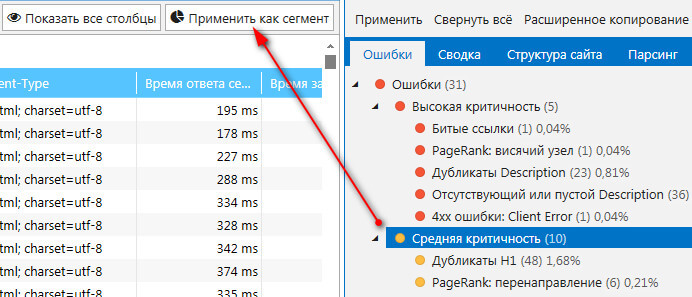
В результате появится дашборд с соответствующими диаграммами, через которые легче определить источники ошибок.

Удобная выгрузка отчетов

Все результаты сканирования сайта можно выгрузить и сохранить в таблице excel или CSV. Для этого в программе необходимо кликнуть по кнопке Экспорт и выбрать тот раздел, в формате которого вы хотите увидеть результаты.

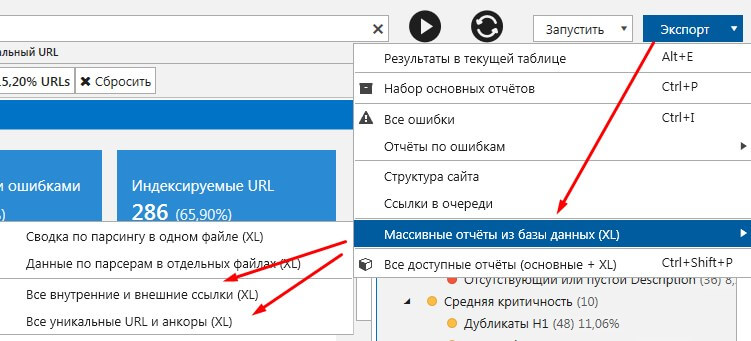
Это может быть набор основных отчетов, все ошибки, отчеты по ошибкам, в том числе битые ссылки, ссылки с неправильным форматом URL, изображения без атрибута ALT, редиректы; массивные отчеты из базы данных, в том числе все внутренние и внешние ссылки, уникальные URL и анкоры; отчет по структуре сайта, и т.д.

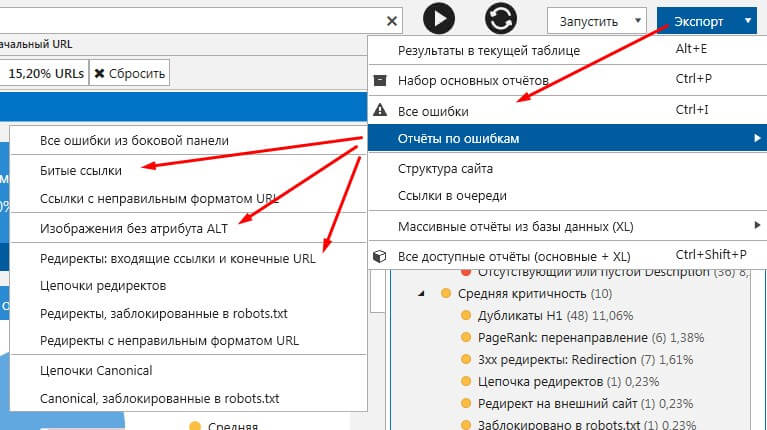
Дополнительные инструменты

О дополнительных инструментах Netpeak Spider я уже упоминала в первой статье, но не будет лишним еще раз повторить. Для анализа своего сайта вы можете воспользоваться дополнительными инструментами:

Расчет внутреннего PageRank
Валидатор XML Sitemap
Генератор Sitemap

Расчет внутреннего PageRank определяет висячий узел. Висячие узлы – это URL, которые получают ссылочный вес, но не передают его дальше. Проще говоря, это страница, на которую идут входящие ссылки, а исходящих ссылок нет.

С помощью Netpeak Spider нас воем блоге я обнаружила такую ошибку. Дело в том, что я удалила некоторые рубрики с сайта, а статьи раскидала по другим рубрикам. Но как оказалось, в одной из моих статей была ссылка на удаленную рубрику. В результате образовался висячий узел, от которого необходимо избавиться. Netpeak Spider считает эту ошибку критичной.

Если на вашем блоге карта сайта Sitemap не генерируется автоматически, ее можно сгенерировать с помощью инструмента Netpeak Spider – Генератор Sitemap. В результате данная карта будет отвечать рекомендациям Google и Яндекс, и будет соответствовать протоколу Sitemap.

Сохранение шаблонов настроек

Наверное, с этого обновления и нужно было начинать, т.к. работа со всеми программами начинается с настроек.

Теперь Netpeak Spider позволяет сохранять шаблоны настроек. Для этого в настройках вам нужно лишь кликнуть по кнопке Сохранить и ввести название ваших настроек. При следующем запуске анализа сайта нет необходимости снова выставлять нужные настройки – просто выберите сохраненный вариант.

Виртуальный robots.txt

Так же в настройках можно настроить виртуальный robots.txt или протестировать любую директиву из «роботса» перед заливкой на сайт.

Анализ списка URL

Если вдруг у вас возникла необходимость проанализировать на ошибки не весь сайт, а только некоторые страницы, вы можете это сделать, добавив списком URL (из файла) через кнопку Экспорт в программе.

Быстрый поиск по таблице

Теперь, чтобы найти определенный URL, можно воспользоваться новой функцией Быстрый поиск по таблице. Просто вставьте интересующий вас адрес в поле поиска, и система выдаст вам готовый результат.

Удобный фильтр

Ну и в заключение хочу познакомить вас с удобным фильтром, который позволяет найти группу ошибок в один клик. Для этого в таблице правой кнопкой мыши кликните по ошибке и выберите функцию Фильтровать по значению. Система отберет все страницы, где встречается эта ошибка.

Заключение

Как видите, с Netpeak Spider проводить анализ сайта на ошибки стало еще проще, при минимальных затратах времени и ресурсов вашего компьютера. Интуитивный функционал, всплывающие подсказки, выгрузка отчетов в виде таблиц позволит работать с этой программой любому новичку. Ну а продвинутые пользователи найдут для себя здесь современные решения для работы над задачами разной сложности.

Автор статьи Ольга Абрамова

Денежные ручейки

SEMPRO 2018: SEO-эксперименты с Дмитрием Шаховым

16 марта в Киеве прошла конференция SEMPRO 2018, посвященная продвижению на западный рынок. Во время своего выступления на мероприятии Дмитрий Шахов (владелец и руководитель Remarka.info, организатор крупнейшей в Калининграде SEO-конференции Baltic Digital Days) и Денис Китайчук (SEO-специалист Webline Promotion) поделились результатами экспериментов, целью которых было подтвердить или опровергнуть устоявшиеся представления об отдельных аспектах работы поисковых систем.

В докладе рассматривались следующие вопросы:

Висячие узлы. Страшны ли они?
Ссылки на 404. Страшны ли они?
Влияние сквозных ссылок на ранжирование: плюс или минус?
Редиректы: когда теряется анкорный вес?
Биение на пассажи: какие символы бьют?
Влияние на ранжирование атрибутов изображений.

Рассмотрим каждый из аспектов выступления подробнее.

Вредны ли висячие узлы?

Гипотеза: ссылочный вес, передающийся на висячие узлы (страницы без исходящих ссылок), уходит в никуда.

Следствие 1: страницы со ссылками на висячие узлы теряют ссылочный вес, и это ухудшает показатели страницы.

Следствие 2: если разместить на хорошо ранжируемой странице ссылки на такие документы, она должна просесть в выдаче.

Эксперимент: для проверки гипотезы экспериментаторы разместили ссылки на запароленные архивы (они играли роль висячих узлов) на страницах, которые стабильно держались в выдаче, дождались переиндексации и подождали еще около месяца.

Результат: позиции по запросам практически не изменились.

Вывод: ссылки на висячие узлы на посадочных в небольшом количестве не являются проблемой.

Вредны ли ссылки на 404?

Гипотеза: если страница отдает 404 (документ не найден), то передаваемый на нее ссылочный вес теряется.

Следствие 1: страница со ссылками на 404 теряет статический вес, и это ухудшает ее ранжирование.

Следствие 2: если разместить на странице ссылки на несуществующие документы, она просядет в выдаче.

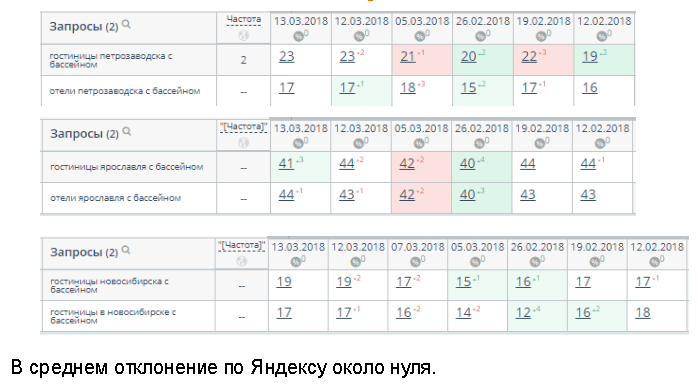
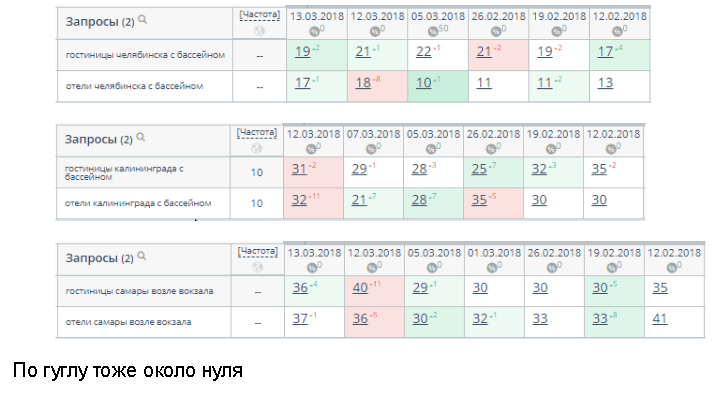
Эксперимент: на страницы, которые стабильно удерживают позиции в выдаче поисковых систем, размещены ссылки на несуществующие страницы, дождались переиндексации и подождали еще месяц. Затем сравнили позиции до и после размещения

Результат: позиции практически не изменились ни в Яндексе, ни в Google.

Вывод: исходящие ссылки на 404 (подвид висячих узлов) тоже не влияют на ранжирование страниц-доноров.

Полезны ли сквозные входящие ссылки?

Гипотеза: «сквозняки» (ссылки, размещенные на всех страницах сайта-донора) передают большой ссылочный вес и улучшают ранжирование страницы-акцептора.

Альтернативная гипотеза: «сквозняки» неестественны, оцениваются алгоритмами как ссылочный спам и ухудшают ранжирование.

Эксперимент: на анализируемые страницы было размещено по 3–5 сквозных ссылок со сторонних трастовых сайтов. Изменение позиций оценивалось в течение 1–2 (для разных акцепторов по-разному) месяцев.

Результат: позиции в Яндексе практически не изменились. Позиции в Google либо тоже не показали роста, либо незначительно выросли по некоторым запросам.

Полезны ли сквозные входящие ссылки 1.png

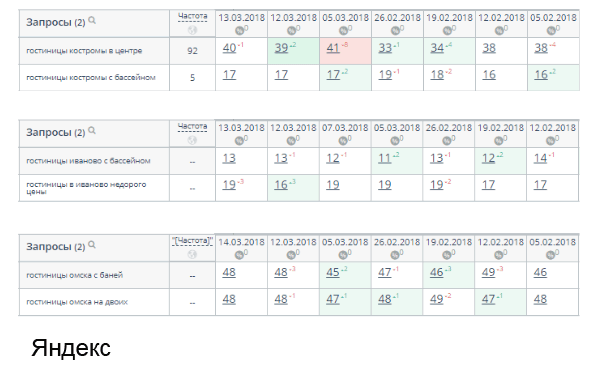
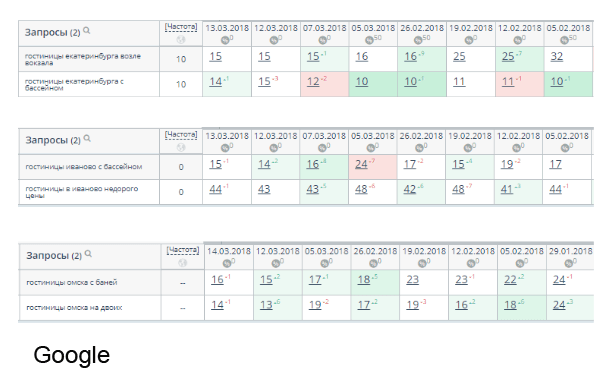
Вывод: для обоих поисковых систем не отмечено падения от наличия сквозных ссылок. Рост есть по отдельным запросам в Google, так что при грамотной ссылочной стратегии из сквозных ссылок можно извлекать пользу.

Какие символы и теги разбивают пассажи?

Гипотеза: с точки зрения алгоритмов Яндекса некоторые теги и символы разбивают пассаж, и разделенные ими слова не считаются связанными – это не позволяет ранжироваться документам по фразам, части которых находятся в разных пассажах.

Следствие 1: если между словами в тексте будет располагаться разбивающий пассаж элемент, этот документ не будет находиться при цитатном поиске по запросу, включающему разбитые слова.

Эксперимент: созданы страницы, содержащие разные символы и теги в теле текста. После индексации документа все символы поочередно проверялись цитатным поиском.

Результаты представлены в таблице:

Какие символы и теги разбивают пассажи.png

Выводы: список символов и тегов, которые разбивали пассаж ранее, не изменился.

Как учитываются в поиске Alt и другие атрибуты изображения

Гипотеза 1: Alt, Title, Name и другие атрибуты изображения индексируются и влияют на:

ранжирование изображения в поиске по картинкам;
ранжирование всех изображений документа в поиске по картинкам;
ранжирование самого документа в основном поиске.

Гипотеза 2: Title страницы, текст вокруг изображения и анкоры влияют на ранжирование изображение в поиске по картинкам.

Эксперимент: на страницы были добавлены изображения с ключевыми фразами в значениях атрибутов, окружающем тексте, анкорах и т.п. (см. таблицу ниже). После индексации экспериментаторы проверили, находятся ли изображения и страницы по ключевым фразам в поиске по картинкам и основном поиске Яндекса и Google.

Результаты представлены в таблице.

Как учитываются в поиске Alt и другие атрибуты изображения.png

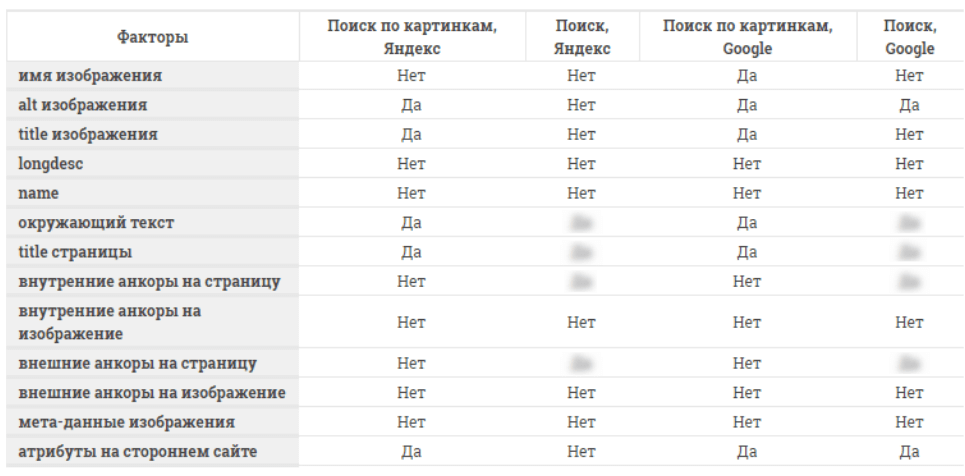
Выводы: при ранжировании в поиске по картинкам Яндекс использует значения атрибутов Alt и Title изображения, а также Title страницы и окружающий изображение текст. В основном поиске атрибуты изображений не учитываются вообще. Google рассматривает атрибуты как часть документа — атрибуты одного изображения влияют на нахождение всех изображений в поиске по картинкам. Alt учитывается в основной выдаче как текст страницы. Имя изображения также учитывается в поиске по картинкам.

HostRank или PageRank, вычисляемый по графу хостов

Как уже упоминалось в предыдущей части нашего с вами материала, в ряду случаев наличие висячих узлов может оказывать существенное влияние на ранжирование документов в органическом поиске. Ориентируясь на Рис. 14 можно сказать, что как при равномерном, так и неравномерном перемещении пользователя наша с вами виртуальная страница получает более высокое значение Google PR.

Например, при допущении равномерного перемещения с какого-либо висячего документа к прочим страницам нашей системы мы бы имели следующую матрицу переходов:

В ином случае мы можем обозначить за С={1, 2} то подмножество узлов нашей модели, которое имеет сильную связанность, а прочие узлы, на которое подмножество С ссылается лишь в одностороннем порядке обозначим за D={3}. Тогда матрица переходов (α= 0.85) принимает вид:

Отсюда, нормированное значение PageRank (x1, x2, z) = (0.31746, 0.31746, 0.365079). Надо сказать, что виртуальная страница может получать существенно большее значение веса Google PR даже при введении запрета на телепортацию в ее содержимое пользователя поисковой системы.

Мёртвые (битые) ссылки в построении выдачи

Если само по себе признание документа висячим, еще не ставит под сомнение качество содержащегося в нем контента (мы можем иметь дело с аналитическими отчетами, научными публикациями и т.д.) и поисковая система всегда может произвести все необходимые оценки его содержимого, то ситуация с теми веб-ресурсами, которые возвращают клиентские ошибки вида 404 Not Found (документ не найден и/или не существует) или 403 Forbidden (доступ к ресурсу был запрещен) обстоит совершенно по-иному. Существуют две основные причины появления подобного рода ссылок:

Созданная ранее web-страница по тем или иным причинам впоследствии была удалена вебмастером. В таком случае мы говорим, что цитируемый сайтом-реципиентом интернет-документ устарел и более не поддерживается администратором ресурса.
Страница никогда не существовала в принципе, и текущая исходящая ссылка со страницы сайта была создана вследствие какой-либо ошибки администратора. В таком случае, мы говорим о крайне низком уровне модерации веб-ресурса, поскольку качественный сайт предполагает тщательный отбор тех адресов, которым следует передавать нашу голосующую способность.

В обоих случаях, те интернет-документы, которые содержат в своем контенте исходящие ссылки на несуществующие или запрещенные страницы следует рассматривать как своего рода отклонение от корректно функционирующей системы и, по всей логике вещей, они не должны оказывать влияния на результаты поисковой выдачи. Все-таки основополагающий принцип Google PageRank состоит в том, что вес страницы рассчитывается исходя из ссылающихся на страницу документов, а не из тех особенностей (в данном контексте имеется в виду отдача 404 и 403 ошибок) соседей по сети, которые с нею связаны. В нашем распоряжении имеется неподтвержденная информация о том, что в современном интернете наблюдается тенденция к увеличению объема подобного рода умерших по причине своей неактуальности ссылок. Мы ознакомились с рядом исследований [2, 3], посвященных прогнозам полураспада URL-адресов на последующие 4-5 лет. В частности, [2] описывает процесс исчезновения в зоне .COM более 50% отслеживаемых web-страниц в первые 24 месяца. Более того, в процессе обхода более чем 1 млрд. документов мы обнаружили, что около 6% из них возвращают нам код 404, что натолкнуло нас на здравую мысль о том, что в перспективе проблема глобального учета подобного вида отмерших страниц будет только усугубляться. Вопрос увеличения доли битых страниц во многом перекликается с наблюдениями Najork и Wiener [4], выполнявших поиск в ширину и, соответственно, стремившихся найти наибольший ранг документа на раннем этапе обхода. Напомним, что суть данного обхода и разметки вершин веб-графа сводится к тому, что началу обхода приписывается метка 0, а смежным с ней вершинам — 1; после чего мы имеем возможность рассмотреть окружение 1-ой вершины и пометить окружающие ее узлы меткой 2, и т.д.

Если анализировать отсканированный нами 1,1 млрд. страниц, то мы обнаружим следующую картину: после значительного всплеска и незначительного затухания процента обнаруженных нами ссылок на несуществующие web-документы, их доля будет неуклонно расти по мере индексации веба. Причиной этому является то, что все большее количество страниц за время нашей работы утрачивало свою актуальность и выдавало 404 ошибку. Поскольку текущая работа обнаруживает наличие прямой корреляции между ссылками на несуществующие HTML-документы и снижением качества цитирующих их площадок, можно предположить то, что качественная оптимизация и продвижение сайтов должна ставить своей целью поддержание актуальной ссылочной структуры обслуживаемого веб-ресурса. В дальнейшем мы опишем вам некоторые поисковые алгоритмы, которые могут выполнять пессимизацию голосующей способности страниц сайтов, имеющих в своем содержимом ссылки на штрафные узлы. Мы надеемся, что учет подобного рода данных позволит нам улучшить качество персонального поиска и более эффективно управлять сайтами в процессе сканирования.

Небольшой пример

Рассмотрим теперь пример, при котором ссылки на штрафные узлы будут иметь для наших подсчетов существенное значение. На Рис. 15 показано 4 документа, один из которых является безисходным.

Если заниматься подсчетом Google PageRank с α= 0.85, то для трех сильно связанных документов и одной виртуальной страницы получаем:

Если же мы сделаем допущение, что узел 3 имеет не одну, а четыре висячие ссылки, тогда наши новые веса составят:

Как и следовало ожидать, голосующая способность виртуального узла 3 возросла, но одновременно с этим вес документа 2 существенно снизился. Таким образом, ссылки на документы, отдающие нам коды ошибок 404 и/или 403, могут оказывать значительное воздействие на своих ближайших соседей по всемирной паутине.

Ссылки на штрафные узлы

В данном блоке мы рассмотрим с вами несколько модификаций классического алгоритма PageRank, которые могут улучшить ранжирование документов, имеющих исходящие ссылки на штрафные страницы. В их число входят: алгоритм возврата, петельный алгоритм, переходы с весами и BHITS.

1. Алгоритм Возврата

Суть данного метода заключается в том, что в случае наличия на какой-либо страницы исходящей мёртвой ссылки на штрафной документ, ее голосующая способность должна быть пропорционально разделена между имеющимися рабочими ссылками, а оставшееся (штрафное) значение возвращено тем страницам, которые вызвали увеличение ее ранга на этапе предыдущей итерации. В конце концов, мы достигаем эффекта ограничения притока голосующей способности на штрафные узлы со страниц наших web-сайтов. В уже известной нам модели случайного серфинга пользователя данная методика соответствовала бы попаданию пользователя на страницу без исходящих ссылок и его последующего возврата к нужным файлам посредством использования интернет-обозревателя (браузера). В качестве наглядного примера, описывающего нам алгоритм возврата, можем представить страницу i, которая ссылается на штрафной веб-документ p. Для x_i имеем:

Мы хотим вернуть часть (скажем, β_i, где 0<β_i<1) голосующей способности тем интернет-страницам, которые указывают на наш штрафной документ (то есть такой j, где (j,i) ∈ E). Мы можем сделать это посредством изменения расчета PageRank таким образом, чтобы

где B, как и А, представляют собой стохастическую матрицу, а сумма элементов в каждом столбце равна единице. То есть, e^TB =e^TA = e^T. Мы полагаем, что оштрафованный голос i следует распределит между его донорами в пропорциях β_ia_ij, оставляя нашей странице только часть (1-β_i) первоначального целостного значения Google PageRank равного 1. В матричном выражении тот случай, когда мы возвращаем голос только одной странице-донору может быть представлен следующим образом:

где a₁^T является первым столбцом матрицы А (за исключением а₁₁), и:

является таким нормализирующим коэффициентом, что В считается стохастической матрицей. Естественно, если голосующая способность возвращаются нескольким web-документам, мы распределяем общее значение PR в определенных соотношениях (1-β_i) между донорами нашей странички. На практике, данная модификация известного алгоритма Google PageRank подразумевает дополнительный шаг не только на каждой его итерации, но и после умножения значения вектора В, хотя, стоит заметить, что вторая ситуация встречается достаточно редко. Если же заводить разговор о более конкретных примерах, то описанная выше операция может достаточно эффективно применяться к страницам, указывающим на те ресурсы, которые отдают 404 ошибку. Обозначим за gi число «хороших» исходящих ссылок со страницы i, а bi количество «плохих» (штрафных) линков. Тогда мы можем оштрафовать страницу i следующим образом:

Если мы представим, что на нашем рисунке 15 имеется 8 исходящих ссылок с документа 3, из которых 4 отдают нам 404 ошибку (мертвые ссылки), а оставшиеся 4-ре признаются рабочими, то, посредством применения данного алгоритма, получаем уже новые значения PageRank (0.292287, 0.312162, 0.1666, 0.228948) для всех (3 и 1 виртуальный узел) наших интернет-страничек. Видим, что документ 3 имеет существенно меньшее (сниженное) значение голосующей способности по сравнению с его соседями 1 и 2. Здорово? Идем дальше.

2. Петельный алгоритм

Существует утверждение, что на каждом шаге наш пользователь может как проследовать по исходящей по ссылке с вероятностью α, так и перейти на какую-либо случайную страницу в сети с вероятностью 1-α. Петельный алгоритм заключается в том, что мы добавляем нашему документу ссылку на самого себя, тем самым, создавая ребро, инцидентное одной и тоже вершине. После того, как мы это сделали (предполагается, что все возможные петли до этого шага были заранее удалены с нашего графа), мы переходим по ней с вероятностью γ_i, которая будет менее значительной в том случае, если веб-документ имеет множество исходящих ссылок на штрафные странички. Таким образом, те сайты, которые не имеют в своем содержимом мёртвых линков, будут сохранять свой PR в случае нашего перехода по нашей петельной ссылке, а наличие хотя бы одной единственной ссылки на несуществующий файл будет снижать их первоначальную голосующую способность. Для расчета параметра γi нам необходимо выбрать вероятность γ и использовать формулу γ_i=γ⋅g_i/b_i+g_i, где b_i обозначается количество исходящих линков со страницы i к штрафным документам, а g_i — тех ссылок, которые ведут к актуальным интернет-сайтам. Однако для того, чтобы наша матрица была стохастической, мы должны скорректировать вероятность телепортации с 1-α до 1-α-(_γb_i/b_i+g_i). В принципе, существует несколько моделей, описывающих работу данного алгоритма, в наиболее простой из которых мы просто добавляем на каждую хорошую страницу ссылку на саму себя и всякий раз осуществляем случайный переход по исходящим линкам (в том числе и по тем, на которые являются петлями) с равномерной вероятностью. Однако мы можем усложнить себе задачу таким образом, при котором параметр γ_i будет подбираться для каждой странички нашего сайта индивидуально, а также, помимо вероятности перехода нашего пользователя по петельному линку, добавим в нашу модель вероятность перехода 1-γ_i в соответствии с классической формулой Google PageRank. Несмотря на большое обилие всевозможных модификаций данного алгоритма, все они достигают своей основной цели — поток голосующей способности к штрафным сайтам ограничивается.

3. Алгоритм весовых переходов

В предыдущей части мы уже занимались обработкой штрафных страниц (например, с кодами ответа HTTP 404 Not Found) на нашем графе под видом висячих узлов и минимизировали их воздействие (см. раздел «Обработка висячих страниц»), но в отличие от стандартной процедуры, которая предполагает последующее равномерное/выборочное перераспределение веса виртуального узла (n+1), мы предлагаем альтернативный механизм смещенного перераспределения, при котором оштрафованные документы получают меньшее значение голосующей способности. Для этого, используя приведенные выше обозначения для хороших и плохих документов, взвесим исходящие ссылки из виртуального узла к качественному документу в С (или ко всему набору) с коэффициентом p и к штрафному узлу с pg_i /(g_i + b_i), где p подбирается таким образом, что сумма весов всех вершин нашего графа будет давать 1.

4. Алгоритм BHITS

Ниже представлена модификация классического алгоритма HITS [5], которая является производной от случайного блуждания пользователя как в прямом, так и обратном направлении, однако, наряду с этим, основными его отличительными характеристиками от более известного прототипа является то, что работа BHITS осуществляется вне зависимости от запросов и рангов интернет-документов. В этом смысле он больше напоминает методологию описанную SALSA [6] или в [7], но суть его, как и во всех описанных ранее алгоритмах, заключается в некотором снижении голосующей способности тех web-документов, которые цитируют штрафные сайты. Соответственно случайному серфингу нашего пользователя, каждый последующий шаг вперед будет рассчитываться в нашем случае по аналогии с PR, а в случае попадания на висячий узел мы будем вынуждены вернуться назад. Важно отметить, что возврат на невисячем узле обеспечивается в нашей модели посредством петельного линка, а процедура возвращения с висячего разделяется на два типа. Для первого из них мы будем передавать свой голос виртуальному узлу (справедливо для попадания на штрафной документ), а для второго типа, который учитывает нештрафной ресурс, — равномерно распределять текущую оценку страницы между всеми обратными ссылками. Мы полагаем, что все сайты представляет собой связанные между собой цифровые документы, что, безусловно, подтверждается нашими сканнерами, однако нам также следует предположить, что нашим роботам-индексаторам известны все внутренние ссылки, связывающие данный набор разрозненных интернет-страниц, поскольку в противном случае алгоритм не сможет быть запущен. Поэтому, мы будем учитывать только сильные связи, и любая страница без входящих ссылок будет расцениваться в рамках поставленной перед нами задачи как штрафная. Взамен операции возвращения по входящим на них ребрам, как и в классической модели PR, будем применять случайную телепортацию на любое множество документов в сети. Результатом этого процесса становится как «возврат» голосующей способности тем сайтам, которые цитируют из своего контента нештрафные странички, так и перераспределение рангов, присваиваемых некачественным web-узлам. Если матрицу, описывающую PageRank марковского процесса, обозначить за Р, тогда матрица для алгоритма BHITS обозначается как BP, в которой B есть ни что иное, как матрица кодирующая обратный шаг пользователя. С учетом того, что штрафные страницы, как правило, оказываются в самом конце поисковой выдачи, то давайте обозначим полустепень захода узла j через δ(j), а вероятность перехода нашего пользователя с j на i через b_ij = 1/δ(j). Тогда, для описания обратного шага мы получим следующую матрицу:

BP является матрицей переходных вероятностей для цепи Маркова по той простой причине, что она является продуктом двух прочих стохастических матриц. Эта марковская цепь будет создавать стационарное распределение вероятностей, то есть такое распределение, которое не будет меняться с течением времени, но вполне очевиден тот факт, что для тех веб-документов, которые ссылаются на штрафные сайты/страницы, вероятность будет меньшей, нежели чем в стандартном алгоритме Google PR.

Проблематика практической реализации

Учитывая все возрастающий объем глобальной сети, проблема эффективного практического внедрения любого алгоритма ранжирования является достаточно существенной. Первая тройка описанных выше алгоритмов, которые основываются на модификации классической модели Google PageRank, а если говорить более конкретно, на изменениях матрицы А, не потребует от нас значительных вычислительных затрат. Почему? Дело в том, что все эти дополнения по своей сути носят локальный характер и, кроме соблюдения требований нормализированности матрицы, изменения записей в i-строке будут зависеть только от количества штрафных и хороших исходящих ссылок из i-го узла, b_i и g_i. Отсюда, у нас появляется возможность не только предварительно вычислять модифицированные матрицы за линейное время (вектор b и g), но и вносить все необходимые изменения в процессе наших итераций. Четвертый алгоритм BHITS представляется для практического внедрения куда более сложным, и основная его проблема заключается в том, что он требует учёта всех существующих в интернете висячих узлов. Вспомнив же, что в ходе нашей исследовательской работы нами было проиндексировано только 1 из 5 млрд. HTML-страниц (думается, что число висячих узлов в пять раз превышает обнаруженный нами объем), сделаем логичный вывод о том, что такой подход явно не подходит для крупномасштабной реализации и нам следует использовать методологию, базирующуюся на PageRank.

Алгоритм HostRank

До текущего момента мы в основном затрагивали висячие узлы, игнорируя прочие особенности веба, которые также могут быть учтены при подсчете PR документов. Оригинальная парадигма данного алгоритма моделировала сеть как некоторый набор страничек, по которым пользователь может перемещаться как посредством прохождения по ссылкам, так и телепортируясь на случайные узлы по причине утрата интереса к существующим и/или для выхода на сайты прочих тематик. Безусловно, она была достаточно упрощенной и не могла отразить реального пользовательского поведения в полном смысле этого слова, в частности можно сослаться на то, что пользователь не может осуществлять равномерный случайный выбор документов или даже быть осведомленным в доступном для него наборе URL-адресов. Ряд недавних исследований предполагает, что подавляющий процент пользовательских сессий начинается с обращения к поисковым системам, далее идет сам вопрос и следование по предложенным ссылкам на странице поисковой выдачи. Продолжительность сессии складывается из прохождения по ссылкам на оригинальный веб-документ и ознакомления с его содержимым, возможного возвращения к странице результатов и/или переформулировки запроса до тех пор, пока у пользователя поисковой машины сохраняется потребность в получении необходимой ему информации. Однако в случае начала новой сессии, пользователь уже не обращается к случайному узлу, а возвращается к поисковой машине для формулирования очередного запроса и именно это поведение исключается в классической парадигме Google PageRank, особенно в той части, что в пользовательском перемещении был заложен неоднородный по своему распределению набор всевозможных узлов.

Еще одной вариацией на тему модели интернет серфинга, несколько позже положенного в классический PageRank, является то, что пользователь выбирает для своего случайного перехода страницу из ряда трастовых узлов, в принципе это то, о чем мы писали в части алгоритма доверия Google TrustRank. Впоследствии, данная схема была использована как средство для увеличения персонализирующей составляющей (алгоритм Topic-Sensitive PageRank [1]) поискового механизма Google. Согласимся, что это было бы эффективной моделью для тех пользователей, которые осуществляют свое перемещение к каким-либо URL-адресам из набора имеющихся в их браузере закладок или являются частью аудитории крупных интернет-порталов. Однако в случае с теми же самыми порталами мы будем иметь неравномерное распределение рандомных перемещений, поскольку такие интернет-ресурсы очень быстро меняют свое содержимое и генерируют огромное число новых ссылок в краткий период времени, которых с момента последнего визита пользователя просто не существовало! В [8] отмечается, что вероятностные значения, присваиваемые алгоритмом PageRank распадаются в соответствии со степенным законом распределения вероятностей, и это необходимо учитывать в модели развивающегося веба. Ими было предположено, что телепортация осуществляется равномерно на случайно избираемую страничку.

На Рис. 16 показано распределение значений PR, вычисленного посредством трастовой и рандомной телепортации (0.5) к одному из авторитетных сайтов (microsoft.com и yahoo.com). И хотя наши наблюдения во многом подтверждают данные [8], мы видим, что стратегия телепортации оказывает глубокое влияние на гипотетическое распределение вероятностей для попадания пользователей на страницу сайта. В частности, если ссылочная структура веба была бы иерархической, в которой каждая предыдущая страница, связанная с последующей, тогда бы распределение уменьшалось экспоненциально с продвижением вглубь иерархии, а окончание (кривой) распределения показывало бы результаты более близкие к экспоненциальному, нежели чем к степенному закону распределения. Попутно заметим, что было бы очень заманчиво предлагать пользователям перемещаться по страницам на основании присваиваемых им значений PR.

Использование иерархической структуры

Одним из предположений, сделанных в оригинальной работе Lawrence Page и Sergey Brin [9] было случайное перемещение к цифровым документам верхнего уровня страниц сайта, что во многом увязывается с нашей склонностью восприятия информации, построенной по иерархическому принципу. Кроме того, исходя из отсканированных нами страниц мы обнаружили, что 62,4% проиндексированных ссылок оказались внутренними, а оставшиеся исходящие линки, как правило, вели на главные страницы веб-сайтов (см. Табл. 2)

Глубина	Доля
0	0.75
1	0.089
2	0.035
3	0.017
4	0.005
5	0.002
6	0.001

Данные структурные особенности веба показывают нам очень высокий уровень компрессии для графа хостов и позволяют использовать блок-ориентированный подход для ускорения сходимости Google PageRank. С учетом иерархической структуры самих сайтов, а также того факта, что в качестве источника цитирования вебмастера предпочитают ставить обратную ссылку не на какую-либо внутреннюю страницу сайта, а именно на главную, мы считаем необходимым исследовать страницы интернет-сайтов как элементы единого организма, а также присваивать им ранговые значения, исходя из информационной ценности. Для данных расчетов используется алгоритм HostRank. Говоря более формально, в том случае, если имеется такой URL на хосте S, которой ссылается на URL хоста D (имена хостов представляют собой узлы на нашем графе), то мы строим между ними ориентированное ребро. Помимо этого, мы можем назначить ребрам между хостами некоторые весовые значения (в сумме они будут давать нам единицу), которые отразят нам количество ссылок с URL-источника к URL-цели. Затем, в первоначальном подсчете PR заменим этими весами элементы a_ij = 1/d_j. Несмотря на то, что включение реберных весов потребует от нас дополнительной информации для каждого ребра данного графа, они могут улучшить качество тех поисковых результатов, которые отражают сильные связи.

В качестве альтернативы мы могли бы использовать веса, состоящие из числа обособленных URL-целей. По той простой причине, что мы имеем дело с малыми графами (в нашей выборке имелось около 48 млн. хостов, хотя многие из них не были проиндексированы по разным причинам), вычисление HostRank оказывается существенно простой задачей нежели чем самого Google PageRank, а следовательно он может быть объединен с другими оптимизационными подходами, опирающиеся на более сложные алгоритмы линейной алгебры; быть более эффективным, чем диспетчеризация ввода/вывода (I/O) и аппроксимаций, использующих только локальную информацию.

networkx.algorithms.link_analysis.pagerank_alg.pagerank — документация NetworkX 2.4

Домашняя страница проекта | Исходный код NetworkX

2,4

Установить
Учебник
Номер ссылки
- Введение
- Типы графиков
- Алгоритмы
  - Аппроксимации и эвристика
  - Ассортативность
  - Астероидальный
  - Двудольный
  - Граница
  - Мосты
  - Центральность
  - Цепи
  - хордовый
  - Клика
  - Кластеризация
  - Раскраска
  - Коммуникабельность
  - Сообщества
  - Компоненты
  - Возможности подключения
  - Ядра
  - Покрытие
  - циклов
  - Отрубы
  - Направленные ациклические графы
  - Меры расстояния
  - Дистанционные регулярные графики
  - Доминирование
  - Доминирующие наборы
  - Эффективность
  - Эйлерова
  - Потоки
  - Графическая последовательность градусов
  - Иерархия
  - Гибрид
  - Изоляты
  - Изоморфизм
  - Анализ ссылок
    - PageRank
    - Просмотров
  - Прогнозирование связи
  - Самый низкий общий предок
  - Соответствие
  - Несовершеннолетние
  - Максимальный независимый набор
  - неслучайность
  - Мораль
  - Классификация узлов
  - Операторы
  - Планарность
  - Планарный чертеж
  - Взаимность
  - Rich Club
  - Кратчайшие пути
  - Меры сходства
  - Простые пути
  - Маленький мир
  - с метрическая
  - Разбрызгиватели
  - Конструкционные отверстия
  - Своп
  - Турнир
  - Переход
  - Дерево
  - Триады
  - Жизнеспособность
  - Ячейки Вороного
  - Индекс Винера
- Функции
- Генераторы графиков
- Линейная алгебра
- Преобразование в другие форматы данных и обратно
- Перемаркировка узлов
- Чтение и запись графиков
- Рисунок
- Случайность
- Исключения
- Коммунальные услуги
- Глоссарий
Руководство разработчика
Протокол выпуска
Лицензия
кредитов
Цитирование
Библиография
Примеры

NetworkX
Документы »
Ссылка »
Алгоритмы »
Анализ ссылок »
networkx.алгоритмы.link_analysis.pagerank_alg.pagerank
.
机器学习手记 [8] — Python Networkx 库中 PageRank 算法实现源码分析 _ 虾米 ning 的博客 -CSDN 博客 _networkx pagerank

对 Page 讲解的很多，代码也很多很杂，所以为了质量的 PageRank 算法的实现，
阅读了 Python Networkx 库上多余删除了，有兴趣可以直接下这个库查看源码
源码的地址在 http://networkx.github.io/download.html
体的 pagerank 代码我已经上传到网盘在 http://pan.baidu.com/s/1ntOafh4

PageRank 最主要的地方在于对两个问题的解决，一个是 dangling nodes ，一个 spider trap
前者是说，的链接，图就是出0003 0。
者是说，进入到一个网页或者几个网页单个网页，或者几个网页之间引用，这样资源进去后就一直在里面，出不来， раковина ранга 问题。
对于 болтается узлы 我们可以计算他们的 PR 贡献值, 然后均分给所有节点
spider trap ，需要用心灵漂移的方式去。
Networkx 库里面，主要 PageRank 的方法（PS 为什么是三种我直观觉得是因为这是三个人写的，因为连某些效果完全相同的初始化语句，三个写的都不一样）
1 pagerank 函数
以图结构为基础
通过迭代收敛方法计算 PR 值 (PageRank 值)
2 pagerank_numpy 函数
将图转换为 numpy 邻接矩阵
通过 google_matrix numpy的主特征向量，即为所 PR 值
3 pagerank_scipy 函数
将图转换 sparse 稀疏矩阵
通过迭代收敛方法 PR 值
"" "Анализ PageRank структуры графа.«»» # Лицензия BSD. # NetworkX: http: //networkx.lanl.gov/ импортировать networkx как nx @not_implemented_for ('мультиграф') def pagerank (G, альфа = 0,85, персонализация = Нет, max_iter = 100, tol = 1.0e-6, nstart = None, weight = 'weight', dangling = Нет): "" "Возвращает PageRank узлов в графе. параметры ----------- G: график Граф NetworkX.在 PageRank 算法里面是有向图 альфа: float, необязательно 稳定系数, 默认 0.85, 心灵漂移 телепортация 系数，用于解决 паучья ловушка 问题 персонализация: dict, необязательно 个性化向量，确定在分配中各个节点的权重格式举例，比如四个点的情况: {1: 0.25,2: 0,25,3: 0,25,4: 0,25} 默认个点权重相等，给某个节点分配些权重，需保证重和为 1. max_iter: целое число, необязательно 最大迭代次数 tol: float, необязательно 迭代阈值 nstart: словарь, необязательно 整个网络各节点 PageRank 初始值 вес: ключ, по желанию 各边权重 dangling: dict, необязательно 存储的是 dangling 边的信息 ключ --dangling 边的尾节点，也就是 dangling node 节点 значение --dangling 边的权重 PR 按多大程度将资源分配给 dangling node 是根据 personalization 向量分配的 Это должно быть выбрано, чтобы привести к неприводимому переходу матрица (см. примечания в разделе google_matrix).Часто бывает, что dangling dict должен быть таким же, как dict персонализации. Ноты ----- 特征值计算是通过迭代方法进行的，不能保证收敛，当超过最大迭代次数时还不能减小到值就会报错 «»» # 步骤一：图结构的准备 ------------------------------------------ -------------------------------------- если len (G) == 0: возвращение {} если не G.is_directed (): D = G.to_directed () еще: D = G # Создайте копию в (справа) стохастической форме W = nx.stochastic_graph (D, вес = вес) N = W.количество_узлов () # 确定 PR 向量的初值 если nstart равен None: x = dict.fromkeys (W, 1.0 / N) # 和为 1 еще: # Нормализованный вектор nstart s = float (сумма (nstart.values ())) x = dict ((k, v / s) для k, v в nstart.items ()) если персонализация отсутствует: # Назначьте единый вектор персонализации, если он не задан p = dict.fromkeys (W, 1.0 / N) еще: missing = set (G) - установить (персонализация) если отсутствует: поднять NetworkXError ('Словарь персонализации' 'должно иметь значение для каждого узла.' 'Отсутствующие узлы% s'% отсутствуют) s = float (сумма (personalization.values ())) p = dict ((k, v / s) для k, v в personalization.items ()) # 归一化处理 если висячий - Нет: # Использовать вектор персонализации, если висячий вектор не указан dangling_weights = p еще: отсутствует = набор (G) - набор (болтается) если отсутствует: поднять NetworkXError ('Словарь висящих узлов' 'должно иметь значение для каждого узла.' 'Отсутствующие узлы% s'% отсутствуют) s = float (сумма (dangling.values ())) dangling_weights = dict ((k, v / s) для k, v в dangling.items ()) dangling_nodes = [n для n в W, если W.out_degree (n, вес = вес) == 0,0] #dangling_nodes dangling 节点 #danglesum dangling 节点 PR 总值 #dangling 初始化默认为 персонализация #dangling_weights 根据 dangling 而生成，决定 dangling node 资源如何分配给全局的矩阵 # 迭代计算 ----------------------------------------------- --------------------- # PR = альфа * (A * PR + висящий 分配) + (1-альфа) * 平均分配 # 就是三部分， A * PR 其实是我们用图分配的， dangling 分配则是 dangling node 的 PR 值进行， (1-alpha) 分配则是天下为公的的的的 # 其实通俗的来说，我们可以 PageRank 看成抢夺大赛，有三种抢夺机制。 # 1 ， A * PR 这种是自由分配，大家都愿意参与竞争交流的分配 # 2 ， болтаться 是强制分配，有点类似打倒土豪分田地的感觉，你不参与自由市场那好，我们就特地帮你强制分。 # 3 ，平均分配，其实有个大家实现共产主义了，不让 паучья ловушка 这种 раковина ранга 的节点捞太多油水，其实客观 dangling 分配。 # 从图和矩阵的角度来说，可以这样理解，我们这个矩阵可以看出是个有向图 # 矩阵要收敛 -> 矩阵有唯一解 -> n 阶方阵对应有向图是强连通的 -> 两个节点相互可达， 1 能到 2,2 能到 1 # 如果是个强连通图，就是我们上面说的第 1 种情况，自由竞争，我们可以确定是收敛的 # 不然就会有 ловушка для пауков 造成 раковина ранга 问题 для _ в диапазоне (max_iter): xlast = x x = dict.fromkeys (xlast.keys (), 0) #x 初值 danglesum = alpha * sum (xlast [n] для n в dangling_nodes) # 第 2 部分：计算 dangling_nodes 的 PR 总值 для n в x: для nbr в W [n]: x [nbr] + = alpha * xlast [n] * W [n] [nbr] [вес] # 第 1 部分: 将节点 n 的 PR 资源分配给各个节点，循环之 для n в x: x [n] + = danglesum * dangling_weights [n] + (1.0 - alpha) * p [n] # 第 3 部分：节点 n висячие узлы 和均分的值 # 迭代检查 err = sum ([abs (x [n] - xlast [n]) для n в x]) если err
. Висячий модификатор | Что такое свисающий модификатор? Крэйг Шрайвс Модификатор свисания Висячий модификатор - это модификатор, изменять который нечего. Модификатор предназначен для описания слова или уточнения его значения. Модификатор не может этого сделать, если слово не существует. Другими словами, висячий модификатор - это ошибка, вызванная неспособностью использовать слово, которое модификатор должен изменять. Понял? Сделайте быстрый тест. Простые примеры висящих модификаторов Все свисающие модификаторы на этой странице затенены. При входе в комнату мой взгляд привлек скелет. (Ничто в этом предложении не вошло в комнату. Скелет не попал. Мой глаз - нет.) Придерживаясь строгой диеты, ее вес резко снизился. (Ничто в этом предложении не соответствовало строгой диете. Ее вес - нет.) Другие термины для модификатора висячих Висячие модификаторы также известны как «висячие модификаторы», «плавающие модификаторы» или «висячие причастия». Висячие модификаторы контрастируют с: Неуместные модификаторы.Неуместный модификатор не имеет четкой ссылки на то, что он предназначен для изменения. Джон ударил мужчину кремовым тортом . (Мужчина получил кремовый торт в лицо или это был тот, у кого кремовый торт? При неуместном модификаторе модифицируемая вещь присутствует (это то, чем он отличается от модификатора висячих), но модификатор не связывает к этому ясно.) Модификаторы прищуривания. Модификатор прищуривания может реально изменить текст слева или справа. Говорить быстро людей раздражает. (Быстрая речь раздражает людей или разговор быстро раздражает людей?) Помните, что с модификатором dangling модифицируемая вещь отсутствует. Сводка видео Вот короткое видео, в котором резюмируется этот урок о модификаторах dangling: Реальные примеры висящих модификаторов Висячие модификаторы обычно возникают из-за того, что писатели забегают вперед.Они предполагают, что то, о чем они говорят, настолько очевидно из контекста, что забывают об этом упомянуть. Прочитав ваше письмо, мой кот останется дома, пока утята не улетят. (Совершенно ясно, что владелец кошки прочитал письмо, но владелец не упоминается. Следовательно, «прочитав ваше письмо» - это висячий модификатор. Это не относится ни к чему в предложении. Ни кошки, ни утята не могут читать. ) Правильная версия будет: Прочитав Ваше письмо, мы оставим кошку дома, пока утята не улетят. (Здесь «прочитав твое письмо» изменяет «мы».) Вот еще один висячий модификатор: Поместив мой комплект в три огромных сумки, мой маленький Джек Рассел мог сказать, что приближается долгое путешествие. (Ничто в этом предложении не упаковывало комплект. Поэтому «Упаковать мой комплект в три огромных сумки» - это модификатор висящего положения. Он ни к чему не применим.) Правильная версия будет: Помещая свой комплект в три огромных сумки, я знал, что мой маленький Джек Рассел мог сказать, что приближается долгое путешествие. Это может быть сложно. Посмотрите на этот пример модификатора dangling: Скрупулезность и пунктуальность Дэвида достойны восхищения. (Здесь отсутствует слово «Дэвид», потому что «Дэвид» не является заглавным существительным во фразе «трудовая этика Дэвида». «Дотошный и пунктуальный» изменяет заглавное существительное «этика». Предложение говорит нам, что трудовая этика Дэвида дотошен и пунктуален, что нелогично.) Правильная версия будет: Дотошный и пунктуальный, Дэвид обладает замечательной рабочей этикой. (Здесь модификатор «Дотошный и пунктуальный» изменяет «Дэвида» должным образом, а не «трудовую этику Дэвида».) Иногда модификатор может немного болтаться. Это происходит, когда изменяемое слово присутствует, но не рядом с его модификатором. Злобные вонючие существа с огромными бивнями, экипаж корабля с трудом прогнал самцов моржей с пляжа. (На самом деле это неуместный модификатор. Модификатор не болтается полностью, потому что модифицируемый объект («самцы моржей») присутствует.) Подробнее о неуместных модификаторах. Прочтите о модификаторах прищуривания. Действительно ли свисающий модификатор является ошибкой? Висячие модификаторы обычно не приводят к двусмысленности, потому что отсутствующий термин почти всегда подразумевается или даже упоминается либо в недавнем предложении, либо в форме притяжательного детерминатора. Давайте еще раз рассмотрим два приведенных выше примера. После строгой диеты резко похудела. (Мы отметили этот пример как неправильный, но слово «она» относится к человеку, соблюдающему строгую диету.Поэтому технически упоминается модифицируемая вещь.) Прочитав ваше письмо, мой кот останется дома, пока утята не улетят. (В этом примере слово «мой» относится к человеку, прочитавшему письмо. Таким образом, технически упоминается изменяемый объект.) Это используется некоторыми грамматиками, чтобы заявить, что большинство висящих модификаторов (то есть те, в которых модифицируемая вещь достаточно очевидна) не являются ошибками. Почему меня должны волновать свисающие модификаторы? Несмотря на то, что думают некоторые грамматики, мы думаем, что использование висячего модификатора скажет вашим читателям, разбирающимся в грамматике, что вы плохо мыслите. Кроме того, знание модификаторов свисания позволяет вам сообщить своему боссу или вашим товарищам, что они использовали модификатор свисания, что, несомненно, является победой в чьей-либо книге. С точки зрения его способности набирать очки, он, вероятно, превосходит только модификатор прищуривания. Чтобы убедиться, что вы сами не используете модификатор висячие, предполагайте, что любой модификатор, который вы используете, является висячим, пока вы не прибьете его к термину, который он модифицирует. Проходя по кладбищу, деревья превратились в длиннопалых упырей. (Если бы вы писали это предложение, у вас должны были прозвучать предупреждающие колокола, прежде чем вы достигнете конца «деревьев».) Вот несколько версий без модификатора dangling: Прогуливаясь по кладбищу, я увидел, что деревья превратились в длиннопалых упырей. Когда я шел по кладбищу, деревья превратились в длиннопалых упырей. (Часто лучше обойти модификатор, изменив его формулировку.) Чтобы избежать неуместного модификатора, поместите свой модификатор рядом (обычно слева) от термина, который он изменяет.Например: При переходе дороги автобус сбил Джанет. ("Джанет" присутствует. Следовательно, это неуместный модификатор, т.е. он не полностью свисает.) Джанет, переходя дорогу, сбила автобус. (Это один из вариантов размещения модификатора рядом с «Джанет». Он намного аккуратнее.) Ключевые моменты Предположим, что ваш модификатор болтается, пока вы не убедитесь, что это не так. Поместите модификатор рядом с термином, который он изменяет (обычно сразу слева). Помогите нам улучшить грамматику Monster Вы не согласны с чем-то на этой странице? Вы заметили опечатку? Сообщите нам, используя эту форму. См. Также Что такое модификаторы? Что такое неуместный модификатор? Что такое модификатор прищуривания? Что такое ограничивающий модификатор? Словарь грамматических терминов .

как правильно оптимизировать ваш сайт

Desktop vs. SaaS — что выбрать?

Структура страниц

Программное исполнение

Контент

No birds: Развитие PageRank

PageRank с математической стороны

Примечание

Висячие узлы (dangling nodes)

Метод удаления

Считать связанными со всеми другими страницами

Шаг назад (step back)

Петля (self-link)

Телепортация

Ускорение метода степеней

Метод Гаусса-Зейделя (Gauss-Seidel method)

Методы экстраполяции (Extrapolation methods)

Адаптивный метод (Adaptive method)

Метод блочной структуры (Block Structure Method)

Численные методы

Параллелизация

Оптимизация ввода-вывода

Эволюция графа

Персонализация

Темы, которые будут рассмотрены в следующих постах

Оптимизация ввода-вывода

Siterank

Технический аудит сайта программой Netpeak Spider

Настройка Netpeak Spider

Как Netpeak Spider отображает информацию о скорости

Проверка заголовков, мета-тегов, альтов

Висячий узел – фишка Netpeak Spider

Работа с техническими параметрами

Заключение

Две техники SEO, которые дадут рост трафика уже через месяц. Читайте на Cossa.ru

Техника 1. Перелинковка сайта на основе PageRank

Алгоритм перелинковки сайта

Техника 2. Подготовка текстов на основе алгоритма семантического анализа

Результат

Вывод

Анализ сайта на ошибки: онлайн программа Netpeak Spider

Высокая скорость сканирования сайтов

Обновление таблицы после исправления ошибок и удаление URL

Новая вкладка Параметры

Сегментация и дашборд

Удобная выгрузка отчетов

Дополнительные инструменты

Сохранение шаблонов настроек

Виртуальный robots.txt

Анализ списка URL

Быстрый поиск по таблице

Удобный фильтр

Заключение

SEMPRO 2018: SEO-эксперименты с Дмитрием Шаховым

Вредны ли висячие узлы?

Вредны ли ссылки на 404?

Полезны ли сквозные входящие ссылки?

Какие символы и теги разбивают пассажи?

Как учитываются в поиске Alt и другие атрибуты изображения

HostRank или PageRank, вычисляемый по графу хостов

Мёртвые (битые) ссылки в построении выдачи

Небольшой пример

Ссылки на штрафные узлы

1. Алгоритм Возврата

2. Петельный алгоритм

3. Алгоритм весовых переходов

4. Алгоритм BHITS

Проблематика практической реализации

Алгоритм HostRank

Использование иерархической структуры

networkx.algorithms.link_analysis.pagerank_alg.pagerank — документация NetworkX 2.4

机器 学习 手记 [8] — Python Networkx 库 中 PageRank 算法 实现 源码 分析 _ 虾米 ning 的 博客 -CSDN 博客 _networkx pagerank

Висячий модификатор | Что такое свисающий модификатор?

Модификатор свисания

Простые примеры висящих модификаторов

Другие термины для модификатора висячих

Сводка видео

Реальные примеры висящих модификаторов

Действительно ли свисающий модификатор является ошибкой?

Почему меня должны волновать свисающие модификаторы?

机器学习手记 [8] — Python Networkx 库中 PageRank 算法实现源码分析 _ 虾米 ning 的博客 -CSDN 博客 _networkx pagerank

`Добавить комментарий Отменить ответ`