Баллистика корабельной артиллерии — наука о движении тел, брошенных в пространстве.

 Рис. 1. Артиллерия линейного корабля «Марат»
Рис. 1. Артиллерия линейного корабля «Марат»Баллистика (от греч. βάλλειν — бросать) — наука о движении тел, брошенных в пространстве, основанная на математике и физике. Она занимается, главным образом, исследованием движения снарядов, выпущенных из огнестрельного оружия, ракетных снарядов и баллистических ракет.
Основные понятия

 Рис. 2. Элементы стрельбы корабельной артиллерии
Рис. 2. Элементы стрельбы корабельной артиллерииОсновной задачей стрельбы является попадание в цель. Для этого орудию необходимо придать строго определённое положение в вертикальной и горизонтальной плоскостях. Если навести орудие так, чтобы ось канала ствола была направлена на цель, то в цель мы не попадём, так как траектория полёта снаряда будет всегда проходить ниже направления оси канала ствола, снаряд до цели не долетит. Для формализации терминологического аппарата рассматриваемой тематики, введём основные определения, используемые при рассмотрении теории артиллерийской стрельбы.
Точкой падения называется точка пересечения траектории с горизонтом орудия.
Горизонтом орудия называется горизонтальная плоскость, проходящая через точку вылета.
Линией возвышения называется продолжение оси канала ствола наведённого орудия.
Линией бросания ОВ называется продолжение оси канала ствола в момент выстрела. В момент выстрела орудие вздрагивает, вследствие чего снаряд бросается не по линии возвышения ОА, а по линии бросания ОВ (см. рис. 2).
Линией цели ОЦ называется линия, соединяющая орудие с целью (см. рис. 2).
Линией прицеливания (визирования) называется линия, идущая от глаза наводчика через оптическую ось прицела в точку наводки. При стрельбе прямой наводкой, когда линия прицеливания направлена в цель, линия прицеливания совпадает с линией цели.
Линией падения называется касательная к траектории в точке падения.

 Рис. 3. Стрельба по вышележащей цели
Рис. 3. Стрельба по вышележащей цели 
 Рис. 4. Стрельба по нижележащей цели
Рис. 4. Стрельба по нижележащей целиУглом возвышения (греческая фи)
Дальность стрельбы из орудия зависит от угла возвышения и условий стрельбы. Следовательно, чтобы добросить снаряд до цели, надо орудию придать такой угол возвышения, при котором дальность стрельбы будет соответствовать расстоянию до цели. В таблицах стрельбы указано какие углы прицеливания нужно придать орудию, чтобы снаряд полетел на нужную дальность.
Углом бросания (греческая тета ноль) называется угол между линией бросания и горизонтом орудия (см. рис. 2).
Углом вылета (греческая гамма) называется угол между линией бросания и линией возвышения. В морской артиллерии угол вылета имеет малую величину и его иногда в расчёт не принимают, полагая, что снаряд бросается под углом возвышения (см. рис. 2).
Углом прицеливания (греческая альфа) называется угол между линией возвышения и линией прицеливания (см. рис. 2).
Углом места цели (греческая эпсилон) называется угол между линией цели и горизонтом орудия. При стрельбе корабля по морским целям угол места цели равен нулю, так как линия цели направлена по горизонту орудия (см. рис. 2).
Углом падения (греческая тета с латинской буквой с) называется угол между линией цели и линией падения (см. рис. 2).
Углом встречи (греческая мю) называется угол между линией падения и касательной к поверхности цели в точке встречи (см. рис. 2).
От значения величины этого угла сильно зависит стойкость брони корабля, по которому ведётся огонь, к пробитию снарядами. Очевидно, чем ближе этот угол к 90 градусам, тем вероятность пробития выше, верно и обратное.
Плоскостью стрельбы называется вертикальная плоскость, проходящая через линию возвышения.
При стрельбе корабля по морским целям линия прицеливания направлена по горизонту, в этом случае угол возвышения равен углу прицеливания.
При стрельбе корабля по береговым и воздушным целям угол возвышения равен сумме угла прицеливания и угла места цели (см. рис. 3).
При стрельбе береговой батареи по морским целям угол возвышения равен разности угла прицеливания и угла места цели (см. рис. 4).
Таким образом, величина угла возвышения равна алгебраической сумме угла прицеливания и угла места цели. Если цель выше горизонта, угол места цели имеет знак «+», если цель ниже горизонта, угол места цели имеет знак «-«.
Влияние сопротивления воздуха на траекторию полёта снаряда
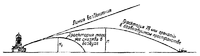
 Рис. 5. Изменение траектории полёта снаряда от сопротивления воздуха
Рис. 5. Изменение траектории полёта снаряда от сопротивления воздухаТраектория полёта снаряда в безвоздушном пространстве представляет собой симметричную кривую линию, называемую в математике параболой. Восходящая ветвь совпадает по форме с нисходящей ветвью и, следовательно, угол падения равен углу возвышения.
При полёте в воздухе снаряд расходует часть скорости на преодоление сопротивления воздуха. Таким образом, на снаряд в полёте действуют две силы — сила тяжести и сила сопротивления воздуха, которая уменьшает скорость и дальность полёта снаряда, как проиллюстрировано на рис. 5. Величина силы сопротивления воздуха зависит от формы снаряда, его размеров, скорости полёта и от плотности воздуха. Чем длиннее и заострённее головная часть снаряда, тем сопротивление воздуха меньше. Форма снаряда особенно сказывается при скоростях полёта, превышающих 330 метров в секунду (то есть при сверхзвуковых скоростях).

 Рис. 6. Недальнобойный и дальнобойный снаряды
Рис. 6. Недальнобойный и дальнобойный снарядыСила сопротивления воздуха пропорциональна скорости его полёта, но не прямо пропорциональна. Зависимость формализуется более сложно. Вследствие действия сопротивления воздуха у траектории полёта снаряда восходящая ветвь длиннее и отложе нисходящей. Угол падения больше угла возвышения.
Помимо уменьшения дальности полёта снаряда и изменения формы траектории, сила сопротивления воздуха стремится опрокинуть снаряд, как это видно из рис. 7.

 Рис. 7. Силы, действующие на снаряд в полёте
Рис. 7. Силы, действующие на снаряд в полётеСледовательно, невращающийся продолговатый снаряд под действием сопротивления воздуха будет переворачиваться. При этом снаряд может попасть в цель в любом положении, в том числе боком или дном, как показано на рис. 8.

 Рис. 8. Вращение снаряда в полёте под действием силы сопротивления воздуха
Рис. 8. Вращение снаряда в полёте под действием силы сопротивления воздухаЧтобы снаряд в полёте не переворачивался, ему придают вращательное движение с помощью нарезов в канале ствола.
Если же рассмотреть воздействие воздуха на вращающийся снаряд, то можно увидеть, что это приводит к боковому отклонению траектории от плоскости стрельбы, как изображено на рис. 9.

 Рис. 9. Деривация
Рис. 9. ДеривацияДеривацией называется отклонение снаряда от плоскости стрельбы вследствие его вращения. Если нарезы вьются слева вверх направо, то снаряд отклоняется вправо.
Влияние угла возвышения и начальной скорости снаряда на дальность его полёта
Дальность полёта снаряда зависит от углов возвышения, под которыми он бросается. Увеличение дальности полёта с увеличением угла возвышения происходит только до некоторого предела (40-50 градусов), при дальнейшем увеличении угла возвышения, дальность начинает уменьшаться.
Углом предельной дальности называется угол возвышения, при котором получается наибольшая дальность стрельбы при данной начальной скорости и снаряде.
При стрельбе в безвоздушном пространстве наибольшая дальность полёта снаряда получается при угле возвышения 45 градусов. При стрельбе в воздухе величина угла предельной дальности отличается от этого значения и у разных орудий бывает неодинаковой (обычно меньше 45 градусов). Для сверхдальнобойной артиллерии, когда снаряд значительную часть пути летит на большой высоте в сильно разреженном воздухе, угол предельной дальности бывает более 45 градусов.
Для орудия данного образца и при стрельбе определенным типом боеприпаса каждому углу возвышения соответствует строго определенная дальность полёта снаряда. Следовательно, чтобы забросить снаряд на нужное нам расстояние, необходимо орудию придать угол возвышения, соответствующий этому расстоянию.
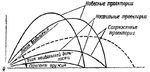
Траектории снарядов, выпущенных при углах возвышения меньших, чем угол предельной дальности, называются настильными траекториями.
Траектории снарядов, выпущенных при углах возвышения больших, чем угол предельной дальности, называются ‘
Рассеивание снарядов
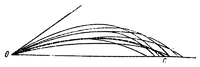
 Рис. 10. Рассеивание снарядов
Рис. 10. Рассеивание снарядовЕсли из одного и того же орудия, одинаковым боеприпасом, при одном и том же направлении ствола орудия, при одинаковых, на первый взгляд, условиях произвести несколько выстрелов, то снаряды не попадут в одну точку, а полетят по разным траекториям, образуя пучок траекторий, как проиллюстрировано на рис. 10. Это явление называется рассеиванием снарядов.
Причиной рассеивания снарядов является невозможность достижения абсолютно одинаковых условий для каждого выстрела. В таблице приведены основные факторы, вызывающие рассеивание снарядов и возможные пути уменьшения этого рассеивания.
| Основные группы причин рассеивания | Условия, порождающие причины рассеивания | Меры борьбы за уменьшение рассеивания |
|---|---|---|
| 1. Разнообразие начальных скоростей |
(размеры и расположение ведущего пояска, досылка снарядов).
|
|
| 2. Разнообразие углов бросания |
|
|
| 3. Разнообразие условий в полёте снаряда | Разнообразие влияния воздушной среды (плотность, ветер). | — |
Площадь, на которую падают снаряды, выпущенные из орудия при одном и том же направлении канала ствола, называется площадью рассеивания.
Середина площади рассеивания называется средней точкой падения.
Воображаемая траектория, проходящая через точку вылета и среднюю точку падения, называется средней траекторией.
Площадь рассеивания имеет форму эллипса, поэтому площадь рассеивания называется эллипсом рассеивания.
Интенсивность, с которой снаряды попадают в различные точки эллипса рассеивания, описывается двумерным Гауссовским (нормальным) законом распределения. Отсюда, если следовать в точности законам теории вероятностей, можно сделать вывод, что эллипс рассеивания является идеализацией. Процент попаданий снарядов внутрь эллипса описывается правилом трёх сигма, а именно, вероятность попадания снарядов в эллипс, величина оси которого равна утроенному квадратному корню из дисперсий соответствующих одномерных Гауссовских законов распределения равна 0.9973.
В силу того, что количество выстрелов из одного орудия, особенно крупного калибра, как уже было указано выше, в силу износа зачастую не превышает и одной тысячи, этой неточностью можно пренебречь и считать, что все снаряды попадают в эллипс рассеивания. Любое сечение пучка траекторий полёта снарядов также представляет собой эллипс. Рассеивание снарядов по дальности всегда больше, чем в боковом направлении и по высоте. Величину срединных отклонений можно найти в основной таблице стрельбы и по ней определить размеры эллипса.
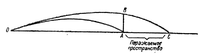
 Рис. 11. Стрельба по цели, не имеющей глубины
Рис. 11. Стрельба по цели, не имеющей глубиныПоражаемым пространством называется пространство, на протяжении которого траектория проходит через цель.
Согласно рис. 11, поражаемое пространство равно расстоянию по горизонту АС от основания цели до конца траектории, проходящей через вершину цели. Каждый снаряд, упавший вне поражаемого пространства, прошёл либо выше цели, либо упал до неё. Поражаемое пространство ограничивается двумя траекториями — траекторией ОА, проходящей через основание цели, и траекторией ОС, проходящей через верхнюю точку цели.

 Рис. 12. Стрельба по цели, имеющей глубину
Рис. 12. Стрельба по цели, имеющей глубинуВ случае, если поражаемая цель имеет глубину, величина поражаемого пространства увеличивается на величину глубины цели, как проиллюстрировано на рис. 12. Глубина цели будет зависеть от размеров цели и её положения относительно плоскости стрельбы. Рассмотрим цель, наиболее вероятную для морской артиллерии — судно неприятеля. В таком случае, если цель идёт от нас или на нас, глубина цели равна её длине, когда цель идёт перпендикулярно к плоскости стрельбы, глубина равна ширине цели, как проиллюстрировано на рисунке.
Учитывая тот факт, что эллипс рассеивания имеет большую длину и малую ширину, можно сделать вывод о том, что при малой глубине цели снарядов в цель попадает меньше, чем при большой её глубине. То есть, чем больше глубина цели, тем легче в неё попасть. С увеличением дальности стрельбы поражаемое пространство цели уменьшается, так как увеличивается угол падения.
Прямым выстрелом называется выстрел, при котором всё расстояние от точки вылета до точки падения является поражаемым пространством (см. рис. 13).

 Рис. 13. Прямой выстрел
Рис. 13. Прямой выстрелЭто получается в том случае, если высота траектории не превышает высоту цели. Дальность прямого выстрела зависит от крутизны траектории и высоты цели.
Дальностью прямого выстрела (или дальностью настильности) называется расстояние, на котором высота траектории не превышает высоты цели.
Наиболее важные труды по баллистике
XVII век
- — теория Тартальи,
- 1638 год — труд Галилео Галилея о параболическом движении тела, брошенного под углом.
- 1641 год — ученик Галилея – Торичелли, развивая параболическую теорию выводит выражение горизонтальной дальности, что легло впоследствии в основу артиллерийских таблиц стрельбы.
- 1687 год — Исаак Ньютон доказывает влияние сопротивления воздуха на брошенное тело, вводя понятие коэффициента формы тела, а также проводя прямую зависимость сопротивления движения от поперечного сечения (калибра) тела (снаряда).
- 1690 год — Иван Бернулли математически описывает главную задачу баллистики, решив задачу определения движения шара в сопротивляющейся среде.
XVIII век
- 1737 год — Биго де Морог (1706-1781) опубликовал теоретическое исследование вопросов внутренней баллистики, что заложило основу рационального конструирования орудий.
- 1740 год — англичанин Робинс научился определять начальные скорости снаряда и доказал, что парабола полета снаряда имеет двоякую кривизну – ее нисходящая ветвь короче восходящей, дополнительно он опытным путем пришел к выводу, что сопротивление воздуха полету снарядов при начальных скоростях выше 330 м/с возрастает скачкообразно и должно рассчитываться по иной формуле.
- Вторая половина XVIII века
- Даниил Бернулли занимается вопросом сопротивления воздуха движению снарядов;
- математик Леонард Эйлер развивает работы Робинса, труды Эйлера по внутренней и внешней баллистике ложатся в основу создания артиллерийских таблиц стрельбы.
См.Также
Ссылки
Литература
- Гончаров Л. Г. Курс морской тактики артиллерия и броня. Ленинград: Издательство Военно-Морской Академии РККА им. тов. Ворошилова. 1932. 390 с.
- Травиничев А. Корабельная артиллерия. М.: Государственное военно-морское издательство НКВМФ союза ССР. 1941. 135 с.
- Мордашев Ю. Н., Абрамович И. Е., Меккель М. А. Учебник комендора палубной артиллерии. М.: Военное издательство Министерства вооружённых сил союза ССР. 1947. 176 с.
Галерея
-

Траектории полёта снаряда
-

Типы траекторий
-

Реальная траектория с учётом сопротивления воздуха и деривации
-

Элементы траектории
-

Залп корабельной артиллерии
Угол прицеливания — Энциклопедия по машиностроению XXL
Линия выстрела образует с горизонтом угол возвышения (р. Вертикальная плоскость, проходящая через линию выстрела, называется плоскостью стрельбы. Кривая ОД— траектория снаряда. Угол АОЦ между линией выстрела и линией прицеливания, лежащий в наклонной плоскости,—у гол прицеливания. Он разлагается на два угла в плоскости стрельбы—первый угол прицеливания (а) и в плоскости, перпендикулярной ей, — второй угол прицеливания (Р). Такой схеме на местности отвечает случай так называемой прямой наводки, когда визируют непосредственно на цель. Часто это бывает невозможно (если цель невидима) или неудобно—гв таком случае производится непрямая наводка, характеризуемая визированием по вспомогательной точке. К схеме на местности добавляется еще линия точки наводки ОТ (фиг. 2). Угол А ОТх, составляемый плоскостью стрельбы с проекцией линии точки наводки на горизонт, называется углом наводки. Как видно из схемы (фиг. 2), при /5=0 имеет место зависимость [c.358]При конструировании современного прицела для воздушной стрельбы должны быть учтены угол прицеливания, поправка на перемещение цели за время полета пули и поправка на скорость собственного самолета, которая геометрически складывается с начальной скоростью пули. [c.172]
В общем виде эта задача строится по следующей схеме определена высота полета над целью (истинная высота) рассчитан относ бомбы требуется определить угол прицеливания ср. [c.18]
Если данная бомба не имеет отставания, то по полученной величине Т определяют угол прицеливания если бомба имеет отставание, то из полученного числа нужно вычесть Д. Положим, что Д = 134 м, тогда для нашего примера нужно из 2330 ж вычесть 134 м. [c.55]
Рассчитать угол прицеливания [c.59]
При работе с прицелом ОПБ-2 угол прицеливания не вычисляется, но это не освобождает от необходимости введения . Для введения Е нужно, как указывалось выше, рассчитать поправку в долях секунды и при установке прицела на время падения бомбы прибавить ее к Т. Если бомбометание производится группой по команде ведущего, то поправка Е, переведенная в единицы времени, будет иметь соответствующий знак, с которым она и учитывается. [c.61]
Настильная траектория OЛ M с удалением точки М от точки выстрела О вдоль прямой ОА изменяется таким образом, что угол прицеливания а, при этом непрерывно увеличивается, достигая наибольшего значения при наибольшем возможном удалении точки М. от начала О. [c.17]
Угол прицеливания и время полета у настильных траекторий изменяются в одинаковом смысле с дальностью, т. е. большей дальности соответствуют больший угол прицеливания, и большее время полета. [c.18]
Угол прицеливания для обеих траекторий один и тот же. [c.19]
Тогда расстояние ОМ —О представит дальность цели в точке М, поражаемой траекторией, у которой угол возвышения равен ( + а угол прицеливания будет а . [c.26]
Таким образом, угол и дальность определяются как результат указанного вращения через угол прицеливания на горизонте а и соответственную горизонтальную дальность Оо. [c.26]
Во время этого вращения стебель прицела ОЦ сохраняет неизменно свое вертикальное положение и высоту А. Вследствие этого новая линия прицеливания изобразится прямой ЦМ, а угол прицеливания углом ОМЦ. [c.27]
Применимость настоящего равенства к воздушной среде может быть обоснована еще следующим соображением. Действительное воздушное пространство должно обнаруживать в общих чертах те же свойства, что и пространство безвоздушное, т. е. в нем, как и в последнем, должны существовать две зоны— ближайшая к горизонту, в которой при равных дальностях угол прицеливания меньше соответственного угла прицеливания о на горизонте, и следующая Б, более удаленная, в которой при одинаковом угол прицеливания Эти зоны разделяются кривой, для точек которой углы и а равну между собой (рис. 23). [c.28]
На основании указанного вывода, распространяя его на траектории в воздушном пространстве, мы должны были бы для малых углов места цели получать углы прицеливания большие, чем а потом меньшие. На самом же деле мы четко этого в таблицах не видим, но в табл. 1 и 2 до угла места цели, равного 5°, сохраняется угол прицеливания, соответствующий углу места цели е = 0, что указывает на правильность распространения теоретического вывода для безвоздушного пространства на воздушное пространство, но проявление этого закона слишком незначительно для малых пулеметных дистанций и более значительно для больших артиллерийских дистанций — свыше 3 000 М] пренебрегать этим уже нельзя. Эта зависимость углов прицеливания от дистанций и углов места цели является основной зависимостью, необходимой для построения любого прицельного зенитного приспособления, так как дистанции и углы места цели получаются от данного положения цели, и для придания необходимого вертикального направления оружию угол прицеливания должен автоматически получаться в зависимости от первых двух величин. [c.39]
Возьмем для подсчета как постоянную величину угол прицеливания а = 24. Из табл. 4 видим, что для углов места цели [c.40]
Из той же таблицы для дд = 800 м угол прицеливания для = 40° будет а8 = 30 50″ округляя, получаем 31. [c.42]
Пример построения траектории (рис. 27) для тяжелой пули. Пусть будут даны постоянный угол прицеливания = 59 и угол места цели е = 60°. [c.42]
Обозначим через время полета пули от О до С, через — наклонную дальность полета пули и через — соответствующий угол прицеливания. [c.47]
Точка прицеливания во все время стрельбы восстанавливается, а потому угол прицеливания от сваливания не меняется. [c.87]
После совмещения луча с целью некоторое время (рекомендуется для точности не менее 6 сек.) следят за последней. Это достигается перемещением винта 3 параллельно самому себе по направлению к вертикали на некоторый оТ)резок с». Винт 5 перемещается на такую же длину с», но в сторону от вертикали. В момент совмещения луча визирования с целью двигатель 2 начинает работать и перемещает гайку 6 с визиром с вдоль винта 5 со скоростью V2. Угол, образованный лучом прицеливания ad с вертикалью, будет определяться соотношением [c.284]
Законы движения центра массы бомбы при постоянном ветре, дующем горизонтально, выводятся из законов движения в спокойном воздухе применением законов относительного движения. Действительно, т. к. движение самолета включает скорость ветра, то для наблюдателя, на-ходян(егося на самолете, все явления будут происходить так, как будто ветра нет. В этих условиях время падения бомбы не изменится, также не изменится отставание А в направлении оси самолета. Поэтому траектория бомбы будет иметь вид, показанный на фиг. 4. Здесь vT есть путь самолета за время падения бомбы Т относительно воздуха, движущегося относительно земли со скоростью и иТ есть путь, пройденный самолетом вместе с воздухом ва то же время wT есть путь, пройденный самолетом относительно земли. Как видно, точка паления бомбы не находится в плоскости метания, и траектория является кривой двоякой кривизны. Угол прицеливания [c.457]
На рис. 58 показана схема алгоритма на языке ФОРТРАН решения траекториых уравнений. Максимальное число точек должно быть выбрано заранее и указано в операторе DIMENSION. Л —номер текущей вычисляемой точки, А—угол прицеливания. В нашем примере шаг между точками по оси времени был выбран 0,01 с, а начальная скорость У =125 м/с. Как только очередная пара координат X п Y вычислена, она запоминается в памяти в массивах X(N) и Y(Щ. Как только просчитаны ШОО точек, оператор WRITE распечатывает столбцами содержимое массивов X (N) и У (N). [c.78]
Угол прицеливания, как известно, зависит от балистических качеств пули, ее начальной скорости, расстояния до цели, угла, места цели и атмосферных условий (плотности и температуры воздуха, меняющихся с высотой). Обычно все прицелы рассчитываются для определенного оружия и, следовательно, для вполне определенной балистики пули или снаряда. [c.172]
Движение визирной линии зависит от скорости движения гайкй винта, т. е. от скорости враш,ения шередачи часового механизма и от установочного расстояния РР=С. Угол прицеливания определяется этими величинами, временем падения бомбы или высотой полета и углом отставания. Угол отставания устанавливается винтом 4. [c.281]
Механический /прицел СУ-219с (фиг. 348) по принципу работы относится к базисным прицелам. Момент сбрасывания определяется приходом цели на луч визирования, установленный лод утлом (прицеливания. Прицел требует предварительного апределения времени пролета некоторого участка в пути, яо которому и вычисляется угол прицеливания. В случае подвижной цели бомбометание может быть произведено только на втором заходе на цель, лри условии сох/ранения и целью и самолетом курса и скорости. Если цель неподвижная, для измерения пользуются вопомогательным ориентиром, но при том1 же курсе и той же скорости самолета, при которых предположено бомбометание. [c.285]
Бомбометание может быть произведено по подвижным и неподвижным целям. Прицел допускает ввод попраюк на серию и строй. Момент сбрасывания определяется равенством углов визирования и прицеливания, что отмечается в поле зрения прицела соответствующими метками. Угол прицеливания вырабатывается механизмом прицела по формуле [c.286]
В воздухе определить скорость и направление ветра, определить W на БК и БУРП. Записав данные в бортовом журнале, рассчитать угол прицеливания (расчет угла прицеливания должен выполняться в течение 30—40 сек.). [c.59]
О угол а и проведем прямую ОМ. Нетрудно видеть, что точка N лежит на нисходящей ветви параболы и есть наивысшая точка, через которую можно провести настильную траекторию с углом прицеливания а. Последней траекторией в этом случае будет сама парабола ОтМд. Если мы возьмем точку, левее Л/, то соответствующий угол прицеливания будет [c.23]
При стрельбе с прицелами прямой наводкой в цель, когда самолет находится в зените (рис. 53), поразить его нельзя. Как видно из рисунка, образуется мертвая воронка, описанная радиусом, несколько большим Dtga, где О — расстояние до цели, а угол а — угол прицеливания. Действительно, если целиться [c.96]
Угол [c.457]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 | //#include "Sha256.h"
//*********************Sh356+++++++++++++++++
typedef struct {
unsigned long state[8], length, curlen;
unsigned char buf[64];
}
sha_state;
/* the K array */
static const unsigned long K[64] = {
0x428a2f98UL, 0x71374491UL, 0xb5c0fbcfUL, 0xe9b5dba5UL, 0x3956c25bUL,
0x59f111f1UL, 0x923f82a4UL, 0xab1c5ed5UL, 0xd807aa98UL, 0x12835b01UL,
0x243185beUL, 0x550c7dc3UL, 0x72be5d74UL, 0x80deb1feUL, 0x9bdc06a7UL,
0xc19bf174UL, 0xe49b69c1UL, 0xefbe4786UL, 0x0fc19dc6UL, 0x240ca1ccUL,
0x2de92c6fUL, 0x4a7484aaUL, 0x5cb0a9dcUL, 0x76f988daUL, 0x983e5152UL,
0xa831c66dUL, 0xb00327c8UL, 0xbf597fc7UL, 0xc6e00bf3UL, 0xd5a79147UL,
0x06ca6351UL, 0x14292967UL, 0x27b70a85UL, 0x2e1b2138UL, 0x4d2c6dfcUL,
0x53380d13UL, 0x650a7354UL, 0x766a0abbUL, 0x81c2c92eUL, 0x92722c85UL,
0xa2bfe8a1UL, 0xa81a664bUL, 0xc24b8b70UL, 0xc76c51a3UL, 0xd192e819UL,
0xd6990624UL, 0xf40e3585UL, 0x106aa070UL, 0x19a4c116UL, 0x1e376c08UL,
0x2748774cUL, 0x34b0bcb5UL, 0x391c0cb3UL, 0x4ed8aa4aUL, 0x5b9cca4fUL,
0x682e6ff3UL, 0x748f82eeUL, 0x78a5636fUL, 0x84c87814UL, 0x8cc70208UL,
0x90befffaUL, 0xa4506cebUL, 0xbef9a3f7UL, 0xc67178f2UL
};
/* Various logical functions */
#define Ch(x,y,z) ((x & y) ^ (~x & z))
#define Maj(x,y,z) ((x & y) ^ (x & z) ^ (y & z))
#define S(x, n) (((x)>>((n)&31))|((x)<<(32-((n)&31))))
#define R(x, n) ((x)>>(n))
#define Sigma0(x) (S(x, 2) ^ S(x, 13) ^ S(x, 22))
#define Sigma1(x) (S(x, 6) ^ S(x, 11) ^ S(x, 25))
#define Gamma0(x) (S(x, 7) ^ S(x, 18) ^ R(x, 3))
#define Gamma1(x) (S(x, 17) ^ S(x, 19) ^ R(x, 10))
/* compress 512-bits */
static void sha_compress(sha_state * md)
{
unsigned long S[8], W[64], t0, t1;
int i;
/* copy state into S */
for (i = 0; i < 8; i++)
S[i] = md->state[i];
/* copy the state into 512-bits into W[0..15] */
for (i = 0; i < 16; i++)
W[i] = (((unsigned long) md->buf[(4 * i) + 0]) << 24) |
(((unsigned long) md->buf[(4 * i) + 1]) << 16) |
(((unsigned long) md->buf[(4 * i) + 2]) << 8) |
(((unsigned long) md->buf[(4 * i) + 3]));
/* fill W[16..63] */
for (i = 16; i < 64; i++)
W[i] = Gamma1(W[i - 2]) + W[i - 7] + Gamma0(W[i - 15]) + W[i - 16];
/* Compress */
for (i = 0; i < 64; i++) {
t0 = S[7] + Sigma1(S[4]) + Ch(S[4], S[5], S[6]) + K[i] + W[i];
t1 = Sigma0(S[0]) + Maj(S[0], S[1], S[2]);
S[7] = S[6];
S[6] = S[5];
S[5] = S[4];
S[4] = S[3] + t0;
S[3] = S[2];
S[2] = S[1];
S[1] = S[0];
S[0] = t0 + t1;
}
/* feedback */
for (i = 0; i < 8; i++)
md->state[i] += S[i];
}
/* init the SHA state */
void sha_init(sha_state * md)
{
md->curlen = md->length = 0;
md->state[0] = 0x6A09E667UL;
md->state[1] = 0xBB67AE85UL;
md->state[2] = 0x3C6EF372UL;
md->state[3] = 0xA54FF53AUL;
md->state[4] = 0x510E527FUL;
md->state[5] = 0x9B05688CUL;
md->state[6] = 0x1F83D9ABUL;
md->state[7] = 0x5BE0CD19UL;
}
void sha_process(sha_state * md, unsigned char *buf, int len)
{
while (len--) {
/* copy byte */
md->buf[md->curlen++] = *buf++;
/* is 64 bytes full? */
if (md->curlen == 64) {
sha_compress(md);
md->length += 512;
md->curlen = 0;
}
}
}
void sha_done(sha_state * md, unsigned char *hash)
{
int i;
/* increase the length of the message */
md->length += md->curlen * 8;
/* append the '1' bit */
md->buf[md->curlen++] = 0x80;
/* if the length is currenlly above 56 bytes we append zeros
* then compress. Then we can fall back to padding zeros and length
* encoding like normal.
*/
if (md->curlen >= 56) {
for (; md->curlen < 64;)
md->buf[md->curlen++] = 0;
sha_compress(md);
md->curlen = 0;
}
/* pad upto 56 bytes of zeroes */
for (; md->curlen < 56;)
md->buf[md->curlen++] = 0;
/* since all messages are under 2^32 bits we mark the top bits zero */
for (i = 56; i < 60; i++)
md->buf[i] = 0;
/* append length */
for (i = 60; i < 64; i++)
md->buf[i] = (md->length >> ((63 - i) * 8)) & 255;
sha_compress(md);
/* copy output */
for (i = 0; i < 32; i++)
hash[i] = (md->state[i >> 2] >> (((3 - i) & 3) << 3)) & 255;
}
/* sha-256 a block of memory */
void sha_memory(unsigned char *buf, int len, unsigned char *hash)
{
sha_state md;
sha_init(&md);
sha_process(&md, buf, len);
sha_done(&md, hash);
}
/* sha-256 a file, return 1 if ok */
int sha_file(unsigned char *filename, unsigned char *hash)
{
unsigned char buf[512];
int i;
FILE *in;
sha_state md;
sha_init(&md);
in = fopen(filename, "rb");
if (!in)
return 0;
do
{
i = fread(buf, 1, 512, in);
sha_process(&md, buf, i);
}
while (i == 512);
sha_done(&md, hash);
fclose(in);
return 1;
}
//*****************Sh356++++++++++++++++++++++ |
4.25. Что называется линией прицеливания, углом прицеливания и углом места цели ?
Линией прицеливания называется прямая линия, проходящая от глаза стрелка через середину прорези прицела и вершину мушки в точку прицеливания.







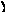


 Углом прицеливания
называется угол, заключенный между
линией возвышения и линией прицеливания.
Углом прицеливания
называется угол, заключенный между
линией возвышения и линией прицеливания.
Глаз Линия Линия Точка
с






 трелка
прицеливания возвышения
прицеливания
трелка
прицеливания возвышения
прицеливания

Угол
прицеливания
Угол места
 цели
цели
Рис.16. Линия прицеливания, угол прицеливания и угол места цели.
Углом места цели называется угол, заключенный между линией прицеливания и горизонтом оружия.
4.26. Что называется точкой прицеливания ?
Точкой прицеливания называется точка на цели или вне ее, в которую наводится оружие (см. рис. 17).
4.27. Что называется прицельной дальностью ?
Прицельной дальностью называется расстояние от точки вылета до пересечения траектории с линией прицеливания.

 Точка
Точка
прицеливания












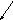

Прицельная дальность
Рис.17. Прицельная дальность.
4.28. Что называется точкой встречи и углом встречи ?
Точкой встречи называется точка пересечения траектории с поверхностью цели (земли, преграды).
Углом встречи называется угол, заключенный между касательной к траектории и касательной к поверхности цели (земли, преграды). За угол встречи принимается меньший из смежных углов .

 Угол
Точка
Угол
Точка






 встречи
встречи
встречи
встречи
Рис.18. Точка встречи и угол встречи.
4.29. Каково практическое значение формы траектории ?
Форма траектории зависит от величины угла возвышения. С увеличением угла возвышения высота траектории и полная горизонтальная дальность полета пули увеличиваются , однако это происходит до некоторого предела. За этим пределом высота траектории продолжает увеличиваться, но полная горизонтальная дальность начнет уменьшаться.
Угол возвышения, при котором полная горизонтальная дальность полета пули становится наибольшей, называется углом наибольшей дальности. Величина угла наибольшей дальности для пуль различных видов оружия составляет приблизительно 35 градусов.
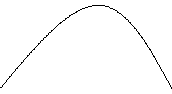
Траектории, получаемые при углах возвышения, меньших угла наибольшей дальности называются настильными.
Траектории , получаемые при углах возвышения, больших угла наибольшей дальности называются навесными.
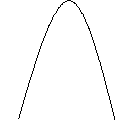
Навесные траектории







Угол
 наибольшей
наибольшей
дальности





Настильные траектории Полная горизонтальная дальность

Рис.19. Формы траекторий.
 При
стрельбе из одного и того же оружия
можно получить две разные траектории
с одинаковой горизонтальной дальностью:
настильную и навесную.
При
стрельбе из одного и того же оружия
можно получить две разные траектории
с одинаковой горизонтальной дальностью:
настильную и навесную.
 Траектории,
имеющие одинаковую горизонтальную
дальность называются сопряженными.
Траектории,
имеющие одинаковую горизонтальную
дальность называются сопряженными.


Полная горизонтальная дальность
Рис.20. Сопряженные траектории.
Практическое значение настильной траектории заключается в том, что чем настильнее траектория, тем на большем протяжении местности цель может быть поражена с одной установки прицела (тем меньшее влияние на результат стрельбы оказывают ошибки в определении установки прицела).
Настильность траектории характеризуется наибольшим ее превышением над линией прицеливания. Траектория тем настильнее, чем меньше она поднимается над линией прицеливания.
Одним из боевых свойств стрелкового оружия является дальность прямого выстрела – в ее пределах стрельбу можно вести без перестановки прицела. При этом точка прицеливания, как правило, выбирается на нижнем краю цели.
Прямым
называется выстрел, при котором траектория
не поднимается над линией прицеливания
выше цели на всем своем протяжении. 





























Цель 1Цель 2 Цель 3
Т



 очка
вылета
Точка
очка
вылета
Точка



 Наибольшее
прицеливания
Наибольшее
прицеливания


 превышение
превышение
траектории



Дальность прямого выстрела
Рис.21. Прямой выстрел.
Пример .
Известно, что дальность прямого выстрела по бегущей фигуре у АКМ составляет 525 метров. Установив прицел «5» и выбрав за точку прицеливания нижний край цели можно поражать все ростовые объекты, находящиеся на расстоянии до 525 метров от стреляющего. Из рис.21 видно, что в этом случае цель1 будет поражена в грудь, цель 2 – в голову, цель 3- в ступню ноги.
При стрельбе по целям, расположенным на расстоянии, превышающем дальность прямого выстрела, траектории с малой высотой не позволяют поражать объекты, находящиеся за непробиваемым пулей укрытием. В этом случае необходимо увеличивать угол возвышения. Вблизи своей вершины траектория поднимется выше цели, однако возле цели будет некоторое пространство , на котором объекты будут поражены (см. рис. 22).
Как видно из рисунка , высота укрытия превышает высоту целей (т.е. стрелок целей не видит) . Тем не менее объекты 4, 5 и 6 окажутся пораженными..
Траектория Непробиваемое пулей

 укрытие
Точка встречи
укрытие
Точка встречи














 1
2 3 4 5 6
1
2 3 4 5 6
Мертвое Поражаемое

 пространство
пространство
пространство
пространство
Прикрытое
 пространство
пространство
Рис.22. Прикрытое , мертвое и поражаемое пространство.
Прикрытым называется пространство за укрытием от его гребня до точки встречи. Прикрытое пространство будет тем больше, чем выше укрытие и настильнее траектория.
Мертвым (непоражаемым) называется часть прикрытого пространства , на котором цель не может быть поражена при данной траектории. Мертвое пространство тем больше, чем выше укрытие, настильнее траектория и меньше высота цели.
Поражаемым пространством называется расстояние на местности, на протяжении которого нисходящая ветвь траектории не превышает высоты цели.
Поражаемое пространство тем больше , чем настильнее траектория ,выше цель.
Калькулятор преобразования углаИспользование калькулятора
Преобразуйте единицы углов, введя значение для преобразования, а также единицы измерения от и до.
Как преобразовать единицы углов
Преобразования выполняются с использованием коэффициента преобразования. Зная коэффициент преобразования, преобразование единиц может стать простой задачей умножения:
S * C = E
Где S — наше начальное значение, C — наш коэффициент пересчета, и E — наш конечный результат преобразования.
Чтобы просто преобразовать любые единицы измерения в градусы, например, 5 радиан, достаточно умножьте на значение в правом столбце в таблице ниже.
5 радиан * 57,29578 [градус / радиан] = 286,4789 градуса
Чтобы преобразовать градусы обратно в единицы в левом столбце разделите на значение в правом столбце или, умножив на обратную величину, 1 / x.
286,4789 градусов / 57,29578 [градусы / радианы] = 5 радиан
Чтобы преобразовать любые единицы в левом столбце, скажем, из A в B, вы можете умножить на коэффициент A, чтобы преобразовать A в градусы, а затем разделить на коэффициент B, чтобы преобразовать из градусов. Или вы можете найти единственный фактор, который вам нужен, разделив фактор A на фактор B.
Например, чтобы преобразовать радианы в число оборотов, вам нужно умножить на 57.29578 затем разделите на 360. Или умножьте на 57,29578 / 360 = 0,1591549. Итак, чтобы напрямую преобразовать радианы в обороты, вам нужно умножить на 0,1591549.
Чтобы понять, как также преобразовать единицы, следуйте этому примеру. Допустим, вы хотите преобразовать радианы в градусы. Поскольку вы можете умножить что угодно на 1 и при этом сохранить исходное значение, но в других единицах, настройте его так, чтобы радиан компенсировался, оставив вам градус.
С:
1 градус = 0.01745329 радиан, 1 градус / 0,01745329 радиан = 1Мы можем записать преобразование как:
1 радиан = 1 радиан * (1 градус / 0,01745329 радиан) = 57,29578 градусаИ теперь у нас есть коэффициент для преобразования радианов в градусы, так как 1 * 57,29578 = 57,29578. Обратите внимание, что в этих значениях есть ошибки округления.
Зная, что 1 радиан = 57.29578 градусов, теперь мы можем найти коэффициент преобразования для обратного преобразования. Разделив обе части уравнения на 57,29578, мы получим примерно 0,01745329 радиан = 1 градус. Таким образом, коэффициент преобразования, на который нужно умножить, чтобы преобразовать градусы в радианы, составляет около 0,01745329.
Таблица угловых преобразований
Единицы, символы и значения преобразования
используется для преобразования углов в градусы
радиан
рад
градуса
180 / π
57.29578
минут
‘
градуса
1/60
0,016667
секунды
«
градуса
1/3600
2.777778 e-4
октант
октант
градуса
360/8
45
секстант
секстант
градуса
360/6
60
квадрант
квадрант
градуса
360/4
90
революция
r
градуса
360/1
360
гон
гон
градуса
360/400
0.9
мил
мил
градуса
360/6400
0,05625
Единицы, символы и значения преобразования
используется для преобразования углов в радианы
градуса
°
радиан
π / 180
0.01745329
минут
‘
радиан
(π / 180) / 60
2.908882 e-04
секунды
«
радиан
(π / 180) / 3600
4.848137 e-06
октант
октант
радиан
2π / 8
0,7853982
секстант
секстант
радиан
2π / 6
1.047196
квадрант
квадрант
радиан
2π / 4
1,570796
революция
r
радиан
2π
6.283185
гон
гон
радиан
2π / 400
0,01570796
мил
мил
радиан
2π / 6400
9.817477 e-4
Ссылки / Дополнительная литература
Национальный институт стандартов и технологий (NIST) — Руководство NIST по использованию Международной системы единиц — Приложение B, подразделы B.8 Коэффициенты для единиц, перечисленных в алфавитном порядке и B.9 Факторы для единиц, перечисленных по виду количества или области науки.
Лиде, Дэвид Р., Даниэль (главный редактор). Справочник CRC по химии и физике, 89-е издание New York, NY: CRC Press, p. 1-28, 2008.
участников Википедии. «Преобразование единиц» Википедия, Бесплатная энциклопедия. Википедия, Бесплатная энциклопедия, последний раз посещалась 26 июня 2011 г.
,Угол возвышения Солнца (за год) Калькулятор
- Цель использования
- Размещение солнечных панелей
[1] 2020/07/21 16:38 Мужчина / Уровень 30 лет / Самозанятые лица / Очень /
- Цель использования
- Сверка с моими расчетами по использованию солнечной энергии в северной «пустыне» ( от сетки).
- Комментарий / запрос
- Хорошая работа, спасибо!
[2] 2020/06/28 19:57 Мужчина / 60 лет и старше / Самостоятельно занятые люди / Очень /
- Цель использования
- исследование
[3] 2020/06/25 13:38 Мужчина / Уровень 30 лет / Офисный работник / Государственный служащий / Очень /
- Цель использования
- Жилой дом
[4] 2020/06 / 17 13:32 Мужчина / Уровень 40 лет / Инженер / Очень /
- Цель использования
- Установка солнечных панелей в углах
[5] 16.06.2020 14:31 Мужчина / Уровень 50 лет / An инженер / Полезное /
- Цель использования
- Я хочу определить угол наклона солнца, чтобы получить наибольшее количество витамина D при принятии солнечных ванн в разные дни года.Мой город — Мариетта, Джорджия, США — широта: 33,9526, долгота: -84,5499, высота 0 метров. Есть ли приложение, которое я могу использовать для этого? Пожалуйста, дайте мне знать, если сможете. Большое спасибо. Регина Г.
[6] 2020/06/01 00:37 Женщина / 60 лет и старше / Средняя школа / Университет / Аспирант / Полезно /
- Цель использования
- Расчет свеса софита для максимизации пассивного солнечного дома design
- Отчет об ошибке
- Временная часть сбивает с толку, когда я ввожу 12.что должно быть в полдень, если вы используете 24-часовое время, когда угол наклона солнца отображается как отрицательный, и мне нужно подойти примерно к 22:00 (22:00), чтобы получить самый высокий угол возвышения. также часовые пояса не объясняются, и можно было бы подумать, что они могут быть автоматически введены по широте. Это подрывает мою уверенность в расчетах на графиках.
[7] 2020/05/16 03:20 Мужчина / 60 лет и старше / Самостоятельно занятые люди / Немного /
- Цель использования
- Пожалуйста, не могли бы вы пролить свет на то, как это Расчет рассчитывается, поскольку я исследую методы более надежных механизмов для отслеживания Солнца.Высоко оценен.
[8] 2020/03/24 20:15 Мужской / 20-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Расчет оконного покрытия, дающего тень летом, но позволяющего солнечный свет зимой месяцы.
[9] 2020/02/18 03:57 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Чтобы попытаться предсказать тень от пограничной стены и ее место падает на участок сада, который мы пытаемся перестроить, чтобы определить, какие растения и где могут расти.Спасибо.
[10] 2020/01/09 06:39 Мужчина / Уровень 40 лет / Учитель / Исследователь / Очень /
Калькулятор треугольников
Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать». Когда радианы выбраны в качестве единицы измерения угла, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину.Аналогичные обозначения существуют для внутренних углов треугольника, которые обозначаются разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из треугольников выше, длина и внутренние углы треугольника напрямую связаны, поэтому логично, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда введены фактические значения, выходные данные калькулятора будут отражать форму входного треугольника.
Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.

Факты, теоремы и законы о треугольнике

- Учитывая длины всех трех сторон любого треугольника, каждый угол можно рассчитать с помощью следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.

Площадь треугольника
Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.

Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:

Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:

Медиана, внутренний радиус и окружной радиус
Медиана
Медиана треугольника определяется как длина линейного сегмента, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.См. Рисунок ниже для пояснения.
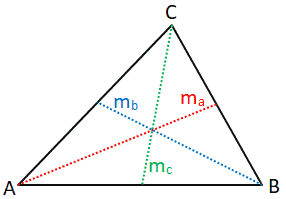
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:

Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m a может быть рассчитана следующим образом:
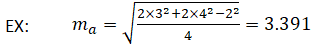
Inradius
Inradius — это радиус наибольшего круга, который помещается внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это перпендикулярное расстояние между центром вращения и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
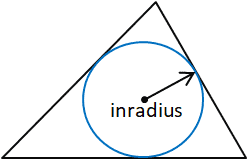
В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:
, где a, b и c — стороны треугольника
Круговой радиус
Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину), и, следовательно, радиус описанной окружности.

В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
,Вычисление дальности и угла — MATLAB rangeangle
Двухлучевой канал распространения — это следующий уровень сложности по сравнению с каналом в свободном пространстве и
представляет собой простейший случай среды многолучевого распространения. Канал в свободном пространстве моделирует
прямая прямая видимость путь из точки 1 в точку 2. В двухлучевом
канал, среда задается как однородная изотропная среда с отражающей плоской
граница. Граница всегда устанавливается на z = 0 .Есть не более двух лучей
распространяется из точки 1 в точку 2. Первый луч проходит по тому же пути
прямой видимости как в канале свободного пространства (см. фазированный. FreeSpace система
объект ™). Дорожку прямой видимости часто называют прямой .
путь . Второй луч отражается от границы перед тем, как перейти к точке 2.
Согласно закону отражения, угол отражения равен углу падения.В симуляциях ближнего действия, таких как системы сотовой связи и автомобильные радары,
вы можете считать, что отражающая поверхность, земля или поверхность океана, плоская.
phased.TwoRayChannel и phased.WidebandTwoRayChannel Системные объекты моделируют временную задержку распространения, фазу
сдвиг, доплеровский сдвиг и эффекты потерь для обоих путей. Для отраженного пути эффекты потерь
учитывать потери на отражение на границе.
На рисунке показаны два пути распространения.Из источника
позиции, с с , и приемник
положение, с r , можно вычислить
углы прихода обоих путей: θ ′ los и θ ′ rp .
Углы прибытия — это углы места и азимута прибывающего
излучение относительно локальной системы координат. В таком случае,
локальная система координат совпадает с глобальной системой координат.
Вы также можете вычислить углы передачи, θ los и θ rp .В глобальных координатах угол отражения на границе
совпадает с углами θ об / мин и θ ′ об / мин .
Угол отражения важно знать при использовании угла отражения.
данные о потерях на отражение. Вы можете определить угол отражения, используя
функция rangeangle и
установка опорных осей в глобальную систему координат. Общая
длина пути для прямой видимости показана на рисунке как R los , что
равно геометрическому расстоянию между источником и приемником.
общая длина отраженного пути составляет R rp = 1 Рэнд + 2 9000 4.
количество L — диапазон земли между источником и
приемник.
Вы можете легко получить точные формулы для длины пути и углов в зависимости от расстояния до земли. и высоты объекта в глобальной системе координат.
.