Как вычислить расстояние до объекта по фотографии
В связи с известным событием по всему интернету развернулись бурные дискуссии, участники которых обвиняют своих оппонентов то в незнании программы средней школы, то в непонимании того очевидного факта, что в военное время косинус угла может достигать четырёх.Не желая в эти дискуссии ввязываться, я лучше на наглядном примере покажу вам, как, имея на руках фотографию какого-либо известного объекта и немного вспомогательной информации, можно с большой точностью по совсем не сложным формулам рассчитать, на каком расстоянии этот объект находился от фотографа в момент съёмки. По возможности я постараюсь каждый шаг сопровождать иллюстрацией, расчётом или ссылкой на источник. Итак, приступим.
Как известно, простейший объектив для фотоаппарата можно сделать из одной двояковыпуклой линзы. Конечно, существуют фотоаппараты вообще без объектива (так называемые пинхол-камеры, предок которых — камера-обскура), но в данном случае они нам не слишком интересны. Для начала мы рассмотрим, как строится изображение в простейшем однолинзовом объективе, а затем я покажу, что те же методы хорошо подходят и для сложных объективов, сочетающих в себе более десятка последовательно расположенных линз.
Напомню вам схему хода лучей в тонкой линзе из школьного курса геометрической оптики:
На этой схеме d — расстояние от линзы до объекта, D — расстояние от линзы до изображения объекта (на матрице или плёнке), а f — фокусное расстояние линзы.
Формула тонкой линзы из того же курса связывает эти три расстояния:
Теперь ещё раз посмотрим на оптическую схему: h — это линейный размер объекта съёмки, а H — размер его уменьшенного изображения. Нетрудно заметить, что h = d tan α, а H = D tan α (это следует из свойств прямоугольного треугольника). Подставив эти величины в формулу тонкой линзы, увидим, что tan α сокращается, и в результате получим следующее уравнение:
«Неудобная» величина D ушла, а остальные мы знаем или можем легко вычислить. На основе этого уравнения получаем вот такую формулу расстояния до объекта: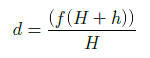
Ну а теперь давайте проверим её на практике.
Вот фотография, которую я сделал из своего окна:
На ней запечатлён дом 1 по 3-му Дорожному проезду, что в Москве. Это 22-этажная башня серии И-700А.
Какую полезную информацию можно извлечь из данной фотографии? Напомню, для расчёта нам нужны неизвестные пока величины h, H и f. h — это реальная высота дома (в метрах). Сходу я её не нагуглил, зато выяснил вот что: высота потолков в этом доме — 2,64 м, а толщина перекрытий — 0,22 м. Наверняка при измерении высоты потолков не учитывалась толщина напольного покрытия. Точно она мне не известна, так что, немного округлив, примем высоту одного этажа равной 2,9 м. Хорошо видны 23 панели, таким образом, высота видимого участка составляет примерно 66,7 м. Запомним эту величину и приступим к анализу фотографии.
H — это размер изображения дома на матрице фотоаппарата. По фотографии мы можем подсчитать его в пикселях, но, как известно, размер пикселя — это всё равно что размер ангела: точных данных ни у кого нет. Но здесь нужно вспомнить, что конкретные физические размеры имеет матрица фотоаппарата. Лезем в поисковик и узнаём, что для камеры Nikon D90 размер матрицы составляет 2,36 × 1,58 см, а разрешение — 4288 × 2848 пикс. Наша фотография не была кадрирована или повёрнута, поэтому мы можем узнать точный линейный размер изображения дома на матрице, составив пропорцию. Но чтобы делать это не вручную, воспользуемся программой Adobe Photoshop, где есть масса полезных инструментов.
По умолчанию Photoshop, конечно, не знает, какого размера должна быть наша фотография, и указывает ей разрешение 300 пикс./дюйм, или 118,11 пикс./см:
Но мы, зная физический размер матрицы и количество пикселей по длинной стороне снимка, делаем такой расчёт: 4288 / 2,36 (размер матрицы в сантиметрах), и получаем правильное разрешение — 1817 пикс./см. Вписываем его в соответствующее окошко и, чтобы не изменились реальные размеры фотографии, а лишь были пересчитаны её длина и ширина в см, указываем в верхних полях «100 проц»:
Как видите, при этом в поле «Размер печатного оттиска» появились уже известные нам размеры матрицы: 2,36 × 1,57 см. Точнее, в спецификации было указано 1,58 см, но это несущественная погрешность.
Теперь при помощи инструмента «Линейка» измерим высоту видимого участка дома (23 панели) на фотографии (смотрите в правый верхний угол):
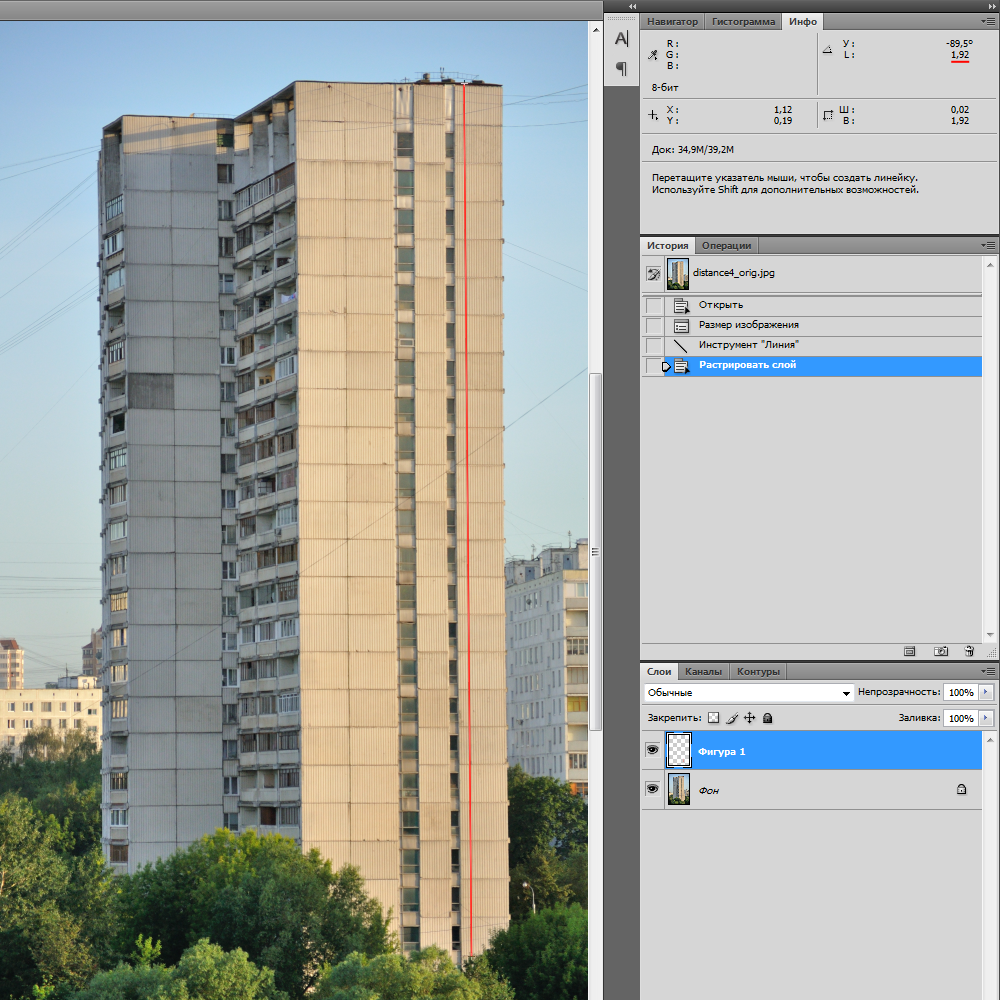
Получается, что высота изображения дома на матрице составляет 1,92 см, или 0,0192 м.
Осталось только выяснить фокусное расстояние, но для этого, к счастью, ничего считать не нужно: оно сразу прописывается при съёмке в метаданных фотографии (EXIF). Открываем их в фоторедакторе и видим:
Фокусное расстояние при съёмке составляло 105 мм, или 0,105 м, то есть я снимал дом с максимально возможным для этого объектива приближением.
Ну что ж, теперь у нас есть все данные для расчёта. Подставляем их в формулу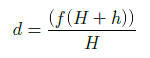
и получаем: d = (0,105(0,0192 + 66,7)) / 0,0192 = 364,9 м. Внимательный читатель наверняка заметил, сколь ничтожно мала величина H в сравнении с h, поэтому нашу формулу смело можно упростить до вида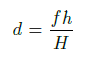
Для любых фотографий относительно крупных объектов, сделанных с расстояния больше 10 м, она будет давать практически тот же результат.
Ну а теперь самое интересное — нужно проверить, верна ли была использованная нами формула? Ведь в начале я говорил, что мы рассматриваем упрощённую конструкцию объектива, а не реальную. Может быть, наши расчёты не имеют ничего общего с действительностью? К счастью, это легко выяснить. Заходим на Яндекс.Карты и переходим в точку с координатами 55.604364, 37.611455. Затем активируем инструмент «Линейка» и ставим на карте две точки: одну — возле окна, из которого было сделано фото, а другую — возле стены дома, на которой мы считали панели:
Получаем 365 м. Ну не красота, а? Величины совпали с точностью до 0,1 м! Конечно, такая точность в известной мере является результатом везения, потому что и при измерении размеров изображения, и при подсчёте высоты этажей, и при расстановке точек на карте я вполне мог допускать погрешности в 1–3%. Но, как бы то ни было, в конечном итоге расчётная и измеренная величины сошлись.
Скептически настроенный читатель может подумать, что я подгонял цифры, и что для другой фотографии всё будет по-другому. Что ж, у меня есть ещё одно фото того же дома, сделанное с аналогичной точки, но совсем с другим фокусным расстоянием:
Проделаем для него те же измерения и расчёты. У меня получилось, что размер изображения дома составляет 0,39 см, а фокусное расстояние — 21 мм. Подставляем эти числа в упрощённую формулу и получаем d = (0,021 × 66,7) / 0,0039 = 359,2 м. Результат немного отличается, но всё равно в рамках погрешности совпадает с измеренным по карте. Расхождение несложно объяснить: камера указывает фокусное расстояние как целое число, то есть и 20,51, и 21,49 мм она покажет как 21 мм. А это уже даёт погрешность 2,4%.
Впрочем, самых въедливых скептиков наверняка не убедил и этот пример. Ведь в обоих случаях я использовал один и тот же объектив — а что, если формула работает для него чисто по совпадению? Справедливое замечание. Чтобы проверить, так ли это, я возьму кадр, сделанный не только другим объективом, но и другим фотоаппаратом, причём не цифровым, а плёночным.
Вот фотография, которую мы будем анализировать:

Её много лет назад сделал мой отец на свой «Зенит-Е» с объективом Гелиос-44-2. Фокусное расстояние этого объектива составляет 58 мм. Определить физический размер изображения дома очень просто: у меня есть слайд, который я оцифровал с определённым разрешением, и сканер прописал его в свойствах файла. Тут даже пересчитывать ничего не нужно, достаточно воспользоваться линейкой.
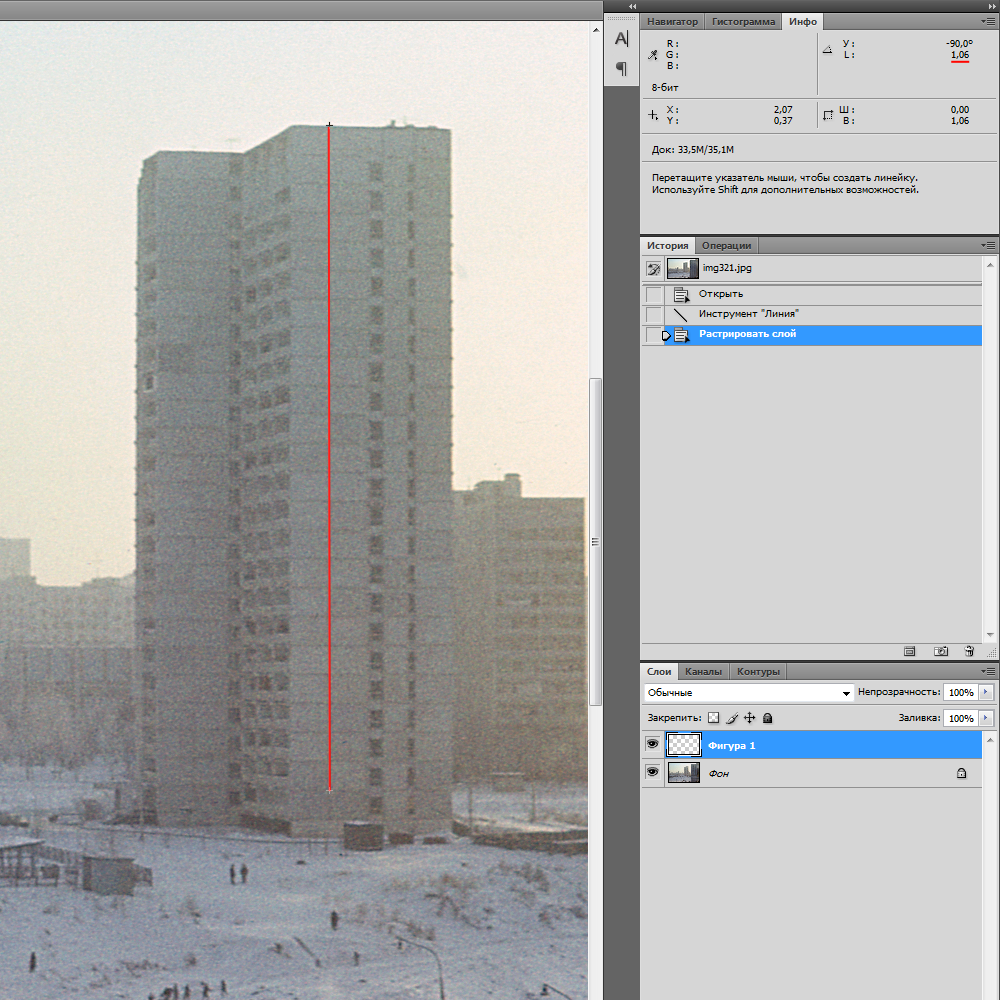
Участок из тех же 23-х панелей имеет на слайде высоту 1,06 см. Подставляем значения в формулу: d = (0,058 × 66,7) / 0,0106 = 365 м. Полное совпадение!
Что ж, мы получили интересные результаты: выходит, простая формула для тонкой линзы позволяет получать весьма точные (и легко проверяемые) результаты при анализе реальных фотографий, а не «сферических коней в вакууме». Почему же так происходит, если реальный объектив представляет собой не одну линзу, а целый бутерброд из линз? Ответ на этот вопрос поможет дать статья Википедии. Для сложного объектива при расчёте вводят не одну, а две главные плоскости. Фактически, расстояния d и D, которые вы видели на схеме в самом начале этого поста, в этом случае отсчитываются от разных (хотя и не слишком удалённых друг от друга) точек. Но расстояние D, даже небольшое изменение которого могло бы существенно повлиять на результат просто в силу небольших размеров этого плеча оптической системы, нам, к счастью, знать не нужно, потому что производитель объектива уже рассчитал и нанёс на его корпус фокусное расстояние, через которое величину D, как было показано выше, легко выразить. А что касается изменения расстояния от передней главной плоскости до объекта, то какими бы толстыми ни были линзы и каким бы длинным ни был объектив (мы, конечно, говорим о реальных конструкциях, а не воображаемых объективах размером с дом), при расстоянии до объекта съёмки в несколько сотен метров, как в нашем случае, величиной в десяток-другой сантиметров можно смело пренебречь.
На основании вышеизложенного легко вывести формулу для соотношения расстояний до объектов, запечатлённых на одной и той же фотографии. Причём знать фокусное расстояние объектива и размер матрицы в этом случае уже будет не нужно, поскольку они сократятся при составлении пропорции.
Как видите, даже знаний из программы средней школы достаточно, чтобы убедиться в полной некомпетентности отдельных «экспертов». Любите математику и не давайте себя обмануть!
Как измеряют расстояния до удалённых астрономических объектов?: yuritkachev — LiveJournal
Нередко в научно-популярных статьях по астрономии мы читаем, что расстояние до того или иного космического объекта, о котором идёт речь, составляет тысячи, миллионы или даже миллиарды световых лет. Как же удалось измерить столь колоссальные расстояния? Об этом мы и поговорим сегодня.
 Галактика Треугольник, удалённая от Земли на 2,7 миллиона световых лет
Галактика Треугольник, удалённая от Земли на 2,7 миллиона световых летНаиболее давним методом измерения расстояний до удалённых объектов является так называемый метод параллактического смещения. Он работает не только в космосе, но и на Земле.
Предположим, к примеру, что вам надо измерить расстояние до дерева, находящегося на другом берегу реки. Для того, чтобы сделать это, не переплывая реку с рулеткой в руках, можно проделать следующую процедуру: выбрать некий отрезок (его ещё называют базисом), длина которого строго известна, а затем измерить углы, которые образуются между базисом и направлением на объект в противоположных концах базиса.
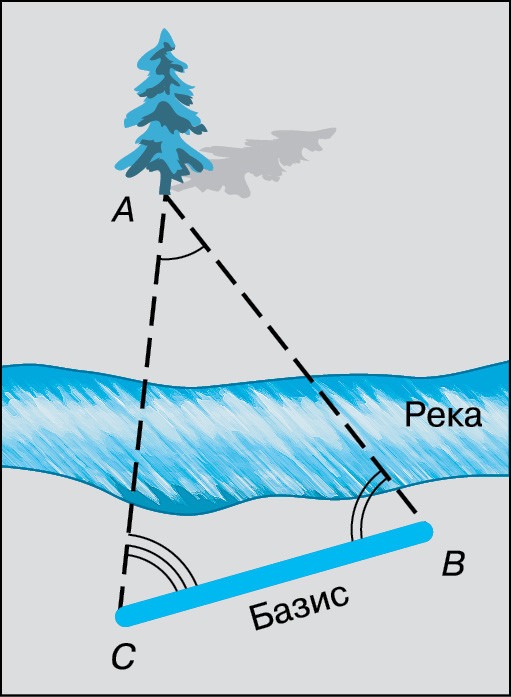 Классическая иллюстрация явления параллакса из не менее классического учебника по астрономии Воронцова-Вельяминова
Классическая иллюстрация явления параллакса из не менее классического учебника по астрономии Воронцова-ВельяминоваЗная длину базиса (СВ) и углы АСВ и СВА можно без труда решить данный треугольник и найти длину отрезка АС (или АВ), определив таким образом расстояние до объекта.
Разумеется, чем больше расстояние до объекта, тем больший базис нам нужно выбрать. Поэтому для измерения расстояний до космических объектов (даже ближайших) нужно выбирать достаточно значительные. Например, расстояния вроде диаметра Земли, а ещё лучше диаметра орбиты Земли вокруг Солнца. Если замерить угол, под которым видна, скажем, звезда из одной и той же точки в некий момент времени, а затем повторить измерение ровно через полгода, то можно посчитать параллактическое смещение именно с таким базисом.
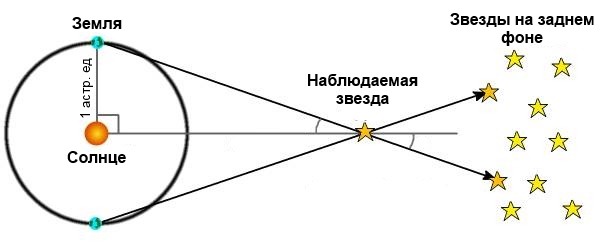
Таким образом астрономам удалось определить расстояние до многих звёзд Млечного Пути; однако для более удалённых объектов, вроде иных галактик (даже ближайших) этот метод уже не работает: параллактическое смещение оказывается слишком незначительным.
Для измерения расстояния до таких объектов используется так называемый закон Хаббла. Чтобы понять, что это такое и как оно работает, нам нужно отклониться немного в сторону.
Как известно, Вселенная расширяется. Однако её расширение многие представляют неверно. Не слишком сведующим в современной космологии представляется, что расширение Вселенной происходит подобно тому, как разлетаются в разные стороны осколки взорвавшейся гранаты. Но это не так. Фактически, можно сказать, что ничто во Вселенной никуда не разлетается: просто пространство между объектами как бы «разбухает»: 1 световой год через некоторое время превращается в 1,1 световых года.
И нам кажется, как будто наблюдаемый объект за это время удалился от нас на 0,1 светового года. Соответственно, 10 световых лет за тот же промежуток времени превратятся уже в 11, то есть, чем дальше от нас находится космический объект, тем быстрее он от нас удаляется. Это явление и называется законом Хаббла. Считается, что скорость убегания космических объектов прямо пропорциональна расстоянию до них, то есть, вычисляется по формуле V=H x r, где r — расстояние от объекта, а H — некая константа, именуемая постоянной Хаббла.
 Крупномасштабная структура Вселенной. Точки — отдельные галактики
Крупномасштабная структура Вселенной. Точки — отдельные галактикиРазумеется, значимое влияние этот закон оказывает лишь на больших (космических)
Таким образом, чтобы рассчитать расстояние до объекта, нам надо «всего лишь» знать его скорость — ну и постоянную Хаббла, конечно.
Как узнать скорость удалённого от нас объекта? Ну, это относительно просто. Уже достаточно давно известно такое явление как красное (или голубое) смещение: изменение частоты волны в зависимости от того, с какой скоростью и в какую сторону относительно наблюдателя движется её источник. Вы наверняка наблюдали нечто подобное, когда едущая вам навстречу машина начинала сигналить: звук кажется более высоким, пока она приближается к вам, а затем делается более низким, когда она минует вас и начинает удаляться. С космическими объектами в принципе то же самое: если объекты приближаются к нам, то их спектр «голубеет», а если удаляются — то краснеет.
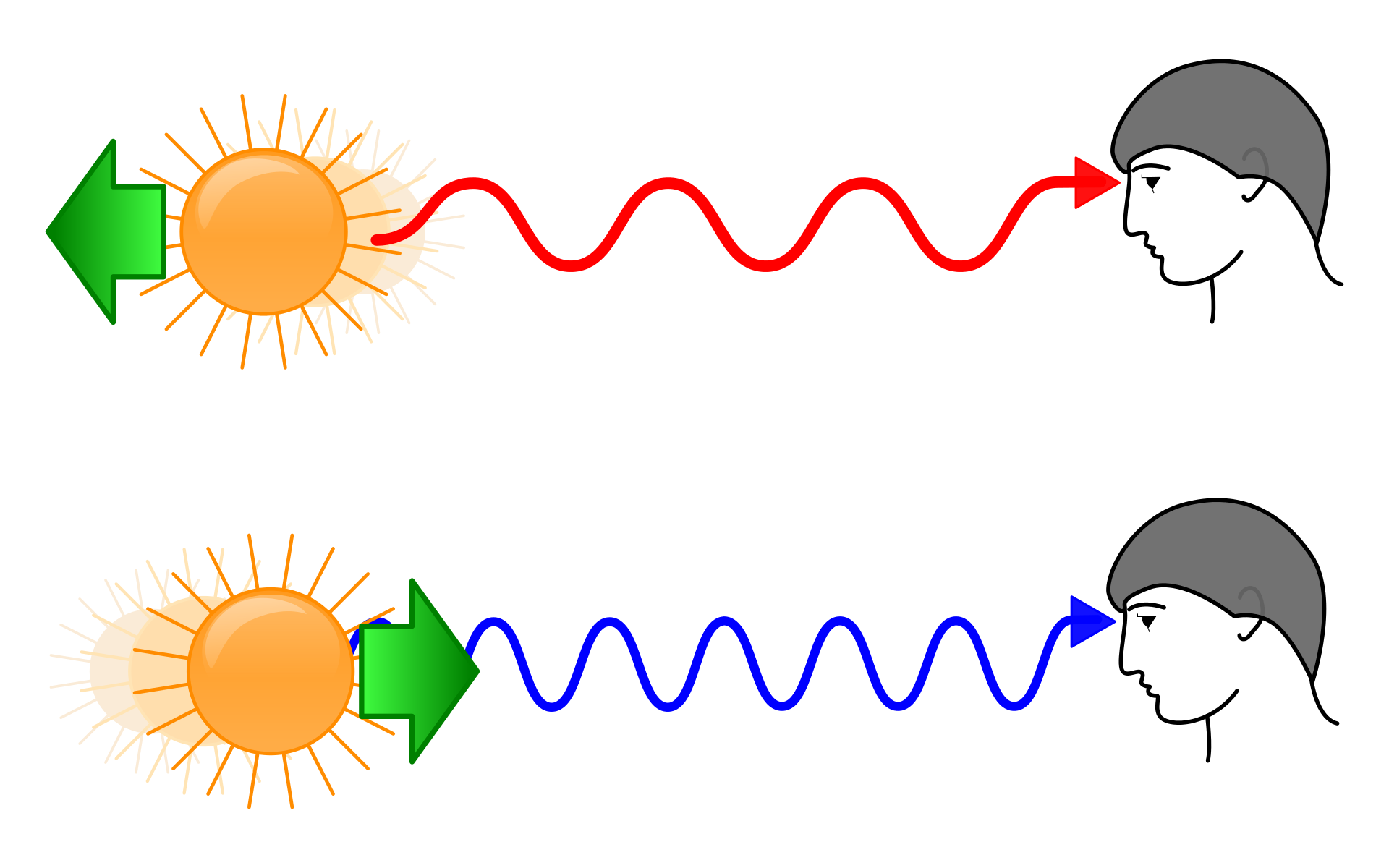
Причём чем быстрее они удаляются — тем быстрее краснеют. И если замерить, насколько он «покраснел», то из стандартных выражений, получаемых в теории относительности, можно посчитать его скорость.
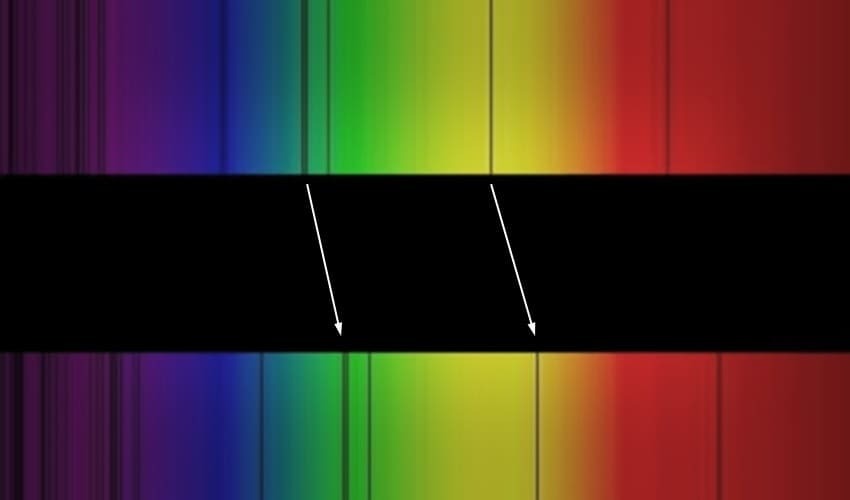
Но для того, чтобы по скорости определить расстояние по закону Хаббла, нужно знать ещё постоянную Хаббла, то есть, коэффициент пропорциональности между скоростью объекта и расстоянием до него.
Для этого нужен некий эталонный удалённый объект, расстояние до которого мы могли бы определить каким-то другим, независимым способом — например, по его светимости, то есть потому, насколько ярким его свет кажется с Земли. Известно, что видимая светимость объекта с изменением расстояния изменяется по формуле обратных квадратов: скажем, свет фонарика на расстоянии в 2 метра примерно в 4 раза менее ярок, чем если смотреть на тот же фонарик с расстояния в 1 метр. И если мы возьмём два объекта, имеющих, как нам известно, равную светимость, расстояние до одного из которых нам при этом известно, то мы можем измерить, насколько второй объект ярче (или тусклее) первого, и на этом расстоянии вычислить, насколько он дальше или ближе первого. Такие объекты-эталоны в астрономии называют стандартными свечами.
Есть несколько видов таких объектов. Одним из них являются цефеиды — особый вид звёзд, яркость которых периодически изменяется со временем. Наблюдая за ближайшими цефеидами, астрономы установили, что амплитуда колебаний яркости и период этих колебаний связаны вполне определённым соотношением. Таким образом, если две цефеиды имеют равный период изменений яркости, то они светятся одинаково. И если мы измерим их наблюдаемую с Земли яркость (опять же, методом прямых наблюдений), то можно сказать, насколько дальше от Земли находятся одна из этих звёзд относительно другой. Если при этом более близкая звезда находится достаточно близко для того, чтобы замерить расстояние до неё методом параллакса, то можно затем, используя закон обратных квадратов, посчитать и расстояние до более удалённой звезды.
 Изменения яркости цефеиды V1 в галактике Андромеды; полный цикл составляет 31 день
Изменения яркости цефеиды V1 в галактике Андромеды; полный цикл составляет 31 деньИ когда телескопы стали достаточно мощны для того, чтобы различить отдельные звёзды в других галактиках, а затем и для того, чтобы выделить среди них цефеиды и посчитать расстояние до них, стало возможным определить и расстояние до этих галактик. Ну а зная его, мы смогли определить значение постоянной Хаббла
 Цефеиды в галактике NGC 5584 (удалённой на 70 миллионов световых лет от Земли)
Цефеиды в галактике NGC 5584 (удалённой на 70 миллионов световых лет от Земли)Именно закон Хаббла и красное смещение являются наиболее актуальными методами измерения расстояний до удалённых объектов во Вселенной.
Вычисление расстояния до наблюдаемого объекта по изображениям со стереопары
В данной работе предлагается алгоритм для вычисления расстояния до наблюдаемого объекта по изображениям со стереопары.
Актуальность данной работы заключается в том, что определение расстояния до объекта по изображениям с двух камер — одна из ключевых задач систем компьютерного зрения. В лабораториях по всему миру ведутся исследования практического применения стереозрения для извлечения информации об окружающем мире.
Одно из применений стереозрения — навигация подвижных роботов. Например, Национальное управление по воздухоплаванию и исследованию космических пространств (НАСА) разработала робота (марсоход Mars Exploration Rover) для исследования поверхности планеты Марс. С помощью системы стереозрения робот может определять расстояние до препятствия и успешно обходить его.
Используемое вработе оборудование.
- две USB-камеры;
- шаблон шахматной доски размера 594 x 841 мм;
- ноутбук с операционной системой MacOS, Python 2.7;
- рулетка измерительная.
Подготовительные работы перед разработкой алгоритма.
- Изготовление шаблона шахматной доски размером 594 x 841 мм на основе стандартного шаблона библиотеки с открытым исходным кодом OpenCV. Данный шаблон имеет 6 узлов по вертикали и 9 узлов по горизонтали.
- Создание стенда из двух USB-камер, закрепленных на твердой, ровной поверхности, расположенных на фиксированном расстоянии друг от друга.
Разработка алгоритма.
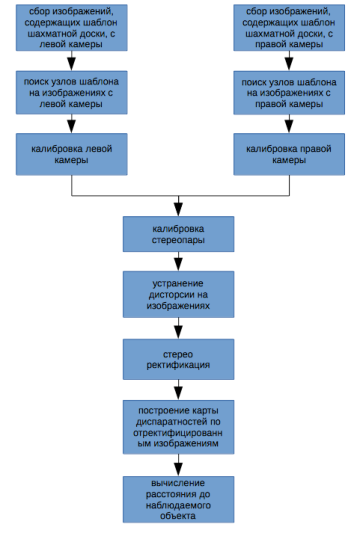
Рис. 1. Алгоритм вычисления расстояния до объекта
На рисунке 1 представлен алгоритм вычисления расстояния до наблюдаемого объекта. Приведем подробное пояснение каждого из шагов.
Шаг 1. На первом шаге производится сбор изображений, на которых изображен шаблон шахматной доски в различных положениях, с левой и правой камер стереопары. Для корректной работы реализации алгоритма необходимо, чтобы шаблон шахматной доски полностью попадал в область видимости камер стереопары и занимал как можно большую площадь кадра.
Шаг 2. На втором шаге производится поиск узлов шаблона шахматной доски на изображениях, полученных на шаге 1. Поиск узлов шаблона осуществляется при помощи библиотечной функции OpenCV find Chessboard Corners(). Координаты узлов шаблона сохраняются для дальнейшего использования.
Шаг 3. На третьем шаге производится калибровка каждой из стереопар по-отдельности. Калибровка камер стереопары осуществляется при помощи библиотечной функции OpenCV calibrate Camera().
Шаг 4. На четвертом шаге производится калибровка всей стереопары. Данные, полученные на третьем шаге подаются на вход библиотечной функции OpenCV stereo Calibrate(), которая считает внутренние параметры стереопары. После процедуры стерео калибровки мы получаем фокусное расстоянии камер в пикселях и координаты принципиальных точек камер.
Шаг 5. На пятом шаге производится устранение дисторсии на изображениях, полученных на первом шаге. Устранение дисторсии производится при помощи библиотечных функций OpenCV init Undistort Rectify Map() и remap(). После выполнения данного шага, все прямые линии наблюдаемых объектов окружающего мира становятся прямыми линиями на изображении.
Шаг 6. На шестом шаге производится ректификация изображений, полученных на шаге 5. Ректификация заключается в выравнивании деформированных изображений, полученных на шаге 5, таким образом, чтобы эпиполярные линии изображений с левой камеры совпадали с эпиполярными линиями изображений с правой камеры. Данную процедуру выполняет библиотечная функция OpenCV stereo Rectify().
Шаг 7. На седьмом шаге для каждой пары соответствующих изображений с левой и правой камер производится построение карты диспаратностей (или карты глубины (depth map)) по изображениям, полученным на шестом шаге. Каждый пиксель карты диспаратностей содержит в себе информацию о том, сколько пикселей по оси OX находится между соответствующие пикселями изображений объекта с левой и правой камер. Построение карты диспаратностей осуществляется на основе алгоритма SGBM при помощи библиотечной функции OpenCV Stereo SGBM.
Шаг 8. На восьмом шаге производится вычисление расстояния до наблюдаемого объекта. Вычисление расстояния до объекта напрямую связано с информацией, которую несет в себе карта диспаратностей, построенная на седьмом шаге.
Приведем вывод формулы для нахождения расстояния до наблюдаемого объекта.
Дано:
- расстояние между камерами стереопары (базовое расстояние, base length)
- фокусное расстояние камеры стереопары

- карта диспаратностей
Найти: расстояние до наблюдаемого объекта 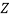
Решение:
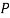 – наблюдаемый объект
– наблюдаемый объект
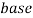 – расстояние между камерами стереопары (в метрах)
– расстояние между камерами стереопары (в метрах)
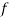 – фокусное расстояние камеры стереопары (в пикселях)
– фокусное расстояние камеры стереопары (в пикселях)
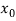 – координата по оси OX точки объекта P на изображении с левой камеры
– координата по оси OX точки объекта P на изображении с левой камеры
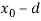 – координата по оси OX точки объекта P на изображении с правой камеры
– координата по оси OX точки объекта P на изображении с правой камеры
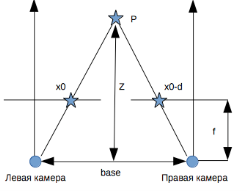
Рис. 2. Пояснительный рисунок
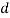 – диспаратность точки x0 объекта P (в пикселях)
– диспаратность точки x0 объекта P (в пикселях)
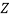 – расстояние до наблюдаемого объекта (в метрах)
– расстояние до наблюдаемого объекта (в метрах)
Посмотрев на Рисунок 2, можно заметить подобные треугольники. Из подобных треугольников следует соотношение: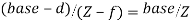
Из данного соотношения следует, что 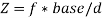
Получили формулу, для вычисления расстояния до наблюдаемого объекта.
Проанализировав данную формулу, можно сделать следующие выводы:
- Расстояние до точки объекта обратно пропорционально диспаратности данной точки. Это свидетельствует о том, что точки, расположенные дальше от плоскости стереопары имеют меньшую диспаратность, нежели точки, расположенные ближе к плоскости стереопары.
- Значение диспаратности прямо пропорционально расстоянию между камерами. Чем больше расстояние между камерами, тем выше диспаратность.
- Разрешение карты диспаратностей линейно зависит от разрешения изображения. Чем выше разрешение изображения, тем более аккуратной получается карта диспаратностей.
Экспериментальная часть.
В данной части работы пройдемся по шагам алгоритма и рассмотрим артефакты, полученные на каждом шаге описанного выше алгоритма. Также построим зависимость ошибки определения диспаратноcтей от расстояния до наблюдаемого объекта.
Приведем наглядные иллюстрации результата работы алгоритма и построим зависимость ошибки определения диспаратноcтей от расстояния до наблюдаемого объекта.
Таблица 1
Действительные расстояния от плоскости стереопары до наблюдаемых объектов
Объект | Расстояние от стереопары до объекта (м) |
Поверхность стола | 2.3 |
Первая книга | 3.11 |
Вторая книга | 3.45 |
Третья книга | 3.72 |
Доска | 4.15 |
Таблица 2
Значения диспаратностей точек наблюдаемых объектов, взятые из карты диспаратностей
Объект | Координата точки объекта (x, y) | Значение диспаратности |
Поверхность стола | (324, 274) | 56.5 |
Первая книга | (508, 207) | 42.0 |
Вторая книга | (415, 199) | 37.6875 |
Третья книга | (335, 200) | 35.0625 |
Доска | (230, 116) | 31.0 |
Под ошибкой определения диспаратности будем понимать модуль разности значения диспаратностей, соответствующего вычисленным расстояниям (на основе базового расстояния, фокусного расстояния и значения диспаратностей) и значения диспаратностей, соответствующего действительным расстоянием.

Рис. 3. Изображение с правой камеры (этап сборки кадров с камеры с изображением шахматной доски)

Рис. 4. Изображение с левой камеры (этап сборки кадров с камеры с изображением шахматной доски)

Рис. 5. Изображение с левой камеры с найденным шаблоном (этап поиска узлов шаблона шахматной доски на изображениях)

Рис. 6. Отректифицированное изображение с правой камеры с устраненной дисторсией (этап ректификации и устранения дисторсии)

Рис. 7. Отректифицированное изображение с левой камеры с устраненной дисторсией (этап ректификации и устранения дисторсии)

Рис. 8. Изображение сцены с наблюдаемыми объектами (стол, три книги и доска, расположенные на расстоянии друг от друга)

Рис. 9. Карта диспаратностей для изображений с правой и левой камеры (стол, три книги и доска, расположенные на расстоянии друг от друга)
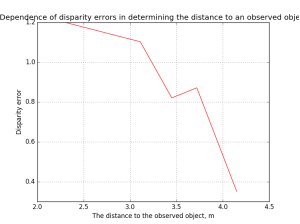
Рис. 10. Зависимость ошибки определения диспаратности от расстояния до наблюдаемого объекта
Вывод.
По графику видно, что наибольшее значение ошибки определения диспаратности для расстояния до наблюдаемого объекта от 2.30 до 4.15 метров составляет всего 1.2, что свидетельствует о хорошем качестве карты диспаратностей.
Заключение.
В данной работе был разработан алгоритм вычисления расстояния до наблюдаемого объекта по изображениям со стереопары. Приведены расчеты ошибки определения диспаратностей в зависимости от расстояния до наблюдаемого объекта.
Литература:
- Richard Hartley, Andrew Zisserman. Multiple View Geometry in Computer Vision, 2nd Edition
- https://www.python.org/
- http://opencv.org/
Основные термины (генерируются автоматически): шаг, изображение, правая камера, шахматная доска, левая камера, расстояние, библиотечная функция, SGBM, вычисление расстояния, устранение дисторсии.
Как в Figma измерить расстояние от объекта до другого объекта
Фигма обладает вполне стандартным набором линеек и привязок, но есть у нее и несколько полезных дополнительных функций.
Как включить линейку
Линейку можно включить из меню View > Rulers, либо сочетанием Shift + R.
 Включение линеек из меню
Включение линеек из менюЧтобы поместить линию на макет, надо перетянуть зажатую мышь с линейки в область макета. А чтобы удалить линию, надо перетянуть ее обратной в область линейки.
Видео: линейки в Figma
Тег video не поддерживается вашим браузером 
Как измерить расстояние между элементами
Чтобы измерить расстояние, следуйте простым инструкциям:
- Выделите первый элементы
- Зажмите alt (Windows) / Option (Mac)
- Наведите курсор на другие элементы
При этом элементы должны находиться в одном фрейме, а расстояния будут показаны как по вертикали, так и по горизонтали.
Видео: расстояния между объектами в Figma
Тег video не поддерживается вашим браузером 
Также прямо в процессе вы можете двигать выбранный элемент с помощью стрелок клавиатуры, чтобы наиболее точно расположить его на экране.
Расстояние X и Y
В параметрах элемента есть его значения X и Y — они показывают расстояние от левого и верхнего края фрейма. При этом если речь идет об экземпляре компонента, то все его внутренние элементы будут считать расстояние от краев фрейма элемента.

В эти поля вы можете вручную вписать значения, но, кроме того, Фигма умеет считать простые математические выражения. Вы можете задать X = 100+500, а Фигма сама посчитает финальное значение 600. Это удобно, если вы располагаете несколько элементов с не «круглыми» значениями длин и высот.
4 шага к пониманию фокусных расстояний
Почему вы должны знать, что такое фокусное расстояние?
Знать, что такое фокусное расстояние и в чем заключаются особенности, особенно важно при покупке объективов. Этот урок даст вам информацию о том, как работают объективы с различным фокусным расстоянием, как использовать их творчески и выбрать те, которые подходят именно вам.
Шаг 1 – Что это на самом деле означает?
Фокусное расстояние вашего объектива в основном определяет, какой масштаб изображения будет в ваших фотографиях: чем больше число, тем больше будет эффект увеличения и приближения.
Очень часто неправильно понимают фокусное расстояние, говоря что оно измеряется от передней или задней линзы. В действительности это расстояние от точки конвергенции до сенсора или пленки в фотоаппарате. Посмотрите на диаграмму ниже, где это объясняется
Шаг 2 – Различные фокусные расстояния и как они используются
Сверхширокоугольный 12-24 мм
Эти объективы считаются узкоспециализированными и не часто входят в комплект объективов обычного фотографа. Они создают столь широкий угол обзора, что изображение может выглядеть искаженным, так как наши глаза не привыкли к такого рода диапазонам. Они часто используются в событийной и архитектурной фотографии, для съемки в ограниченном пространстве. Широкоугольные объективы как бы помещают фотографа в центр событий, делая его уже не наблюдателем, а участником, создают эффект присутствия. Они не очень подходят для портретной съемки, так как увеличивают перспективу настолько, что черты лица могут искажаться и выглядеть неестественно.
Широкоугольный 24-35 мм
Здесь вы найдете много комплектных объективов для полнокадровых камер, они начинаются с фокусного расстояния 24 мм, когда угол широкий, но искажения еще не столь выражены. Эти объективы широко применяются для репортажной фотографии, фотожурналистами для документальных съемок, поскольку они обладают достаточно широким углом, чтобы включить большое количество объектов, и при этом искажения не столь значительны.
Стандартный 35-70 мм
Именно в этом диапазоне фокусных расстояний 45-50 мм угол зрения объектива будет примерно соответствовать тому, как видят наши глаза (исключая боковое зрение). Я лично хотел бы использовать этот диапазон при съемке на улице или на встречах с друзьями в пабе или за обеденным столом. Стандартный объектив, такой как 50 мм f/1.8 – отличный недорогой и дает отличные результаты. Объектив с фиксированным фокусным расстоянием всегда даст лучшее качество изображения, чем зум. Это потому, что он построен с единственной целью. Он делает одну работу хорошо, а несколько заданий плохо.
Начальное телефото 70-105 мм
Этот диапазон обычно является крайним для комплектных объективов. С него начинаются телеобъективы и фикс-объективы для портретной съемки (около 85 мм). Это хороший выбор для портретной съемки, так как им можно снимать крупноплановые портреты без искажений, а также получать отделение объекта от фона.
Теле 105-300 мм
Объективы в этом диапазоне часто используются для далеких сцен, таких как здания, горы. Они не подходят для пейзажей, так как сжимают перспективу. Линзы более длиннофокусного диапазона в основном используются для съемки спорта или диких животных.
Шаг 3 – Как фокусное расстояние влияет на перспективу?
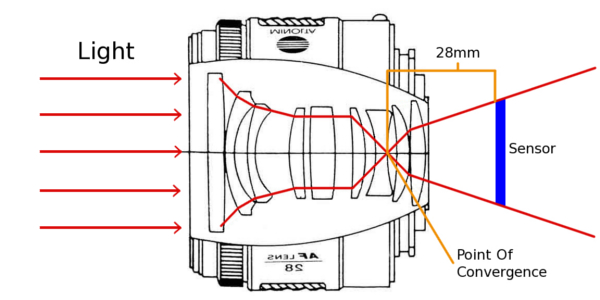
Об этом я уже говорил в предыдущем разделе, но чтобы дать вам более полное представление о влиянии фокусного расстояния на перспективу, я сделал 4 фото одних и тех же предметов на разных фокусных расстояниях и сравнил их. Три предмета (банки с супом) находились в одном и том же положении на расстоянии 10 см друг от друга на каждой фотографии. Стоит отметить, что снимки сделаны на кроп-камеру, поэтому фокусное расстояние будет несколько больше.

Теперь поговорим о том, что такое кроп-фактор. В сущности это означает, что если любую линзу для полного кадра (EF, FX и т.д.) поставить на тушку с кроп-фактором, то часть изображения обрежется. Коэффициент обрезки будет составлять примерно 1.6. В реальном выражении это означает, что если вы снимаете объективом 35 мм, получите результат, как будто снимали объективом 50 мм.
Как это работает – показано на рисунках ниже. Это фактически зуммированое изображение, сужение угла зрения объектива.
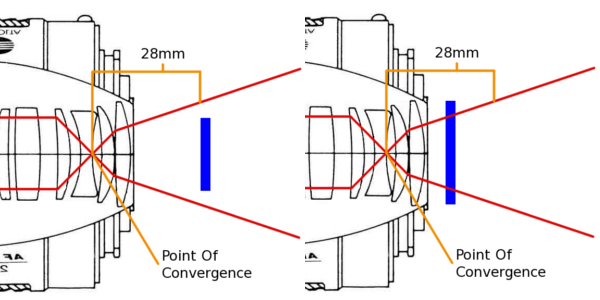
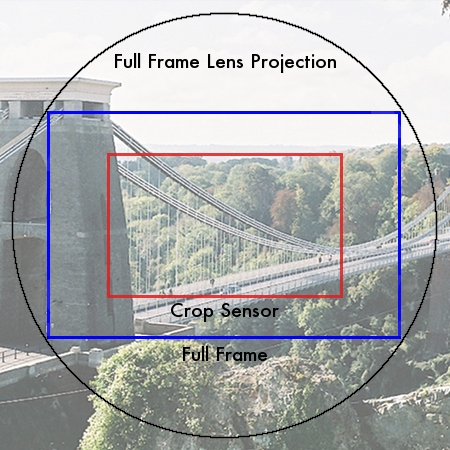
Даже на объективах, которые сконструированы для кроп-камер (EF-S, DX), будет наблюдаться подобный эффект, так как фокусные расстояния всегда указывается для полного кадра. Просто эти объективы на полном кадре дадут сильный эффект виньетирования, так как изображение проецируется не на всю площадь кадра.
Вот и все! И еще два совершенно разных снимка, сделанных на разных фокусных расстояниях. Первый на 24 мм, второй на 300 мм (оба на камере с кроп-сенсором).


Фокусное расстояние объектива – что это такое и зачем?
Что такое фокусное расстояние объектива?
Фокусное расстояние объектива – это физическая характеристика объектива, определяющая его возможности: увеличение и угол обзора, перспективу и размытие заднего плана. А технически это расстояние между матрицей фотокамеры и точкой фокусировки объектива, в которой сходится преломляемое изображение.
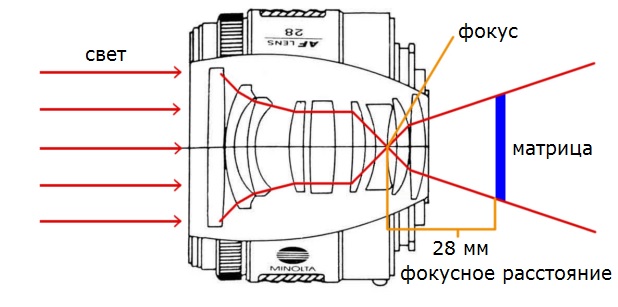 Точку фокусировки называют по-разному:
Точку фокусировки называют по-разному:
- фокус;
- фокальная точка;
- оптический центр объектива;
- точка конвергенции;
- точка схождения лучей.
Фокусное расстояние измеряется в миллиметрах и определяет угол обзора объектива.
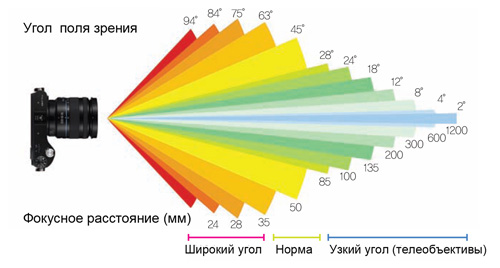
В зависимости от угла обзора объективы делятся на:
- Широкоугольные объективы (ширики) – охватывают фокусные расстояния от 8 до 35 мм, при этом объектив с фокусным расстоянием 8 мм дает обзор 180 градусов, а 35 мм – 63 градуса. Такие объективы используются для съемки пейзажей, интерьеров, некрупных портретов в узких улочках или для съемки большого количества людей в небольшом помещении, где нет возможности отойти подальше. Такие объективы дают масштабную картинку, однако есть и минус – искажения по краям снимка, поэтому людей лучше размещать по центру.
- Портретные объективы (портретники) – охватывают фокусные расстояния от 35 до 85 мм и считаются нормой, то есть дают меньше всего искажений и лучше всего подходят для съемки портретов. Угол обзора тут от 63 до 28 градусов.
- Длиннофокусные объективы (телевики) – охватывают фокусные расстояния от 85 до 600 мм и рассчитаны на съемку удаленных объектов с большим приближением. Используются в основном для съемки дикой природы, репортажа и слежки – ситуаций, когда ближе подойти просто невозможно. Если, к примеру, на 135 мм угол обзора примерно 18 градусов, то на сверхдлиннофокусном объективе 600 мм он сужается до 4 градусов. Дальше только телескопы.
Получается, чем меньше фокусное расстояние, тем больше объектов помещается в кадр и тем больше искажения этих объектов. А чем больше фокусное расстояние, тем лучше объектив приближает удаленные объекты и задний план.
Как влияет фокусное расстояние объектива на картинку?
Давайте посмотрим, как влияет фокусное расстояние объектива на картинку, на примерах фотографий Екатерины Пикулиной, которая фотографировала свою дочь примерно с расстояния трех метров до объекта съемки.



На широкоугольных объективах на первый план выходит красота пейзажа и архитектуры, а человек в кадре является лишь дополнением картинки, подчеркивает собой масштаб окружающего ландшафта. Обратите внимания на вертикальные линии: пространство так растянуто, что искажения видны невооруженным глазом.

Примерно такой угол обзора у человеческих глаз.

А пропорции и перспективу человеческий глаз воспринимает примерно так.

На портретных объективах обычно получается самое красивой размытие заднего плана.


На фокусных расстояниях больше 105 мм при съемке с трех метров даже маленький ребенок в кадр не влезет.
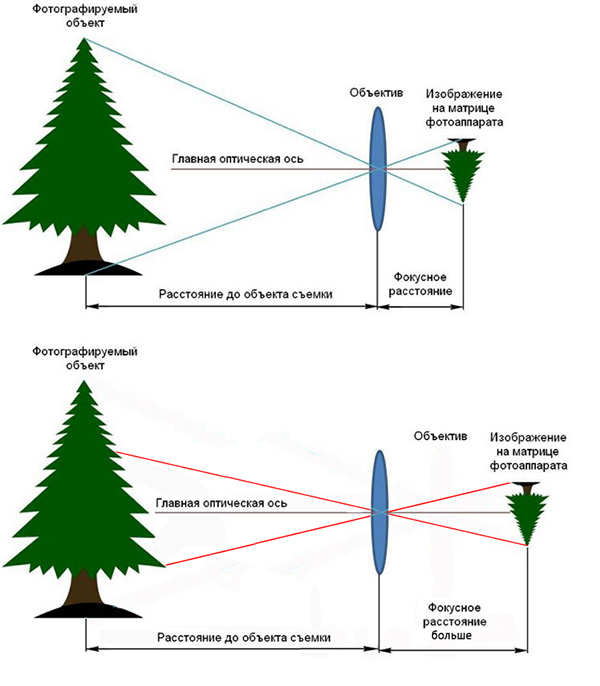
Схематически влияние фокусного расстояния объектива на масштаб снимаемого объекта при неизменном расстоянии до объекта можно представить вот так:
Фокусное расстояние человеческих глаз
Глаза человека имеют обзор до 125 градусов по вертикали и до 150 градусов по горизонтали (при условии, что оба глаза открыты). Если эти цифры перевести в фокусное расстояние в миллиметрах, то получится 22,3 мм (большинство исследователей сходятся именно на этой цифре). По углу обзора глаза похожи на широкоугольный объектив, однако перспективу и пространственные отношения между объектами мы воспринимаем примерно так, как на картинке портретного объектива (примерно 43 мм).
Фиксы и зумы
Но даже если прочесть всю информацию про фокусное расстояние объективов, все равно возникают вопросы: Объектив с каким фокусным расстоянием выбрать? Какое фокусное расстояние наиболее универсально? И что лучше: зум или фикс?
Фикс – это объектив с фиксированным фокусным расстоянием, например, только 85 мм или только 135 мм. А если хочешь приблизить или отдалить объект, придется это делать ножками, отходя или подходя к объекту съемки.
Плюсы фиксов:
- Светосила – у фиксов может быть светосила от f 1,4 (а топовые от f 0,95), тогда как у зумов обычно она стартует от f 2,8 (есть пару исключений, но они очень дорогие).
- Вес – фиксы намного легче зумов, поэтому в использовании они комфортнее.
- Стоимость – фиксы дешевле зумов аналогичного качества и светосилы.
- Качество фото – у фиксов хорошая контрастность, звенящая резкость, низкая дисторсия, эффективное подавление бликов и засветок, минимальные хроматические аберрации.
- Срок службы – поскольку в фиксах нет подвижных линз, они меньше подвержены поломке.
- Использование фильтров – светосила фиксов позволяет использовать творческие фильтры.
Минусы фиксов:
- Необходимость много бегать во время съемки вместо того, чтобы просто крутить колесико на объективе.
- Необходимость покупать дополнительные объективы для покрытия всех необходимых фокусных расстояний.
- Необходимость иметь один зум для путешествий, чтобы не тянуть с собой весь набор фиксов.
- Необходимость менять объективы во время съемки, когда приближение-отдаление ногами не помогает.
- Необходимость использовать нейтрально-серый фильтр при хорошей светосиле объектива и открытой диафрагме в солнечный день.
- Необходимость оперативной смены объектива в полевых условиях чревато загрязнением оптики.

Зум – это объектив с переменным фокусным расстоянием заданного диапазона, например, 18–55 мм или 24–70 мм.
Плюсы зумов:
- Удобство при съемке: нет необходимости бегать вперед-назад при съемке крупных и общих планов.
- Универсальность: нет необходимости брать разные объективы для съемки разных планов и жанров.
Минусы зумов:
- Большой вес – множество линз для охвата разных фокусных расстояний дают определенный вес, не особо комфортный при съемке с рук.
- Малая светосила – из-за большого количества линз такие объективы пропускают меньше света, что будет критично при съемке в помещении и в темное время суток.
- Отсутствие резкости – из-за того, что линз в зум-объективе много и они постоянно в движении, они физически не могут обеспечить такую резкую картинку, как фиксы.
- Высокая стоимость – зумы производить сложнее, поэтому они стоят дороже аналогичных по качеству фиксов.
- Быстрый износ – в сравнении с фиксами, зумы быстрее выходят из строя, так как в них больше подвижных элементов.
Достоинства и недостатки зумов и фиксов не однозначны, так как объектив нужно подбирать под конкретные задачи. Фикс 24 мм может идеально подходить для съемки интерьеров квартир, однако совсем не подойдет для съемки футбола. Поэтому при выборе объектива нужно опираться на личные предпочтения фотографа.
Как фокусное расстояние объектива влияет на перспективу?
В связи с фокусным расстоянием объектива необходимо также пару слов сказать о перспективе.
Перспектива – это соотношение дистанций и размеров объекта съемки и остальных объектов кадра.
Широкоугольные объективы расширяют пространство так, что в кадр попадает больше объектов, чем на стандартный или длиннофокусный объектив. Например, если вы фотографируете девушку в узкой улочке Парижа на объектив 24 мм, то, кроме девушки, в кадр попадут противоположные стены домов этой улочки, брусчатка и небо с Эйфелевой башней вдалеке.

Дома на горизонте, кажется, очень далеко. Перспектива растянута.
Длиннофокусные объективы приближают не только объект съемки, но и задний план к объекту съемки. Например, если вы фотографируете девушку на фоне Эйфелевой башни на 135 мм, то будет казаться, что башня намного ближе к девушке, чем есть на самом деле.

Дома на горизонте, кажется, очень близко. Перспектива сжата.
Получается, что широкоугольные объективы (с небольшим фокусным) растягивают перспективу, а телеобъективы (с большим фокусным) сжимают ее.
Как влияет фокусное расстояние объектива на размытие?
Красота размытия заднего плана – характеристика субъективная.
Размытие зависит от многих факторов:
1. Строения линз объектива. Творческое размытие заднего плана, свойственное объективам типа Gelios 58 мм или Lensbaby 50 мм, является техническим браком оптики, однако эффект радиального размытия многим фотографам очень нравится.
2. Светосилы и значения диафрагмы. Чем светосильнее объектив, тем шире можно открыть диафрагму и получить меньшую глубину резко изображаемого пространства, то есть размыть задний план.

3. Расстояния от фотографа до объекта и от объекта до фона. Степень размытия заднего плана будет тем больше, чем объект съемки отдален от фона.

4. Фокусного расстояния объектива. Поскольку ширик позволяет взять в кадр больше пространства, то и размытого фона (обычно, неоднородного: небо, земля, деревья, здания) при открытой диафрагме в кадре будет больше; а телевик в кадр берет только объект съемки, а задний план за объектом приближает, за счет чего размытый фон при открытой диафрагме получается более однородным и красивым.

На фото с мишкой показано, как меняется степень размытия фона в зависимости от фокусного расстояния при одинаковых настройках камеры. Поскольку на 105 мм перспектива сжата, то и размытый фон получился более однородным.

Как рассчитать фокусное расстояние для кропа?
Поскольку фокусное расстояние объектива – это расстояние от точки фокусировки до матрицы, и размер матрицы камеры не влияет на эту физическую величину. Однако размер матрицы влияет на конечное изображение. Давайте разберемся, каким образом.
Фулфрейм-камера – это камера с полноразмерной матрицей – дорогим сенсорным элементом, который улавливает лучи света и проявляет изображение.
Кроп-камера – это камера с уменьшенной матрицей, которая была разработана для удешевления производства и доступности камер большинству фотолюбителей.
Объективы производятся как для фулфрейма, так и для кропа.
Если объектив для фулфрейма надеть на кроп-камеру, то мы получим урезанное, более плотно кадрированное изображение, чем на фулфрейме.

А если объектив для кропа надеть на фулфрейм, то, наоборот, у изображения появится виньетка в виде черной рамки. Правда, этого можно избежать, если в камере есть автокроп.
 Слева объектив для фулфрейма, справа объектив для кропа. Зеленая – фулфрейм-матрица, желтая – кроп-матрица.
Слева объектив для фулфрейма, справа объектив для кропа. Зеленая – фулфрейм-матрица, желтая – кроп-матрица.
В зависимости от размера матрицы меняется угол обзора и размер изображения, получаемого на одинаковых фокусных расстояниях.
Получается, что на угол обзора влияет не только фокусное расстояние объектива, но и размер матрицы фотоаппарата.
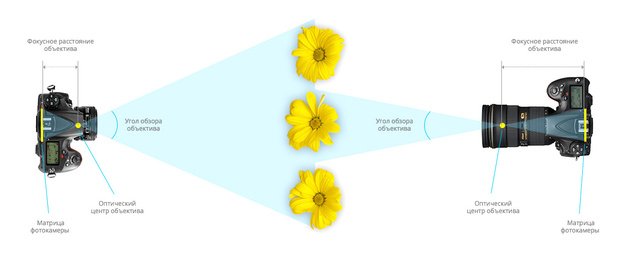
Зависимость улга обзора объектива от фокусного расстояния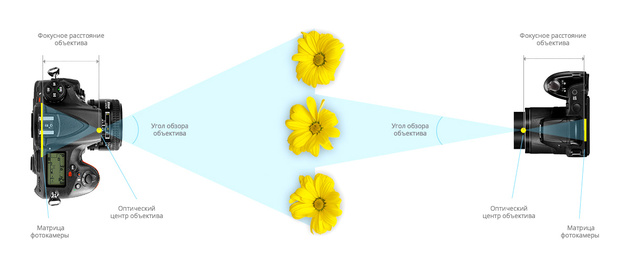
Зависимость угла обзора объектива от размера матрицы камеры
Чтобы разобраться с тем, какому фокусному расстоянию соответствует тот или иной угол обзора объектива, было введено два понятия: кроп-фактор и эквивалентное фокусное расстояние.
Эквивалентное фокусное расстояние позволяет узнать, какое фокусное расстояние будет иметь объектив с таким же углом обзора на полнокадровой (или пленочной) фотокамере. Эта характеристика будет полезна тем, кто задумался о покупке новой фотокамеры с матрицей другого размера и хочет выбрать подходящую для нее оптику, узнать, как на новой камере будут работать его старые объективы.
Кроп-фактор – это условный множитель, отражающий изменение угла обзора объектива при его использовании с матрицами меньшего размера. Например, диагональ матрицы формата APS-C меньше полнокадровой примерно в 1,5 раза. Так что кроп-фактор для матрицы APS-C будет равен 1,5. А вот диагональ матрицы формата Nikon CX меньше полнокадровой в 2,7 раз. Поэтому ее кроп-фактор будет равняться 2,7.
Теперь, зная кроп-фактор, мы сможем рассчитать и эквивалентное фокусное расстояние для объектива 50 мм. Чтобы на кроп-камере с объективом 50 мм получить такую же картинку, как на фулфрейм, нужно фокусное расстояние умножить на кроп-фактор.
50*1,5=75 мм (На кроп-камере с объективом 50 мм получится примерно такое же по размеру изображение, как на фулфрейм-камере с объективом 75 мм).
РЕЗЮМЕ
Теперь, зная все тонкости, на которые влияет фокусное расстояние объектива, вы сможете сделать правильный выбор. Самое главное, это ответить для себя на несколько вопросов:
- В каком жанре фотографии вы снимаете? Для свадебной съемки зум-объектив предпочтительней, в то время как для портретов лучше подойдет портретный фикс. Для детских фотосессий на улице идеально подходит светосильный фикс 85 мм благодаря его светосиле и размытию.
- Какая светосила объектива необходима? Если планируете использовать объектив в разных условиях освещения, вам понадобится светосила f-1.4, а для фотосессий на улице достаточно f-1.8-2.
- Как часто вы будете менять оптику? Если в этом есть необходимость, вы можете приобрести три фикса, которые перекроют наиболее востребованный диапазон фокусных расстояний. А если менять объективы во время съемки неудобно, то лучше подумать про качественный зум.
- Какой бюджет вы готовы выделить на покупку оптики? Если вы не уверены, приобретите для начала объектив с фокусным расстоянием 50 мм и светосилой f-1.8, а потом поймете, каких фокусных расстояний вам не хватает и докупите еще.
Вконтакте
Определение расстояния от точки съемки до объекта съемки. Фотокомпозиция
Определение расстояния от точки съемки до объекта съемки
Изменение второй координаты точки съемки, то есть расстояния между точкой съемки и объектом съемки при постоянном значении двух других координат, приводит прежде всего к изменению масштаба изображения. Он увеличивается с приближением точки съемки к объекту и уменьшается с увеличением этого расстояния.
Таким образом, выбор расстояния, с которого будет вестись съемка, связан с выбором крупности изображения, или, как еще говорят, с выбором крупности плана.
Выбирая крупность плана, фотограф ограничивает рамкой кадра изображаемое пространство и, следовательно, отбирает из всего имеющегося перед ним материала лишь определенную его часть, на которой и сосредоточивается внимание зрителя. Определение масштаба изображения и крупности плана является действенным способом изобразительной трактовки содержания, темы снимка.
Отбирая материал по смысловому значению, фотограф рассматривает его также и со стороны изобразительной, со стороны композиционного размещения элементов объекта съемки в границах кадра.
Действительно, при неправильном определении расстояния от точки съемки до объекта съемки и находящихся в прямой зависимости от него масштаба изображения и крупности плана снимок теряет композиционную завершенность, а вместе с ней и выразительность. Бывает и так, что потеря четкости и определенности композиции приводит к тому, что мысль автора становится непонятной.
Например, съемка натюрморта (фото 12) велась с очень большого расстояния, ничем не обусловленного в данном случае. Масштаб изображения здесь мал, и крупность плана недостаточна. Вследствие этого предметы не заполнили картинной плоскости, в верхней части кадра осталось слишком много свободного места, в то время как нижняя часть кадра оказалась перегруженной предметами.

Фото 12. Пример съемки при слишком малом масштабе изображения
Фотограф с одинаковым безразличием зафиксировал все предметы, никак не организовав их в пределах картинной плоскости, и поэтому все они выглядят совершенно равнозначными, в снимке нет никаких акцентов. Это обстоятельство и отсутствие четкой композиции приводит к тому, что взгляд зрителя с полным безразличием и отсутствием всякой заинтересованности скользит по предметам, затерявшимся в свободных пространствах кадра. В результате снимок не производит впечатления законченности фотокартины и выглядит случайным, поскольку в нем нельзя найти никакого композиционного принципа организации материала.
Таким образом, автору снимка не удалось получить гармоничной композиции. Её можно было достигнуть соответствующим размещением отдельных элементов в прямоугольнике фотографического кадра и правильным определением расстояния от точки съемки до объекта. Эти приемы позволяют добиться стройности композиции.
При съемке натюрморта (фото 13) точка съемки находилась слишком близко к объекту, поэтому изображенные в кадре предметы масштабно преувеличены, выглядят более крупными, чем они есть в действительности. В результате предметы не сразу узнаются зрителем: на снимке изображен светофильтр, о чем мы догадываемся не по фотографическому изображению, а по надписи «ЖС-18» на оправе светофильтра.

Фото 13. Пример слишком крупного масштаба изображения
Несмотря на то, что по формальным признакам картинная плоскость в этом случае заполнена вполне грамотно, композиционное решение снимка нельзя признать удачным. Причина заключается в том, что здесь не выполнено главное требование, предъявляемое к натюрморту, и не решена главная задача этого жанра – правдивый и выразительный показ предметов в их действительном виде и назначении.
При съемке натюрморта (фото 14) расстояние от точки съемки до объекта съемки и масштаб изображения определены правильно. Предметы, составляющие натюрморт, закономерно размещены в прямоугольнике кадра, картинная плоскость рационально использована для выразительного раскрытия темы. В результате возникает четкое и ясное композиционное решение кадра, а отсюда – законченность и целостность фотографического снимка. Поэтому определению расстояния, с которого должен сниматься тот или иной объект, следует уделять самое пристальное внимание.
Фото 14. А. Альварес (ВГИК). Натюрморт
На фото 15, а, б, в один и тот же объект снят с трех различных расстояний. На первом из них объект взят слишком общим планом, вследствие чего в кадре оказалось свободное незаполненное пространство в верхнем правом углу, в то время как левая часть снимка перегружена предметами. В результате в снимке нарушено равновесие, поэтому возникает желание кадрировать снимок, обрезать его сверху и справа.

а
б
в
Фото 15. X. Файзиев (ВГИК). Различные варианты композиционного решения натюрморта
Во втором варианте этой композиции (фото 15, б) картинная плоскость заполнена более правильно, однако и здесь еще имеется некоторая перегруженность нижней левой части кадра.
Попутно следует обратить внимание на слишком резкую и определенную линию стола в обоих вариантах композиции; она четко делит кадр на две части, что в какой-то степени нарушает его цельность. Для устранения этого недостатка следовало плоскость стола и плоскость стены сделать более близкими по тональности. Можно было также иначе распределить резкость по глубине изображаемого пространства, сделав тем самым линию стола менее резкой.
В третьем варианте композиции (фото 15, в) взят еще более крупный масштаб изображения. Внимание зрителя здесь останавливается только на главных объектах. Но исключение из кадра лампы обедняет снимок, делает эффект освещения менее определенным, лишает снимок световой обстановки, настроения. Эта точка слишком близка для съемки данного объекта.
Но изменение расстояния от точки съемки до объекта оказывает влияние не только на масштаб изображения предметов. Изменением масштаба не исчерпывается все значение определения расстояния между точкой установки фотоаппарата и объектом для общего изобразительного строя снимка.
От расстояния, с которого ведется съемка, зависит такой первостепенной важности момент, как перспектива фотографического снимка. Этот вопрос будет рассмотрен подробно в главе четвертой, в связи с задачей изображения трехмерного пространства на двухмерной плоскости снимка.
Поделитесь на страничкеСледующая глава >
DRIVE Labs: определение расстояния
Примечание редактора: это последняя публикация из серии NVIDIA DRIVE Labs , в которой с инженерной точки зрения рассматриваются отдельные проблемы автономных транспортных средств и способы их решения с помощью NVIDIA DRIVE. Следите за нашими предыдущими публикациями, здесь .
Простое правило: если вы не умеете судить о расстоянии, не садитесь за руль. Проблема: судить о расстоянии совсем не просто.
У людей, конечно же, есть два синхронизированных визуальных сенсора с высоким разрешением — наши глаза — которые позволяют нам измерять расстояния с помощью обработки стереозрения в нашем мозгу.
Однако сопоставимая система стереовидения с двумя камерами в беспилотном автомобиле была бы очень чувствительной. Если камеры даже немного рассинхронизированы, это приводит к так называемому «рассогласованию по времени», что приводит к неточным оценкам расстояния.
Вот почему мы выполняем определение расстояния до объекта, используя данные с одной камеры. Однако использование только одной камеры представляет собой ряд проблем.
До появления глубоких нейронных сетей обычным способом вычисления расстояния до объектов по изображениям с одной камеры было предположение, что земля плоская.Исходя из этого предположения, трехмерный мир был смоделирован с использованием двумерной информации из изображения камеры. Геометрия оптики будет использоваться для оценки расстояния от объекта до эталонного транспортного средства.
Но это не всегда работает в реальном мире. Подъем или спуск с холма может привести к неточным результатам, потому что земля неровная.
Такие неверные оценки могут иметь негативные последствия. Автоматический круиз-контроль, проверка безопасности при смене полосы движения и выполнение смены полосы движения — все это зависит от правильной оценки расстояния.
Завышение расстояния — определение того, что объект находится дальше, чем он есть — может привести к невозможности включения автоматического круиз-контроля. Или, что еще более важно, невозможность задействовать функции автоматического экстренного торможения.
Неправильное определение препятствия ближе, чем оно может привести к другим сбоям, таким как включение круиз-контроля или экстренное торможение, когда они не нужны.
На расстоянии с помощью глубокого обучения
Чтобы понять это правильно, мы используем сверточные нейронные сети и данные с одной фронтальной камеры.DNN обучена предсказывать расстояние до объектов, используя данные радаров и лидарных датчиков в качестве достоверной информации. Инженеры знают, что эта информация точна, потому что прямые отражения передаваемых сигналов радара и лидара предоставляют точную информацию о расстоянии до объекта, независимо от топологии дороги.
Обучая нейронные сети на данных радара и лидара вместо того, чтобы полагаться на предположение о плоской поверхности, мы позволяем DNN оценивать расстояние до объектов с одной камеры, даже когда транспортное средство движется вверх или вниз по склону.
 Камера DNN обнаружение расстояния до объекта в туннеле автомагистрали. Зеленые ограничивающие рамки обозначают обнаружение объектов. Число в верхней части каждого поля — это радиальное расстояние в метрах между центром задней оси эго-автомобиля и обнаруженным объектом.
Камера DNN обнаружение расстояния до объекта в туннеле автомагистрали. Зеленые ограничивающие рамки обозначают обнаружение объектов. Число в верхней части каждого поля — это радиальное расстояние в метрах между центром задней оси эго-автомобиля и обнаруженным объектом.В нашей обучающей реализации конвейер создания и кодирования наземных данных автоматизирован. Таким образом, DNN можно обучить с помощью такого количества данных, которое может быть собрано датчиками, без того, чтобы ручная маркировка ресурсов стала узким местом.
Мы используем оценку расстояния до объекта на основе DNN в сочетании с обнаружением объекта и отслеживанием с помощью камеры как для продольного управления (ускорение и замедление), так и для бокового управления (рулевое управление). Чтобы узнать больше о вычислении расстояния до объекта с использованием DNN, посетите нашу страницу DRIVE Networks.
.python — функция Django Distance не возвращает объект Distance
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
