Фото УЗИ при беременности, фото плода при УЗИ во время беременности
4-5 недель
Фото УЗИ плода при беременности 4-5 недельСамый ранний срок, на котором можно разглядеть с помощью трансвагинального УЗИ плодное яйцо в полости матки — это 30-й день гестации, или 4-5 акушерских недель беременности. Уровень ХГЧ крови при этом должен быть не менее 1000 мЕд/мл. В это время ещё не видно ни эмбриона, ни желточного мешка. При визуализации двух плодных яиц можно утверждать, что это дихориальная многоплодная беременность. При визуализации одного плодного яйца можно утверждать, что это монохориальная беременность. Но на этом сроке мы ещё не можем сказать сколько эмбрионов находится в каждом плодном яйце. Кроме того, во время однократного УЗИ мы ещё не можем сказать, прогрессирует ли данная беременность, так как у эмбриона ещё нет сердцебиения. Средний внутренний диаметр (СВД) плодного яйца на этом сроке 2-10 мм.
В заключении будет указано: Маточная беременность малого срока.![]()
Подробнее об УЗИ на ранних сроках беременности
5-6 недель
Фото УЗИ плода при беременности 5-6 недельНа этом сроке внутри плодного яйца появляется белое колечко — это желточный мешок.
В стенке желточного мешка образуются очаги эритропоэза, которые формируют капиллярную сеть, поставляя эритробласты (ядерные эритроциты) в первичную кровеносную систему плода. Желточный мешок является источником первичных половых клеток, которые мигрируют из его стенки к закладкам гонад эмбриона. До 6-й недели после оплодотворения желточный мешок, играя роль «первичной печени», продуцирует многие важные для эмбриона белки — альфа-фетопротеин, трансферрины, альфа2-микроглобулин. К концу I триместра беременности этот провизорный орган перестает функционировать и редуцируется.
Нормальные размеры желточного мешка 2-6 мм. Если в плодном яйце визуализируются два желточных мешка, значит это монохориальная многоплодная беременность. Но если внутри плодного яйца виден один желточный мешок, а эмбрион ещё отчётливо не визуализируется, то это всё ещё может оказаться монохориальная моноамниотическая двойня.
Эмбрион в начале 5-й недели практически неразличим на стенке желточного мешка, но уже к концу недели копчико-теменной размер (КТР) эмбриона достигает 3 мм.
СВД плодного яйца 11-16 мм.
Читайте также: Вредно ли УЗИ при беременности? Опасно ли УЗИ? Как часто можно делать УЗИ?
6 — 7 недель
Фото УЗИ плода при беременности 6-7 недельВнутри плодного яйца мы видим «колечко с драгоценным камнем» 🙂 — это желточный мешок и уже хорошо различимый эмбрион, расположенные рядом. Сердце эмбриона начинает биться в начале 6-й акушерской недели беременности. Именно наличие пульсации сердца является достоверным ультразвуковым признаком прогрессирующей беременности. При КТР ≥6 мм и отсутствии пульсации сердца делается заключение об остановке развития данного эмбриона. Нормальная частота сердечных сокращений (ЧСС) эмбриона в самом начале 6-й недели 70-90 ударов в минуту, но уже к концу недели становится более 100 уд. в мин. На ранних сроках беременности большее значение имеет не ЧСС, а как таковое наличие или отсутствие сердечных сокращений.![]()
Наличие одного желточного мешка, одного эмбриона и одного пульсирующего сердца в подавляющем большинстве случаев говорит об одноплодной беременности. Но в очень редких случаях это могут в последствии оказаться неразделившиеся близнецы.
СВД плодного яйца 13-23 мм. КТР эмбриона 4-9 мм.
Читайте также: «Не хочу УЗИ, хочу ребёнка!». Почему УЗИ при беременности необходимо.
7 — 8 недель
Фото УЗИ плода при беременности 7-8 недельРасстояние между эмбрионом и желточным мешком постепенно увеличивается и становится хорошо различим желточный проток (ductus vitellinus), соединяющий между собой желточный мешок и кишечник эмбриона. Так же, как и желточный мешок, проток на более поздних сроках запустевает и рассасывается, но если это не происходит по каким-то причинам, то у человека формируется слепое выпячивание стенки подвздошной кишки — дивертикул Меккеля.
До этого срока хорион имеет кольцевидную форму, окружает плодное яйцо со всех сторон и пока ещё нельзя сказать к какой стенке матки прикрепился эмбрион.
В случае монохориальной двойни ещё не видно амниотических оболочек и при наличии двух желточных мешков всё ещё нельзя сказать является ли данная беременность моно или диамниотической. Если плодное яйцо содержит два желточных мешка и два плода с наличием сердечной активности, в последующем количество амниотических полостей может быть больше, чем количество плацент (монохориальная диамниотическая) или одинаковым (монохориальная моноамниотическая). В этом случае точно определить амниональность возможно после 8 недель, когда амниотические оболочки начинают четко визуализироваться.
ЧСС эмбриона 130-160 ударов в минуту.
СВД плодного яйца 24-30 мм, КТР эмбриона 9-15 мм.
8 — 9 недель
Фото УЗИ плода при беременности 8-9 недельВо время УЗИ у эмбриона уже можно отчётливо различить отдельные сегменты — голову, туловище, конечности. Появляется первая двигательная активность. Становятся хорошо видны амниотические оболочки и уже можно говорить о количестве амниотических пузырей при многоплодной беременности. Происходит дифференцировка хориона на гладкий, обращённый в сторону полости матки, и ветвистый, из которого впоследствии будет формироваться плацента, так что уже можно говорить о преимущественном расположении хориона по передней или задней стенке матки.
Появляется первая двигательная активность. Становятся хорошо видны амниотические оболочки и уже можно говорить о количестве амниотических пузырей при многоплодной беременности. Происходит дифференцировка хориона на гладкий, обращённый в сторону полости матки, и ветвистый, из которого впоследствии будет формироваться плацента, так что уже можно говорить о преимущественном расположении хориона по передней или задней стенке матки.
ЧСС эмбриона увеличивается до 160-180 ударов в минуту.
СВД плодного яйца 31-37 мм. КТР эмбриона 16-22 мм.
9 — 10 недель
Фото УЗИ плода при беременности 9-10 недельПродолжается развитие эмбриона. Уже отчётливо видны ручки ножки, а на хорошем аппарате порой удаётся разглядеть даже пальчики на руках и ногах. Частота сердцебиения на этом сроке достигает 170-190 ударов в минуту. Шевеления эмбриона становятся активными, и есть работы, показывающие, что чем активнее ребёнок, тем длиннее будет пуповина (хотя тут может быть и обратная зависимость).![]()
СВД плодного яйца 38-44 мм. КТР эмбриона 23-30 мм.
шагинян.рф — Акушерство и Гинекология
ВЗРОСЛЫЕ (репродуктивный период)
| Параметр | Нормальное значение |
|
Размеры тела матки: длина толщина ширина |
42-61 мм 28-42 мм 42-60 мм |
|
Эндометрий: Сразу после менструации в 1-ую фазу цикла на 5-7 день цикла в периовуляторный период во 2-ую фазу цикла перед менструацией менопауза (стойкая) менопауза на фоне ЗГТ |
1-6 мм до 9 мм до 7 мм 10-12 мм 12-13 мм до 15 мм до 5 мм до 10 мм |
|
Шейка матки: длина цервикальный канал в периовуляторный период |
до 30-40 мм до 4-5 мм |
|
Яичники: длина толщина ширина объём на 5-7 день цикла (неовулирующего) объём овулирующего объём в постменопаузе антральные фолликулы доминантный фолликул |
20-39 мм 15-25 мм 20-30 мм 3-9 см3 до 15 см3 до 4,5 см3 / до 2,2 см3 4-10 шт до 10 мм в d 15-25 мм |
СВД плодного яйца и срок беременности* (A.
| СВД плодного яйца | Срок, нед./дн. | СВД плодного яйца | Срок, нед./дн. |
| 1 мм | — | 26 мм | 7/4 |
| 2 мм | 4/6 | 27 мм | 7/5 |
| 3 мм | 5/0 | 28 мм | 7/6 |
| 4 мм | 5/1 | 29 мм | 8/0 |
| 5 мм | 5/2 | 30 мм | 8/1 |
| 6 мм | 5/2 | 31 мм | 8/2 |
| 7 мм | 5/3 | 32 мм | 8/3 |
| 8 мм | 5/4 | 33 мм | 8/3 |
| 9 мм | 5/5 | 34 мм | 8/4 |
| 10 мм | 5/5 | 35 мм | 8/5 |
| 11 мм | 5/6 | 36 мм | 8/6 |
| 12 мм | 6/0 | 37 мм | 9/0 |
| 13 мм | 6/1 | 38 мм | 9/1 |
| 14 мм | 6/2 | 39 мм | 9/2 |
| 15 мм | 6/2 | 40 мм | 9/3 |
| 16 мм | 6/3 | 41 мм | 9/4 |
| 17 мм | 6/4 | 42 мм | 9/5 |
| 18 мм | 6/5 | 43 мм | 9/6 |
| 19 мм | 6/6 | 44 мм | 9/6 |
| 20 мм | 6/6 | 45 мм | 10/0 |
| 21 мм | 7/0 | 52 мм | 11/0 |
| 22 мм | 7/1 | 59 мм | 12/0 |
| 23 мм | 7/2 | 66 мм | 13/0 |
| 24 мм | 7/3 | 72 мм | 14/0 |
| 25 мм | 7/4 | 73 мм | 14/1 |
КТР эмбриона/плода и срок беременности* (Hadlock, ± 5 дней)
| КТР эмбриона/плода | Срок, нед. /дн. /дн. |
КТР эмбриона/плода | Срок, нед./дн. |
| 2,0 мм | 5/5 | 34,7 мм | 10/3 |
| 2,4 мм | 5/6 | 36,1 мм | 10/4 |
| 3,2 мм | 6/0 | 37,5 мм | 10/5 |
| 4,0 мм | 6/1 | 39,0 мм | 10/6 |
| 4,9 мм | 6/2 | 40,5 мм | 11/0 |
| 5,7 мм | 6/3 | 42,1 мм | 11/1 |
| 6,6 мм | 6/4 | 43,7 мм | 11/2 |
| 7,5 мм | 6/5 | 45,4 мм | 11/3 |
| 8,3 мм | 6/6 | 47,1 мм | 11/4 |
| 9,2 мм | 7/0 | 48,9 мм | 11/5 |
| 10,1 мм | 7/1 | 50,7 мм | 11/6 |
| 11,0 мм | 7/2 | 52,6 мм | 12/0 |
| 11,9 мм | 7/3 | 54,5 мм | 12/1 |
| 12,8 мм | 7/4 | 56,4 мм | 12/2 |
| 13,7 мм | 7/5 | 58,4 мм | 12/3 |
| 14,6 мм | 7/6 | 60,3 мм | 12/4 |
| 15,6 мм | 8/0 | 62,3 мм | 12/5 |
| 16,5 мм | 8/1 | 64,3 мм | 12/6 |
| 17,5 мм | 8/2 | 66,3 мм | 13/0 |
| 18,5 мм | 8/3 | 68,2 мм | 13/1 |
| 19,5 мм | 8/4 | 70,1 мм | 13/2 |
| 20,5 мм | 8/5 | 72,0 мм | 13/3 |
| 21,5 мм | 8/6 | 73,9 мм | 13/4 |
| 22,6 мм | 9/0 | 75,7 мм | 13/5 |
| 23,7 мм | 9/1 | 77,5 мм | 13/6 |
| 24,8 мм | 9/2 | 79,3 мм | 14/0 |
| 25,9 мм | 9/3 | 81,0 мм | 14/1 |
| 27,1 мм | 9/4 | 82,7 мм | 14/2 |
| 28,2 мм | 9/5 | 84,4 мм | 14/3 |
| 29,5 мм | 9/6 | 86,0 мм | 14/4 |
| 30,7 мм | 10/0 | 87,6 мм | 14/5 |
| 32,0 мм | 10/1 | 89,2 мм | 14/6 |
| 33,3 мм | 10/2 | 90,7 мм | 15/0 |
* Указаны акушерские сроки беременности.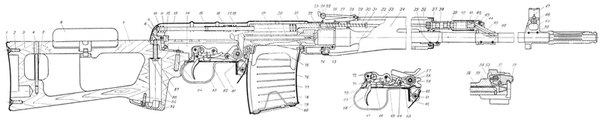 Срок от зачатия = минус 2 недели.
Срок от зачатия = минус 2 недели.
Пневматическая винтовка СВД (Драгунова): характеристики, модификации, цены
Пневматические винтовки находят широкое применение в нашей жизни. Это и спортивные соревнования, и игровые сражения, и охота. Они намного менее травматичные, чем боевые, поскольку для выстрела используют не настоящие боевые, а пластиковые пули или шарики. Кроме того, эти орудия влаго- и морозоустойчивы и имеют более короткий цикл перезарядки.
Виды механизмов, применяющихся в пневматической винтовке
Чаще всего в пневматическом оружии для страйкбола используются такие механизмы:
- Пневмоэлектрический: под действием электрического разряда в сжатой газовой среде происходит горение металла. Это создает импульс для выстрела пули.
- Пружинно-поршневой. Массивный поршень приводится в действие за счет увеличения давления воздуха, которое дает энергия сжатой пружины. Пружинно-поршневые винтовки выпускаются как с нарезным стволом, который перезаряжается способом перелома, так и с неподвижным стволом, который взводится специальным рычагом.

Мишени для соревнований и для развлекательной стрельбы. Здесь можно узнать как правильно их сделать своими руками с помощью принтера и А4.
Отличия винтовок для страйкбола
Оружие, использующееся для игры в страйкбол, обладает характерными особенностями. Перечислим их:
- Страйкбольная винтовка поражает цели небольшими шариками из пластика. Скорость выстрела при этом может достигать 200 м/сек.
- Электропневматические орудия для страйкбола обладают практически 100% фотографической идентичностью с настоящими боевым оружием.
- Для проведения игры на большой открытой местности предпочтительны штурмовые и снайперские винтовки, например, СВД.
- Приобретение страйкбольной винтовки не сопряжено с долгой процедурой получения разрешения и лицензии. Поскольку официально оно вообще не считается оружием.

- Орудия для страйкбола имеют средний уровень прицельности и ограниченное количество шариков.
- Модели среднего и высокого ценового сегмента оснащены системой Хоп-ап, повышающей точность прицела.
- В пружинно-поршневом страйкбольном оружии взводить затвор нужно каждый раз перед выстрелом, чтобы привести в движение пружину и дослать шарик в ствол.
Видео-обзор винтовки СВД King Arms для страйкбола:
Сравнительный анализ производителей винтовок СВД
Пневматическая винтовка СВД представляет собой копию легендарной снайперской винтовки Драгунова, адаптированную под пневматику.
Перед приобретением той или иной модели винтовки целесообразно изучить ассортимент моделей, который предлагает нам рынок пневматического оружия.
Технические характеристики пневматических винтовок Драгунова различных марок
| Параметр/марка оружия | CYMA SVD CM057 | King Arms Dragunov SVD Rifle AEG (120936) | ASG SVD-S | A&K SVD Spring Rifle |
| Страна-производитель | Китай | Тайвань | Китай | Китай |
| Скорость выстрела, м/с | 130-140 | 131 | 95 | 130 |
| Калибр, мм | 7. | 6 | 8 | 7.62 |
| Вес, г | 3100 | 3175 | 3500 | 2690 |
| Емкость магазина, шаров | 120 | 200 | 200 | 60 |
| Источник энергии | Электро-пневматический | Пружинно-поршневой | Пружинно-поршневой | Пружинно-поршневой полуавтоматический, газоотвод |
| Размер, см | Длина в разложенном виде – 1090, со сложенным прикладом — 838 | Общая длина 1210 | Общая длина 1100, длина ствола 550 | Общая длина 1200 |
| Материал | Корпус из металла, приклад и цевье — пластик | Металл | Ложе из пластика | Корпус металлический, цевье и приклад пластиковые |
| Мощность, Дж | 0.5 | 1.4 | 0.9 | 0.5 |
| Тип пуль | Пластиковые шарики | Пластиковые шарики весом | Пластиковые шарики | Пластиковые шарики |
| Тип спуска | Регулируемый | Не регулируемый | Не регулируемый | Не регулируемый |
| Тип предохранителя | автоматический | ручной | ручной | ручной |
| Прицельные приспособления, дополнительная комплектация | Регулируемый Хоп-ап.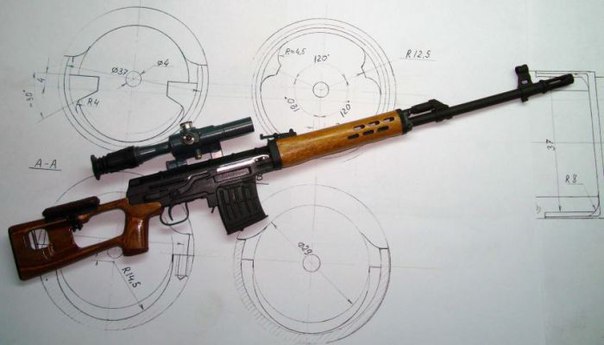 | Регулируемый целик | Регулируемый Хоп-ап | Регулируемый хоп-ап |
| Средняя цена, р | 13000 | 10500 | 8400 | 5000 |
| Базовая комплектация | Винтовка, аккумулятор, бункерный магазин, шомпол, зарядное устройство, шары | Винтовка, магазин, шомпол | Винтовка, инструкция, магазин | привод, инструкция, магазин |
CYMA CM057 СИД 3к
Внешний вид пневматической винтовки Драгунова SVD CYMAВсе габариты данной винтовки идентичны оригиналу. Оружие укомплектовано переключателем огня, имеющим 2 положения (полуавтомат и предохранитель) и съемной накладкой под щеку. Особенностью данной модели является расположение аккумулятора в цевье.
Преимущества
- Удобно расположенный центр тяжести, маневренность и ухватливость.
- Компактный размер как в сложенном, так и в раскрытом виде.
- Идеальная длина стволика для используемой ЦПГ.

- Надежный механизм СВД RS.
King Arms Dragunov SVD Rifle AEG (120936)
Как выглядит пневматическая винтовка SVD Rifle AEGДанная пневматическая копия СВД произведена из качественного пластика и металла. Специально для удобства игры в страйкбол оружие снабжено системой AEG для нагнетания нужного давления воздуха. На винтовке закреплено специальное электромеханическое устройство, содержащее аккумулятор, насос и подающее приспособление. При срабатывании спускового крючка оно одновременно создает давление для выстрела и подает шарик.
Стрельба производится одиночными выстрелами. Параметры модели King Arms Dragunov SVD Rifle AEG позволяют поражать цели с высокой точностью на отдалении до 50 м.
Также в модели предусмотрена возможность модернизации базового комплекта дополнительной оптикой, которая крепится к стволу по принципу «ласточкиного хвоста».
Высокие результаты, которые показывает данное орудие, делают его востребованным широким кругом людей. Среди них историки-любители, участвующие в реконструкции военных действий времен Второй Мировой войны, участники непрофессиональных спортивных соревнований и охотники, которые успешно охотятся с ее помощью на птиц и крупных грызунов.
Среди них историки-любители, участвующие в реконструкции военных действий времен Второй Мировой войны, участники непрофессиональных спортивных соревнований и охотники, которые успешно охотятся с ее помощью на птиц и крупных грызунов.
ASG SVD-S
Обзор пневматической винтовки SVD-SЭта модель повторяет винтовку СВД, которая в 1990 г. была модернизирована в СВДС (снайперская винтовка Драгунова складная). Пистолетная рукоять и вытянутый приклад дают возможность с легкостью двигаться по полю для игры, без труда удерживая компактное орудие в руках.
Плюсы
- Регулируемый хоп-ап.
- Возможность доустановки прицела.
- Емкий магазин.
Выбираем пневматическую винтовку для охоты в этой статье. Сравнение нескольких моделей винтовок с разными калибрами и типами системы.
A&K SVD Spring Rifle
Пневматическая винтовка Драгунова SVD Spring RifleБлагодаря высочайшему качеству сборки орудия и отсутствия каких-либо люфтов между деталями из металла создается полное ощущение работы с настоящим боевым оружием.
Металлический прицел идентичен тому, что используется в модели АК47. Имеется прицельная планка с V-подобным профилем, имеющим калибровочные деления, рассчитанные до 1200 м с интервалом в 10 м.
Цевье и приклад сделаны из ударопрочного пластика. Крышка затвора, корпус, ствол, и прицел – металлические. Поршень взводится в ручном режиме при помощи язычка шторки затвора.
Возможна эффективная модернизация винтовки путем замены пружины на более мощную и использования стволика меньшего размера.
Кроме того, можно увеличить скорость выстрела до 155 м\с и облегчить передергивание затвора данной модели путем докомплектации ее поршнем Conversion Kit, содержащим CO2-клапан.Каждая модель имеет свои достоинства и характерные черты. Тщательно изучив их и сравнив между собой, можно сделать выбор в пользу той пневматической винтовки, параметры которой подходят вам больше всего. Так, если стоит цель купить бюджетный вариант неплохого качества, то имеет смысл рассмотреть модель ASG SVD-S, преимуществами которой является складной механизм, возможность комплектации точным прицелом и регулируемый Хоп-ап. Если же качество для вас значит больше, чем цена, то смело выбирайте орудие марки CYMA SVD CM057. Эта мощная электропневматическая винтовка, которая отсутствует в калибре 4,5 мм, но богатой базовой комплектацией с лихвой окупает затраченные на ее приобретение средства.
Тщательно изучив их и сравнив между собой, можно сделать выбор в пользу той пневматической винтовки, параметры которой подходят вам больше всего. Так, если стоит цель купить бюджетный вариант неплохого качества, то имеет смысл рассмотреть модель ASG SVD-S, преимуществами которой является складной механизм, возможность комплектации точным прицелом и регулируемый Хоп-ап. Если же качество для вас значит больше, чем цена, то смело выбирайте орудие марки CYMA SVD CM057. Эта мощная электропневматическая винтовка, которая отсутствует в калибре 4,5 мм, но богатой базовой комплектацией с лихвой окупает затраченные на ее приобретение средства.
Непревзойденное оружие снайпера
Снайперская винтовка Драгунова – надежное, выносливое, безотказное в самых суровых условиях оружие.
СВД зарекомендовала себя в конфликтах в Афганистане, Чечне и других горячих точках в разных странах мира и была одним из самых желанных военных трофеев. С момента ее создания в 1963 году было создано всего несколько модификаций.
С момента ее создания в 1963 году было создано всего несколько модификаций.
7,62 мм снайперская винтовка Драгунова была создана в 1963 году группой конструкторов под руководством Евгения Драгунова. В 1958 году коллектив, возглавляемый Драгуновым, одержал победу в конкурсе на создание самозарядной снайперской винтовки для Советской Армии, проводимого Главным Ракетно-Артиллерийским Управлением (ГРАУ) Генштаба Советской Армии (СА). Перед Драгуновым стояла сложная задача – добиться высочайшей точности оружия и на одну цель расходовать один патрон. Формула «One kill – one shot» используется профессиональными снайперами при оценке степени оптимальности работы. И поставленная задача была полностью выполнена.
В 1963 году СВД была принята на вооружение СА, став штатным оружием армейских снайперов. Сейчас СВД стоит на вооружении многих стран мира.
Это самозарядная винтовка, в которой использована такая же работа автоматики, как и в АК-47, но с измененной системой использования энергии газов.![]()
Среди очевидных преимуществ – точность, удобство и практичность. Благодаря удачной балансировке винтовку удобно держать в руках. Еще одна особенность – не сильная отдача. Прицельная стрельба из СВД может вестись даже на дистанциях свыше 800 м.
Специально для СВД был создан «снайперский» патрон с пулей со стальным сердечником, однако винтовка может использовать всю номенклатуру отечественных патронов 7.62х54R, что позволило решить проблему обеспечения снайперов боеприпасами.
ТТХ
Калибр: 7.62x54R мм
Механизм: Полуавтоматический, газоотвод
Масса без патронов и прицела: 4.3 кг
Длина общая: 1225 мм
Длина ствола: 620 мм
Высота с оптическим прицелом: 230 мм
Ширина с оптическим прицелом: 88 мм
Магазин: 10 патронов, коробчатый
Темп стрельбы: 30 выстрелов/мин
Начальная скорость пули: 830 м/с
Скорострельность: до 30 в/м
Дульная энергия: 4064 дж
Прицел: ПСО-1, 4Х кратность
Точность: Меньше 2 угловых минут на 600м
Прицельная дальность с открытым прицелом: 800 м
Прицельная дальность с оптическим прицелом: 1300 м
Прицельная дальность с ночным прицелом: 300 м
Производитель – Ижевский машиностроительный завод.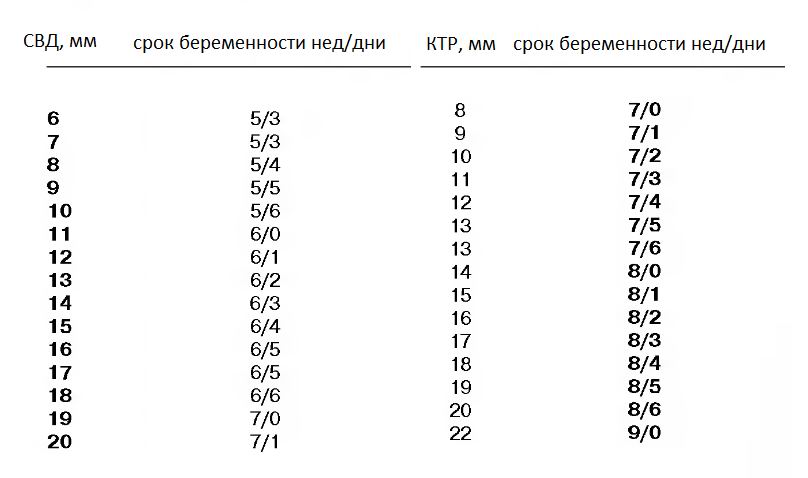
До настоящего момента появилось всего несколько модификаций винтовки.
Так, специально для ВДВ был разработан вариант винтовки со складывающимся прикладом – СВД-С, признанный зарубежными специалистами лучшей самозарядной снайперской винтовкой в мире.
Еще одна модификация – СВУ (снайперская винтовка укороченная) по системе булл-пап. В процессе создания обнаружилась возможность без ущерба укоротить ствол на 100 мм. На этой модификации опробовано ствольное устройство, совмещающее глушитель, пламегаситель и дульный тормоз. Это позволило снизить уровень звука выстрела, что обеспечило возможность максимальной маскировки снайпера при условиях боя в городе.
В начале 90-х был разработан так называемый «снайперский автомат» СВД – СВУ-АС (снайперская винтовка укороченная, автоматическая, с сошками). Основной заказчик – МВД.
В мае 2013 года «Ижмаш» представил первый образец снайперской винтовки ВС-121, разработанный на платформе снайперской винтовки Драгунова. Использование компоновки булл-пап сделало оружие более компактным, легким и сбалансированным. ВС-121 оснащена тактическим глушителем. При этом на нее могут быть установлены все современные оптико-электронные приборы, используемые снайперами. На сегодняшний день образец проходит испытания.
Использование компоновки булл-пап сделало оружие более компактным, легким и сбалансированным. ВС-121 оснащена тактическим глушителем. При этом на нее могут быть установлены все современные оптико-электронные приборы, используемые снайперами. На сегодняшний день образец проходит испытания.
«Ижмаш» – крупнейший российский производитель боевого автоматического и снайперского оружия, управляемых артиллерийских снарядов, а также широкого спектра гражданской продукции – охотничьих ружей, спортивных винтовок, станков и инструмента. Предприятие основано в 1807 году. Продукция «Ижмаша» поставляется в 27 стран мира, включая США, Великобританию, Германию, Норвегию, Италию, Канаду, Казахстан и Таиланд.
Матрицы и линейная алгебра (математика)
Матрицы и линейная алгебра (математика)| Математика |
Разложение сингулярного значения
Сингулярное значение и соответствующие сингулярные векторы прямоугольной матрицы A являются скаляром и парой векторов и и v , которые удовлетворяют
С сингулярными значениями на диагонали диагональной матрицы и соответствующими сингулярными векторами, образующими столбцы двух ортогональных матриц U и V , мы имеем
Поскольку U и V ортогональны, это становится разложением по сингулярным значениям
Полное разложение по сингулярным значениям матрицы м на n включает в себя м на м U , м на n и n по n V .![]() Другими словами, U и V квадратные и имеют тот же размер, что и A . Если A имеет намного больше строк, чем столбцов, результирующий U может быть довольно большим, но большинство его столбцов умножаются на нули. В этой ситуации декомпозиция размера economy экономит как время, так и хранилище, создавая m -by- n U , n -by- n и тот же V .
Другими словами, U и V квадратные и имеют тот же размер, что и A . Если A имеет намного больше строк, чем столбцов, результирующий U может быть довольно большим, но большинство его столбцов умножаются на нули. В этой ситуации декомпозиция размера economy экономит как время, так и хранилище, создавая m -by- n U , n -by- n и тот же V .
Разложение по собственным значениям — подходящий инструмент для анализа матрицы, когда она представляет отображение из векторного пространства в себя, как это делается для обыкновенного дифференциального уравнения.С другой стороны, разложение по сингулярным значениям является подходящим инструментом для анализа отображения из одного векторного пространства в другое векторное пространство, возможно, с другой размерностью. Большинство систем одновременных линейных уравнений попадают во вторую категорию.
Если A является квадратным, симметричным и положительно определенным, то его разложение на собственное значение и сингулярное значение одинаково.![]() Но, поскольку A отклоняется от симметрии и положительной определенности, разница между двумя разложениями увеличивается.В частности, разложение вещественной матрицы по сингулярным числам всегда является действительным, но разложение по собственным значениям реальной несимметричной матрицы может быть сложным.
Но, поскольку A отклоняется от симметрии и положительной определенности, разница между двумя разложениями увеличивается.В частности, разложение вещественной матрицы по сингулярным числам всегда является действительным, но разложение по собственным значениям реальной несимметричной матрицы может быть сложным.
Для примера матрицы
полное разложение по сингулярным числам —
[U, S, V] =
свд(A) U = -0,6105 0,7174 0,3355 -0,6646 -0,2336 -0,7098 -0,4308 -0,6563 0,6194 S = 14,9359 0 0 5,1883 0 0 V = -0,6925 0.7214 -0,7214 -0,6925
Вы можете проверить, что U * S * V ' равно A с точностью до ошибки округления. Для этой небольшой задачи декомпозиция размера экономии лишь немного меньше.
[U, S, V] = svd (A, 0) U = -0,6105 0,7174 -0,6646 -0,2336 -0,4308 -0,6563 S = 14,9359 0 0 5,1883 V = -0,6925 0,7214 -0,7214 -0,6925
Опять же, U * S * V ' равно A с точностью до ошибки округления.
| Собственные значения | Полиномы и интерполяция |
SVD-Demo: сжатие изображений
О разложении по сингулярным значениям
Матрица размера m × n представляет собой сетку действительных чисел, состоящую из m строк и n столбцов.
В линейной алгебре, разделе математики, матрицы размера m × n описывают линейные отображения из n-мерного в m-мерное пространство.Слово линейный примерно означает, что прямые линии соответствуют прямым линиям, а начало координат в n-мерном пространстве отображается в начало координат в m-мерном пространстве.
Когда у нас есть (m × n) -матрица A и (n × k) -матрица B, мы можем вычислить произведение AB, которое является (m × k) -матрицей.
Отображение, соответствующее AB, — это в точности композиция отображений, соответствующих A и B соответственно.
Разложение по сингулярным значениям (SVD) утверждает, что каждая (m × n) -матрица A может быть записана как произведение
где U и V — ортогональные матрицы, а матрица Σ состоит из убывающих неотрицательных значений на своей диагонали и нулей в других местах.Записи σ 1 & geq; σ 2 & geq; σ 3 & geq; … & Geq; 0 на диагонали Σ называются сингулярными значениями (SV) A. Геометрически, Σ отображает j-й единичный вектор координат n-мерного пространства в j-й вектор координат m-мерного пространства, масштабируемый с коэффициентом σ j . Ортогональность U и V означает, что они соответствуют поворотам (возможно, с последующим отражением) m-мерного и n-мерного пространства соответственно.Следовательно, только Σ изменяет длину векторов.
Использование SVD для сжатия изображений
Мы можем разложить данное изображение на три цветовых канала: красный, зеленый и синий. Каждый канал может быть представлен в виде матрицы (m × n) со значениями от 0 до 255.
Теперь мы сжимаем матрицу A, представляющую один из каналов.
Каждый канал может быть представлен в виде матрицы (m × n) со значениями от 0 до 255.
Теперь мы сжимаем матрицу A, представляющую один из каналов.
Для этого мы вычисляем приближение к матрице A, которое занимает только часть пространства для хранения.Теперь вот что замечательно в SVD: данные в матрицах U, Σ и V сортируются по тому, насколько они вносят вклад в матрицу A в произведении. Это позволяет нам получить довольно хорошее приближение, просто используя только самые важные части матриц.
Теперь выберем число k сингулярных значений, которые мы собираемся использовать для аппроксимации. Чем выше это число, тем лучше качество приближения, но также тем больше данных необходимо для его кодирования.Теперь возьмем только первые k столбцов U и V и верхний левый (k × k) -квадрат матрицы Σ, содержащий k наибольших (и, следовательно, наиболее важных) сингулярных значений. Тогда у нас есть
Количество данных, необходимых для хранения этого приближения, пропорционально цветной области:
сжатый размер = m × k + k + k × n = k × (1 + m + n)
(На самом деле, требуется немного меньше места из-за ортогональности U и V. )
Можно доказать, что это приближение в определенном смысле оптимально.
)
Можно доказать, что это приближение в определенном смысле оптимально.
Эта демонстрация позволяет вам выбрать количество сингулярных значений k и увидеть, как этот выбор влияет на качество приближения и степень сжатия. Обратите внимание, что для всех фотографий график, показывающий особые значения, выглядит как гипербола: есть только несколько действительно больших SV и длинный хвост относительно меньших SV. Напротив, для изображения случайного шума график SV выглядит примерно линейным.
SVD обычно используется в статистике для анализа главных компонентов и в численном моделировании для уменьшения порядка моделей. Для сжатия изображений более сложные методы, такие как JPG, которые учитывают человеческое восприятие, обычно превосходят сжатие с использованием SVD.
Об этой демонстрации
Вычисление SVD выполняется на стороне клиента с помощью WebAssembly.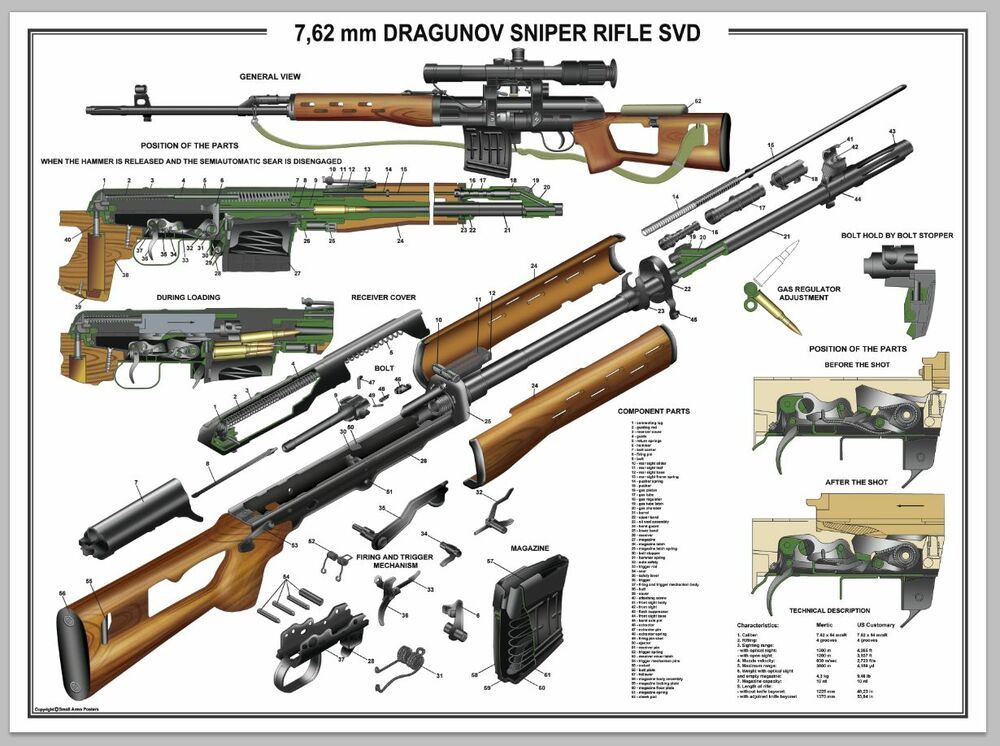 Мы используем алгоритм, реализованный библиотечной алгеброй Rust.SVD всех трех цветовых каналов вычисляются параллельно с использованием одного веб-воркера для каждого канала.
Чтобы обеспечить быстрый предварительный просмотр, мы используем рандомизированный алгоритм для вычисления приблизительного усеченного SVD с 50 сингулярными значениями. Пользовательский интерфейс использует React, response-slick и noUiSlider.
Спасибо создателям всех этих замечательных проектов!
Мы используем алгоритм, реализованный библиотечной алгеброй Rust.SVD всех трех цветовых каналов вычисляются параллельно с использованием одного веб-воркера для каждого канала.
Чтобы обеспечить быстрый предварительный просмотр, мы используем рандомизированный алгоритм для вычисления приблизительного усеченного SVD с 50 сингулярными значениями. Пользовательский интерфейс использует React, response-slick и noUiSlider.
Спасибо создателям всех этих замечательных проектов!
(PDF) Сжатие изображений с использованием разложения по сингулярным числам
5
1234567890
14-я конференция IOP ICSET-2017, публикация
IOP Conf.Серия: Материаловедение и инженерия 263 (2017) 042082 doi: 10.1088 / 1757-899X / 263/4/042082
преобразование кодирования изображений. Этот метод использует сходство между SVD и KLT, и благодаря
эффективность кодирования метода также улучшена. Если цель состоит в том, чтобы использовать преобразование во всех
блоках, которые строят изображение, KLT можно использовать эффективно. Однако улучшение сжатия для данного блока
Однако улучшение сжатия для данного блока
достигается с помощью SVD. Итак, чтобы использовать это преимущество, построена система, которая формирует преобразования SVD
и создает приближения с их помощью.Метод Лагранжа может использоваться для уменьшения искажения
изображения во время реконструкции. Это можно использовать для перехода на KLT. Но ограничение
здесь — количество битов, используемых для восстановления каждого блока, очень велико. Это увеличивает стоимость
, связанную с этим методом. Это можно импровизировать, используя замещающие методы.
T. J. Peters et al. [4] реализовал SVD (разложение по сингулярным значениям) для сжатия изображения микрочипа
–.Огромные объемы информации о ДНК для исследовательских целей хранятся в виде изображений на микрочипе
. Это изображения с высоким разрешением, которые подчеркивают мельчайшие детали изображения. Из-за высокого разрешения
эти изображения имеют тенденцию быть большего размера, что означает, что для хранения на жестком диске
, требуется много места. Поэтому очень важно уменьшить размер изображения без ущерба для качества
Поэтому очень важно уменьшить размер изображения без ущерба для качества
и количества деталей, присутствующих в изображении.Для этого требуется сравнительно сложный процесс
, когда изображения микроматрицы должны быть сгруппированы и классифицированы перед выбором
признаков. SVD может использоваться здесь для разделения изображения на небольшие фрагменты изображения, и на каждом фрагменте изображения
выполняется SVD. Этот метод дает лучшее отношение пикового сигнала к шуму в дополнение к увеличению степени сжатия
.
H. S. Prasantha et al. [5] реализовали другой подход для сжатия изображений с использованием
разложения по сингулярным числам (SVD).Применяя разложение по сингулярным значениям к матрице изображения, достигается сжатие
,изображения .SVD принимает во внимание. В этом способе используется метод сжатия данных
,, в котором операции выполняются с матрицей после того, как изображение
, разложено на матрицы. Для каждого изображения находится матрица и по точкам строится график для разнородных рангов
Для каждого изображения находится матрица и по точкам строится график для разнородных рангов
в [10]. Кроме того, наблюдается, что по мере увеличения ранга в матрице изображения, количество записей также будет увеличиваться
,, что соответственно приводит к повышению качества изображения.За счет этого меньшими рядами достигается большая степень сжатия
.
4. Предлагаемое решение
Матрица изображения, составленная из сигналов RGB. Представление RGB
,не является оптимальным для целей хранения и передачи изображения. Это связано с наличием избыточной информации. Таким образом, предлагаемое решение
пытается улучшить это путем преобразования спектра RGB в спектр YCBCR. Y
представляет яркость.В качестве альтернативы также можно использовать яркость. CB и CR представляют собой синий и красный хромированные компоненты
. Это новое представление обеспечивает приближение к обработке, при которой
основных цветов обрабатываются в воспринимаемую значимую информацию. Это представление разделяет
Это представление разделяет
компоненты Y на два компонента цветности. Эти компоненты могут храниться с более высоким разрешением
или передаваться с более высокой пропускной способностью. Их также можно обрабатывать отдельно, сжимая
или уменьшая полосу пропускания.
В предлагаемой системе предусмотрено использование формата YCBCR для представления исходного изображения, которое находится в представлении
RGB. Затем составляющие компоненты могут быть получены путем разбивки представления YCBCR
. Следовательно, мы получаем 3 компонента, соответствующие Y, CB и CR. Затем СВД наносится на
этих компонентов. Получены их соответствующие компоненты U, ∑ и V; а именно, Uy, ∑y, Vy
, соответствующие y, Ub, ∑b, Vb, соответствующие CB, и Ur, ∑r, Vr, соответствующие CR.Поскольку U и V
,представляют пространственные атрибуты изображения, они могут быть взяты из любого цветового пространства. Однако, поскольку Y
представляет яркость, его необходимо использовать для всех трех компонентов. Потеря информации может быть достигнута с использованием этого подхода. Поскольку Y используется во всех трех компонентах, мы решили использовать U
Потеря информации может быть достигнута с использованием этого подхода. Поскольку Y используется во всех трех компонентах, мы решили использовать U
и компонент V of Y. Все три компонента изображения используются при реконструкции, чтобы уменьшить повреждение
из-за потери.Частотные компоненты для U и V генерируются, и метод определения порога
используется для удаления низкого значения SV из матрицы. Этот метод помогает достичь максимального сжатия
при сохранении качества. Изображение реконструируется с использованием ∑, U и V всех компонентов
.
Jupyter, python, сжатие изображений и svd — интерактивное исследование | Рамеш Путалапатту
Jupyter — это интерактивная среда для блокнотов на основе браузера, в которой мы можем комбинировать текст, выполнение кода и визуализацию.Он поддерживает несколько языков программирования с помощью подключаемых модулей ядра для конкретного языка. Однако он широко используется с Python в сообществах научных вычислений и данных. Наличие большого количества высококачественных библиотек с открытым исходным кодом, полезных для многих задач в области научных вычислений, числовой линейной алгебры, машинного обучения и визуализации, гарантирует, что Python широко используется в этих областях. Блокноты Jupyter — отличная среда для обучения и преподавания благодаря интерактивности.
Наличие большого количества высококачественных библиотек с открытым исходным кодом, полезных для многих задач в области научных вычислений, числовой линейной алгебры, машинного обучения и визуализации, гарантирует, что Python широко используется в этих областях. Блокноты Jupyter — отличная среда для обучения и преподавания благодаря интерактивности.
В этом коротком блоге я рассмотрю несколько тем, чтобы проиллюстрировать интерактивность среды jupyter и доступность высококачественных библиотек Python в экосистеме.
- Расчет π методом Монте-Карло
- Сжатие изображений с использованием разложения по сингулярным числам
Установка jupyter и других важных пакетов по отдельности является громоздкой. Благодаря Continuum Analytics у нас есть дистрибутив Anaconda python, в который включены почти все полезные пакеты.Установите анаконду.
Ранее я писал о вычислении математической константы ππ методом Монтекарло. Он включает в себя создание случайных точек на единичном квадрате и подсчет количества точек внутри единичной четверти круга. Мы напишем функцию
Мы напишем функцию mc_pi для вычисления π. В этой функции мы также визуализируем процесс моделирования Монтекарло с помощью библиотеки matplotlib.
Мы можем написать функцию mc_pi без использования каких-либо явных для циклов — благодаря функциям векторизации в библиотеке numpy.Благодаря концепции, называемой широковещательной передачей в numpy, мы можем вычесть вектор из скаляра (1.0 — unit_circle_x ** 2), чтобы вычислить координату y единичного круга.
Теперь мы воспользуемся модулем ipywidgets для интерактивной передачи параметра функции mc_pi . Модуль ipywidgets предоставляет виджеты для создания элементов управления пользовательского интерфейса в самом блокноте, с которыми пользователь может взаимодействовать. Мы можем перетащить ползунок и наблюдать, как значение pi, вычисленное функцией mc_pi, изменяется с количеством попыток.
Теперь мы рассмотрим, как применить разложение матрицы по сингулярным значениям к проблеме сжатия изображения. SVD раскладывает прямоугольную матрицу M на три части.
SVD раскладывает прямоугольную матрицу M на три части.
- U — матрица левых сингулярных векторов в столбцах
- Σ — диагональная матрица с сингулярными значениями
- V — матрица правых сингулярных векторов в столбцах
SVD по сути предполагает восстановление исходной матрицы как линейной комбинации несколько матриц первого ранга.Матрица ранга один может быть выражена как внешнее произведение двух векторов-столбцов.
Матрица ранга r будет содержать r членов.
Здесь σ1, σ2, σ3… — сингулярные значения. u1, u2, u3… и v1, v2, v3… — левый и правый сингулярные векторы соответственно.
Сжатие изображений с использованием SVD предполагает использование того факта, что очень немногие из сингулярных значений являются большими. Хотя изображения из реального мира имеют полный ранг, они имеют низкий эффективный ранг, что означает, что только некоторые из сингулярных значений SVD изображений будут большими.
Для работы с изображениями в Python мы будем использовать библиотеку обработки изображений skimage (из семейства пакетов sci-kit). В skimage есть модуль под названием data, который предоставляет набор изображений для исследования. Мы загрузим некоторые изображения и конвертируем их в формат серой шкалы. Эти изображения хранятся в объекте python dict gray_images.
В skimage есть модуль под названием data, который предоставляет набор изображений для исследования. Мы загрузим некоторые изображения и конвертируем их в формат серой шкалы. Эти изображения хранятся в объекте python dict gray_images.
Мы будем использовать функцию svd библиотеки numpy.linalg для вычисления svd матрицы в python. Функция svd возвращает U, s, V.
- U имеет левые сингулярные векторы в столбцах
- s — массив numpy ранга 1 с сингулярными значениями
- V имеет правые сингулярные векторы в строках — эквивалентно V, транспонированному в традиционной литературе по линейной алгебре
Восстановленное приближение исходная матрица создается с использованием подмножества сингулярных векторов, как показано ниже в функции compress_svd . Мы используем нарезку массива numpy для выбора k сингулярных векторов и значений. Вместо того, чтобы хранить m × n значений для исходного изображения, теперь мы можем хранить k (m + n) + k значений.
reconst_matrix = np.dot (U [:,: k], np.dot (np.diag (s [: k]), V [: k ,:]))
Функция compress_show_gray_images ниже принимает имя изображения (img_name) и количество сингулярных значений / векторов (k), которые будут использоваться в сжатой реконструкции. Он также отображает сингулярные значения и изображение.
Используйте представленный ниже интерактивный виджет, чтобы изучить, как качество реконструированного изображения зависит от k.
Цветные изображения представлены в Python как трехмерные массивы numpy — третье измерение для представления значений цвета (красный, зеленый, синий).Однако метод svd применим к двумерным матрицам. Поэтому нам нужно найти способ преобразовать трехмерный массив в двухмерные массивы, применить svd и восстановить его обратно как трехмерный массив. Это можно сделать двумя способами. Ниже мы покажем оба этих метода.
- Метод изменения формы
- Метод слоев
Метод изменения формы для сжатия цветного изображения
Этот метод включает выравнивание третьего измерения массива изображений во второе измерение с использованием метода изменения формы numpy.
image_reshaped = image.reshape ((original_shape [0], original_shape [1] * 3))
SVD-декомпозиция применяется к полученному преобразованному массиву и восстанавливается с желаемым количеством сингулярных значений / векторов. Массив изображений преобразуется обратно в три измерения с помощью другого вызова метода изменения формы.
image_reconst = image_reconst.reshape (original_shape)
Вот интерактивный виджет для изучения сжатия цветных изображений с помощью метода изменения формы.Перетаскивая ползунок для изменения kk, наблюдайте за изменением качества изображения. Кроме того, мы можем исследовать различные изображения, выбирая их в раскрывающемся виджете.
В функции compress_show_color_images_layer мы обрабатываем цветное изображение как стек из 3 отдельных двухмерных изображений (красный, синий и зеленый слои). Мы применяем усеченную реконструкцию svd к каждому двумерному слою отдельно.
image_reconst_layers = [compress_svd (image [:,:, i], k) [0] для i в диапазоне (3)]
И мы собираем восстановленные слои вместе.
image_reconst = np.zeros (image.shape)
для i в диапазоне (3):
image_reconst [:,:, i] = image_reconst_layers [i]
Вот виджет для изучения метода слоев для сжатия цветных изображений.
Полный блокнот ipython, использованный для этого сообщения в блоге, доступен по этому адресу github.
Low Processing Fee Journal в EEE / ECE / E & I / ECE / ETE — Impact Factor-7.122
Анализ методом конечных элементов системы электромагнитного прерывания
DR.M.BROWN
Факультет электротехники и вычислительной техники, Йоркский университет, Торонто, Канада
Аннотация PDF 10.15662 / IJAREEIE.2018.0706001
Новый алгоритм адаптивного медианного фильтра для удаления шумов при обработке изображений и сигналов
Ракеш M R
Доцент кафедры ECE, AJIET Mangaluru, Карнатака, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706002
Внедрение системы мониторинга теплиц на основе Интернета вещей с использованием протокола сжатия данных в WSN
Кранти В.
 Никам, д-р С.П. Мохани
Никам, д-р С.П. МоханиМ.Студент технического факультета, факультет электроники и телекоммуникаций, Государственный инженерный колледж, Джалгаон, Махараштра, Индия
Доцент кафедры электроники и телекоммуникаций Государственного инженерного колледжа, Джалгаон, Махараштра, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706003
Проектирование и размещение UPFC и генератора в системе шины IEEE для повышения напряжения
Нишант Кумар Багеле, Сантош Кумар
М.Технический специалист, Департамент электротехники и электроники, MITS, Бхопал, Индия,
Профессор кафедры электротехники и электроники, Массачусетский технологический институт, Бхопал, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706004
Разработка и внедрение системы удаленной домашней безопасности на базе GSM с использованием микроконтроллера Arduino UNO (ATMEGA 328)
Эльбакуш Э., Азиз К.

Колледж инженерии и вычислений, Университет Аль-Гурайр, Дубайский академический город, Дубай, ОАЭ
Аннотация PDF 10.15662 / IJAREEIE.2018.0706005
Интеллектуальное отслеживание энергии и перегрузки с помощью Labview
К. Нилима Правина, С. Суварна, М. Роха, Д. Мадхусудхан
Доцент кафедры EEE, Инженерный колледж Малла Редди (автономный), Телангана, Индия
PG Студент [EPS], кафедра EEE, Инженерный колледж Малла Редди (автономный), Телангана, Индия
PG Студент [EPS], кафедра EEE, Инженерный колледж Малла Редди (автономный), Телангана, Индия
PG Студент [EPS], Dept.EEE, Инженерный колледж Малла Редди (Автономный), Телангана, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706006
Воздействие электромобилей на индийские распределительные системы
Pallavi Rodge, Кантилал Джоши
Магистр технических наук, кафедра электротехники, инженерный колледж Г. Х. Райзони, Нагпур, Индия
Х. Райзони, Нагпур, Индия
Доцент кафедры электротехники, инженерный колледж Г. Х. Райзони, Нагпур, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706007
Максимальная точка мощности (MPP) подключенной фотоэлектрической системы с постоянным облучением, использующей схему возрастающей проводимости
Арти Пандей, Бхупендра Сингх Ниранджан
PG Студент [Power System], кафедра EEE, Университет информационных технологий Махариши, Лакхнау, США, Индия
PG Студент [Power System], кафедра EEE, Университет информационных технологий Махариши, Лакхнау, США, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706008
Моделирование соединения трех-семи фазного трансформатора с помощью программного обеспечения MATLAB
Muktshri Sadaphal, Varsha Sharma
Магистр технических наук, Департамент электротехники и электроники, Инженерно-технологический колледж RSR Rungta, Бхилаи (C.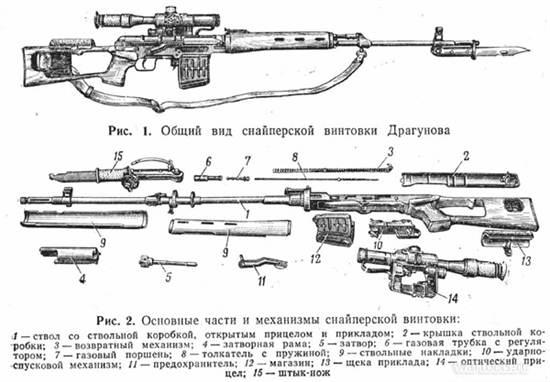 G.) Индия
G.) Индия
Доцент кафедры электротехники и электроники, Инженерно-технологический колледж RSR Rungta, Бхилаи (C.G.) Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706009
Подавление гармоник с помощью активных и пассивных фильтров гармоник, а также обнаружение неисправностей с помощью MATLAB Simulation
Джхума Дас, Ашутош Мишра
Магистр технических наук, Департамент электротехники и электроники, Инженерно-технологический колледж RSR Rungta, Бхилаи (C.G.) Индия
Доцент кафедры электротехники и электроники, Инженерный и технологический колледж RSR Рунгта, Бхилаи (C.G.) Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706010
Реализация методов модуляции AM и DSB-SC на FPGA
Д-р Р. Пракаш Рао
Доцент кафедры электроники и техники связи, Инженерный колледж Матрусри, # 16-1-486, Сайдабад, Хайдарабад, Индия
Аннотация PDF 10.15662 / IJAREEIE. 2018.0706011
2018.0706011
Многофункциональная самобалансирующаяся мобильная платформа со смартфоном
гл.Deepthi, Ch. Киран Кумар
Магистр технических наук, факультет ECE, Колледж MRCET, Хайдарабад, Телангана, Индия
Доцент кафедры ECE, Колледж MRCET, Хайдарабад, Телангана, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706012
Разработка цифрового осциллографа с использованием микроконтроллера TI MSP430G2553
Вишал Раман Гайквад
Доцент кафедры электронной инженерии, Инженерный колледж Валчанда, Сангли, Махараштра, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706013
Система индукционного нагревателя, управляемая усилителем класса E с замкнутым контуром FOPID
M.P.S. Саравана Сентил
Преподаватель (старший класс), Департамент дошкольного образования, Раджагопальский политехнический колледж, Гудиятам, Тамил Наду, Индия
Аннотация PDF 10. 15662 / IJAREEIE.2018.0706014
15662 / IJAREEIE.2018.0706014
Обзор моделирования и методов слияния мультисенсорных данных (MSDF): приложения на автономном подводном аппарате (AUV) для морской эксплуатации
К.Читра, Ч.Камарадж
Доцент кафедры электроники и приборостроения, Инженерно-технологический колледж PSN (автономный), Тирунелвели, Тамилнад, Индия1
Профессор и руководитель отдела морской инженерии Инженерно-технологического колледжа PSN (автономный), Тирунелвели, Тамилнад, Индия 2
Аннотация PDF 10.15662 / IJAREEIE.2018.0706015
Разработка и реализация эффективных и интеллектуальных интеллектуальных бункеров на основе IOT с использованием Raspberry Pi
К.Парватисам, Б. Дивакар
Доцент кафедры ECE, Адитья колледж инженерии и технологий, Какинада, Андхра-Прадеш, Индия
Доцент кафедры ECE, Колледж инженерии и технологий Адитья, Какинада, Андхра-Прадеш, Индия
Аннотация PDF 10. 15662 / IJAREEIE.2018.0706016
15662 / IJAREEIE.2018.0706016
Обзор развития системы измерения большой площади
Джоти С. Бхонсле
Доцент кафедры электротехники Инженерно-технологического института имени Приядаршини, Нагпур, Махараштра, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706017
Моделирование ветряной турбины по аэродинамической эффективности в системе преобразования энергии ветра
Кумарасвами Лелла
Партнер проекта, CPRI, Бангалор, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706018
Подход с использованием генетических алгоритмов для управления нелинейной системой
Sucheta Sampatrao Yadav, V.M. Панчада
Студент кафедры электротехники, г.Институт инженерии и технологий Х. Райсони, Пуна, Университет Савитрибай Фуле Пуна, Пуна, Индия
Профессор, кафедра электротехники, инженерно-технологический институт им. Г. Х. Райзони, Пуна, Университет Савитрибай Фуле Пуна, Пуна, Индия
Аннотация PDF 10. 15662 / IJAREEIE.2018.0706019
15662 / IJAREEIE.2018.0706019
Управляемый данными в реальном времени алгоритм для диагностики промышленных отказов с использованием систем на базе Ethernet
Пранита А. Раут, Уттам Л.Bombale
PG Студент, факультет электронных технологий, Университет Шиваджи, Колхапур, Махараштра, Индия
Доцент кафедры электронных технологий, Университет Шиваджи, Колхапур, Махараштра, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706020
Повышение крутящего момента при низких оборотах в электромобилях с использованием силового электронного трансформатора
Ашиш Шукла
M.Tech студент, кафедраEEE, Институт науки и технологий доктора К. В. Рамана, Биласпур, Чхаттисгарх, Индия,
Аннотация PDF 10.15662 / IJAREEIE.2018.0706021
Устройство контроля уровня мусора, использующее Интернет вещей с ESP8266
Джубин Дипаккумар Котари
Департамент информационных технологий, Университет Кэмпбеллсвилля, Кэмпбеллсвилл, Кентукки
Аннотация PDF 10. 15662 / IJAREEIE.2018.0706029
15662 / IJAREEIE.2018.0706029
Обзор повышения стабильности фильтра активной мощности гибридной серии с помощью контроллера скользящего режима
Рупали М.Патил, Калпеш М.Махаджан
PG Студент [EPS], кафедра EE, Инженерный колледж KCES и ИТ, Джалгаон, Махараштра, Индия
Доцент кафедры ЭО, Технический колледж KCES и информационных технологий, Джалгаон, Махараштра, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706022
Оптимизация полосы пропускания с использованием Пи-образной фрактальной патч-антенны для широкополосных приложений
Э. Прити Диман, Э. Капил Арора, Э. Парвеш Кумар
М.Студент технологического факультета ДОО, Колледж RPIIT, Карнал, Индия
HOD, Департамент ECE, Колледж RPIIT, Карнал, Индия
Старший инженер, Bharat Electronics Ltd (Министерство обороны), Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706023
Защита сельскохозяйственных культур и правильное использование дождевой воды с помощью IOT
Ракхи Патил, Гаятри.
HOD и доцент кафедры E&IE, Инженерный колледж RYM, Баллари, Карнатака, Индия
Доцент кафедрыиз E&IE, Инженерный колледж RYM, Баллари, Карнатака, Индия
Доцент кафедры E&IE, Инженерный колледж RYM, Баллари, Карнатака, Индия
Доцент кафедры EEE, Инженерный колледж RYM, Баллари, Карнатака, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706024
Интеллектуальный мониторинг окружающей среды на основе Интернета вещей с использованием беспроводной сенсорной сети
С. М. Ширсат, Н. Б. Вагхайл
Доцент кафедры КИПиА, П.R.E.C. Лони, Ахмеднагар, Махараштра, Индия
M.E. Студент кафедры КИПиА, P.R.E.C. Лони, Ахмеднагар, Махараштра, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706025
Обзор развития волоконно-оптических сетей связи: прогресс и проблемы
Сандип Сингх, Махендра Сингх Мина, профессор (доктор) Джанак Кумар Б.
 Патель
ПательM.Tech. Студент, факультет электроники и техники связи, Университет Амити, Харьяна, Гуруграм, Индия,
Доцент кафедры электроники и техники связи, Университет Амити, Харьяна, Гуруграм, Индия
Профессор и Х.О. Д., Департамент электроники и коммуникационной техники, Университет Амити, Харьяна, Гуруграм, Индия,
Аннотация PDF 10.15662 / IJAREEIE.2018.0706026
Беспроводная связь на основе магнитной индукции ближнего поля
Викрам Чекури, Сурааг Сунил Теллакула, Кунал Мехра, Анураг Джейкоб, Абхай Харбханджанка
Доцент кафедры EEE, Институт технологий и менеджмента BMS, Бангалор, Индия
Студент, факультет EEE, Институт технологий и менеджмента BMS, Бангалор, Индия
Аннотация PDF 10.15662 / IJAREEIE.2018.0706027
Идентификация проксимального кариеса по панорамным рентгеновским снимкам зубов
Harshini S, Hasini M S, Шенбагавалли A, Нирмала K
UG Студент, кафедра BME, инженерный колледж SSN, Ченнаи, Тамилнад, Индия
UG Студент, кафедра BME, инженерный колледж SSN, Ченнаи, Тамилнад, Индия
UG Студент, кафедра BME, инженерный колледж SSN, Ченнаи, Тамилнад, Индия
Доцент кафедрыBME, инженерный колледж SSN, Ченнаи, Тамилнад, Индия,
Аннотация PDF 10. 15662 / IJAREEIE.2018.0706028
15662 / IJAREEIE.2018.0706028
Сжатие изображений с использованием SVD
1. сжатие по шкале серого:
Исходное изображение: ЦВЕТЫ
Получение изображения в оттенках серого, т.е. отбрасывание цветов RGB:
megray <-grayscale (изображение)
plot (megray, axes = FALSE, main = "Grayscale image") Теперь «мегрей» хранит матрицу, содержащую данные изображения в оттенках серого.
Получение разложения по одному значению матрицы «мегерая»:
svd1 <-svd (масштаб (мегрей))
ул (свд1) ## Список из 3
## $ d: число [1: 186] 122.* \) Итак, давайте уменьшим количество векторов до \ (5 \), \ (10 \), \ (25 \), \ (35 \) и \ (50 \):
# матричное умножение U, D и V *
# включая только первые 5 одиночных векторов
приблизительно5 <-svd1 $ u [, 1: 5]% *% diag (svd1 $ d [1: 5])% *% t (svd1 $ v [, 1: 5])
# включая только первые 10 сингулярных векторов
Approx10 <-svd1 $ u [, 1:10]% *% diag (svd1 $ d [1:10])% *% t (svd1 $ v [, 1:10])
# включая только первые 20 сингулярных векторов
приблизительно25 <-svd1 $ u [, 1:25]% *% diag (svd1 $ d [1:25])% *% t (svd1 $ v [, 1:25])
# включая только первые 20 сингулярных векторов
приблизительно35 <-svd1 $ u [, 1: 35]% *% diag (svd1 $ d [1:35])% *% t (svd1 $ v [, 1:35])
# включая только первые 20 сингулярных векторов
приблизительно50 <-svd1 $ u [, 1:50]% *% diag (svd1 $ d [1:50])% *% t (svd1 $ v [, 1:50])
Если мы теперь изобразим приведенные выше уменьшенные матрицы как изображения, мы увидим 4 изображения для приведенных выше приближений:
номинал (mfrow = c (2,3), mar = c (1,1,1,1))
#plotting для уменьшенных изображений
сюжет (как. cimg (приблизительно 5), main = "(a) 5 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (Approx10), main = "(b) 10 сингулярных векторов", axes = FALSE)
график (as.cimg (приблизительно25), main = "(c) 25 сингулярных векторов", оси = FALSE)
график (as.cimg (приблизительно35), main = "(c) 35 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (приблизительно 50), main = "(c) 50 сингулярных векторов", оси = FALSE)
plot (as.cimg (megray), main = "(d) Full image", axes = FALSE)
cimg (приблизительно 5), main = "(a) 5 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (Approx10), main = "(b) 10 сингулярных векторов", axes = FALSE)
график (as.cimg (приблизительно25), main = "(c) 25 сингулярных векторов", оси = FALSE)
график (as.cimg (приблизительно35), main = "(c) 35 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (приблизительно 50), main = "(c) 50 сингулярных векторов", оси = FALSE)
plot (as.cimg (megray), main = "(d) Full image", axes = FALSE)
Исходная матрица изображения имеет ранг 187, а матрицы сжатого изображения имеют ранги 5, 10, 25, 35 и 50.Мы можем заметить, что даже после снижения рейтинга более чем на 150, качество изображения остается почти таким же. ## 2. Цветное изображение Сжатие: Загрузка изображения:
библиотека (тепловизор)
номинальная (c (1,1))
## NULL
изображение <-load.image ("flower.jpg")
plot (image, main = "FLOWER", axes = FALSE)
Ниже мы видим, что большая часть дисперсии объясняется первыми 25 векторами изображения:
svd1 <-svd (масштаб (оттенки серого (изображение)))
участок (svd1 $ d ^ 2 / сумма (svd1 $ d ^ 2))
Исходное изображение представляет собой смесь трех изображений с красными , зелеными и синими компонентами соответственно. Разделение компонентов RGB:
Разделение компонентов RGB:
R = изображение [,, 1]
G = изображение [,, 2]
B = изображение [,, 3]
Как объяснялось выше, исходное изображение представляет собой не что иное, как смесь трех изображений ниже:
номинал (mfrow = c (1,3))
номинал (mfrow = c (1,3), mar = c (1,1,1,1))
cscale <- функция (v) rgb (v, 0,0)
оттенки серого (изображение)%>% график (цветовая шкала = cscale, rescale = FALSE, axes = FALSE)
cscale <- функция (v) rgb (0, v, 0)
оттенки серого (изображение)%>% график (цветовая шкала = cscale, rescale = FALSE, axes = FALSE)
cscale <- функция (v) rgb (0,0, v)
оттенки серого (изображение)%>% график (цветовая шкала = cscale, rescale = FALSE, axes = FALSE)
Single Value Декомпозиция изображений RGB и их группировка в один список.* \) для каждой матрицы подцветов и объединение их в один трехмерный массив. Повторение процесса для первых 5,10,25 и 50 векторов.
номинал (mfrow = c (2,3), mar = c (1,1,1,1))
for (j in c (5,10,25,35,50)) {
comp <- sapply (svdRGB, function (i) {
сжатый = i $ u [, 1: j]% *% diag (i $ d [1: j])% *% t (i $ v [, 1: j])
}, simpleify = 'массив')
comp <-as.cimg (comp)
plot (comp, axes = FALSE, main = paste ("Rank =", j))
}
## Предупреждение в as.cimg.array (comp): предполагается, что третье измерение соответствует
## цвет
## Предупреждение в as.cimg.array (comp): если третье измерение соответствует
## цвет
## Предупреждение в as.cimg.array (comp): предполагается, что третье измерение соответствует
## цвет
## Предупреждение в as.cimg.array (comp): предполагается, что третье измерение соответствует
## цвет
## Предупреждение в as.cimg.array (comp): предполагается, что третье измерение соответствует
## цвет
сюжет (изображение, оси = FALSE, main = "Rank = 187")
Разложение единственного числа
Разложение по сингулярным числам (SVD) приобретает все большее значение в
обработка сигналов. Это продвинутая операция линейной алгебры, которая
создает основу для пространства строк и столбцов матрицы и
указание ранга матрицы. При адаптивной обработке сигналов
ранг матрицы и базис полезны для уменьшения влияния
вмешательство. Для комплексной матрицы A размера m × n сингулярное значение
разложение A равно
Это продвинутая операция линейной алгебры, которая
создает основу для пространства строк и столбцов матрицы и
указание ранга матрицы. При адаптивной обработке сигналов
ранг матрицы и базис полезны для уменьшения влияния
вмешательство. Для комплексной матрицы A размера m × n сингулярное значение
разложение A равно
где U - унитарная матрица размера m × m, ∑ - матрица m × n, в которой верхняя часть n × n является диагональю
матрица со всеми действительными элементами, отсортированными в порядке убывания, а V
является унитарной матрицей размера n × n.Если m> n, то определим где U a - размер m × n, U b - размер m × (m - n), и
Σ a имеет размер n × n. Тогда A = U a Σ a V H называется уменьшил SVD матрицы A. В этом контексте SVD определил
в уравнении (1) иногда называют полный SVD для контраста. Обратите внимание, что U a не является унитарным, но он
имеет ортогональные столбцы. Когда m
Когда m Для приложений обработки сигналов нас обычно больше всего интересуют
в приведенном разложении, в матрице U и в сингулярном
значения (значения на диагонали Σ).Мы предоставляем количество операций для приведенной декомпозиции, предполагая, что
производятся все три матрицы. Интересующие размеры матрицы данных и
количество связанных операций приведено в таблице 1.
Таблица 1: Входные параметры СВД. Параметр
Имена Описание Значения Набор 1 Набор 2 Набор 3 м Строки матрицы 500 180 150 № Столбцы матрицы 100 60 150 W r1 Фиксированная рабочая нагрузка (Мфлоп) 101 15 72 Вт r2 Рабочая нагрузка на итерацию (Mflop) 0. 24
24 0,88 0,54
Полный алгоритм SVD состоит из трех основных этапов, которые описаны ниже.
более подробно в Голубе и Ван Лоане [2, алгоритм 5.2.5]. Во-первых, если m × n
матрица A имеет намного больше строк, чем столбцов, QR-факторизация
выполнила. Этот шаг выполняется, если m> 5n / 3 [2, с. 252], что является
Обычно это происходит при обработке сигналов. Определить
где Q a - размер m × n, Q b - размер m × (m - n), а R a имеет размер n × n.Разложение A = Q a R a называется сокращенное разложение QR A. Матрица Q a не является унитарной, но она
имеет ортогональные столбцы. Уменьшенная QR-факторизация может быть получена
модифицированный алгоритм Грама-Шмидта, описанный у Голуба и Ван
Заем [2, алгоритм 5.2.5]. Если выполняется полная СВД,
вычисляется полный QR: если выполняется сокращенный SVD, сокращенный QR
вычислено. В оставшейся части этого изложения мы описываем сокращенную SVD
алгоритм для матрицы с m ≥ n. Мы предполагаем, что на первом этапе мы
выполнить сокращенное разложение QR с помощью алгоритма MGS для получения
Мы предполагаем, что на первом этапе мы
выполнить сокращенное разложение QR с помощью алгоритма MGS для получения где R - верхнетреугольная матрица размера n × n, а U 1 - матрица размера m × n с ортогональными столбцами. (Обратите внимание, что QR-факторизация
описанный на странице "Факторизация QR" - это полный QR; следовательно, a
здесь используется другой алгоритм.)
На следующем этапе R уменьшается до двухдиагональной формы , чтобы
состоят из главной диагонали и единственной диагонали входов выше
что с оставшимися элементами в матрице
ноль [2, с.253]. Это достигается с помощью Householder
трансформирует, производит
где U 2 и V 2 являются унитарными и имеют размер n × n, а матрица B n × n является двухдиагональной. Матрица B, созданная на этом этапе
уже не сложный, а реальный, хотя матрицы U 2 и V 2 являются
сложный. Последний шаг - итеративное приведение B к диагональной форме и
упорядочение сингулярных значений. Это достигается с помощью Гивенса.
вращения [2, с. 454].В конце этого шага мы создали
матрицы n × n ортогональные матрицы U 3 и V 3 такие, что так что разложение по сингулярным числам исходной матрицы A может быть выражено как
Это достигается с помощью Гивенса.
вращения [2, с. 454].В конце этого шага мы создали
матрицы n × n ортогональные матрицы U 3 и V 3 такие, что так что разложение по сингулярным числам исходной матрицы A может быть выражено как A = U 1 U 2 U 3 Σ (V 3 V 2 ) H
= UΣV H
с U = U 1 U 2 U 3 и V = V 3 V 2 . Поскольку точное количество итераций, необходимых для производства SVD, основано
на данных, измерение эффективности должно учитывать
фактическое количество выполненных шагов итераций.Мы объясняем это
определение рабочей нагрузки W как линейной функции двух чисел W 1 и W 2 , приведенные в таблице 1,
где d - количество итераций, выполненных при редукции
из B в диагональную форму, W 2 - это оценка количества
операций с плавающей запятой на шаг итерации, а W 1 - это
оценка количества операций с плавающей запятой в остатке
алгоритма.



 cimg (приблизительно 5), main = "(a) 5 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (Approx10), main = "(b) 10 сингулярных векторов", axes = FALSE)
график (as.cimg (приблизительно25), main = "(c) 25 сингулярных векторов", оси = FALSE)
график (as.cimg (приблизительно35), main = "(c) 35 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (приблизительно 50), main = "(c) 50 сингулярных векторов", оси = FALSE)
plot (as.cimg (megray), main = "(d) Full image", axes = FALSE)
cimg (приблизительно 5), main = "(a) 5 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (Approx10), main = "(b) 10 сингулярных векторов", axes = FALSE)
график (as.cimg (приблизительно25), main = "(c) 25 сингулярных векторов", оси = FALSE)
график (as.cimg (приблизительно35), main = "(c) 35 сингулярных векторов", оси = FALSE)
сюжет (as.cimg (приблизительно 50), main = "(c) 50 сингулярных векторов", оси = FALSE)
plot (as.cimg (megray), main = "(d) Full image", axes = FALSE) 
 Это продвинутая операция линейной алгебры, которая
создает основу для пространства строк и столбцов матрицы и
указание ранга матрицы. При адаптивной обработке сигналов
ранг матрицы и базис полезны для уменьшения влияния
вмешательство. Для комплексной матрицы A размера m × n сингулярное значение
разложение A равно
Это продвинутая операция линейной алгебры, которая
создает основу для пространства строк и столбцов матрицы и
указание ранга матрицы. При адаптивной обработке сигналов
ранг матрицы и базис полезны для уменьшения влияния
вмешательство. Для комплексной матрицы A размера m × n сингулярное значение
разложение A равно  Когда m
Когда m 24
24 Мы предполагаем, что на первом этапе мы
выполнить сокращенное разложение QR с помощью алгоритма MGS для получения
Мы предполагаем, что на первом этапе мы
выполнить сокращенное разложение QR с помощью алгоритма MGS для получения Это достигается с помощью Гивенса.
вращения [2, с. 454].В конце этого шага мы создали
матрицы n × n ортогональные матрицы U 3 и V 3 такие, что так что разложение по сингулярным числам исходной матрицы A может быть выражено как
Это достигается с помощью Гивенса.
вращения [2, с. 454].В конце этого шага мы создали
матрицы n × n ортогональные матрицы U 3 и V 3 такие, что так что разложение по сингулярным числам исходной матрицы A может быть выражено как