Золотое сечение и числа Фибоначчи – Fib0.ru – Суть числа
Иллюстрация Золотого сечения
Золотое сечение: тайна вселенной
Золотое сечение – это всеобъемлющее проявление структурной гармонии. Оно встречается во всех сферах вселенной в природе, науке, искусстве во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.
Наверняка вам не раз приходилось задумываться, почему Природа способна создавать такие удивительные гармоничные структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие. В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Никто не сможет однозначно ответить на этот вопрос, но в нашей книге мы постараемся приоткрыть завесу и рассказать вам об одной из тайн мироздания – Золотом Сечении или, как его еще называют, Золотой или Божественной Пропорцией. Золотое Сечение называется числом PHI (Фи) в честь великого древнегреческого скульптора Фидия (Phidius), который использовал это число в своих скульптурах.
Не одно столетие ученые применяют уникальные математические свойства числа PHI и эти исследования продолжаются и в наши дни. Это число нашло широкое применение во всех областях современной науки, о чем мы так же попытаемся популярно рассказать на страницах нашего сайта Fib0. Также существует ряд и последовательность фибоначчи что это Вы узнаете далее…
Определение золотого сечения
Наиболее простое и ёмкое определение золотого сечения – малая часть относится к большей, как большая – ко всему целому. Приблизительная его величина 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как ассиметричную симметрию, называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.
Числа фибоначчи в истории
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге Божественная пропорция, иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой Отца, а целое Святой дух.
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Отношение соседних чисел ряда Фибоначчи в пределе стремится к Золотому сечению. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член. Сейчас ряд Фибоначчи – это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Со временем правило правило в зависимости от ударения и контекста может обозначать следующее: Правило — требование для исполнения неких условий ( на поведение) всеми участниками какого-либо действия (игры, золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его математическое эстетство вызывало много критики.
Универсальный код природы
Даже не вдаваясь в расчеты, золотое сечение и Числа фибоначчи можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы материальный мир Вселенной, в сущности — основной объект изучения естественных наук к спиральным формам, называя спираль кривой жизни. Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Формула золотого сечения
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек это универсальная форма может означать: Форма предмета — взаимное расположение границ (контуров) предмета, объекта, а также взаимное расположение точек линии для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя Витрувианского человека Леонардо, создал собственную шкалу гармонических пропорций, повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке живое разумное социальное , субъект общественно-исторической деятельности и культуры ему подчинены практически все части тела, но главный показатель золотого нечто, изготовленное из золота сечения это деление тела В математике: Тело (алгебра) — множество с двумя операциями (сложение и умножение), обладающее определёнными свойствами точкой пупа.
Искусство пространственных форм
Художник Василий Суриков говорил, что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика. Долгое время художники следовали этому закону интуитивно, но после Леонардо ди сер Пьеро да Винчи (итал да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек может означать: Точка — абстрактный объект в пространстве, не имеющий никаких измеримых характеристик, кроме координат золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге Александр Сергеевич Пушкин в селе Михайловском, отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
Слово, звук и кинолента
Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи 5, 8, 13, 21, 34.
Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом Пиковой дамы является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) это и есть точка золотого сечения.
Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.
Кинорежиссер Сергей Эйзенштейн сценарий своего фильма Броненосец Потёмкин сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух в Одессе. Переход на сцены в городе и есть золотая середина фильма.
Гармония Золотого сечения
Научно-технический прогресс имеет длительную историю и прошел в своем историческом развитии несколько этапов (вавилонская и древнеегипетская культура, культура Древнего Китая и Древней Индии, древнегреческая культура, эпоха Средневековья, эпоха Возрождения, промышленная революция 18 в., великие научные открытия 19 в., научно-техническая революция 20 в.) и вошел в 21-й век, который открывает новую эпоху в истории человечества – эпоху Гармонии. Именно в античный период было сделано ряд выдающихся математических открытий, оказавших определяющее влияние на развитие материальной и духовной культуры, среди которых Вавилонская 60-ричная система счисления и позиционный принцип представления чисел, тригонометрия и геометрия Евклида, несоизмеримые отрезки, Золотое Сечение и Платоновы тела, начала теории чисел и теории измерения. И, хотя каждый из этих этапов имеет свою специфику, вместе с тем он обязательно включает содержание предшествующих этапов. В этом и состоит преемственность в развитии науки. Преемственность может осуществляться в различных формах. Одной из сущностных форм ее выражения являются фундаментальные научные идеи, которые пронизывают все этапы научно-технического прогресса и оказывают влияние на различные области науки, искусства, философии и техники.
К разряду таких фундаментальных идей относится идея Гармонии, связанная с Золотым Сечением. По словам Б.Г. Кузнецова, исследователя творчества Альберта Эйнштейна, великий физик свято верил в то, что наука, физика в частности, всегда имела своей извечной фундаментальной целью “найти в лабиринте наблюдаемых фактов объективную гармонию”. О глубокой вере выдающегося физика в существование универсальных законов гармонии мироздания свидетельствует и еще одно широко известное высказывание Эйнштейна: «Религиозность ученого состоит в восторженном преклонении перед законами гармонии».
В древнегреческой философии Гармония противостояла Хаосу и означала организованность Вселенной, Космоса. Гениальный русский философ Алексей Лосев так оценивает основные достижения древних греков в этой области:
“С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления – Золотого Сечения… Их (древних греков) систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».
«Закон золотого деления должен быть диалектической необходимостью. Это – та мысль, которую, насколько мне известно, я провожу впервые», – убежденно высказывался Лосев более полувека назад в связи с анализом культурного наследия древних греков.
А вот еще одно высказывание, касающееся Золотого Сечения. Оно было сделано в 17 веке и принадлежит гениальному астроному Иоганну Кеплеру, автору трех знаменитых «Законов Кеплера». Свое восхищение Золотым Сечением Кеплер выразил в следующих словах:
«В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем».
Напомним, что старинная задача о делении отрезка в крайнем и среднем отношении, которая упоминается в этом высказывании, – это и есть Золотое Сечение!
Числа Фибоначчи в науке
В современной науке существует много научных групп, профессионально изучающих Золотое Сечение, числа Фибоначчи и их многочисленные приложения в математике, физике, философии, ботанике, биологии, медицине, компьютерной науке. Множество художников, поэтов, музыкантов используют в своем творчестве «Принцип Золотого Сечения». В современной науке сделано ряд выдающихся открытий, основанных на числах Фибоначчи и Золотом Сечении. Открытие “квази-кристаллов”, сделанное в 1982 г. израильским ученым Даном Шехтманом, основанное на Золотом Сечении и “пентагональной” симметрии, имеет революционное значение для современной физики. Прорыв в современных представлениях о природе формообразования биологических объектов, в начале 90-х годов сделан украинским ученым Олегом Боднаром, создавшим новую геометрическую теорию филлотаксиса. Белорусский философ Эдуард Сороко сформулировал «Закон структурной гармонии систем», основанный на Золотом Сечении и играющий важную роль в процессах самоорганизации. Благодаря исследованиям американских ученых Эллиотта, Пректера и Фишера числа Фибоначчи активно вошли в сферу бизнеса и стали основой из оптимальных стратегий в сфере бизнеса и торговли. Эти открытия подтверждают гипотезу американского ученого Д. Винтера, руководителя группы “Планетарные сердцебиения”, согласно которой не только энергетический каркас Земли, но и строение всего живого основаны на свойствах додекаэдра и икосаэдра – двух “Платоновых тел”, связанных с Золотым Сечением. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни, представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная – от Метагалактики и до живой клетки – построена по одному принципу – бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции Золотого Сечения!
Украинский профессор и доктор наук Стахов А.П. смог создать некую формулу золотого сечения. Суть этого обобщения предельно проста. Если задаться неотрицательным целым числом р = 0, 1, 2, 3, … и разделить отрезок “AB” точкой С в такой пропорции, чтобы было:
CB/AC=(AB/CB)
То универсальной формулой золотого сечения является выражение:
xp+1 = xp + 1
Числа Фибоначчи и золотое сечение: взаимосвязь
Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Золотое сечение
Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.
В основе его лежит теория о пропорциях и соотношениях делений отрезков, которое было сделано еще древним философом и математиком Пифагором. Он доказал, что при разделении отрезка на две части: X (меньшую) и Y (большую), отношение большего к меньшему будет равно отношению их суммы (всего отрезка):
X : Y = Y : X+Y.
В результате получается уравнение: х2 – х – 1=0, которое решается как х=(1±√5)/2.
Если рассмотреть соотношение 1/х, то оно равно 1,618…
Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.
Числа Фибоначчи
Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Также ученый привел ряд закономерностей:
- Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.
- Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
- Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.
Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.
Спираль Архимеда и золотой прямоугольник
Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.
Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1. Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.
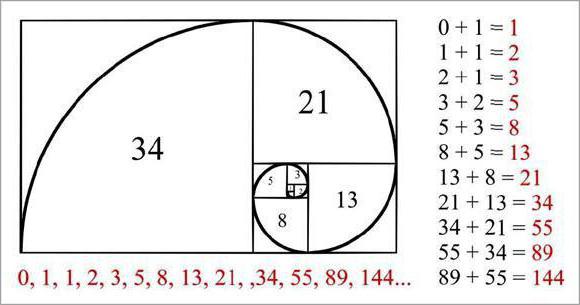
История применения золотых пропорций
Многие древние памятники архитектуры Египта возведены с использованием золотых пропорций: знаменитые пирамиды Хеопса и др. Архитекторы Древней Греции широко использовалиих их при возведении архитектурных объектов, таких как храмы, амфитеатры, стадионы. Например, были применены такие пропорции при строительстве античного храма Парфенон, театра Диониса (Афины) и других объектов, которые стали шедеврами древнего зодчества, демонстрирующими гармонию, основанную на математической закономерности.
В более поздние века интерес к золотому сечению поутих, и закономерности были забыты, однако опять возобновился в эпоху Ренессанса вместе с книгой францисканского монаха Л. Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».
Витрувианский человек Леонардо
Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.
Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.
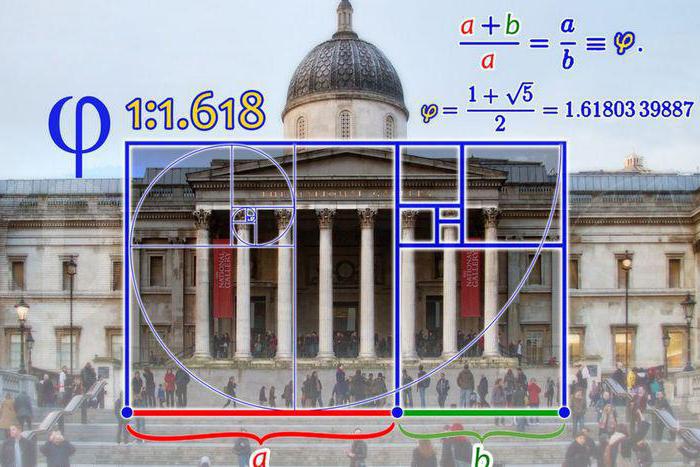
С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.
Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.
Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.
Исследования золотого сечения в 16-19 веках
Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.
В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.
Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.
Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.
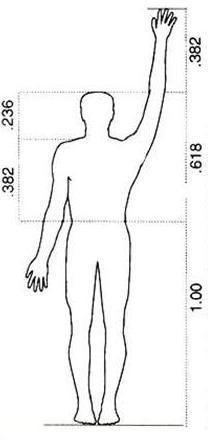
Число Фибоначчи и золотое сечение в природе
В растительном и животном мире существует тенденция к формообразованию в виде симметрии, которая наблюдается в направлении роста и движения. Деление на симметричные части, в которых соблюдаются золотые пропорции, — такая закономерность присуща многим растениям и животным.
Природа вокруг нас может быть описана с помощью чисел Фибоначчи, например:
- расположение листьев или веток любых растений, а также расстояния соотносятся с рядом приведенных чисел 1, 1, 2, 3, 5, 8, 13 и далее;
- семена подсолнуха (чешуя на шишках, ячейки ананаса), располагаясь двумя рядами по закрученным спиралям в разные стороны;
- соотношение длины хвоста и всего тела ящерицы;
- форма яйца, если провести линию условно через широкую его часть;
- соотношение размеров пальцев на руке человека.
И, конечно, самые интересные формы представляют закручивающиеся по спирали раковины улиток, узоры на паутине, движение ветра внутри урагана, двойная спираль в ДНК и структура галактик — все они включают в себя последовательность чисел Фибоначчи.
Использование золотого сечения в искусстве
Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи. Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.
Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.
Золотое сечение в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
Применение пропорций в дизайне
В дизайне одежды все модельеры делают новые образы и модели с учетом пропорций человеческого тела и правил золотого сечения, хотя от природы не все люди имеют идеальные пропорции.
При планировании ландшафтного дизайна и создании объемных парковых композиций с помощью растений (деревьев и кустарников), фонтанов и малых архитектурных объектов также могут применяться закономерности «божественных пропорций». Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.
Все элементы парка находятся в таких соотношениях, чтобы с помощью геометрического строения, взаиморасположения, освещения и света, произвести на человека впечатление гармонии и совершенства.
Применение золотого сечения в кибернетике и технике
Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.
Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.
Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.
Современные исследования теории о золотой пропорции
Начиная с середины 20 века, интерес к проблемам и влиянию закономерностей золотых пропорций на жизнь человека, резко возрастает, причем со стороны многих ученых различных профессий: математиков, исследователей этноса, биологов, философов, медицинских работников, экономистов, музыкантов и др.
В США с 1970-хгодов начинает выпускаться журнал The Fibonacci Quarterly, где публикуются работы на эту тему. В прессе появляются работы, в которых обобщенные правила золотого сечения и ряда Фибоначчи используют в различных отраслях знаний. Например, для кодирования информации, химических исследований, биологических и т.д.
Все это подтверждает выводы древних и современных ученых о том, что золотая пропорция многосторонне связана с фундаментальными вопросами науки и проявляется в симметрии многих творений и явлений окружающего нас мира.
Последовательность чисел Фибоначчи: формула, таблица, золотое сечение
Числа Фибоначчи – это последовательность чисел, которая начинается с цифр 0 и 1, а каждое последующее значение является суммой двух предыдущих.
Формула последовательности Фибоначчи
Например:
- F0 = 0
- F1 = 1
- F2 = F1+F0 = 1+0 = 1
- F3 = F2+F1 = 1+1 = 2
- F4 = F3+F2 = 2+1 = 3
- F5 = F4+F3 = 3+2 = 5
Золотое сечение
Соотношение двух последовательных чисел Фибоначчи сходится к золотому сечению:
где φ – это золотое сечение = (1 + √5) / 2 ≈ 1,61803399
Чаще всего, это значение округляют до 1,618 (или 1,62). А в округленных процентах пропорция выглядит так: 62% и 38 %.
Таблица последовательности Фибоначчи
| n | Fn |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
microexcel.ru
C-код (Си-код) функции
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n > 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
Числа Фибоначчи, «Золотое сечение» — и мировые финансовые рынки (перевод с elliottwave com)
Волны Эллиотта часто связаны друг с другом через последовательность ФибоначчиЧисла Фибоначчи — последовательность, которая начинается с 0 и 1, и каждое последующее число является суммой двух предыдущих (0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Д.).
После первых нескольких чисел в последовательности отношение любого числа к следующему более высокому составляет приблизительно 0,618 к 1; его отношение к следующему более низкому числу составляет приблизительно 1,618 к 1. Это известно как Золотое сечение.
Отношения Фибоначчи появляются по всей природе, от формы галактик и морских раковин до молекул и даже человеческого тела: Классическая книга Уолл-стрит «Принцип волн Эллиотта» от Фроста и Пректера объясняет, почему эти коэффициенты должны представлять большой интерес для глобальных инвесторов:
Последовательность Фибоначчи управляет количеством волн, которые формируются в движении совокупных цен на акции …
Долгосрочные и краткосрочные рыночные графики часто заполнены отношениями Фибоначчи. Вот пример из той же книги:Показывая последовательность 1930-1942 гг., рыночные колебания охватывают приблизительно 260, 160, 100, 60 и 38 пунктов соответственно, что близко напоминает сокращающийся список коэффициентов Фибоначчи: 2,618, 1,618, 1,00, 0,618 и 0,382.
Какое отношение Фибоначчи имеет к сегодняшним движениям на мировом фондовом рынке?
Вот пример из нашей перспективы глобального рынка в августе:Вы заметите, как Азиатский индекс Infotech начал восходящий поворот направо в точке, где волна (ii в кружке) достигла 61,8% волны (i в кружке). Это всего лишь один пример того, как фондовый рынок во всем мире часто соответствует Золотому сечению.
Отношения Фибоначчи также показывают другие возможности в других частях земного шара.
перевод отсюда
реализация и сравнение / Хабр
Введение
Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.
Код предназначен для Python 3, хотя должен идти и на Python 2.
Для начала – напомню определение:
Fn= Fn-1+ Fn-2
и F1= F2=1.
Замкнутая формула
Пропустим детали, но желающие могут ознакомиться с выводом формулы. Идея в том, чтобы предположить, что есть некий x, для которого Fn = xn, а затем найти x.
что означает
сокращаем xn-2
Решаем квадратное уравнение:
Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:
что и используем для вычисления Fn.
from __future__ import division
import math
def fib(n):
SQRT5 = math.sqrt(5)
PHI = (SQRT5 + 1) / 2
return int(PHI ** n / SQRT5 + 0.5)
Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления Fn красиво с математической точки зрения, но уродливо — с компьютерной.
Рекурсия
Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:
fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1
Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека
Запоминание
У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.
Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.
M = {0: 0, 1: 1}
def fib(n):
if n in M:
return M[n]
M[n] = fib(n - 1) + fib(n - 2)
return M[n]
(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)
Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии
Динамическое программирование
После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.
Это решение часто приводится в качестве примера динамического программирования.
def fib(n):
a = 0
b = 1
for __ in range(n):
a, b = b, a + b
return a
Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.
Матричная алгебра
И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что
А обобщение этого говорит о том, что
Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.
Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что
где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.
def pow(x, n, I, mult):
"""
Возвращает x в степени n. Предполагает, что I – это единичная матрица, которая
перемножается с mult, а n – положительное целое
"""
if n == 0:
return I
elif n == 1:
return x
else:
y = pow(x, n // 2, I, mult)
y = mult(y, y)
if n % 2:
y = mult(x, y)
return y
def identity_matrix(n):
"""Возвращает единичную матрицу n на n"""
r = list(range(n))
return [[1 if i == j else 0 for i in r] for j in r]
def matrix_multiply(A, B):
BT = list(zip(*B))
return [[sum(a * b
for a, b in zip(row_a, col_b))
for col_b in BT]
for row_a in A]
def fib(n):
F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply)
return F[0][1]
Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи
Сравнение быстродействия
Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.
n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.
Теоретические замечания
Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:
Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности Fn. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в Аn — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).
Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» {11}. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.
Золотое сечение и пропорции Фибоначчи
Мы уже писали о 10 правилах композиции. Однако есть еще одно правило которое поможет вам улучшить ваши познания в работе с композицией.
Числа Фибоначчи — элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени итальянского математика средневековой Европы Леонардо Пизанского по прозвищу Фибоначчи, что обозначает «хороший сын родился».
Числа Фибоначчи так же называют золотым сечением. Не вдаваясь в математику, можно сказать лишь одно — изображения, которые согласуются с золотым сечением и числами Фибоначчи особенно благоприятны для человеческого глаза.
Многие фотографы и дизайнеры придерживаются пропорций 1:1.618 для построения более удачной композиции.
Эта последовательность была хорошо известна в Индии, где применялась в метрических науках. Позже многие исследователи начали замечать эту последовательность в природе и космосе.
Как на практике работать с композицией читайте в статье «9 советов по композиции от Стива Маккарри».
Следующие два видео и последующие за ним изображения помогут вам лучше понять как это работает на практике.
Ниже представлены фотографии, которые сделаны с применением пропорций Фибоначчи.
Последовательность Фибоначчи и принципы Золотого сечения :: SYL.ru
Последовательность Фибоначчи, ставшая известной большинству благодаря фильму и книге «Код да Винчи», это ряд чисел, выведенный итальянским математиком Пизанским Леонардо, более известным под псевдонимом Фибоначчи, в тринадцатом веке. Последователи ученого заметили, что формула, которой подчинен данный ряд цифр, находит свое отображение в окружающем нас мире и перекликается с другими математическими открытиями, тем самым открывая для нас дверь в тайны мироздания. В этой статье мы расскажем, что такое последовательность Фибоначчи, рассмотрим примеры отображения этой закономерности в природе, а также сравним с другими математическими теориями.
Формулировка и определение понятия
Ряд Фибоначчи – это математическая последовательность, каждый элемент которой равен сумме двух предыдущих. Обозначим некой член последовательности как хn. Таким образом, получим формулу, справедливую для всего ряда: хn+2=хn+хn+1. При этом порядок последовательности будет выглядеть так: 1, 1, 2, 3, 5, 8, 13, 21, 34. Следующим числом будет 55, так как сумма 21 и 34 равна 55. И так далее по такому же принципу.
Примеры в окружающей среде
Если мы посмотрим на растение, в частности, на крону из листьев, то заметим, что они распускаются по спирали. Между соседними листьями образуются углы, которые, в свою очередь, образуют правильную математическую последовательность Фибоначчи. Благодаря этой особенности каждый отдельно взятый листочек, который растет на дереве, получает максимальное количество солнечного света и тепла.
Математическая загадка Фибоначчи
Известный математик представил свою теорию в виде загадки. Звучит она следующим образом. Можно поместить пару кроликов в замкнутое пространство для того, чтобы узнать, какое количество пар кроликов родится в течении одного года. Учитывая природу этих животных, то, что каждый месяц пара способна производить на свет новую пару, а готовность к размножению у них появляется по достижении двух месяцев, в итоге он получил свой знаменитый ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 — где показано количество новых пар кроликов в каждом месяце.
Последовательность Фибоначчи и пропорциональное соотношение
Этот ряд имеет несколько математических нюансов, которые обязательно нужно рассмотреть. Он, приближаясь медленнее и медленнее (асимптотически), стремится к некоему пропорциональному соотношению. Но оно иррациональное. Другими словами, представляет собой число с непредсказуемой и бесконечной последовательностью десятичных чисел в дробной части. Например, соотношение любого элемента ряда варьируется около цифры 1,618, то превосходя, то достигая его. Следующее по аналогии приближается к 0,618. Что есть обратно пропорциональным к числу 1,618. Если мы поделим элементы через один, то получим 2,618 и 0,382. Как вы уже поняли, они также являются обратно пропорциональными. Полученные числа называются коэффициентами Фибоначчи. А теперь объясним, для чего мы выполняли эти вычисления.
Золотое сечение
Все окружающие нас предметы мы различаем по определенным критериям. Один из них – форма. Какие-то нас привлекают больше, какие-то меньше, а некоторые и вовсе не нравятся. Замечено, что симметричный и пропорциональный объект гораздо легче воспринимается человеком и вызывает чувство гармонии и красоты. Цельный образ всегда включает в себя части различного размера, которые находятся в определенном соотношении друг с другом. Отсюда вытекает ответ на вопрос о том, что называют Золотым сечением. Данное понятие означает совершенство соотношений целого и частей в природе, науке, искусстве и т. д. С математической точки зрения рассмотрим следующий пример. Возьмем отрезок любой длины и разделим его на две части таким образом, чтобы меньшая часть относилась к большей как сумма (длина всего отрезка) к большей. Итак, примем отрезок с за величину один. Его часть а будет равна 0,618, вторая часть b, выходит, равна 0,382. Таким образом, мы соблюдаем условие Золотого сечения. Отношение отрезка c к a равняется 1,618. А отношение частей c и b – 2,618. Получаем уже известные нам коэффициенты Фибоначчи. По такому же принципу строятся золотой треугольник, золотой прямоугольник и золотой кубоид. Стоит также отметить, что пропорциональное соотношение частей тела человека близко к Золотому сечению.
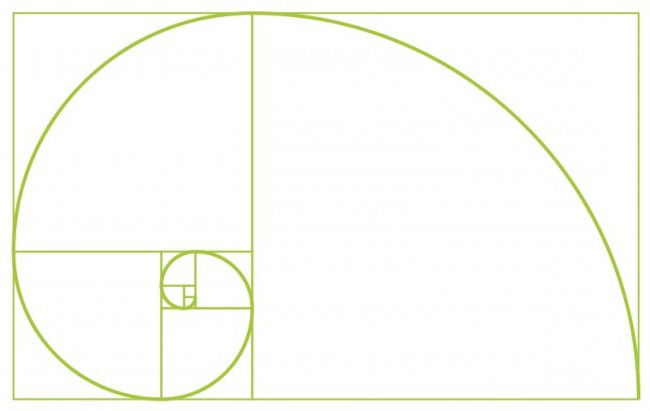
Последовательность Фибоначчи – основа всего?
Попробуем объединить теорию Золотого сечения и известного ряда итальянского математика. Начнем с двух квадратов первого размера. Затем сверху добавим еще квадрат второго размера. Подрисуем рядом такую же фигуру с длиной стороны, равной сумме двух предыдущих сторон. Аналогичным образом рисуем квадрат пятого размера. И так можно продолжать до бесконечности, пока не надоест. Главное, чтобы величина стороны каждого последующего квадрата равнялась сумме величин сторон двух предыдущих. Получаем серию многоугольников, длина сторон которых является числами Фибоначчи. Эти фигуры называются прямоугольниками Фибоначчи. Проведем плавную линию через углы наших многоугольников и получим… спираль Архимеда! Увеличение шага данной фигуры, как известно, всегда равномерно. Если включить фантазию, то полученный рисунок можно проассоциировать с раковиной моллюска. Отсюда можем сделать вывод, что последовательность Фибоначи – это основа пропорциональных, гармоничных соотношений элементов в окружающем мире.
Математическая последовательность и мироздание
Если присмотреться, то спираль Архимеда (где-то явно, а где-то завуалированно) и, следовательно, принцип Фибоначчи прослеживаются во многих привычных природных элементах, окружающих человека. Например, все та же раковина моллюска, соцветия обычной брокколи, цветок подсолнечника, шишка хвойного растения и тому подобное. Если заглянем подальше, то увидим последовательность Фибоначчи в бесконечных галактиках. Даже человек, вдохновляясь от природы и перенимая ее формы, создает предметы, в которых прослеживается вышеупомянутый ряд. Тут самое время вспомнить и о Золотом сечении. Наряду с закономерностью Фибоначчи прослеживаются принципы данной теории. Существует версия, что последовательность Фибоначчи — это своего рода проба природы адаптироваться к более совершенной и фундаментальной логарифмической последовательности Золотого сечения, которая практически идентична, но не имеет своего начала и бесконечна. Закономерность природы такова, что она должна иметь свою точку отсчета, от чего отталкиваться для создания чего-то нового. Отношение первых элементов ряда Фибоначчи далеки от принципов Золотого сечения. Однако чем дальше мы его продолжаем, тем больше это несоответствие сглаживается. Для определения последовательности необходимо знать три его элемента, которые идут друг за другом. Для Золотой последовательности же достаточно и двух. Так как она является одновременно арифметической и геометрической прогрессией.
Заключение
Все-таки, исходя из вышесказанного, можно задать вполне логичные вопросы: «Откуда появились эти числа? Кто этот автор устройства всего мира, попытавшийся сделать его идеальным? Было ли всегда все так, как он хотел? Если да, то почему возник сбой? Что будет дальше?» Находя ответ на один вопрос, получаешь следующий. Разгадал его — появляются еще два. Решив их, получаешь еще три. Разобравшись с ними, получишь пять нерешенных. Затем восемь, далее тринадцать, двадцать один, тридцать четыре, пятьдесят пять…
Что такое последовательность Фибоначчи (также известная как серия Фибоначчи)?
Леонардо Фибоначчи открыл последовательность, сходящуюся на фи.
В 1202 году нашей эры Леонардо Фибоначчи написал в своей книге «Liber Abaci» простую числовую последовательность, которая является основой невероятной математической взаимосвязи, лежащей в основе фи. Эта последовательность была известна индийским математикам еще в VI веке нашей эры, но именно Фибоначчи представил ее на западе после своих путешествий по Средиземноморью и Северной Африке.Он также известен как Леонардо Боначчи, так как его имя происходит от итальянского слова, означающего «сын Боначчи».
Начиная с 0 и 1, каждое новое число в последовательности представляет собой просто сумму двух перед ним.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. , ,
Эта последовательность показана на правом поле страницы в Liber Abaci, где экземпляр книги находится в Национальной библиотеке Фиренце. Нажмите, чтобы увеличить.
Связь последовательности Фибоначчи с золотым сечением такова: отношение каждой последующей пары чисел в последовательности приблизительно равно Phi (1.618.. .), поскольку 5, разделенное на 3, будет 1.666…, а 8, разделенное на 5, будет 1.60.
В таблице ниже показано, как отношения последовательных чисел в последовательности Фибоначчи быстро сходятся на Фи. После 40-го числа в последовательности это соотношение с точностью до 15 десятичных знаков.
1.618033988749895. , ,
Легко вычислить любое число в последовательности Фибоначчи!
Вот два способа использования phi для вычисления n-го числа в последовательности Фибоначчи (f n ).
Если вы считаете, что 0 в последовательности Фибоначчи соответствует n = 0, используйте эту формулу:
f n = Phi n /5 ½
Возможно, лучше рассматривать 0 в последовательности Фибоначчи как соответствующее 1-му числу Фибоначчи, где n = 1 для 0. Затем вы можете использовать эту формулу, открытую и введенную Джорданом Малачи Дантом в апреле 2005 г .:
f n = Phi n / (Phi + 2)
Оба подхода представляют пределы, которые всегда округляются до правильного числа Фибоначчи и приближаются к фактическому числу Фибоначчи с увеличением n.
Отношение последовательных чисел Фибоначчи сходится на phi
| Последовательность в последовательности | Результат Фибоначчи число (сумма двух чисел перед ним) | Отношение каждого номера к номеру перед ним (это составляет фи) | Разница от Phi | |
0 | 0 | |||
| 1 | 1 | |||
| 2 | 1 | 1.000000000000000 | +0.618033988749895 | |
| 3 | 2 | 2.000000000000000 | -0,381966011250105 | |
| 4 | 3 | 1.500000000000000 | +0.118033988749895 | |
| 5 | 5 | 1.666666666666667 | -0,048632677916772 | |
| 6 | 8 | 1.600000000000000 | +0.018033988749895 | |
| 7 | 13 | 1.625000000000000 | -0,006966011250105 | |
| 8 | 21 | 1,615384615384615 | +0,002649373365279 | |
| 9 | 34 | 1,61 | 119-0,001013630297724 | |
| 10 | 55 | 1,617647058823529 | +0,000386929926365 | |
| 11 | 89 | 1,618181818181818 | -0,000147829431923 | |
| 12 | 144 | 1.617977528089888 | +0,000056460660007 | |
| 13 | 233 | 1.618055555555556 | -0,000021566805661 | |
| 14 | 377 | 1.618025751072961 | +0,000008237676933 | |
| 15 | 610 | 1.618037135278515 | -0,000003146528620 | |
| 16 | 987 | 1.618032786885246 | +0,000001201864649 | |
| 17 | 1 597 | 1.618034447821682 | -0,000000459071787 | |
| 18 | 2 584 | 1.618033813400125 | +0,000000175349770 | |
| 19 | 4 181 | 1.618034055727554 | -0,000000066977659 | |
| 20 | 6 765 | 1.618033963166707 | +0,000000025583188 | |
| 21 | 10 946 | 1.618033998521803 | -0,000000009771909 | |
| 22 | 17 711 | 1.618033985017358 | +0,000000003732537 | |
| 23 | 28 657 | 1.6180339 | 597 | -0,000000001425702 |
| 24 | 46 368 | 1.618033988205325 | +0,000000000544570 | |
| 25 | 75 025 | 1.618033988957902 | -0,000000000208007 | |
| 26 | 121 393 | 1.618033988670443 | +0.000000000079452 | |
| 27 | 196 418 | 1.618033988780243 | -0,000000000030348 | |
| 28 | 317 811 | 1.618033988738303 | +0,000000000011592 | |
| 29 | 514 229 | 1.618033988754323 | -0,000000000004428 | |
| 30 | 832 040 | 1.618033988748204 | +0,000000000001691 | |
| 31 | 1,346,269 | 1.618033988750541 | -0,000000000000646 | |
| 32 | 2 178 309 | 1.618033988749648 | +0,000000000000247 | |
| 33 | 3 524 578 | 1.618033988749989 | -0,000000000000094 | |
| 34 | 5 702 887 | 1.618033988749859 | +0,000000000000036 | |
| 35 | 9 227 465 | 1.618033988749909 | -0.000000000000014 | |
| 36 | 14 930 352 | 1.618033988749890 | +0,000000000000005 | |
| 37 | 24 157 817 | 1.618033988749897 | -0,000000000000002 | |
| 38 | 39 088 169 | 1.618033988749894 | +0,000000000000001 | |
| 39 | 63 245 986 | 1.618033988749895 | -0,000000000000000 | |
| 40 | 102,334,155 | 1.618033988749895 | +0,000000000000000 |
Тауфик Мохаммед отмечает, что число 13, которое некоторые считают несчастливым, находится в позиции 7, счастливом числе!
Последовательность Фибоначчи и азартные игры или лотереи
Некоторые люди надеются, что числа Фибоначчи дадут преимущество при выборе номеров лотереи или ставок в азартных играх. На самом деле результаты азартных игр определяются случайными исходами и не имеют особой связи с числами Фибоначчи.
Тем не менее, существуют системы ставок, используемые для управления способом размещения ставок, а система Фибоначчи, основанная на последовательности Фибоначчи, является разновидностью прогрессии Мартингейла. В этой системе, часто используемой для казино и онлайн-рулетки, схема размещаемых ставок соответствует прогрессии Фибоначчи: то есть каждая ставка должна быть суммой двух предыдущих ставок до тех пор, пока не будет сделан выигрыш. Если число выигрывает, ставка возвращается на два числа в последовательности, потому что их сумма была равна предыдущей ставке.
В системе Фибоначчи ставки остаются ниже прогрессии Мартингейла, которая каждый раз удваивается. Обратной стороной является то, что в системе рулетки Фибоначчи ставка не покрывает все потери в неудачной полосе.
Важное предупреждение: системы ставок не изменяют основных коэффициентов игры, которые всегда в пользу казино или лотереи. Они могут быть просто полезны для более методичной игры со ставками, как показано в примере ниже:
| Круглый | Сценарий 1 | Сценарий 2 | Сценарий 3 |
| Ставка 1 | Ставка 1 и проигрыш | Ставка 1 и проигрыш | Сделайте ставку 1 и выиграйте |
| Ставка 2 | Ставка 1 и проигрыш | Ставка 1 и проигрыш | Сделайте ставку 1 и выиграйте |
| Ставка 3 | Сделайте ставку 2 и выиграйте | Ставка 2 и проигрыш | Ставка 1 и проигрыш |
| Ставка 4 | – | Сделайте ставку 3 и выиграйте | Ставка 1 и проигрыш |
| Ставка 5 | – | – | Сделайте ставку 2 и выиграйте |
| Чистый результат | Даже на 0 | Меньше на 1 | Впереди на 2 |
c — Рекурсия Фибоначчи с использованием золотого сечения (золотого числа)
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
чисел Фибоначчи (0,1,1,2,3,5,8,13, …)
Последовательность Фибоначчи — это последовательность чисел, где каждое число сумма двух предыдущих чисел, кроме первых двух чисел, которые равны 0 и 1.
Формула последовательности Фибоначчи
Например:
Ф 0 = 0
Ф 1 = 1
F 2 = F 1 + F 0 = 1 + 0 = 1
F 3 = F 2 + F 1 = 1 + 1 = 2
F 4 = F 3 + F 2 = 2 + 1 = 3
F 5 = F 4 + F 3 = 3 + 2 = 5
,..
Схождение золотого сечения
Отношение двух последовательных чисел Фибоначчи сходится к золотое сечение:
φ — золотое сечение = (1 + √5) / 2 ≈ 1,61803399
Таблица последовательности Фибоначчи
| n | F n |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
Калькулятор последовательности Фибоначчи
TBD
C-код функции Фибоначчи
двойное число Фибоначчи (целое число без знака)
{
двойной f_n = n;
двойной f_n1 = 0.0;
двойной f_n2 = 1.0;
, если (n> 1) {
для (int к = 2; к <= п; k ++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
,Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — одна из самых известных формул в математике.
Каждое число в последовательности представляет собой сумму двух предшествующих ему чисел. Итак, последовательность такова: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Математическое уравнение, описывающее его: Xn + 2 = Xn + 1 + Xn
Опора средней школы и студентов, его называли «секретным кодом природы» и «универсальным правилом природы». Говорят, что он определяет размеры всего, от Великой пирамиды в Гизе до культовой морской ракушки, которая, вероятно, украшала обложку вашего школьного учебника математики.
И, скорее всего, почти все, что вы знаете об этом, неверно.
Разрозненная история
Итак, что же на самом деле стоит за этой знаменитой сценой?
Многие источники утверждают, что он был впервые открыт или «изобретен» Леонардо Фибоначчи. Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский, сказал Кейт Девлин, математик из Стэнфордского университета. По словам Девлина, только в 19 веке историки придумали прозвище Фибоначчи (что примерно означает «сын клана Боначчи»), чтобы отличить математика от другого известного Леонардо Пизанского.[Большие числа, определяющие Вселенную]
Но Леонардо Пизанский на самом деле не обнаружил последовательность, — сказал Девлин, который также является автором книги «В поисках Фибоначчи: поиски заново забытого математического гения, изменившего мир» (Принстон University Press, 2017). Древние санскритские тексты, в которых использовалась индуистско-арабская система счисления, впервые упоминают об этом, и те, которые предшествуют Леонардо Пизанскому на столетия.
«Это было всегда», — сказал Девлин Live Science.
Однако в 1202 году Леонардо Пизанский опубликовал огромный фолиант «Liber Abaci», математическую «поваренную книгу» о том, как производить вычисления », — сказал Девлин.«Liber Abaci», написанная для торговцев, излагает индуистско-арабскую арифметику, полезную для отслеживания прибылей, убытков, остатков ссуд и т. Д., Сказал Девлин.
В одном месте книги Леонардо Пизанский вводит последовательность с задачей с участием кроликов. Задача состоит в следующем: начните с кролика-самца и кролика-самки. Через месяц они созревают и производят помет с еще одним кроликом и самкой. Через месяц эти кролики размножаются и выходят, как вы уже догадались, еще один самец и самка, которые также могут спариваться через месяц.(Не обращайте внимания на невероятно невероятную биологию.) Сколько кроликов у вас будет через год? Оказывается, ответ — 144, и формула, использованная для получения этого ответа, теперь известна как последовательность Фибоначчи. [11 самых красивых математических уравнений]
«Liber Abaci» впервые представила последовательность в западном мире. Но после нескольких скудных параграфов о разведении кроликов Леонардо из Пизы никогда больше не упоминал последовательность. Фактически, об этом почти забыли до 19 века, когда математики больше узнали о математических свойствах последовательности.В 1877 году французский математик Эдуард Лукас официально назвал задачу о кролике «последовательностью Фибоначчи», — сказал Девлин.
Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но не такие волшебные, как могут показаться. (Изображение предоставлено Shutterstock)Воображаемое значение
Но каково именно значение последовательности Фибоначчи? Помимо того, что это изящный инструмент обучения, он обнаруживается в нескольких местах на природе. Однако, по словам Девлина, архитектурой вселенной управляет не какой-то секретный код.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение (которое даже не является истинным соотношением, потому что это иррациональное число). Проще говоря, соотношение чисел в последовательности, когда последовательность стремится к бесконечности, приближается к золотому сечению, которое составляет 1,6180339887498948482 … Оттуда математики могут вычислить так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотое сечение. [9 самых значительных чисел в мире]
«Золотое сечение», кажется, действительно отражает некоторые типы роста растений, — сказал Девлин.Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Сосновые шишки имеют золотую спираль, как и семена подсолнечника, согласно «Филлотаксису: Системное исследование морфогенеза растений» (Cambridge University Press, 1994). Но столько же растений не соблюдают это правило.
«Это не« единственное Божье правило »для выращивания растений, скажем так, — сказал Девлин.
И, возможно, самый известный пример из всех, морская раковина, известная как наутилус, на самом деле не выращивает новые клетки согласно последовательности Фибоначчи, сказал он.
Когда люди начинают рисовать связи с человеческим телом, искусством и архитектурой, связи с последовательностью Фибоначчи переходят от неубедительной к полностью вымышленной.
«Потребовалась бы большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, большая часть которой является просто повторением одних и тех же ошибок разными авторами», — писал Джордж Марковски, математик, который тогда работал в Университете штата Мэн. в статье 1992 года в College Mathematics Journal.
Большая часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Цайзинга.Цейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. Золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения. С тех пор люди говорили, что золотое сечение можно найти в размерах Пирамиды в Гизе, Парфенона, «Витрувианского человека» Леонардо да Винчи и ряда зданий эпохи Возрождения. По словам Девлина, общие утверждения о том, что это соотношение «исключительно приятно» для человеческого глаза, были сформулированы некритически.
Все эти утверждения, когда они проверяются, оказываются в значительной степени ложными, сказал Девлин.
«Мы хорошие распознаватели образов. Мы можем видеть закономерности независимо от того, есть они или нет», — сказал Девлин. «Это все просто принятие желаемого за действительное».
,