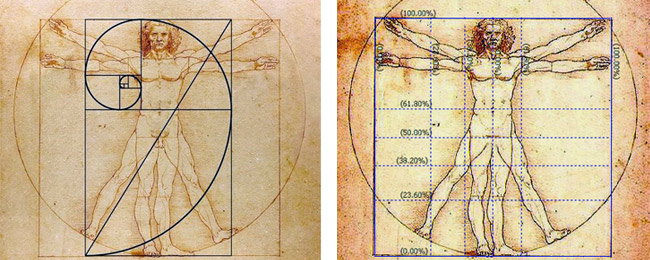
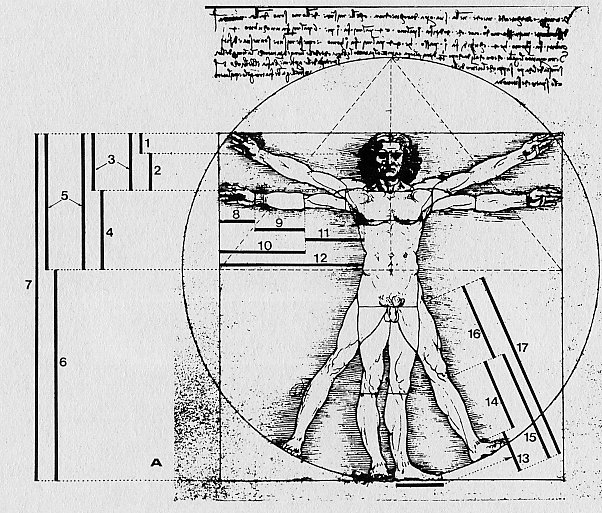
Золотое сечение. Божественная пропорция | Журнал Ярмарки Мастеров
Золотое сечение (лат. Sectio aurea) — термин, знакомый многим. Освежим немного нашу память, друзья!
Золотое сечение, или золотая пропорция — идеальное соотношение величин, лежащее в основе гармонии природы и человека. «Золотое сечение» имеет массу удивительных свойств (из разряда «Ух, ты! Занимательная геометрия»), возможно, именно поэтому, ему приписывается некое божественное происхождение и ряд вымышленных свойств.
Если выражаться сухо по-научному, то ЗС — это соотношение величин или отрезков, при котором отношение большей части к меньшей равно отношению всей величины к большей части. Приблизительное округленное процентное соотношение частей — 62% и 38%.
Числовая величина золотого сечения – 1, 6180339887 (и это еще округление =)) до десятого знака!)
![]()
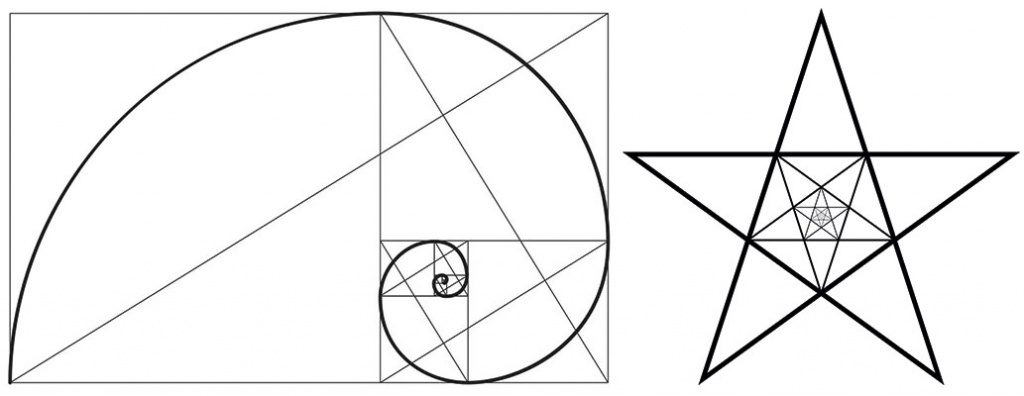
Пример золотого сечения в лучах пятиконечной звезды.
С Вашего позволения, я опущу многострочные математические фомулы и фомулировки =) Перейдем сразу к Прекрасному!
Зачатки этого понятия встречаются еще в античной литературе, датированной 300 гг. до нашей эры, а «божественная пропорция» широко применялась в трудах и работах мастеров Эпохи Возрождения. Иоган Кеплер, астроном 16 в. назвал золотое сечение одним из сокровищ геометрии. Он впервые обращает внимание то, как проявляется ЗС в ботанике (рост растений и строение стеблей и соцветий).
В середине 19 в. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение лежит в основе некой среднестатистической пропорции человеческого тела. Деление тела точкой пупка – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 к 8 = 1,625 и несколько ближе подходят к ЗС, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 к 5 = 1,6. Пропорции золотого сечения проявляются и в отношении всех частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
![]()
![]()
![]()
![]()
На протяжении веков существовало общеприянтое мнение, что рукотворные объекты, созданные с применением принципа ЗС, воспринимаются Человеком как наиболее гармоничные, совершенные. Пропорции золотого сечения можно выделить в проекциях египетских пирамид. Соотношение сторон плана Парфенона в Афинском Акрополе также являет собой не простое кратное число, а бесконечно дробное (догадайтесь, какое?). Таковыми же являются соотношение сторон планов и фасадов многих византийских церквей, романских готических соборов. Принято считать, что еще со времен Ренессанса многие художники и архитекторы сознательно используют принципы золотого сечения в своих творениях.
![]()
Золотое сечение на примере фасада храма Парфенона
Однако же, бытует и мнение, что значение ЗС в искусстве сильно преувеличенно, порой притянуто за уши исследователями, либо основано наошибочных расчетах. Тут каждый останется при своем. Помню, как на втором курсе в архитектурном нас, лопоухих, профессора пытались приобщить к прекрасному и долго-долго втолковывали про принципы золотого сечения в зодчестве, ряды Фибоначчи и прочее-прочее =)) Но настоящее понимание этой волшебной геометрии пришло ко мне много позже, при изучении бионики (один из стилей архитектуры), которая базируется именно на совершенстве природных форм. Согласитесь, мы не в силах оспаривать очевидное, а примеры идеальной пропорции встречаются сплошь и рядом: в раковинах аммонитов, в расположении ветвей на стебле растения, прожилках листьев. Ведь все, что приобретало какую-то форму, образовывалось, росло, осуществляло свое развитие в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали. Раковина закручена по спирали. И вообще, представление о золотом сечении будет неполным, если не сказать о спирали. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали: увеличение ее шага всегда равномерно.
![]()
Спираль Архимеда
Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке , семян подсолнечника, шишек сосны проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».
![]()
Стебель цикория
Полюбуйтесь, как наглябно иллюстрирует природа принципы Золотого сечения! Совершенные спирали без изъян, соотношения витков которых строго соответсвует канонам и принципам построения ЗС.
![]()
© Copyright: Tihomir Balkonskiy
![]()
© Copyright: Kibardindesign
![]()
![]()
![]()
Материалы взяты из Интернета.
Текст преимущественно авторский =)
Спасибо за Ваше внимание, Даша Самаркина
Можете объяснить по-простому, что такое золотое сечение и почему его так часто везде используют?
Золотое сечение — правило пропорции, не случайно его еще называют божественной гармонией.
Коротко эта пропорция определяется так: «меньшая часть относится к большей, как большая ко всему целому «.
В математике золотое сечение называют «асимметричной симметрией», оно выражается вполне конкретной формулой. Само понятие впервые использовал Пифагор, а число золотого сечения получило «имя» древнегреческого архитектора Фидия — число «фи» (греческая буква φ). Равно это число (с округлением) 1,62, а в процентном выражении золотое сечение выглядит, как 62% и 38%.
По канонам этой пропорции создавались произведения искусства еще древними египтянами, так что можно сказать, что золотое сечение сопровождает человеческую цивилизацию на протяжении всего ее развития.
Пропорции, если не совсем точные, то все же максимально близкие к золотому сечению, присутствуют везде — в искусстве, в природе и в самом человеке. Поэтому не совсем верно говорить, что его используют искуственно, оно просто является своеобразным маркером того, что красиво и гармонично.
Вот, например, можете и Вы убедиться, если измерите сами себя 🙂
Число «фи» или близкое к нему получится, если вычислить отношение расстояния от плеч до макушки к размеру головы; отношение расстояния от пупка до коленок и от коленок до ступней. И лицо воспринимается как более красивое, чем ближе его пропорции к идеальным: от подбородка до крайней точки верхней губы и от нее до носа пропорция близка к 1:1,62.
По правилу божественной гармонии «устроены» шишки, раковины моллюсков, чешуйки на плодах ананаса. Его обнаружили в молекуле ДНК и в спиралевидных галактиках.
Настоящие произведения искусства, которые человек подсознательно воспринимает, как прекрасные, тоже основаны на этой пропорции — будь это живопись, музыка, скульптура, архитектура и так далее.
Гармония в нашей жизни рулит! А гармония — это и есть золотое сечение 🙂
Гармонии и Вам!
🍀 Божественная гармония: что такое золотое сечение: пропорции и принципы
Эта гармония поражает своими масштабами…
Здравствуйте, друзья!
Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.
Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)
Что такое золотое сечение?
Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.
Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».
До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.
Золотое сечение в математике
Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.
В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.
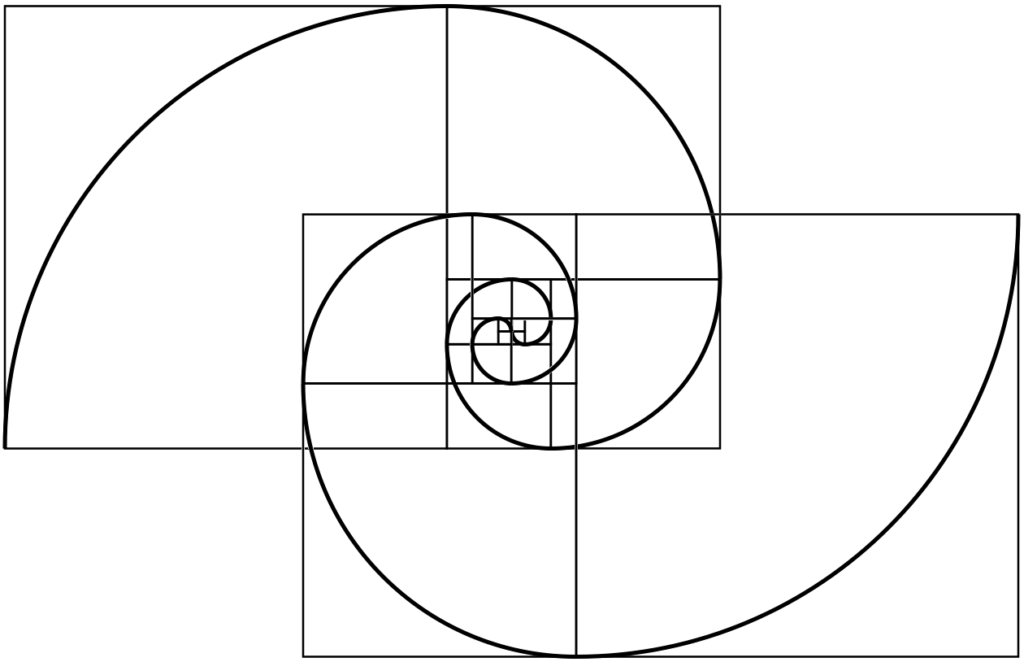
Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Ряд Фибоначчи и золотое сечение
Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ — Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».
Сама последовательность выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… и дальше до бесконечности.
Если словами, то последовательность Фибоначчи — это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.

Причем здесь золотое сечение? Сейчас увидите.
Спираль Фибоначчи
Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.

Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.
Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».

Золотая спираль — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение.

В общем и целом, с точки зрения математики, золотое сечение — идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.
Золотое сечение в природе, человеке, искусстве
Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.
И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.
Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.
Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.
Пропорции золотого сечения в человеке
Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.
Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:
-
от плеч до макушки к размеру головы = 1:1.618
-
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
-
от пупка до коленок и от коленок до ступней = 1:1.618
-
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».
Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.
Золотое сечение в природе и ее явлениях
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:
-
в завитках человеческого уха мы можем увидеть золотую спираль;
-
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
-
и в молекуле ДНК;
-
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.
Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.
Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:
-
Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
-
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
-
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
-
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.
Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.
Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.
Золотое сечение в искусстве
Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.
-
Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
-
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
-
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
-
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
-
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.
Золотые котики Фибоначчи
Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)
А все дело в том, что кошки — идеальны! Не верите? Сейчас докажу вам это математически!
Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)
* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.
На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!
P. S. Изображения взяты с сайта medium.com.
Онлайн калькулятор: Золотое сечение
Калькулятор ниже находит параметры, соответствующие золотому сечению. Про само золотое сечение рассказано под калькулятором

Золотое сечение
ТипДлинный отрезокКороткий отрезокСуммарный отрезокТочность вычисленияЗнаков после запятой: 8
Длинный отрезок
Короткий отрезок
Суммарный отрезок
Золотое сечение
save Сохранить extension Виджет
Золотое сечение — термин, обозначающий деление отрезка на два в соотношении, при котором большая часть относится к меньшей также как весь отрезок относится к большей. Также употребляют термин деление в крайнем и среднем отношении.
Отношение это фиксированное, его можно найти. Представим, что b у нас единица. Тогда значение a должно равняться искомому отношению, и его надо найти — переименуем его в более привычное x и проведем ряд преобразований:
Последнее есть квадратное уравнение. Его положительный корень:
и есть отношение золотого сечения. Число это иррациональное:
Для практических целей иногда используют приближение — большая часть равна 0,62 всей величины, меньшая — 0,38 (это видно, если ввести длину 1, и выбрать тип «суммарный отрезок» в калькуляторе сверху).
Золотое сечение известно еще со времен Евклида (ок. 300 лет до н. э.), и у него много забавных свойств, про которые можно почитать в: Википедии, например, к нему стремится отношение последовательных чисел Фибоначчи.
Для полноты ликбеза скажем, что почему-то считается, что объекты, содержащие золотое сечение, воспринимаются людьми как наиболее гармоничные. Ну а вот целая занятная статья, где золотое сечение находят буквально во всем.
Золотое сечение — Википедия
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Первая тысяча знаков значения Φ[1].
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число
- Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}
Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2],
- φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}
Отсюда следует, что
- φ=Φ−1{\displaystyle \varphi =\Phi -1}.
Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.
Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.
Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом.
Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5].
История
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.
Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6].
Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16]
Математические свойства
- 1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
- Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:
- Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}
- Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби
- Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,
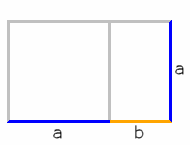 Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения
Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения- Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.
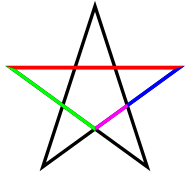 Золотое сечение в пятиконечной звезде
Золотое сечение в пятиконечной звезде- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.
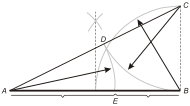 Построение золотого сечения
Построение золотого сечения- Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}
- Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }[17].
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
- Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны[18].
- ∑n=1∞(−1)n+1n2(2nn)=2ln2φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]
Золотое сечение в науке
Общее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.
Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).
Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.
Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23].
Золотое сечение и гармония в искусстве
Золотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
- Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
- Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3378 дней].
- Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.
Примеры сознательного использования
Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 603 дня].
Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.
Золотое сечение в биологии и медицине
 Золотое сечение в природе
Золотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник?] и др.
См. также
Примечания
- ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
- ↑ 1 2 Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
- ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
- ↑ Devlin’s Angle, The Myth That Will Not Go Away
- ↑ В. Лаврус, Золотое сечение
- ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
- ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
- ↑ Herz-Fischler, 2013, p. 168.
- ↑ Livio, 2008, p. 6-7.
- ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
- ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
- ↑ Herz-Fischler, 2013, p. 169.
- ↑ Livio, 2008, p. 7.
- ↑ Herz-Fischler, 2013, p. 169-170.
- ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
- ↑ Системы счисления.
- ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
- ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
- ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
- ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
- ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
- ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
- ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.
Литература
- Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
- Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
- Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
- Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
- Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
- Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
- Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
- Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в
- Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.
Ссылки
Золотое сечение | Блог 4brain
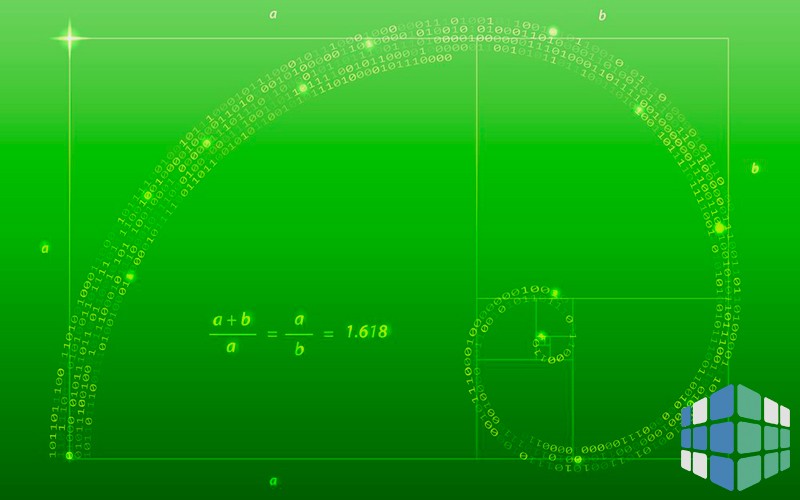
Золотым сечением называют число, полученное путем деления линии на две части таким образом, что более длинная часть (а), разделенная на меньшую часть (b), равна полной длине линии (а+b), разделенной на более длинную часть (а). Такое отношение часто символизируют с помощью литеры Ф (читается как «фи») – 21-й буквы греческого алфавита. В форме уравнения это выглядит так:
a / b = (a + b) / a = 1.6180339887498948420…
Как и в случае с π (пи, отношение длины окружности к ее диаметру), число Ф является бесконечным. Обычно его округляют до значения 1,618.
История открытия золотой середины
Это число было найдено и открыто много раз, поэтому у него так много разных названий — золотая середина, золотое сечение, божественная пропорция и т.д. Исторически его можно увидеть в архитектуре многих древних творений, таких как Великие Пирамиды и Парфенон. В пирамиде Гизы длина каждой стороны основания составляет 230,5 метров при высоте 146,6 метров. Отношение основания к высоте составляет примерно 1,5717, что близко к золотой пропорции.
Фидий (500 г. до н.э. — 432 г. до н.э.) был греческим скульптором и математиком, который, как считается, применил Ф, создавая скульптуры для Парфенона. Платон (428 г. до н.э. — 347 г. до н.э.) считал, что золотое сечение является наиболее универсальным связующим звеном математических отношений. Позднее Евклид (365 г. до н.э. — 300 г. до н.э.) связал золотое сечение с построением пентаграммы.
Последовательность Фибоначчи и золотое сечение
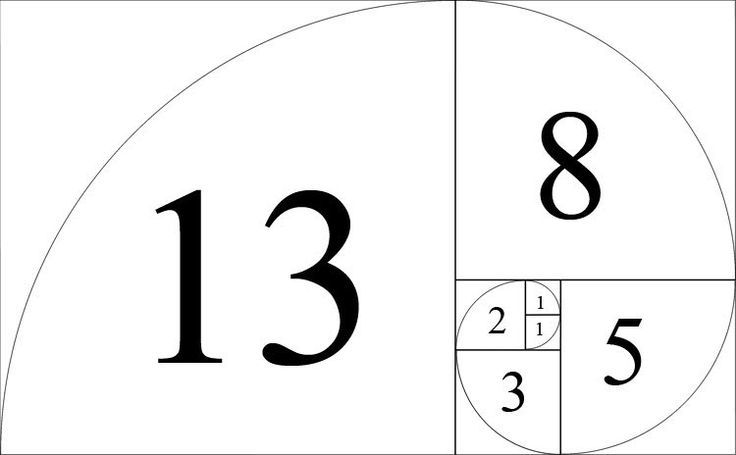
Около 1200 года математик Леонардо Фибоначчи открыл уникальные свойства последовательности Фибоначчи. Эта последовательность непосредственно связана с золотым сечением, потому что если взять любые два последовательных числа Фибоначчи, их отношение будет очень близко к золотому сечению. По мере того как числа возрастают, соотношение приближается к значению 1,618. Например, соотношение 3 к 5 составляет 1,666. Но соотношение 13 к 21 составляет 1,625. Возрастая, соотношение 144 к 233 составляет 1,618. Все эти числа являются последовательными числами в последовательности Фибоначчи.
Такие соотношения из ряда Фибоначчи, близкие к значению золотого сечения, могут быть применены к пропорциям прямоугольника, называемого золотым прямоугольником. Он известен как одна из наиболее визуально совершенных из всех геометрических форм — следовательно, правило золотого сечения очень широко применяется во всех видах визуального искусства. Золотой прямоугольник также связан с золотой спиралью, которая создается путем создания смежных квадратов измерений Фибоначчи.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.
Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.
Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.
Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.
Золотое сечение – МИР БОЕВЫХ ИСКУССТВ
Золотое сечение (лат. Sectio aurea) – это термин, введенный в обиход немецким математиком Мартином Омом в 1835 году.
Однако задолго до того, как термин «Золотое сечение» стал известен, его принципы использовались Пифагором, Евклидом, Аристотелем, Леонардо да Винчи, Микеланджело и другими.
Первое научное обоснование Золотого сечения было дано монахом Лукой Пачоли в 1509 году в книге «Божественная пропорция», иллюстрации к которой предположительно были созданы Леонардо да Винчи.

Золотое сечение — это идеальное соотношение величин, где:
Большая часть относится к меньшей, как вся величина к большей части.
Приблизительное процентное соотношение частей Золотого сечения составляет 62% и 38%.
Лука Пачоли усматривал в Золотом сечении Божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой Дух.
Число Фи
В основе Золотого сечения лежит Число Фи.
Точное значение Числа Фи (1000 знаков после запятой):
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

Однако для удобства Число Фи округляют до 3-х знаков после запятой — 1, 618
Число Фи имеет интересные математические свойства:
1) Каждое третье число Фибоначчи четно;
2) Каждое четвертое кратно 3;
3) Каждое пятнадцатое оканчивается нулем
Если разделить единицу на Число Фи, то получится число 0,618… — те же самые десятичные знаки после запятой, что и у числа Фи.
1/Ф = Ф-1 1/1,618 = 0,618
Используя Число Фи можно составить 3 идеальные фигуры.
1 – идеальная звезда, в которой отрезки HF и FC, а так же другие стороны треугольников и соответствующие стороны внутреннего пятиугольника относятся как 1/1.618.
2 – идеальная спираль, которая образована ¼ окружностей вписанных в квадраты, стороны которых являются последовательностью числового ряда Фибоначчи и относятся как 1/1.618.
3 – идеальный прямоугольник, который состоит из квадрата и прямоугольника и меньшая сторона малого прямоугольника (B) относится к стороне квадрата (A) как 1/1.618, а так же сторона квадрата (A) относится к большей стороне большого прямоугольника (A+B) как 1/1.618.
Мистики называют Число Фи основой всего живого на земле.
Все растения, животные, люди наделены физическими пропорциями, приблизительно равными корню от соотношения Числа Фи к 1.
Так, например, если измерить расстояние от плеча до кончиков пальцев, затем разделите его на расстояние от локтя до тех же кончиков пальцев. Получите число 1.618
Расстояние от верхней части бедра до пола, поделенное на расстояние от колена до пола — это снова Число Фи.
Сумма двух первых фаланг пальца в соотношении со всей длиной пальца = Числу Фи.
Последовательность Фибоначчи
Правило Золотого сечения также связывают с именем первого крупного математика средневековой Европы — Леонардо Пизанским, более известным, как Фибоначчи.
В своем труде «Liber Abaci», датируемым 1202 годом, описывая решение одной из задач, ученый вывел числовой ряд, известный сейчас как «Последовательность Фибоначчи».
Элементы данной числовой последовательности:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584…
Особенностью числового ряда Фибоначчи является то, что первые два числа в нем равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел.
На отношение этой последовательности к Золотой пропорции обратил внимание немецкий математик, астроном и первооткрыватель законов движения планет Солнечной системы Иоганн Кеплер, писавшей о Золотой пропорции так:
«Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
В настоящее время Последовательность Фибоначчи является арифметической основой для расчетов пропорций Золотого сечения во всех его проявлениях.
Принципы Золотого сечения используются абсолютно во всех сферах жизни. Не являются исключением и боевые искусства. Так, например, теоретическая основа базовых принципов Системы Кадочникова построена на принципах Золотого сечения.
Принципы Золотого сечения составляют основу практически всех стилей восточных единоборств, а также современных школ боевых искусств.
Траектории движений Айкидо, захваты Циньна, базовые движения Славяно-горицкой борьбы, техники Звериных стилей Ушу и многое другое – это наглядная демонстрация принципов Золотого сечения в боевых искусствах.
Умение видеть пропорции Золотого сечения при основании техники боевых искусств, позволяет существенно упростить освоение приемов и позволяет с легкостью применять их на практике.
золотого сечения | Примеры, определение и факты
Золотое сечение , также известное как золотое сечение , золотая середина или божественная пропорция , в математике иррациональное число (1 + квадратный корень из √5) / 2 , часто обозначается греческой буквой ϕ или τ, что приблизительно равно 1,618. Это отношение отрезка линии, разрезанного на две части разной длины, при котором отношение всего сегмента к таковому более длинного сегмента равно отношению более длинного сегмента к более короткому.Происхождение этого числа можно проследить до Евклида, который упоминает его как «крайнее и среднее соотношение» в Elements . С точки зрения современной алгебры, если длина более короткого сегмента составляет одну единицу, а длина более длинного сегмента — x единиц, возникает уравнение ( x + 1) / x = x / 1; это может быть преобразовано в квадратное уравнение x 2 — x — 1 = 0, для которого положительным решением будет x = (1 + квадратный корень из √5) / 2, золотое сечение.
Древние греки признавали это свойство «разделения» или «разделения на части», фраза, которая в конечном итоге была сокращена до просто «раздел». Прошло более 2000 лет, когда и «пропорции», и «сечение» были названы «золотыми» немецким математиком Мартином Омом в 1835 году. Греки также заметили, что золотое сечение обеспечивает наиболее эстетически приятную пропорцию сторон прямоугольника. , идея, которая была усилена в эпоху Возрождения, например, благодаря работе итальянского эрудита Леонардо да Винчи и публикации De divina пропорционально (1509; Божественная пропорция ), написанной итальянским математиком Лукой Пачоли и проиллюстрированной Леонардо.
Витрувианский человек, исследование фигур Леонардо да Винчи ( c. 1509), иллюстрирующее пропорциональный канон, установленный классическим римским архитектором Витрувием; в Академии изящных искусств Венеции. Foto Marburg / Art Resource, New YorkЗолотое сечение встречается во многих математических контекстах. Его геометрически можно построить с помощью линейки и компаса, и это происходит при исследовании архимедовых и платоновых тел. Это предел отношений последовательных членов последовательности чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13,…, в котором каждый член после второго является суммой двух предыдущих, а также значение самой простой из непрерывных дробей, а именно 1 + 1 / (1 + 1 / (1 + 1 / (1 + ⋯.
В современной математике золотое сечение встречается при описании фракталов, фигур, которые проявляют самоподобие и играют важную роль в изучении хаоса и динамических систем.
Получите эксклюзивный доступ к контенту из нашего 1768 First Edition с подпиской. Подпишитесь сегодня ,Что такое золотое сечение? Как применить его к своим проектам
Хотите привлечь клиентов красивой графикой? Прочтите, чтобы узнать о золотом сечении и о том, как оно может повысить ставки на ваши изображения. Затем перейдите в редактор Shutterstock и используйте инструменты сетки и кадрирования для создания великолепных дизайнов, соответствующих этому мощному принципу дизайна.
Слово «золотой» означает ценность, совершенство и успех. Мы видели, как это применимо ко всему: от редкого и драгоценного яйца до эпохи культового кино до выигрышного лотерейного билета.Однако для маркетологов есть один такой отзыв, который имеет значение…
Золотое сечение.
Концепции золотого сечения тысячи лет. Он составляет основу многих классических произведений искусства и архитектуры, от Великой пирамиды в Гизе в Египте до «Парада цирка » художника Жоржа Сёра , и вы часто найдете его в энциклопедиях и научных статьях. Однако его историческое значение не означает, что он устарел; на самом деле золотое сечение может быть невероятно ценным для бизнеса.Использование этого при разработке маркетинговых материалов, логотипов и веб-сайта может привести к созданию более привлекательных визуальных ресурсов для вашего бренда.
Вы просто должны знать, как им пользоваться.
Определение золотого сечения
Чтобы понять золотое сечение, вы должны знать, как и где оно началось. Этот поиск ведет нас в Древнюю Грецию. Золотое сечение, также называемое греческой буквой фи , относится к числу 1,61803398875.
С математической точки зрения это число известно как иррациональное, то есть оно состоит из бесконечного ряда цифр, которые не повторяются и не могут быть выражены в виде простой дроби (во многом как знаменитое пи ).Согласно Британской энциклопедии, математическая концепция золотого сечения возникла около 500 г. до н. Э. Некоторые благодарят греческих ученых Евклида и Пифагора за его оттачивание.
Однако, чтобы по-настоящему понять концепцию, вы должны посмотреть на золотое сечение так:
(А + В) / А = А / В.
Разделите строку на две части. Более длинная часть (A), разделенная на более короткую (B), равна всей длине линии, разделенной на более длинную часть. Чтобы создать золотое сечение, деления исходной линии должны быть равны 1.618.
Мы знаем — это сложно описать словами, поэтому вот удобная визуализация, которая вам поможет.

Когда впервые появилась идея золотого сечения, греки поняли, что с его помощью можно создать очень визуально привлекательный прямоугольник, который мы теперь называем золотым прямоугольником. Они стали рассматривать эту форму и ее пропорции в контексте дизайна. Оказывается, когда вы применяете соотношение от 1 к 1,61 к изображению, макету или композиции, оно будет выглядеть естественно и сбалансировано.

Неудивительно, что с тех пор люди используют золотое сечение. Это основа многих древних построек и картин, которые мы считаем красивыми. Некоторые говорят, что золотое сечение представлено в произведениях художника Сальвадора Дали « Таинство Тайной вечери» , Микеланджело «Сотворение Адама» и даже в Стоунхендже. Сегодня вы найдете его на веб-страницах, фотографиях и в логотипах некоторых самых популярных мировых брендов.
Золотое сечение в природе
Как это актуально для вас и вашего бизнеса? Чтобы ответить на этот вопрос, мы должны исследовать золотое сечение в другой форме.

Золотая спираль тесно связана с золотым сечением. Он создается путем рисования непрерывной дуги, которая проходит через каждую часть золотого прямоугольника, создавая плавную спираль. Возможно, греки придумали математическое объяснение того, почему существует Золотая спираль, но она появилась задолго до них. Вы найдете доказательства этого повсюду в природе в форме ракушек, цветочных лепестков, сосновых шишек, семенных головок и спиральных галактик. Это также видно на телах некоторых животных, включая дельфинов, морских звезд и пчел.
Золотая спираль также связана с Последовательностью Фибоначчи, которая станет отличным знаком для поклонников книги Дэна Брауна «Код да Винчи ». Согласно этой математической концепции, каждое число в последовательности создается путем сложения двух предыдущих чисел вместе (например, 1, 1, 2, 3, 5, 8).
Кстати, теория итальянского математика Фибоначчи также появляется в природе. Когда вы превращаете эту последовательность в узор, вы получаете изгибающуюся спираль. Подсчитайте эти спирали, и вы обычно получите число Фибоначчи.Как поясняет Live Science, «Спираль Фибоначчи — это серия соединенных четверть окружностей, нарисованных внутри массива квадратов с числами Фибоначчи для измерений. Квадраты идеально сочетаются друг с другом из-за характера последовательности, где следующее число равно сумме двух перед ним ».
 Изображение предоставлено space_heater
Изображение предоставлено space_heaterЭто возвращает нас к Золотой спирали. Живая наука продолжает: «Любые два следующих друг за другом числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое примерно равно 1.618034. Чем больше пара чисел Фибоначчи, тем точнее приближение ». Больше не нужно задаваться вопросом, что такого особенного в объекте или форме, что делает их такими поразительными. Скорее всего, ему есть за что поблагодарить математику за его непреходящую красоту.
 Изображение от Victority
Изображение от VictorityТам, где встречаются математика и красота
Учитывая связь между математикой и природой, неудивительно, что человеческое тело также имеет доказательства золотого сечения. От пропорций вашей руки (длина пальца относительно предплечья и плеча) до формы лица Моны Лизы — все они соответствуют тому, что Лука Пачоли назвал Божественной пропорцией в 1509 году, и тем, что называл Леонардо да Винчи как Золотое сечение.Да Винчи использовал золотое сечение в своем Витрувианском человеке. Его использовали и такие художники, как Рембрандт.

Многие ученые и статистики приложили немало усилий, чтобы оценить степень, в которой золотое сечение отвечает за то, как мы воспринимаем красоту лица. Согласно этим теориям, если вы вычислите ширину и длину человеческого лица и разделите длину на ширину, и вы получите число, близкое к золотому сечению, то это лицо будет красивым. Расположение глаз, носа и рта, а также расстояние между ними также влияют на наше влечение.
Когда вы можете представить себе, как все эти формулы объединяются для создания различных форм и узоров, становится намного легче увидеть их ценность в повседневной жизни. Подобно тому, как золотое сечение можно использовать для создания привлекательных произведений архитектуры и искусства, оно жизненно важно для современного дизайна.
Золотое сечение в дизайне
веб-страниц, рекламных объявлений, обложек журналов и иллюстраций выигрывают от макета, основанного на этом древнем математическом принципе.Золотое сечение можно использовать для управления размещением объектов, формой логотипа и т. Д.

Макет и контент в Интернете и за его пределами
Давайте начнем с рассмотрения роли, которую он играет в макете и содержании. В веб-дизайне золотое сечение может применяться к тому, где и как размещаются столбцы текста. Например, страница с широким блоком содержания слева и более узким столбцом справа привлекает внимание зрителя и выделяет самое важное.Если на вашем сайте ширина 960 пикселей, ширина левого столбца должна быть 593 пикселя, а ширина правого столбца — 367 пикселей. Вместе они создают желаемую пропорцию.
В зависимости от вашего макета, размер ваших столбцов может не совпадать так, как вам хотелось бы (хотя использование калькулятора золотого сечения может помочь). Это нормально. Ваша конечная цель — максимально приблизиться к соотношению 1: 1,61, при котором основной блок контента в 1,6 раза больше, чем боковая панель.

У этой стратегии пользовательского интерфейса (UI) есть дополнительное преимущество: она помогает читателю перемещаться по видео, фотографиям и тексту. Вы найдете примеры такого типа макета в Интернете по той простой причине, что он эффективен. Взгляните на домашнюю страницу такого сайта, как Fast Company или BuzzFeed, и вы заметите характерный двухколоночный макет.
То же самое можно сказать и о Salon.com. Помещая привлекательные фотографии и популярные видео в двух столбцах, составляющих золотое сечение, Salon обеспечивает визуальный баланс, который перенаправляет посетителя сайта от одного текущего контента к другому.Макет одновременно эстетически приятный и функциональный, помогая посетителю определить, как лучше всего перемещаться по странице, а также продвигая наиболее интересный контент Салона.
 Скриншот из Salon
Скриншот из SalonКак золотое сечение — и его круги — влияют на расстояние и форму
Золотое сечение также может помочь вам принять решение о расстоянии: где разместить элемент дизайна по отношению к другому, оптимальное количество белого пространства и т. Д.
Вернитесь к этому золотому прямоугольнику и подумайте, как он может помочь вам решить, где разместить меньший, менее важный блок контента на странице вашего сайта, или даже как включить отрицательное пространство в ваш новый логотип.Скорее всего, вы обнаружите, что это позволяет сосредоточить вашу работу и сокращает время, необходимое для создания изображения, которое понравится и вам, и вашим клиентам.
Если, однако, вы все еще не можете понять, как математика может улучшить ваши брендированные визуальные ресурсы, возможно, будет полезно принять несколько иную точку зрения. Возьмите этот золотой прямоугольник и нарисуйте идеальный круг внутри каждой его части. С точки зрения размера и пропорции эти формы — так называемые золотые круги — соответствуют золотому сечению, и теперь их можно перемещать по своему усмотрению.

Независимо от того, пересекаются ли они или перекрываются, золотые круги можно применять к любому дизайну, независимо от того, полируете ли вы существующий логотип или начинаете с нуля. Их наложение на текущую работу позволяет вам вносить коррективы, которые гарантируют, что ваш конечный результат будет соответствовать желанному золотому сечению.
Если слухи верны, Золотое сечение и связанные с ним Золотые круги были задействованы в дизайне логотипа Twitter. Когда вы видите эти круги, нанесенные на культовую синюю птицу, это имеет смысл.Похоже, что логотип очень точно соответствует формуле золотого сечения, что может объяснить, почему результат так запоминается.
Птица Twitter — далеко не единственный логотип, в котором используются Золотые круги. Говорят, что логотип Pepsi, как и логотип Google, также придерживается золотого сечения. Графические дизайнеры нередко используют эту технику для создания идеально пропорциональных форм и узоров, которые кажутся зрителю четкими и чистыми.
Иногда простой акт перестановки ваших Золотых кругов до тех пор, пока они не будут напоминать более знакомый объект, может вдохновить вас на следующий дизайн логотипа.Как и во всем, практика ведет к совершенству, и экспериментирование с тем, что могут сделать Golden Circles, является ключом к созданию жизнеспособного дизайна.
 Изображение SAAC
Изображение SAACПомня об этом, в прошлом году творческий профессионал Кази Мохаммед Эрфан поставил перед собой задачу создать 25 логотипов, которые соответствуют золотому сечению. Преобразуя каждую часть формулы в коллекцию золотых кругов и используя эти формы в качестве ориентира, он смог создать динамическую группу логотипов, охватывающих негативное пространство, демонстрирующих баланс и, что наиболее важно, воплощающих суть бизнеса, который они представляют. ,
 Изображение предоставлено Кази Мохаммедом Эрфаном
Изображение предоставлено Кази Мохаммедом Эрфаном
Золотое сечение в фотографии
Помимо веб-дизайна и дизайна логотипов, золотое сечение также имеет место в фотографии. Когда вам нужно создать или выбрать интересное изображение, пропорции и масштаб невероятно важны и входят в число основных строительных блоков сильной фотографической композиции. Расположение объекта таким образом, чтобы он соответствовал макету золотой спирали — с фокусом изображения внутри кривой спирали — может помочь вам создать более привлекательную композицию, соответствующую принципам золотого сечения.
Чтобы упростить этот процесс, многие фотографы используют «сетку phi ». Разделив золотой прямоугольник и перекрывающую его золотую спираль на девять частей, вы получите сетку, которая поможет вам с композицией. Посмотрите, где пересекаются линии сетки. Это те области, которые естественным образом привлекают человеческий глаз, поэтому вам следует расположить различные элементы фотографии именно там, чтобы добиться визуальной гармонии.

Сеточные войны: оценка альтернативного правила третей
Но есть и другой подход к фотографической композиции, и это Правило третей.Этот принцип также включает сетку из девяти частей. Однако по правилу третей все фигуры на сетке имеют одинаковый размер.
Здесь также рекомендуется размещать интересующие вас объекты на пересечении линий или вдоль самих линий. Результат предназначен для получения сбалансированной фотографии. Представьте, что вы кладете на видоискатель лист миллиметровой бумаги. Как объекты в поле вашего зрения совпадают с прямоугольниками квадратов на странице? Эти пересечения служат ориентиром для того, где вы должны разместить на фотографии основные и второстепенные достопримечательности.

Многие цифровые фотоаппараты предлагают возможность наложения шаблона сетки по правилу третей на экран специально, чтобы облегчить пользователям создание отличной фотографии, но со временем создание изображения таким образом становится второй натурой. Однако имейте в виду, что из этого правила есть некоторые исключения. При прямом хедшоте часто лучше забыть об этих линиях сетки и центрировать лицо на экране.
 Изображение Софии Журавец
Изображение Софии ЖуравецМожно подумать, что две подобные практики — золотое сечение и правило третей — будут работать вместе в гармонии.Однако когда дело доходит до компоновки изображений, есть некоторая неуверенность в том, какая стратегия лучше. Оба служат в качестве полезных чертежей, которые могут улучшить вашу способность создавать привлекательные фотографии или дизайн. Но они не созданы равными.
Как отмечает DNews Discovery Communications, сетка phi особенно эффективна при съемке пейзажей, поскольку она «дает более сбалансированное изображение» и «делает фотографии более естественными и менее жесткими». С Правилом третей у вас может получиться фотография, которая выглядит на слишком составной на , и это может показаться натянутым.
В следующий раз, когда вы будете просматривать пейзажные фотографии в поисках идеального изображения для своей электронной кампании, почтового сообщения или публикации в социальных сетях, помните о золотом сечении. Представьте себе сетку фи, наложенную на каждое изображение, и подумайте, как и куда попадают фокусные точки фотографии. Как только вы поймете, что искать, вы увидите золотое сечение повсюду и получите ценное представление о том, почему фотография может поразить вас и ваших клиентов именно так.
 Изображение Танмой Мишра
Изображение Танмой МишраНачало работы с золотым сечением
Если у вас уже есть изображения, которые вы надеетесь использовать в маркетинговых и рекламных целях, но которые не соответствуют золотому сечению или Правилу третей, мужайтесь.Просто редактируя изображения, вы можете сместить фокус зрителя и воспользоваться преимуществами более мастерской композиции.
Более плотное кадрирование может выделить самую важную часть фотографии. В редакторе Shutterstock вы можете быстро обрезать фотографию до любого размера или выбрать один из предустановленных размеров в социальных сетях для удобного обмена по каналам. Используйте инструмент сетки, чтобы наметить направляющие линии золотого сечения и посмотреть, как ваше изображение работает в нем.

На первый взгляд, золотой прямоугольник, золотая спираль, последовательность Фибоначчи, сетка фи и все, что с ними связано, могут показаться сложными.Идея о том, что ряд чисел может создать что-то естественное и красивое, не совсем интуитивна.
Но, как свидетельствует то, как его используют дизайнеры, художники-графики и фотографы, золотое сечение превратилось из малоизвестной математической теории в надежную технику, которая занимает почетное место в современном мире. Это мощное правило, которое нужно держать в заднем кармане и применять к курированию изображений, веб-дизайну и даже макетам блогов. Обладая фундаментальным пониманием, вы лучше подготовлены к выбору изображений и разработке дизайна, которые привлекают клиентов, повышая вовлеченность и улучшая визуальный авторитет вашего бренда.
Откройте для себя Shutterstock Editor — простой способ персонализировать свой дизайн.
Откройте для себя редактор
,Золотое сечение — RationalWiki
Прямоугольник с соотношением сторон, равным золотому сечению. Это вроде бы особенно приятно визуально.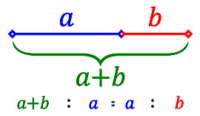 Золотое сечение: Золотое сечение, применяемое к делению линии.
Золотое сечение: Золотое сечение, применяемое к делению линии.Золотое сечение , золотая середина , золотое число или золотое сечение — математическая константа

Что еще более важно, это соотношение двух величин A и B, такое, что отношение от A к B (где A — меньшее) такое же, как отношение от B к A + B; это происходит из-за того, что это действительный положительный корень  .
.
Обычно считается, что он приятен и гармоничен для человеческого восприятия и является основой многих классических архитектур. Использование греческой буквы фи (φ) для обозначения золотого сечения было предложено математиком Марком Барром из первой буквы Фидия (древнегреческий, Φειδίας), скульптора, который якобы использовал ее в создание статуй Парфенона.
Золотое сечение тесно связано с последовательностью Фибоначчи.  Помимо прочего, отношения последовательных чисел Фибоначчи сходятся к фи:
Помимо прочего, отношения последовательных чисел Фибоначчи сходятся к фи:
| 1/1 | = | 1.000000 |
| 2/1 | = | 2,000000 |
| 3/2 | = | 1.500000 |
| 5/3 | = | 1,666666 |
| 8/5 | = | 1,600000 |
| 13/8 | = | 1,625000 |
| 21/13 | = | 1,615385 |
| 34/21 | = | 1.619048 |
| 55/34 | = | 1,617647 |
| 89/55 | = | 1,618182 |
| 144/89 | = | 1,617978 |
| 233/144 | = | 1.618056 |
| 377/233 | = | 1.618026 |
| 610/377 | = | 1.618037 |
| 987/610 | = | 1.618033 |
Phi woo [править]
Фи и числа Фибоначчи наделяют множеством очень увлекательных математических свойств, но некоторые чудаки готовы продвинуть их дальше, добавив хорошую дозу парейдолии. [1] [2] Классический пример — раковины наутилуса: часто говорят, что это золотые спирали, хотя на самом деле это просто логарифмические спирали с отношениями обычно около 1,3 или около того. Другие утверждают, что нашли золотое сечение или числа Фибоначчи в красоте человеческого лица, исторической архитектуре (иногда законной), продуктах Apple, планетах, музыкальных инструментах, идеальных корпусах для громкоговорителей … список можно продолжать и продолжать.Во многих случаях они действительно находят золотое сечение в объекте X, но это не особый результат; при достаточной настойчивости вы можете найти золотое сечение почти в чертовом любом .
 Aloe polyphylla , демонстрирующее золотое сечение посредством филлотаксиса
Aloe polyphylla , демонстрирующее золотое сечение посредством филлотаксисаРазница между реальным случаем «магии» золотого сечения и простым наблюдением кривошипа состоит в том, что наличие золотого сечения может быть фактически объяснено. То есть золотое сечение должно присутствовать как в теоретических моделях, описывающих X, так и в измеренных результатах в X.Изучая филлотаксис, ботаники не только наблюдали рост семян подсолнечника по спирали, пронумерованной Фибоначчи, но и дали научное объяснение тому, почему это происходит: пример золотого сечения, законно появляющийся в природе.
Нумерологическое ухаживание, окружающее фи и Фибоначчи, является примером строгого закона малых чисел; , то есть маленьких чисел (или визуально различимых соотношений между 1 и 2) не так много, и они будут появляться во многих несвязанных местах.См. Также теорию Рамсея.
Между тем, в стране креационистов… Годдидит. [3]
Библиография [править]
- Золотое сечение: История Фи, самое удивительное число в мире Марио Ливио (2002) Broadway Books. ISBN 0767908155.
Ссылки [править]
См. Также [править]
,Phi: Золотое сечение | Живая наука
Число фи, часто известное как золотое сечение, — это математическое понятие, известное людям со времен древних греков. Это иррациональное число, такое как пи, и е, что означает, что его члены бесконечно идут после десятичной точки без повторения.
На протяжении веков вокруг фи было построено множество преданий, например, идея, что он олицетворяет совершенную красоту или уникально встречается в природе.Но многое из этого не имеет под собой реальных оснований.
Определение phi
Phi можно определить, взяв палку и разбив ее на две части. Если соотношение между этими двумя частями такое же, как соотношение между всей палкой и большим сегментом, считается, что эти части находятся в золотом сечении. Впервые это было описано греческим математиком Евклидом, хотя он назвал это «делением на крайнее и среднее отношение», согласно математику Джорджу Марковскому из Университета штата Мэн.2 = phi + 1
Это представление может быть преобразовано в квадратное уравнение с двумя решениями: (1 + √5) / 2 и (1 — √5) / 2. Первое решение дает положительное иррациональное число 1.6180339887… (точки означают, что числа продолжаются бесконечно), и это обычно называется фи. Отрицательное решение — -0,6180339887 … (обратите внимание, как совпадают числа после десятичной точки) и иногда его называют малым фи.
Последний и довольно элегантный способ представления фи выглядит следующим образом:
5 ^ 0.5 * 0,5 + 0,5
Это пять в половинной степени, умноженная на половину плюс половину.
Связанный: 11 самых красивых математических уравнений
Phi тесно связан с последовательностью Фибоначчи , в которой каждое последующее число в последовательности находится путем сложения двух предыдущих чисел. Эта последовательность идет 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Это также связано со многими заблуждениями.
Взяв отношение последовательных чисел Фибоначчи, вы можете становиться все ближе и ближе к фи. Интересно, что если вы расширите последовательность Фибоначчи назад — то есть до нуля и на отрицательные числа — соотношение этих чисел будет приближать вас к отрицательному решению, маленький фи -0,6180339887…
Существует ли золотое сечение в природа?
Хотя люди знают о фи уже давно, большую известность он приобрел только в последние столетия.По словам Нотта, итальянский математик эпохи Возрождения Лука Пачоли написал книгу под названием «De Divina Proportione» («Божественная пропорция») в 1509 году, в которой обсуждалась и популяризовалась фи.
Пачоли использовал рисунки, сделанные Леонардо да Винчи , которые включали фи, и возможно, что да Винчи был первым, кто назвал его «sectio aurea» (латинское «золотое сечение»). Только в 1800-х годах американский математик Марк Барр использовал греческую букву Φ (фи) для обозначения этого числа.
Как свидетельствуют другие названия числа, такие как божественная пропорция и золотое сечение, фи приписывают множество чудесных свойств. Писатель Дэн Браун включил длинный отрывок в свой бестселлер «Код да Винчи» (Doubleday, 2000), в котором главный герой обсуждает, как фи представляет собой идеал красоты и встречается на протяжении всей истории. Более трезвые ученые обычно опровергают подобные утверждения.
Например, энтузиасты фи часто упоминают, что некоторые измерения Великой пирамиды в Гизе , такие как длина ее основания и / или высота, находятся в золотом сечении.Другие утверждают, что греки использовали фи при проектировании Парфенона или в своих прекрасных скульптурах.
Энтузиасты Фи любят указывать, что пирамиды Гизы, построенные между 2589 и 2504 годами до нашей эры, были построены в золотом сечении. Но измерения по своей природе неточны и произвольны, поэтому пирамиды не являются точными примерами золотого сечения. (Изображение предоставлено Дэном Брекволдтом Shutterstock)Но, как отметил Марковский в своей статье 1992 года в журнале College Mathematics Journal , озаглавленной «Заблуждения о золотом сечении»: «измерения реальных объектов могут быть только приблизительными.Поверхности реальных объектов никогда не бывают идеально плоскими ». Далее он написал, что неточности в точности измерений приводят к еще большим неточностям, когда эти измерения помещаются в соотношения, поэтому заявления о древних зданиях или искусстве, соответствующих фи, следует принимать с большой долей вероятности. крупица скепсиса
Часто говорят, что размеры архитектурных шедевров близки к фи, но, как отмечал Марковский, иногда это означает, что люди просто ищут соотношение, которое дает 1,6, и называют это фи.Найти два отрезка с соотношением 1,6 не составляет особого труда. Выбор места измерения может быть произвольным и при необходимости отрегулирован, чтобы приблизить значения к фи.
Попытки найти фи в человеческом теле также поддаются подобным заблуждениям. В недавнем исследовании утверждалось, что золотое сечение обнаруживается в разных пропорциях человеческого черепа. Но, как сказал Live Science :
Дейл Риттер, ведущий преподаватель анатомии человека в Медицинской школе Альперта (AMS) при Университете Брауна в Род-Айленде, сказал Live Science :
: ) наука в нем… с таким количеством костей и таким количеством интересных точек на этих костях, я мог бы предположить, что где-то еще в скелетной системе человека будет хотя бы несколько «золотых соотношений».
Связано: Фотографии: большие числа, определяющие Вселенную
И хотя фи считается обычным явлением в природе, его значение преувеличено. Лепестки цветов часто имеют числа Фибоначчи, такие как пять или восемь, а сосновые шишки растут свои семена наружу по спирали чисел Фибоначчи. Но есть столько же растений, которые не следуют этому правилу, так и те, которые соблюдают, — сказал Live Science Кейт Девлин, математик из Стэнфордского университета .
Люди утверждали, что морские ракушки, такие как раковины наутилуса, обладают свойствами, присущими фи.Но, как указывает Девлин на своем веб-сайте , «наутилус действительно наращивает свою раковину по логарифмической спирали, то есть спирали, которая поворачивается на постоянный угол по всей своей длине, что делает его везде самоподобным. постоянный угол — это не золотое сечение. Жалко, я знаю, но вот оно. »
Хотя фи, безусловно, представляет собой интересную математическую идею, именно мы, люди, придаем значение тому, что мы находим во Вселенной. Защитник, смотрящий через очки цвета фи, может повсюду видеть золотое сечение.Но всегда полезно выйти за рамки конкретной точки зрения и спросить, действительно ли мир соответствует нашему ограниченному пониманию его.
Дополнительные ресурсы:
.