Как определить высоту объекта вблизи или на расстоянии? Основные 5 способов! | Строю для себя
Иллюстрация — Как узнать высоту?Приветствую Вас, уважаемый читатель!
Как-то в юности я занимался альпинизмом и ориентированием на местности, и не знаю как сейчас, но в то время нужно было обязательно знать раздел «Выживание в экстремальных условиях», чтобы сдать экзамен и получить какой-либо разряд!
Собственно, решил поделиться с Вами и написать вкратце данную статью, полагая, что это будет очень познавательно и интересно! На самом деле способов еще гораздо больше, чем описано здесь, но они практически схожи, и вы в процессе чтения, вникнув в суть — сможете сами моделировать ситуации, и понять, что всё не так уж и сложно.
Ну что же, поехали…
Конечно не часто, но бывают в нашей жизни ситуации и обстоятельства, когда нужно знать высоту или расстояние до какого-либо объекта, например дома, дерева, да или похвастаться перед подругой))).Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал «стрелял» обходя высотки и не мешали кроны деревьев… ))) А мало ли, что еще…
Как ни парадоксально, но не забираясь с рулеткой на объект — расчет сделать не сложно, при том, что каждый метод может дать довольно точный результат. Конечно, с точностью до миллиметров не вычислить искомое значение, но погрешность будет точно уж небольшой.
Высота по отбрасываемой тени
Если погода солнечная и четко прослеживается тень, выбираем на объекте нижнюю контрольную точку от которой берет начало отбрасываемая тень будь-то дома, дерева, столба и пр.
Далее, ищем конец тени и производим замер длины тени.
После чего фиксируем в вертикальном положении любой предмет (на фото ниже — это обычный колышек) и аналогично замеряем длину его тени, а потом еще и высоту от точки начала тени до верхушки предмета.
Надеюсь, что у вас нет сомнения, что на фотографии треугольники с катетами Х1, Y1 и X2, Y2 подобны? Расчет строится на геометрическом свойстве подобных треугольников в которых отношения сторон равны и искомая высота объекта Y1 находится так:
Y1 (Высота столба) = (Y2*X1) / X2
Авторское фото — Вычисление высоты столбаПодручный предметЗдесь требуется отойти от объекта и с помощью подручного предмета на вытянутой руке (ручки, карандаша, палки) замерить высоту.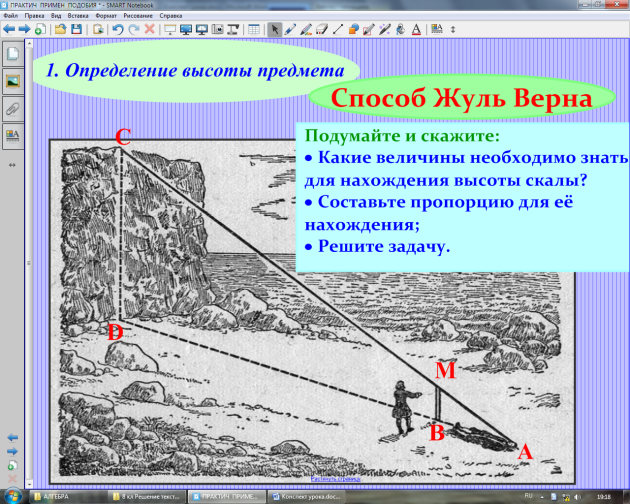 Конец предмета должен совпасть с верхней точкой объекта, а нижнюю точку требуется зафиксировать большим пальцем руки.
Конец предмета должен совпасть с верхней точкой объекта, а нижнюю точку требуется зафиксировать большим пальцем руки.
Разверните предмет горизонтально так, чтобы низ его по-прежнему оставался у основания объекта, а кончик касался земли и указывал на определенную точку. Важно запомнить эту точку или, если есть помощник, попросить встать на эту точку. Как раз эта точка будет являться точкой проекции верхушки на землю и теперь остается только замерить расстояние.
Угол падения и угол отражения
А если солнца нет и идет дождь, тоже не беда!
Согласно закону преломления из физики, о том что угол падения равен углу отражения — в зеркальном отражении любой лужи вы можете найти верхушку объекта и зная свой рост и расстояния соответственно, — получить искомую высоту (см.рисунок ниже).
Иллюстрация — ОтражениеЗафиксируйте точку О любым предметом, брошенным в лужу. Таким образом вы сможете измерить расстояния ОА, ОА1.
Зная все необходимые величины и основываясь на свойствах подобных треугольников, получите высоту, которая будет равна:
АВ = (А1В1 * ОА) / ОА1
Барометр и немного юмораНам понадобится немного знаний физики. 2;
2;
t — время по секундомеру, с.
Определяем высоту объекта на расстоянии от вас
Для определения высоты нам в любом случае требуется расстояние до объекта, но основание его нам не доступно, — по-этому измерение нельзя произвести непосредственно.
Чтобы вычислить расстояние, нам нужно:
- Остановиться напротив объекта и зафиксировать эту точку (На рисунке точка А).
- Повернуться под прямым углом (на 90 град.) и сделать несколько шагов. Эта точка будет являться точкой О (здесь нужно воткнуть длинный предмет, например палку).
- Пройти то же расстояние, что и от А к О, и в том же направлении. Отметить каким-либо предметом (точка В).
- Повернуться под прямым углом (на 90 град.) и удаляться от объекта (в сторону точки Y) до тех пор, пока установленный ваш предмет в точке О не будет совмещен с объектом.
- Расстояние от вас (Y) до точки В — это и есть расстояние от точки А до объекта (Х).
Теперь, зная расстояние до объекта, переходим к вычислению его высоты.
Для простоты построения опять же подобных треугольников — берется шест с подвижной планкой (две доски сбиваются гвоздем). Устройство фиксируется в точке А, планка настраивается (при помощи врожденного глазомера в каждого из нас) на верхнюю точку объекта (Х1) — как показано на иллюстрации, после чего фиксируется.
Далее, отмечается на земле точка С.
В итоге мы получаем два треугольника СХХ1 и САА1, которые подобны между собой. Зная расстояние ХС, АС и АА1 находим искомую высоту Н объекта!
Высота Н = (АА1 * ХС) / АС.
____________________
Если Вам было интересно, ставьте палец вверх и подписывайтесь на канал!
1. Если диагонали равны, то это не значит, что у вас ровный дом. Почему? Рассказываю историю!
2. Почему основной типоразмер изделий металлопроката составляет в длину 11,7 м.?
3. Варианты построения прямых углов при строительстве дома и проверка углов при уже возведенном сооружении.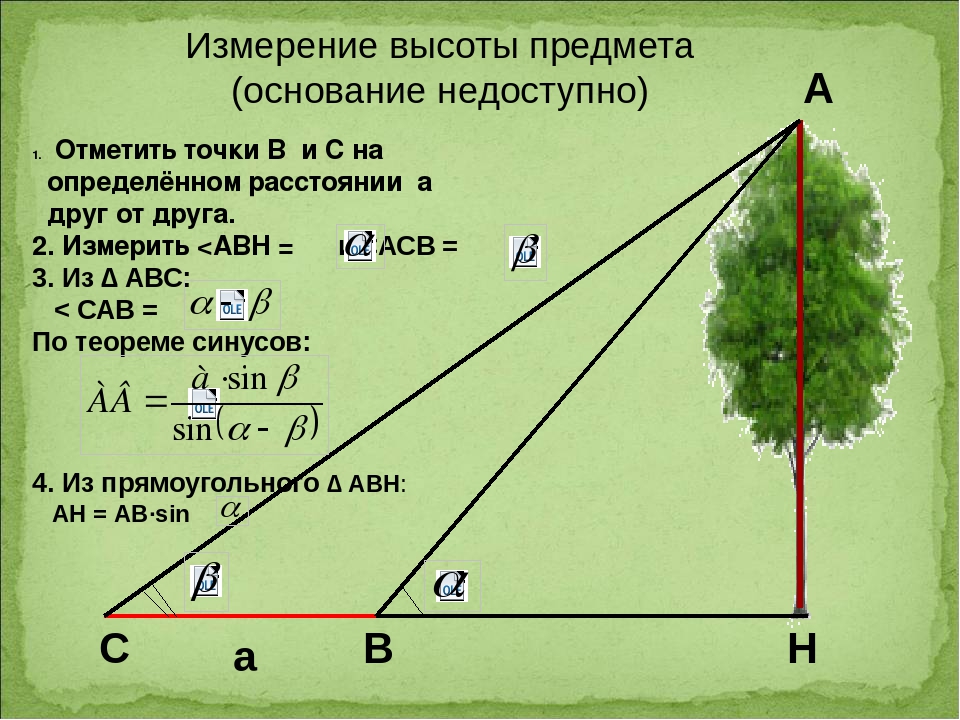
Способ определения высоты дерева и предмета по тени, шесту, луже
В полевых условиях иногда бывает очень важно и полезно владеть простейшими прикладными способами измерений на местности. Например способами определения высоты дерева или любого другого предмета на местности.
Простые способы определения высоты дерева или любого другого предмета по тени, шесту, лужице или зеркалу, прямоугольному треугольнику.
Высоту дерева или любого другого предмета на местности очень просто можно определить по тени, шесту, лужице или зеркальцу, и прямоугольному треугольнику.
Способ определения высоты дерева или другого предмета по своему росту и длине тени.
Если на ровном месте измерить шагами длину своей тени, а затем длину тени, отбрасываемой деревом или предметом, то искомую высоту легко вычислить из пропорции :
АК/ак = КЕ/ке
где АК — высота дерева (В), КЕ — тень дерева (D), ак — ваш рост (b), ке — ваша тень (d).
Например длина вашей тени d равна трем шагам.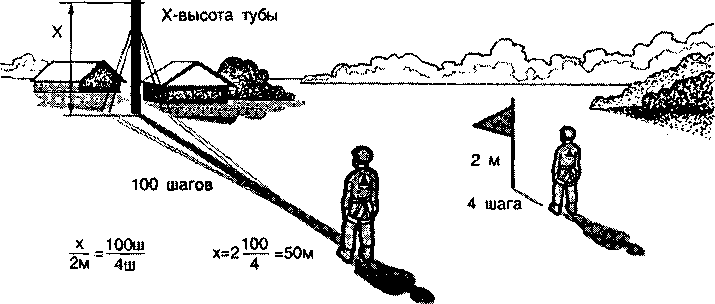 Тень дерева D равна девяти шагам. То есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост за 1,5 метра, то высота дерева будет В = 1,5 х 3 = 4,5 метра.
Тень дерева D равна девяти шагам. То есть тень дерева длиннее вашей тени в три раза. Если принять ваш рост за 1,5 метра, то высота дерева будет В = 1,5 х 3 = 4,5 метра.
Способ определения высоты дерева или другого предмета по шесту и своему росту.
Этот же способ можно применить при пасмурной погоде, когда тени от предметов не видны. В этом случае для измерения нужно взять шест, равный длине вашего роста. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева равна расстоянию от вашей головы до основания дерева, то есть АС = ВС.
Способ определения высоты дерева или другого предмета по лужице или зеркальцу.
По лужице, зеркальцу или гелиографу высоту дерева или любого другого предмета на местности, можно измерять следующим образом. Станьте так, чтобы лужица поместилась между вами и деревом (В). Найдите точку, из которой видна отраженная в воде вершина дерева. Измеряемое дерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы также можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.
Измеряемое дерево будет во столько раз выше вас, во сколько расстояние от него до лужицы (ВО) больше расстояния от лужицы до вас (АО). Вместо лужицы также можно воспользоваться зеркальцем, положив его горизонтально так, чтобы увидеть вершину дерева.
Способ определения высоты дерева или другого предмета с помощью прямоугольного треугольника с двумя острыми углами по 45 градусов.
С помощью прямоугольного треугольника с двумя острыми углами по 45 градусов, высоту дерева или другого предмета определяют так. Отходя от дерева на некоторое расстояние и прикладывая треугольник к глазам так, чтобы один из его катетов был параллелен оси дерева. Второй — параллелен земной поверхности, а гипотенуза представляла собой линию визирования.
Затем добиваются такого положения, чтобы линия визирования прошла через вершину дерева. В этом случае высота дерева D равна расстоянию от наблюдателя до дерева и плюс рост наблюдателя.
По материалам книги «Карта и компас — мои друзья».
Клименко А.И.
Статьи схожей тематики:
- Камусные лыжи, форма и особенности изготовления камусных лыж, крепления для обуви, лыжная палка каек.
- Охотничьи нарты, волокуши, тобогганы, народные приспособления для перевозки грузов и тяжестей в полевых условиях, устройство и конструкция.
- Разведывательная подготовка подразделений специального назначения, способы ведения войсковой разведки и обеспечение, учебно-практическое пособие.
- Поняги, крошни, пестери и горбовик для облегчения переноски грузов на охоте или в полевых условиях, устройство.
- Постройка парусно-гребной байдарки, конструкция, постройка корпуса, парусное вооружение, оборудование байдарки, навыки плавания, перечень основных материалов для постройки байдарки.

- Самостоятельное изготовление разборной туристической байдарки, конструкция, чертежи, изготовление и окраска каркаса, изготовление деки и оболочки, окончательная сборка и оснащение байдарки.
«Определение высоты предмета, основание которого неизвестно»
Как определить высоту предмета, основание которого неизвестно
При ориентировании на местности, например, в туристическом походе, иногда требуется определить высоту того или иного удаленного предмета или объекта. Если расстояние до него известно, то выполнить расчеты не составляет труда. А как быть, когда до основания нужного объекта не добраться, а измерить расстояние нет возможности? На помощь приходит знание геометрии.
Вам понадобится
— шест;
— астролябия.
Инструкция
1
При определении высоты удаленного предмета, основание которого недоступно, а расстояние до него нельзя измерить непосредственно, используйте простые вычисления с приемением подручных предметов или специальных приспособлений. Первый этап – определение расстояния до объекта.
Первый этап – определение расстояния до объекта.
2
Допустим, что от предмета с неизвестной вам высотой (точка Х) вас отделяет непреодолимое препятствие, например, река. Выберите на своей стороне точку А, располагающуюся примерно напротив нужного вам объекта.
3
Теперь повернитесь под прямым углом вправо и сделайте 15-20 шагов. В этом месте воткните в землю ветку или палочку. Это будет точка О. Проделайте точно такое же число шагов в том же направлении. Вы получили точку В; отметьте ее также каким-либо предметом.
4
От точки В двигайтесь под прямым углом, удаляясь от берега. В тот момент, когда точка вашего нахождения будет располагаться между объектом (точка Х) и точкой О, остановитесь. Расстояние от вас до точки В будет равно расстоянию от первой точки (А) до точки Х, обозначаемой нужный вам объект. Измерить расстояние теперь можно шагами, а затем перевести их в метры.
5
Теперь, когда расстояние до объекта известно, переходите к определению его высоты.
6
Отметьте на поверхности земли точку В, чтобы в этой точке прямая АА’ пересекалась бы с поверхностью земли. Треугольники А’С’В и АСВ будут подобными, поскольку имеют общий угол и по углу, равному 90 градусов. Из этого следует, что:
А’С’ / АС = ВА’ / ВА или
Высота предмета, таким образом, будет равняться: А’С’ = АС х ВА’ / ВА.
7
Следующий способ предполагает более сложные вычисления. Допустим, вам требуется определить высоту АН удаленного предмета. Отметьте на определенном расстоянии от основания Н точку В и измерьте при помощи астролябии угол АВН, а затем по этим данным из прямоугольного треугольника АНВ найдите высоту объекта по формуле:
По линейным размерам. Чтобы определить расстояние этим способом, надо:
держать перед собой линейку на расстоянии вытянутой руки (50-60 см от глаза) и измерить по ней в миллиметрах видимую ширину или высоту предмета, до которого требуется определить расстояние;
— действительную высоту (ширину) предмета, выраженную в сантиметрах, разделить на видимую высоту (ширину) в миллиметрах, и результат умножить на б (постоянное число) , получим расстояние.
Например, если столб высотой 4 м (400 см) закрывается по линейке 8 мм, то расстояние до него будет 400 х 6 = 2400; 2400: 8 = 300 м (действительное расстояние). Чтобы определять расстояния таким способом, требуется хорошо знать линейные размеры различных объектов, либо иметь эти данные под рукой .
Инструкция
1
Самый нехитрый способ определить расстояние на местности связан с использованием глазомера. Главное тут – натренированная зрительная память и умение мысленно отложить на видимой местности постоянную меру длины, например, 50 или 100 м. Закрепите в памяти эталоны и при необходимости сравните с ними то расстояние, которое вам необходимо измерить на местности. Один из самых простых эталонов – расстояние между столбами линии электропередач, которое составляет обычно около 50 м.
2
Измеряя расстояние посредством мысленного откладывания постоянной меры, учитывайте, что местные предметы будут казаться уменьшенными в зависимости от их удаления. Иными словами, при удалении в два раза предмет покажется в два раза меньше.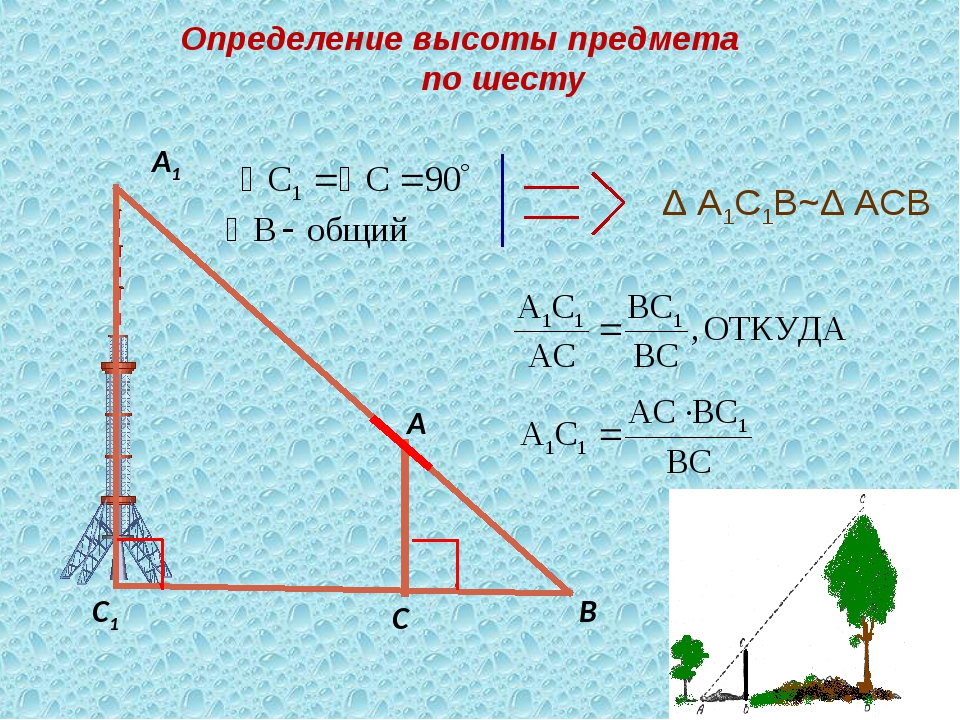
3
При использовании глазомера имейте ввиду, что в условиях недостаточной видимости (в тумане, в сумерки, пасмурную погоду, при дожде и т. п. ) предметы кажутся расположенными дальше, чем есть на самом деле. Точность такого способа, прежде всего, зависит от тренированности наблюдателя. Обычная ошибка на расстоянии в километр составляет около 15%.
4
Используйте способ определения расстояний по линейным размерам. Для этого возьмите линейку и держите ее на расстоянии вытянутой руки. Измерьте по линейке в миллиметрах видимую ширину (высоту) объекта, до которого измеряете расстояние. Действительную ширину (высоту) предмета, известную вам, переведите в сантиметры, затем разделите на видимый размер в миллиметрах, а результат умножьте на 6 (постоянная величина) . Получившийся результат будет искомым расстоянием до объекта.
5
Третий способ определить расстояние на местности – по угловой величине. Для этого требуется знать линейную величину объекта (длину, высоту или ширину) , а также угол в тысячных, под которым виден наблюдаемый объект.
D = L х 1000 / A;
где D — расстояние до объекта; L — линейная величина объекта; A — угол, под которым видна линейная величина объекта; 1000 — постоянная величина.
6
Для определения угловой величины следует знать, что отрезку длиной 1 мм, расположенному на расстоянии 50 см от глаза, будет соответствовать угол в 2 тысячных. Соответственно, для отрезка в 1 см угловая величина будет равна 20 тысячных и так далее. Запомните угловые величины (в тысячных) некоторых подручных средств:
Большой палец руки (толщина) – 40;
Мизинец (толщина) – 25;
Карандаш — 10-11;
Спичечная коробка (ширина) – 50;
Спичечная коробка (высота) — 30
Спичка (толщина) – 2.
Рис. 499 Измерение по тени
Есть несколько простых способов определения высоты предметов. С некоторыми из них охотники должны быть знакомы.
По тени. В солнечный день не составляет труда измерение высоты предмета, предположим дерева, по его тени. Нужно лишь руководствоваться следующим правилом: высота измеряемого дерева во столько раз больше высоты известного вам предмета (например, палки или ружья), во сколько раз тень от дерева больше тени от палки.
Если при нашем измерении тень от ружья или палки будет в два раза больше длины ружья или палки, то высота дерева будет в два раза
Рис. 500.Измерение по шесту
меньше длины его тени (рис. 499). В том же случае, когда тень от ружья или палки будет равна их длине, высота дерева также равна своей тени.
По шесту. Этот способ можно применять, когда нет солнца и не видно тени от предметов.
Для измерения нужно взять шест, равный по длине вашему росту (рис. 500). Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста.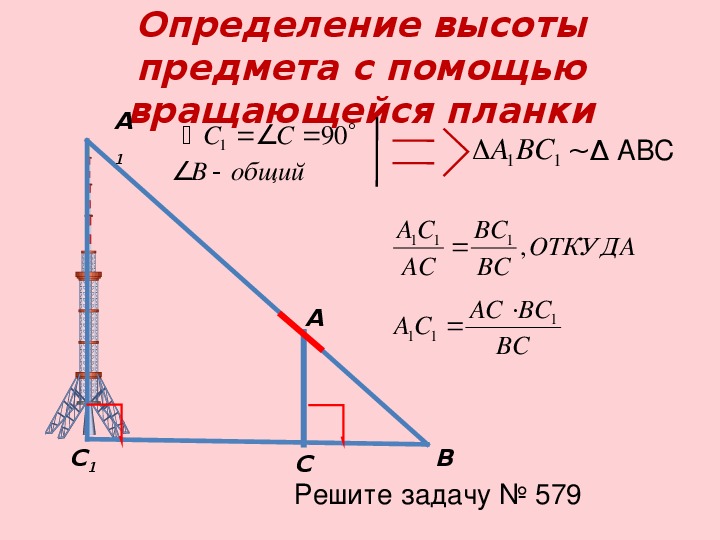
Рис. 501. Измерение с помощью лужи
По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц.
Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета.
Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние
от него до лужицы больше, чем расстояние от лужицы до вас (рис. 501).
Для глазомерного определения тех или иных предметов неплохо знать истинную высоту некоторых предметов, с которыми охотникам приходится нередко встречаться.
Высоты некоторых известных предметов (в м)
Телеграфный столб 6-8 (среднее- 6, 4 м)
Железнодорожный вагон 3, 5
Железнодорожная будка 4, 9
Молодой лес 6, 0
Всадник 2, 2
Человек 1, 7
Этаж дома 4, 0
ОПРЕДЕЛЕНИЕ ШИРИНЫ ВОДОЕМОВ
Рис.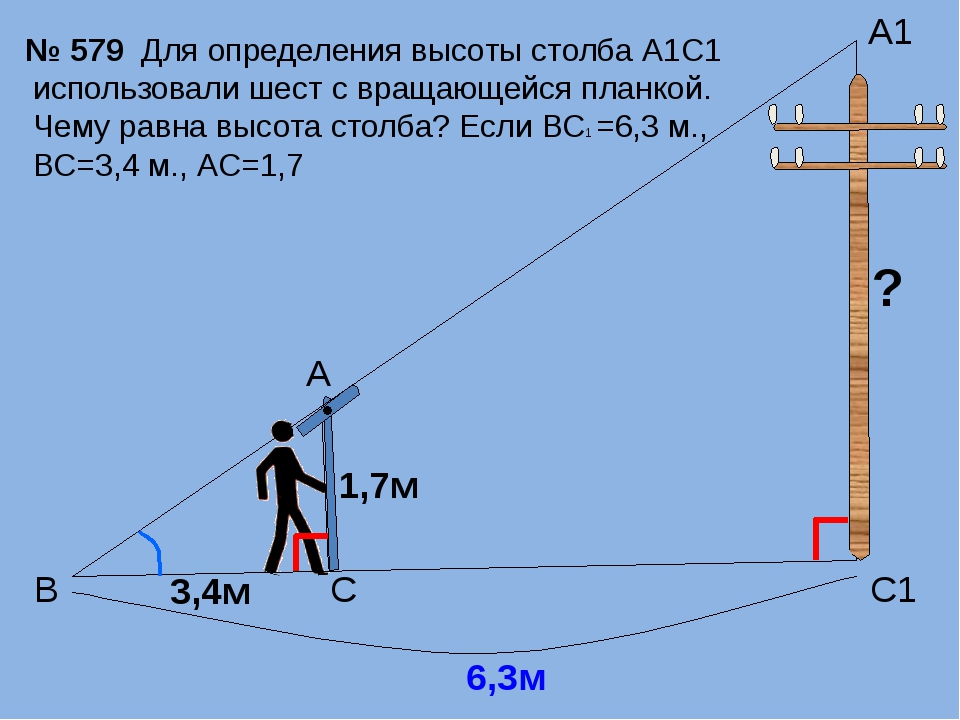 502. Первый способ определения ширины водоемов
502. Первый способ определения ширины водоемов
Рис. 503. Второй способ определения ширины водоемов
Рис. 504. Третий способ определения ширины водоемов
Первый способ. Нужно подойти как можно ближе к воде и заметить на противоположном берегу два каких-либо предмета, расположенных у самой кромки воды. Затем нужно взять травинку (палочку, бечевку) и, держа ее горизонтально за концы обеими вытянутыми руками, закрыть один глаз. Глядя поверх травинки, надо закрыть ею промежуток между замеченными ориентирами.
После этого следует отметить точку, в которой вы находитесь, сложить травинку пополам и отойти от водоема под прямым углом до другой точки, из которой расстояние между ориентирами закроется укороченной травинкой. Расстояние от этой точки до реки, где вы производили
измерение в первый раз, и будет равно ширине водоема (рис. 502).
Второй способ. Нужно подойти к воде, засечь на противоположном берегу какой-либо ясно видимый предмет А, расположенный у самой кромки воды, и отметить точку своего стояния камнем или колышком Б.
Затем нужно пройти вдоль берега по линии, перпендикулярной к направлению между
|
ОПРЕДЕЛЕНИЕ ВЫСОТЫ НЕКОТОРЫХ ПРЕДМЕТОВ
Есть несколько простых способов определения высоты предметов.
С некоторыми из них охотники должны быть знакомы. Если при нашем измерении тень от ружья или палки будет в два раза больше длины ружья или палки, то высота дерева будет в два раза
меньше длины его тени (рис. 499). В том же случае, когда тень
от ружья или палки будет равна их длине, высота дерева также равна
своей тени.
По луже. Этот способ можно удачно применять после дождя,
когда на земле появляется много лужиц. Измеряемый предмет, например дерево, будет во столько раз выше
вас, во сколько расстояние ОПРЕДЕЛЕНИЕ ШИРИНЫ ВОДОЕМОВ
Первый способ. Нужно подойти как можно ближе к воде и
заметить на противоположном берегу два каких-либо предмета, расположенных
у самой кромки воды. Затем нужно взять травинку (палочку, бечевку)
и, держа ее горизонтально за концы обеими вытянутыми руками, закрыть
один глаз. Глядя поверх травинки, надо закрыть ею промежуток между
замеченными ориентирами. Второй способ. Нужно подойти к воде, засечь на противоположном
берегу какой-либо ясно видимый предмет А, расположенный у самой
кромки воды, и отметить точку своего стояния камнем или колышком
Б. Третий способ. Нужно надвинуть на голову фуражку или кепку,
подойти к самому берегу и посмотреть на него так, чтобы козырек
прикрывал берег (рис. 504). Слышимость и видимость
Звук проходит в воздухе около 330 м в секунду, иначе говоря,
примерно 1 км в 3 сек. ЛИЧНЫЕ ЭТАЛОНЫ ОХОТНИКА
Для того, чтобы успешно и безошибочно производить все глазомерные
измерения на местности, каждый охотник должен заблаговременно
определить в сантиметрах свои измерительные эталоны, записать
их в книжку и хорошенько запомнить. ПОХОДНЫЕ ЭТАЛОНЫ ОХОТНИКА
МЕСТНЫЕ ПРИЗНАКИ ОЖИДАЕМОЙ ПОГОДЫ
Сотни лет подмечали люди, что происходит в природе перед ненастьем
и перед наступлением хорошей погоды. Подмечали без приборов, глядя
на солнце, луну и звезды, на птиц и животных, на цветы и травы.
Эти наблюдения людей систематизировались и стали точными. Признаки хорошей погоды
Стадо идет домой спокойно, коровы обычно не мычат. Признаки ненастной погоды
Утром появляется радуга, и в ней преобладают красные цвета. Признаки надвигающейся грозы
Признаки надвигающегося сильного ветра
На горизонте, над багрово-красной зарей возникают клочья легких
облаков, они утолщаются и очерчиваются все резче и резче.
Штормовые предостережения
Признаки надвигающейся бури
|
Школьный туризм
Определение высоты объекта, ширины реки
В ходе выполнения определения местоположения может возникнуть необходимость определения высоты и ширины объекта. Один из способов определения: длина палки относится к длине своей тени, как длина дерева — к своей
Один из способов определения: длина палки относится к длине своей тени, как длина дерева — к своей
CЕ:BC=AD:АB, отсюда AD=(CEхAB):BC
Шариковая ручка
Приспособление для письма всегда найдется в письменном столе, а нам оно поможет в определении высоты объекта, используя метод перспективы. Вместо ручки можно использовать карандаш, ровную палочку или любой другой похожий предмет. Также нам понадобится ассистент и рулетка. Отходим на такое расстояние, когда нам будет виден объект измерений целиком. Зажав ручку в кулаке, вытягиваем прямую руку перед собой таким образом, чтобы ее кончик совпадал с вершиной объекта. Вытягиваем большой палец руки в сторону параллельно земле, чтобы в итоге получился прямой угол. Затем поворачиваем кисть с шариковой ручкой на 90 градусов, в итоге большой палец у нас смотрит в землю параллельно измеряемому объекту, а кончик ручки указывает на место, куда необходимо переместиться ассистенту.
Мы спроецировали высоту объекта параллельным переносом на землю. Теперь не составит особого труда измерить полученное расстояние рулеткой от
ассистента до столба, оно и будет равно определяемой высоте. Метод хорошо подходит для полевых условий, достаточно точный, однако требует
наличие помощника.
Теперь не составит особого труда измерить полученное расстояние рулеткой от
ассистента до столба, оно и будет равно определяемой высоте. Метод хорошо подходит для полевых условий, достаточно точный, однако требует
наличие помощника.
Измерение по тени
Есть несколько простых способов определения высоты предметов. С некоторыми из них туристы должны быть знакомы.
По тени. В солнечный день не составляет труда измерение высоты предмета, предположим дерева, по его тени. Нужно лишь руководствоваться следующим правилом: высота измеряемого дерева во столько раз больше высоты известного вам предмета, например палки, во сколько раз тень от дерева больше тени от палки. Если при нашем измерении тень от палки будет в два раза больше длины палки, то высота дерева будет в два разаИзмерение по шесту
В том же случае, когда тень от ружья или палки будет равна их длине, высота дерева также равна своей тени.
По шесту. Этот способ можно применять, когда нет солнца и не видно тени от предметов. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было
видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева будет равна линии, проведенной от вашей головы до
основания дереваменьше длины его тени.
Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было
видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева будет равна линии, проведенной от вашей головы до
основания дереваменьше длины его тени.
Измерение с помощью лужи
По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.
Примечание. Вместо лужицы можно Пользоваться положенным горизонтально зеркальцем
Определение ширины реки
Один из способов определения.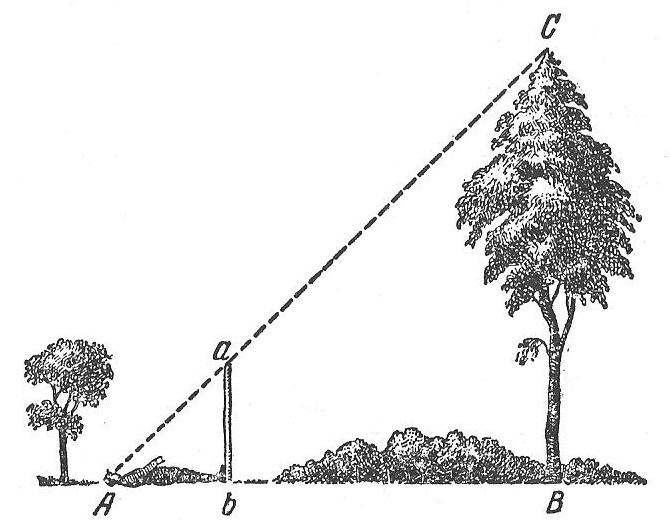
Напротив предмета на противоположном берегу поставить веху А. Повернувшись на 90 и пройдя 20 м, поставить веху В.
В этом же направлении пройти вдвое меньше метров (точка С). Повернувшись на 90, идти пока веха В и предмет не будут
на одной линии. Расстояние СД умножить на 2.
Принцип измерения ширины реки основан на построении равнобедренных треугольников.
 Таким простым способом, не применяя не каких средств, можно измерить примерную ширину реки в походных условиях.
Таким простым способом, не применяя не каких средств, можно измерить примерную ширину реки в походных условиях.В жизни уметь ориентироваться на местности необходимо для того, чтобы дойти до цели. Эти навыки необходимы людям многих профессий.
Измерить расстояние, например, ширину реки, можно так, как предлагают авторы учебника. Способ несколько сложный, но эффективный. Надо только потренироваться, заранее зная истинную ширину объекта. Можно измерить так, как предлагают некоторые авторы пособий по выживанию. Мною этот способ был опробован и дал неплохие результаты. Надо сказать, что действует он на ширину объекта не более 50 метров.
Предположим, вам надо измерить ширину реки. Тогда выбирайте такое место, чтобы справа и слева от вас была ровная,
легко проходимая местность. Повернувшись в сторону противоположного берега, сделайте следующее: приложите ладонь ко лбу,
наклоняйте ребро ладони таким образом, чтобы кромка противоположного берега совместилась с ребром ладони.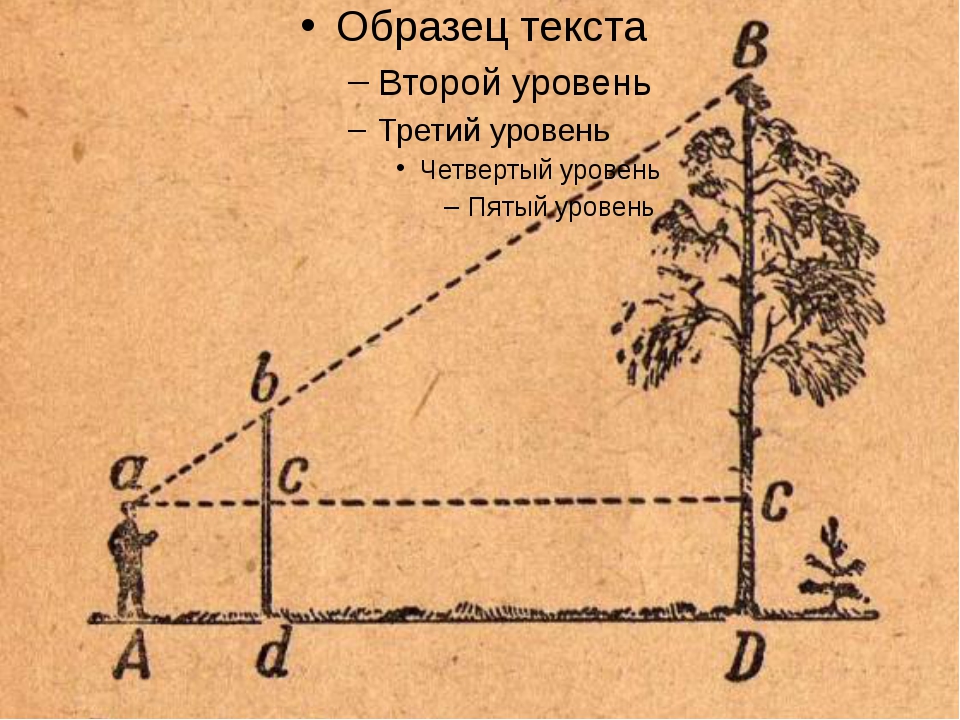 Зафиксируйте такое положение и повернитесь вправо или влево, где будет ровная легко проходимая местность.
Зафиксируйте такое положение и повернитесь вправо или влево, где будет ровная легко проходимая местность.
Не отрывая ладони, найдите на этом открытом участке точку совмещения с ребром ладони, запомните её приметы и отсчитайте количество пар шагов до неё. Умножьте это количество на 150 см. В итоге получится расстояние, равное ширине реки.
Измерение ширины реки при помощи травинки. Выбираем на противоположном берегу, в непосредственной близости от него, два заметных предмета и, стоя по другую сторону реки с вытянутыми руками, в которых зажата травинка, закрываем промежуток между выбранными предметами. Один глаз должен быть закрыт.
После этого, сложив травинку пополам, отходим от берега реки до тех пор, пока расстояние между выбранными предметами не закроется сложенной травинкой. Затем измеряем промежуток между двумя точками своего стояния. Расстояние между ними будет равно ширине реки.
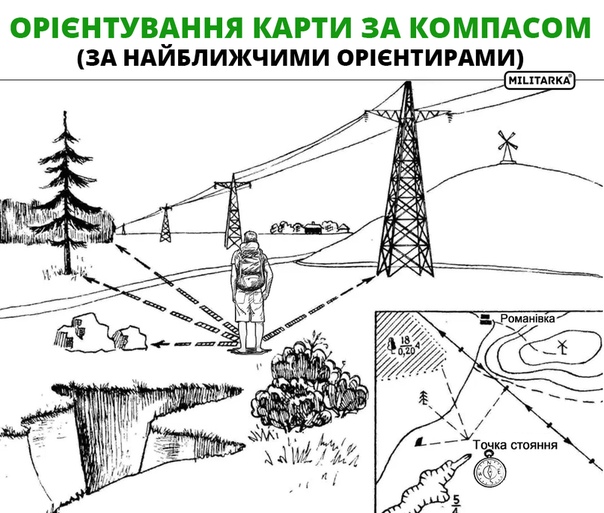
Измерение высоты площадки дальнего вида по способу жюля верна ( «таинственный остров»)
2. Измерение высоты площадки Дальнего Вида по способу Жюля Верна.
Измерение высоты площадки Дальнего Вида по способу Жюля Верна.
( «Таинственный остров»)
Возьмем шест футов 12 длиною. Приготовим отвес: камень, привязанный концу веревки. Не доходя до гранитной стены фунтов 500, воткнем шест фута на два в песок, прочно укрепив с помощью отвеса. Отходя от шеста на такое расстояние, чтобы, лежа на песке, можно было на одной прямой линии видеть и край шеста, и край гребня. Эту точку отметим колышком. Построив два подобных прямоугольных треугольника, найдем искомую длину. У меньшего треугольника одним катетом будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза – луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой хотим определить, и расстояние от колышка до основания этой стены; гипотенуза – луч зрения, совпадающий с направлением гипотенузы первого треугольник.
(см. рис.5 в приложении),
3. Определение высоты предмета.
1) С помощью вращающейся планки.
Предположим, что нам нужно определить высоту какого – нибудь предмета, например высоту столба А1С1. Для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку С1 столба. Отметим на поверхности земли точку В, в которой прямая А1А пересекается с поверхностью земли. Прямоугольные треугольники А1С1В и АСВ подобны по первому признаку подобия треугольников ( угол А1 = углу А = 90о, угол В – общий). Из подобия треугольников следует:
Измерив расстояния ВА1 и ВА (расстояние от точки В до основания столба и расстояние до шеста с вращающейся планкой), зная длину АС шеста, по полученной формуле определяем высоту А1С1 столба. (см. рис.6 в приложении)
2) С помощью тени.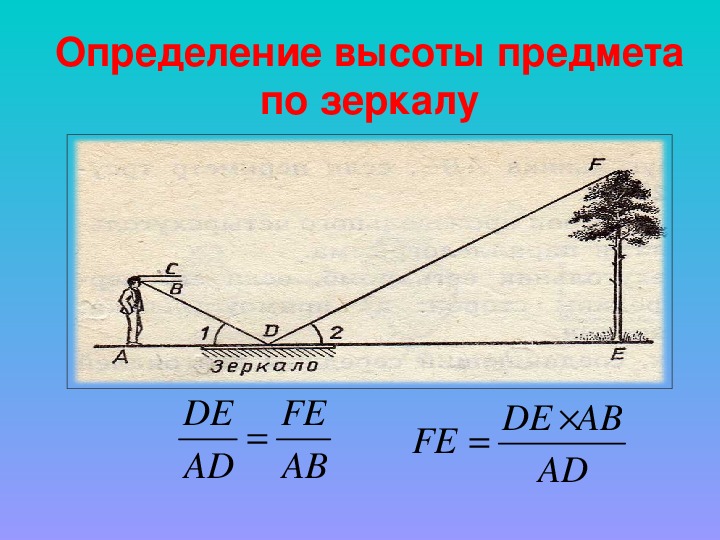
Измерение следует проводить в солнечную погоду. Измерим длину тени дерева и длину тени человека. Построим два прямоугольных треугольника, они подобны. Используя подобие треугольников, составим пропорцию (отношение соответственных сторон), из которой и найдём высоту дерева. Таким образом, можно определить высоту дерева, используя построение прямоугольных треугольников в выбранном масштабе. (см. рис.7 в приложении)
3) С помощью зеркала.
Для определения высоты предмета можно использовать зеркало, расположенное на земле горизонтально. Луч света, отражаясь от зеркала, попадает в глаз человека. Используя подобие треугольников можно найти высоту предмета, зная рост человека (до глаз), расстояние от глаз до макушки человека и измеряя расстояние от человека до зеркала, расстояние от зеркала до предмета (учитывая, что угол падения луча равен углу отражения). (см. рис.8 в приложении)
4) С помощью чертёжного прямоугольного треугольника.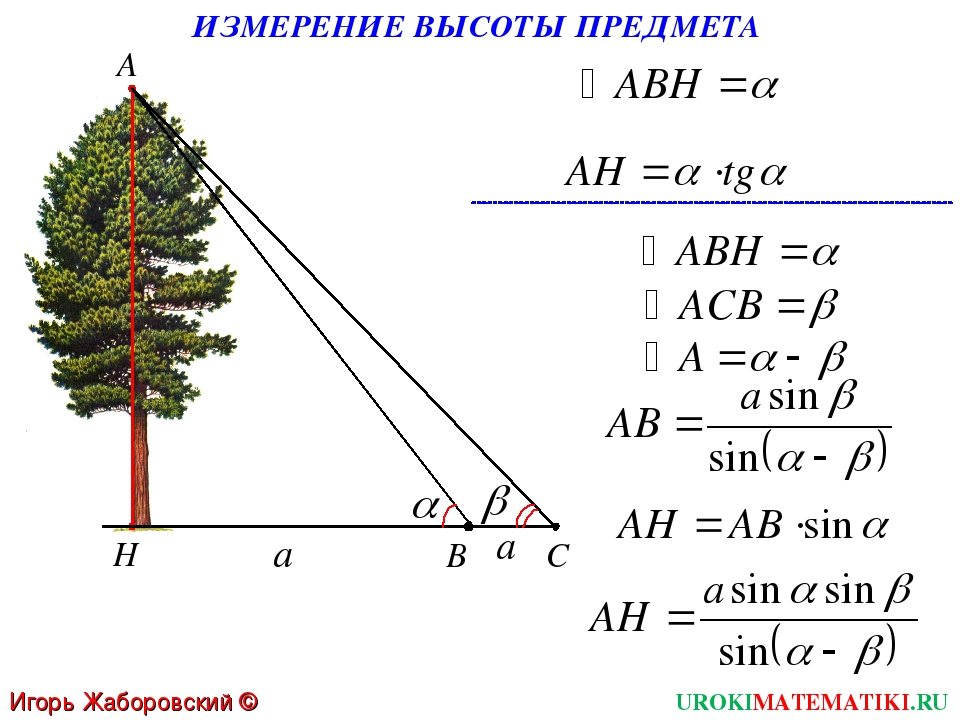
На уровне глаз расположим прямоугольный треугольник, направив один катет горизонтально поверхности земли, другой катет, направив на предмет, высоту которого измеряем. Отходим от предмета на такое расстояние, чтобы второй катет “прикрыл” дерево. Если треугольник ещё и равнобедренный, то высота предмета равна расстоянию от человека до основания предмета (прибавив рост человека). Если треугольник не равнобедренный, то используется снова подобие треугольников, измеряя катеты треугольника и расстояние от человека до предмета (используется и построение прямоугольных треугольников в выбранном масштабе). Если треугольник имеет угол в 300, то используется свойство прямоугольного треугольника: против угла в 300 лежит катет вдвое меньше гипотенузы.
5) С помощью чертёжного прямоугольного равнобедренного треугольника.
Вполне можно обойтись при измерении высоты и без помощи теней. Мы можем воспользоваться свойством равнобедренного прямоугольного треугольника, обратившись к услугам весьма простого прибора, который легко изготовить из дощечки и трех булавок. На дощечке любой формы, даже на куске коры, если у него есть плоская сторона, намечают три точки- вершины равнобедренного прямоугольного треугольника – и в них втыкают торчком по булавке. Пусть у вас нет под рукой чертежного треугольника для построения прямого угла, нет и циркуля для откладывания равных сторон. Перегибаем тогда любой лоскут бумаги один раз, а затем поперек первого сгиба еще раз так, чтобы обе части первого сгиба совпали, — и получаем прямой угол. Та же бумажка пригодится и вместо циркуля, чтобы отмерить равные расстояния.
На дощечке любой формы, даже на куске коры, если у него есть плоская сторона, намечают три точки- вершины равнобедренного прямоугольного треугольника – и в них втыкают торчком по булавке. Пусть у вас нет под рукой чертежного треугольника для построения прямого угла, нет и циркуля для откладывания равных сторон. Перегибаем тогда любой лоскут бумаги один раз, а затем поперек первого сгиба еще раз так, чтобы обе части первого сгиба совпали, — и получаем прямой угол. Та же бумажка пригодится и вместо циркуля, чтобы отмерить равные расстояния.
Прибор может быть целиком изготовлен в бивуачной обстановке. Обращение с ним не сложнее изготовления. Отойдя от измеряемого дерева, держим прибор так, чтобы один из катетов треугольника был направлен отвесно, для чего можем пользоваться ниточкой с грузиком, привязанной к верхней булавке. Приближаясь к дереву или удаляясь от него, найдем такое место A, из которого, глядя на булавки a и с, увидим, что они покрывают верхушку C дерева: это значит, что продолжение гипотенузы ac проходит через точку C. Тогда, очевидно расстояние aB равно CB, так как = 45° .Следовательно, измерив, расстояние aB (или, на ровном месте, одинаковое с ним расстояние AD) и прибавив BD, т. е. возвышение aA глаза над землей, получим искомую высоту дерева. (см. рис.9 в приложении)
Тогда, очевидно расстояние aB равно CB, так как = 45° .Следовательно, измерив, расстояние aB (или, на ровном месте, одинаковое с ним расстояние AD) и прибавив BD, т. е. возвышение aA глаза над землей, получим искомую высоту дерева. (см. рис.9 в приложении)
6) Предположим, что требуется определить высоту АН какого – то предмета.
Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим АВН. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = НВ tg АВН. Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии а друг от друга и измерим углы АВН и АСВ: АВН =, АСВ = , ВАС = – . Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ:
Из прямоугольного треугольника АВН находим высоту АН предмета:
АН = АВ sin . Тогда
Тогда
(см. рис.10 в приложении)
7).Измерение высоты дерева при помощи шеста
Высоту деревьев можно определить при помощи шеста. Этот способ состоит в следующем.
Запасшись шестом выше своего роста, воткнем его в землю отвесно на некотором расстоянии от измеряемого дерева. Отойдем от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, мы увидим на одной линии с ней верхнюю точку b шеста. Затем, не меняя положения головы, смотрим по направлению горизонтальной прямой aC, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросим помощника сделать в этих местах пометки, и наблюдение окончено. Остаётся только на основании подобия треугольников abc и aBC вычислить ВС из пропорции ВС : bc = aC : ас. Значит,
Расстояния bc, aC легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние CD (которое также измеряется непосредственно), чтобы узнать искомую высоту дерева. (см. рис.11 в приложении)
(см. рис.11 в приложении)
8). Метод завала
Нужен прямой шест длиной около метра. Встать на такое место, откуда сможем, хорошо видеть как комель, так и верхушку дерева. Если бы дерево завалили на самом деле, мы должны видеть его верхушку с места своего расположения. Удаление от дерева сначала может быть 20-30 метров. Попросим товарища пойти к стволу дерева и вытянуть руку под прямым углом. Держать шест в вытянутой руке в прямом положении. Переместится, не двигая шеей, на такое расстояние, чтобы дерево казалось такой же длины, как и шест. В этом случае верхушка дерева должна совпадать с верхней частью шеста, а комель соответствовать большому пальцу руки, находящейся в нижней части шеста. Во время перемещения постоянно держать шест в прямом положении, а руку прямо. В качестве другого варианта можно, не меняя места расположения, переместить руку по шесту, т.е. поменять длину. «;Завалить»; дерево. Продолжая держать руку прямой, повернуть шест так, чтобы нижняя часть шеста (которую мы держим) оставалась бы все время на месте, т. е. совпадала с комлем, а верхняя часть шеста (которая соответствует верхушке) как бы упала на землю под прямым углом. Если не видно место предполагаемого падения верхушки, изменить место расположения. Попросить товарища перейти от ствола к месту верхушки «;заваленного»; дерева. Когда найдем это место, попросите товарища измерить шагами длину «;заваленного»; дерева.
е. совпадала с комлем, а верхняя часть шеста (которая соответствует верхушке) как бы упала на землю под прямым углом. Если не видно место предполагаемого падения верхушки, изменить место расположения. Попросить товарища перейти от ствола к месту верхушки «;заваленного»; дерева. Когда найдем это место, попросите товарища измерить шагами длину «;заваленного»; дерева.
Возможные ошибки :
Руку важно держать прямой весь период измерения. Изгибая руку, мы получим неправильный результат. Если будем двигать шеей во время измерения, результат будет плохой. «;Заваливать»; дерево перпендикулярно. Товарищ тоже должен перемещаться перпендикулярно по отношению к линии дерева и вашего расположения. (см. рис.12 в приложении)
4. Определение расстояния до недоступной точки.
1). Предположим, что нам нужно найти расстояние от пункта А до недоступного пункта В. Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябии измеряем углы А и С. На листке бумаги строим какой – нибудь треугольник А1В1С1, у которого А1 = А, С! = С и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольник АВС подобен треугольнику А1В1С1, то
Затем с помощью астролябии измеряем углы А и С. На листке бумаги строим какой – нибудь треугольник А1В1С1, у которого А1 = А, С! = С и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольник АВС подобен треугольнику А1В1С1, то
Для удобства вычислений удобно построить треугольник А1В1С1 так, чтобы
(см. рис.13 в приложении)
2). Измерение расстояния между точками А и В, разделёнными препятствием (рекой).
Выберем на берегу реки две доступные точки А и В, расстояние между которыми может быть измерено. Из точки А видны и точка В и точка С, взятая на противоположном берегу. Измерим расстояние АВ, с помощью астролябии измеряем углы А и В,
АСВ = 1800 – ( А + В).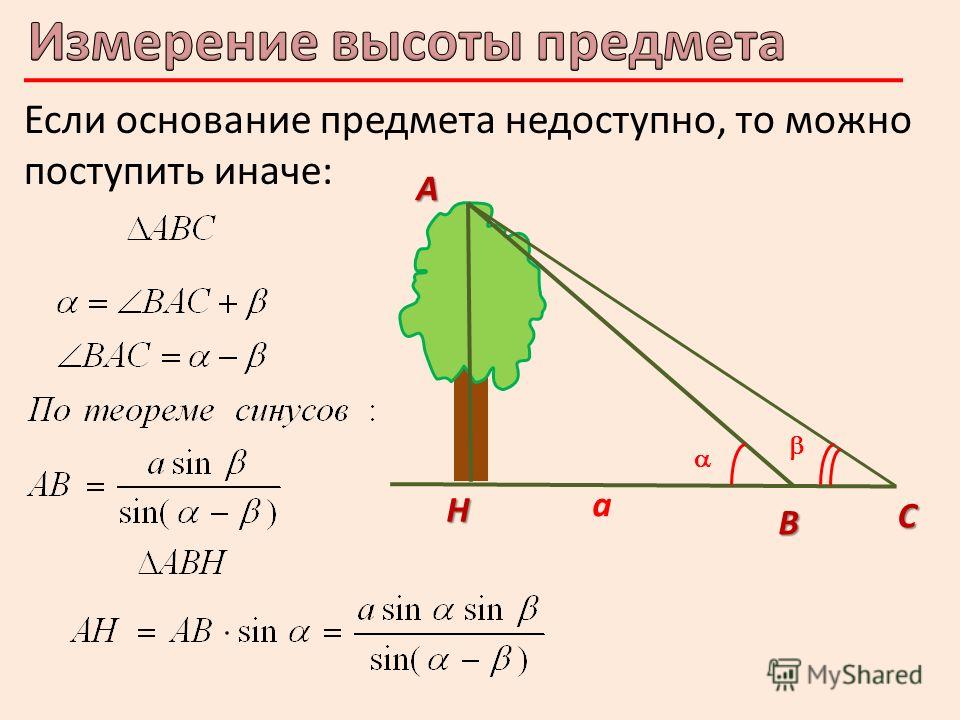 Зная одну сторону треугольника и все углы, по теореме синусов находим искомое расстояние.
Зная одну сторону треугольника и все углы, по теореме синусов находим искомое расстояние.
АС = АВ (см. рис.14 в приложении)
3). Измерение расстояния между точками А и В, разделёнными препятствием (озером).
Точки А и В доступны. Выбираем третью точку С, из которой видны точки А и В и могут быть непосредственны измерены расстояния до них. Получается треугольник, у которого даны АСВ (измеряется с помощью астролябии) и стороны АС и ВС. На основании этих данных по теореме косинусов можно определить величину стороны АВ – искомое расстояние.
(см. рис.15 в приложении)
5. Определение ширины водоемов.
Над озером тихим,
С полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Более цветка над водой,
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода
Здесь глубока?
(Перевод В.И. Лебедева)
1. Подойдем как можно ближе к воде и заметим на противоположном берегу два каких-либо предмета, расположенных у самой кромки воды. Затем нужно взять травинку (палочку, бечевку) и, держа ее горизонтально за концы обеими вытянутыми руками, закрыть один глаз. Глядя поверх травинки, надо закрыть ею промежуток между замеченными ориентирами. После этого следует отметить точку, в которой мы находимся, сложить травинку пополам и отойти от водоема под прямым углом до другой точки, из которой расстояние между ориентирами закроется укороченной травинкой. Расстояние от этой точки до реки, где мы производили измерение в первый раз, и будет равно ширине водоема. (см. рис.16 в приложении)
2. Подойдем к воде, засечем на противоположном берегу какой-либо ясно видимый предмет А, расположенный у самой кромки воды, и отметим точку своего стояния камнем или колышком Б.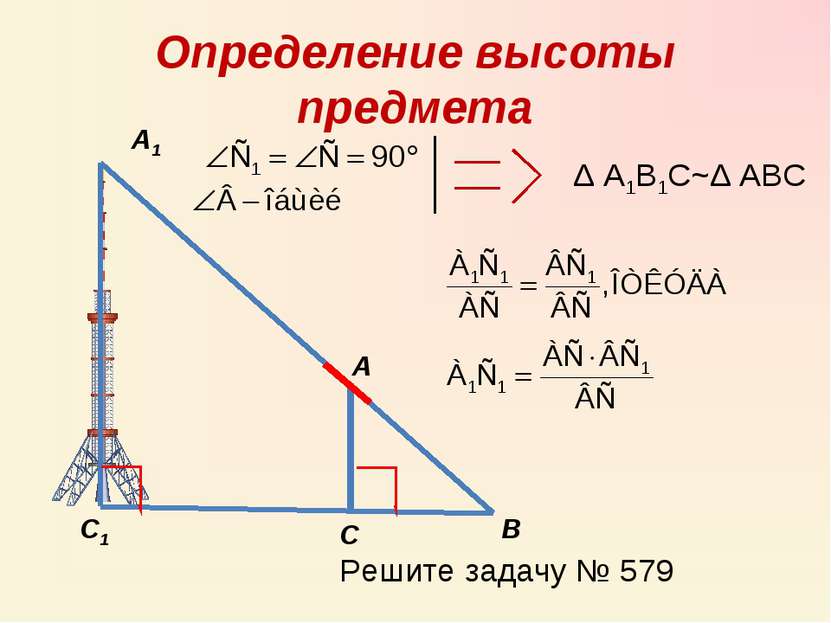 Затем нужно пройти вдоль берега по линии, перпендикулярной к направлению между А и Б, ровно 30 шагов, воткнуть палку В, отсчитать еще 30 шагов и сделать новую заметку Г. После этого, повернувшись спиной к берегу, нужно идти от заметки Г до точки Д, пока палка не окажется на одной линии с предметом за рекой (Л). Расстояние ГД и будет равно ширине водоема. (см. рис.17 в приложении)
Затем нужно пройти вдоль берега по линии, перпендикулярной к направлению между А и Б, ровно 30 шагов, воткнуть палку В, отсчитать еще 30 шагов и сделать новую заметку Г. После этого, повернувшись спиной к берегу, нужно идти от заметки Г до точки Д, пока палка не окажется на одной линии с предметом за рекой (Л). Расстояние ГД и будет равно ширине водоема. (см. рис.17 в приложении)
3. Станем на берегу реки в точке А против заметного предмета (камень, дерево) на противоположном берегу (точка В). Затем сделать под прямым углом вдоль берега определённое количество шагов (например, 20) и воткнуть палочку (точка О). От этой точки отсчитать столько же шагов (точка С) и идти под прямым углом к линии АС до точки Д, которая с точкой О и В будет на одной прямой. Таким образом, ширина реки АВ = СД. Этим способом можно также определить расстояние от всякого недоступного предмета.
(см. рис.18 в приложении)
4. Ширину реки можно определить и так: рассматривая два подобных треугольника АВС и АВ1С1. Точка А выбрана на берегу реки, В1 и С у кромки поверхности воды, ВВ1 – ширина реки, измеряя при этом АС, АС1, АВ1
Точка А выбрана на берегу реки, В1 и С у кромки поверхности воды, ВВ1 – ширина реки, измеряя при этом АС, АС1, АВ1
.
6. Геометрия звездного неба
Стихотворение “Из века в век”.
Из века в век идет человек,
Из века в век переходит земля.
Моря переходят из века в век,
Озера, реки, леса и поля.
Из века в век — солнце над Землей,
Из года в год луна по ночам,
И звезды в небе — надо мной,
И ночью пути освещают нам.
И хочется мне сохранить этот мир –
Пусть все переходит из века в век!
Ведь жизнь – божий дар!
Жизнь – пышный пир,
И пусть же “пирует” на нем человек!
Аня Кротова.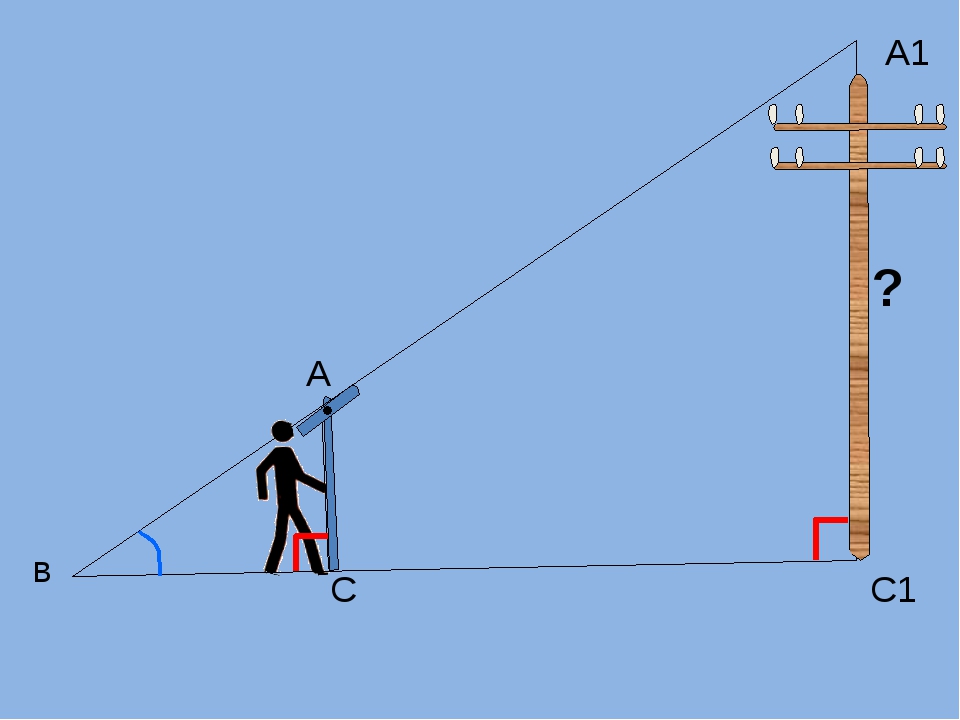 г. Абаза.
г. Абаза.
Единственная точка звездного купола в нашем северном полушарии, которая сохраняет неподвижность, — та, куда упирается мысленное продолжение земной оси. Этот северный «полюс мира» приходится невдалеке от яркой звезды на конце хвоста Малой Медведицы — Полярной звезды. Найдя ее на нашем северном небе, мы тем самым найдем и положение северного полюса мира. Отыскать же ее нетрудно, если найти сначала положение всем известного созвездия Большой Медведицы: проведите прямую линию через ее крайние звезды, как показано на рисунке, и, продолжив ее на расстояние, примерно равное длине всего созвездия, мы наткнемся на Полярную.
Это одна из тех точек на небесной сфере, которые понадобятся нам для определения географической широты. Вторая — так называемый «зенит» — есть точка, находящаяся на небе отвесно над вашей головой. Другими словами: зенит есть точка на небе, куда упирается мысленное продолжение того радиуса Земли, который проведен к занимаемому вами месту.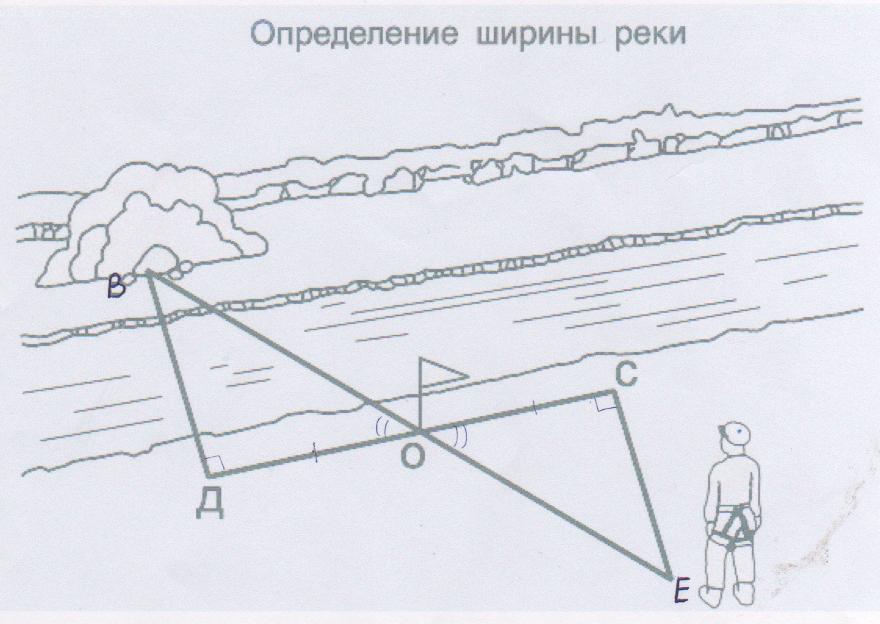 Градусное расстояние по небесной дуге между вашим зенитом и Полярной звездой есть в то же время градусное расстояние вашего места от земного полюса. Если зенит отстоит от Полярной на 30°, то мы отдалены от земного полюса на 30°, а значит, отстоим от экватора на 60°; иначе говоря, находимся на 60-й параллели.
Градусное расстояние по небесной дуге между вашим зенитом и Полярной звездой есть в то же время градусное расстояние вашего места от земного полюса. Если зенит отстоит от Полярной на 30°, то мы отдалены от земного полюса на 30°, а значит, отстоим от экватора на 60°; иначе говоря, находимся на 60-й параллели.
Следовательно, чтобы найти широту какого-либо места надо лишь измерить в градусах (и его долях) «зенитное расстояние» Полярной звезды: после этого останется вычесть эту величину из 90°—и широта определена. Практически можно поступать иначе. Так как дуга между зенитом и горизонтом содержит 90°, то, вычитая зенита расстояние Полярной звезды из 90°, мы получаем в остатке не что иное, как длину небесной дуги от Полярной до горизонта; иначе говоря, мы получаем «высоту» Полярной звезды над горизонтом. Поэтому географическая широта какого-либо места равна высоте Полярной звезды над горизонтом этого места.
Теперь понятно, что нужно сделать для определения широты. Дождавшись ясной ночи, отыщем на небе Полярную звезду и измеряем ее угловую высоту над горизонтом; результат сразу даст нам искомую широту места. Если хотим быть точным, мы должны принять в расчет, что Полярная звезда не строго совпадает с полюсом мира, а отстоит от него на 1°. Поэтому Полярная звезда не остается совершенно неподвижной, она описывает около неподвижного небесного полюса маленький кружок, располагаясь то выше его, то ниже, то справа, то слева — на 1,25°. Определив высоту Полярной звезды в самом высоком и в самом низком ее положении (астроном сказал бы: в моменты ее верхней и нижней «кульминаций»), мы берем среднее из обоих измерений. Это и есть истинная высота полюса, а следовательно, и искомая широта места. Но если так, то незачем избирать непременно Полярную звезду: можно остановиться на любой незаходящей звезде и, измерив ее высоту в обоих крайних положениях над горизонтом, взять среднюю из этих измерений. В результате получится высота полюса над горизонтом, т. е широта места.
Дождавшись ясной ночи, отыщем на небе Полярную звезду и измеряем ее угловую высоту над горизонтом; результат сразу даст нам искомую широту места. Если хотим быть точным, мы должны принять в расчет, что Полярная звезда не строго совпадает с полюсом мира, а отстоит от него на 1°. Поэтому Полярная звезда не остается совершенно неподвижной, она описывает около неподвижного небесного полюса маленький кружок, располагаясь то выше его, то ниже, то справа, то слева — на 1,25°. Определив высоту Полярной звезды в самом высоком и в самом низком ее положении (астроном сказал бы: в моменты ее верхней и нижней «кульминаций»), мы берем среднее из обоих измерений. Это и есть истинная высота полюса, а следовательно, и искомая широта места. Но если так, то незачем избирать непременно Полярную звезду: можно остановиться на любой незаходящей звезде и, измерив ее высоту в обоих крайних положениях над горизонтом, взять среднюю из этих измерений. В результате получится высота полюса над горизонтом, т. е широта места. Но при этом необходимо уметь улавливать моменты наивысшего и наинизшего положения избранной звезды, что усложняет дело; да и не всегда удается это наблюдать в течение одной ночи. Вот почему для первых приближенных измерений лучше работать с Полярной звездой, пренебрегая небольшим удалением ее от полюса.
Но при этом необходимо уметь улавливать моменты наивысшего и наинизшего положения избранной звезды, что усложняет дело; да и не всегда удается это наблюдать в течение одной ночи. Вот почему для первых приближенных измерений лучше работать с Полярной звездой, пренебрегая небольшим удалением ее от полюса.
До сих пор мы воображали себя находящимися в северном полушарии. Как поступили бы вы, очутившись в южном полушарии? Точно так же, с той лишь разницей, что здесь надо определять высоту не северного, а южного полюса мира. Близ этого полюса, к сожалению, нет яркой звезды вроде Полярной в нашем полушарии. Знаменитый Южный Крест сияет довольно далеко от южного полюса, и если мы желаем воспользоваться звездами этого созвездия для определения широты, то придется брать среднее из двух измерений — при наивысшем и наинизшем положении звезды. Герои романа Жюля Верна, при определении широты своего «таинственного острова», пользовались именно этим красивым созвездием южного неба.
(см. рис.19 в приложении)
ЧастьII
Примеры из жизни мудрых людей (Опрос людей, которые работали на природе)
Мне стало очень интересно, а что же знают об измерении на местности мудрые люди, которых я знаю. Стала расспрашивать.
1). Случай во время Великой Отечественной войны «Измерение ширины реки».
Вот этот случай рассказала мне моя соседка, а её отец был одним из лучших математиков в классе, когда учился в школе. Был участником Великой Отечественной войны.
Его отделению было приказано измерить ширину реки, через которую предстояло организовать переправу.…Подобравшись к кустарнику вблизи реки, отделение залегло, а он вместе с другим солдатом выдвинулся ближе к реке, откуда был хорошо виден занятый фашистами берег. В таких условиях измерить ширину реки нужно было и на глаз. Но они поступили следующим образом: встали лицом к реке и надвинули фуражку на глаза так, чтобы нижний обрез козырька точно совпал с линией противоположного берега.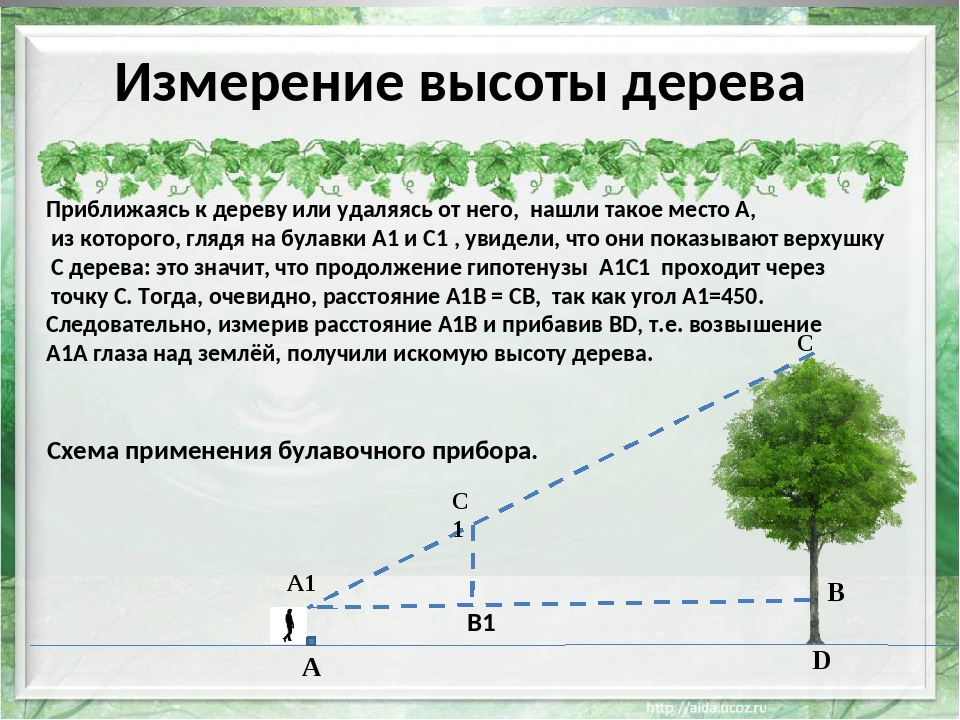 Козырек можно заменить ладонью руки или записной книжкой, плотно приложенной ребром ко лбу. Затем, не изменяя положения головы, надо повернуться направо или налево, или даже назад ( в ту сторону где поровнее площадка, доступная для измерения расстояния) и заметить самую длинную точку, видимую из под козырька. Расстояние до этой точки и будет примерно равно ширине реки.
Козырек можно заменить ладонью руки или записной книжкой, плотно приложенной ребром ко лбу. Затем, не изменяя положения головы, надо повернуться направо или налево, или даже назад ( в ту сторону где поровнее площадка, доступная для измерения расстояния) и заметить самую длинную точку, видимую из под козырька. Расстояние до этой точки и будет примерно равно ширине реки.
Этим способом они и воспользовались. Затем вместе они ползком добрались до этой точки, измеряя расстояние шнуром.
(см. рис.20 в приложении)
2). Измерения лесника Никитина Николая Николаевича
а).Измерение высоты дерева
Рассказ Николая Николаевича:
«Втыкаем в землю на некотором расстоянии от дерева планку. Место для нее выбирают так, чтобы, лежа за ней, (рост — 1,7 м) видеть верхушку дерева на одной прямой линии с верхней точкой планки. Расстояние от основания дерева до планки измерялось с помощью рулетки (СН = 9 м), высота планки была известна заранее (АС=1,5м), а вот расстояние С В и измерять не пришлось (СВ = 1,7 м).
, значит -высота дерева».
Если проверить с точки зрения геометрии, т.е использовать подобие треугольников, получается:
°, — общий угол для треугольников ВСА и ВНА. Значит, треугольники ВСА и ВНА – подобны. Т.е
, где ВН=СН+СВ. По этому признаку подобия решается эта задача.
АН- высота дерева. (см. рис.21 в приложении)
в).Измерение высоты дерева
Рассказ Николая Николаевича:
«Случается так, что неудобно подойти вплотную к основанию измеряемого дерева. Тогда поступали так: был придуман простейший прибор из двух планок. Две планки АВ и СД скрепляются под прямым углом так, чтобы АВ=ВС, а ВД=АВ. Вот и весь прибор. (см. рис в приложении) Чтобы измерить им высоту, держат его в руках, направив планку СД вертикально (для чего при ней имеется отвес – шнурок с грузиком), и становятся последовательно в двух местах: сначала в точке А, где располагают прибор концом с вверх, а затем в точке А’, подальше, где прибор держат вверх концом d.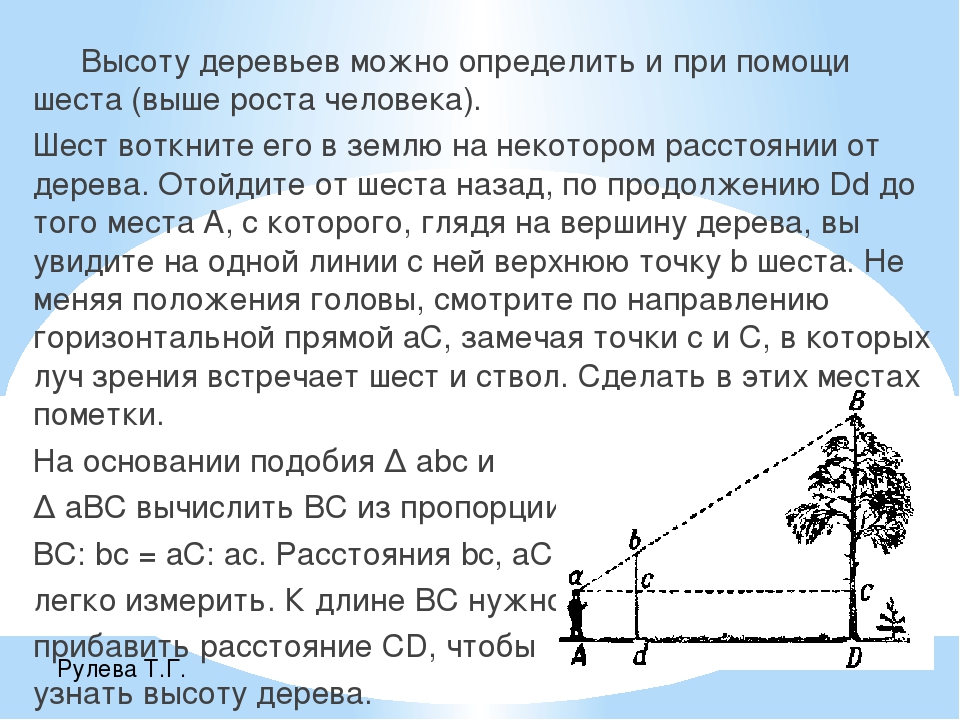 Точка А’ избирается так, чтобы, глядя из а на конец с, видеть его на одной прямой с верхушкой дерева. Точку А’ отыскивают так, чтобы, глядя из а’ на точку d’, видеть ее совпадающей с В. В отыскании этих двух точек А и А’ заключается все измерение, потому что искомая высота дерева ВС равна расстоянию А А’» (см рис в приложении)
Точка А’ избирается так, чтобы, глядя из а на конец с, видеть его на одной прямой с верхушкой дерева. Точку А’ отыскивают так, чтобы, глядя из а’ на точку d’, видеть ее совпадающей с В. В отыскании этих двух точек А и А’ заключается все измерение, потому что искомая высота дерева ВС равна расстоянию А А’» (см рис в приложении)
Если рассмотреть этот случай, то равенство вытекает из того, что аС=ВС, а’С=2ВС. Значит,
а’С’- аС=ВС.
«Через годы появились высотомеры лесоводов, которым мы пользовались в последние годы работы»- объяснил нам Николай Николаевич.
«Этим прибором тоже можно определить высоту дерева, к которому нельзя подойти. Поступают следующим образом: Надо направить прибор на вершину В дерева с двух точек Аи А’. Пусть в А мы определили, что ВС=0,9АС, а в точке А’ определили, что ВС= 0,4 А’С.
Тогда АС=; А’С’=, значит, АА’= А’С-АС= — =ВС.
Получили, АА’=ВС. , или ВС=А’А.
, или ВС=А’А.
3).Измерения охотоведа Юрия Ивановича Ланин
а).В условиях путешествий очень важно уметь без помощи приборов определять расстояния и размеры предметов. Способность человека оценивать на глаз без помощи приборов, расстояния до окружающих его предметов и размеры предметов называется глазомером. Это индивидуальная особенность человека, но ее можно развить путем постоянных и терпеливых упражнений. Глазомерное определение расстояний производится различными способами.
В условиях путешествий возникает необходимость в измерении расстояния до недоступных предметов.
Например, на противоположном берегу реки человек идет параллельно берегу слева направо. Вытянув руку по направлению движения пешехода, смотрим одним правым глазом на конец пальца, ожидая, когда человек заслонится им. В тот же момент закроем правый глаз и откроем левый — человек словно отскочит назад. Считаем, сколько шагов сделает пешеход, прежде чем снова поравняется с нашим пальцем.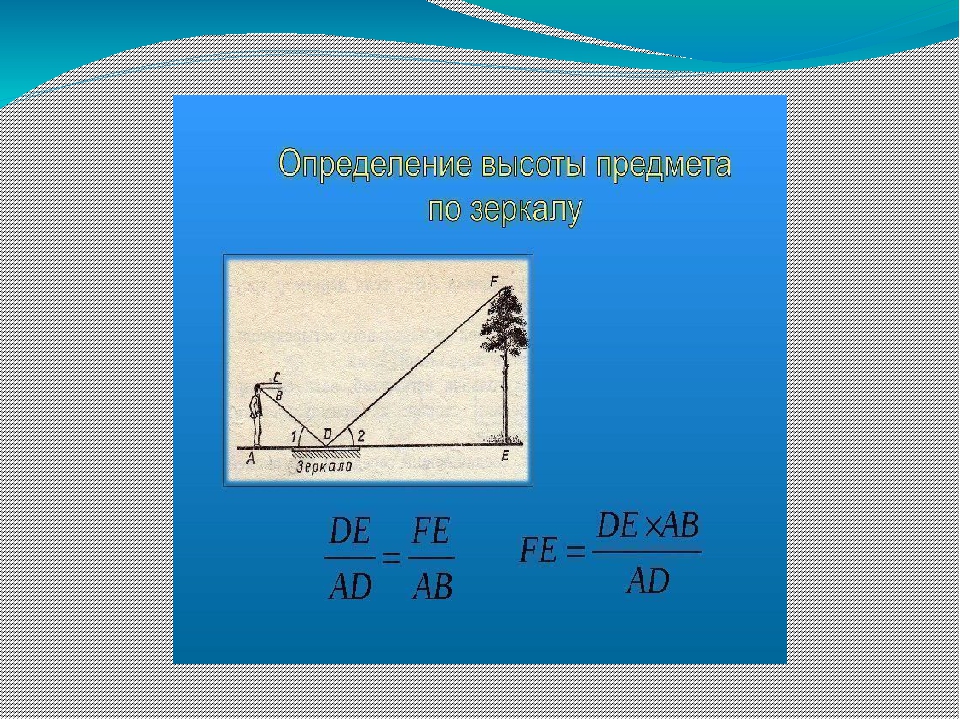
Расстояние от нас до человека на другом берегу реки определяется из пропорции:
Пример. Расстояние между зрачками глаз Г = 6 см, от конца вытянутой руки до глаза Л = 60 см. Пешеход прошел расстояние П, равное 18 шагам; в среднем шаг равен 75 см. Подставляя эти величины в формулу, получаем :
(см. рис.22 в приложении)
в). Измерение по луже.
Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц.
Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между нами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета.
Измеряемый предмет, например дерево, будет во столько раз выше нас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до нас( расстояния можно мерить шагами).
(см. рис.23 в приложении)
рис.23 в приложении)
4). Определение глубины колодца строителем А.В. Таратиным.
Определить глубину колодца можно с помощью шеста. Требуется найти глубину х колодца по известной длине Н шеста и ширине d колодца, а также отрезку L, отсекаемому лучом зрения наблюдателя на границе колодца.
Значит, . Это получается из подобия треугольников. Так как , то получается та величина, который нам предложил строитель Александр Витальевич.
.(см. рис.24 в приложении)
5). Еще один случай во время Великой Отечественной войны «Построение моста»
Вот как однажды было на одном из фронтов Великой Отечественной войны, где служил прадедушка Александровой Кристины, Степан Ильич Сергеев. Подразделению разведчика Сергеева было приказано построить мост через реку. На противоположном берегу засели фашисты. Для разведки места постройки моста выделили разведывательную группу во главе с Сергеевым. … В ближайшем лесном массиве они измерили диаметр и высоту наиболее типичных деревьев и посчитали количество деревьев, которые можно было использовать для постройки.
… В ближайшем лесном массиве они измерили диаметр и высоту наиболее типичных деревьев и посчитали количество деревьев, которые можно было использовать для постройки.
Высоту деревьев определяли при помощи шеста.
6). Определение на местности расстояний по линейным размерам предметов заслуженным учителем физики В.Г.Гавриловым.
Определение расстояний по линейным размерам предметов заключается в следующем. С помощью линейки, расположенной на расстоянии 50 см от глаза, измеряют в миллиметрах высоту (ширину) наблюдаемого предмета. Затем действительную высоту (ширину) предмета в сантиметрах делят на измеренную по линейке в миллиметрах, результат умножают на постоянное число 5 и получают искомую высоту предмета в метрах.
Например, телеграфный столб высотой 6 м закрывает на линейке отрезок 10 мм.
Следовательно, расстояние до него:
:
Точность определения расстояний по линейным величинам составляет 5-10% длины измеряемого расстояния.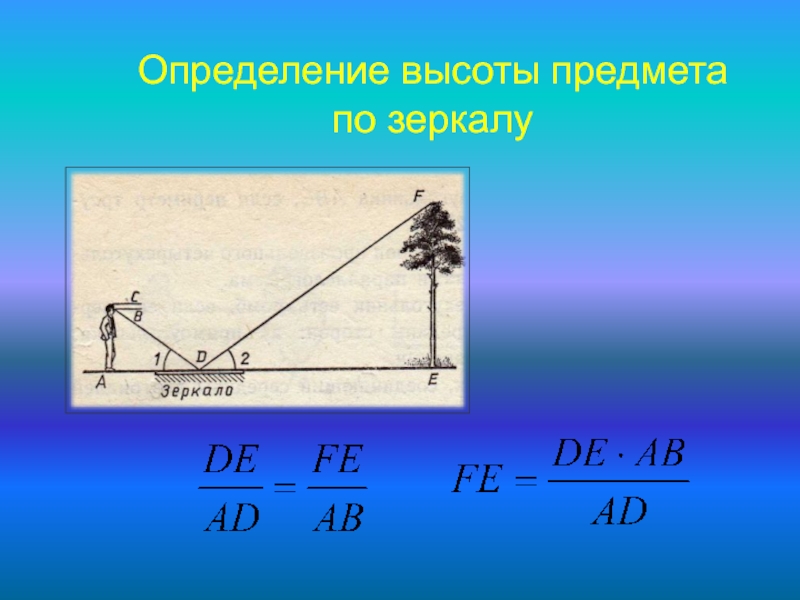 (см. рис.25 в приложении)
(см. рис.25 в приложении)
ЧастьIII
Практическая часть- личные исследования.
Измерения голыми руками.
«Измерь самого себя – и ты станешь настоящим геометром!» — воскликнул средневековый философ Марсилио Фичино.
Конечно, измерить самого себя и стать настоящим геометром очень трудно. Не всякому удается сделать это за всю жизнь, но если говорить о чем-то более простом, то с уверенностью можно сказать, что каждому человеку, научившемуся считать и писать, неоднократно приходилось что-либо измерять: высоту дерева, собственный вес, длину прыжка и многое другое. Но не всегда в путешествии мы имеем сантиметровую ленту. Хорошо бы каждому из нас обзавестись «живым метром», чтобы в случае нужды пользоваться им для измерений.
Полезно также помнить, что у большинства людей расстояние между концами расставленных рук равно росту – правило, подмеченное гениальным художником и ученым Леонардо да Винчи: оно позволяет пользоваться нашими «живыми метрами».
Искусство мерить шагами.
Очутившись на шоссе, мы можем выполнить ряд интересных геометрических упражнений. Прежде всего, воспользуемся шоссе, чтобы измерить длину своего шага и скорость ходьбы. Это даст возможность измерять расстояния шагами – навык, который приобретается довольно легко после недолгих упражнений. Главное здесь- приучить себя делать шаги всегда одинаковой длины. На шоссе через каждые 100 м установлен белый столб, пройдя такой 100-метровый промежуток своим обычным шагом и сосчитав число шагов, вы легко найдете среднюю длину своего шага. Отметим любопытное соотношение, обнаруженное многократными измерениями: средняя длина шага взрослого человека равна примерно половине его роста, считая до уровня глаз. Если, например, рост человека до уровня глаз 1,4 м, то длина его шага – около 70 см Проверим это утверждение:
На улице зима, потому длину шага мы измерили в школьном коридоре. Отмерили расстояние 10м и шагами прошлись 3 раза. Получили в среднем у меня 13 шагов, а у Алексея 12. Нашли длину шага у Алексея и свою: . Посмотрев на таблицу и диаграмму (см таблица 1 и диаграмма1 в приложении) можно сделать вывод, что на самом деле длина шага человека равна половине его роста, считая до уровня глаз с точностью 0,03м.
Отмерили расстояние 10м и шагами прошлись 3 раза. Получили в среднем у меня 13 шагов, а у Алексея 12. Нашли длину шага у Алексея и свою: . Посмотрев на таблицу и диаграмму (см таблица 1 и диаграмма1 в приложении) можно сделать вывод, что на самом деле длина шага человека равна половине его роста, считая до уровня глаз с точностью 0,03м.
Правильность первой гипотезы доказана.
Измерение столба в школьном дворе.
Для измерения высоты столба измеряем:
тень столба-13м;
тень Алексея — 2,3м;
рост Алексея – 1,68м.
Чтобы найти высоту столба .
Вывод: Высота столба должна быть 9-9,5 м. Этот расчет получился у нас точный. Посоветовались с техником по техническим документациям из Урмарской подстанции Гурьевой Татьяной Михайловной
Измерение березы, которую посадил мой отец Николаев Сергей Михайлович( с помощью зеркала)
Для измерения высоты дерева измеряем:
Мой рост до глаз ( m)– 1,47м;
Расстояние от глаз до макушки (n) – 10 см;
Расстояние от меня до зеркала (c ) – 1м;
Расстояние от зеркала до березы (k) – 9 м;
Высота березы – l.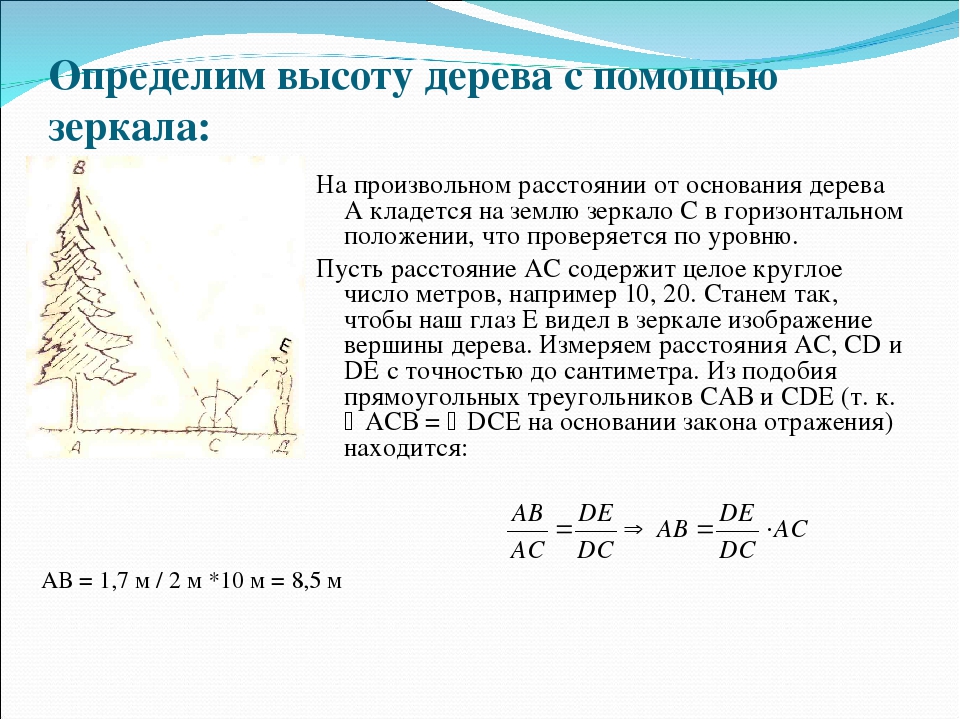
Чтобы найти высоту березы:
5. Измерение школьного здания( с помощью шеста)
Для измерения высоты школьного здания измеряем:
Длина шеста (m) – 1м;
Рост Алексея (n)– 1,67м;
Расстояние от шеста до здания школы (b) – 13,5м;
Высота здания – l.
Чтобы найти высоту школьного здания:
Вывод: Я думаю, что этот ответ точный. Узнала, поговорив с бывшим директором нашей школы Николаем Михайловичем Софроновым. Он сказал, что высота всего здания 11м и нужно вычесть 2м (крыша). А мы измеряли здание без крыши.
Измерение ширины оврага, через которое мы ходим в школу.
Для измерения ширины оврага, откуда мы ходим в школу, измеряем:
MA=8м;
AK=5м;
KB=5м;
МN – ширина оврага. Чтобы найти ширину оврага рассмотрим подобные треугольники.
Чтобы найти ширину оврага рассмотрим подобные треугольники.
Получаем:
Значит, MN=16-8=8м.
Вывод: Этот ответ тоже с небольшой погрешностью. Провела общественный опрос о ширине оврага. Вычисляя глазомером, Софронов В.А, Софронов Н.М, Артюков Ю.И, Артюкова В.Г – учителя и работники нашей школы, ответили 15-17м. А у нас получилось среднее арифметическое этих чисел.
Измерение высоты памятника ( с помощью линейки)
Для измерения высоты памятника измеряем:
Расстояние от глаза до линейки(m) – 0,5м;
Расстояние от памятника до меня (n)- 65 м;
Длина линейки(a) – 0,25м
Высота памятника(l)
Чтобы найти высоту памятника:
.
Заключение
Практические работы на местности обогатили меня новыми знаниями о природе родного края, развили интерес к его изучению, расширили знания по географии, геометрии. Знания, полученные при выполнении исследовательской работы, остаются в моей памяти надолго, развивая навыки научно-исследовательской работы
Знания, полученные при выполнении исследовательской работы, остаются в моей памяти надолго, развивая навыки научно-исследовательской работы
Были исследованы различные способы измерения высоты деревьев, столбов, ширины рек, озер, оврагов. Полученные знания достаточно легко применяются на практике. По проблеме исследования был проведен эксперимент.
Эксперимент проходил в три этапа:
1 этап – теоретический. Находила исторические данные и общие данные практического направления по теме «Использование и измерений на местности при изучении некоторых тем школьного курса геометрии».
2 этап – поисковый. Здесь я искала людей, у которых работа была связана моей темой и случаи измерения на природе из жизни мудрых людей.
3 этап – практический. Здесь была проведена экспериментальная проверка знаний, полученных в ходе теоретического и поискового этапов.
На третьем этапе эксперимента проводилась проверка гипотез.
В ходе проведения исследовательской работы я пришла к выводам:
1.Длина шага человека равна половине его роста.
2. Высоту столба, дерева можно измерить не только при помощи тени.
3. Если человек знает подобие треугольников, возникнет необходимость их применения в жизни.
Таким образом, эксперимент подтвердил выдвинутые гипотезы: длина шага человека равна половине его роста и если человек знает подобие треугольников, возникнет необходимость их применения в жизни, гипотеза о том, что высоту столба, дерева можно измерить только при помощи тени не подтвердился. Высоту столба, дерева можно измерить по разным способам: по луже, по зеркалу, используя шест, планку и так далее.
В ходе исследовательской деятельности повысился у меня интерес к геометрии. Дальнейшие мои задачи продолжить эту тему, рассматривая задачи: измерение глубины реки, озера, оврага, нахождение нижней высоты облаков.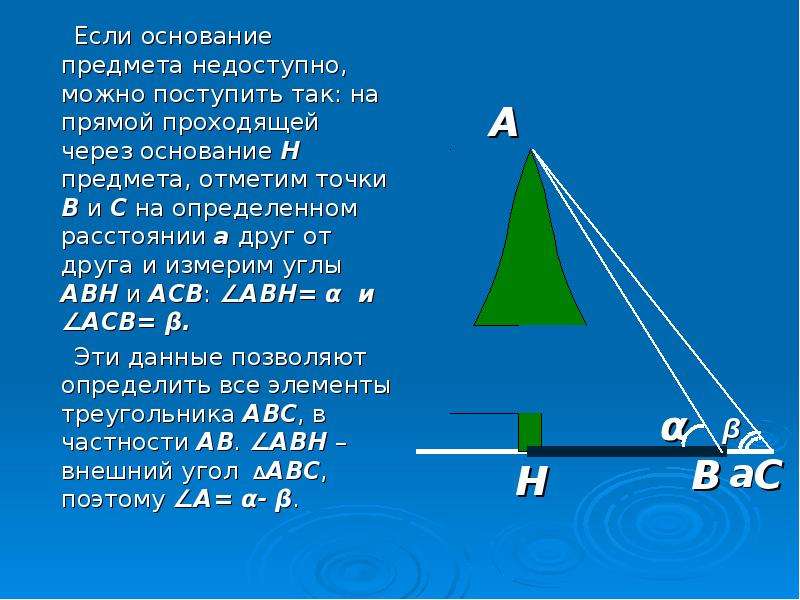 Хотела бы продолжить личные исследования по теме: «Геометрия в звездном небе».
Хотела бы продолжить личные исследования по теме: «Геометрия в звездном небе».
Используемая литература:
В.Н.Руденко. Геометрия Просвещение 2001
Л.С.Атанасян. Геметрия. Просвещение 2009
Научно- практический и методический журнал. Математика в школе.№ 2 Издательство «Школьная пресса»
Газета. Математика. Издательский дом «Первое сентября»
Я.И.Перельман. Занимательная геометрия.
А.В.Волошинов. Пифагор. Просвещение 1993
А.П.Савин и др.Я познаю мир. Москва АСТ.2000
Б.В.Гнеденко и др. Энциклопедический словарь юного математика. Москва «Педагогика»1985
Г.И.Глейзер. История математики в школе.Просвещение.1985.
Определение высоты предмета — математика, презентации
Конкурс «Чувашская Республика в математических задачах»
Номинация:
«Задачи о храмах и монастырях Чувашской Республики»
Иванов Никита Валерьевич
ученик 8 класса МБОУ «Арабосинская ООШ»
Кузьмин Дмитрий Олегович
ученик 8 класса МБОУ «Арабосинская ООШ»
Руководитель: Кузьмина Юлия Николаевна
учитель математики МБОУ «Арабосинская ООШ»
Урмарского района Чувашской Республики
e-mail : laruylia196@yandex. ru
ru
Церковь Святого Николая Чудотворца деревни Арабоси Урмарского района
Задача на измерение на местности.
Задача.
Определить высоту церкви Святого Николая Чудотворца (в метрах) деревни Арабоси Урмарского района после восстановления.
Цель: измерить недоступную высоту церкви Николая Чудотворца разными способами.
Задачи:
- изучить различные способы определения недоступной высоты предмета;
- провести соответствующие измерения и вычисления;
- оформить результат, сделать выводы.
Церковь Святого Николая Чудотворца
деревни Арабоси Урмарского района
Этапы выполнения работы:
- 1 этап: теоретический. Изучение способов определения недоступной высоты предмета.
- 2 этап: практический. Определение недоступной высоты предмета разными способами.

- 3 этап: сравнительный. Сравнение полученных данных с помощью диаграммы. Выявление самого точного способа определения недоступной высоты предмета.
Из архивного материала
- На территории села Арабоси Урмарского района расположена Церковь Святого Николая Чудотворца, построенная на средства казны в 1893 году, однопрестольная. Церковь деревянная, теплая, длина с колокольней 10 сажень, наибольшая ширина 3 саж. 2 аршина, высота до верхнего карниза 2 саж., на церкви одна глава. Иконостас: длина 3 саж., высота 2 саж., колокольня 2-ярусная, высота 6 сажень. Штат причта: священник и диакон.
- Закрыта в 1931 году. Сохранилась до наших дней со значительными утратами. После регистрации в 2001 г. полностью восстановлена и перестроена на средства благотворителей, администрации района и прихожан. Престольные праздники: 6 декабря (19 декабря), 9 мая (22 мая)
(Браславский Л.Ю. «Православные храмы Чувашии». http://www. nikola-ygodnik.narod.ru/Raznoe_093.html
nikola-ygodnik.narod.ru/Raznoe_093.html
Описание о Николае Чудотворце
- Святитель Николай родился во второй половине III века в городе Патары, области Ликии в Малой Азии. Родители его были из благородного рода и весьма зажиточны, что не мешало им быть благочестивыми христианами, милосердными к бедным и усердными к Богу. Сия благословенная чета, за свою богоугодную жизнь, многие милостыни и великие добродетели, удостоилась произрастить святую ветвь, «как дерево, посаженное при потоках вод, которое приносит плод свой во время свое.» (Пс.1,3).
- Ещё при жизни своей святитель Николай прославился как умиротворитель враждующих, защитник невинно осужденных и избавитель от напрасной смерти.
- Святитель Николай Чудотворец, архиепископ Мирликийских, самый наверно известный во всем мире святой. На основании фактов из его жития ему молятся и о помощи на море, и о путешествующих, и о замужестве дочерей, и в крайней бедности и во многих других нуждах.

- http://www.nikola-ygodnik.narod.ru/Raznoe_093.html
Встреча с настоятелем церкви Леонидом Ермолаевым
В каждой области, в каждом районе, населённом пункте есть свои достопримечательности. Отец Леонид рассказал нам историю церкви, о её архитектуре, как проводилась работа по её восстановлению. Над восстановлением церкви работало множество прихожан во главе с настоятелем. Церковь, возведенная в центре д. Арабоси, имеет очень большое значение не только для жителейдеревни, но и для верующих всего района.
Разные способы измерения высоты здания церкви
1 способ. Измерения Фалеса Милетского
Существует много различных способов для измерения высоты предмета. Самый лёгкий и самый простой способ – это способ, которым ещё за шесть веков до нашей эры древнегреческий мудрец Фалес Милетский определил высоту египетской пирамиды. В чём заключалась его работа? Чтобы определить высоту пирамиды, он воспользовался длиной её тени. Фалес воткнул в землю вертикально длинную палку и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды». ВЕ = ДЕ – высота пирамиды.
Фалес воткнул в землю вертикально длинную палку и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды». ВЕ = ДЕ – высота пирамиды.
Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия».
Наши действия. 10.03.2015 г. Мы попробовали измерить высоту церкви по Фалесу. Погода солнечная. Поставили палку длиной 1м.50 см на землю вертикально и ждали, когда тень от неё станет равной 1м. 50 см. Это случилось в 10 ч. 25 мин. Быстро измерили длину тени церкви. MK=KN= 1,5м., АС=ВС= 12,7 м. Высота церкви равна 12,7 м.
В
N
K
С
А
М
2 способ. Жюль Верн. Роман «Таинственный остров».
«Таинственный остров» (фр. L’Île mystérieuse ) — роман-робинзонада французского писателя впервые опубликованный в 1874 году. «Взяв прямой шест, длиной 12 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком. Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам. По свойству подобных треугольников вычислили высоту гранитной стены».
Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком. Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам. По свойству подобных треугольников вычислили высоту гранитной стены».
Наши действия. 11.03.2015 г. Мы измерили высоту церкви по Жюль Верну. Палка длиной 1м 60 см, таков рост Димы, поставлена вертикально на землю, у его ног так, чтобы лёжа на земле, можно было на одной прямой линии видеть и конец палки, и верхнюю точку церкви. Чтобы не испачкаться, мы постелили картон. Я измерил расстояние от уровня глаз Димы до основания церкви. Это расстояние равно АС. AN=MN=1,6 м. AC =ВС= 12,3м. Высота церкви 12,3 м .
Это расстояние равно АС. AN=MN=1,6 м. AC =ВС= 12,3м. Высота церкви 12,3 м .
В
М
С
А
N
3 способ. Измерение высоты с помощью фотоаппарата.
Наши действия.
11.03.2015 г.
Сфотографировали церковь и в полный рост Никиту. На снимке рост Никиты- 1,2 см, а в действительности -1,55 м. Соответственно: высота церкви на снимке – 8,2см, в действительности – х м.
Решение: Напишем пропорцию и решим её:
=
Х 10,9
Высота церкви 10,9 м.
4 способ. Измерение высоты предмета с помощью зеркала.
Наши действия. 12.03.2015 г. Зеркало положили на землю, на ровное место. Дима отошёл от зеркала назад на такое расстояние, чтобы в зеркале была видна верхняя точка здания церкви. Это место я отметил мелом. Измерил расстояние от точки, отмеченной мелом до ног Димы (1,3 м.) и до основания церкви (10,7м.). Если рост Димы 1,6 м, то до уровня глаз-1,5 м. Решение: АВ=1,5м., ВО=1,3 м., ОN=10,7 м. Используя подобие треугольников AOВ и MОN по двум углам, нашли МN 12,4 м. Высота церкви 12,4 м.
Решение: АВ=1,5м., ВО=1,3 м., ОN=10,7 м. Используя подобие треугольников AOВ и MОN по двум углам, нашли МN 12,4 м. Высота церкви 12,4 м.
М
А
О
N
В
5 способ. Измерение высоты с помощью прямоугольного равнобедренного треугольника
Наши действия. Для измерения высоты по этому способу нам необходим прямоугольный равнобедренный треугольник. Один катет должен быть параллелен поверхности земли и должен находиться на уровне глаз. По гипотенузе нашли верхнюю точку здания церкви. Измерили расстояние от ног Димы (наблюдателя) до основания здания церкви и оно равно 10,6 м. Тогда высота церкви равна сумме этого расстояния и высоты Димы до уровня глаз, т.е. 10,6 м. + 1,5 м. = 12,1 м.
Высота церкви 12,1 м.
6 способ. Определение высоты здания на глаз (среднее арифметическое)
Наши действия.
В нашем классе 13 учеников. Мы с Димой участвуем в решении задачи. Значит, 11 учеников определили примерно на глаз высоту здания церкви, предварительно установив рядом с зданием церкви вертикально метровую линейку.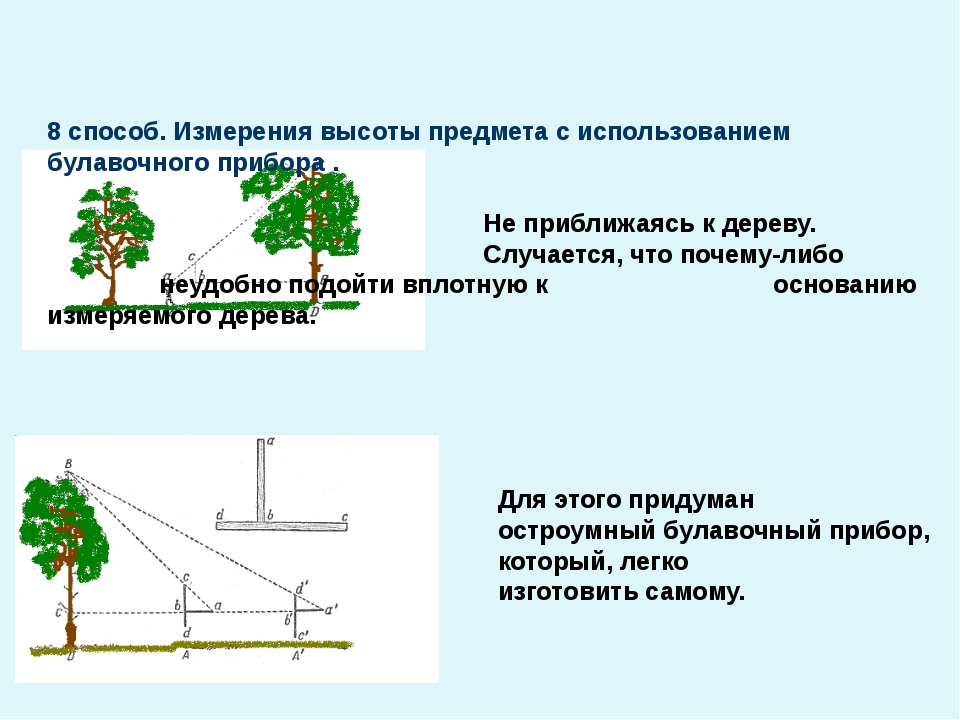 Нашли среднее арифметическое полученных данных.
Нашли среднее арифметическое полученных данных.
(14+13+16+12+14+13+12+15+13+13+12) : 11 = 13,3
Высота церкви 13,3 м.
7 способ. С помощью воздушного шара, наполненного гелием.
Наши действия.
Один ученик стоит рядом с зданием и отпускает шарик наполненный гелием и привязанной к тонкой нитке. Освободить нитку до тех пор, пока второй ученик (наблюдающий) увидит шарик на уровне вершины здания. Измерить длину выпущенной части верёвки, которая равна высоте здания. Длина нити равнялась 11,2 м.
Высота церкви равна 11,2 м.
8 способ. Измерения высоты предмета с использованием булавочного прибора . Не приближаясь к дереву. Случается, что почему-либо неудобно подойти вплотную к основанию измеряемого дерева. Для этого придуман остроумный булавочный прибор, который, легко изготовить самому.
Таблица подсчёта высоты церкви Николая Чудотворца д. Арабоси
Арабоси
№
Способ вычисления
1
Полученный результат (в м.)
По Фалесу
2
12.7
По Жюль Верну
3
12.3
Способ фотоаппарата
4
5
Способ зеркала
10,9
Способ прямоугольного треугольника
6
12,4
12.1
Среднее арифметическое
7
13,3
Способ гелиевого шара
8
11,2
Действительная высота церкви
12,7
Диаграмма вычислений высоты церкви Николая Чудотворца в д. Арабоси
Вывод
Мы хотели показать, что высоту здания можно измерить разными способами и постарались измерить высоту церкви Николая Чудотворца д. Арабоси. Но все полученные результаты дают погрешность. Считаем, что более точный результат получается по Фалесу (способ шеста).
Список использованных источников
- Я.И.Перельман «Занимательная геометрия».
- Жюль Верн. Роман «Таинственный остров».
- Атанасян. Учебник «Геометрия» 8 класса.
- Браславский Л.Ю. «Православные храмы Чувашии».
- http://www.nikola-ygodnik.narod.ru/Zitie_001.htm
- Книга «Святитель Николай Чудотворец», составители — Андрей Вознесенский, Фёдор Гусев.
- Издание Сретенского монастыря, Москва, 2005 г., 664 стр.)
- http://www.nikola-ygodnik.narod.ru/Raznoe_093.html
Практические приемы для оценки высоты и ширины объектов
Когда вы находитесь в поле, путешествуете по земле или выполняете какое-либо количество работ и задач на открытом воздухе, вам может потребоваться по разным причинам измерить высоту и ширину таких объектов, как деревья и реки. Но часто эти объекты настолько велики и недоступны, что пытаться измерить их рулеткой было бы безрассудно и непрактично.
К счастью, есть несколько небольших практических приемов, которые разведчики веками использовали для оценки высоты и ширины объектов, используя только палки и немного геометрии.Хотя существуют приложения для смартфонов, которые могут делать то же самое, чтобы стать более антихрупкими, всегда полезно знать, как делать такие вещи без технологий. К тому же это весело.
Примечание. Для многих из этих методов вам необходимо знать длину обычного темпа в футах и дюймах, поскольку для определения размеров требуется стимуляция. Чтобы определить длину вашего шага, сделайте обычный шаг и измерьте расстояние от пятки задней ноги до носка передней.
Как оценить высоту в полевых условияхЕсли вы рубите деревья, вам нужно заранее узнать, какой они высоты, чтобы они не упали на вашу машину или кемпинг. Но как измерить высоту дерева, не взбираясь на вершину рулеткой?
Вот несколько традиционных приемов, используемых лесорубами и разведчиками для оценки высоты деревьев и других высоких объектов, таких как скалы каньона и водопады.
Способ валки
- Отойдите достаточно далеко от измеряемого объекта, чтобы вы могли видеть его верх и низ.Держите палку вертикально на расстоянии вытянутой руки, чтобы верхняя часть палки касалась верхней части объекта.
- Поверните руку на 90 градусов, чтобы она выровнялась с горизонтом, имитируя падение объекта, отсюда и термин «валка».
- Пусть ваш напарник встанет в том месте, где вам кажется, что кончик палки заканчивается. Поместите туда маркер, как камень или другую палку.
- Измерьте расстояние между маркером и основанием объекта, чтобы оценить его высоту.
Метод палки
Этот метод требует относительно ровной поверхности, чтобы получить хорошую оценку.
- Найдите палку длиной с вашу руку.
- Вытяните руку прямо так, чтобы палка была направлена вверх (под углом 90 градусов к вытянутой руке).

- Идите назад, пока не увидите, что кончик палки совпадает с верхушкой дерева. Теперь ваши ноги находятся примерно на таком же расстоянии от дерева, как и оно высоко.
Метод пропорционального стержня
Это разновидность метода палки, требующая второго человека.
- Попросите напарника (рост которого известен) встать рядом с измеряемым объектом.
- Встаньте достаточно далеко от объекта, чтобы вы могли видеть его верх и низ. Возьмите карандаш или палку на расстоянии вытянутой руки и одним глазом взгляните на палку так, чтобы ее верхушка касалась макушки головы вашего друга.
- Поместите ноготь большого пальца на палку в том месте, где она, кажется, касается основания ствола дерева. Теперь переместите ручку вверх, чтобы примерно увидеть, сколько раз это измерение входит в высоту дерева.
- Умножьте число, полученное на шаге 3, на рост вашего друга, чтобы определить приблизительную высоту объекта.

Метод тени
Этот метод работает только в солнечный день.Земля должна быть относительно ровной, так как любой уклон будет мешать измерению.
- Измерьте тень, отбрасываемую деревом (от основания дерева до тени его вершины), и обозначьте эту длину как AB.
- Измерьте тень, отбрасываемую кем-либо или объектом известной высоты. Обозначьте эту длину как CD.
- Вычислите высоту дерева по следующей формуле (AB x высота вашего тела) / CD = ~ высота объекта.
Допустим, вы путешествуете по суше и подходите к спокойной реке, которую вам нужно пересечь.Вы знаете, что можете легко проплыть 100 ярдов, но река кажется шире. Как можно определить ширину реки, не промокнув и без рулетки?
Или, допустим, вы пришли в овраг. Как узнать, как далеко находится другая сторона, чтобы вы могли соединить мост, чтобы пересечь ее?
Вот два метода, которые могут решить эти дилеммы и дать вам приблизительную оценку ширины.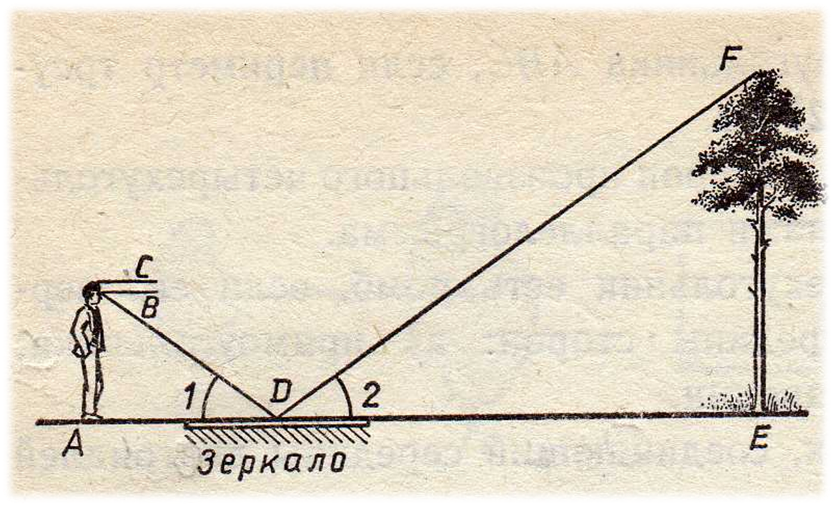
Наполеон / Метод приветствия
- Стойте как можно ближе к берегу реки.
- Склоните голову, подбородок к груди. Поднесите руку ко лбу ладонью вниз (как будто отдаете честь).
- Опустите руку так, чтобы ее передний край касался противоположного берега.
- Поверните все тело на четверть оборота влево или вправо, «перенося» расстояние до берега, на котором вы стоите. Обратите внимание на точку, в которой кажется, что край вашей руки касается берега, на котором вы стоите. Приходите к этому. Расстояние до точки, которой кажется, касается края вашей руки, примерно равно ширине реки.
Шаговый метод
Для этого метода требуется немного геометрии, но он может дать вам довольно точную оценку ширины реки.
- Выберите объект на противоположной стороне реки, например дерево или камень, и отметьте его буквой «А».
- Поместите палку на свою сторону реки точно напротив ориентира A.
 Отметьте эту палку буквой B.
Отметьте эту палку буквой B.
- Пройдите вдоль берега под углом 90 градусов от точки B определенное количество шагов.Скажем, 50 шагов. Поместите туда палку. Отметьте это точкой «C».
- Продолжайте идти половину расстояния, которое вы только что прошли. В нашем примере это 25 шагов. Поместите сюда палку и отметьте ее буквой D.
- Поверните от реки и идите до тех пор, пока маркеры C и A не выровняются по прямой. Поместите сюда палку и отметьте ее буквой «E».
- Идите и считайте шаги от точки D до точки E. Расстояние между D и E составляет ½ расстояния через реку.Удвойте это число, и вы получите расстояние в шагах через реку. Умножьте количество шагов на длину вашего шага, чтобы получить расстояние в футах.
Projectile Motion
Projectile Motion Движение снаряда Предмет выбрасывается прямо с вершины здания высотой h футов с начальной скоростью v футов в секунду. Высота объекта как функция времени может быть смоделирована функцией h (t) = –16t 2 + vt + h, где h (t) — высота объекта (в футах) через t секунд после него. брошен. Высота объекта как функция времени может быть смоделирована функцией h (t) = –16t 2 + vt + h, где h (t) — высота объекта (в футах) через t секунд после него. брошен.Если нам задана начальная скорость (или скорость) объекта и высота здания, мы можем использовать эту модель, чтобы определить, сколько времени требуется, чтобы объект достиг разной высоты. В этой модели предполагается, что объект не попадает в верхнюю часть здания на обратном пути к земле и что сопротивление ветра минимально. |
Вот шаги, необходимые для решения проблем движения снаряда:
| Шаг 1 : | Установите данное уравнение равным соответствующей высоте. |
| Шаг 2 : | Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. |
| Шаг 3 : | В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. |
Пример 1 — Мяч бросается прямо вверх с вершины здания высотой 128 футов с начальной скоростью 32 фута в секунду.Высота мяча как функция времени может быть смоделирована функцией h (t) = –16t 2 + 32t + 128. Сколько времени потребуется, чтобы мяч коснулся земли?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. | |
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители.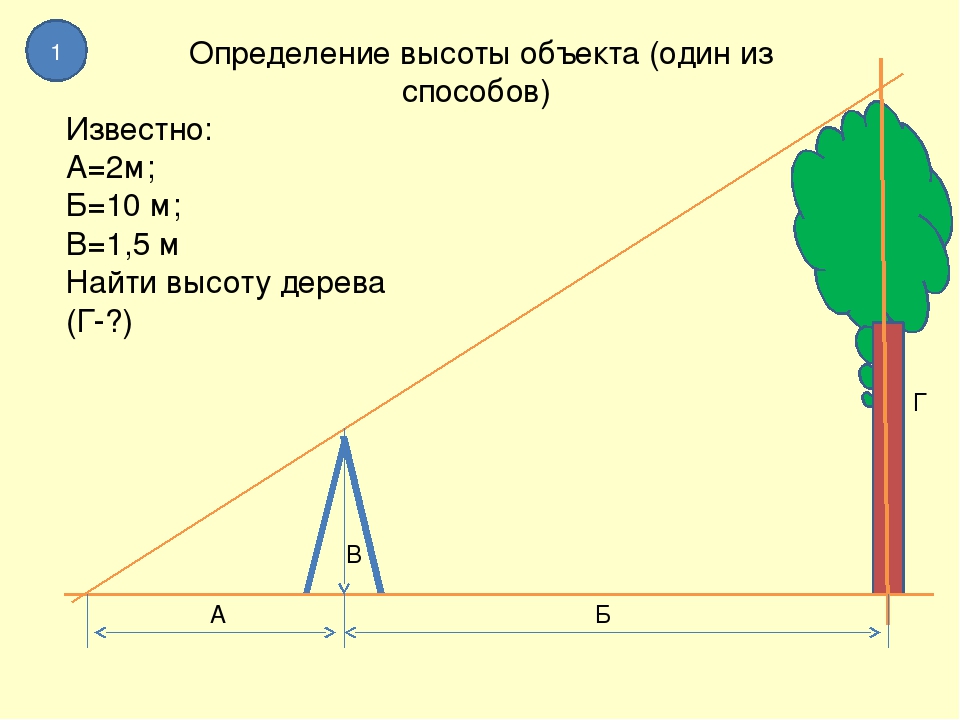 | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз. |
Пример 2 — Мяч бросается прямо вверх с вершины здания высотой 288 футов с начальной скоростью 48 футов в секунду.Высота мяча как функция времени может быть смоделирована функцией h (t) = –16t 2 + 48t + 288. Когда мяч достигнет высоты 320 футов?
| Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным 320, потому что мы хотим определить, когда высота будет 320 футов. | |
Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 320 футов один раз на пути вверх и еще раз на пути вниз. |
Щелкните здесь для практических задач
Пример 3 — Ракета запускается прямо с вершины здания высотой 24 фута с начальной скоростью 92 фута в секунду.Высота ракеты как функция времени может быть смоделирована функцией h (t) = –16t 2 + 92t + 24. Сколько времени потребуется, чтобы ракета ударилась о землю?
Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным нулю, потому что высота земли равна нулю. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. В этом случае есть только один положительный ответ, который имеет смысл, потому что мяч ударяется о землю только один раз. |
Щелкните здесь для практических задач
Пример 4 — Мяч падает прямо в воздухе с высоты 4 фута с начальной скоростью 64 фута в секунду.Высота мяча как функция времени может быть смоделирована функцией h (t) = –16t 2 + 64t + 4. Когда мяч достигнет высоты 52 фута?
Шаг 1 : Установите данное уравнение равным соответствующей высоте. В этом случае мы устанавливаем уравнение равным 52, потому что мы хотим определить, когда высота будет 52 фута. В этом случае мы устанавливаем уравнение равным 52, потому что мы хотим определить, когда высота будет 52 фута. | |
| Шаг 2 : Решите уравнение, найденное на шаге 1, установив уравнение равным нулю и разложив уравнение на множители. | |
| Шаг 3 : В зависимости от проблемы определите, какой ответ или ответы верны. Не забудьте указать единицы в своем окончательном ответе. В этом случае есть два положительных ответа, которые имеют смысл, потому что мяч достигнет 52 футов один раз на пути вверх и еще раз на пути вниз. |
Щелкните здесь для практических задач
Измерение высоты деревьев и других высоких объектов (здания, столбы, водонапорные башни, антенны,…)
Тема
Наблюдение за деревьями для поиска закономерностейКонцепты
- Есть отношения
между высотой объекта и его тенью.

- Существует взаимосвязь между расстоянием от дерева и углом к вершине этого дерева от точки на этом расстоянии.
- Есть отношения среди пород деревьев.
- Есть отношения среди хвойных пород.
- Есть отношения
среди лиственных деревьев.
Основные вопросы
- Как узнать высоту? Посмотрите шесть способов измерения роста.
- Насколько велики деревья?
- Насколько велико это дерево?
- Что размеры деревьев важны?
- Что значит, какое высокое дерево? иметь в виду?
- Что значит размер багажника иметь в виду?
- Что значит размер корона означает?
- Почему людям нужно знать размеры деревьев?
- Пропорциональны ли деревья?
- Есть ли связь к диаметру ствола и его высоте?
- Есть ли связь к высоте и багажнику?
- Это есть связь до высоты е и короны размер?
- У некоторых видов деревьев иметь уникальные пропорции?
- Какая еще информация можно собрать о деревьях, чтобы людям было полезно знать?
Материалы
50 метровый шнур со счетчиком метки и один метр в сантиметрах, транспортир, клинометр, листы диаграммы бумага, калькулятор
Мероприятие 1
Сфотографируйте и соберите информацию о нескольких
виды деревьев. Может измерить высоту, диаметр и макушку
несколько похожих и разных видов (видов) деревьев, зафиксируйте
данные, систематизируйте их, нарисуйте в масштабе, нанесите на график и обнаруживайте закономерности.
Может измерить высоту, диаметр и макушку
несколько похожих и разных видов (видов) деревьев, зафиксируйте
данные, систематизируйте их, нарисуйте в масштабе, нанесите на график и обнаруживайте закономерности.
Справочная информация
Окружность дерева можно измерить напрямую шнуром cm и m.
Диаметр дерева можно рассчитать по формуле окружность или оценивается прямым измерением или с помощью Biltmore палка.
Crown можно измерить косвенно снизу дерево на земле с помощью шнурка cm и m.
Высота дерева можно оценить несколькими способами. Посмотрите шесть способов измерения роста.
Измерение высоты деревьев, построек, столбов,
Найдите дерево, здание, столб или другой высокий предмет.
Угадай высоту.
Каково ваше предположение? ________________
Не забудьте пометить свой ответ
относительно футов и дюймов, метров и сантиметров. Число само по себе бессмысленно.
Число само по себе бессмысленно.
Сначала ваш догадки могут быть не очень близкими, но тем более догадок и замеров тем точнее вы будете.
Есть несколько способов измерения высота без точного измерения сверху вниз рукой.
Один из способов — использовать человека в качестве измерителя. палка . Проще выбрать человека, которому три года, четыре или пять футов высотой.
Пусть этот человек встанет рядом к столбу или дереву перед ним.
Замерщик должен отойдите на 25-50 футов от обоих, в зависимости от высоты, чем выше, тем дальше.
Используйте прозрачную сетку или линейку.
Просматривая прозрачную пленку, медленно отойдите от них, чтобы найти место, где ученик перед деревом или шестом отмеряет точно определенное количество квадратов на сетке. или дюймов на линейке, и вы сможете увидеть все дерево или столб на сетке.
Посчитайте, сколько квадратов на
сетка человек и сколько там квадратов из
землю до вершины дерева.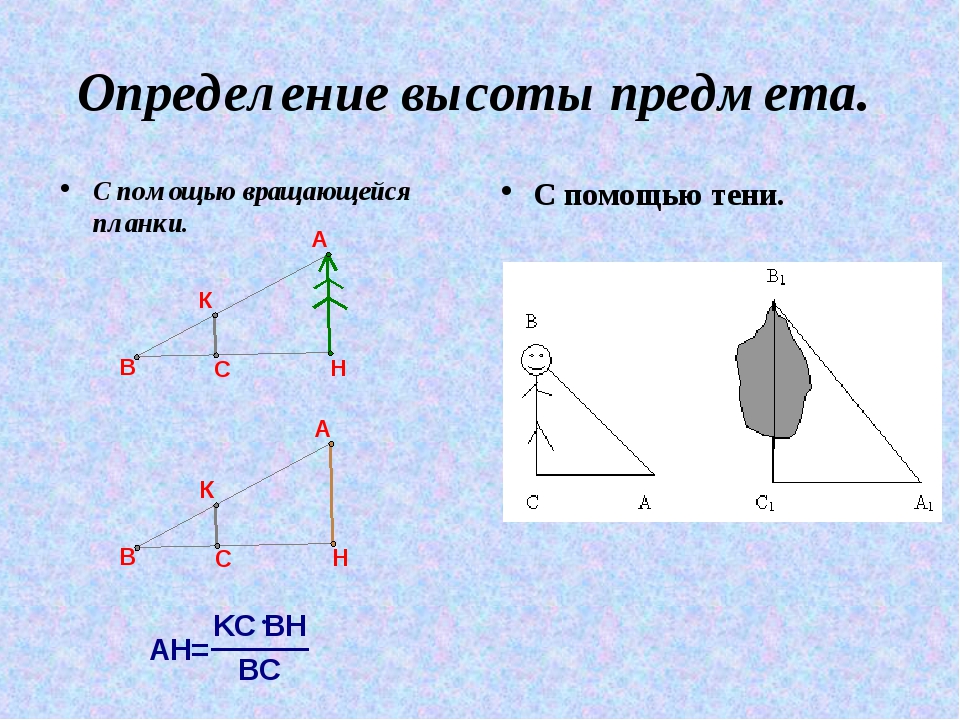
Если вы использовали линейку и человек, стоящий у столба, измерял один дюйм, что дерево измерялось в дюймах?
Если требуется шесть дюймов, чтобы дотянуться верхушка шеста и один дюйм представляет человека, нарисуйте это масштабировать на листе бумаги.
Если один дюйм = четыре фута, то дерево будет = 6 X 4 или 24. футов в высоту.
Измерьте столб или дерево в обоих направлениях (сетка и линейка) и запишите результаты на миллиметровой бумаге и включите любые примечания, которые могут быть полезным.Какую информацию нужно запомнить?
Ученые часто пишут свои результаты так они их не забудут.
Использование теней для измерения:
Арифметика очень важна в науке и почти
все ученые используют арифметику или другую математику для решения
проблемы. Если столб или дерево стоит на ровной поверхности и это солнечно
день, его тень можно использовать, чтобы определить, насколько он высоко.
Возьмите объект или человек, рост которого известен за пределами и измерьте длину его тени.
Затем измерьте тень от дерева или шеста неизвестной высоты.
Рост ученика: _______________________
Длина тени ученика: ________________
Длина тени дерева: ___________________
Теперь можно определить высоту дерева, используя эту информацию и идею пропорции. Студенты высота пропорциональна тени ученика таким же образом высота дерева пропорциональна длине тени дерева.
Постановка задачи
На листе миллиметровой бумаги нарисуйте линию, шкала для обозначения роста ученика и другого перпендикуляра к нему, чтобы представить длину тени ученика.
Используйте тот же масштаб и нарисуйте еще одну линию, чтобы обозначить длину дерева. тень.
Нарисуйте еще одну линию, перпендикулярную ему, чтобы обозначить высоту дерево.
Сравните количество единиц, используемых для рисования тени ученика на
рост студента.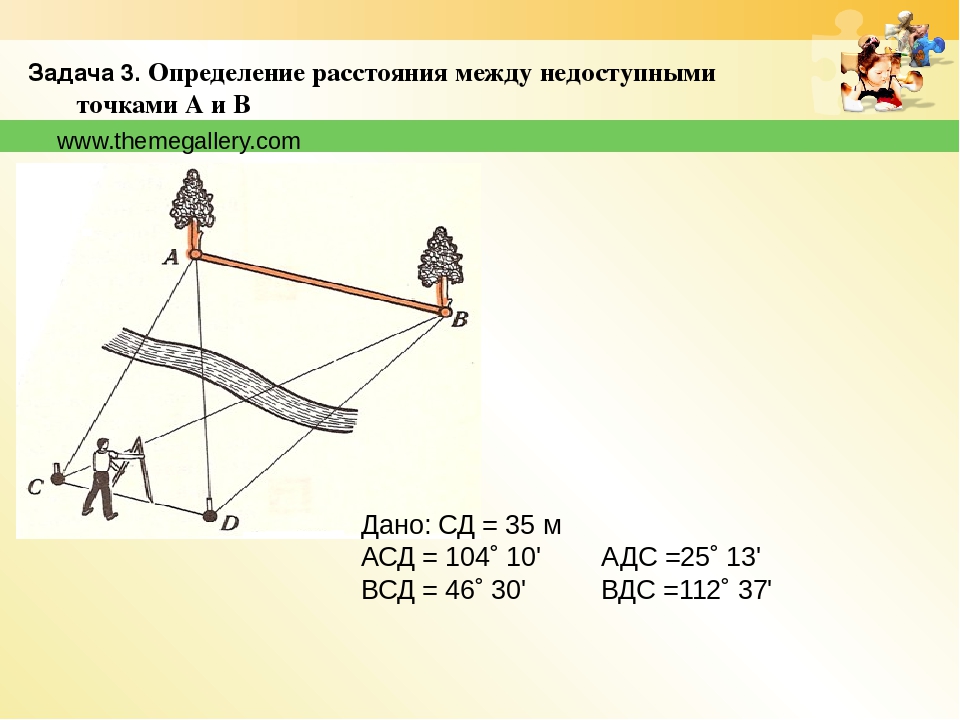
Используйте это соотношение, чтобы нарисовать высоту дерева. Затем вы можете использовать масштаб, чтобы найти высоту дерева.
Математическая установка пропорции:
| Рост ученика | Длина тени студента | Высота дерева | Длина тени дерева |
|---|---|---|---|
| 4 фута | 3 фута | ? | 21 фут |
Используя данные с предыдущей страницы, найдите длину мачты (x).
| Рост ученика | Длина ученической тени | Высота дерева | Длина тени дерева |
|---|---|---|---|
Использование клинометра для измерения высоты
Клинометр может быть
используется для измерения угла возвышения дерева или столба.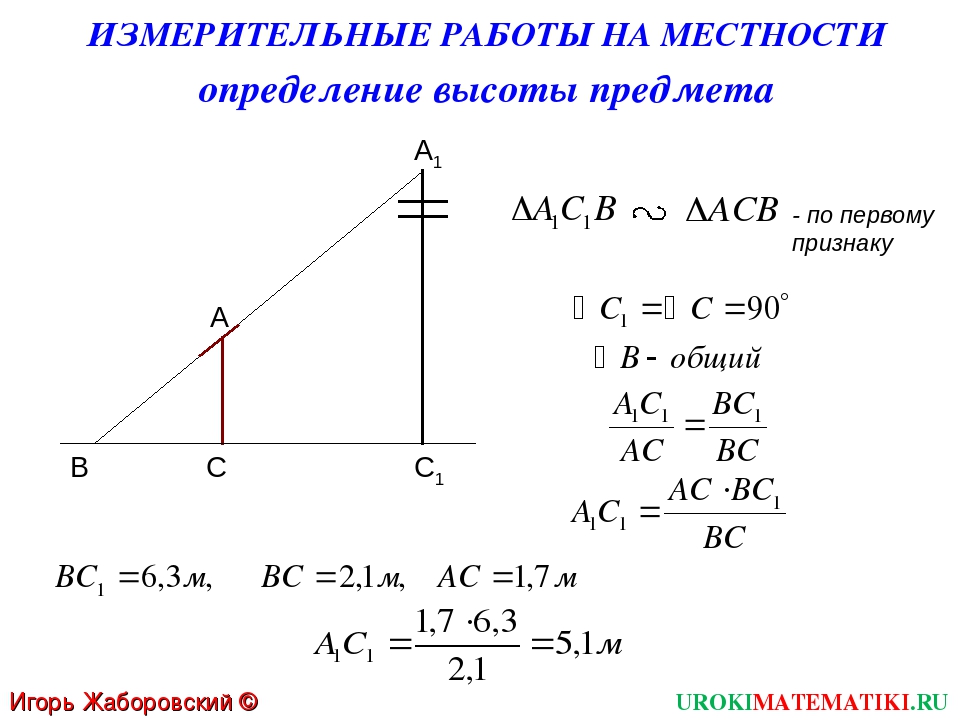
Материалы
Большой пластиковый транспортир или (бумажный принт транспортира, наклеенного на картон), соломка, нить 30 см, шайба или другой груз.
- Используйте пластиковый транспортир или бумажно-картонный транспортир и скотчем соломинку к прямому краю транспортира.
- Используйте отверстие в транспортире или аккуратно проделайте отверстие в центре транспортира где встречается с соломинкой.
- Нажать на веревку через отверстие и завяжите узел с другой стороны так что он не выживет.
- Привяжите свой вес к другой конец строки.
Чтобы использовать клинометр, вы
потребуются два человека: один будет смотреть сквозь соломинку и устанавливать верхнюю часть
объект и один для считывания градусов, которые строка делает с транспортиром.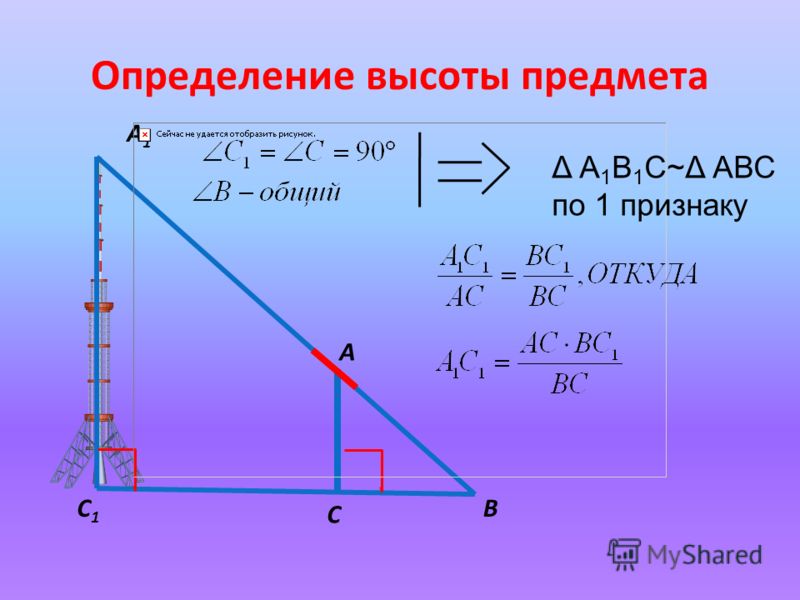
- Измерение расстояние на земле 50 м (для высоких деревьев) или 25 м (для небольших деревья) от ствола дерева, которое вы хотите измерить.
- в В 50 или 25 м от дерева встаньте лицом к нему вместе с партнером. Один из вас видит верхушку дерева через клинометр, пока другой читает градусы.
- Выбрать лист миллиметровой бумаги и нарисуйте базовую линию в масштабе для На расстоянии 25 или 50 метров вы стояли от дерева.
- Вкл. один конец масштабированной линии длиной 25 или 50 м нарисуйте другую линию перпендикулярно (90 градусов) к нему. Эта линия представляет высоту дерева.
- Вкл.
другой конец масштабной линии длиной 25 или 50 м нарисуйте линию,
составляет (90 градусов минус угол, измеренный клинометром). Ты
возможно потребуется изучить приведенные ниже диаграммы и убедить
сами какой угол вы измерили и как нарисовать чертеж в масштабе
найти высоту дерева.

- г. линию, проведенную под этим углом, можно продолжить, пока она не пересечется (пересекает) линию, представляющую дерево.
- Это отрезок линии представляет высоту дерева за вычетом высота глаз зрителя.
- Использование какая бы шкала ни использовалась для масштабирования 25 или 50 м для определения фактическая высота дерева.
Дополнительная информация:
Палочка Билтмора — Инструмент измерения дерева
The B iltmore Stick — это
умный инструмент для измерения диаметра ствола, высоты стоящих деревьев,
и бревна для оценки пиломатериалов. Он был разработан примерно в середине 18-го века.
века на основе пропорциональности и подобных треугольников.Похоже на
метровая палочка или мерка. Однако расстояние между метками приращения,
для измерения диаметра или высоты уменьшайте по мере увеличения диаметра или высоты.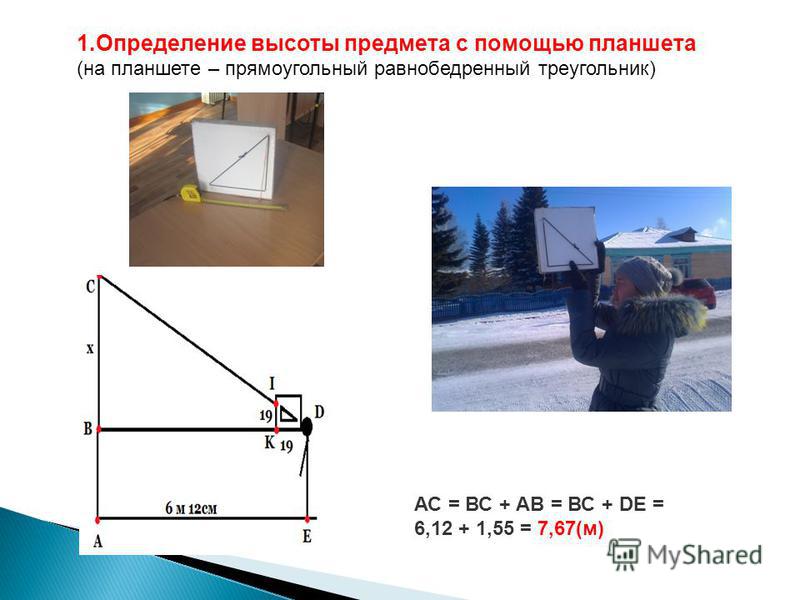 Он используется для оценок, в то время как другие методы могут использоваться для более точного
измерения. Тем не менее, палка Билтмора по-прежнему является важной частью
набор инструментов лесовладельца, который можно приобрести в любом лесном хозяйстве.
Вы даже можете сделать свой собственный.
Он используется для оценок, в то время как другие методы могут использоваться для более точного
измерения. Тем не менее, палка Билтмора по-прежнему является важной частью
набор инструментов лесовладельца, который можно приобрести в любом лесном хозяйстве.
Вы даже можете сделать свой собственный.
Также используется для измерения объем доской ножки дерева с двумя измерениями: 1.Торговый высота в 16-футовых бревнах и 2. Диаметр на высоте 4,5 фута от земли. Фактическая таблица объемов напечатана на флешке.
Для измерения диаметра — удерживать
палка на высоте четырех с половиной (4,5) футов от земли, перпендикулярно
к стволу дерева, напротив дерева, и около 25 дюймов
из глаз. Совместите нулевую отметку с одной стороны ствола. Без
двигая головой, расположите другую сторону туловища и посмотрите, что
инкремент на палке самый близкий.Количество пробелов на
палка, что размах ствола — это размер ствола.
Как это работает — Составьте диаграмму. Нарисуйте линию, изображающую палку. Нарисуйте круг, чтобы представить дерево. Нарисуйте еще одну линию, чтобы обозначить первую линию обзора. Он должен быть перпендикулярен линии стик на нулевой отметке. и касательная к одной стороне древесного круга. Нарисуйте еще одну линию представляют собой линию обзора до правого края дерева. Должно быть на расстоянии 25 дюймов от линии палки и пересекать касательную линию.Он должен выходить так, чтобы касаться другой стороны круг дерева. Место, где линия пересекает линию стикера, представляет собой диаметр дерева. Поскольку радиус не находится на прямой линии, необходимо произвести корректировку. В противном случае чтение было бы много слишком высоко (точка на диаметре дерева, где линии пересекаются вне багажника).
Если мы выберем дерево с
диаметр 20 дюймов, мы знаем, что радиус равен десяти. Мы также знаем расстояние
от глаза до палки 25 дюймов, стандартное расстояние.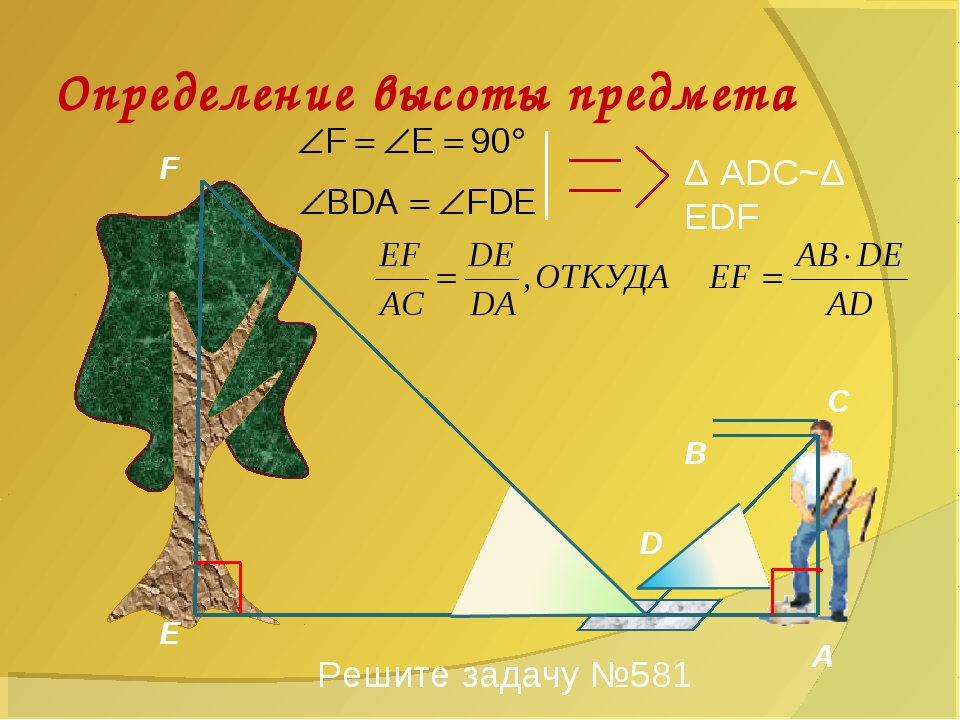 Расстояние
от глаза до центра дерева — радиус плюс 25 дюймов. С помощью
эту информацию угол можно найти. Поскольку два треугольника — это
То же самое, мы знаем, что тангенс двойного угла — это величина палки.
делится на расстояние от глаза до палки (tan 2a = d / 25). Сейчас же
мы просто подставляем значение двойного угла в формулу и решаем
d = 25 * tan (2 * (arctan [R / (R + 25)]). Вы можете понять, как использовать
электронное устройство для решения уравнения.Если у тебя другая рука
размер больше 25 дюймов, вы можете изменить это значение, чтобы оно соответствовало вашей руке
длина так будет удобнее.
Расстояние
от глаза до центра дерева — радиус плюс 25 дюймов. С помощью
эту информацию угол можно найти. Поскольку два треугольника — это
То же самое, мы знаем, что тангенс двойного угла — это величина палки.
делится на расстояние от глаза до палки (tan 2a = d / 25). Сейчас же
мы просто подставляем значение двойного угла в формулу и решаем
d = 25 * tan (2 * (arctan [R / (R + 25)]). Вы можете понять, как использовать
электронное устройство для решения уравнения.Если у тебя другая рука
размер больше 25 дюймов, вы можете изменить это значение, чтобы оно соответствовало вашей руке
длина так будет удобнее.
Таблица ниже содержит размеры ручки в дюймах для 25-дюймового досягаемости.
Измерьте и отметьте дерево
диаметры на вашей палке, которые соответствуют вашим значениям по длине
палка. Когда вы закончите, покройте всю палку прозрачным финишом.
например, прозрачная аэрозольная краска или полиуретановый лак для долговечности.
| Дерево | Рукоять | Дерево | Рукоять | |
|---|---|---|---|---|
| 10 | 8,6 | 30 | 21,8 | |
| 11 | 9,3 | 31 | 22,4 | |
| 12 | 10,1 | 32 | 23 | |
| 13 | 10.8 | 33 | 23,6 | |
| 14 | 11,5 | 34 | 24,2 | |
| 15 | 12,2 | 35 | 24,8 | |
| 16 | 12,9 | 36 | 25,4 | |
| 17 | 13.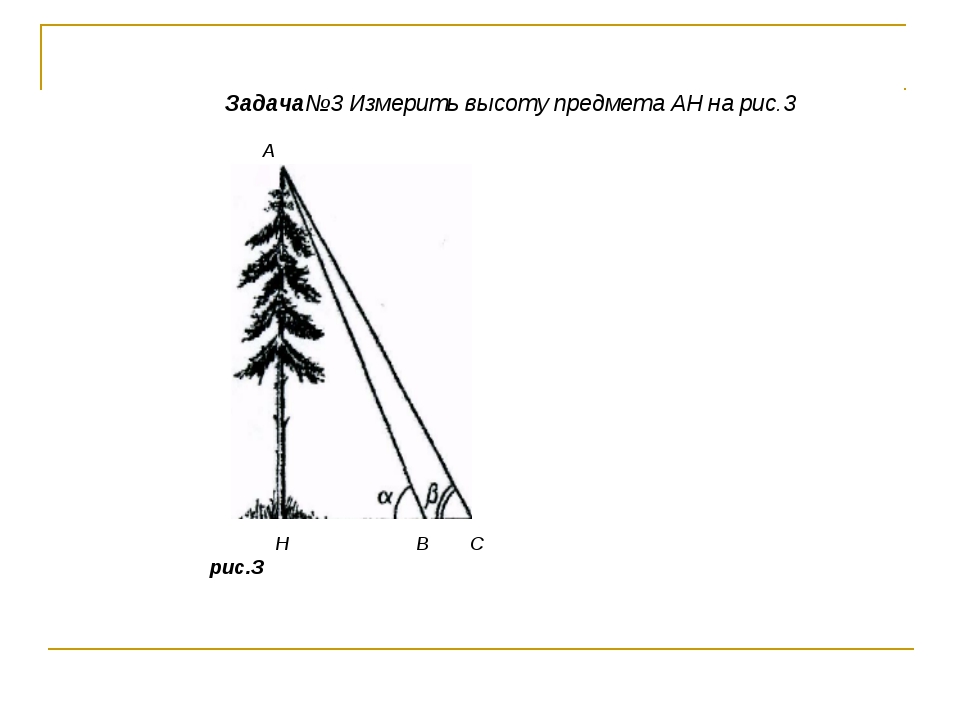 6 6 | 37 | 26 | |
| 18 | 14,2 | 38 | 26,5 | |
| 19 | 14,9 | 39 | 27,1 | |
| 20 | 15,6 | 40 | 27,7 | |
| 21 | 16.2 | 41 | 28,3 | |
| 22 | 16,9 | 42 | 28,8 | |
| 23 | 17,5 | 43 | 29,4 | |
| 24 | 18,1 | 44 | 30 | |
| 25 | 18.8 | 45 | 30,5 | |
| 26 | 19,4 | 46 | 31,1 | |
| 27 | 20 | 47 | 31,7 | |
| 28 | 20,6 | 48 | 32,2 | |
| 29 | 21. 2 2 |
Измерения высоты
Вы можете легко добавить измерения высоты к своей палке, что упрощает оценку высоты дерева. Формула для этого очень проста. Используйте тот же «охват» или расстояние от глаза до палки. Вам также необходимо знать расстояние от тебя стоишь с дерева. Рекомендуется расстояние 100 футов. в качестве основы. Некоторые палки имеют весы на 100 и 66 футов (одна цепь).
Для определения высоты дерева (или другого объекта) держите палку вертикально в обычном достигать. Совместите нулевую точку с нижней частью дерева. Прочтите высоту в точке, где верхушка дерева пересекает палку.
Чтобы рассчитать размер ручки (S) на базовом расстоянии 100 футов:
S = 25 * (H / 100)
Для базы 66 футов:
S = 25 * (H / 66)
Если у вас есть досягаемость,
больше или меньше 25 дюймов, вы можете изменить формулу соответственно. Теперь измерьте свою палку и отметьте ее. Обязательно пометьте весы как 100-футовые.
основание или основание 66 футов.
Теперь измерьте свою палку и отметьте ее. Обязательно пометьте весы как 100-футовые.
основание или основание 66 футов.
В качестве последней функции на вашем палка, разметить стандартные дюймы. Это может быть здорово. Вам не нужно положить все чешуйки на одну сторону — есть несколько сторон и ровные края использовать. Просверлите отверстие на одном конце и прикрепите кожаные или нейлоновые ремешки, как ремешок на запястье. И закончить прозрачным покрытием.
Для измерения дерева товарного высота Товарная высота относится к длине годного к употреблению дерева и измеряется от высоты пня до точки отсечки вверху.Точка отсечения будет варьируются в зависимости от местности, продукта и количества конечностей.
Стенд 66 футов (приблизительно
12 шагов) от дерева, которое вы хотите измерить. Держите палку в
вертикальное вертикальное положение в 25 дюймах от глаза с числом «16 футов»
бревна «сторона палки, обращенная к вам. Обычно это край
палки.
Обычно это край
палки.
Количество журналов может быть считывайте прямо с ручки, начиная с расчетной высоты пня вверх.На самом деле вы не измеряете общий рост, а оцениваете его в 16 футов. разделы журнала. С этой товарной высотой, оцененной в бревнах, плюс диаметр, можно оценить объем дерева.
Для измерения объема дерева: удерживайте палка против дерева на высоте груди (DBH) 4,5 фута и 25 дюймов от вашего глаза. Переместите джойстик вправо или влево от елка до нулевого или левого конца объемной стороны палки совпадает с левым краем дерева.Прицеливание с правой стороны от палки, где она касается внешней коры (двигая только глазами) показывает диаметр в верхней строке, а ниже — число опор доски для деревьев разного количества бревен.
Для измерения объема бревен: Позиция
шкалу «диаметра бревна» на малом конце бревна, поместив
палка в месте среднего диаметра (или
несколько значений и среднее значение). Объемы бревен разного диаметра и
длины от 8 до 16 футов можно прочитать на плоской стороне палки с надписью «бревно»
шкала».
Объемы бревен разного диаметра и
длины от 8 до 16 футов можно прочитать на плоской стороне палки с надписью «бревно»
шкала».
Бревна длиной более 16 футов масштабируется как два бревна с учетом конусности бревен длиной 22 фута и более. А 20-футовое бревно, например, 15 дюймов в диаметре, будет масштабировано. в виде двух 10-футовых бревен диаметром 15 дюймов каждое
Шесть способов измерения роста
| Метод или концепция | Требуемая информация | Процедура |
|---|---|---|
| Прямое измерение | Стандартная линейка известного размера Прямой контакт с известным и неизвестным объектом | Поместите объект с известным размером рядом с объектом с неизвестным размером |
| Доля | Объект известной высоты на том же месте, что и объект неизвестной высоты Масштабная высота известного и неизвестного объекта | Поместите объект, высота которого известна, рядом с объектом, высота которого неизвестна. На одинаковом расстоянии от обоих используйте линейку или сетку и измерьте масштабированную высоту как известного, так и неизвестного объекта Изобразите обе в масштабе и используйте известную высоту для вычисления неизвестного |
| Доля | Объект известной высоты и известной длины тени на его высоте Объект неизвестной высоты и известной длины тени на его высоте | Поместите объект, высота которого известна, рядом с объектом, высота которого неизвестна. Измерьте известную высоту и неизвестную высоту. Изобразите как в масштабе, так и используя известную высоту, чтобы изобразить неизвестное |
| Два угловых измерения и расстояние | Расстояние от объекта Угловая мера на расстоянии от низа объекта до верха объекта. | Встаньте на известном расстоянии (50 метров) на уровне низа неизвестной высоты объекта. Измерьте угол от низа до верха объекта Проведите линию для обозначения высоты объекта Проведите снизу линию, представляющую высоту объекта, так, чтобы она была перпендикулярной и равной расстоянию от объекта, на котором был измерен угол. Проведите линию под измеренным углом, пока она не пересечет линию, представляющую неизвестную высоту. Измерьте высоту в масштабе чертежа |
| Два угловых измерения и расстояние | Расстояние от объекта Угловая мера на расстоянии от низа объекта до верха объекта. | Встаньте внизу неизвестной высоты предмета. Измерьте угол от низа до верха объекта Отойдите от объекта неизвестной высоты до угла 45 градусов. Измерьте расстояние от точки под углом 45 градусов до нижней части объекта. |
| Использовать таблицу тригонометрии |
Доктор. Заметки Роберта Свитленда
Заметки Роберта Свитленда
[Домашняя страница: homeofbob.com & thehob.net. ]
% PDF-1.4
%
314 0 объект
>
эндобдж
xref
314 102
0000000016 00000 н.
0000003083 00000 н.
0000003242 00000 н.
0000003989 00000 н.
0000004169 00000 п.
0000004347 00000 н.
0000004527 00000 н.
0000004706 00000 н.
0000004820 00000 н.
0000004932 00000 н.
0000004959 00000 н.
0000005270 00000 н.
0000005595 00000 н.
0000005975 00000 н.
0000006396 00000 н.
0000006912 00000 н.
0000007397 00000 н.
0000007977 00000 н.
0000008565 00000 н.
0000009202 00000 н.
0000009549 00000 н.
0000009952 00000 н.
0000010083 00000 п.
0000010473 00000 п.
0000010978 00000 п.
0000011631 00000 п.
0000012227 00000 п.
0000012690 00000 п.
0000012907 00000 п.
0000017115 00000 п.
0000017260 00000 п.
0000017647 00000 п.
0000017838 00000 п.
0000018137 00000 п.
0000018462 00000 п.
0000018644 00000 п.
0000025165 00000 п.
0000025615 00000 п.
0000025884 00000 п.
0000026030 00000 н.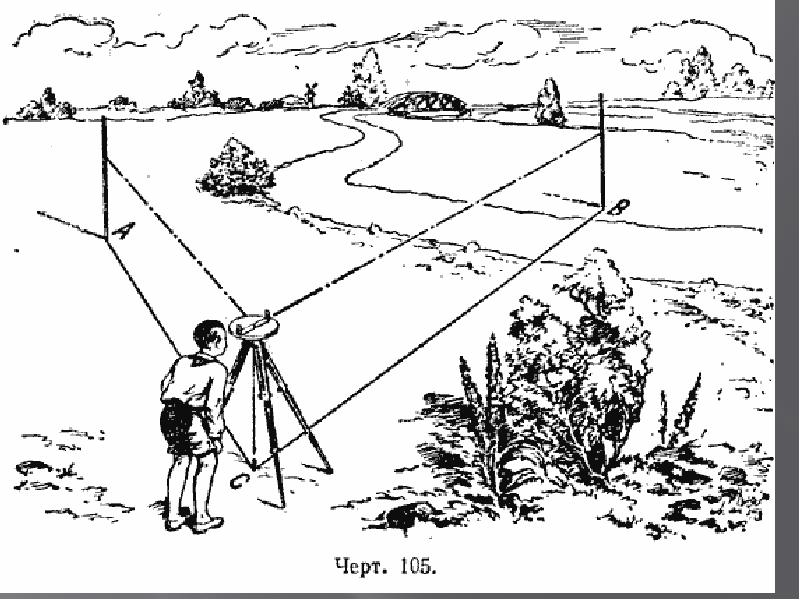 0000026233 00000 п.
0000026423 00000 п.
0000031663 00000 п.
0000037273 00000 п.
0000042717 00000 п.
0000048291 00000 п.
0000054240 00000 п.
0000060097 00000 п.
0000065258 00000 п.
0000073369 00000 п.
0000074952 00000 п.
0000075122 00000 п.
0000083497 00000 п.
0000083758 00000 п.
0000086875 00000 п.
0000089033 00000 п.
0000089119 00000 п.
0000089189 00000 п.
0000089308 00000 п.
0000089378 00000 п.
0000089476 00000 п.
0000098186 00000 п.
0000098485 00000 п.
0000098804 00000 п.
0000098831 00000 п.
0000099251 00000 п.
0000101120 00000 н.
0000101461 00000 п.
0000102001 00000 н.
0000102261 00000 н.
0000102348 00000 п.
0000102783 00000 н.
0000103028 00000 н.
0000104092 00000 н.
0000104395 00000 н.
0000104931 00000 н.
0000105199 00000 п.
0000106134 00000 п.
0000106417 00000 н.
0000107399 00000 н.
0000107693 00000 п.
0000108049 00000 н.
0000108137 00000 н.
0000108520 00000 н.
0000108779 00000 н.
0000109086 00000 н.
0000109443 00000 п.
0000109712 00000 н.
0000026233 00000 п.
0000026423 00000 п.
0000031663 00000 п.
0000037273 00000 п.
0000042717 00000 п.
0000048291 00000 п.
0000054240 00000 п.
0000060097 00000 п.
0000065258 00000 п.
0000073369 00000 п.
0000074952 00000 п.
0000075122 00000 п.
0000083497 00000 п.
0000083758 00000 п.
0000086875 00000 п.
0000089033 00000 п.
0000089119 00000 п.
0000089189 00000 п.
0000089308 00000 п.
0000089378 00000 п.
0000089476 00000 п.
0000098186 00000 п.
0000098485 00000 п.
0000098804 00000 п.
0000098831 00000 п.
0000099251 00000 п.
0000101120 00000 н.
0000101461 00000 п.
0000102001 00000 н.
0000102261 00000 н.
0000102348 00000 п.
0000102783 00000 н.
0000103028 00000 н.
0000104092 00000 н.
0000104395 00000 н.
0000104931 00000 н.
0000105199 00000 п.
0000106134 00000 п.
0000106417 00000 н.
0000107399 00000 н.
0000107693 00000 п.
0000108049 00000 н.
0000108137 00000 н.
0000108520 00000 н.
0000108779 00000 н.
0000109086 00000 н.
0000109443 00000 п.
0000109712 00000 н. 0000110008 00000 н.
0000111239 00000 н.
0000111539 00000 н.
0000111901 00000 н.
0000116253 00000 н.
0000116536 00000 н.
0000119120 00000 н.
0000119159 00000 н.
0000121635 00000 н.
0000121700 00000 н.
0000150356 00000 н.
0000150395 00000 н.
0000002902 00000 н.
0000002336 00000 н.
трейлер
] / Назад 278093 / XRefStm 2902 >>
startxref
0
%% EOF
415 0 объект
> поток
hb«c` * a`g` Ā
0000110008 00000 н.
0000111239 00000 н.
0000111539 00000 н.
0000111901 00000 н.
0000116253 00000 н.
0000116536 00000 н.
0000119120 00000 н.
0000119159 00000 н.
0000121635 00000 н.
0000121700 00000 н.
0000150356 00000 н.
0000150395 00000 н.
0000002902 00000 н.
0000002336 00000 н.
трейлер
] / Назад 278093 / XRefStm 2902 >>
startxref
0
%% EOF
415 0 объект
> поток
hb«c` * a`g` Ā
Фотограмметрия
Фотограмметрия — это наука об измерениях по фотографиям.Сюда входит расчет расстояний и длин, высоты объектов и измерений площади. Фотограмметрия существует с момента развития современной техники фотографии. Если масштаб изображения известен, расстояния или длины объектов можно легко вычислить, измерив расстояние на фотографии и умножив его на масштабный коэффициент.
Масштаб
Помните, что масштаб — это отношение размера или расстояния объекта на фотографии к его фактическому размеру. Масштаб для аэрофотоснимков обычно выражается в виде репрезентативной дроби (1 единица на фотографии равна «x» единицам на земле). Если масштаб известен, расстояния на фотографии можно легко преобразовать в реальные расстояния от земли.
Масштаб для аэрофотоснимков обычно выражается в виде репрезентативной дроби (1 единица на фотографии равна «x» единицам на земле). Если масштаб известен, расстояния на фотографии можно легко преобразовать в реальные расстояния от земли.
Расчет расстояния и площади
Расстояние и длина
Если масштаб аэрофотоснимка известен, можно легко вычислить расстояния, длины и площади объектов. Вы просто измеряете расстояние на фотографии (расстояние на фотографии) и умножаете расстояние на коэффициент масштабирования.Помните, что масштаб всегда равен отношению расстояния фотографии к расстоянию до земли.
Пример: Масштаб аэрофотоснимка — 1:15 000. На фотографии вы измеряете длину моста 0,25 дюйма, какова длина моста в футах в реальной жизни?
Площадь
Важно помнить, что площадь измеряется в квадратных единицах. Чтобы определить прямоугольную область, длина умножается на ширину, поэтому, если вы измеряете и то, и другое и конвертируете эти расстояния, помните, что если вы умножаете их вместе, полученные единицы возводятся в квадрат. Например, если площадь составляет 100 метров на 500 метров, это будет 50 000 квадратных метров. Теперь, если вы хотите изменить это число на квадратные футы, вы бы не умножали на 3,28 (3,28 фута на метр), а умножали на 10,76 (3,28 x 3,28).
Например, если площадь составляет 100 метров на 500 метров, это будет 50 000 квадратных метров. Теперь, если вы хотите изменить это число на квадратные футы, вы бы не умножали на 3,28 (3,28 фута на метр), а умножали на 10,76 (3,28 x 3,28).
Пример: Аэрофотоснимок имеет масштаб 1: 10 000. На фото длина поля составляет 10 мм, а ширина 7 мм. Насколько велико (в гектарах) поле в реальной жизни? Учтите, что 10 000 квадратных метров = 1 Га.
Расчет высоты объекта
Как и при вычислении масштаба, существует несколько методов определения высоты высоких объектов (например, деревьев или зданий) на аэрофотоснимках. В одиночных аэрофотоснимках используются два основных метода: метод рельефа / радиального смещения и теневые методы.
Метод разгрузки / радиального смещения
Величина смещения изображения между верхом и низом объекта называется его рельефным смещением и связана с высотой объекта и расстоянием от объекта до главной точки. Этот метод можно использовать только в том случае, если измеряемый объект находится достаточно далеко от основной точки для измерения смещения, а верх и низ объекта видны на фотографии.
Этот метод можно использовать только в том случае, если измеряемый объект находится достаточно далеко от основной точки для измерения смещения, а верх и низ объекта видны на фотографии.
Пример: длина перемещенного здания составляет 2,01 мм, а радиальное расстояние до главной точки составляет 56,43 мм. Если высота полета над поверхностью составляет 1220 м, какова высота здания?
Если вы можете измерить длину тени и узнать угол наклона солнца, высоту объекта можно рассчитать с помощью простой тригонометрии.Если вы знаете, когда и где был сделан аэрофотоснимок, вы можете определить угол наклона солнца с помощью солнечного калькулятора NOAA. При использовании этого калькулятора вы хотите использовать для расчетов угол возвышения Солнца (El).
Измерение высоты Задание
Измерение высоты ЗаданиеНазначение:
Для измерения высоты высокого объекта (дерева, фонарного столба, флага
полюс), используя Закон Отражения.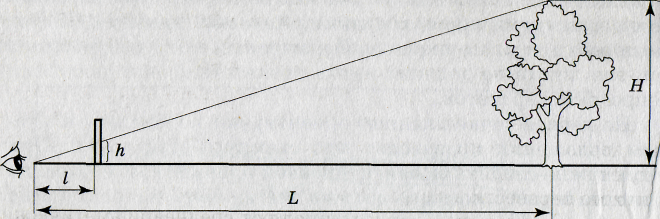
Обсуждение:
Очень легко использовать Закон Отражения и некоторые простые геометрия для измерения высоты объекта, который был бы очень трудно измерить напрямую. Пожалуйста, изучите диаграмму ниже.
На этой диаграмме ab человек наблюдает изображение вершины флагштока, используя поверхность чаши с водой в качестве отражающей поверхность. Закон Отражения гарантирует, что два треугольника сформированы похожи (вы понимаете, почему?)
На схеме ниже «h» — это высота глаз человека над головой. поверхности воды, а «d» — горизонтальное расстояние от человека в центр чаши.»H» обозначает высоту флагштока, а «D» — горизонтальное расстояние от флагштока до миска с водой. Три расстояния h, d и D легко измерить.
Оборудование:
миска | метровая палка | вода |
маленькое зеркало | бумага темного цвета |
Процедура:
- Выберите высокий предмет (возможно, у вашего учителя есть предложение),
флагшток или столб, например.

- Налейте немного воды в небольшую миску и поставьте миску на землю в нескольких метрах от высокого объекта.
- Двигайтесь вокруг, пока не увидите изображение вершины столба. отражается в поверхности воды. Если у вас проблемы с просмотром отраженное изображение, можно положить немного темной бумаги в дно чаши. (Если ветерок дует, поверхность воды слишком много, чтобы сформировать четкое изображение, вы можете аккуратно пропустить небольшой зеркало на поверхности воды и используйте зеркало для своего отражающая поверхность.)
- Измерьте расстояние от чаши до ступней (d), расстояние от чаши до основания фонарного столба (D), и запишите их в свою таблицу данных (показан образец таблицы данных ниже).
- Измерьте расстояние по вертикали от чаши до глаза (h).
- Переместите чашу на другое расстояние от шеста и повторите
ваши измерения, пока вы не убедитесь, что у вас достаточно
данные.

Результатов:
- Используйте аналогичные треугольники (как показано выше) для расчета высоты. вашего высокого объекта для каждого испытания. Покажите пример расчета и запишите свои результаты в таблицу данных.
- Рассчитайте среднюю высоту ваших измерений.
Выводы:
Насколько точно совпадают ваши измерения роста? Как вы думаете это точный способ измерения высоты? Почему? Какие факторы больше всего повлияют на точность этого метода?
В чем преимущество использования воды в качестве отражающей поверхности для это занятие, вместо того, чтобы просто положить зеркало на землю?
Ссылка:
IHETS AP Physics Lab # 2 — сентябрь 1992 г.
../../../Help.html
последнее обновление 14 августа 1997 г., автор: JL Stanbrough
Тени и углы: измерение высоты объектов по спутниковым изображениям
Распространенной особенностью пространственного анализа является то, что данные часто представляются в двухмерном формате. Вид карты — это здорово, и мы все знаем, какую ценность могут иметь такие пространственные продукты, но иногда можно использовать творческий подход для извлечения ценных трехмерных данных из двухмерного представления.Один из таких примеров этой способности находится на спутниковых и аэрофотоснимках в форме объекта, который обычно считается закрывающим и нежелательным: тени.
Вид карты — это здорово, и мы все знаем, какую ценность могут иметь такие пространственные продукты, но иногда можно использовать творческий подход для извлечения ценных трехмерных данных из двухмерного представления.Один из таких примеров этой способности находится на спутниковых и аэрофотоснимках в форме объекта, который обычно считается закрывающим и нежелательным: тени.
Благодаря прекрасным метаданным, которые поставляются со спутниковыми изображениями, тени можно использовать для оценки высоты отбрасывающих их объектов. На каждом спутниковом изображении записана информация о дате сбора, угле отклонения от надира (в градусах от ортогонального к поверхности к датчику) космического корабля во время съемки, азимуте солнца, углу наклона солнце от горизонта и данные о местоположении с привязкой к местности.Обладая этой информацией, а также способностью измерять расстояния в вашей любимой программе ГИС и базовым пониманием тригонометрии, тени становятся возможностью получить достаточно количественное представление о высоте объектов на земле. А теперь давайте рассмотрим простой пример.
А теперь давайте рассмотрим простой пример.
Выше представлено изображение Бурдж-Халифа в Дубае с помощью WorldView-2, которое, как вы можете узнать, имеет нынешний титул самого высокого здания в мире.Этот снимок был сделан под углом 0,8758449 ° от надира или, по сути, прямо над зданием. Сама тень простирается по относительно ровной поверхности, в основном не закрыта большими зданиями или холмами, и есть хороший вид на ее конечную точку. По всем этим причинам это изображение является отличным местом для применения метода оценки, основанного на автоматизированном методе, который был разработан и более подробно описан Шеттигарой и Сумерлингом (см .: Определение высоты протяженных объектов с использованием теней на изображениях SPOT ).Ниже представлена упрощенная схема этой техники, которая соответствует объему и потребностям данной статьи.
Рисунок 2 — Упрощенная диаграмма, изображающая ключевые переменные, участвующие в оценке высоты объекта.
Хотя в статье Шеттигара и Сумерлинга описывается метод, который можно использовать с автоматическими макросами обнаружения и измерения теней для количественной оценки высоты нескольких объектов с разумной точностью, он также включает в себя схему базовой тригонометрии, доступной для выполнения оценок первого порядка. высота.Первая часть решения включает в себя вычисление высоты здания по углу солнечного света и длине тени:
tan (Высота Солнца) = (Высота объекта) / (Длина тени)
Метаданные изображения, используемого здесь, сообщают о Высота Солнца составляет 46,733 °, а измеренная длина тени составляет 746,421 метра, поэтому я рассчитал, что высота объекта составляет 792,997 метра.
Поскольку этот метод предназначен для количественной оценки высот объектов на изображениях на заднем плане, в него включен ряд упрощений, чтобы сделать его быстрым и простым в использовании.Одним из таких упрощений является использование высоты объекта, полученной в Расчете 1, для замены фактической высоты Бурдж-Халифы для определения длины тени, которая скрывается от поля зрения датчика за самим зданием. Это может быть или не быть необходимым шагом, в зависимости от того, насколько вы уверены, что можете измерить фактическую длину тени, но в этом случае датчик находится на той же стороне здания, что и солнце, поэтому давайте посмотрим на процесс. .
Это может быть или не быть необходимым шагом, в зависимости от того, насколько вы уверены, что можете измерить фактическую длину тени, но в этом случае датчик находится на той же стороне здания, что и солнце, поэтому давайте посмотрим на процесс. .
Чтобы найти заблокированную длину тени, на втором этапе решения используется угол отклонения датчика от надира и оценка высоты объекта, полученная выше.В этом случае качество оценки повышается за счет выдающегося угла отклонения от надира 0,8758449 °, но изображения с углами отклонения датчика от надира, равными, скажем, 30 °, все равно выиграют от этого второго расчета:
тангенса (Off-Nadir Angle) = (Blocked Length of the Shadow) / (Height of the Object)
Результат может быть добавлен к измеренной длине тени, а затем высота объекта может быть пересчитана с измененной ценить. В этом случае я считаю, что значение Blocked Length of the Shadow равно 12.400 метров, что исправляет общую длину тени до 758,841 метра. При повторном подключении к первому уравнению это дает расчетную высоту Бурдж-Халифа 806,192 метра.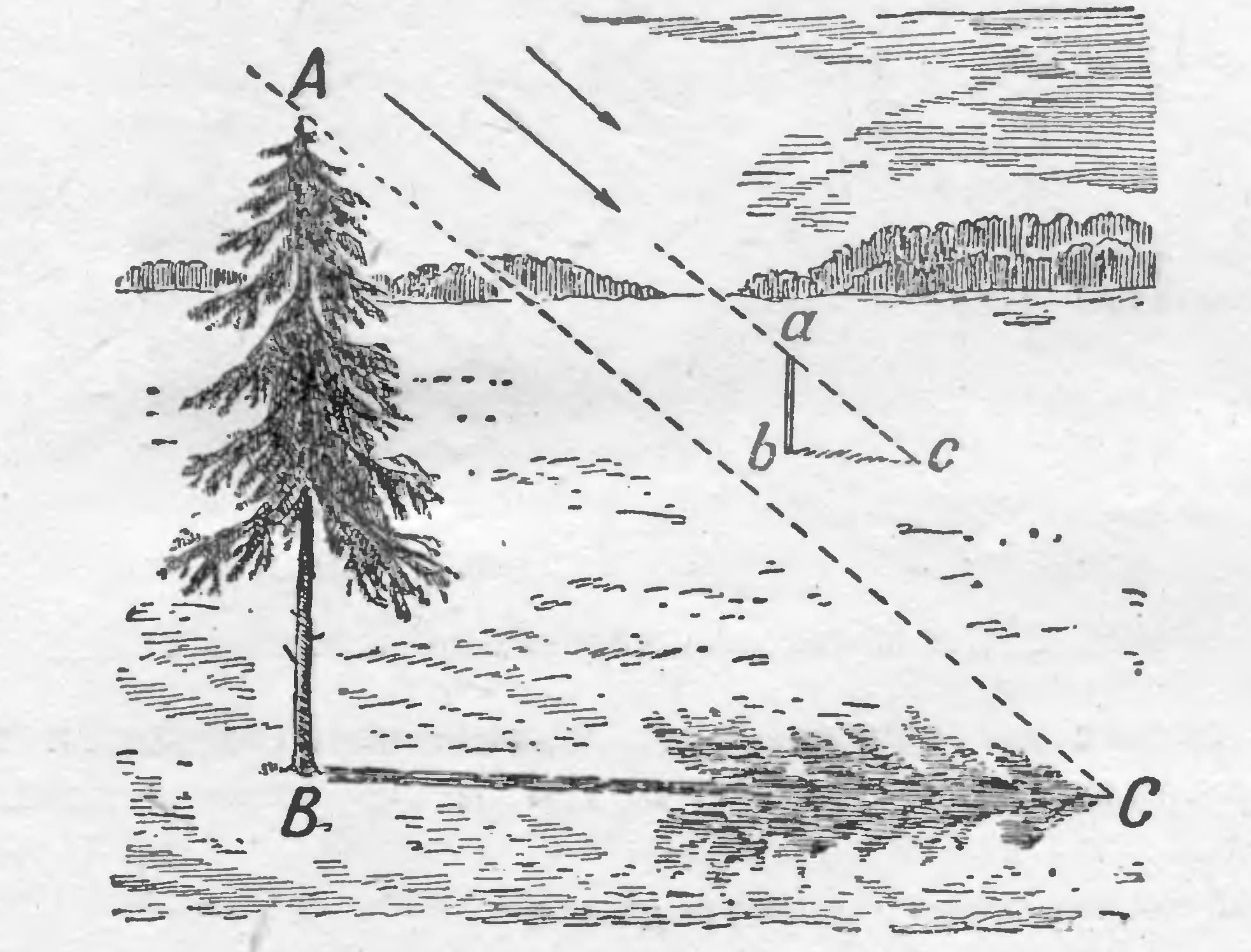 Поскольку Google сообщает, что фактическая высота Бурдж-Халифы составляет 828 метров, это дает относительную ошибку в 2,633%, что я считаю довольно выдающейся. Обратите внимание, что этот метод можно использовать аналогичным образом, если солнце и датчик находятся на противоположных сторонах объекта, и не стесняйтесь писать мне, если вам нужна дополнительная информация по этому поводу.
Поскольку Google сообщает, что фактическая высота Бурдж-Халифы составляет 828 метров, это дает относительную ошибку в 2,633%, что я считаю довольно выдающейся. Обратите внимание, что этот метод можно использовать аналогичным образом, если солнце и датчик находятся на противоположных сторонах объекта, и не стесняйтесь писать мне, если вам нужна дополнительная информация по этому поводу.
Итак, очевидно, что этот метод работает; и он может оказаться полезным в ряде мест, где невозможно легко измерить высоту объектов в полевых условиях, таких как водопад Игуасу или излучающие элементы Шипрок в Нью-Мексико. Представленная здесь техника может быть расширена и объединена с автоматическим обнаружением и измерением теней для определения высоты нескольких объектов в сцене, таких как деревья. Попробуйте и дайте мне знать, как это работает для вас!
О картографировании Apollo
Кэмерон Виндхэм — выпускник Колледжа Помона со степенью в области геологии, в настоящее время работает в картографической службе Apollo, расположенной в Боулдере, штат Колорадо.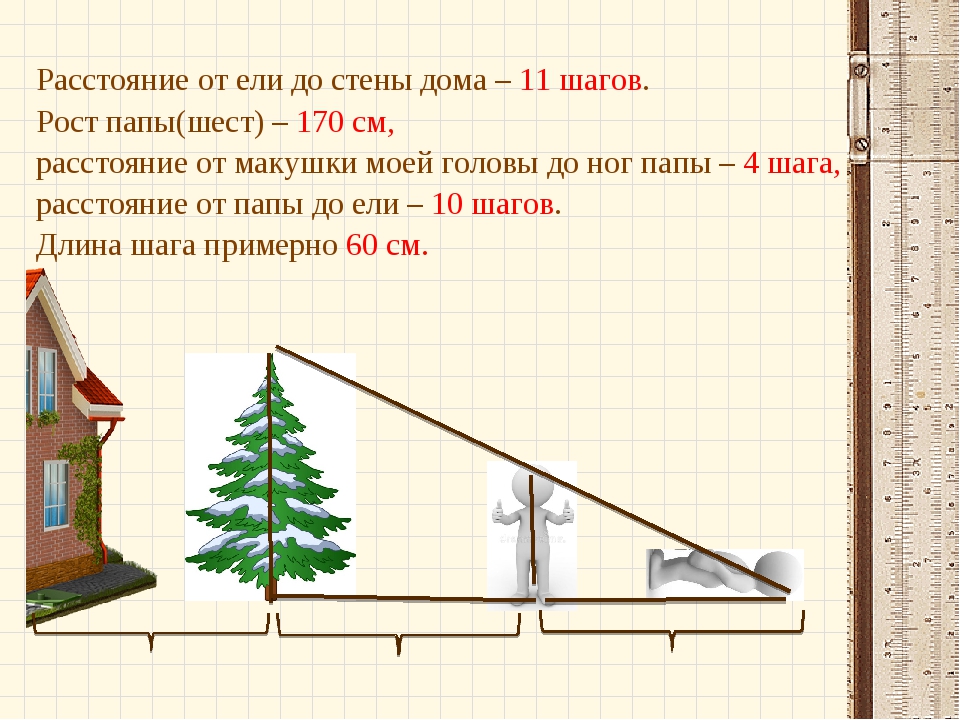

 Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал «стрелял» обходя высотки и не мешали кроны деревьев… ))) А мало ли, что еще…
Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал «стрелял» обходя высотки и не мешали кроны деревьев… ))) А мало ли, что еще…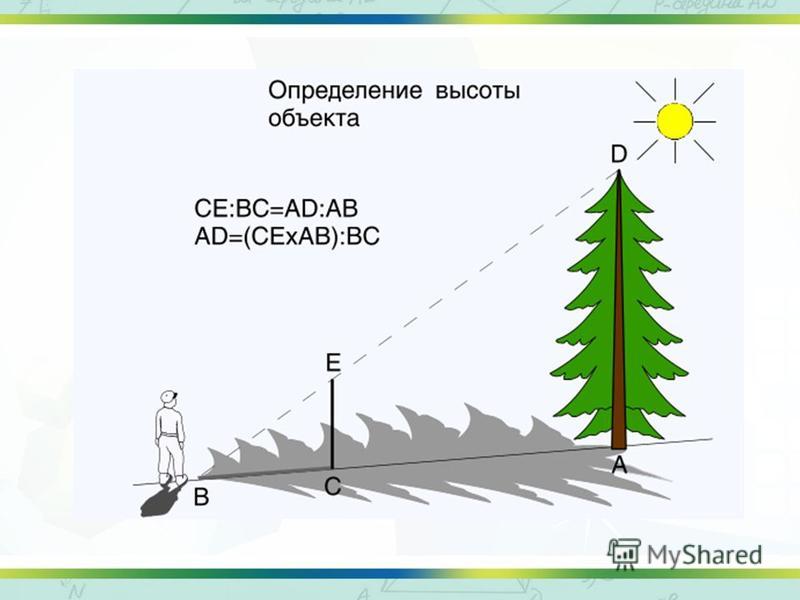
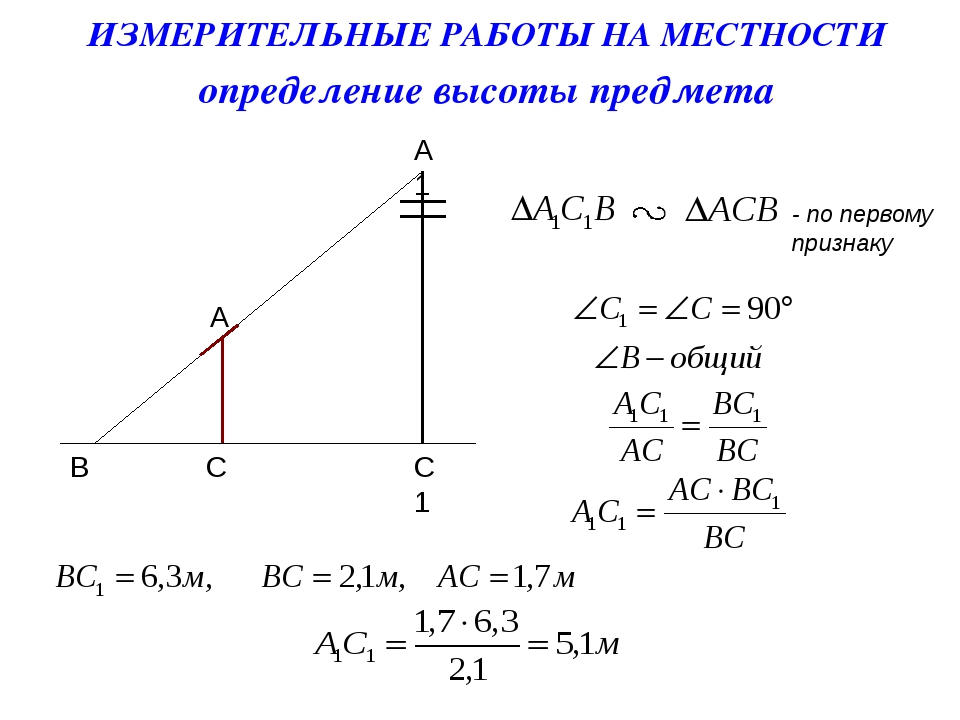
 Тогда высота дерева будет равна линии,
проведенной от вашей головы до основания дерева.
Тогда высота дерева будет равна линии,
проведенной от вашей головы до основания дерева. 501).
501). 502. Первый способ определения
ширины водоемов
502. Первый способ определения
ширины водоемов
 После этого, повернувшись спиной
к берегу, нужно идти от заметки Г до точки Д, пока палка не окажется
на одной линии с предметом за рекой (Л). Расстояние ГД и будет
равно ширине водоема (рис. 503).
После этого, повернувшись спиной
к берегу, нужно идти от заметки Г до точки Д, пока палка не окажется
на одной линии с предметом за рекой (Л). Расстояние ГД и будет
равно ширине водоема (рис. 503).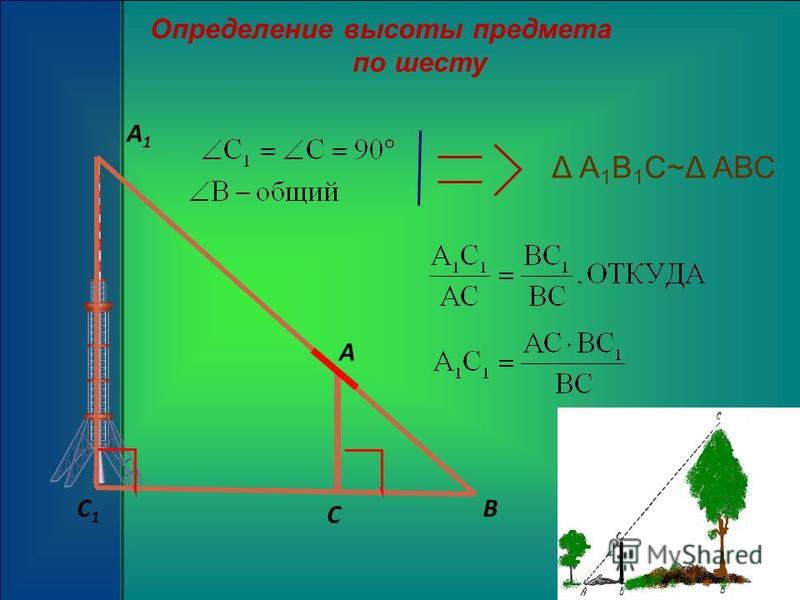 Отсчитав, сколько секунд прошло от виденной
вспышки молнии, выстрела, пароходного или паровозного гудка, удара
молотом и т. д., можно довольно точно определить расстояние до
источника звука.
Отсчитав, сколько секунд прошло от виденной
вспышки молнии, выстрела, пароходного или паровозного гудка, удара
молотом и т. д., можно довольно точно определить расстояние до
источника звука.
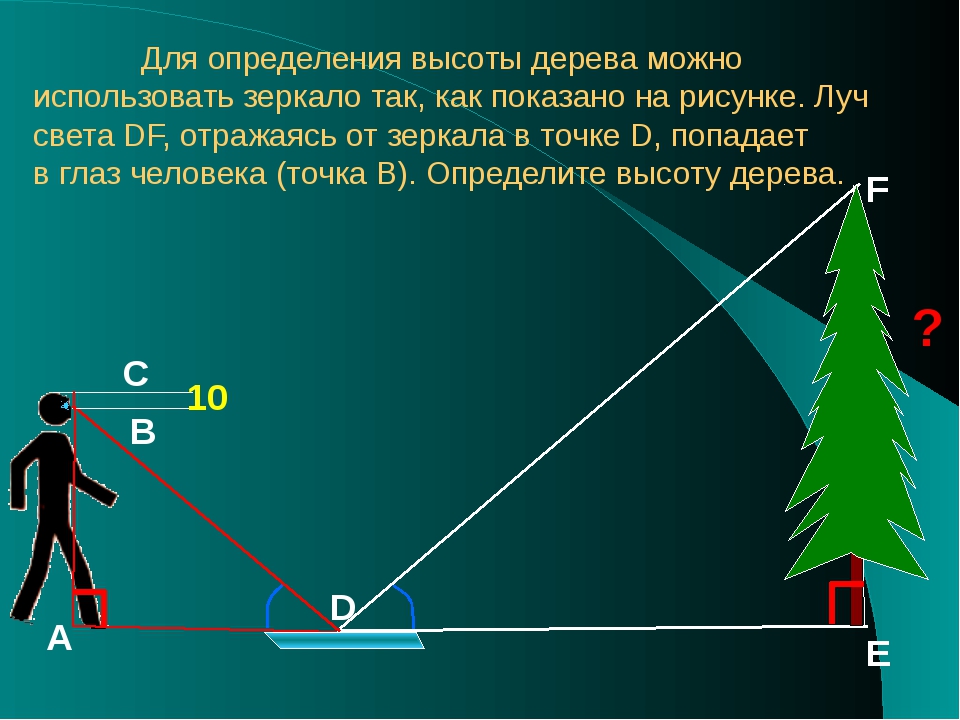 д., пользуясь теми предметами, которые находятся
под руками. Чтобы облегчить эту работу, приводятся соответствующие
образцы мер или готовые мерки. Некоторая часть этих мерок уже
была указана в таблице угломерного измерения расстояний.
д., пользуясь теми предметами, которые находятся
под руками. Чтобы облегчить эту работу, приводятся соответствующие
образцы мер или готовые мерки. Некоторая часть этих мерок уже
была указана в таблице угломерного измерения расстояний. и две монеты по 5 коп. дают 8 см. Одна монета в 1 коп.
и три монеты по 5 коп. дают 9 см. Такую же длину образуют 6 монет
достоинством по 1 коп. Четыре монеты по 5 коп. образуют длину
в 10 см.
и две монеты по 5 коп. дают 8 см. Одна монета в 1 коп.
и три монеты по 5 коп. дают 9 см. Такую же длину образуют 6 монет
достоинством по 1 коп. Четыре монеты по 5 коп. образуют длину
в 10 см.

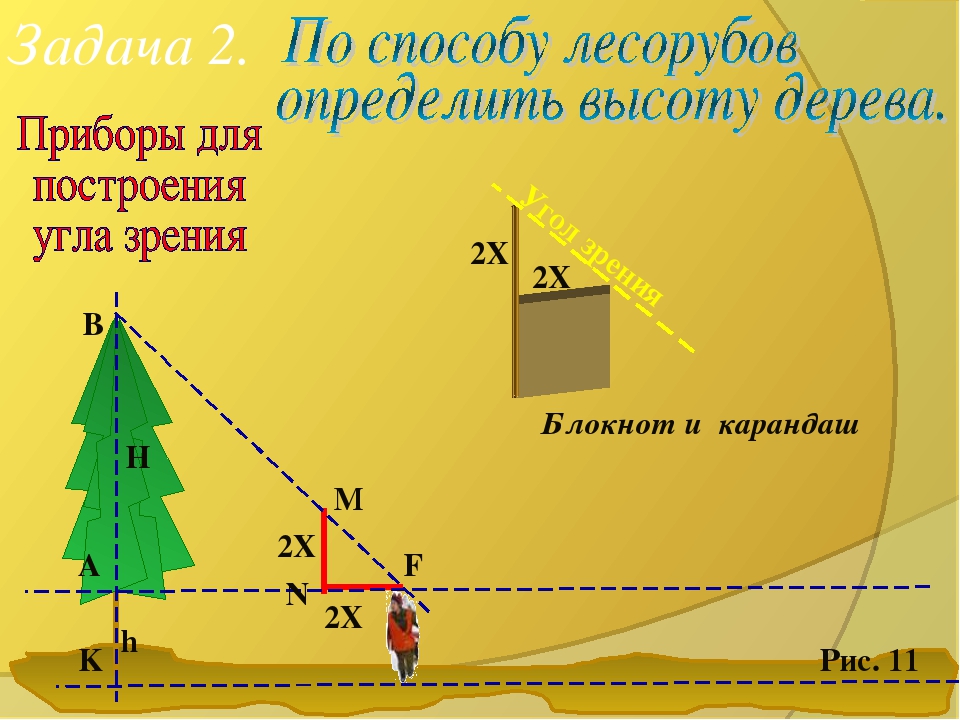 .. В полдень погода изменилась. Ее
можно было бы описать в двух словах: туман и дождь. Мы опять просидели
весь день в палатках… К вечеру поднялся сильный ветер. Царствовавшая
дотоле тишина в природе вдруг нарушилась. Застывший воздух пришел
в движение и одним могучим порывом сбросил с себя апатию.
.. В полдень погода изменилась. Ее
можно было бы описать в двух словах: туман и дождь. Мы опять просидели
весь день в палатках… К вечеру поднялся сильный ветер. Царствовавшая
дотоле тишина в природе вдруг нарушилась. Застывший воздух пришел
в движение и одним могучим порывом сбросил с себя апатию.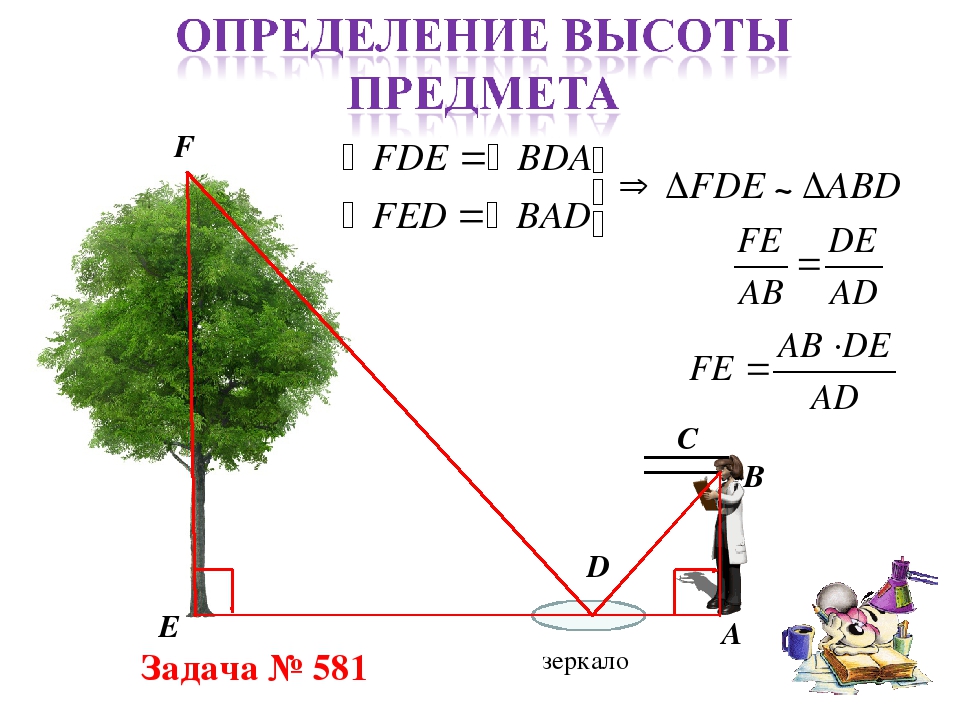 А это обычно бывает перед затяжным дождем или
перед пургой. Прогноз Дерсу оказался безошибочным: к ночи разыгралась
пурга.
А это обычно бывает перед затяжным дождем или
перед пургой. Прогноз Дерсу оказался безошибочным: к ночи разыгралась
пурга.
 Солнце садится при безоблачном
небе.
Солнце садится при безоблачном
небе.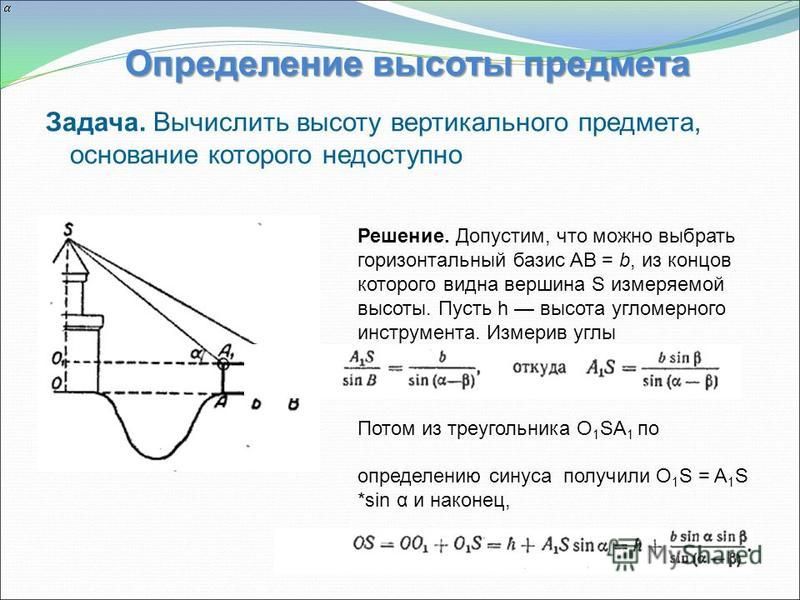
 Словно вянут голубые цветы цикория
и желтые цветы чистотела. Складываются мохнатые листочки красного
лугового клевера.
Словно вянут голубые цветы цикория
и желтые цветы чистотела. Складываются мохнатые листочки красного
лугового клевера.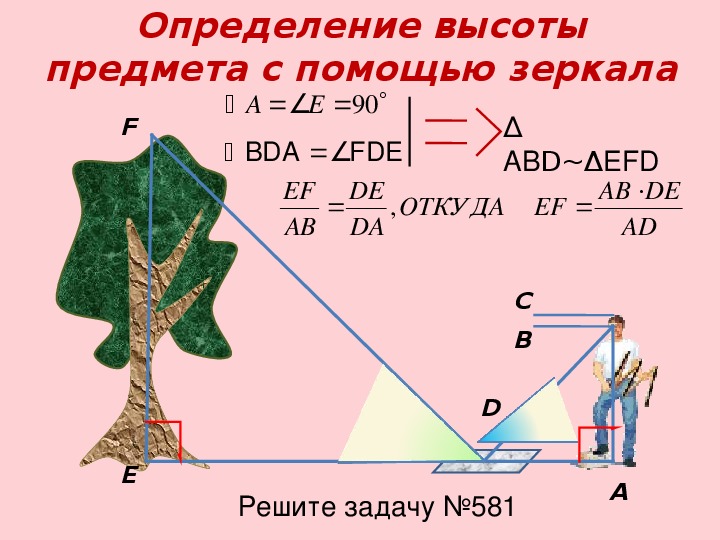
 Г Комовский, Спутник юного туриста.
Учпедгиз, Москва, 1952, стр. 41.).
Г Комовский, Спутник юного туриста.
Учпедгиз, Москва, 1952, стр. 41.). Давление:
Давление: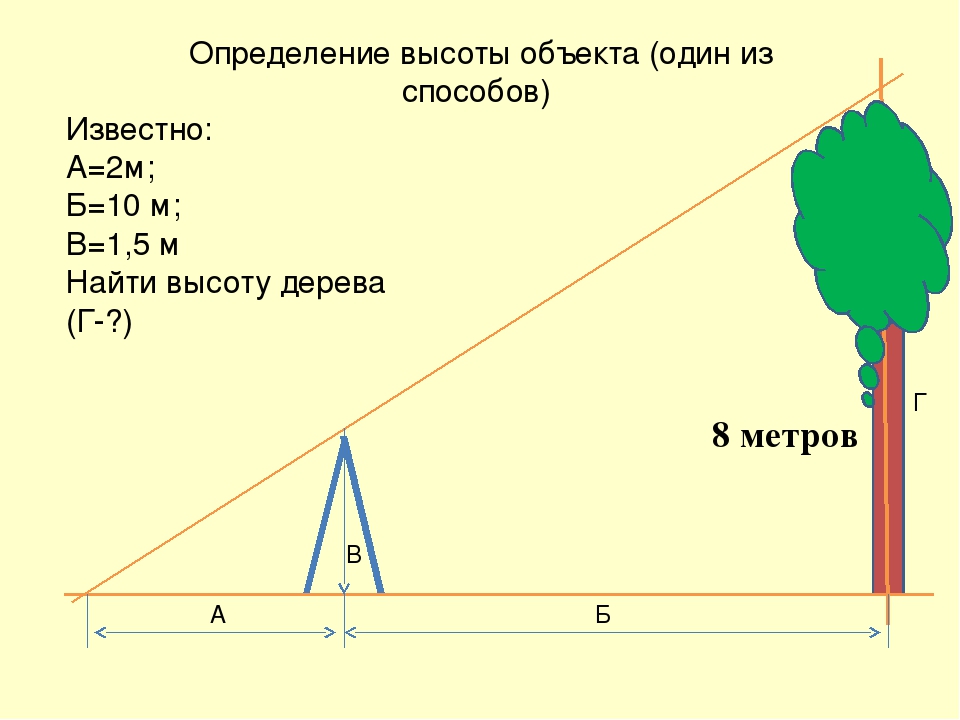 .. Пл.
.. Пл. ……………. Пл.
……………. Пл.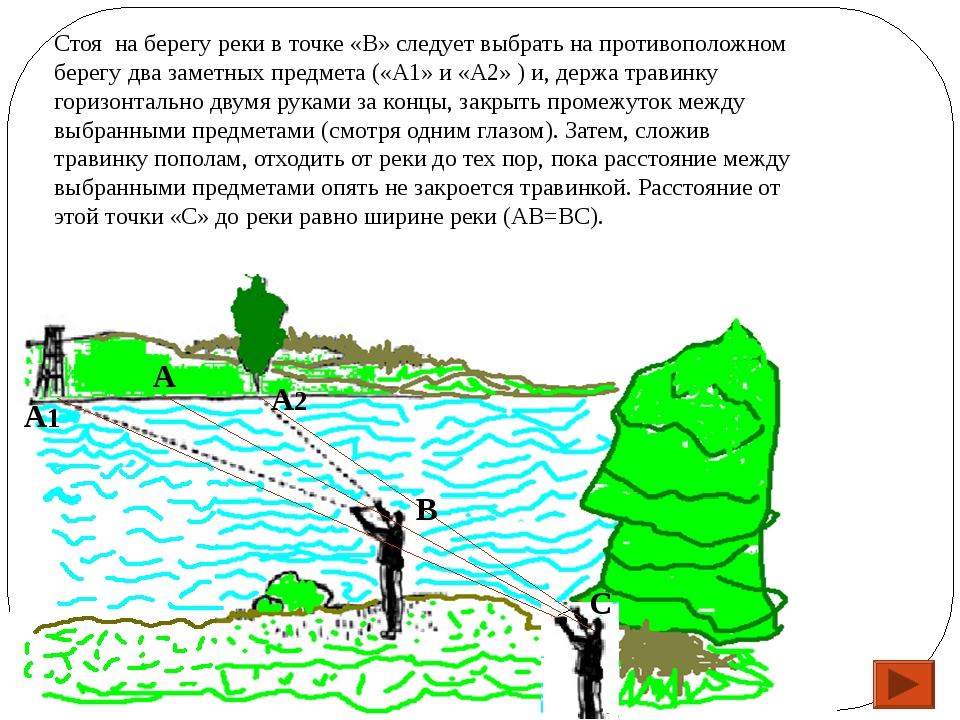 ……. Хор.
……. Хор. с подветренной стороны
(со стороны, обратной ветру)…………… Хор.
с подветренной стороны
(со стороны, обратной ветру)…………… Хор.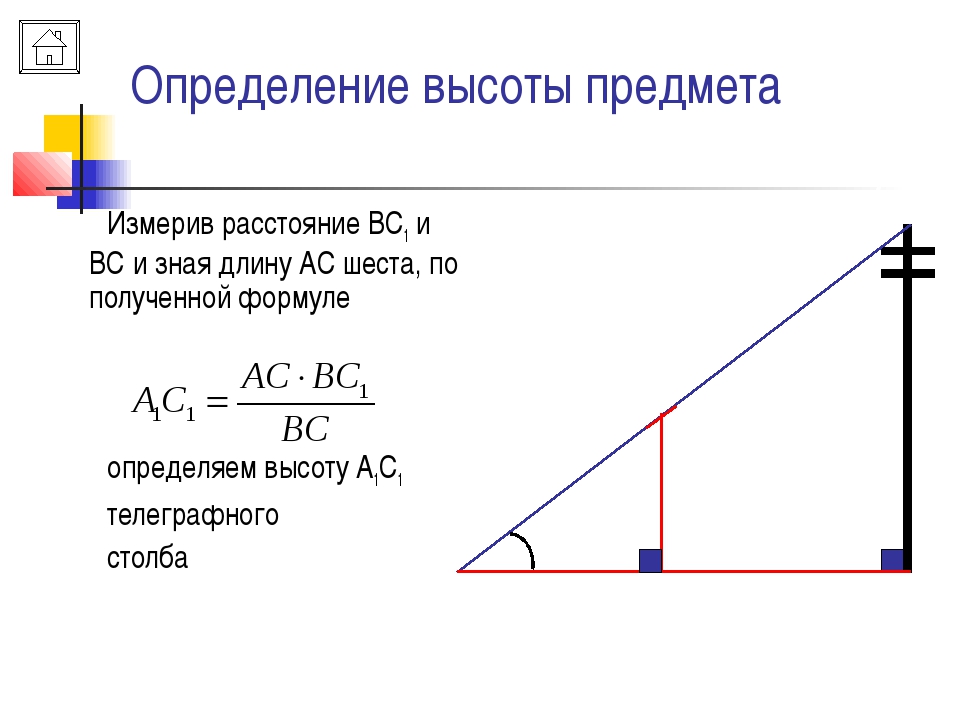 .. Хор.
.. Хор.

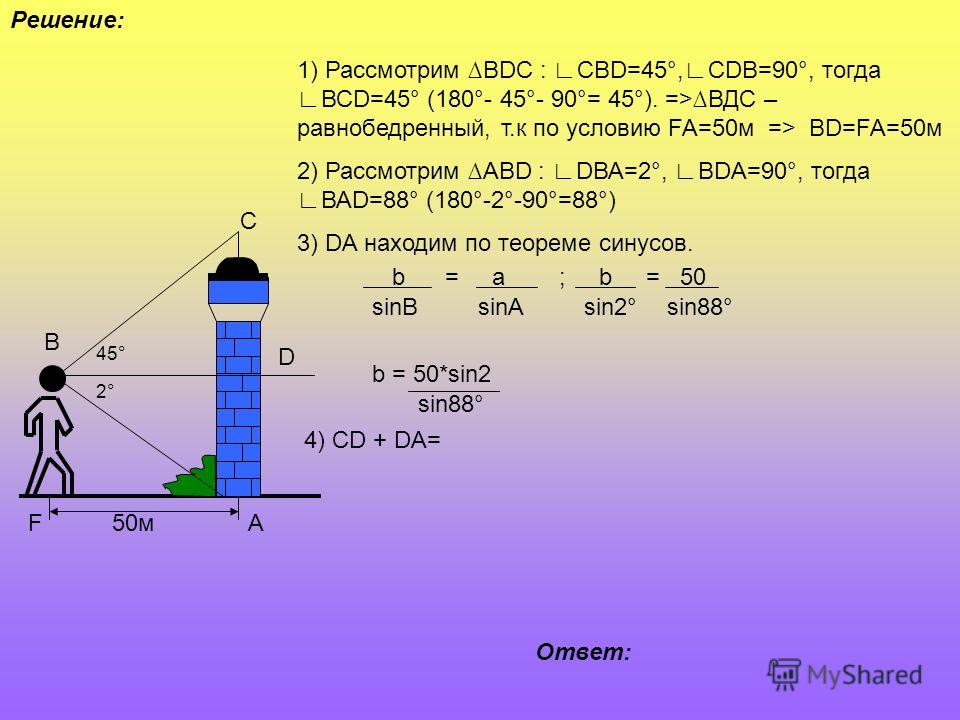
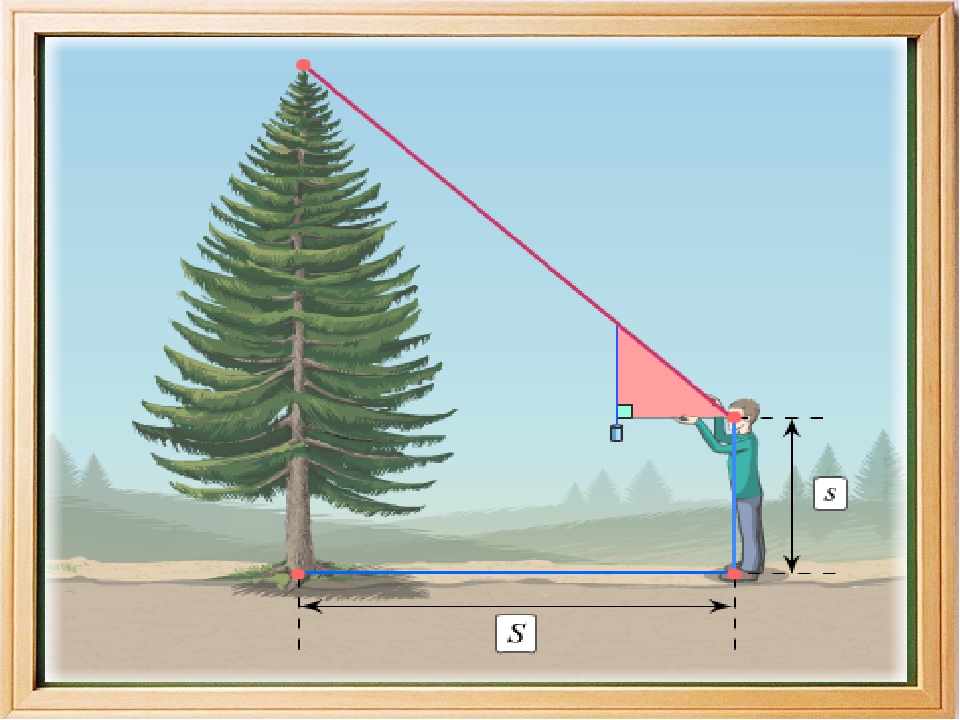

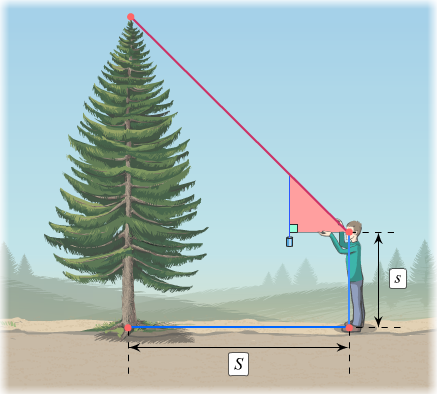


 Отметьте эту палку буквой B.
Отметьте эту палку буквой B.