Определение золотое сечение: Золотое сечение и симметрия — Мастерок.жж.рф

Содержание

Золотое сечение: зачем оно нужно — Рамблер/новости

Золотое сечение это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени. [С-BLOCK] Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

История

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой — Отца, а целое — Святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях. [С-BLOCK]

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды. [С-BLOCK]

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века. Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела — 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль. Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции. Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента

Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения. [С-BLOCK]

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Золотое сечение: как это работает

Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени. Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

История

Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзьенашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящён математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

Рис. Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.

Представление о золотых пропорциях имели и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причём та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.

Рис. Построение шкалы отрезков золотой пропорции

Рис. Цикорий

Рис. Ящерица живородящая

Рис. Яйцо птицы

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гёте отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.

Искусство пространственных форм

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции. Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

Гёте, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввёл в научный обиход термин морфология.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Золотое сечение и симметрия

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863…1925) считал золотое сечение одним из проявлений симметрии.

Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии. Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Слово, звук и кинолента

Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух – в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Источники: http://russian7.ru; http://n-t.ru.

Приглашаем к обсуждению темы в нашей группе — https://vk.com/dostoyanieplaneti

* * *

Рекомендуем к ознакомлению:

Геометрия Великой пирамиды

Наука вторит индийским ведам

Золотое сечение, что это такое. Золотое сечение: как это работает.

Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение.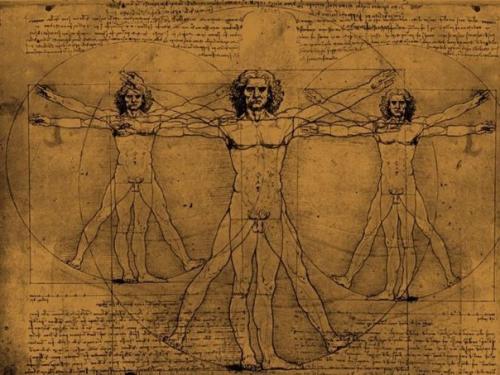
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1, 6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение в формах пространства и времени действует.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «Асимметричную Симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.

История.
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах лука пачоли в книге «Божественная Пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял сына, большой — отца, а целое — святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. на отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два Младших Члена Этой Нескончаемой Пропорции в Сумме Дают Третий Член, а Любые два Последних Члена, Если их Сложить, Дают Следующий Член, Причем та же Пропорция Сохраняется до Бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях

Фибоначчи числа — гармоническое деление, мера красоты. Золотое сечение в природе, человеке, искусстве, архитектуре, скульптуре, дизайне, математике, музыке https://psihologiyaotnoshenij.com/stati/zolotoe-sechenie-kak-eto-rabotaet

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «Математическое Эстетство» вызывало много критики.

Природа.
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «Кривой Жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение днк и даже структура галактик заключают в себе ряд Фибоначчи.

Человек.
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

Адольф цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13: 8 ближе к золотому сечению, чем пропорции женского тела — 8: 5.

Искусство пространственных форм.
Художник Василий суриков говорил, «что в Композиции Есть Непреложный Закон, Когда в Картине Нельзя Ничего ни Убрать, ни Добавить, Даже Лишнюю Точку Поставить Нельзя, это Настоящая Математика». Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. в. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в Селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке великие пирамиды гизы, собор парижской богоматери, храм Василия блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента.
Формы временно? Го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой Дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853: 535=1, 6) — это и есть точка золотого сечения.

Советский музыковед э. к. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.
Кинорежиссер Сергей эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Золотое сечение примеры. Как получили золотое сечение

Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.

Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.

На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.

Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:

Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.

К сведению! В отличие от классического золотого соотношения, архитектурная версия подразумевает соотношение сторон отрезка в пропорции 44:56.

Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.

Золотое сечение, что это такое. Понятие золотого сечения

Итак, золотое сечение – это золотая пропорция, которая также является гармоническим делением. Для того чтобы объяснить это более понятно, рассмотрим некоторые особенности формы. А именно: форма является чем-то целым, ну а целое, в свою очередь, всегда состоит из некоторых частей. Эти части, вероятнее всего, обладают разными характеристиками, по крайней мере разными размерами. Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.

Значит, другими словами, мы можем утверждать, что золотое сечение – это соотношение двух величин, которое имеет свою формулу. Использование такого соотношения при создании формы помогает сделать ее максимально красивой и гармоничной для человеческого глаза.

Золотое сечение тату. Значение татуировки спираль

В татуировке спирали заложено намного больше смысла чем это кажется на первый взгляд. Такой простой узор построен по так называемому принципу золотого сечения, который встречается в природе повсюду. Причем этот принцип известен с древних времен, что подтверждается его наличием в основании египетских пирамид.

Символика татуировок со спиралями

В татуировках Та-моко или в тех же кельтских узорах спирали встречаются очень часто, и это не удивительно. Отсутствие прямых углов этой фигуры символизирует связь с природой, которая не любит прямые углы, старается всегда их сгладить. Татуировка спирали означает единство с природой, как правило такую тату делают спокойные, рассудительные люди.

Но это лишь общее значение, нередко люди пытаются узнать о значении татуировки в виде спирали, на самом деле путая ее с другими татуировками. Часто татуировка спиралевидного панциря вводит людей в заблуждение, она в последнее время весьма популярна. Одна значение абсолютно другое, она подходит замкнутым людям, одиночкам, обычно перенесших какое-то потрясение и не желающим о нем делиться, а в его честь делают такую наколку.

Весьма похожа на спираль татуировка волны , которая символизирует любовь к морю или татуировка черного солнца , о значении которой мы подробно писали.

Нередко татуировку спирали делают в качестве оберега, так как это символ цикличности жизни, он передают энергию мира и существования. Наносить изображение спирали можно на плечи, предплечья, грудь и спину. Больше татуировка подходит женщинам, так как еще одно значение татуировки – женское начало.

Я рекомендую наносить татуировку спирали с поперечными линиями, чтобы однозначно идентифицировать ее как символ цикличности времени и связи с природой.

Золотое сечение в человеке. Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

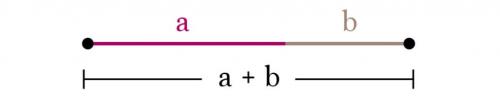
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

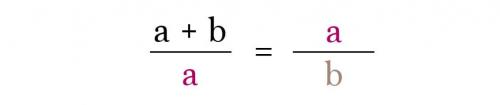
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

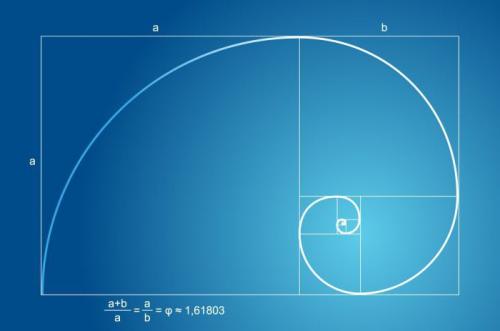
Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Принцип золотого сечения. Успешное творение или правило золотого сечения

Запечатление момента – именно в этом заключается миг творения художника или фотографа. Кроме вдохновения, мастер должен следовать строго определенным правилам, коими предстают: контраст, размещение, равновесие, правило соблюдения третей и многие другие. Но приоритетным все же признается правило золотого сечения, оно же правило третей.

Просто о сложном

Если в упрощенном виде преподносить основу правила золотого сечения, то фактически — это деление воспроизводимого момента на девять равных частей (три по вертикали на три по горизонтали). Впервые специально его ввел Леонардо да Винчи, выстраивая все свои композиции в этой своеобразной сетке. Именно он практически подтвердил, что ключевые элементы изображения должны быть сосредоточены в точках пересечения вертикальных и горизонтальных линий.

Правило золотого сечения в фотографии подлежит определенной коррекции. Кроме девятисегментной сетки рекомендуется использовать и так называемые треугольники. Принцип их построения основывается на правиле третей. Для этого из крайней верхней точки проводится диагональ в нижнюю, а из противоположной верхней – луч, делящий уже существующую диагональ в одной из внутренних точек пересечения сетки. Ключевой элемент композиции должен быть отображен в среднем по величине из получившихся треугольников. Здесь стоит сделать ремарку: приведенная схема построения треугольников отображает лишь их принцип, а, значит, имеет смысл экспериментировать с приведенной инструкцией.

Как использовать сетку и треугольники?

Правило золотого сечения в фотографии действует по определенным нормам в зависимости от того, что изображается на ней.

Фактор горизонта. Согласно правилу третей, его следует располагать по горизонтальным линиям. При этом, если запечатляемый объект находится выше уровня горизонта, то фактор проходит через нижнюю линию, и наоборот.

Расположение главного объекта. Классическим считается такое расположение, при котором центральный элемент находится в одной из точек пересечения. Если фотограф выделяет два объекта, то они должны быть по диагонали или в параллельных точках.

Использование треугольников. Правило золотого сечения в рассматриваемом случае отступает от канонов, но незначительно. Объект не обязан располагаться в точке пересечения, но находится максимально близко к ней в среднем треугольнике.

Направление. Используется данный принцип съемки в динамичной фотографии и заключается в том, что перед движимым объектом должно оставаться две трети пространства снимка. Это обеспечит эффект перемещения вперед и указание цели. В противном случае фотография может остаться недопонятой.

Корректировка правила золотого сечения

Несмотря на то, что правило третей в существующей теории построения композиции считается классическим, всё больше фотографов склонны отказываться от него. Мотивация у них проста: анализ картин известных художников показывает, что правило золотого сечения не выдерживается. С данным утверждением можно поспорить.

Рассмотрим всем известную Джоконду, которую противники использования правила третей приводят в качестве примера (забывая, что сам да Винчи стоял у истоков его практического использования). Их аргументами служит то, что мастер не посчитал нужным расположить ключевые элементы картины по точкам пересечения, как этого требует классическое изображение. Но они упускают из вида фактор горизонтальных линий, согласно которому голова и торс изображаемой расположены таким образом, что силуэт в целом не «режет глаз». Кроме того, в данном произведении в большей степени использована спираль, о которой в большинстве случаев забывают теоретики фотографии. И так можно опровергнуть утверждения относительно практически каждого творенияя, приводимого в качестве примера.

Правило золотого сечения можно использовать, а можно отказаться от него, если требуется подчеркнуть дисгармоничность композиции. Однако утверждать, что оно не является ключевым в формировании арт-объекта, невозможно.

Золотое сечение в архитектуре. Как получили золотое сечение

Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.

Золотое сечение лица. Золотое сечение — пропорция лица

Многие грезят идеальной внешностью, но далеко не все имеют четкое представление о том, какие пропорции можно считать гармоничными. Формула золотого сечения лица неразрывно связана с числом 1,618 и прочими соотношениями. Так, пропорции красоты можно описать следующим образом:

отношение высоты и ширины лица должно равняться 1,618;
если разделить длину рта и ширину крыльев носа, то получится 1,618;
при делении расстояний между зрачками и бровями, опять-таки, получается 1,618;
длина глаз должна совпадать с расстоянием между ними, а также с шириной носа;
участки лица от линии роста волос до бровей, от переносицы до кончика носа, и нижняя часть до подбородка должны быть равными;
если от зрачков провести вертикальные линии к уголкам губ, то получится три равных по ширине участка.

Нужно понимать, что в природе совпадение всех параметров встречается достаточно редко. Но в этом нет ничего дурного. Это вовсе не значит, что лица, не соответствующие идеальным пропорциям, можно назвать некрасивыми или немиловидными. Напротив, именно «дефекты» порой придают лицу незабываемый шарм.

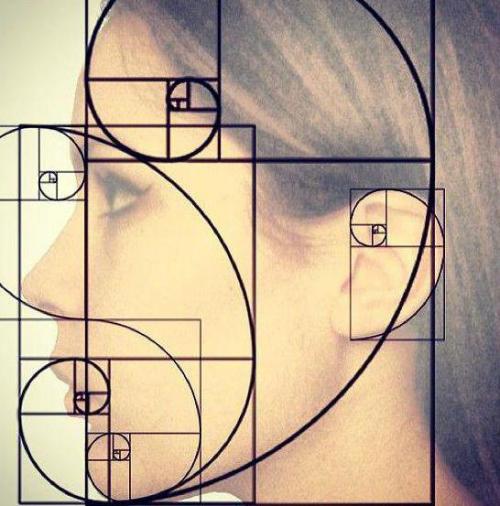
Золотое сечение в композиции. Основы композиции — Золотое сечение

Золотое сечение в композиции рисунков в paint.net
Математически «Золотое сечение» можно описать так — отношение целого к большей его части должно равно отношению большей части к меньшей. Проиллюстрируем на примере отрезка.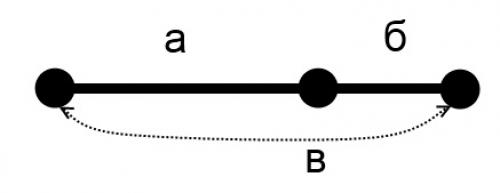
В нашем случае весь отрезок В разделен на две части – большую А и меньшую Б. Тогда, если В/А будет равно А/Б, деление отрезка будет осуществлено по принципу, называемому «Золотое Сечение».
Не совсем точно, но близко к «Золотому сечению», например соотношение 2/3 или 5/8. Числа в подобных соотношениях нередко называют «золотыми».
Зачем эта информация нам для рисования в paint.net? «Золотое сечение» важно для композиции. Считается, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. Именно в подобных соотношениях выбирали размеры хостов для своих картин известные художники.
Рассмотрим упрощенный вариант построения «Золотого сечения» для композиции рисунка, или правило «Трети». Заключается правило трети в том, что мы мысленно делим кадр, на три части по горизонтали и вертикали и в точках пересечения воображаемых линий, размещаем ключевые и важные детали нашего рисунка или фотоколлажа.
Принцип «золотого сечения» можно применять при кадрировании изображения. Так, например, кадр, сформированный по правилу «золотого сечения», из большой фотографии может иметь следующий вид.

Золотое сечение в музыке. Метод золотого сечения в музыкальных произведениях

«Золотое сечение» – это понятие, скорее, математическое и его изучение – задача науки. Это деление некоей величины на две части в таком отношении, когда болььшая часть так будет относиться к меньшей, как целое к большей. Данное отношение оказывается равным трансцендентному числу Ф=1,6180339… с удивительными свойствами.

Метод золотого сечения — это поиск значений функции на заданном отрезке. Данный метод основывается на принципе деления отрезка в так называемой золотой пропорции. Наибольшее распространение он получил для поиска экстремальных значений при решении задач, связанных с оптимизацией. Кроме математики, метод золотого сечения используется в самых разных сферах, начиная от архитектуры, искусства и заканчивая астрономией. Так, например, известный советский режиссёр Сергей Эйзенштейн использовал его в своей картине «Броненосец Потёмкин», а Леонардо да Винчи – при написании им знаменитой «Джоконды».

Метод золотого сечения применяется и в музыке. Оказалось, что в музыкальных произведениях очень часто встречается эта золотая пропорция. В начале 20 века на заседании Московского музыкального кружка было сделано сообщение, содержащее информацию о том, какое применение находит золотое сечение в музыке. Сообщение с огромным интересом слушали члены музыкального кружка композиторы С. Рахманинов, С. Танеев, Р. Глиэр и другие. Доклад музыковеда Розенова Э.К. «Закон золотого сечения в музыке и поэзии» положил начало исследованиям математических закономерностей, связанных с золотой пропорцией, в музыке. Он проанализировал музыкальные произведения Моцарта, Баха, Бетховена, Вагнера, Шопена, Глинки и других композиторов и показал, что в их произведениях присутствует эта «божественная пропорция».

Кульминация многих музыкальных произведений располагается не в центре, а немного смещена к концу произведения в соотношении 62:38 – это и есть точка золотой пропорции. Доктор искусствоведения, профессор Л. Мазель заметил, изучая восьмитактные мелодии Шопена, Бетховена, Скрябина, что во многих творениях этих композиторов кульминация, как правило, приходится на слабую долю пятого, то есть на точку золотого сечения – 5/8. Л. Мазель считал, что практически у каждого композитора – приверженца гармонического стиля можно найти подобную музыкальную структуру: пять тактов подъёма и три такта спуска. Это говорит о том, что метод золотого сечения активно применялся композиторами сознательно либо бессознательно. Вероятно, такое структурное расположение кульминационных моментов придает музыкальному произведению гармоническое звучание и эмоциональную окраску.

Серьёзное исследование музыкальных произведений на предмет проявления в них золотой пропорции предпринял композитор и музыковед Л. Сабанеев. Он изучил около двух тысяч творений разных композиторов и пришёл к выводу, что примерно в 75% случаев золотое сечение присутствовало в музыкальном произведении хотя бы один раз. Самое большое количество произведений, в которых встречается золотая пропорция, он отмечал у таких композиторов, как Аренский (95%), Бетховен (97%), Гайдн (97%), Моцарт (91%), Скрябин (90%), Шопен (92%), Шуберт (91%). Наиболее пристально он исследовал этюды Шопена и пришёл к выводу, что золотое сечение было определено в 24 этюдах из 27. Только в трёх этюдах Шопена золотая пропорция не была обнаружена. Иногда структура музыкального произведения включала в себя одновременно и симметричность, и золотое сечение. Например, у Бетховена многие произведения делятся на симметричные части, и в каждой из них проявляется золотое сечение.

Итак, можно сказать, что наличие золотого сечения в музыкальном произведении является одним из критериев гармоничности музыкальной композиции.

Золотое сечение: Как это работает?

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.

История

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Природа

Человек

Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

Искусство пространственных форм

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

Слово, звук и кинолента

Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.

Источник: Academic Painting

Правило золотого сечения в дизайне интерьера

Формула идеальных гармоничных пропорций или правило «золотого сечения» известно человечеству с незапамятных времен. Его описывает Евклид в своих «Началах», о нем упоминает Пифагор. Руководствуясь этой формулой, великие архитекторы проектировали Парфенон, египетские пирамиды, Тадж-Махал, Храм Василия Блаженного. Тот же принцип использовали Фидий, Леонардо Да Винчи, Микеланджело, знаменитые художники, математики, композиторы. Определение золотого сечения в дизайне помогает создавать удивительно гармоничные пространства, в которых приятно находиться и комфортно жить.

Общие принципы и определение

Суть правила «золотого сечения» сводится к тому, что большая часть целого относится к целому точно так же, как и меньшая часть – к большей части и наоборот. В цифровом выражении эта пропорция равна примерно 1,618, иначе это число называют числом «Фи», в честь древнегреческого архитектора Фидия. Если рассматривать правило в процентном соотношении, то большая часть составляет 62% от целой величины, а меньшая – около 38%.

То же определение легко сформулировать иначе. Так, в геометрии принято изображать «золотой прямоугольник», меньшая из сторон которого относится к большей как 0,618 к 1. Если от этого прямоугольника «отрезать» квадрат со стороной, равной меньшей из сторон, вы получите новый «золотой прямоугольник», и так – до бесконечности. В итоге искомые прямоугольники образуют своего рода спираль.

Золотое сечение в природе

Самое удивительное состоит в том, что человек лишь дал определение золотому сечению, записав его формулу. В природе этому правилу подчиняется строение многих предметов и объектов, к появлению которых люди не имеют никакого отношения. В качестве примеров можно привести ракушки улиток, моллюсков, рога животных, расположение лепестков цветов, семечек подсолнуха, «чешуек» ананасов и шишек, фаланги человеческих пальцев и многое другое.

Где используется человеком?

Отыскав заветную формулу определения золотого сечения, выдающиеся умы человечества нашли ей применение в самых разных областях науки и искусства:

в математике;
в архитектуре;
в живописи;
в ландшафтном дизайне;
в полиграфии и рекламе;
в дизайне интерьеров.

Немалую роль в популяризации правила золотого сечения сыграл средневековый математик Фибоначчи (Леонардо Пизанский). Он открыл последовательность цифр, иллюстрирующую формулу. Ряд Фибоначчи состоит из чисел, где каждое последующее число является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21 и так до бесконечности. Все эти числа подчиняются правилу золотого сечения.

Леонардо Да Винчи использовал знаменитую «золотую» спираль для написания «Моны Лизы» и других шедевров. Дело в том, что и картины, и архитектурные сооружения, созданные в рамках указанных пропорций, представляют собой удивительно гармоничные, приятные взгляду, красивые композиции, несмотря на асимметрию. Именно поэтому правило золотого сечения активно используют современные художники, ландшафтные дизайнеры, создатели рекламных слоганов, логотипов, сайтов компаний, афиш, обложек, виртуальных, печатных изданий.

Что касается строительства и дизайна интерьеров, в начале прошлого века Ле Корбюзье существенно облегчил жизнь архитекторам и планировщикам, придумав систему под названием «модулор». В ее основе лежит принцип определения золотого сечения и пропорции человека с поднятой рукой. Сами помещения и их обстановка проектируются, исходя из антропометрических данных будущих обитателей, обеспечивая максимальный комфорт, удобство, ощущение гармонии.

Использование в дизайне интерьеров

Определение золотого сечения в дизайне поможет создать благоприятную атмосферу и уют даже в типовой квартире, построенной без учета ваших антропометрических данных. Вы всегда можете «подогнать» окружающее пространство под себя, проведя нехитрые подсчеты и расположив детали, объекты, мебель на оптимальном уровне и местах, подобрав верное соотношение цветов, размеров.

Размеры и зонирование

Идеальным считается помещение в виде прямоугольника, стороны которого пропорциональны числам 5 и 8, но и неидеальные параметры поддаются корректировке. То же можно сказать о высоте потолка, которая визуально меняется с помощью нехитрых дизайнерских приемов. Зонирование комнат также основывается на правиле «62%». Например, зона отдыха в кухне-гостиной занимает не более 5/8 от всего пространства, как и любая большая часть комнаты при делении на функциональные зоны.

Если речь идет о дизайне стен в классическом двухцветном формате или об отделке стеновыми панелями, то для помещений с потолками высотой более 3 метров стоит использовать правило «двух третей»: расстояние от потолка до начала декоративных панелей или высокого плинтуса должно составлять около 60% от общей высоты. Для невысоких комнат применяется дополнительное деление нижней или верхней части, что позволяет «приподнять» потолки. Определение высоты следующего, меньшего фрагмента состоит в умножении высоты одной из частей на 0,618.

Цвета

Выбор оттенков для дизайна любой жилой комнаты основан на принципах определения золотого сечения. Примерно 60% поверхностей оформляется в едином базовом оттенке, 30% отводится под активный тон, а 5-10% остается для ярких акцентов. Цветовая гамма выбирается, исходя из вкусов, пожеланий владельца, выбранного стиля, практичности, размера затрат. При этом 62% отводятся под фоновые обои или окраску, 30% оттенка-компаньона идет на мебель и акцентные стены, ковры, 10% – на декор. Допускается увеличение количества цветов в комнате до 4, но при этом яркие тона все равно займут минимальные позиции. Основной тон комнаты составит 62%, расцветка мебели – 24%, различный декор – 9%, акценты – до 5% общей палитры.

Меблировка

Расстановка крупногабаритной мебели, основанная на определении «золотого прямоугольника», позволяет создать ощущение уюта за счет идеальных пропорций. Так, меньшая часть углового дивана должна составлять 1/3 от длины его большей части, а журнальный столик – не более 2/3. Классический диван, установленный вдоль стены, занимает примерно 2/3 ее длины. Высота спинок диванов, кресел, тумб не должна превышать 3/8 стены. Что касается прикроватных тумбочек, обычно их высота равняется 1/3 расстояния от пола до потолка, а светильники в изголовье располагают не выше отметки в 2/3 размера стен по вертикали. Если присмотреться, то схожих пропорций придерживаются многие производители, устанавливая правильные соотношения между длиной и высотой шкафов, комодов, книжных стеллажей. Покупателям остается лишь выбрать размер, стиль мебели, идеально подходящей к габаритам и дизайну их квартир.

Декор

Под предметами декора подразумевают достаточно крупные или яркие аксессуары. Картины, зеркала прямоугольной формы размещают так, чтобы их нижняя граница находилась на уровне 1/3 высоты стены (если речь идет о вертикальном варианте). Расположенные горизонтально картины принято вешать так, чтобы их нижняя рама отступала от пола на 5/8 стены. При этом сами картины, зеркала, панно, телевизионные панели, как правило, приближены по своим параметрам к «золотому прямоугольнику». Главное правило, которому должны подчиняться аксессуары в вашей квартире, гласит: размеры каждого последующего предмета должны быть меньше предыдущего во столько раз, во сколько раз больший предмет меньше самого крупного.

Простые практические советы

Рассчитайте ряд Фибоначчи для дизайна вашего дома, взяв за основу, как когда-то Ле Корбюзье, высоту потолков. Это значение надо умножить на 0,618, и вы получите следующее число. Таким образом последовательность продолжают до бесконечности, используя полученные значения для создания гармоничного интерьера. Если вы планируете поделить стены при помощи карнизов, плинтусов и бордюров, определение размера нижней части сводится к двукратному умножению общей высоты на 0,618. Остальное пространство отводится под верхний фриз и карниз (увеличив его на несколько сантиметров, вы сделаете потолок выше). Еще один совет: мебель должна занимать не больше 60% площади комнаты, чтобы не вызывать ощущения захламленности и тесноты.

Используя принцип определения золотого сечения при дизайне дома или квартиры, не старайтесь встроить все предметы меблировки, декора в знаменитую спираль, состоящую из золотых прямоугольников. Руководствуйтесь не только математикой, но и интуицией, собственным вкусом, чувством прекрасного, ведь красота и гармония – это нечто большее, чем сухие формулы.

Мне нравится 1

Похожие посты

Оставить комментарий

Золотое сечение для дизайна и жизни

Золотое сечение, или божественная пропорция — самое загадочное правило дизайна и вызывает много споров. Разбираемся, как использовать его, чтобы ваши дизайны выделялись.

Что общего у пирамиды в Гизе и Мона Лизы с логотипом Пепси? И то, и другое создано с помощью золотого сечения. В этой статье мы разберем, что это такое и как его использовать в создании дизайна.

Правило золотого сечения

Золотое сечение — пропорция, которую заметили еще древние египтяне. Чтобы её получить, нужно разделить линию на две части так, чтобы длинная часть соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной. Оказывается, эта пропорция всегда равняется 1,618. Это число еще называют числом «фи».

Сохранившиеся постройки древности тоже подчинены правилу золотого сечения

Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.

Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.

Принцип и формула золотого сечения

На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.

Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.

Последовательность Фибоначчи — не только математическая формула

Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.

Как построить прямоугольник с идеальными пропорциями

Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.

Построение прямоугольника с золотым сечением

Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).

Это явно неспроста. Хотя далеко не все подчиняется этой закономерности

Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.

Как разделить отрезок по правилу золотого сечения

Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Ничего особенного, но взгляд не оторвать. Знаете почему?

Итак, порядок деления отрезка по правилу золотого сечения:

Берем отрезок, делим его пополам.
Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
Полученную точку C соединяем прямой с другим концом отрезка (A).
На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.

Деление отрезка на участки с идеальным соотношением

Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.

Идеальный треугольник и пентаграмма

Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

Построение пентаграммы

Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.

Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

Применение в строительстве

Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Исаакиевский собор — можете посчитать ради интереса

Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.

Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно

Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.

Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

Не только прямые линии можно использовать

По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.

Золотое соотношение во внутреннем оформлении

Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:

Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.
  Пример подбора цвета по правилам правильной пропорциональности
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Пропорциональность — важная вещь
Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.

Золотое сечение в ландшафтном дизайне

При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

Правило треугольника в садовом дизайне
От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.

Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.

Золотое сечение — Простая английская Википедия, бесплатная энциклопедия

С одним числом a и другим меньшим числом b соотношение двух чисел находится путем их деления. Их соотношение составляет a / b . Другое соотношение получается путем сложения двух чисел и деления их на большее число на . Новое соотношение составляет ( a + b ) / a . Если эти два соотношения равны одному и тому же числу, то это число называется золотым сечением .Греческая буква φ {\ displaystyle \ varphi} (фи) обычно используется в качестве названия золотого сечения. ^[1] ^[2]

Например, если b = 1 и a / b = φ {\ displaystyle \ varphi}, то a = φ {\ displaystyle \ varphi} , Второе соотношение ( a + b ) / a будет тогда (φ + 1) / φ {\ displaystyle (\ varphi +1) / \ varphi}. Поскольку эти два соотношения равны, это правда:

φ знак равно φ + 1φ {\ Displaystyle \ varphi = {\ гидроразрыва {\ varphi +1} {\ varphi}}}

Один из способов написать это число —

φ = 1 + 52 = 1.61803 … {\ displaystyle \ varphi = {\ frac {1 + {\ sqrt {5}}} {2}} = 1,61803 …} ^[1] ^[2]

5 {\ displaystyle {\ sqrt {5}}} похоже на любое число, которое при умножении само на себя дает 5 (или какое число умножается): 5 × 5 = 5 {\ displaystyle {\ sqrt {5}} \ раз {\ sqrt {5}} = 5}.

Золотое сечение — иррациональное число. Если человек попытается написать это число, это никогда не остановится и никогда не создаст узор, но начнется оно так: 1.6180339887 … Важная особенность этого числа состоит в том, что человек может вычесть из него 1 или разделить на него 1.В любом случае число будет продолжаться и никогда не остановится.

φ − 1 = 1,6180339887 …− 1 = 0,6180339887 … 1 / φ = 11,6180339887 … = 0,6180339887 … {\ displaystyle {\ begin {array} {ccccc} \ varphi -1 & = & 1.6180339887 …- 1 & = & 0.6180339887 … \\ 1 / \ varphi & = & {\ frac {1} {1.6180339887 …}} & = & 0.6180339887 … \ end {array}}}

${\begin{array}{ccccc}\varphi -1&=&1.6180339887...-1&=&0.6180339887...\\1/\varphi &=&{\frac {1}{1.6180339887...}}&=&0.6180339887...\end{array}}$

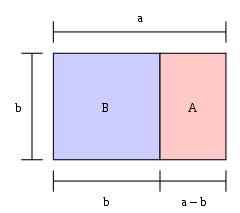Большой прямоугольник BA — золотой прямоугольник; то есть пропорция b: a равна 1: φ {\ displaystyle \ varphi}. Для любого такого прямоугольника и только для прямоугольников этой конкретной пропорции, если мы удалим квадрат B , то, что останется, A , будет еще одним золотым прямоугольником; то есть с теми же пропорциями, что и исходный прямоугольник.

Если длина прямоугольника, разделенная на его ширину, равна золотому сечению, то прямоугольник является «золотым прямоугольником». Если с одного конца золотого прямоугольника отрезать квадрат, то другой конец будет новым золотым прямоугольником. На рисунке большой прямоугольник (синий и розовый вместе) представляет собой золотой прямоугольник, потому что a / b = φ {\ displaystyle a / b = \ varphi}. Синяя часть (B) — это квадрат, а розовая часть (A) — это еще один золотой прямоугольник, потому что b / (a − b) = φ {\ displaystyle b / (a-b) = \ varphi}.Большой прямоугольник и розовый прямоугольники имеют одинаковую форму, но розовый прямоугольник меньше и повернут.

Числа Фибоначчи — это список чисел. Человек может найти следующий номер в списке, сложив два последних числа вместе. Если человек делит число в списке на число, которое было перед ним, это соотношение все ближе и ближе к золотому сечению.

Число Фибоначчи	делится на предыдущий	соотношение
1
1	1/1	= 1.0000
2	2/1	= 2,0000
3	3/2	= 1,5000
5	5/3	= 1,6667
8	8/5	= 1,6000
13	13/8	= 1,6250
21	21/13	= 1,6154 …
34	34/21	= 1.6190 …
55	55/34	= 1,6177 …
89	89/55	= 1,6182 …
…	…	…
	φ {\ displaystyle \ varphi}	= 1,6180 …

$\varphi$ Использование золотого угла позволяет оптимально использовать солнечный свет. Это вид сверху. $\varphi$

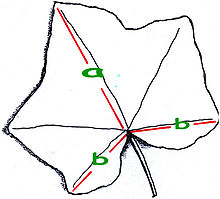
В природе золотое сечение часто используется для расположения листьев или цветов.В них используется золотой угол приблизительно 137,5 градусов. Листья или цветы, расположенные под таким углом, лучше всего используют солнечный свет.

↑ ^1.0 ^1.1 «Сборник математических символов». Математическое хранилище . 2020-03-01. Проверено 10 августа 2020.
↑ ^2,0 ^2,1 Вайсштейн, Эрик В. «Золотое сечение». mathworld.wolfram.com . Проверено 10 августа 2020.

Свойства золотого сечения, внешний вид и обзор приложений

Что делает одно число таким интересным, что о нем писали древние греки, художники эпохи Возрождения, астроном 17 века и писатель 21 века? У этого числа много названий. Это «золотое» число, 1.61803399, представленное греческой буквой фи, известно как золотое сечение, золотое число, золотая пропорция, золотое сечение, золотое сечение, божественная пропорция и божественное сечение.Об этом написал Евклид в «Элементах» около 300 г. до н.э., Лука Пачоли, современник Леонардо да Винчи, в «De Divina Proportione» в 1509 году, Иоганн Кеплер около 1600 года и Дэн Браун в 2003 году в своем бестселлере. , «Код да Винчи.» С выпуском фильма «Код да Винчи» стремление узнать Фи стало еще более популярным в поп-культуре. Очарование «Кода да Винчи» заключалось в том, что он творчески объединил вымысел с фактами и мифами из искусства, истории, теологии и математики, так что читатель никогда не узнал, что было правдой, а что нет.Этот сайт изучает это золотое число Фи и его математический кузен, последовательность Фибоначчи (0, 1, 1, 2, 3, 5, 8,…), оба из которых играют роль в сюжете этого загадочного убийства, и проводит различие между миф и математика.

Математика золотого сечения

Это золотое сечение действительно уникально по своим математическим свойствам и широко распространено по всей природе. «Те, кто испытывает математические трудности», могут быть больше заинтересованы в появлении Фи в природе, его применении в искусстве, архитектуре и дизайне и его потенциале для понимания более духовных аспектов жизни, но давайте начнем с самых чистых фактов о Фи, которые встречаются в математике.

Почти каждый узнал о числе Пи в школе, но относительно немногие учебные программы включали Фи, возможно, по той самой причине, что понимание всех его проявлений часто выводит человека за пределы академического в сферу духовного просто потому, что Фи открывает необычно частая константа дизайна, применимая ко многим аспектам жизни. И Пи, и Фи — иррациональные числа с бесконечным числом цифр после десятичной точки, что обозначено многоточием «…».

Где Pi или p (3.14…) — это отношение длины окружности к ее диаметру, Phi или Φ (1,618…) — это золотое сечение, которое получается, когда линия делится очень особым и уникальным образом. Для иллюстрации предположим, что вас попросили взять веревку и перерезать ее. Есть любое количество мест, где вы можете разрезать его, и каждое место приведет к разному соотношению длины маленького отрезка к большому и большого отрезка ко всей струне. Однако есть одна уникальная точка, в которой отношение большой части к меньшей части точно такое же, как отношение всей струны к большей части, и в этот момент это золотое соотношение обоих частей равно 1.618 к 1, или Phi.

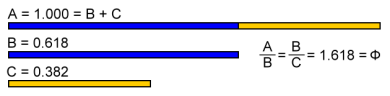
Что делает это намного больше, чем просто интересным упражнением в математике, так это то, что эта пропорция проявляется во всем творении и широко проявляется на лице и теле человека. Его можно найти в пропорциях многих других животных, в растениях, в Солнечной системе и даже в ценах и динамике движения фондовых рынков и валютных курсов. Таким образом, его привлекательность варьируется от математиков до врачей, натуралистов, художников, инвесторов и мистиков.

Отчасти уникальность Phi заключается в том, что его можно получить многими другими способами, кроме сегментации линии.

Фи — единственное число, квадрат которого больше самого себя на единицу, математически выраженный как Φ² = Φ + 1 = 2,618.
Phi также является единственным числом, обратное значение которого меньше самого себя на единицу, выраженное как 1 / Φ = Φ — 1 = 0,618.

Эти два качества phi могут быть выражены алгебраически как a + 1 = a² и a-1 = 1 / a. Затем это можно изменить и выразить как a²-a -1 = 0.Это квадратное уравнение, единственное положительное решение которого:

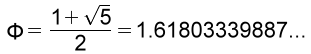
Φ = (1 + √5) / 2 = 1,61803398874989484820…

Если 1,618 отображается в верхнем регистре как Phi или Φ, его близнец или обратное значение 0,618 часто отображается в нижнем регистре как phi или φ. Фи — иррациональное число, число, которое не может быть выражено как отношение двух целых чисел.

Последовательность Фибоначчи

Последовательность Фибоначчи, также являющаяся элементом графика в «Коде да Винчи», представляет собой еще один способ математического вывода Фи.Сериал довольно простой. Начните с 0 и прибавьте 1, чтобы получить 1. Затем повторите процесс сложения каждых двух чисел в серии, чтобы определить следующее: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее. Этот узор также встречается в диагоналях Треугольника Паскаля. Связь с золотым сечением или фи определяется путем деления каждого числа на предыдущее. Чем дальше вы продвигаетесь в серии, тем ближе результат к Фи. Например:

1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1,666
13/8 = 1,625
21/13 = 1,615

Если вы пойдете дальше в ряд, и вы обнаружите, что 233/144 = 1,61805, очень близкое приближение к Phi, который с десятью десятичными знаками равен 1,6180339887.

Геометрия золотого сечения

Золотое сечение также встречается в геометрии, появляясь в базовых конструкциях равностороннего треугольника, квадрата и пятиугольника, помещенных внутри круга, а также в более сложных трехмерных телах, таких как додекаэдры, икосаэдры и «шары Баки», которые были названы в честь Бакминстера Фуллера и являются основой форм как мяча Carbon 60, так и футбольных мячей.

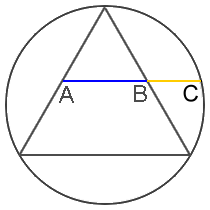
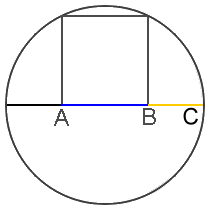
Иоганн Кеплер (1571-1630), открывший истинную эллиптическую природу орбит планет Солнечной системы, описал это так: «У геометрии есть два великих сокровища: одно — это Теорема Пифагора; другой — разделение линии на крайнее и среднее соотношение. Первое мы можем сравнить с мерой золота; второй мы можем назвать драгоценным камнем ». (См. Другие предложения)

Природа и жизнь

Есть много других увлекательных математических соотношений и странностей как в Фи, так и в рядах Фибоначчи, которые можно исследовать более глубоко, но сейчас давайте сделаем шаг в сторону от чисто математических и погрузимся в природу, где проявляются Фи и ряд Фибоначчи. сами по себе повсеместно, но не повсеместно.Числа Фибоначчи часто встречаются в числе лепестков цветка и в спиралях растений. Позиции и пропорции основных размеров многих животных основаны на Фи. Примеры включают части тела муравьев и других насекомых, размеры крыльев и расположение глазковидных пятен у бабочек, спирали морских раковин и положение спинных плавников морских свиней. Даже спирали человеческой ДНК воплощают пропорции фи.

Восприятие красоты

Еще более интригующим является то, что Фи проявляется во всей человеческой форме, в лице, теле, пальцах, зубах и даже в нашей ДНК, а также влияние, которое это оказывает на наше восприятие человеческой красоты.Некоторые утверждают, что красота в глазах смотрящего, но есть свидетельства, подтверждающие, что то, что мы воспринимаем как красоту в женщинах и мужчинах, основано на том, насколько близко пропорции лица и тела приближаются к Фи. Кажется, что Фи встроена в наше сознание как проводник красоты. По этой причине Phi применяется как в пластической хирургии лица, так и в косметической стоматологии в качестве руководства для достижения наиболее естественных и красивых результатов в чертах лица и внешнем виде.

Искусство, архитектура и дизайн

При всех уникальных математических свойствах Фи и его внешнем виде на протяжении всего творения неудивительно, что человечество не только заметило это число и создаваемое им золотое сечение, но и использовало его, чтобы запечатлеть красоту и гармонию природы в своей собственной творения в искусстве, архитектуре и других областях дизайна.В некоторых случаях применение Фи человечеством неоспоримо. В других случаях это все еще является предметом споров. Великая пирамида Египта, кажется, воплощает золотое сечение в соотношении ее основания, высоты и гипотенузы, но ее отсутствующая внешняя оболочка и отсутствие упоминания Фи в древнеегипетских писаниях затрудняют окончательное доказательство того, что это было намеренно. , Греки знали о Фи во время строительства Парфенона, и, хотя его габаритные размеры лишь приблизительно соответствуют золотому сечению, есть свидетельства его использования в конструкции балки на вершине колонн.Путаница в этих вопросах приводит к тому, что и это оспаривается. Известно, что Леонардо да Винчи использовал Фи, известную в 1500-х годах как «Божественная пропорция», в ряде своих картин. Другие художники, в том числе Рафаэль, Сандро Боттичелли и Жорж Сёра, тоже. В то время как это неоспоримо, некоторые люди творчески наложить золотые спирали к изображениям, где другие не считают, что они должны были художником. Размеры драгоценных скрипок Страдивари, построенных около 1700 года, показывают взаимосвязь Фи.Он играет важную роль в музыке и акустике. Более современные применения золотого сечения в архитектуре можно увидеть в Нотр-Даме в Париже, здании Секретариата штаб-квартиры ООН в Нью-Йорке и Си-Эн Тауэр в Торонто. Он широко используется при разработке продуктов и логотипов многими крупными корпорациями. Он даже использовался в дизайне одежды высокой моды, например, в «Phi Collection», объявленной в 2004 году и освещавшейся Vogue, Elle и Vanity Fair. Это также основа для The Fashion Code, руководства по стилю женской одежды.Различные исследования проверяли, является ли золотой прямоугольник самым приятным для человеческого глаза прямоугольником. Результаты исследований неоднозначны, но обычно указывают на прямоугольники с формой, близкой к золотому прямоугольнику, как на наиболее приятные.

Солнечная система и Вселенная

Как ни странно, мы даже находим отношения золотого сечения в Солнечной системе и Вселенной. Диаметры Земли и Луны образуют треугольник, размеры которого основаны на математических характеристиках фи.Расстояния планет от Солнца удивительно близко коррелируют с экспоненциальными степенями Фи. Красивые кольца Сатурна очень близки по размерам к золотому сечению диаметра планеты. В 2003 году НАСА опубликовало данные о том, что Вселенная имеет форму додекаэдра, основанного на Фи.

Новые открытия с использованием золотого сечения

Золотое сечение продолжает открывать новые двери в нашем понимании жизни и Вселенной. Он появился в 1970-х годах, когда Роджер Пенроуз открыл «Плитки Пенроуза», позволившие укладывать поверхности плиткой с пятикратной симметрией, что раньше считалось невыполнимой задачей.Он снова появился в 1980-х годах в трехмерной молекулярной структуре квазикристаллов, недавно открытой форме материи. Вступая в 21 век, кажется, что Фи возрождается в интеграции знаний в самых разных областях науки, включая время и квантовую физику.

Духовные аспекты

Описание этой золотой пропорции как Божественной пропорции, возможно, уместно, потому что многие видят ее как дверь к более глубокому пониманию красоты и духовности в жизни, раскрывающую скрытую гармонию или взаимосвязь во многом из того, что мы видим.Это невероятная роль для одного числа, но, опять же, это одно число сыграло невероятную роль в истории человечества и в основах самой жизни. Таким образом, нелегко провести грань между его математическим и мистическим аспектами.

Фи не упоминается явно в Библии или других древних писаниях, но мы находим, что размеры, данные Богом Ною для Ковчега и Моисею для Ковчега Завета, отражают соотношение 5 к 3, числа Фибоначчи с соотношением из 1.666 и достаточно близкое приближение к Phi. Кааба, самое священное место ислама в Мекке, находится очень близко к золотому сечению расстояния между северным и южным полюсами Земли. Довольно любопытно, что даже символ Фи, круг с линией, проведенной через него, можно представить как ноль, или пустоту, разделенную на единицу, или Единство, чтобы создать красоту, аналогично тому, как Бог создает вселенную из ничего.

Путешествие открытий

В вопросах разума видеть — значит верить, но в вопросах веры — это вера, которая сначала открывает дверь для видения.Подобно тому, как нам нужны два глаза, чтобы добавить глубины нашему восприятию в видении, и вера, и разум служат нам, добавляя глубины нашему пониманию жизни и вселенной, в которой мы живем. Некоторые скажут вам, что появление золотого сечения является доказательством замысла Бога. Однако большинство религий показывают, что мы познаем Бога через веру, а не доказательства. Некоторые скажут вам, что нет даже никаких доказательств золотого сечения, что мы просто воспринимаем закономерности, которых на самом деле не существует. Однако попытайтесь выяснить, основаны ли их взгляды на доказательствах или просто на отражении их собственных атеистических или натуралистических представлений о жизни.

Лучший способ узнать для себя, где появляется Фи и где она воображается, — это непредвзято исследовать, изучать и делать собственные выводы на основе фактов и последствий. Вы можете узнать больше о золотом сечении здесь, на сайте www.GoldenNumber.net, и загрузить бесплатную пробную версию программного обеспечения для проектирования золотого сечения PhiMatrix, чтобы легко находить и применять пропорции Фи для себя. Наслаждайтесь номемоном «фи», будь то для углубления вашего понимания и оценки красоты и гармонии в жизни или для применения его в ваших собственных художественных творениях, таких как Леонардо да Винчи и другие мастера до вас.Я приветствую вас поделиться своими мыслями и выводами с нашим онлайн-сообществом.

Гэри Мейснер
The Phi Guy
Автор www.goldennumber.net
Разработчик программного обеспечения PhiMatrix на www.phimatrix.com

Золотое сечение — определение золотого сечения по The Free Dictionary

Золотое сечение между колесной базой и протектором обеспечивает высокий уровень предельных характеристик и маневренности. Золотое сечение для коммуникации состоит в том, что 80 процентов того, что вы говорите, должно быть положительным или нейтральным и только 20 процентов должно быть критическим или директивным. , традиционный золотой эль в американском стиле пэйл-эля, является идеальным компаньоном для шотландской говядины, используемой в этом рецепте, которая поступает только от крупного рогатого скота, который родился и вырос в Шотландии.Создавая Essence Professional, мы неустанно стремимся к золотому сечению идеально сбалансированных пропорций, чтобы придать дизайну вневременной характер ». Его концентрический узор напоминает расположение чешуек на сосновой шишке — один из бесчисленных примеров золотого сечения. Пока Макс пытается выявить закономерности, скрытые на фондовом рынке (или, по его примеру, « рост и убыль популяций карибу »), сам фильм густо заполнен числовыми узорами — наиболее заметными из них. последовательность Фибоначчи и связанное с ней золотое сечение.Последовательность Фибоначчи, получившая прозвище создателя Леонардо Боначчи, имеет простое рекурсивное определение: возьмите один в качестве первого члена, один в качестве второго члена, а затем найдите каждый последующий член, добавив два предыдущих члена. Я использую «Золотой термин». Пропорции и арматуры сакральной геометрии, которые представляют собой сеточные системы для визуально и умственно / психически приятного композиционного баланса. Основываясь на математических принципах золотого сечения Леонардо да Винчи, пекарь Стивен Лансалотта создал то, что он назвал «Диета да Винчи».Вскоре ABH стал синонимом «брови в Instagram». Опередив всех остальных, они владеют патентом на «метод формирования бровей с золотым сечением», которому будут следовать многие учебники, которые вы увидите при создании идеальных бровей ». Золотое сечение или золотое сечение часто символизируют с помощью 21-го Буква греческого алфавита, известная как фи. Заимствованная из греческой архитектуры и золотого сечения, которое способствует созданию органических и естественных композиций, немецкий творческий человек переосмыслил древность со своей точки зрения: красота, культура и современность.Они используют золотое сечение повсюду, демонстрируя его через соборы, Парфенон, египетские пирамиды и штаб-квартиру Организации Объединенных Наций. ,

История золотого сечения

Хотя пропорция, известная как золотое сечение, всегда существовала в математике и в физической вселенной, неизвестно, когда именно она была впервые открыта и применена человечеством. Разумно предположить, что он, возможно, был обнаружен и повторно открыт на протяжении всей истории, что объясняет, почему он получил несколько названий.

Использование в архитектуре потенциально относится к древним египтянам и грекам

Похоже, что египтяне могли использовать и пи, и фи в дизайне Великих пирамид.Некоторые считают, что греки основали дизайн Парфенона на этой пропорции, но это является предметом некоторых предположений.

Фидий (500 г. до н.э. — 432 г. до н.э.), греческий скульптор и математик, изучил фи и применил его для создания скульптур Парфенона.

Платон (около 428 г. до н.э. — 347 г. до н.э.) в своих взглядах на естествознание и космологию, представленных в его «Тимее», считал золотое сечение наиболее связывающим из всех математических соотношений и ключом к физике космоса.

Евклид (365 г. до н.э. — 300 г. до н.э.) в «Элементах» упоминает разделение линии в точке 0,6180399… как «разделение линии в крайнем и среднем соотношении». Позже это привело к использованию термина «среднее значение» в золотой середине. Он также связал это число с построением пентаграммы.

Ряд Фибоначчи был открыт около 1200 г. н.э.

г.

Леонардо Фибоначчи, итальянец, родившийся в 1175 году нашей эры (2), обнаружил необычные свойства числового ряда, который теперь носит его имя, но нет уверенности, что он вообще осознавал его связь с фи и золотым сечением.Его наиболее заметным вкладом в математику была работа, известная как Liber Abaci, которая оказала решающее влияние на принятие европейцами арабской десятичной системы счета над римскими цифрами. (3)

Впервые он был назван «Божественной пропорцией» в 1500-х гг.

Леонардо да Винчи представил иллюстрации к диссертации, опубликованной Лукой Пачоли в 1509 году и озаглавленной «De Divina Proportione» (1), возможно, самой ранней ссылкой в литературе на другое ее название — «Божественная пропорция».Эта книга содержит рисунки пяти Платоновых тел, сделанные Леонардо да Винчи.

Художники эпохи Возрождения широко использовали золотую середину в своих картинах и скульптурах для достижения баланса и красоты. Леонардо да Винчи, например, использовал его, чтобы определить все основные пропорции своей картины «Тайная вечеря», от размеров стола, за которым сидели Христос и ученики, до пропорций стен и окон на заднем плане.

Иоганн Кеплер (1571-1630), открывший эллиптическую природу орбит планет вокруг Солнца, также упомянул «Божественную пропорцию», сказав о ней следующее:

«У геометрии есть два великих сокровища: одно — это теорема Пифагора; другой — разделение линии на крайнее и среднее соотношение.Первое мы можем сравнить с мерой золота; второй мы можем назвать драгоценным камнем ».

«Золотое сечение» было придумано в 1800-х годах.

Считается, что Мартин Ом (1792–1872) был первым, кто использовал термин «золотой» для описания золотого сечения. использовать этот термин. В 1815 году он опубликовал «Die reine Elementar-Mathematik» (Чистая элементарная математика). Эта книга известна тем, что в ней впервые встречается термин «goldener schnitt» (золотое сечение).

Термин «фи» не использовался до 1900-х гг.

Только в 1900-х годах американский математик Марк Барр использовал греческую букву фи (Φ) для обозначения этой пропорции.Это появилось в «Кривых жизни» (стр. 420) в 1914 году Теодора Андреа Кук. К тому времени эта вездесущая пропорция была известна как золотая середина, золотое сечение и золотое сечение, а также Божественная пропорция. Фи — первая буква Фидия (1), который использовал золотое сечение в своих скульптурах, а также греческий эквивалент буквы «F», первой буквы Фибоначчи. Фи — это также 21-я буква греческого алфавита, а 21 — одно из чисел ряда Фибоначчи. Иероглиф фи также имеет интересное богословское значение.

Последние выступления Фи в математике и физике

Phi продолжает открывать новые двери в нашем понимании жизни и Вселенной. Он появился в 1970-х годах, когда Роджер Пенроуз открыл «Плитки Пенроуза», которые впервые позволили укладывать поверхности плиткой с пятикратной симметрией. Он снова появился в 1980-х годах в квазикристаллах, недавно открытой форме материи.

Фи как дверь к пониманию жизни

Описание этой пропорции как Золотой и Божественной, возможно, уместно, потому что многие считают ее открывающей дверь к более глубокому пониманию красоты и духовности в жизни.Это невероятная роль для одного числа, но опять же, это одно число сыграло невероятную роль в истории человечества и во Вселенной в целом.

Источник — «Божественная пропорция: исследование математической красоты» Х. Э. Хантли

(1) Стр.25
(2) Стр.157
(3) Стр.158

Золотое сечение: зачем оно нужно — Рамблер/новости

Золотое сечение: как это работает

Золотое сечение, что это такое. Золотое сечение: как это работает.

Золотое сечение, что это такое. Золотое сечение: как это работает.

Золотое сечение примеры. Как получили золотое сечение

Золотое сечение, что это такое. Понятие золотого сечения

Золотое сечение тату. Значение татуировки спираль

Символика татуировок со спиралями

Золотое сечение в человеке. Золотое сечение в математике

Принцип золотого сечения. Успешное творение или правило золотого сечения

Золотое сечение в архитектуре. Как получили золотое сечение

Золотое сечение лица. Золотое сечение — пропорция лица

Золотое сечение в композиции. Основы композиции — Золотое сечение

Золотое сечение в музыке. Метод золотого сечения в музыкальных произведениях

Золотое сечение: Как это работает?

Определение

История

Природа

Человек

Искусство пространственных форм

Слово, звук и кинолента

Правило золотого сечения в дизайне интерьера

Общие принципы и определение

Золотое сечение в природе

Где используется человеком?

Использование в дизайне интерьеров

Размеры и зонирование

Цвета

Меблировка

Декор

Простые практические советы

Золотое сечение для дизайна и жизни

Правило золотого сечения

Как построить прямоугольник с идеальными пропорциями

Как разделить отрезок по правилу золотого сечения

Идеальный треугольник и пентаграмма

Применение в строительстве

Золотое соотношение во внутреннем оформлении

Золотое сечение в ландшафтном дизайне

Золотое сечение — Простая английская Википедия, бесплатная энциклопедия

Свойства золотого сечения, внешний вид и обзор приложений

Математика золотого сечения

Последовательность Фибоначчи

Геометрия золотого сечения

Природа и жизнь

Восприятие красоты

Искусство, архитектура и дизайн

Солнечная система и Вселенная

Новые открытия с использованием золотого сечения

Духовные аспекты

Путешествие открытий

Золотое сечение — определение золотого сечения по The Free Dictionary

История золотого сечения

Использование в архитектуре потенциально относится к древним египтянам и грекам

Ряд Фибоначчи был открыт около 1200 г. н.э.

Впервые он был назван «Божественной пропорцией» в 1500-х гг.

«Золотое сечение» было придумано в 1800-х годах.

Термин «фи» не использовался до 1900-х гг.

Последние выступления Фи в математике и физике

Фи как дверь к пониманию жизни

Добавить комментарий Отменить ответ